A Compensatory Fuzzy Logic Model in Technical Trading
Abstract
1. Introduction
- Semantic modelling using the opportunities associated with the approaches’ characteristics of science of vagueness, the multivalued approach, and language labels modeled by membership functions.
- The use of expert knowledge as source for modeling, as a particular means of addressing knowledge engineering.
- The use of different expressions of knowledge, for example, sets of rules of conditional propositions typically used to deal with fuzzy systems for automatic fuzzy control and other applications.
- The simultaneous use of different scenarios, made possible using fuzzy sets and fuzzy logic domain.
- The incorporation of subjective and qualitative approaches in a harmonic manner with quantitative approaches.
2. Background
2.1. Literature Review
2.2. Compensatory Fuzzy Logic—An Outline
- I.
- Compensation Axiom, and.
- II.
- Symmetry or Commutativity Axiom, and.
- III.
- Strict Growth AxiomIf are different to zero and then, and.
- IV.
- Veto AxiomIf for any then, andIf for any then.
- V.
- Fuzzy Reciprocity Axiom.
- VI.
- Fuzzy Transitivity AxiomIf and , then.
- VII.
- De Morgan’s Laws:and.
- Evaluating the convenience of an alternative according to a predicate, obtained from expressions of the decision-maker’s preferences.
- Searching for new convenient alternatives using the predicate.
- Assessing the truth degree of an expression using facts and expert opinions.
- Assessing the truth degree of an expression using facts associated with a probabilistic sample.
- Discovering new knowledge expressed in natural language using heuristics and optimization.
- Demonstrating and discovering new knowledge by reasoning.
2.3. Technical Analysis
3. Compensatory Fuzzy Logic Model for Trading Based on Technical Analysis
- A financial asset is good for the portfolio if it has presented high volume and high volatility systematically during a long period of time.
- An asset should be bought (long position) at moment if all valid rules of technical analysis for the bullish trend or oscillation are satisfied and all the general indicators are in favor of that operation.
- An asset should be sold (short position) at moment if all valid rules of technical analysis for the bearish trend or oscillation are satisfied and all the general indicators are in favor of that operation.
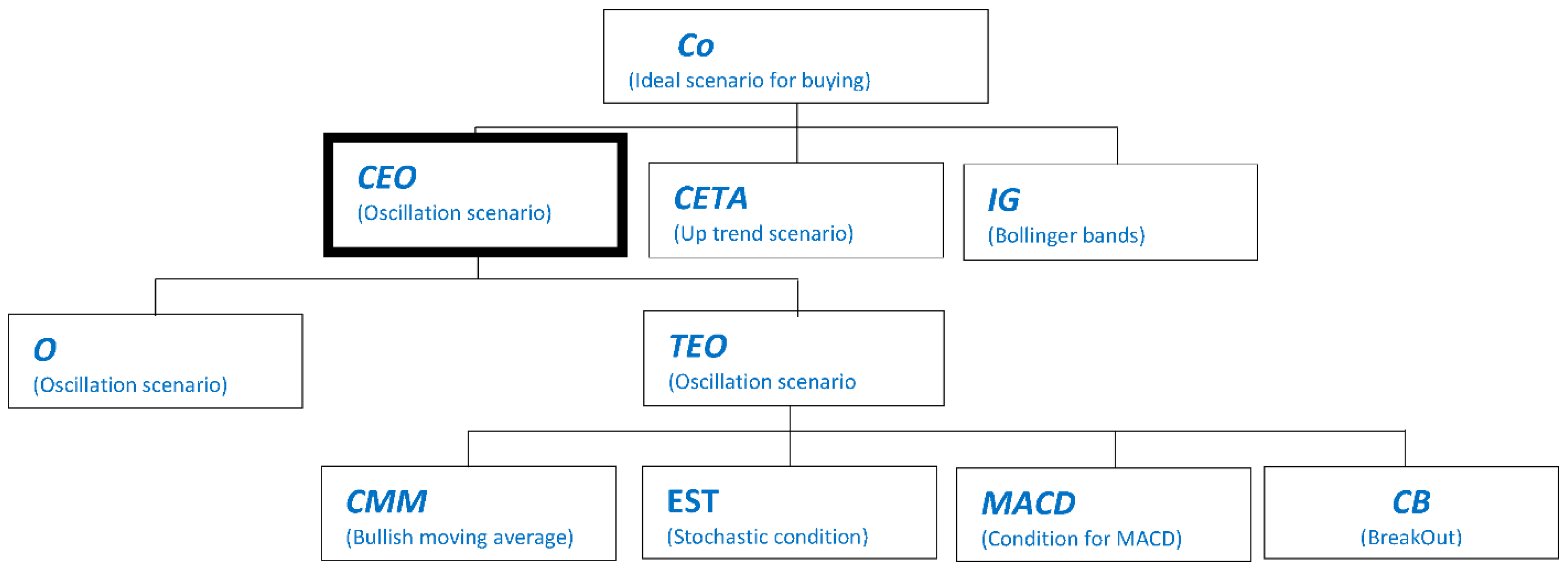
3.1. Buying Model
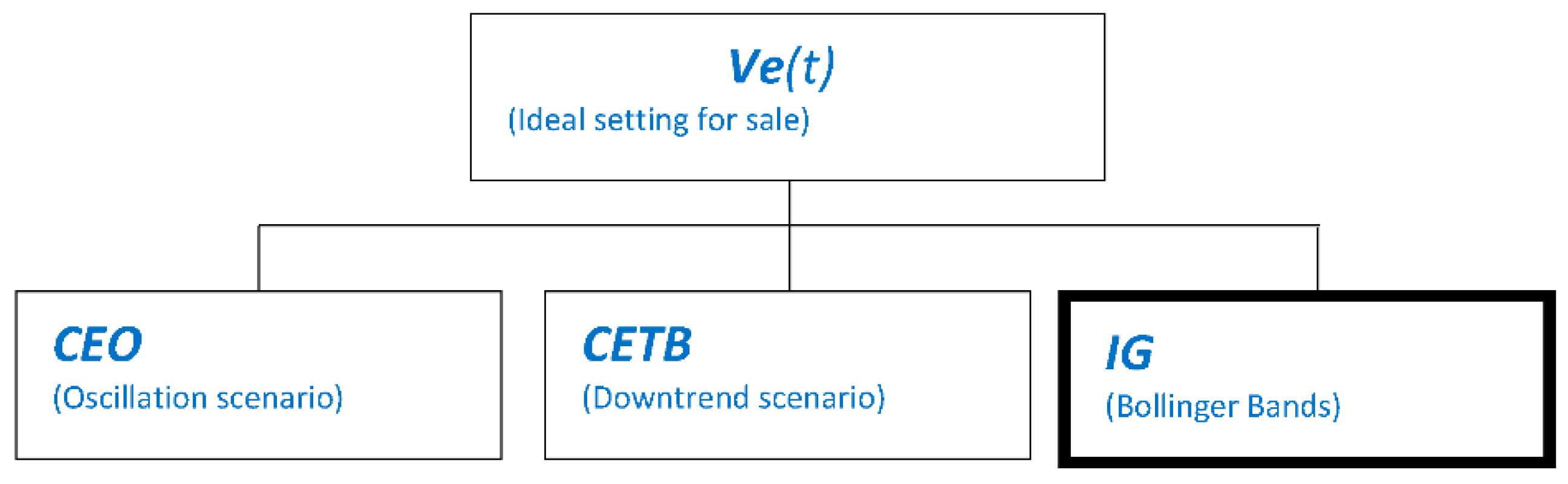
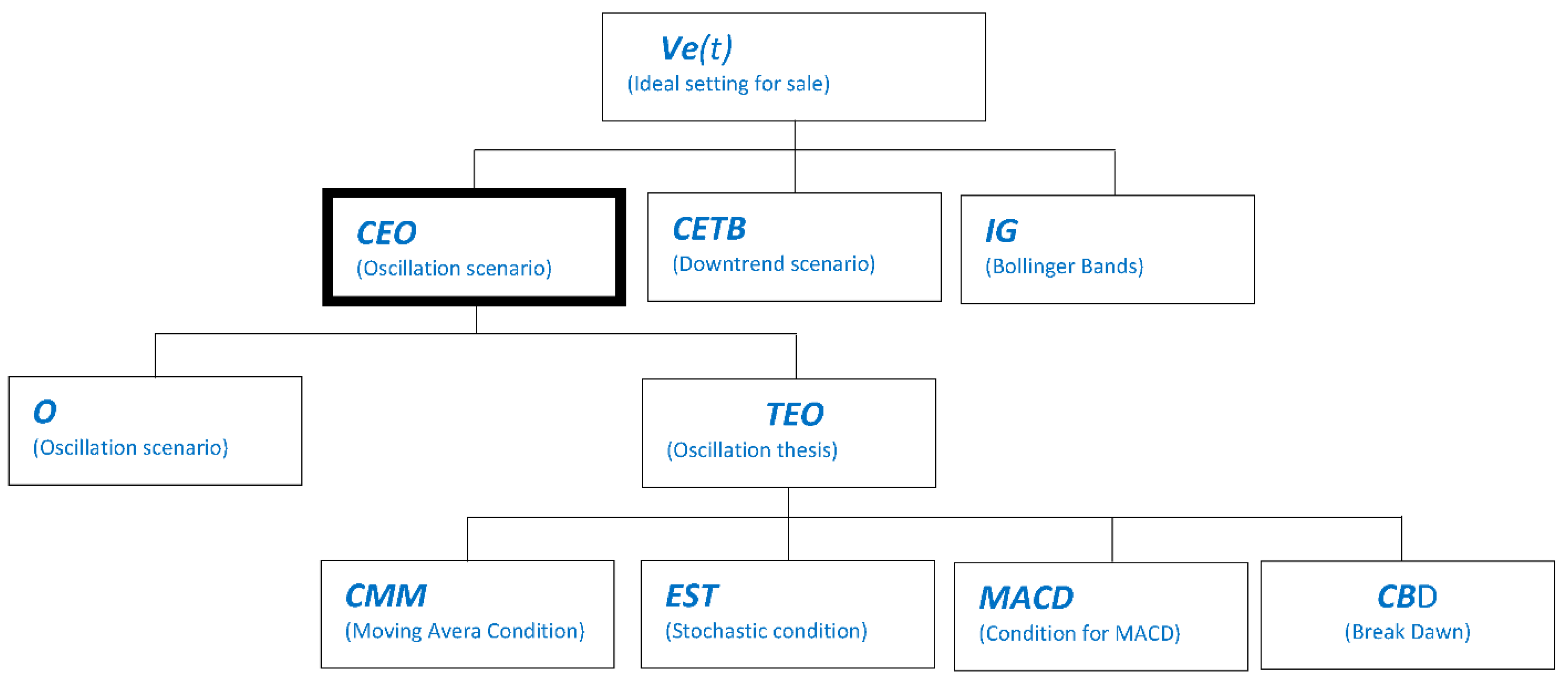
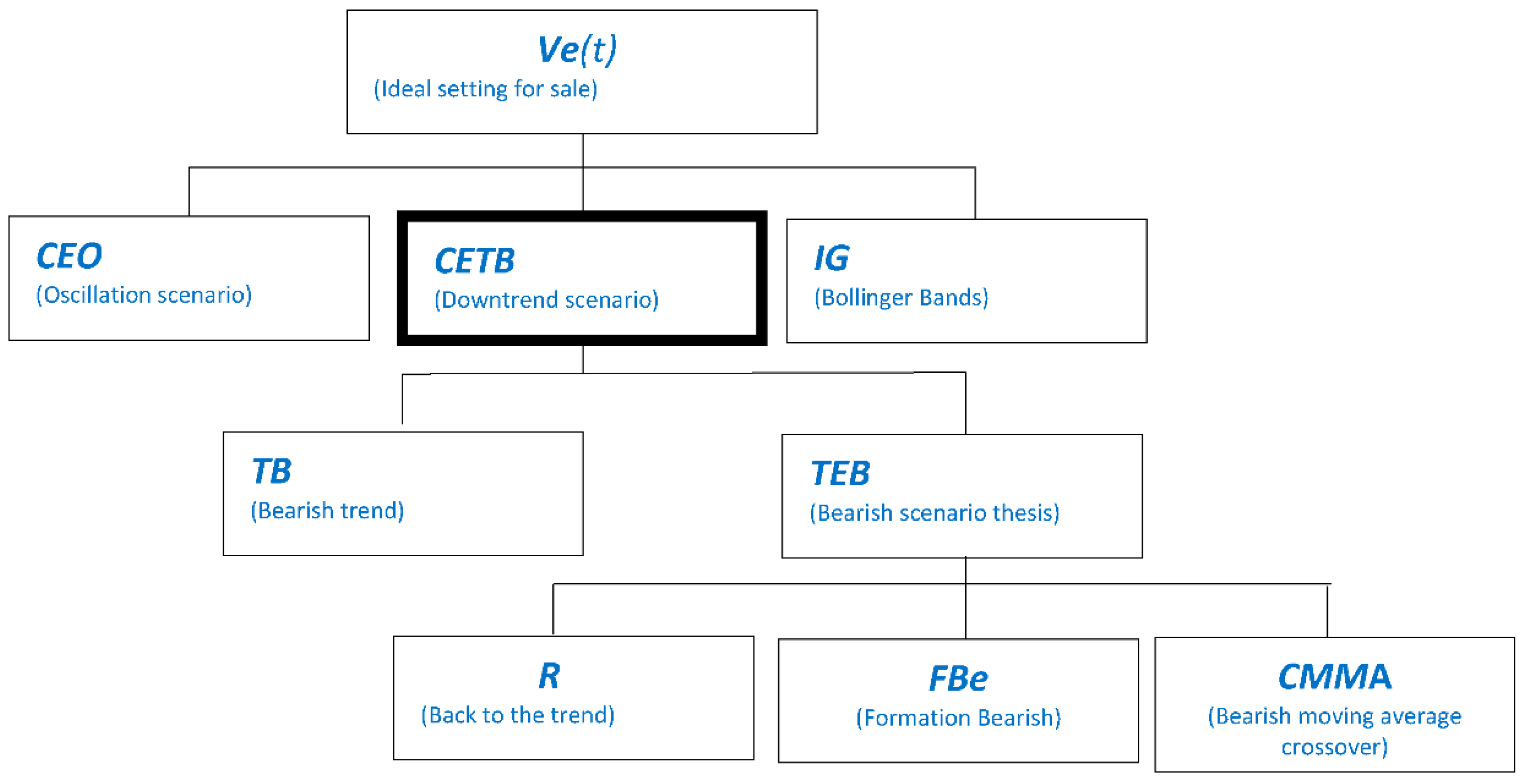
3.2. Selling Model
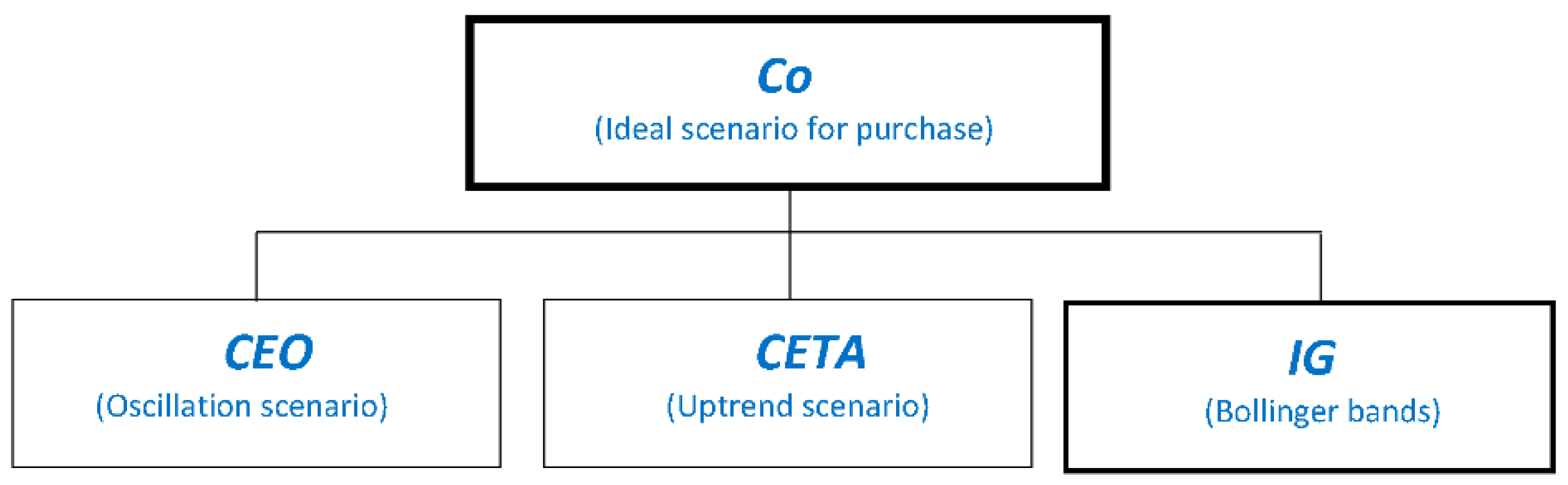
- CEO(t): The conditional associated with the scenario of oscillation at moment t is satisfied.
- CETB(t): The conditional associated with the bearish scenario at moment t is satisfied.
- IG(t): Conditions associated with general indicators such as Bollinger bands are satisfied.
- CMM(t): moving average condition,
- EST(t): Stochastic oscillator condition
- MACD(t): Moving Average Convergence Divergence (MACD)condition
- CBD(t): moving average condition for clear situation of break down
- R(t): The graphic of price returns to a line of tendency or to a moving average
- FBE(t): There is a bearish candle sheet formation in time t
3.3. Overall Procedure
- From a set of pre-screened assets, calculate the truth value of the predicate G(a, t) that models the expression “asset a is good for the portfolio according to the available information during time t”.
- If G(a, t) is greater than a predefined value greater than 0.5, then asset a is incorporated to the set of “good” assets.
- Calculate, for each asset in the set of “good” assets, the value of the predicate Co(t) (see Equation (1)).
- If Co(t) for asset a is greater than a predefined value greater than 0.5, then a is incorporated to the set of assets convenient for buying at moment t.
- Calculate, for each asset in the set of “good” assets, the value of the predicate V(t) (see Equations (4) and (5)).
- If V(t) for asset a is greater than a predefined value greater than 0.5, then a is incorporated in the set of assets convenient for selling at moment t.
- -
- If a belongs to (a has been determined as suitable for buying), determine the amount to be invested in asset a as the percentage of resources equivalent to the proportion with which a belongs to regarding the sum of the truth degrees with which the rest of assets in belong to .
- -
- If a belongs to (a has been determined as suitable for selling), determine the amount to be invested in asset a as the percentage of resources equivalent to the proportion with which a belongs to regarding the sum of the truth degrees with which the rest of assets in belong to .
4. An Illustrative Case Study: An Analysis of the Cryptocurrency Market
- The system does not require a central authority.
- The system keeps an overview of cryptocurrency units and their ownership.
- The system defines whether new cryptocurrency units can be created. If new cryptocurrency units can be created, the system defines the circumstances of their origin and how to determine the ownership of these new units.
- Ownership of cryptocurrency units can be proved exclusively cryptographically.
- The system allows transactions to be performed in which ownership of the cryptographic units is changed. A transaction statement can only be issued by an entity proving the current ownership of these units.
- If two different instructions for changing the ownership of the same cryptographic units are simultaneously entered, the system performs at most one of them.
4.1. Experimental Procedure
4.2. Results
5. Conclusions
- Elaboration and application of exhaustive experiments.
- Improvement of the model with the applications of new rules and models of technical analysis.
- Compatibility with human behavior.
- Compatibility with different platforms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Logical Trees of a Buying Model
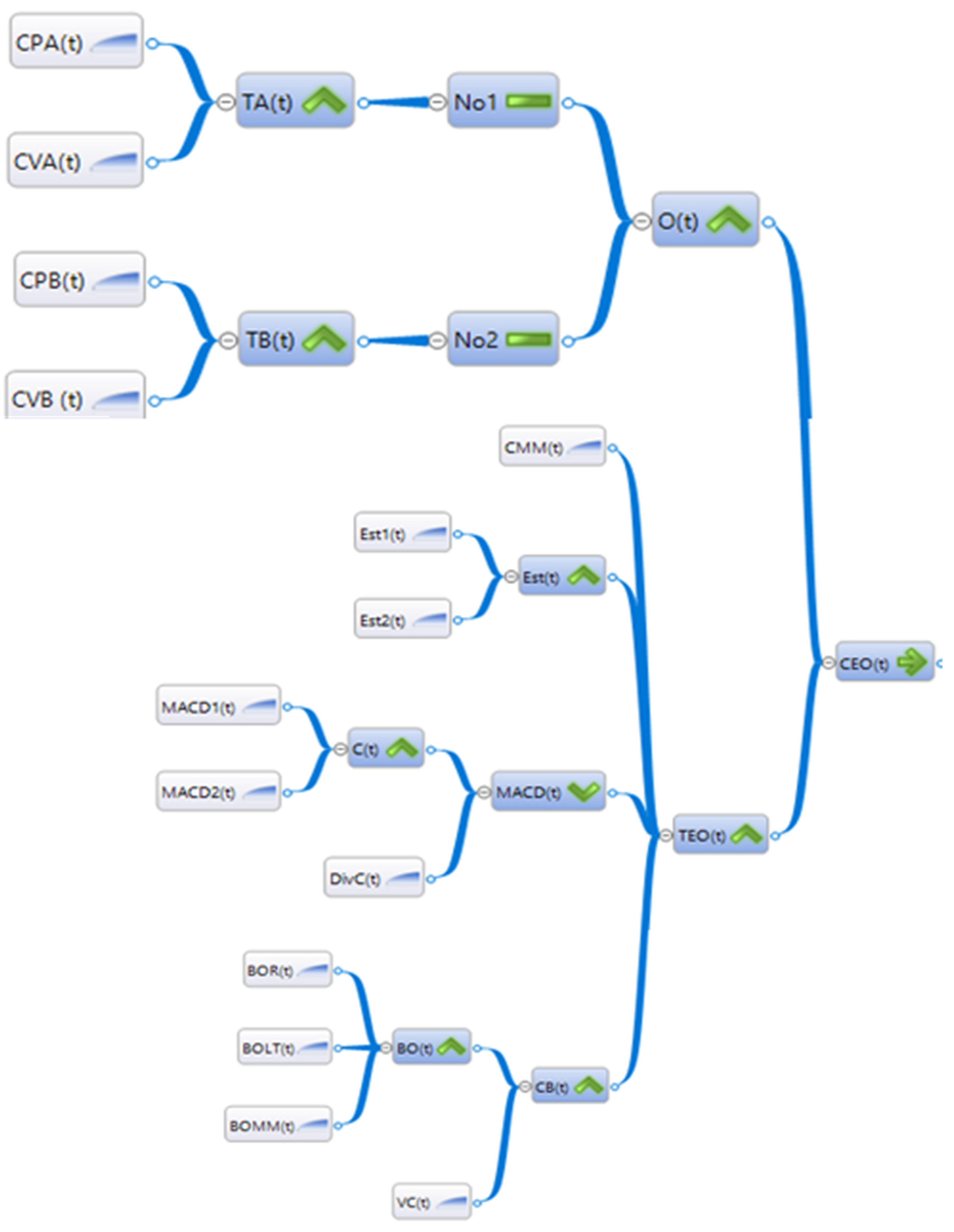

Appendix B. Logical Trees of a Selling Model
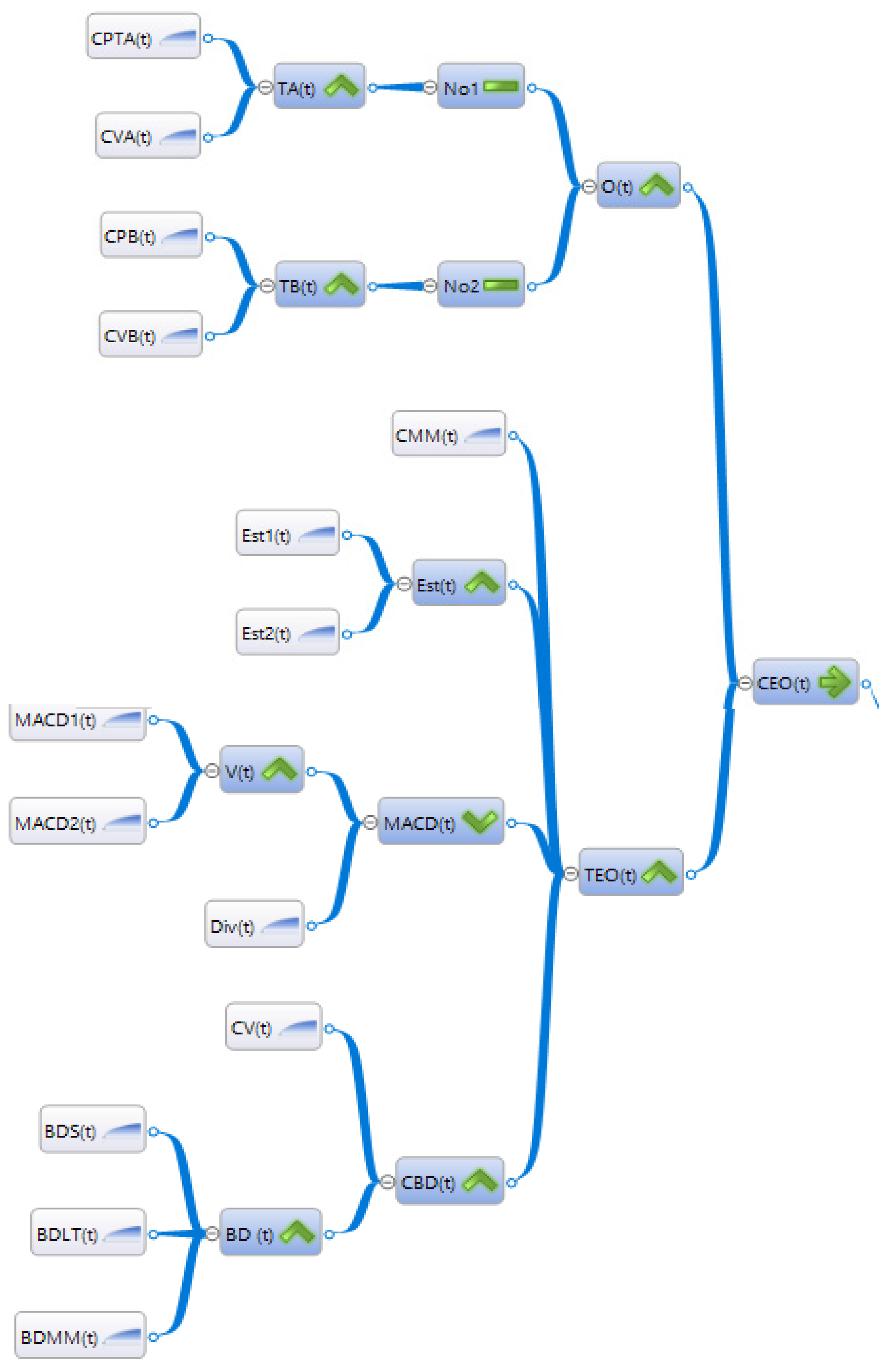
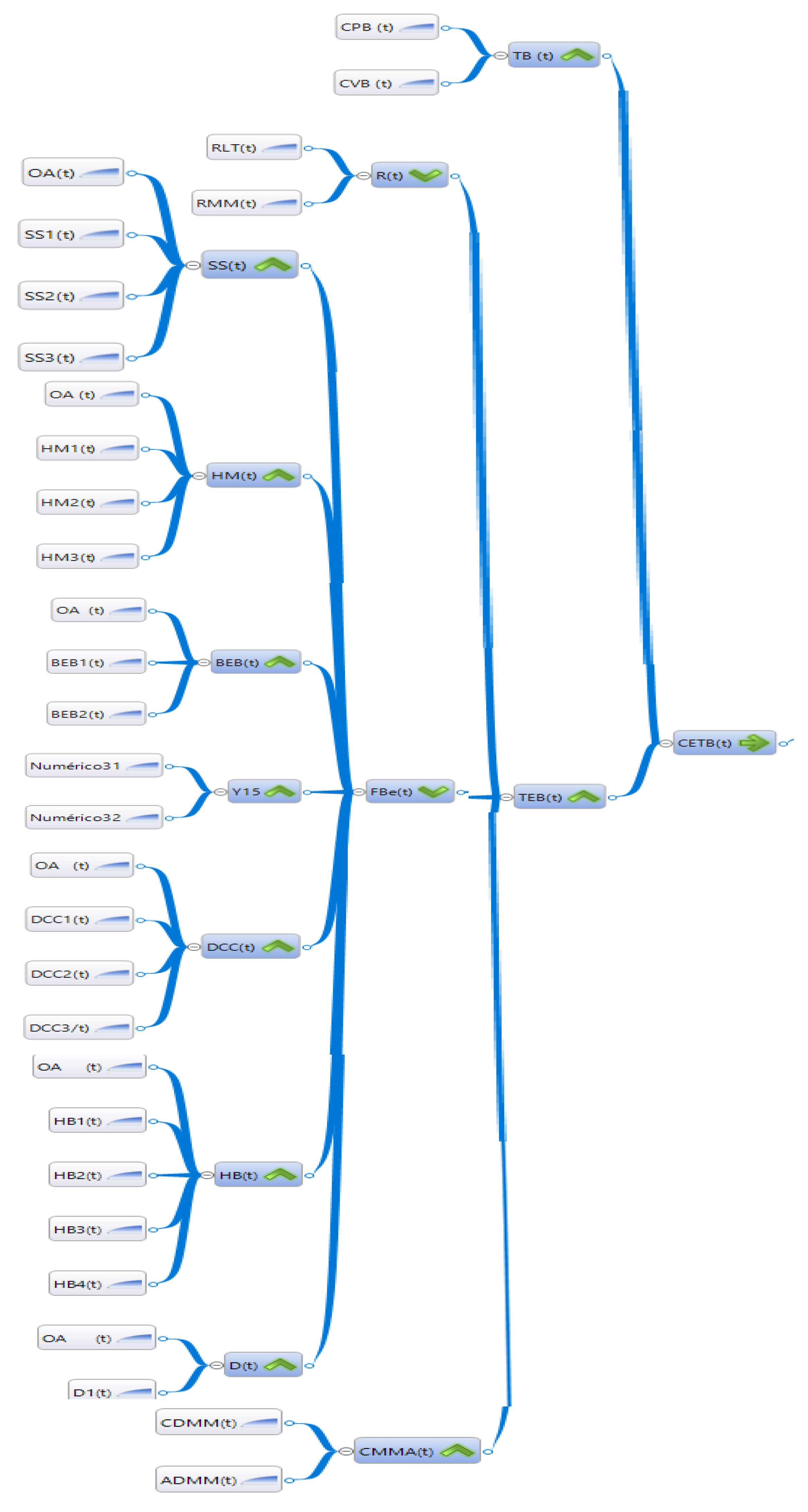
Appendix C. Definitions and Notation Used by the Proposed Models
| Rule | Predicate | Knowledge Expressed by the Predicate | Category |
|---|---|---|---|
| Trend (T) | TA | Bullish trend | GA |
| TB | Bearish trend | GA | |
| OB | Part of a bearish trend. | GA | |
| O | Oscillation trend. | GA | |
| CPA | Peaks going up | GA | |
| CVA | Valleys going up | GA | |
| CPB | Peaks going down | GA | |
| CVB | Valleys going down | GA | |
| Moving Averages (CMM) | CMM | The fast moving average goes through the slow moving average from up to down. | QA |
| Stochastic (Est) | EST1 | The percent “K” goes through the stochastic moving average from up to down. | QA |
| EST2 | Stochastic and moving are above of the line “80”. | QA | |
| MACD | MACD1 | MACD crosses the signal line from top to bottom | QA |
| (MACD) | MACD2 | MACD and signal line are above of the line “0” | QA |
| Divergence (DIV) | DIV | The prices grow but macd’s histography is decreasing. | QA |
| Breakdown (BD) | BDS | There is a breakdown of a support | GA |
| BDLT | Exists a breakdown of a trend line of the actual wave. | GA | |
| BDMM | There is a breakdown of the moving average | GA | |
| Volume (CV) | CV | There is a significant increase in volume | QA |
| Trend line (R) | RLT | Price returns to trend line | GA |
| RLM | Price returns to the moving average | GA | |
| Shooting Star (SS) | SS1 | The upper tail is at least twice as long as the body | C |
| SS2 | The body is at the bottom of the candle | C | |
| SS3 | The lower tail is absent or too small | C | |
| The Hanging Man (HM) | HM1 | The lower tail is twice as long as the body | C |
| HM2 | The body is on top | C | |
| HM3 | The upper tail almost does not exist | C | |
| Bearish Engulfing Bar (BEB) | BEB1 | The first candle is short and green | C |
| BEB2 | The second candle is red and wraps the previous candle | C | |
| Doji (D) | D | Closing and opening prices are very close | C |
| Dark Cloud Cover (DCC) | DCC1 | The first candle is long and green, it is above the trend line | C |
| DCC2 | The second opens above the maximum of the previous candle and is red | C | |
| DCC3 | The second candle closes below half of the previous green candle | ||
| Harammi Bearish (HB) | HB1 | There is a long green candle | C |
| HB2 | It is followed by a red candle that opens below the closing of the previous red candle | C | |
| HB3 | The mentioned red candle is wrapped by the previous green candle | C | |
| HB4 | There is another red candle after the previous one | C | |
| Moving Average (CMMA) | CEMM | Shortly before “t” the price closes below the moving average | QA |
| AEMM | In the following period the price opens below the moving average | QA | |
| Bollinger Bands (IG) | BB | Price is too close or crosses the upper Bollinger curve upwards | QA |
| Rule | Predicate | Knowledge Expressed by the Predicate | Category |
|---|---|---|---|
| Time (t) | t | Time | QA |
| Trend (T) | TA | Bullish trend. | GA |
| TB | Downtrend. | GA | |
| OB | Part of a downtrend | ||
| O | Oscillation stage. | GA | |
| CPA | Spikes on the rise. | GA | |
| CVA | Valleys on the rise. | GA | |
| CPB | Spikes to the downside. | GA | |
| CVB | Valleys to the downside. | GA | |
| Moving Averages | CMM | The fast moving average goes through the slow moving average from down to up | QA |
| Stochastic (EST) | EST1 | The percent “K” goes through the stochastic moving average from down to up | QA |
| EST2 | Stochastic and moving are above of the line “20”. | QA | |
| MACD (MACD) | MACD1 | MACD crosses the signal line from bottom to top | QA |
| MACD2 | MACD and signal line are below of the line “0”. | QA | |
| Divergence (DivC) | DIVC | The prices grow but macd’s histography is decreasing. | QA |
| BreakOut (BO) | BOR | There is a breakout of a resistance. | GA |
| BOLT | Exists a breakout of a trend line of the actual wave. | GA | |
| BOMM | There is a breakout of the moving average. | GA | |
| Volume (VC) | VC | There is a significant increase in volume. | QA |
| Trend line (R) | RLT | Price returns to trend line. | GA |
| RMM | The price returns to the moving average. | GA | |
| The Hammer (HAMM) | RCI | The lower tail is twice as long as the body. | C |
| RC | The body is on top. | C | |
| RCO | The upper tail almost does not exist. | C | |
| Inverted Hammer (H) | RCS | The upper tail is at least twice as long as the body. | C |
| RCUI | The body is at the bottom of the candle. | C | |
| RSI | The lower tail is absent or too small. | C | |
| Bullish Engulfing Bar (BEB) | VV | The first candle is red. | C |
| VR | The second candle is green. | C | |
| E | The candle green wraps the red. | C | |
| Doji (D) | D | closing and opening prices are very close. | C |
| Pircing Line (PL) | PL1 | The first candle is red and closes below the line that the previous candle brought | C |
| PL2 | The second candle opens below the previous one and closes above half of the previous candle. | C | |
| Harami Bullish (HB) | HB1 | There is a long red candle. | C |
| HB2 | It is followed by a green candle that opens above the closing of the previous red candle. | C | |
| HB3 | The mentioned green candle closes below the opening of the previous candle. | C | |
| HB4 | Exist another green candle after the previous candle. | C | |
| Moving Average (CDMM) | CEMM | Shortly before “t” the price closes above the moving average. | QA |
| AEMM | In the following period the price opens above the moving average. | QA | |
| Bollinger Bands (IG) | BB | Price is too close or is going through the lower bollinger curve down. | QA |
References
- Solares, E.; Coello, C.A.C.; Fernandez, E.; Navarro, J. Handling uncertainty through confidence intervals in portfolio optimization. Swarm Evol. Comput. 2019, 44, 774–787. [Google Scholar] [CrossRef]
- Nazário, R.T.F.; Silva, J.L.; Sobreiro, V.A.; Kimura, H. A literature review of technical analysis on financial asset markets. Q. Rev. Econ. Financ. 2017, 66, 115–126. [Google Scholar] [CrossRef]
- Scott, G.; Carr, M.; Cremonie, M. Technical Analysis: Modern Perspectives; CFA Institute Research Foundation: Charlottesville, VA, USA, 2016. [Google Scholar]
- Fernandez, E.; Navarro, J.; Solares, E.; Coello, C.C. A novel approach to select the best portfolio considering the preferences of the decision maker. Swarm Evol. Comput. 2019, 46, 140–153. [Google Scholar] [CrossRef]
- Saul, J.; Jun, M. Modeling Technical Analysis; EPSRC: Swindon, UK, 2018; Chapter 1; p. 3. [Google Scholar]
- Irwin, S.H.; Park, C.-H. What do we know about the profitability of technical analysis? J. Econ. Surv. 2007, 21, 786–826. [Google Scholar] [CrossRef]
- Fama, E. Efficient Capital Markets: A Review of Theory and Empirical Work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Sangvinatsos, A. A Random Walk Down Wall Street: The Time-Tested Strategy for Successful Investing. Quant. Financ. 2016, 17, 1–4. [Google Scholar] [CrossRef]
- Lo, A.W.; Mamaysky, H.; Wang, J. Foundations of technical analysis: Computational algorithms, statistical inference, and empirical implementation. J. Financ. 2000, 55, 1705–1765. [Google Scholar] [CrossRef]
- Market Technicians Association. CMT Level I 2016: An Introduction to Technical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Espin, E.; Téllez, G.; Fernández, E.; Marx-Gómez, J.; Lecich, M.I. Compensatory Logic: A fuzzy normative model for decision making. Investig. Oper. 2006, 27, 188–197. [Google Scholar]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Sugeno, M. Industrial Applications of Fuzzy Control; Elsevier Science Pub. Co.: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Picos., J.C. Modelado Lógico de Relaciones de Preferencia Básicas a partir de Argumentos. PhD. Thesis, Universidad Autónoma de Sinaloa, Culiacán, Sinaloa, México, 2017. [Google Scholar]
- Andriosopoulos, D.; Doumpos, M.; Pardalos, P.M.; Zopounidis, C. Computational approaches and data analytics in financial services: A literature review. J. Oper. Res. Soc. 2019, 70, 1581–1599. [Google Scholar] [CrossRef]
- Gorgulho, A.; Neves, R.; Horta, N. Applying a GA kernel on optimizing technical analysis rules for asset picking and portfolio composition. Expert Syst. Appl. 2011, 38, 14072–14085. [Google Scholar]
- Fernandez, E.; Navarro, J.; Solares, E.; Coello, C.C. Using evolutionary computation to infer the decision maker’s preference model in presence of imperfect knowledge: A case study in portfolio optimization. Swarm Evol. Comput. 2020, 54, 100648. [Google Scholar] [CrossRef]
- Yang, F.; Chen, Z.; Li, J.; Tang, L. A novel hybrid stock selection method with stock prediction. Appl. Soft Comput. 2019, 80, 820–831. [Google Scholar] [CrossRef]
- Yu, L.; Hu, L.; Tang, L. Stock Selection with a Novel Sigmoid-Based Mixed Discrete-Continuous Differential Evolution Algorithm. Ieee Trans. Knowl. Data Eng. 2016, 28, 1891–1904. [Google Scholar] [CrossRef]
- Zhang, R.; Lin, Z.-A.; Chen, S.; Lin, Z.; Liang, X. Multi-factor Stock Selection Model Based on Kernel Support Vector Machine. J. Math. Res. 2018, 10, 9. [Google Scholar] [CrossRef]
- Hajjami, M.; Amin, G.R. Modelling stock selection using ordered weighted averaging operator. Int. J. Intell. Syst. 2018, 33, 2283–2292. [Google Scholar] [CrossRef]
- Amin, G.R.; Hajjami, M. Application of optimistic and pessimistic owa and dea methods in stock selection. Int. J. Intell. Syst. 2016, 31, 1220–1233. [Google Scholar] [CrossRef]
- Peachavanish, R. Stock selection and trading based on cluster analysis of trend and momentum indicators. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 16–18 March 2016; pp. 317–321. [Google Scholar]
- Fu, X.; Du, J.; Guo, Y.; Liu, M.; Dong, T.; Duan, X. A machine learning framework for stock selection. arXiv 2018, arXiv:180601743. [Google Scholar]
- Huang, C.-F. A hybrid stock selection model using genetic algorithms and support vector regression. Appl. Soft Comput. 2012, 12, 807–818. [Google Scholar] [CrossRef]
- Cao, J.; Wang, J. Exploration of stock index change prediction model based on the combination of principal component analysis and artificial neural network. Soft Comput. 2020, 24, 7851–7860. [Google Scholar] [CrossRef]
- Quah, T. DJIA stock selection assisted by neural network. Expert Syst. Appl. 2008, 35, 50–58. [Google Scholar] [CrossRef]
- Gouveia, M.; Neves, E. Performance Evaluation of Portuguese Mutual Fund Portfolios Using the Value-Based Dea Method; Taylor & Francis: Abingdon, UK, 2018. [Google Scholar]
- Galagedera, D.U.; Roshdi, I.; Fukuyama, H.; Zhu, J. A new network DEA model for mutual fund performance appraisal: An application to U.S. equity mutual funds. Omega 2018, 77, 168–179. [Google Scholar] [CrossRef]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investment; John Wiley & Sons: Hoboken, NJ, USA, 1959. [Google Scholar]
- Oshi, M.S.; Paterson, J.M. Introduction to Mathematical p Ortfolio Theory; Cambridge University Press: Cambridge, UK, 2013; pp. 134–145. [Google Scholar]
- Artzner, P.; Delbaen, F.; Eber, J.-M.; Heath, D. Coherent Measures of Risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Acerbi, C.; Nordio, C.; Sirtori, C. Expected shortfall as a tool for financial risk management. arXiv 2001, arXiv:cond-mat/0102304. [Google Scholar]
- Yan, W.; Li, S. A class of multi-period semi-variance portfolio selection with a four-factor futures price model. J. Appl. Math. Comput. 2008, 29, 19–34. [Google Scholar] [CrossRef]
- Szegö, G. Measures of risk. J. Bank. Financ. 2002, 26, 1253–1272. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Rachev, S.T.; Hsu, J.S.; Bagasheva, B.S.; Fabozzi, F.J. Bayesian Methods in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 153. [Google Scholar]
- Greco, S.; Matarazzo, B.; Słowiński, R. Beyond Markowitz with multiple criteria decision aiding. J. Bus. Econ. 2013, 83, 29–60. [Google Scholar] [CrossRef]
- Espin-Andrade, R.A.; Gonzalez, E.; Pedrycz, W.; Fernandez, E. An Interpretable Logical Theory: The case of Compensatory Fuzzy Logic. Int. J. Comput. Intell. Syst. 2016, 9, 612–626. [Google Scholar] [CrossRef]
- Espín-Andrade, R.A.; Bataller, A.C.; Marx-Gomez, J.; Racet, A. Fuzzy Semantic Transdisciplinary Knowledge Discovery Approach for Business Intelligence. In Towards a Trans-Disciplinary Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making; Shaker Verlag GmbH: Aachen, Germany, 2011; pp. 13–34. [Google Scholar]
- Griffioen, G.A.W. Technical Analysis in Financial Markets. SSRN Electron. J. 2003. [Google Scholar] [CrossRef]
- Paulos, J.A. A Mathematician Plays the Asset Market; Basic Books: New York, NY, USA, 2003. [Google Scholar]
- Roberts, H.V. Asset-market “patterns” and financial analysis: Methodological suggestions. J. Financ. 1959, 14, 1–10. [Google Scholar]
- Tabell, E.W.; Tabell, A.W. The case for technical analysis. Financ. Anal. J. 1964, 20, 67–76. [Google Scholar] [CrossRef]
- Beja, A.; Goldman, M.B. On The Dynamic Behavior of Prices in Disequilibrium. J. Financ. 1980, 35, 235–248. [Google Scholar] [CrossRef]
- Jaffe, J.; Keim, D.B.; Westerfield, R. Earnings yields, market values, and asset returns. J. Financ. 1989, 44, 135–148. [Google Scholar] [CrossRef]
- Chui, A.C.; Wei, K.J. Book-to-market, firm size, and the turn-of-the-year effect: Evidence from Pacific-Basin emerging markets. Pac. Basin Financ. J. 1998, 6, 275–293. [Google Scholar] [CrossRef]
- Mostafa, M.M. Forecasting asset exchange movements using neural networks: Empirical evidence from Kuwait. Expert Syst. Appl. 2010, 37, 6302–6309. [Google Scholar] [CrossRef]
- Mehtab, S.; Sen, J. A Robust Predictive Model for Asset Price Prediction Using Deep Learning and Natural Language Processing. SSRN 2019, 3502624. [Google Scholar] [CrossRef]
- Michie, D.; Spiegelhalter, D.J.; Taylor, C.C. Machine learning. Neural Stat. Classif. 1994, 13, 1–298. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Huang, W.; Nakamori, Y.; Wang, S.Y. Forecasting asset market movement direction with support vector machine. Comput. Oper. Res. 2005, 32, 2513–2522. [Google Scholar] [CrossRef]
- Banga, J.S.; Brorsen, B.W. Profitability of alternative methods of combining the signals from technical trading systems. Intell. Syst. Account. Financ. Manag. 2019, 26, 32–45. [Google Scholar] [CrossRef]
- Nicholls, J.F.; Engelbrecht, A.P. Co-evolved genetic programs for stock market trading. Intell. Syst. Account. Financ. Manag. 2019, 26, 117–136. [Google Scholar] [CrossRef]
- Picasso, A.; Merello, S.; Ma, Y.; Oneto, L.; Cambria, E. Technical analysis and sentiment embeddings for market trend prediction. Expert Syst. Appl. 2019, 135, 60–70. [Google Scholar] [CrossRef]
- Man, X.; Luo, T.; Lin, J. Financial Sentiment Analysis (FSA): A Survey. In Proceedings of the 2019 IEEE International Conference on Industrial Cyber Physical Systems (ICPS), Taipei, Taiwan, 6–9 May 2019; pp. 617–622. [Google Scholar]
- Rhea, R. The Dow Theory: An Explanation of its Development and an Attempt to Define its Usefulness as an Aid in Speculation; Fraser Publishing Company: Flint Hill, VA, USA, 1993. [Google Scholar]
- Murphy, J.J. Technical Analysis of the Financial Markets: A Comprehensive Guide to Trading Methods and Applications; Penguin: London, UK, 1999. [Google Scholar]
- Lu, T.H.; Shiu, Y.M.; Liu, T.C. Profitable candlestick trading strategies—The evidence from a new perspective. Rev. Financ. Econ. 2012, 21, 63–68. [Google Scholar] [CrossRef]
- Lansky, J. Possible State Approaches to Cryptocurrencies. J. Syst. Integr. 2018, 9, 19–31. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. SSRN: Rochester, NY, USA, 2008. [Google Scholar]
- Narayanan, A.; Bonneau, J.; Felten, E.; Miller, A.; Goldfeder, S. Bitcoin and Cryptocurrency Technologies: A Comprehensive Introduction; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]

| Date of Analysis | Asset | Operation (Selling or Buying) | Truth Value of the Operation | Result | Opening Price ($) | Closing Price ($) | Return | Number of Days with an Active Operation |
|---|---|---|---|---|---|---|---|---|
| 13/07/2020 | Zcash | S | 1 | Positive | 60.07 | 60.05 | 0.03 | 3 |
| XRP Ripple | S | 0.96 | negative | 0.1956 | 0.2835 | −44.94 | 19 | |
| Litecoin | S | 0.92 | Positive | 43.46 | 42.36 | 2.53 | 3 | |
| Bnb | S | 1 | Positive | 17.95 | 17.26 | 3.84 | 3 | |
| 14/07/2020 | Zcash | S | 1 | Positive | 61.32 | 60.05 | 2.07 | 2 |
| Bnb | S | 0.92 | Positive | 17.89 | 17.26 | 3.52 | 2 | |
| 15/07/2020 | Without operation performed | |||||||
| 16/07/2020 | Zcash | S | 0.92 | Positive | 58.11 | 57.97 | 0.24 | 4 |
| XLM Estelar | S | 0.96 | Positive | 0.0966 | 0.0957 | 0.93 | 4 | |
| Ada | S | 0.88 | Positive | 0.1241 | 0.1218 | 1.85 | 4 | |
| 20/07/2020 | Bitcoin BCH | B | 0.92 | Positive | 227.04 | 230.21 | 1.4 | 2 |
| Etherum Classic | B | 0.84 | Positive | 6.0945 | 6.1849 | 1.48 | 2 | |
| Litecoin | B | 0.88 | Positive | 42.35 | 43.27 | 2.17 | 2 | |
| XLM Estelar | S | 1 | Positive | 0.0983 | 0.0978 | 0.51 | 1 | |
| 21/07/2020 | Spx500 | S | 0.96 | Positive | 3275.07 | 3266.5 | 0.26 | 1 |
| Ger30 | S | 0.96 | Positive | 13,158.79 | 13,136.62 | 0.17 | 1 | |
| Wmt | S | 0.92 | Positive | 132.69 | 132.37 | 0.24 | 1 | |
| Dis | S | 0.92 | Positive | 119.18 | 118.62 | 0.47 | 1 | |
| Home depot HD | S | 1 | Positive | 263.01 | 262 | 0.38 | 10 | |
| 22/07/2020 | Pfe | S | 0.92 | Positive | 38.38 | 37.63 | 1.95 | 5 |
| Home depot HD | S | 0.96 | Positive | 263.59 | 262 | 0.6 | 9 | |
| 27/07/2020 | USD/MXN | B | 1 | Positive | 22.0054 | 22.00735 | 0.01 | 2 |
| Spx500 | S | 0.96 | Positive | 324.08 | 3238.92 | 0.04 | 1 | |
| Ger30 | S | 0.84 | Positive | 12,904.09 | 12,841.64 | 0.48 | 1 | |
| Home depot HD | S | 1 | Positive | 267.42 | 266.45 | 0.36 | 1 | |
| 28/07/2020 | USD/MXN | B | 1 | Positive | 21.9321 | 21.9378 | 0.03 | 1 |
| Pfe | S | 0.96 | Positive | 39.01 | 38.68 | 0.85 | 1 | |
| Home depot HD | S | 0.96 | Positive | 267.09 | 266.43 | 0.25 | 1 | |
| 29/07/2020 | Gold | S | 1 | Positive | 1969.94 | 1953.84 | 0.82 | 1 |
| Ger30 | S | 0.84 | Positive | 12,855.47 | 12,398.54 | 3.56 | 1 | |
| 30/07/2020 | PG | S | 0.96 | Positive | 130.09 | 129.67 | 0.32 | 1 |
| Pfe | S | 0.92 | Positive | 38.28 | 37.99 | 0.76 | 1 | |
| Wmt | S | 0.84 | Positive | 129.19 | 128.21 | 0.76 | 1 | |
| Home depot HD | S | 0.92 | Positive | 264.79 | 262.04 | 1.04 | 1 | |
| Cutting Threshold | ≥0.8 | ≥0.9 | 1 | ||||
|---|---|---|---|---|---|---|---|
| Operation | Number of Operations Advised | NP | NN | NP | NN | NP | NN |
| Buying | 75 | 73 | 2 | 46 | 2 | 5 | 0 |
| Selling | 203 | 186 | 17 | 134 | 11 | 53 | 4 |
| Total | 278 | 259 | 19 | 180 | 13 | 58 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Cándido, N.P.; Espin-Andrade, R.A.; Solares, E.; Pedrycz, W. A Compensatory Fuzzy Logic Model in Technical Trading. Axioms 2021, 10, 36. https://doi.org/10.3390/axioms10010036
Rodríguez-Cándido NP, Espin-Andrade RA, Solares E, Pedrycz W. A Compensatory Fuzzy Logic Model in Technical Trading. Axioms. 2021; 10(1):36. https://doi.org/10.3390/axioms10010036
Chicago/Turabian StyleRodríguez-Cándido, Norma P., Rafael A. Espin-Andrade, Efrain Solares, and Witold Pedrycz. 2021. "A Compensatory Fuzzy Logic Model in Technical Trading" Axioms 10, no. 1: 36. https://doi.org/10.3390/axioms10010036
APA StyleRodríguez-Cándido, N. P., Espin-Andrade, R. A., Solares, E., & Pedrycz, W. (2021). A Compensatory Fuzzy Logic Model in Technical Trading. Axioms, 10(1), 36. https://doi.org/10.3390/axioms10010036







