Abstract
This paper aims to find a statistical model for the COVID-19 spread in the United Kingdom and Canada. We used an efficient and superior model for fitting the COVID 19 mortality rates in these countries by specifying an optimal statistical model. A new lifetime distribution with two-parameter is introduced by a combination of inverted Topp-Leone distribution and modified Kies family to produce the modified Kies inverted Topp-Leone (MKITL) distribution, which covers a lot of application that both the traditional inverted Topp-Leone and the modified Kies provide poor fitting for them. This new distribution has many valuable properties as simple linear representation, hazard rate function, and moment function. We made several methods of estimations as maximum likelihood estimation, least squares estimators, weighted least-squares estimators, maximum product spacing, Cramr-von Mises estimators, and Anderson-Darling estimators methods are applied to estimate the unknown parameters of MKITL distribution. A numerical result of the Monte Carlo simulation is obtained to assess the use of estimation methods. also, we applied different data sets to the new distribution to assess its performance in modeling data.
1. Introduction
Modeling for lifetime distributions have attracted great attention over the years and decades, and their interest has grown over time because the importance of modeling phenomena and pandemics is very important. Researchers in distribution theory prefer to make modeling for data either by introducing a new parameter to make the distribution of interest more flexible or perhaps by producing a new distribution family. Modeling is very interesting in numerous fields, such as industry, engineering, reliability, and medical research, see (Anake et al. [1]) for more reading. The inverted distributions have a great importance due to their applicability in many areas such as biological sciences, life test problems, medical, etc. The density and hazard ratio forms of the inverted distributions show a different structure from the other non-inverted distributions. Many authors used the inverted distributions in many applications, the reader can refer to Abd AL-Fattah et al. [2], Barco et al. [3], Hassan and Abd-Allah [4], Muhammed [5], Chesneau et al. [6], Usman and ul Haq [7], Eferhonore et al. [8] and others. Also, in this paper, we made a statistical modeling for COVID-19 mortality data in two different countries, for more reading about this, see Kumar [9], Khakharia et al. [10], Wang [11], Lalmuanawma et al. [12] and Bullock et al. [13].
The cumulative distribution function (CDF) and probability density function (PDF) of the inverted Topp-Leone distribution (ITL) distribution with shape parameter , have been proposed by Hassan et al. [14] as follows:
and,
Kumar and Dharmaja [15] studied the properties of the exponentiated Kies distribution. The product moments of a modified Kies distribution under type II progressive censored sample, as well as an estimate of the distribution parameters, have been derived, see Dey et al. [16]. A new family of distributions based on the modified Kies (MK) distribution family was presented by Al-Babtain et al. [17]. If is the baseline CDF depending on a parameter vector , then the CDF of the MK family is defined by
where is parameter vector . The PDF of (3) is as below
Referring to the distributions above the two-parameter modified Kies inverted Topp-Leone (MKITL), which has many attractive characteristics, is obtained in this article. The proposed MKITL distribution has a very versatile PDF because it can form either positive skewed, negative skewed, and also symmetric, enabling further flexibility of tail. It can model diminishing, rising, bathtub, and reverse-J hazard rates. One more advantage of the proposed distribution is that it also has an exact closed-form CDF and very convenient to handle. These merits make the distribution an elegant candidate for use in varied areas such as biomedical life testing, reliability, and actuarial data. This article introduced two real data applications and deduced from modeling the results that the new distribution is perfect competitor with some traditional and common distributions with scale and shape parameters such as ITL, Marshall-Olkin exponential, modified Kies exponential, reverse Weibull, reverse exponential, and reverse Rayleigh distributions.
In future studies, we intend to make a new extension bivariate modified Kies inverted Topp-Leone based on copula such as and Muhammed and Almetwally [18], Almetwally and Muhammed [19], El-Morshedy et al. [20], and Kim et al. [21]. We intend to discuss a new application based on a censored sample for MKITL distribution see for more reading, Almetwally et al. [22] and Aslam et al. [23].
The rest of this paper is ordered as follows: In Section 2, we obtain the MKITL distribution. In Section 3, we discuss some of the mathematical properties of the MKITL distribution. In Section 4, we obtain an estimation methods MKITL distribution. In Section 5, we obtain simulation results of MKITL distribution. In Section 6, two applications of real data analysis were obtained. The paper is summarized and concluded in Section 7.
2. MKITL Distribution
By using the ITL distribution with the parameter of and the CDF given (for ) by using Equations (1) and (2). We define the CDF for the distribution MKITL, by substituting in Equation (3) the CDF of the ITL distribution.
and the corresponding PDF is
where is parameter vector . The hazard rate (HR) function of the MKITL distribution is shown as
Figure 1 and Figure 2 demonstrate certain plots of the MKITL distribution for the values specified for and . The diagrams shown in Figure 2 demonstrate that the MKITL distribution HR function can be increased, decreased, and shaped a bathtub. One of the merits of MKITL distribution over an ITL distribution is that the latter is very poor model for data and phenomena that shows increasing, declining shapes, failure rates of the bathtub so it becomes more versatile to evaluate lifetime data than its competitor.
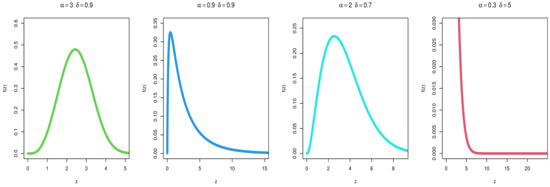
Figure 1.
PDF of the MKITL distribution for certain parameter values.
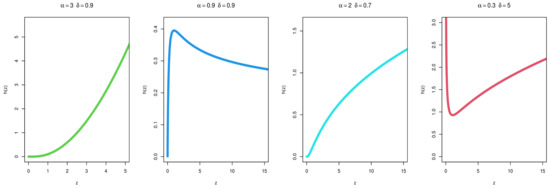
Figure 2.
HF of the MKITL distribution for certain parameter values.
3. All Statistical Properties of the Proposed Distribution of MKITL
3.1. Linear Representation for the MKITL Distribution
We introduce a linear representation in this subsection for the MK family and use it to provide a useful linear representation for the MKITL distribution. A mixture representation of the MK family can be provided as follows,
The last equation of the MKITL distribution can be rewritten with the ITL distribution PDF and CDF.
where . Equation (9) denotes the ITL density with parameter .
3.2. Quantile for the MKITL Distribution
The quantile function of the MKITL distribution, say is derived by inverting (5) as follows:
In particular, the first quartile, say Q1, the second quartile, say Q2, and the third quartile, say Q3 are obtained by setting , respectively, in (10).
3.3. Moments for the MKITL Distribution
4. Methods of Estimation for the Distribution Parameters
We managed to make a solution for the estimation problem of the MKITL distribution parameters using six different estimation methods. These methods are the maximum likelihood estimators (MLE), least squares estimators (LSEs), maximum product of spacing estimators (MPSE), weighted least-squares estimators (WLSE), Cramr-von Mises estimators (CVME) and Anderson-Darling estimators (ADE).
4.1. Maximum Likelihood Estimators
Let be a random sample from the MKITL distribution with parameters and . the log-likelihood function for MKITL distribution is given by
The partial derivatives of with respect to the model parameters and are
and
The MLE of the distribution parameters and can be calculated by finding the maximum value for Equation (13) by finding the first derivative for it with respect to and . The R software can be used to optimise the log-likelihood and obtain the MLE by using the Newton-Rapshon method.
4.2. Least Squares and Weighted Least Squares Methods
Here we introduce two methods of estimation that we can use in this paper; these methods are the least squares (LS) and weighted least square (WLS) methods. They are very important common methods for estimating the parameters of different distributions. Suppose that we have a random sample say from the MKITL distribution with the two parameters and . Now we can calculate both the LS estimators (LSE) and WLS estimators (WLSE) of the MKITL distribution parameters and by making the following equation as minimum as possible
with respect to and , where in case of LSE and in case of WLSE. Furthermore, the LSE and WLSE follow by solving the nonlinear equations
and
4.3. Maxzimum Product of Spacings Method
In this sub section, we will use an alternative method for the MLE method which is called the maximum product of spacings (MPS), this method is used to estimate the parameters of continuous univariate models, this method was introduced by Cheng and Amin [24] and used for censored application by Singh et al. [25], Almetwally and Almongy [26], Basu et al. [27], Almetwally et al. [28], El-Sherpieny et al. [29] and Alshenawy et al. [30] and [31]. Let , be a random sample of size n, the uniform spacing of the MKITL distribution can be defined by
where denotes to the uniform spacings, , and .
The MPS estimators (MPSE) of the MKITL parameters can be obtained by maximizing Equation (20) with respect to and .
4.4. Cramr-von-Mises Method
The Cramr-von-Mises estimators (CVME), can be calculated depending on the difference between both the CDF and the empirical distribution function estimates. For more information see (Luceno [32]).
We can find the estimates by The CVME method for the two parameters of MKITL, which are and by finding the minimum value for Equation (23) with respect to and .
and
4.5. Anderson-Darling Method
Here we introduce another minimum distance estimation method. This method is called the Anderson-Darling estimation (ADE).
We can manipulate the ADE to estimate the parameters of the MKITL distribution by making the Equation (26) at minimum value with respect to and .
5. Simulation Results
In this section, we made an estimation by using six methods of the MKITL parameters, and compared between them to assess the performance of each method by a simulation study. We consider different sample sizes for different parameters values and . We generate random samples from MKITL distribution. For each estimate, we obtain the average values of the estimates (mean) and their corresponding mean squares error (MSE).
The performance of different estimators is evaluated in terms of MSE, i.e., the most efficient method of estimating will be those whose MSE values are closer to zero. Simulation results are obtained via the R program. Table 1, Table 2 and Table 3 show the estimates mean and MSE for MLE, LS, WLS, MPS, CVM, and AD. Moreover, the mean using all estimation methods tends towards the true parameter values, as the sample size increases in most cases.

Table 1.
Mean and MSE of the MLE, LS, MPS, WLS, CVM and AD estimate for MKITL distribution when .

Table 2.
Mean and MSE of the MLE, LS, MPS, WLS, CVM and AD estimate for MKITL distribution when .

Table 3.
Mean and MSE of the MLE, LS, MPS, WLS, CVM and AD estimate for MKITL distribution when .
Concluded Observation on the Simulation Results
- When , and as the value of increases the MSE of the two parameters increases in most cases, while the mean values of both parameters tends to the initial values.
- For a fixed value of , and , by increasing the sample size, the mean values of the parameters tend to the initial values, and MSE decreases.
- In most cases, the MPS was the best method for estimating the parameter referring to the mean values of the parameters and MSE as in Table 1, Table 2 and Table 3, while the AD was the best efficient method for estimating the parameters referring to the mean values of the parameters and MSE in Table 3 when .
- All estimators perform very well and provides very small MSE and the mean value of estimates for all estimators tend to the initial value of the parameters.
- The differences between all estimators values are very small, referring to the MSE values and the mean value of the parameters.
6. Application of Real Data Analysis
This section is devoted to illustrating the potentiality of the MKITL distribution for two real data sets. MKITL distribution is compared with other competitive models, namely: ITL (Hassan et al. [14]), the Marshall-Olkin exponential (MOEx) [Marshall and Olkin [33], modified Kies exponential (MKEx) (Al-Babtain et al. [17]), inverse Weibull (IW), inverse exponential (IE) and inverse Rayleigh (IR) (Ahmad et al. [34]).
Table 4 and Table 5 provide values of Cramr-von Mises (W*), Anderson-Darling (A*) and Kolmogorov- Smirnov (KS) statistic along with its P-value for the all models fitted based on Two real data sets. In addition, these tables contain the MLE and standard errors (SE) of the parameters for the considered models. In Table 4 and Table 5 the MKITL distribution has the highest P-value and the lowest distance of Kolmogorov-Smirnov(KS), W*, and A* value when it compares with all other models used here to fit the COVID-19. Figure 3 and Figure 4 show the fit empirical, histogram, QQ-plot, and PP-plot for the MKITL distribution for COVID-19 data of the United Kingdom and Canada.

Table 4.
MLE, SE, KS test and P-values for COVID-19 data of Canada.

Table 5.
MLE, SE, KS test and P-values for COVID-19 data of The United Kingdom.
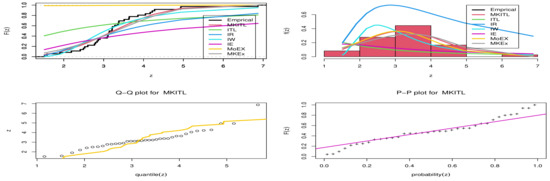
Figure 3.
Cumulative function and empirical CDF, histogram, Q-Q plot and P-P plot for the MKITL distribution for COVID-19 data of Canada.
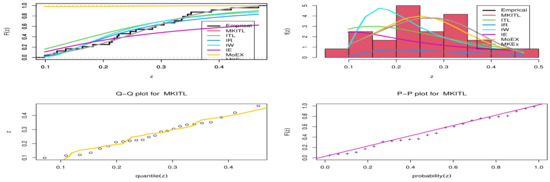
Figure 4.
Cumulative function and empirical CDF, histogram, Q-Q plot and P-P plot for the MKITL distribution for COVID-19 data of The United Kingdom.
6.1. Application 1
Firstly: The data represents a COVID-19 data belong to Canada of 36 days, from 10 April to 15 May 2020 see the link [https://covid19.who.int/].
These data formed of drought mortality rate. The data are as follows: 3.1091 3.3825 3.1444 3.2135 2.4946 3.5146 4.9274 3.3769 6.8686 3.0914 4.9378 3.1091 3.2823 3.8594 4.0480 4.1685 3.6426 3.2110 2.8636 3.2218 2.9078 3.6346 2.7957 4.2781 4.2202 1.5157 2.6029 3.3592 2.8349 3.1348 2.5261 1.5806 2.7704 2.1901 2.4141 1.9048.
6.2. Application 2
Secondly: The data represents a COVID-19 data belong to The United Kingdom of 24 days, from 15 October to 7 November 2020 [https://covid19.who.int/]. These data formed of drought mortality rate. The data are as follows: 0.2240 0.2189 0.2105 0.2266 0.0987 0.1147 0.3353 0.2563 0.2466 0.2847 0.2150 0.1821 0.1200 0.4206 0.3456 0.3045 0.2903 0.3377 0.1639 0.1350 0.3866 0.4678 0.3515 0.3232.
6.3. Concluding Remarks on the Two Application
- Referring to data set one we can see that MKITL provides the highest P-value, and the lowest W*, A* and lowest KS distance.
- From Figure 3 , we can deduce that MKITL was the best model for fitting the first data set.
- Referring to data set two, we can see that MKITL provides the highest P-value, and the lowest A*, W* and KS distance.
- From Figure 4, we can deduce that MKITL was the best model for fitting the second data set.
- Referring to Table 4 we can see that IE, IR, ITL and MOEx distribution provides poor fitting for the first data set.
- Referring to Table 5 we can see that IE, MOEx distribution provides poor fitting for the second data set.
- We can conclude that from both applications that the MKITL distribution provides the best fitting among all its competitive distributions, which gives it superiority in fitting this kind of mortality rate for COVID-19 data.
7. Summary
In this paper, we propose a new two-parameter model, called the modified Kies inverted Topp-Leone distribution, which can be denoted as MKITL distribution. The MKITL distribution is more flexible to analyze lifetime data than other common distributions. Survival function, hazard function, linear representation, quantile, and moments of the MKITL distribution are provided. We compare MLE, LSE, MPSE, WLSE, CVME, and ADE methods, and we conclude the alternative methods of MLE are better than the MLE method. We provide two applications on COVID 19 mortality rate and we proved that the MKITL distribution is the best model among all its competitors to fit this kind of data. The parameter estimation of MKITL distribution is derived by MLE, LSE, MPSE, WLSE, CVME, and ADE. The methods of estimation are used to estimate the model parameters, and simulation results are provided to assess the model performance. Two real-life data proposed model provides a consistently better fit than the MKITL, IE, IW, MOEx, MKEx, and IR distributions.
Author Contributions
All authors contribute equally to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anake, T.A.; Oguntunde, P.E.; Odetunmibi, O.A. On a fractional beta- distribution. Int. J. Math. Comput. 2015, 26, 26–34. [Google Scholar]
- Abd AL-Fattah, A.M.; El-Helbawy, A.A.; Al-Dayian, G.R. Inverted Kumaraswamy Distribution: Properties and Estimation. Pak. J. Stat. 2017, 33, 37–61. [Google Scholar]
- Barco, K.V.P.; Mazucheli, J.; Janeiro, V. The inverse power Lindley distribution. Commun. Stat.-Simul. Comput. 2017, 46, 6308–6323. [Google Scholar] [CrossRef]
- Hassan, A.S.; Abd-Allah, M. On the inverse power Lomax distribution. Ann. Data Sci. 2019, 6, 259–278. [Google Scholar] [CrossRef]
- Muhammed, H.Z. On the inverted Topp Leone distribution. Int. J. Reliab. Appl. 2019, 20, 17–28. [Google Scholar]
- Chesneau, C.; Tomy, L.; Gillariose, J.; Jamal, F. The inverted modified Lindley distribution. J. Stat. Theory Pract. 2020, 14, 1–17. [Google Scholar] [CrossRef]
- Usman, R.M.; ul Haq, M.A. The Marshall-Olkin extended inverted Kumaraswamy distribution: Theory and applications. J. King Saud Univ.-Sci. 2020, 32, 356–365. [Google Scholar] [CrossRef]
- Eferhonore, E.E.; Thomas, J.; Zelibe, S.C. Theoretical Analysis of the Weibull Alpha Power Inverted Exponential Distribution: Properties and Applications. Gazi Univ. J. Sci. 2020, 33, 265–277. [Google Scholar]
- Kumar, S. Monitoring Novel Corona Virus (COVID-19) Infections in India by Cluster Analysis. Ann. Data Sci. 2020, 7, 417–425. [Google Scholar] [CrossRef]
- Khakharia, A.; Shah, V.; Jain, S.; Shah, J.; Tiwari, A.; Daphal, P.; Mehendale, N. Outbreak Prediction of COVID-19 for Dense and Populated Countries Using Machine Learning. Ann. Data Sci. 2020, 8, 1–19. [Google Scholar] [CrossRef]
- Wang, Y.z.J. A call for caution in extrapolating chest CT sensitivity for COVID-19 derived from hospital data to patients among general population. Quant. Imaging Med. Surg. 2020, 10, 798. [Google Scholar] [CrossRef]
- Lalmuanawma, S.; Hussain, J.; Chhakchhuak, L. Applications of machine learning and artificial intelligence for Covid-19 (SARS-CoV-2) pandemic: A review. Chaos Solitons Fractals 2020, 139, 110059. [Google Scholar] [CrossRef] [PubMed]
- Bullock, J.; Pham, K.H.; Lam, C.S.N.; Luengo-Oroz, M. Mapping the landscape of artificial intelligence applications against COVID-19. arXiv 2020, arXiv:2003.11336. [Google Scholar]
- Hassan, A.S.; Elgarhy, M.; Ragab, R. Statistical Properties and Estimation of Inverted Topp-Leone Distribution. J. Stat. Appl. Probab. 2020. forthcoming. [Google Scholar]
- Kumar, C.S.; Dharmaja, S.H.S. The exponentiated reduced Kies distribution: Properties and applications. Commun. Stat.-Theory Methods 2017, 46, 8778–8790. [Google Scholar] [CrossRef]
- Dey, S.; Nassar, M.; Kumar, D. Moments and estimation of reduced Kies distribution based on progressive type-II right censored order statistics. Hacet. J. Math. Stat. 2019, 48, 332–350. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Shakhatreh, M.K.; Nassar, M.; Afify, A.Z. A New Modified Kies Family: Properties, Estimation Under Complete and type-II Censored Samples, and Engineering Applications. Mathematics 2020, 8, 1345. [Google Scholar] [CrossRef]
- Muhammed, H.Z.; Almetwally, E.M. Bayesian and Non-Bayesian Estimation for the Bivariate Inverse Weibull Distribution Under Progressive Type-II Censoring. Ann. Data Sci. 2020. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Muhammed, H.Z. On a bivariate Fréchet distribution. J. Stat Appl Probab. 2020, 9, 1–21. [Google Scholar]
- El-Morshedy, M.; Alhussain, Z.A.; Atta, D.; Almetwally, E.M.; Eliwa, M.S. Bivariate Burr X generator of distributions: Properties and estimation methods with applications to complete and type-II censored samples. Mathematics. 2020, 8, 264. [Google Scholar] [CrossRef]
- Kim, J.M.; Ju, H.; Jung, Y. Copula Approach for Developing a Biomarker Panel for Prediction of Dengue Hemorrhagic Fever. Ann. Data Sci. 2020, 7, 697–712. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Almongy, H.M.; Rastogi, M.K.; Ibrahim, M. Maximum Product Spacing Estimation of Weibull Distribution Under Adaptive Type-II Progressive Censoring Schemes. Ann. Data Sci. 2020, 7, 257–279. [Google Scholar] [CrossRef]
- Aslam, M.; Yousaf, R.; Ali, S. Bayesian Estimation of Transmuted Pareto Distribution for Complete and Censored Data. Ann. Data Sci. 2020, 7, 663–695. [Google Scholar] [CrossRef]
- Cheng, R.C.H.; Amin, N.A.K. Estimating parameters in continuous univariate distributions with a shifted origin. J. R. Stat. Soc. Ser. B (Methodol.) 1983, 45, 394–403. [Google Scholar] [CrossRef]
- Singh, R.K.; Singh, S.K.; Singh, U. Maximum product spacings method for the estimation of parameters of generalized inverted exponential distribution under Progressive Type II Censoring. J. Stat. Manag. Syst. 2016, 19, 219–245. [Google Scholar]
- Almetwally, E.M.; Almongy, H.M. Maximum product spacing and Bayesian method for parameter estimation for generalized power Weibull distribution under censoring scheme. J. Data Sci. 2019, 17, 407–444. [Google Scholar]
- Basu, S.; Singh, S.K.; Singh, U. Estimation of Inverse Lindley Distribution Using Product of Spacings Function for Hybrid Censored Data. Methodol. Comput. Appl. Probab. 2019, 21, 1377–1394. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Almongy, H.M.; ElSherpieny, E.A. Adaptive type-II progressive censoring schemes based on maximum product spacing with application of generalized Rayleigh distribution. J. Data Sci. 2019, 17, 802–831. [Google Scholar]
- El-Sherpieny, E.S.A.; Almetwally, E.M.; Muhammed, H.Z. Progressive Type-II hybrid censored schemes based on maximum product spacing with application to Power Lomax distribution. Phys. A Stat. Mech. Its Appl. 2020, 553, 124251. [Google Scholar] [CrossRef]
- Alshenawy, R.; Al-Alwan, A.; Almetwally, E.M.; Afify, A.Z.; Almongy, H.M. Progressive Type-II Censoring Schemes of Extended Odd Weibull Exponential Distribution with Applications in Medicine and Engineering. Mathematics 2020, 8, 1679. [Google Scholar] [CrossRef]
- Alshenawy, R.; Sabry, M.A.; Almetwally, E.M.; Almongy, H.M. Product Spacing of Stress–Strength under Progressive Hybrid Censored for Exponentiated-Gumbel Distribution. Comput. Mater. Contin. 2021, 66, 2973–2995. [Google Scholar] [CrossRef]
- Luceno, A. Fitting the generalized Pareto distribution to data using maximum goodness of fit estimators. Comput. Stat. Data Anal. 2006, 51, 904–917. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Ahmad, A.; Ahmad, S.P.; Ahmed, A. Transmuted Inverse Rayleigh distribution: A generalization of the Inverse Rayleigh distribution. Math. Theory Model. 2014, 4, 90–98. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).