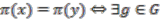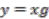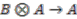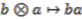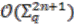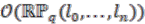Bundles over Quantum RealWeighted Projective Spaces
Abstract
:1. Introduction
 -grading of this coordinate algebra. A typical
-grading of this coordinate algebra. A typical 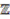 -grading assigns degree ±1 to every generator of this algebra (different from the identity). The degree zero part forms a subalgebra which in particular cases corresponds to quantum complex or real projective spaces (grading of coordinate algebras of quantum spheres [1] or prolonged quantum spheres [2]). Often this grading is strong, meaning that the product of
-grading assigns degree ±1 to every generator of this algebra (different from the identity). The degree zero part forms a subalgebra which in particular cases corresponds to quantum complex or real projective spaces (grading of coordinate algebras of quantum spheres [1] or prolonged quantum spheres [2]). Often this grading is strong, meaning that the product of 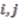 -graded parts is equal to the
-graded parts is equal to the  -part of the total algebra. In geometric terms this reflects the freeness of the circle action.
-part of the total algebra. In geometric terms this reflects the freeness of the circle action.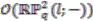 (
(  a positive integer) and
a positive integer) and 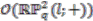 (
( 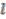 an odd positive integer) identified in [3] as fixed points of weighted circle actions on the coordinate algebra
an odd positive integer) identified in [3] as fixed points of weighted circle actions on the coordinate algebra  of a non-orientable quantum Seifert manifold described in [2]. Our aim is to construct quantum
of a non-orientable quantum Seifert manifold described in [2]. Our aim is to construct quantum 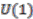 -principal bundles over the corresponding quantum spaces
-principal bundles over the corresponding quantum spaces 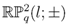 and describe associated line bundles. Recently, the importance of such bundles in non-commutative geometry was once again brought to the fore in [5], where the non-commutative Thom construction was outlined. As a further consequence of the principality of
and describe associated line bundles. Recently, the importance of such bundles in non-commutative geometry was once again brought to the fore in [5], where the non-commutative Thom construction was outlined. As a further consequence of the principality of 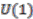 -coactions we also deduce that
-coactions we also deduce that 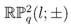 can be understood as quotients of
can be understood as quotients of 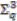 by almost free
by almost free  -actions.
-actions.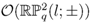 in Section 3. Section 4 contains main results including construction of principal comodule algebras over
in Section 3. Section 4 contains main results including construction of principal comodule algebras over  . We observe that constructions albeit very similar in each case yield significantly different results. The principal comodule algebra over
. We observe that constructions albeit very similar in each case yield significantly different results. The principal comodule algebra over 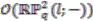 is non-trivial while that over
is non-trivial while that over 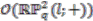 turns out to be trivial (this means that all associated bundles are trivial, hence we do not mention them in the text). Whether it is a consequence of our particular construction or there is a deeper (topological or geometric) obstruction to constructing non-trivial principal circle bundles over
turns out to be trivial (this means that all associated bundles are trivial, hence we do not mention them in the text). Whether it is a consequence of our particular construction or there is a deeper (topological or geometric) obstruction to constructing non-trivial principal circle bundles over 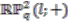 remains an interesting open question.
remains an interesting open question.2. Review of Bundles in Non-Commutative Geometry
2.1. Topological Aspects of Bundles
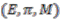 where
where  and
and 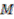 are topological spaces and
are topological spaces and 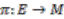 is a continuous surjective map. Here
is a continuous surjective map. Here 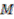 is called the base space,
is called the base space,  the total space and
the total space and 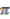 the projection of the bundle.
the projection of the bundle. 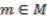 , the fibre over
, the fibre over  is the topological space
is the topological space 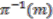 , i.e., the points on the total space which are projected, under
, i.e., the points on the total space which are projected, under 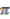 , onto the point
, onto the point  in the base space. A bundle whose fibres are homeomorphic which satisfies a condition known as local triviality are known as fibre bundles. This is formally expressed in the next definition.
in the base space. A bundle whose fibres are homeomorphic which satisfies a condition known as local triviality are known as fibre bundles. This is formally expressed in the next definition. where
where 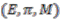 is bundle and
is bundle and  is a topological space such that
is a topological space such that 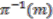 are homeomorphic to
are homeomorphic to  for each
for each 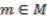 . Furthermore,
. Furthermore, 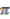 satisfies the local triviality condition.
satisfies the local triviality condition.  , there is an open neighourhood
, there is an open neighourhood 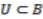 such that
such that 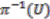 is homeomorphic to the product space
is homeomorphic to the product space 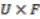 , in such a way that
, in such a way that 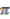 carries over to the projection onto the first factor. That is the following diagram commutes:
carries over to the projection onto the first factor. That is the following diagram commutes: 
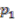 is the natural projection
is the natural projection  and
and 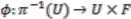 is a homeomorphism.
is a homeomorphism.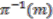 is homeomorphic to
is homeomorphic to  and the Mobius strip is a fibre bundle.
and the Mobius strip is a fibre bundle. 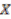 be a topological space which is compact and satisfies the Hausdorff property and G a compact topological group. Suppose there is a right action
be a topological space which is compact and satisfies the Hausdorff property and G a compact topological group. Suppose there is a right action 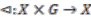 of
of 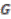 on
on 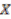 and write
and write  .
.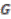 on
on 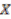 is said to be free if
is said to be free if 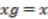 for any
for any 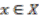 implies that
implies that 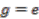 , the group identity.
, the group identity.  is defined as
is defined as 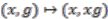 .
.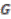 acts freely on
acts freely on 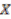 if and only if
if and only if 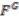 is injective.
is injective.  " Suppose the action is free, hence
" Suppose the action is free, hence 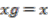 implies that
implies that 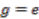 . If
. If 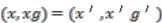 , then
, then 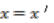 and
and  . Applying the action of
. Applying the action of 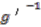 to both sides of
to both sides of  we get
we get  , which implies
, which implies  by the freeness property, concluding
by the freeness property, concluding 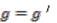 and
and 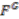 is injective as required.
is injective as required.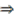 " Suppose
" Suppose 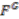 is injective, so
is injective, so 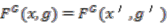 or
or 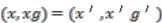 implies
implies 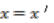 and
and 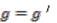 . Since
. Since 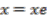 from the properties of the action, if
from the properties of the action, if 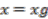 then
then 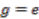 from the injectivity property.
from the injectivity property. 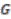 acts on
acts on 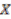 we can define the quotient space
we can define the quotient space 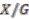 ,
, 
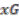 are called the orbits of the points
are called the orbits of the points 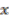 . They are defined as the set of elements in
. They are defined as the set of elements in 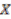 to which
to which 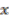 can be moved by the action of elements of
can be moved by the action of elements of 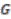 . The set of orbits of
. The set of orbits of 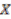 under the action of
under the action of 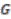 forms a partition of
forms a partition of 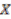 , hence we can define the equivalence relation on
, hence we can define the equivalence relation on 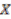 as,
as, 
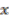 and
and 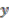 are in the same orbit, i.e.,
are in the same orbit, i.e., 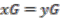 . Given any quotient space, then there is a canonical surjective map
. Given any quotient space, then there is a canonical surjective map 
 to their orbits. We define the pull-back along this map
to their orbits. We define the pull-back along this map 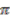 to be the set
to be the set 
 contains elements of
contains elements of 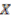 in the first leg and the action of
in the first leg and the action of 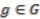 on
on 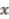 in the second leg. To put it another way, the image records elements of
in the second leg. To put it another way, the image records elements of 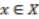 in the first leg and all the elements in the same orbit as this
in the first leg and all the elements in the same orbit as this 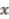 in the second leg. Hence we can identify the image of the canonical map as the pull back along
in the second leg. Hence we can identify the image of the canonical map as the pull back along 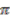 , namely
, namely 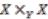 . This is formally proved as a part of the following proposition.
. This is formally proved as a part of the following proposition.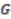 acts freely on
acts freely on 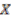 if and only if the map
if and only if the map 
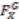 is well-defined since the elements
is well-defined since the elements 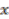 and
and 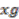 are in the same orbit and hence map to the same equivalence class under
are in the same orbit and hence map to the same equivalence class under 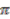 . Using Proposition 2.5 we can deduce that the injectivity of
. Using Proposition 2.5 we can deduce that the injectivity of 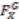 is equivalent to the freeness of the action. Hence if we can show that
is equivalent to the freeness of the action. Hence if we can show that 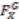 is surjective the proof is complete.
is surjective the proof is complete. . This means
. This means 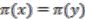 , which implies
, which implies 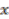 and
and 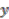 are in the same equivalence class, which in turn means they are in the same orbit. We can therefore deduce that
are in the same equivalence class, which in turn means they are in the same orbit. We can therefore deduce that  for some
for some 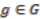 . So,
. So, 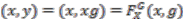 implying
implying  . Hence
. Hence 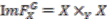 completing the proof.
completing the proof. 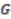 on
on 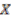 is said to be principal if the map
is said to be principal if the map 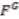 is both injective and continuous (and such that the inverse image of a compact subset is compact in a case of locally compact spaces).
is both injective and continuous (and such that the inverse image of a compact subset is compact in a case of locally compact spaces). 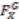 from
from 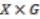 onto the space
onto the space 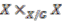 . Principal actions lead to the concept of topological principle bundles.
. Principal actions lead to the concept of topological principle bundles.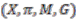 such that
such that- (a)
is a bundle and
is a topological group acting continuously on
with action
,
;
- (b) the action
is principal;
- (c)
such that
;
- (d) the induced map
is a homeomorphism.
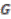 on the total space
on the total space 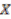 , i.e., principal bundles correspond to principal actions. By Definition
, i.e., principal bundles correspond to principal actions. By Definition  , principal actions occur when the principal map is both injective and continuous, or equivalently, when the action is free and continuous. The third property ensures that the fibres of the bundle correspond to the orbits coming from the action and the final property implies that the quotient space can topologically be viewed as the base space of the bundle.
, principal actions occur when the principal map is both injective and continuous, or equivalently, when the action is free and continuous. The third property ensures that the fibres of the bundle correspond to the orbits coming from the action and the final property implies that the quotient space can topologically be viewed as the base space of the bundle.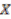 is a topological space and
is a topological space and 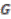 a topological group which acts on
a topological group which acts on 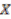 from the right. The triple
from the right. The triple 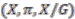 where
where  is the orbit space and
is the orbit space and 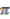 the natural projection is a bundle. A principal action of
the natural projection is a bundle. A principal action of 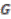 on
on 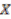 makes the quadruple
makes the quadruple 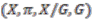 a principal bundle.
a principal bundle. 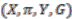 as a
as a 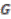 -principal bundle over
-principal bundle over  , or
, or 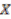 as a
as a 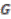 -principal bundle over
-principal bundle over 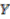 .
.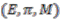 where each fibre
where each fibre 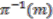 is endowed with a vector space structure such that addition and scalar multiplication are continuous maps.
is endowed with a vector space structure such that addition and scalar multiplication are continuous maps. 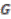 -principal bundle
-principal bundle 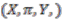 and let
and let 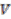 be a representation space of
be a representation space of 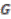 , i.e., a (topological) vector space with a (continuous) left
, i.e., a (topological) vector space with a (continuous) left 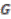 -action
-action 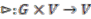 ,
, 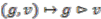 . Then
. Then 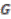 acts from the right on
acts from the right on  by
by 
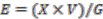 and a surjective (continuous map)
and a surjective (continuous map)  ,
, 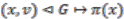 and thus have a fibre bundle
and thus have a fibre bundle 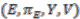 . In the case where
. In the case where 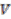 is a vector space, we assume that
is a vector space, we assume that 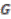 acts linearly on
acts linearly on 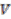 .
.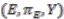 is a continuous map
is a continuous map 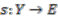 such that, for all
such that, for all 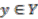 ,
, 
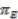 . The set of sections of
. The set of sections of  is denoted by
is denoted by 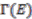 .
. 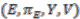 associated to a principal
associated to a principal 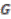 -bundle
-bundle 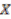 are in bijective correspondence with (continuous) maps
are in bijective correspondence with (continuous) maps 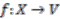 such that
such that 
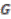 -equivariant maps are denoted by
-equivariant maps are denoted by 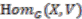 .
. 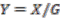 . Given a map
. Given a map 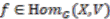 , define the section
, define the section 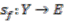 ,
, 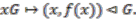
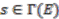 , define
, define 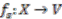 by assigning to
by assigning to 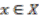 a unique
a unique  such that
such that 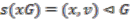 . Note that
. Note that 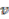 is unique, since if
is unique, since if 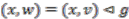 , then
, then 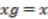 and
and  . Freeness implies that
. Freeness implies that 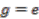 , hence
, hence  . The map
. The map 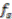 has the required equivariance property, since the element of
has the required equivariance property, since the element of 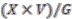 corresponding to
corresponding to 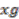 is
is 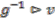 .
. 2.2. Non-Commutative Principal and Associated Bundles
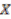 is a complex affine variety with an action of an affine algebraic group
is a complex affine variety with an action of an affine algebraic group 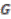 and set
and set  (all with the usual Euclidean topology). Let
(all with the usual Euclidean topology). Let  ,
, 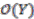 and
and 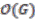 be the corresponding coordinate rings. Put
be the corresponding coordinate rings. Put  and
and 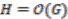 and note the identification
and note the identification 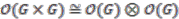 . Through this identification,
. Through this identification,  is a Hopf algebra with comultiplication:
is a Hopf algebra with comultiplication: 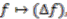
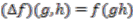 , counit
, counit 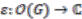 ,
, 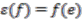 , and the antipode
, and the antipode 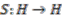 ,
, 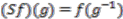 .
.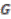 acts on
acts on 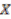 we can construct a right coaction of
we can construct a right coaction of  on
on  by
by 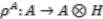 ,
, 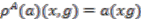 . This coaction is an algebra map due to the commutativity of the algebras of functions involved.
. This coaction is an algebra map due to the commutativity of the algebras of functions involved.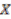 and
and 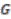 , next we view the space of functions on Y,
, next we view the space of functions on Y, 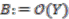 , where
, where  .
. 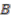 is a subalgebra of
is a subalgebra of 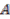 by
by 
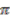 is the canonical surjection defined above. The map
is the canonical surjection defined above. The map 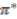 is injective, since
is injective, since 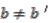 in
in 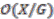 means there exists at least one orbit
means there exists at least one orbit  such that
such that 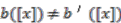 , but
, but 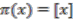 , so
, so 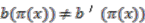 which implies
which implies 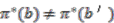 . Therefore, we can identify
. Therefore, we can identify 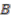 with
with  . Furthermore,
. Furthermore, 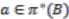 if and only if
if and only if 
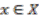 ,
, 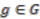 . This is the same as
. This is the same as 
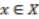 ,
, 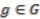 , where
, where 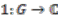 is the unit function
is the unit function  (the identity element of
(the identity element of 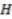 ). Thus we can identify
). Thus we can identify 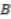 with the coinvariants of the coaction
with the coinvariants of the coaction 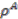 :
: 
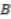 is a subalgebra of
is a subalgebra of 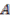 , it acts on
, it acts on 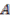 via the inclusion map
via the inclusion map 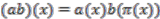 ,
, 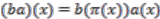 . We can identify
. We can identify 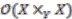 with
with 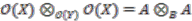 by the map
by the map 
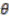 is well defined because
is well defined because 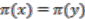 . Proposition 2.6 immediately yields
. Proposition 2.6 immediately yields on
on 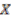 is free if and only if
is free if and only if 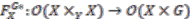 ,
, 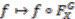 is bijective.
is bijective. 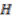 on
on 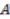 , we can identify
, we can identify  with the canonical map
with the canonical map
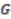 on
on 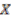 is free if and only if this purely algebraic map is bijective. In the classical geometry case we take
is free if and only if this purely algebraic map is bijective. In the classical geometry case we take 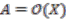 ,
, 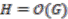 and
and 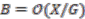 , but in general there is no need to restrict oneself to commutative algebras (of functions on topological spaces). In full generality this leads to the following definition.
, but in general there is no need to restrict oneself to commutative algebras (of functions on topological spaces). In full generality this leads to the following definition. be a Hopf algebra and
be a Hopf algebra and 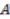 a right
a right  -comodule algebra with coaction
-comodule algebra with coaction 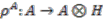 . Let
. Let  , the coinvariant subalgebra of
, the coinvariant subalgebra of 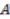 . We say that
. We say that  is a Hopf–Galois extension if the left
is a Hopf–Galois extension if the left 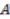 -module, right
-module, right  -comodule map
-comodule map 
 be a Hopf algebra with bijective antipode and let
be a Hopf algebra with bijective antipode and let 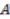 be a right
be a right  -comodule algebra with coaction
-comodule algebra with coaction 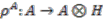 . Let
. Let  denote the coinvariant subalgebra of
denote the coinvariant subalgebra of 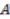 . We say that
. We say that 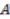 is a principal
is a principal  -comodule algebra if:
-comodule algebra if:- (a)
is a Hopf–Galois extension;
- (b) the multiplication map
,
, splits as a left
-module and right
-comodule map (the equivariant projectivity condition).
 is the Hopf algebra associated to a
is the Hopf algebra associated to a  -algebra of functions on a quantum group [10], then the existence of the Haar measure together with the results of [8] mean that condition (a) in Definition 2.15 implies condition (b) (i.e., the freeness of the coaction implies its principality).
-algebra of functions on a quantum group [10], then the existence of the Haar measure together with the results of [8] mean that condition (a) in Definition 2.15 implies condition (b) (i.e., the freeness of the coaction implies its principality). -comodule algebra
-comodule algebra  with coaction
with coaction 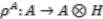 is principal if and only if it admits a strong connection form, that is if there exists a map
is principal if and only if it admits a strong connection form, that is if there exists a map 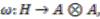 such that
such that



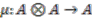 denotes the multiplication map,
denotes the multiplication map, 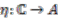 is the unit map,
is the unit map, 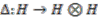 is the comultiplication,
is the comultiplication, 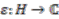 counit and
counit and 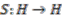 the (bijective) antipode of the Hopf algebra
the (bijective) antipode of the Hopf algebra  , and
, and 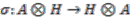 is the flip.
is the flip. 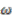 exists, then the inverse of the canonical map
exists, then the inverse of the canonical map  (see Definition 2.14 ) is the composite
(see Definition 2.14 ) is the composite 

 is a principal comodule algebra, then
is a principal comodule algebra, then 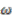 is the composite
is the composite 
 is the left
is the left 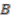 -linear right
-linear right  -colinear splitting of the multiplication
-colinear splitting of the multiplication 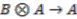 .
.  be a right
be a right  -comodule algebra. The space of
-comodule algebra. The space of 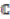 -linear maps
-linear maps 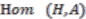 is an algebra with the convolution product
is an algebra with the convolution product
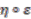 .
. 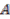 is said to be cleft if there exists a right
is said to be cleft if there exists a right 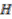 -colinear map
-colinear map 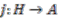 that has an inverse in the convolution algebra
that has an inverse in the convolution algebra 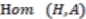 and is normalised so that
and is normalised so that 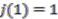 . Writing
. Writing 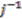 for the convolution inverse of
for the convolution inverse of 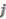 , one easily observes that
, one easily observes that 
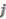 is called a cleaving map or a normalised total integral.
is called a cleaving map or a normalised total integral.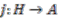 is an
is an 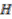 -colinear algebra map, then it is automatically convolution invertible (as
-colinear algebra map, then it is automatically convolution invertible (as 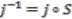 ) and normalised. A comodule algebra
) and normalised. A comodule algebra 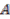 admitting such a map is termed a trivial principal comodule algebra.
admitting such a map is termed a trivial principal comodule algebra. 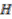 be a Hopf algebra of the compact quantum group. By the Woronowicz theorem [10],
be a Hopf algebra of the compact quantum group. By the Woronowicz theorem [10], 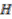 admits an invariant Haar measure, i.e., a linear map
admits an invariant Haar measure, i.e., a linear map 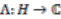 such that, for all
such that, for all 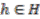 ,
, 
 is the Sweedler notation for the comultiplication. Next, assume that the lifted canonical map:
is the Sweedler notation for the comultiplication. Next, assume that the lifted canonical map: 

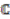 -linear map such that
-linear map such that 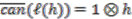 , for all
, for all  . Then, by the Schneider theorem [8],
. Then, by the Schneider theorem [8], 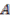 is a principal
is a principal 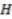 -comodule algebra. Explicitly, a strong connection form is
-comodule algebra. Explicitly, a strong connection form is 
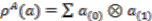 ; see [13].
; see [13]. 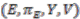 associated to a principal
associated to a principal 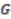 -bundle
-bundle 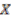 . Since
. Since 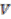 is a vector representation space of
is a vector representation space of 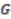 , also the set
, also the set 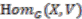 is a vector space. Consequently
is a vector space. Consequently 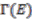 is a vector space. Furthermore,
is a vector space. Furthermore,  is a left module of
is a left module of  with the action
with the action  To understand better the way in which
To understand better the way in which  -module
-module 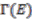 is associated to the principal comodule algebra
is associated to the principal comodule algebra 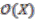 we recall the notion of the cotensor product.
we recall the notion of the cotensor product.  , right
, right  -comodule
-comodule 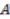 with coaction
with coaction  and left
and left  -comodule
-comodule 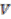 with coaction
with coaction 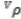 , the cotensor product is defined as an equaliser:
, the cotensor product is defined as an equaliser: 
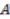 is an
is an  -comodule algebra, and
-comodule algebra, and 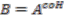 , the
, the 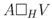 is a left
is a left  -module with the action
-module with the action  In particular, in the case of a principal
In particular, in the case of a principal 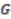 -bundle
-bundle 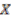 over
over 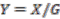 , for any left
, for any left 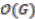 -comodule
-comodule 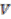 the cotensor product
the cotensor product  is a left
is a left 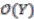 -module.
-module.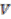 of a vector bundle
of a vector bundle 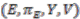 associated to a principal
associated to a principal 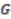 -bundle
-bundle  is finite dimensional. View
is finite dimensional. View 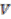 as a left comodule of
as a left comodule of 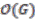 with the coaction
with the coaction 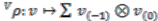 (summation implicit) determined by
(summation implicit) determined by 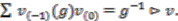 Then the left
Then the left 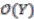 -module of sections
-module of sections 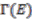 is isomorphic to the left
is isomorphic to the left 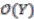 -module
-module  .
. 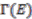 with
with 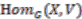 . Let
. Let 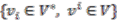 be a (finite) dual basis. Take
be a (finite) dual basis. Take 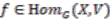 , and define
, and define 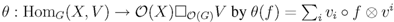 .
. 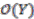 -module map
-module map 
 be a principal
be a principal  -comodule algebra. Set
-comodule algebra. Set 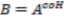 and let
and let 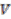 be a left
be a left  -comodule. The left
-comodule. The left 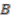 -module
-module 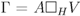 is called a module associated to the principal comodule algebra
is called a module associated to the principal comodule algebra  .
.  is a projective left
is a projective left 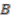 -module, and if
-module, and if 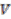 is a finite dimensional vector space, then
is a finite dimensional vector space, then  is a finitely generated projective left
is a finitely generated projective left 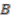 -module. In this case it has the meaning of a module of sections over a non-commutative vector bundle. Furthermore, its class gives an element in the
-module. In this case it has the meaning of a module of sections over a non-commutative vector bundle. Furthermore, its class gives an element in the 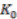 -group of
-group of 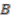 . If
. If  is a cleft principal comodule algebra, then every associated module is free, since
is a cleft principal comodule algebra, then every associated module is free, since  as a left
as a left 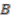 -module and right
-module and right  -comodule, so that
-comodule, so that 
3. Weighted Circle Actions on Prolonged Spheres.
3.1. Circle Actions and ![Axioms 01 00201 i314]() -Gradings.
-Gradings.
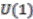 ,
, 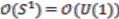 can be identified with the
can be identified with the  -algebra
-algebra 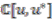 of Laurent polynomials in a unitary variable
of Laurent polynomials in a unitary variable 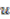 (unitary means
(unitary means 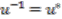 ). As a Hopf
). As a Hopf  -algebra
-algebra 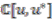 , is generated by the grouplike element
, is generated by the grouplike element 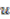 , i.e.,
, i.e.,
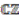 . As a consequence of this interpretation of
. As a consequence of this interpretation of 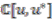 , an algebra
, an algebra  is a
is a 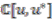 -comodule algebra if and only if
-comodule algebra if and only if  is a
is a 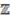 -graded algebra,
-graded algebra, 
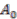 is the coinvariant subalgebra of
is the coinvariant subalgebra of  . Since
. Since 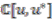 is spanned by grouplike elements, any convolution invertible map
is spanned by grouplike elements, any convolution invertible map 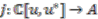 must assign a unit (invertible element) of
must assign a unit (invertible element) of  to
to 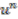 . Furthermore, colinear maps are simply the
. Furthermore, colinear maps are simply the 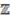 -degree preserving maps, where
-degree preserving maps, where 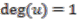 . Put together, convolution invertible colinear maps
. Put together, convolution invertible colinear maps 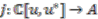 are in one-to-one correspondence with sequences
are in one-to-one correspondence with sequences 
3.2. The ![Axioms 01 00201 i331]() and
and ![Axioms 01 00201 i332]() Coordinate Algebras
Coordinate Algebras
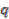 be a real number,
be a real number, 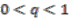 . The coordinate algebra
. The coordinate algebra  of the even-dimensional quantum sphere is the unital complex
of the even-dimensional quantum sphere is the unital complex 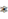 -algebra with generators
-algebra with generators 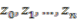 , subject to the following relations:
, subject to the following relations: 

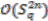 is a
is a 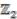 -graded algebra with
-graded algebra with 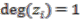 and so is
and so is 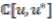 (with
(with  ). In other words,
). In other words, 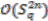 is a right
is a right 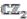 -comodule algebra and
-comodule algebra and 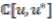 is a left
is a left 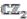 -comodule algebra, hence one can consider the cotensor product algebra
-comodule algebra, hence one can consider the cotensor product algebra  . It was shown in [2] that, as a unital
. It was shown in [2] that, as a unital 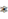 -algebra,
-algebra,  has generators
has generators 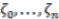 and a central unitary
and a central unitary  which are related in the following way:
which are related in the following way: 

 pairwise coprime numbers
pairwise coprime numbers 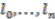 one can define the coaction of the Hopf algebra
one can define the coaction of the Hopf algebra 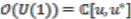 on
on 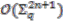 as
as 
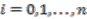 . This coaction is then extended to the whole of
. This coaction is then extended to the whole of 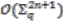 so that
so that 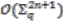 is a right
is a right 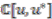 -comodule algebra.
-comodule algebra.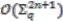 containing all coinvariant elements, i.e.,
containing all coinvariant elements, i.e., 
3.3. The 2D Quantum Real Projective Space ![Axioms 01 00201 i365]()
 which is generated by
which is generated by 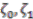 and central unitary
and central unitary 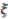 such that
such that 

 is
is 
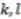 of coprime positive integers, the coaction
of coprime positive integers, the coaction 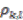 is given on generators by
is given on generators by 
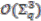 so that the coaction is a
so that the coaction is a  -algebra map. We denote the comodule algebra
-algebra map. We denote the comodule algebra 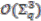 with coaction
with coaction 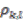 by
by 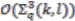 .
.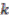 but instead whether
but instead whether 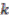 is either even or odd, and hence only cases
is either even or odd, and hence only cases 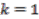 and
and 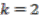 need to be considered [3]. We describe these cases presently.
need to be considered [3]. We describe these cases presently.3.3.1. The Odd or Negative Case
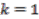 ,
,  is a polynomial
is a polynomial  -algebra generated by
-algebra generated by  ,
, 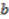 ,
,  which satisfy the relations:
which satisfy the relations: 



 into
into  or the isomorphism of
or the isomorphism of  with the coinvariants of
with the coinvariants of  is provided by
is provided by 
 has the following irreducible
has the following irreducible  -representations. There is a family of one-dimensional representations labelled by
-representations. There is a family of one-dimensional representations labelled by 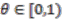 and given by
and given by 
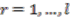 , and given by
, and given by 

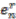 ,
, 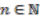 , is an orthonormal basis for the representation space
, is an orthonormal basis for the representation space 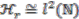 .
.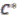 -algebra of continuous functions on
-algebra of continuous functions on 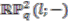 , obtained as the completion of these bounded representations, can be identified with the pullback of
, obtained as the completion of these bounded representations, can be identified with the pullback of 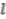 -copies of the quantum real projective plane
-copies of the quantum real projective plane 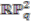 introduced in [14].
introduced in [14].3.3.2. The Even or Positive Case
 and hence
and hence 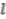 odd,
odd, 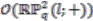 is a polynomial
is a polynomial 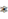 -algebra generated by
-algebra generated by 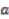 ,
, 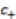 which satisfy the relations:
which satisfy the relations: 

 into
into  or the isomorphism of
or the isomorphism of  with the coinvariants of
with the coinvariants of 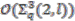 is provided by
is provided by 
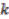 case, there is a family of one-dimensional representations of
case, there is a family of one-dimensional representations of  labelled by
labelled by  and given by
and given by 
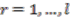 , and given by
, and given by 
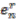 ,
, 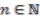 is an orthonormal basis for the representation space
is an orthonormal basis for the representation space  .
.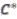 -algebra
-algebra  of continuous functions on
of continuous functions on 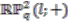 , obtained as the completion of these bounded representations, can be identified with the pullback of
, obtained as the completion of these bounded representations, can be identified with the pullback of 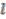 -copies of the quantum disk
-copies of the quantum disk  introduced in [15]. Furthermore,
introduced in [15]. Furthermore, 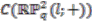 can also be understood as the quantum double suspension of
can also be understood as the quantum double suspension of 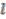 points in the sense of [16, Definition 6.1].
points in the sense of [16, Definition 6.1].4. Quantum Real Weighted Projective Spaces and Quantum Principal Bundles
 and fibre structures given by the circle Hopf algebra
and fibre structures given by the circle Hopf algebra 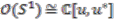 . The question arises as to which quantum space (i.e., a
. The question arises as to which quantum space (i.e., a 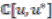 -comodule algebra with coinvariants isomorphic to
-comodule algebra with coinvariants isomorphic to  ) we should consider as the total space within this construction. We look first at the coactions of
) we should consider as the total space within this construction. We look first at the coactions of 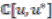 on
on  that define
that define  , i.e., at the comodule algebras
, i.e., at the comodule algebras 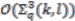 .
. 4.1. The (Non-)Principality of ![Axioms 01 00201 i439]()
 is a principal comodule algebra if and only if
is a principal comodule algebra if and only if 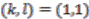 .
.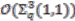 is a prolongation of the
is a prolongation of the 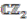 -comodule algebra
-comodule algebra 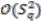 . The latter is a principal comodule algebra (over the quantum real projective plane
. The latter is a principal comodule algebra (over the quantum real projective plane  [14]) and since a prolongation of a principal comodule algebra is a principal comodule algebra [8, Remark 3.11], the coaction
[14]) and since a prolongation of a principal comodule algebra is a principal comodule algebra [8, Remark 3.11], the coaction 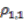 is principal as stated.
is principal as stated. , i.e., it cannot be surjective since we know
, i.e., it cannot be surjective since we know  is in the codomain. We begin by identifying a basis for the algebra
is in the codomain. We begin by identifying a basis for the algebra 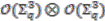 ; observing the relations in Equations (6a) and (6b) it is clear that a basis for
; observing the relations in Equations (6a) and (6b) it is clear that a basis for 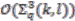 is given by elements of the form
is given by elements of the form 

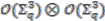 is given by elements of the form
is given by elements of the form 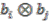 , where
, where  . Applying the canonial map gives
. Applying the canonial map gives 
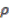 means
means 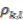 for simplicity of notation. The next stage is to construct all possible elements in
for simplicity of notation. The next stage is to construct all possible elements in  which map to
which map to  . To obtain the identity in the first leg we must use one of the following relations:
. To obtain the identity in the first leg we must use one of the following relations: 


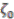 and
and 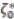 to be equal. We now construct all possible elements of the domain which map to
to be equal. We now construct all possible elements of the domain which map to  after applying the canonical map.
after applying the canonical map.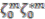 (
(  ); this can be done in fours ways. First, using
); this can be done in fours ways. First, using  ,
, 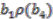 ,
, 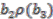 and
and 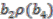 . Now,
. Now, 

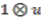 cannot be obtained as an element of the image of the canonical map in this case.
cannot be obtained as an element of the image of the canonical map in this case. (
( 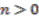 ); this can be done in four ways
); this can be done in four ways  ,
, 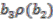 ,
, 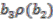 and
and 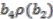 . Now,
. Now, 

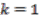 is not a problem provided
is not a problem provided  is not equal to
is not equal to  . This is reviewed at the next stage of the proof. The same conclusion is reached in all four cases.
. This is reviewed at the next stage of the proof. The same conclusion is reached in all four cases.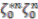 appears only when
appears only when 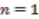 , in which case the relation simplifies to
, in which case the relation simplifies to  , so the next stage involves constructing elements in the domain which map to
, so the next stage involves constructing elements in the domain which map to 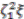 . There are eight possibilities altogether to be checked:
. There are eight possibilities altogether to be checked:  ,
, 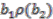 ,
, 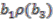 ,
, 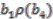 ,
,  ,
, 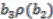 ,
, 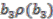 and
and  . The first case gives:
. The first case gives: 

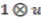 cannot be obtained as an element in the image in this case. Similar calculations for the remaining possibilities show that either
cannot be obtained as an element in the image in this case. Similar calculations for the remaining possibilities show that either 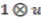 is not in the image of the canonical map, or that if
is not in the image of the canonical map, or that if 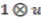 is in the image then
is in the image then  .
.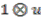 , using the third relation, could be in the image of the canonical map. All possible elements in the domain which could potentially map to this element are constructed and investigated. There are eight possibilities:
, using the third relation, could be in the image of the canonical map. All possible elements in the domain which could potentially map to this element are constructed and investigated. There are eight possibilities: 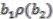 ,
, 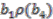 ,
, 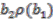 ,
, 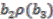 ,
, 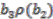 ,
, 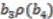 ,
,  and
and  . The first possibility comes out as
. The first possibility comes out as 

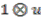 , which is contained in
, which is contained in  , is not in the image of the canonical map, proving that this map is not surjective and ultimately not an isomorphism when
, is not in the image of the canonical map, proving that this map is not surjective and ultimately not an isomorphism when 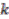 and
and 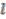 are both not simultaneously equal to
are both not simultaneously equal to  , completing the proof that
, completing the proof that 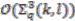 is not a principal comodule algebra in this case.
is not a principal comodule algebra in this case. 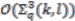 as our total space, then we are forced to put
as our total space, then we are forced to put 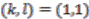 to ensure that the required Hopf–Galois condition does not fail. A consequence of this would be the generators
to ensure that the required Hopf–Galois condition does not fail. A consequence of this would be the generators 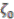 and
and 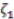 would have
would have 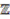 -degree
-degree 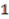 . This suggests that the comodule algebra
. This suggests that the comodule algebra 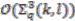 is too restrictive as there is no freedom with the weights
is too restrictive as there is no freedom with the weights 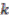 or
or 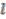 , and that we should in fact consider a subalgebra of
, and that we should in fact consider a subalgebra of  which admits a
which admits a  -coaction that would offer some choice. Theorem 4.1 indicates that the desired subalgebra should have generators with grades
-coaction that would offer some choice. Theorem 4.1 indicates that the desired subalgebra should have generators with grades 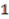 to ensure the Hopf–Galois condition is satisfied. This process is similar to that followed in [4], where the bundles over the quantum teardrops
to ensure the Hopf–Galois condition is satisfied. This process is similar to that followed in [4], where the bundles over the quantum teardrops 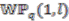 have the total spaces provided by the quantum lens spaces and structure groups provided by the circle group
have the total spaces provided by the quantum lens spaces and structure groups provided by the circle group 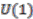 . We follow a similar approach in the sense that we view
. We follow a similar approach in the sense that we view 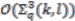 as a right
as a right  -comodule algebra, where
-comodule algebra, where  is the Hopf algebra of a suitable cyclic group.
is the Hopf algebra of a suitable cyclic group. 4.2. The Negative Case ![Axioms 01 00201 i523]()
4.2.1. The Principal ![Axioms 01 00201 i524]() -Comodule Algebra over
-Comodule Algebra over ![Axioms 01 00201 i381]()
 -algebra
-algebra  which is generated by unitary grouplike element
which is generated by unitary grouplike element  and satisfies the relation
and satisfies the relation 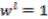 . The algebra
. The algebra  is a right
is a right 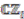 -comodule
-comodule  -algebra with coaction
-algebra with coaction 
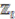 -degree of the generator
-degree of the generator 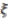 is determined by the degree of
is determined by the degree of 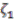 : the relation
: the relation 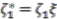 and that the coaction must be compatible with all relations imply that
and that the coaction must be compatible with all relations imply that 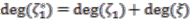 . Since
. Since 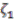 has degree zero,
has degree zero, 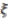 must also have degree zero.
must also have degree zero. given the coaction defined above.
given the coaction defined above. 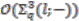 , generated by
, generated by 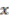 ,
, 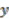 and
and  subject to the following relations
subject to the following relations 
 is central unitary. The embedding of
is central unitary. The embedding of 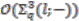 into
into  is given by
is given by  ,
, 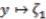 and
and 
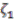 ,
, 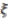 ,
, 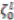 and
and  are coinvariant elements of
are coinvariant elements of  . Apply the coaction to the basis (7) to obtain
. Apply the coaction to the basis (7) to obtain 
 . Hence every coinvariant element is a polynomial in
. Hence every coinvariant element is a polynomial in 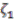 ,
, 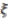 ,
, 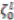 and
and  . Equations (20) are now easily derived from Equations (6) and (18).
. Equations (20) are now easily derived from Equations (6) and (18). 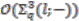 is a right
is a right  -comodule coalgebra with coaction defined as
-comodule coalgebra with coaction defined as 
 must be double the grade of
must be double the grade of 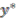 since
since 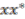 and
and 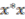 have degree zero, and so
have degree zero, and so 
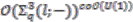 of invariant elements under the coaction
of invariant elements under the coaction  is isomorphic to the
is isomorphic to the  .
.  -subalgebra of
-subalgebra of 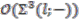 of elements which are invariant under the coaction is generated by
of elements which are invariant under the coaction is generated by  ,
,  and
and 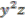 . The isomorphism of
. The isomorphism of 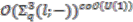 with
with 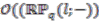 is then obtained by using the embedding of
is then obtained by using the embedding of 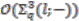 in
in  described in Proposition 4.2, i.e.,
described in Proposition 4.2, i.e., 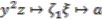 ,
, 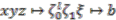 and
and 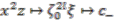 .
.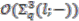 is spanned by elements of the type
is spanned by elements of the type 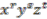 ,
,  , where
, where  and
and 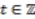 . Applying the coaction
. Applying the coaction 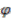 to these basis elements gives
to these basis elements gives 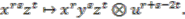 Hence
Hence 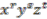 is
is 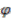 -invariant if and only if
-invariant if and only if 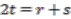 . If
. If 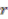 is even, then
is even, then 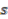 is even and
is even and 
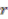 is odd, then so is
is odd, then so is 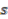 and
and 
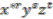 is dealt with similarly, thus proving that all coinvariants of
is dealt with similarly, thus proving that all coinvariants of 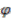 are polynomials in
are polynomials in 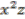 ,
, 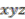 ,
, 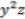 and their
and their 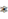 -conjugates.
-conjugates. 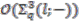 is a non-cleft principal
is a non-cleft principal 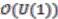 -comodule algebra over
-comodule algebra over 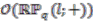 via the coaction
via the coaction 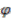 .
. 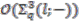 is a principal
is a principal 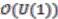 -comodule algebra over
-comodule algebra over 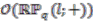 we employ Proposition 2.16 and construct a strong connection form as follows.
we employ Proposition 2.16 and construct a strong connection form as follows.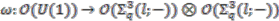 recursively as follows.
recursively as follows. 


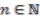 and, for all
and, for all 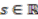 , the deformed or q-binomial coefficients
, the deformed or q-binomial coefficients  are defined by the following polynomial equality in indeterminate
are defined by the following polynomial equality in indeterminate 

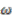 has been designed such that normalisation property, Equation (1a), is automatically satisfied. To check Equation (1b) for
has been designed such that normalisation property, Equation (1a), is automatically satisfied. To check Equation (1b) for 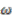 given by Equation (22b) and (22c) takes a bit more work. We use proof by induction, but first have to derive an identity to assist with the calculation. Set
given by Equation (22b) and (22c) takes a bit more work. We use proof by induction, but first have to derive an identity to assist with the calculation. Set 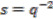 ,
, 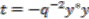 in Equation (23) to arrive at
in Equation (23) to arrive at 

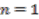 . By Equation (24)
. By Equation (24) 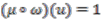 providing the basis. Next, we assume that the relation holds for
providing the basis. Next, we assume that the relation holds for 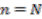 , that is
, that is 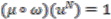 , and consider the case
, and consider the case  ,
, 

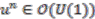 , where
, where 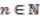 . To show this property holds for each
. To show this property holds for each 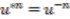 we adopt the same strategy; this is omitted from the proof as it does not provide further insight, instead repetition of similar arguments.
we adopt the same strategy; this is omitted from the proof as it does not provide further insight, instead repetition of similar arguments.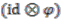 to
to  gives
gives 
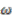 given by Equation (22b) when
given by Equation (22b) when 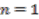 . We now assume the property holds for
. We now assume the property holds for  , hence
, hence 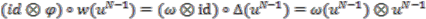 , and consider the case
, and consider the case 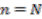 .
. 
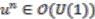 where
where 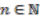 . The case for
. The case for 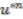 is proved in a similar manner, as is Equation (1d). Again, the details are omitted as the process is identical. This completes the proof that
is proved in a similar manner, as is Equation (1d). Again, the details are omitted as the process is identical. This completes the proof that 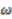 is a strong connection form, hence
is a strong connection form, hence 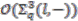 is a principal comodule algebra.
is a principal comodule algebra.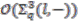 . Since
. Since 
 are scalar multiples of
are scalar multiples of 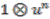 for
for 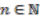 , we can conclude that the only invertible elements in
, we can conclude that the only invertible elements in 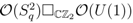 are the elements of the form
are the elements of the form 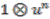 . These elements correspond to the elements
. These elements correspond to the elements 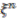 in
in  , which in turn correspond to
, which in turn correspond to 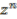 in
in  .
.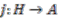 is the cleaving map; to ensure the map is convolution invertible we are forced to put
is the cleaving map; to ensure the map is convolution invertible we are forced to put 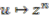 . Since
. Since 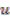 has degree
has degree  in
in 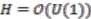 and
and  has degree
has degree 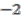 in
in  , the map
, the map 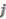 fails to preserve the degrees, hence it is not colinear. Therefore,
fails to preserve the degrees, hence it is not colinear. Therefore,  is a non-cleft principal comodule algebra.
is a non-cleft principal comodule algebra. 4.2.2. Almost Freeness of the Coaction ![Axioms 01 00201 i647]()
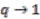 , the algebras
, the algebras  represent singular manifolds or orbifolds. It is known that every orbifold can be obtained as a quotient of a manifold by an almost free action. The latter means that the action has finite (rather than trivial as in the free case) stabiliser groups. As explained in Section 2, on the algebraic level, freeness is encoded in the bijectivity of the canonical map
represent singular manifolds or orbifolds. It is known that every orbifold can be obtained as a quotient of a manifold by an almost free action. The latter means that the action has finite (rather than trivial as in the free case) stabiliser groups. As explained in Section 2, on the algebraic level, freeness is encoded in the bijectivity of the canonical map  , or, more precisely, in the surjectivity of the lifted canonical map
, or, more precisely, in the surjectivity of the lifted canonical map 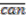 (Equation (2)). The surjectivity of
(Equation (2)). The surjectivity of 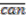 means the triviality of the cokernel of
means the triviality of the cokernel of 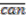 , thus the size of the cokernel of
, thus the size of the cokernel of 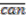 can be treated as a measure of the size of the stabiliser groups. This leads to the following notion proposed in [4].
can be treated as a measure of the size of the stabiliser groups. This leads to the following notion proposed in [4].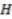 be a Hopf algebra and let
be a Hopf algebra and let 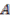 be a right
be a right 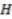 -comodule algebra with coaction
-comodule algebra with coaction 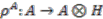 . We say that the coaction is almost free if the cokernel of the (lifted) canonical map
. We say that the coaction is almost free if the cokernel of the (lifted) canonical map 
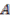 -module.
-module. 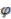 defined in the preceding section is free, at the classical limit
defined in the preceding section is free, at the classical limit 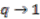
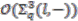 represents a singular manifold or an orbifold. On the other hand, at the same limit,
represents a singular manifold or an orbifold. On the other hand, at the same limit,  corresponds to a genuine manifold, one of the Seifert three-dimensional non-orientable manifolds; see [17]. It is therefore natural to ask, whether the coaction
corresponds to a genuine manifold, one of the Seifert three-dimensional non-orientable manifolds; see [17]. It is therefore natural to ask, whether the coaction  of
of 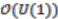 on
on  which has
which has 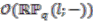 as fixed points is almost free in the sense of Definition 4.5.
as fixed points is almost free in the sense of Definition 4.5. is almost free.
is almost free. 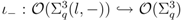 , the
, the  -algebra embedding described in Proposition 4.2. One easily checks that the following diagram
-algebra embedding described in Proposition 4.2. One easily checks that the following diagram 
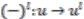 , is commutative. The principality or freeness of
, is commutative. The principality or freeness of 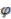 proven in Theorem 4.4 implies that
proven in Theorem 4.4 implies that 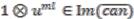 ,
, 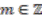 , where
, where 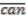 is the (lifted) canonical map corresponding to coaction
is the (lifted) canonical map corresponding to coaction  . This means that
. This means that 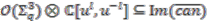 . Therefore, there is a short exact sequence of left
. Therefore, there is a short exact sequence of left  -modules
-modules 
 -module
-module 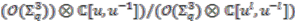 is finitely generated, hence so is
is finitely generated, hence so is 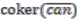 .
. 4.2.3. Associated Modules or Sections of Line Bundles
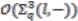 following the procedure outlined at the end of Section 2.2; see Definition 2.21.
following the procedure outlined at the end of Section 2.2; see Definition 2.21.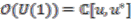 is determined by the grading of a basis element of
is determined by the grading of a basis element of  , say
, say  . More precisely, for any integer
. More precisely, for any integer  ,
,  is a left
is a left  -comodule with the coaction
-comodule with the coaction 
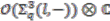 with
with 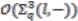 we thus obtain, for each coaction
we thus obtain, for each coaction 

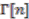 consists of all elements of
consists of all elements of 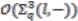 of
of 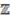 -degree
-degree  . In particular
. In particular 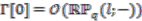 . Each of the
. Each of the 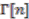 is a finitely generated projective left
is a finitely generated projective left 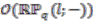 -module, i.e., it represents the module of sections of the non-commutative line bundle over
-module, i.e., it represents the module of sections of the non-commutative line bundle over 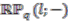 . The idempotent matrix
. The idempotent matrix 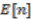 defining
defining 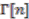 can be computed explicitly from a strong connection form
can be computed explicitly from a strong connection form 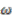 (see Equations (22) in the proof of Theorem 4.4) following the procedure described in [11]. Write
(see Equations (22) in the proof of Theorem 4.4) following the procedure described in [11]. Write 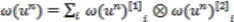 . Then
. Then 
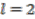 and
and 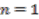 , using Equations (22b) and (22a) as well as redistributing numerical coefficients we obtain
, using Equations (22b) and (22a) as well as redistributing numerical coefficients we obtain 
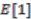 is not hermitian, the left-upper
is not hermitian, the left-upper 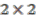 block is hermitian. On the other hand, once
block is hermitian. On the other hand, once 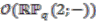 is completed to the
is completed to the  -algebra
-algebra 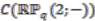 of continuous functions on
of continuous functions on 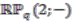 (and then identified with the suitable pullback of two algebras of continuous functions over the quantum real projective space; see [3]), then a hermitian projector can be produced out of
(and then identified with the suitable pullback of two algebras of continuous functions over the quantum real projective space; see [3]), then a hermitian projector can be produced out of 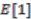 by using the Kaplansky formula; see [18, page 88].
by using the Kaplansky formula; see [18, page 88].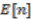 make up a cycle in the cyclic complex of
make up a cycle in the cyclic complex of 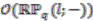 , whose corresponding class in the cyclic homology
, whose corresponding class in the cyclic homology 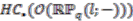 is known as the Chern character of
is known as the Chern character of 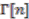 . Again, as an illustration of the usage of an explicit form of a strong connection form, we compute the traces of
. Again, as an illustration of the usage of an explicit form of a strong connection form, we compute the traces of 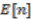 for general
for general 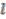 .
.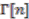 is the class of the polynomial
is the class of the polynomial 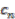 in generator
in generator  of
of 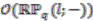 , given by the following recursive formula. First,
, given by the following recursive formula. First, 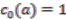 , and then, for all positive
, and then, for all positive  ,
, 

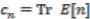 . By normalisation (22a) of the strong connection
. By normalisation (22a) of the strong connection 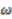 , obviously
, obviously  . In view of Equation (22b) we obtain the following recursive formula
. In view of Equation (22b) we obtain the following recursive formula 
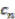 could be a polynomial in
could be a polynomial in 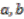 and
and 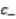 . However, the third of Equations (20) together with Equation (24) and identification of
. However, the third of Equations (20) together with Equation (24) and identification of 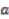 as
as 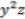 yield
yield 
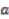 only. As commuting
only. As commuting 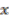 and
and 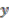 through a polynomial in
through a polynomial in 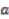 in Equation (28) will produce a polynomial in
in Equation (28) will produce a polynomial in 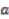 again, we conclude that each of the
again, we conclude that each of the 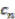 is a polynomial in
is a polynomial in 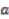 . The second of Equations (20), the centrality of
. The second of Equations (20), the centrality of  and the identification of
and the identification of 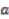 as
as 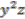 imply that
imply that 
4.3. The Positive Case ![Axioms 01 00201 i717]()
4.3.1. The Principal ![Axioms 01 00201 i585]() -Comodule Algebra over
-Comodule Algebra over ![Axioms 01 00201 i417]()
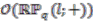 , and proceed by viewing
, and proceed by viewing  as a right
as a right 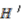 -comodule algebra, where
-comodule algebra, where 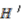 is a Hopf-algebra of a finite cyclic group. The aim is to construct the total space
is a Hopf-algebra of a finite cyclic group. The aim is to construct the total space 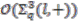 of the bundle over
of the bundle over 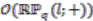 as the coinvariant subalgebra of
as the coinvariant subalgebra of  .
. 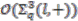 must contain generators
must contain generators 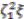 and
and 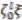 of
of 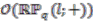 . Suppose
. Suppose 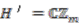 and
and 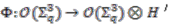 is a coaction. We require
is a coaction. We require  to be compatible with the algebraic relations and to give zero
to be compatible with the algebraic relations and to give zero 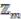 -degree to
-degree to 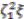 and
and 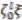 are zero. These requirements yield
are zero. These requirements yield 
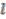 is odd, the simplest solution to these requirements is provided by
is odd, the simplest solution to these requirements is provided by  ,
, 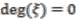 ,
, 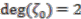 ,
,  . This yields the coaction
. This yields the coaction 
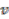 (
(  ) is the unitary generator of
) is the unitary generator of 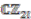 .
.  is extended to the whole of
is extended to the whole of  so that
so that  is an algebra map, making
is an algebra map, making  a right
a right 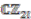 -comodule algebra.
-comodule algebra. is isomorphic to the
is isomorphic to the  -algebra
-algebra 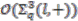 generated by
generated by 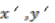 and central unitary
and central unitary  subject to the following relations:
subject to the following relations: 

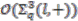 and the coinvariant subalgebra of
and the coinvariant subalgebra of  is given by
is given by  ,
,  and
and 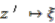 .
. 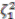 ,
, 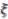 ,
,  and
and 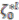 are coinvariant elements of
are coinvariant elements of  . Apply the coaction
. Apply the coaction  to the basis (7) to obtain
to the basis (7) to obtain 
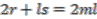 in the first case or
in the first case or 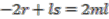 in the second. Since
in the second. Since 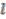 is odd,
is odd,  must be even and then
must be even and then  , hence the invariant elements must be of the form
, hence the invariant elements must be of the form 
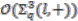 is a right
is a right  -comodule with coaction defined as,
-comodule with coaction defined as, 
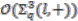 , however the second relation in Equations (30a) tells us that the grade of
, however the second relation in Equations (30a) tells us that the grade of 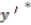 must be the same as that of
must be the same as that of  since,
since, 

 and
and 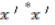 , have degree zero, as do the right had sides,
, have degree zero, as do the right had sides, 
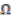 is defined setting the grades of
is defined setting the grades of 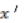 and
and  as 1, and putting the grade of
as 1, and putting the grade of  as
as 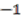 to ensure the coaction is compatible with the relations of the algebra
to ensure the coaction is compatible with the relations of the algebra 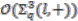 .
. -comodule algebra
-comodule algebra 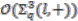 has
has 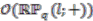 as its subalgebra of coinvariant elements under the coaction
as its subalgebra of coinvariant elements under the coaction 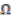 .
. 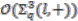 under the coaction
under the coaction 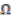 are found using the same method as in the odd
are found using the same method as in the odd 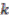 case. A basis for the algebra
case. A basis for the algebra 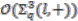 is given by
is given by  ,
,  , where
, where 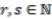 and
and 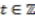 .
.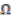 to the first of these basis elements gives,
to the first of these basis elements gives, 
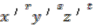 is equivalent to
is equivalent to 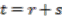 . Simple substitution and re-arranging gives,
. Simple substitution and re-arranging gives, 
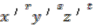 is a polynomial in
is a polynomial in 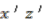 and
and 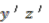 . Repeating the process for the second type of basis element gives the
. Repeating the process for the second type of basis element gives the 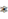 -conjugates of
-conjugates of 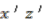 and
and 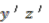 . Using Proposition 4.8 we can see that
. Using Proposition 4.8 we can see that 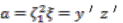 and
and 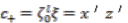 .
. 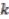 case, although
case, although 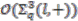 is a principal comodule algebra it yields trivial principal bundle over
is a principal comodule algebra it yields trivial principal bundle over 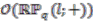 .
.  -comodule algebra
-comodule algebra 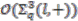 is trivial.
is trivial. 
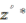 is central unitary in
is central unitary in 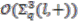 , hence must be convolution invertible. Also,
, hence must be convolution invertible. Also, 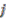 is a right
is a right 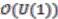 -comodule map since,
-comodule map since, 
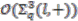 is a trivial principal comodule algebra, all associated
is a trivial principal comodule algebra, all associated  -modules are free.
-modules are free. 4.3.2. Almost Freeness of the Coaction ![Axioms 01 00201 i793]()
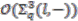 , the principality of
, the principality of 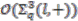 can be used to determine that the
can be used to determine that the 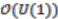 -coaction
-coaction  on
on  that defines
that defines 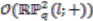 is almost free.
is almost free. is almost free.
is almost free. 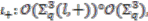 the
the  -algebra embedding described in Proposition 4.8. One easily checks that the following diagram
-algebra embedding described in Proposition 4.8. One easily checks that the following diagram 
 is commutative. By the arguments analogous to those in the proof of Proposition 4.6 one concludes that there is a short exact sequence of left
is commutative. By the arguments analogous to those in the proof of Proposition 4.6 one concludes that there is a short exact sequence of left  -modules
-modules 
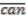 is the lifted canonical map corresponding to coaction
is the lifted canonical map corresponding to coaction  . The left
. The left  -module
-module 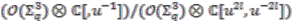 is finitely generated, hence so is
is finitely generated, hence so is 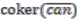 .
. 5. Conclusions
 -coactions on the coordinate algebra of the quantum Seifert manifold
-coactions on the coordinate algebra of the quantum Seifert manifold  weighted by coprime integers
weighted by coprime integers 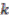 and
and 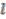 . We concluded that the coaction is principal if and only if
. We concluded that the coaction is principal if and only if 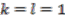 , which corresponds to the case of a
, which corresponds to the case of a 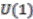 -bundle over the quantum real projective plane. In all other cases the coactions are almost free. We identified subalgebras of
-bundle over the quantum real projective plane. In all other cases the coactions are almost free. We identified subalgebras of 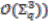 which admit principal
which admit principal  -coactions, whose invariants are isomorphic to coordinate algebras
-coactions, whose invariants are isomorphic to coordinate algebras 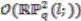 of quantum real weighted projective spaces. The structure of these subalgebras depends on the parity of
of quantum real weighted projective spaces. The structure of these subalgebras depends on the parity of 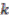 . For the odd
. For the odd 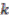 case, the constructed principal comodule algebra
case, the constructed principal comodule algebra 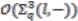 is non-trivial, while for the even case, the corresponding principal comodule algebra
is non-trivial, while for the even case, the corresponding principal comodule algebra 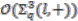 turns out to be trivial. The triviality of
turns out to be trivial. The triviality of 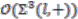 is a disappointment. Whether a different nontrivial principal
is a disappointment. Whether a different nontrivial principal  -comodule algebra over
-comodule algebra over  can be constructed or whether such a possibility is ruled out by deeper geometric, topological or algebraic reasons remains to be seen.
can be constructed or whether such a possibility is ruled out by deeper geometric, topological or algebraic reasons remains to be seen. References
- Soibel’man, Y.S.; Vaksman, L.L. Algebra of functions on the quantum group SU(n + 1), and odd-dimensional quantum spheres. Algebra i Analiz 1990, 2, 101–120. [Google Scholar]
- Brzeziński, T.; Zieliński, B. Quantum principal bundles over quantum real projective spaces. J. Geom. Phys. 2012, 62, 1097–1107. [Google Scholar] [CrossRef]
- Brzeziński, T. Circle actions on a quantum Seifert manifold. In Proceedings of the Corfu Summer Institute 2011 School and Workshops on Elementary Particle Physics and Gravity, Corfu, Greece, 4-18 September 2011.
- Brzeziński, T.; Fairfax, S.A. Quantum teardrops. Comm. Math. Phys. in press.
- Beggs, E.J.; Brzeziński, T. Line bundles and the Thom construction in noncommutative geometry. J. Noncommut. Geom. in press.
- Baum, P.F.; Hajac, P.M.; Matthes, R.; Szymański, W. Noncommutative geometry approach to principal and associated bundles. 2007,arXiv:math/0701033. Available online: http://arxiv.org/abs/math/0701033 (accessed on 10 September 2012).
- Brzeziński, T.; Majid, S. Quantum group gauge theory on quantum spaces. Comm. Math. Phys. 1993, 157, 591–638. [Google Scholar] [CrossRef]
- Schneider, H.-J. Principal homogeneous spaces for arbitrary Hopf algebras. Israel J. Math. 1990, 72, 167–195. [Google Scholar] [CrossRef]
- Hajac, P.M. Strong connections on quantum principal bundles. Comm. Math. Phys. 1996, 182, 579–617. [Google Scholar] [CrossRef]
- Woronowicz, S.L. Compact matrix pseudogroups. Comm. Math. Phys. 1987, 111, 613–665. [Google Scholar] [CrossRef]
- Brzeziński, T.; Hajac, P.M. The Chern-Galois character. Comptes Rendus Math. (Acad. Sci. Paris Ser. I) 2004, 338, 113–116. [Google Scholar]
- Dąbrowski, L.; Grosse, H.; Hajac, P.M. Strong connections and Chern-Connes pairing in the Hopf–Galois theory. Comm. Math. Phys. 2001, 220, 301–331. [Google Scholar] [CrossRef]
- Beggs, E.J.; Brzeziński, T. An explicit formula for a strong connection. Appl. Categor. Str. 2008, 16, 57–63. [Google Scholar] [CrossRef]
- Hajac, P.M.; Matthes, R.; Szymański, W. Quantum real projective space, disc and spheres. Algebr. Represent. Theory 2003, 6, 169–192. [Google Scholar] [CrossRef]
- Klimek, S.; Leśniewski, A. A two-parameter quantum deformation of the unit disc. J. Funct. Anal. 1993, 115, 1–23. [Google Scholar] [CrossRef]
- Hong, J.H.; Szymański, W. Quantum spheres and projective spaces as graph algebras. Comm. Math. Phys. 2002, 232, 157–188. [Google Scholar] [CrossRef]
- Scott, P. The geometries of 3-manifolds. Bull. Lond. Math. Soc. 1983, 15, 401–487. [Google Scholar] [CrossRef]
- Gracia-Bondia, J.M.; Várilly, J.C.; Figueroa, H. Elements of Noncommutative Geometry; Birkhäusäer: Boston, MA, USA, 2001. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Brzeziński, T.; Fairfax, S.A. Bundles over Quantum RealWeighted Projective Spaces. Axioms 2012, 1, 201-225. https://doi.org/10.3390/axioms1020201
Brzeziński T, Fairfax SA. Bundles over Quantum RealWeighted Projective Spaces. Axioms. 2012; 1(2):201-225. https://doi.org/10.3390/axioms1020201
Chicago/Turabian StyleBrzeziński, Tomasz, and Simon A. Fairfax. 2012. "Bundles over Quantum RealWeighted Projective Spaces" Axioms 1, no. 2: 201-225. https://doi.org/10.3390/axioms1020201
APA StyleBrzeziński, T., & Fairfax, S. A. (2012). Bundles over Quantum RealWeighted Projective Spaces. Axioms, 1(2), 201-225. https://doi.org/10.3390/axioms1020201