Abstract
Using the most elementary methods and considerations, the solution of the star-triangle condition  is shown to be a necessary condition for the extension of the operator coalgebra of the six-vertex model to a bialgebra. A portion of the bialgebra acts as a spectrum-generating algebra for the algebraic Bethe ansatz, with which higher-dimensional representations of the bialgebra can be constructed. The star-triangle relation is proved to be necessary for the commutativity of the transfer matrices T(a, b, c) and T(a', b', c').
is shown to be a necessary condition for the extension of the operator coalgebra of the six-vertex model to a bialgebra. A portion of the bialgebra acts as a spectrum-generating algebra for the algebraic Bethe ansatz, with which higher-dimensional representations of the bialgebra can be constructed. The star-triangle relation is proved to be necessary for the commutativity of the transfer matrices T(a, b, c) and T(a', b', c').
 is shown to be a necessary condition for the extension of the operator coalgebra of the six-vertex model to a bialgebra. A portion of the bialgebra acts as a spectrum-generating algebra for the algebraic Bethe ansatz, with which higher-dimensional representations of the bialgebra can be constructed. The star-triangle relation is proved to be necessary for the commutativity of the transfer matrices T(a, b, c) and T(a', b', c').
is shown to be a necessary condition for the extension of the operator coalgebra of the six-vertex model to a bialgebra. A portion of the bialgebra acts as a spectrum-generating algebra for the algebraic Bethe ansatz, with which higher-dimensional representations of the bialgebra can be constructed. The star-triangle relation is proved to be necessary for the commutativity of the transfer matrices T(a, b, c) and T(a', b', c').1. Introduction
In two-dimensional lattice vertex models in which the state of a lattice point is specified by the states of the four links to its neighboring points, the matrix M of local Boltzmann weights can be used to construct the row-to-row transfer matrix by a matrix coproduct operation. In the six-vertex model a link between two lattice points has only two states, call them 0, 1 or ↑, ↓ subject to the “ice-rule” (two arrows point into a vertex, two point out). The matrix M of local Boltzmann weights for the six-vertex model has two types of indices, “vertical” and “horizontal” [1],
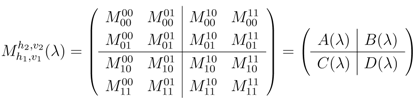
in which
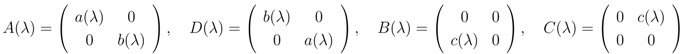
have only vertical indices (for example 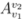 ). All four matrices A, B, C, D typically depend on a set of parameters λ. The matrix C has a non-zero kernel
). All four matrices A, B, C, D typically depend on a set of parameters λ. The matrix C has a non-zero kernel  which is not annihilated by B, and A and D are invertible. This will be a principal ingredient of the solution of the model by the Bethe ansatz.
which is not annihilated by B, and A and D are invertible. This will be a principal ingredient of the solution of the model by the Bethe ansatz.
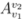 ). All four matrices A, B, C, D typically depend on a set of parameters λ. The matrix C has a non-zero kernel
). All four matrices A, B, C, D typically depend on a set of parameters λ. The matrix C has a non-zero kernel 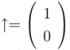 which is not annihilated by B, and A and D are invertible. This will be a principal ingredient of the solution of the model by the Bethe ansatz.
which is not annihilated by B, and A and D are invertible. This will be a principal ingredient of the solution of the model by the Bethe ansatz.The matrix coproduct is a mapping Δ : 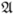 →
→ 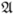 ×
× 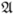 (a tensor product on vertical indices, a dot or matrix product on horizontal)
(a tensor product on vertical indices, a dot or matrix product on horizontal)
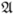 →
→ 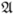 ×
× 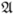 (a tensor product on vertical indices, a dot or matrix product on horizontal)
(a tensor product on vertical indices, a dot or matrix product on horizontal) 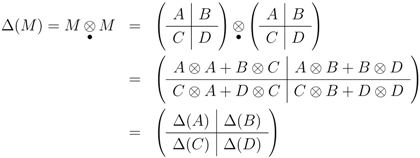
which in matrix index language would be
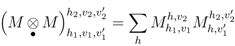
Because the ⊗• product is fundamentally a matrix product (which is associative), Δ is coassociative, so Δ and a compatible counit map ε (see for example [2,3]) define a coalgebra structure on the set 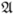 .
.
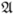 .
.If 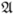 is an algebra and the coproduct and counit of the coalgebra structure on
is an algebra and the coproduct and counit of the coalgebra structure on 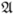 are compatible with the product and unit of the algebra (Δ and ε are algebra homomorphisms), then
are compatible with the product and unit of the algebra (Δ and ε are algebra homomorphisms), then 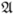 is a bialgebra (simultaneous coalgebra and algebra). The compatibility with the coalgebra structure is a very strong constraint on the algebraic product rules. The existence of an antipode map extends the bialgebra to a Hopf algebra [3].
is a bialgebra (simultaneous coalgebra and algebra). The compatibility with the coalgebra structure is a very strong constraint on the algebraic product rules. The existence of an antipode map extends the bialgebra to a Hopf algebra [3].
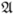 is an algebra and the coproduct and counit of the coalgebra structure on
is an algebra and the coproduct and counit of the coalgebra structure on 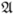 are compatible with the product and unit of the algebra (Δ and ε are algebra homomorphisms), then
are compatible with the product and unit of the algebra (Δ and ε are algebra homomorphisms), then 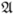 is a bialgebra (simultaneous coalgebra and algebra). The compatibility with the coalgebra structure is a very strong constraint on the algebraic product rules. The existence of an antipode map extends the bialgebra to a Hopf algebra [3].
is a bialgebra (simultaneous coalgebra and algebra). The compatibility with the coalgebra structure is a very strong constraint on the algebraic product rules. The existence of an antipode map extends the bialgebra to a Hopf algebra [3].For a lattice vertex model with n sites per row, we construct the L-matrix of Boltzmann weights whose horizontal components are higher dimensional representations of the elements  (λ),
(λ),  (λ),
(λ),  (λ), … of
(λ), … of 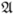
 (λ),
(λ),  (λ),
(λ),  (λ), … of
(λ), … of 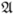
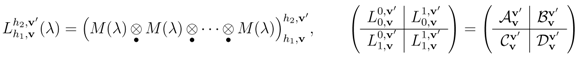
The transfer matrix for a lattice model with such a matrix M of Boltzmann weights is obtained from an iterated coproduct,
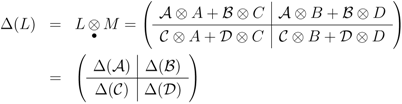
by summing over the last set of horizontal indices
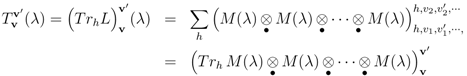
This is the trace of the L-matrix over its horizontal components
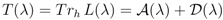
Define the complementary product in which the tensor is on the horizontal indices, and matrix product on the vertical (note that the horizontal space sub-matrices depend on different parameter sets, carefully compare with Equation 3)
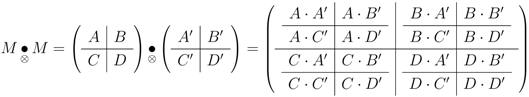
The matrices A, B, C, D and  ,
,  ,
,  and
and  are functions of the parameter-sets λ (un-primed depend on λ, primed are functions of λ'), which for the six-vertex model is a collection of three energies upon which a, b, c depend.
are functions of the parameter-sets λ (un-primed depend on λ, primed are functions of λ'), which for the six-vertex model is a collection of three energies upon which a, b, c depend.
 ,
,  ,
,  and
and  are functions of the parameter-sets λ (un-primed depend on λ, primed are functions of λ'), which for the six-vertex model is a collection of three energies upon which a, b, c depend.
are functions of the parameter-sets λ (un-primed depend on λ, primed are functions of λ'), which for the six-vertex model is a collection of three energies upon which a, b, c depend.For commutativity of the transfer matrix [T(λ), T(λ')] = 0, which makes the model integrable if a sufficiently large set of mutually commuting matrices can be found, it is sufficient that there exists an invertible matrix R such that [1]
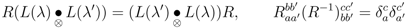
since if we write out the horizontal components
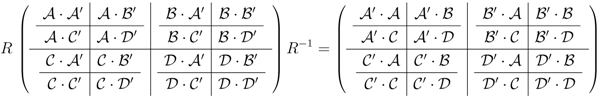
(explicitly using invertibility of R) and take traces we obtain the desired commutativity
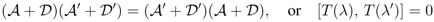
A sufficient condition that makes Equation 10 true is [1]
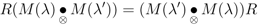
Equation 13 becomes the Yang–Baxter equation (with a spectral parameter) if R = M(μ) for some choice of parameter μ, and this is not possible if M is not invertible.
If Equation 13 is written out in detail for the six-vertex model, with λ = (a, b, c), λ' = (a', b', c') and μ= (a'', b'', c'') and μ is eliminated from the resulting system of cubic equations, one obtains a much simpler constraint under which Equation 12 is true, which is the solution of the star-triangle relation
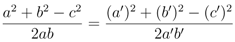
Suppose that one begins with a matrix M of local Boltzmann weights (possibly not invertible), which we think of as a low-dimensional representation of some operator coalgebra, and uses it to construct a transfer matrix for a lattice model by the matrix coproduct construction. Under what conditions can the coalgebra be extended to a bialgebra, or perhaps even a Hopf algebra?
The purpose of this paper is to show that Equation 14 is a necessary condition for the matrix coalgebra of the spectrum-generating operators  ,
,  ,
,  ,
,  with lowest dimensional representation given in Equation 2 (the six-vertex model) to extend to a bialgebra with matrix coproduct. A bialgebra need not be a Hopf algebra, and a Hopf algebra need not have an R-matrix. We show that, at least in the case of the six-vertex model, commuting transfer matrices are one of the bialgebra product relations. The star-triangle relation is therefore necessary for integrability. Whether or not the star-triangle equation is necessary for [T(λ), T(λ')] = 0 for any given model is still an open problem (see for example P. 418 of [4]), one which seems to have been abundantly acknowledged but largely unaddressed in the literature.
with lowest dimensional representation given in Equation 2 (the six-vertex model) to extend to a bialgebra with matrix coproduct. A bialgebra need not be a Hopf algebra, and a Hopf algebra need not have an R-matrix. We show that, at least in the case of the six-vertex model, commuting transfer matrices are one of the bialgebra product relations. The star-triangle relation is therefore necessary for integrability. Whether or not the star-triangle equation is necessary for [T(λ), T(λ')] = 0 for any given model is still an open problem (see for example P. 418 of [4]), one which seems to have been abundantly acknowledged but largely unaddressed in the literature.
 ,
,  ,
,  ,
,  with lowest dimensional representation given in Equation 2 (the six-vertex model) to extend to a bialgebra with matrix coproduct. A bialgebra need not be a Hopf algebra, and a Hopf algebra need not have an R-matrix. We show that, at least in the case of the six-vertex model, commuting transfer matrices are one of the bialgebra product relations. The star-triangle relation is therefore necessary for integrability. Whether or not the star-triangle equation is necessary for [T(λ), T(λ')] = 0 for any given model is still an open problem (see for example P. 418 of [4]), one which seems to have been abundantly acknowledged but largely unaddressed in the literature.
with lowest dimensional representation given in Equation 2 (the six-vertex model) to extend to a bialgebra with matrix coproduct. A bialgebra need not be a Hopf algebra, and a Hopf algebra need not have an R-matrix. We show that, at least in the case of the six-vertex model, commuting transfer matrices are one of the bialgebra product relations. The star-triangle relation is therefore necessary for integrability. Whether or not the star-triangle equation is necessary for [T(λ), T(λ')] = 0 for any given model is still an open problem (see for example P. 418 of [4]), one which seems to have been abundantly acknowledged but largely unaddressed in the literature.We will prove that Equation 14 is necessary for commutativity of the transfer matrices for the six-vertex model by constructing a complete closed set of quadratic operator products that annihilate the entire vector space basis of the physical states. The operator products are found by exploiting the recursive nature of the coalgebra, and the requirement that the coproduct be an algebra homomorphism. If these products annihilate the lowest dimensional (single-site) state space, the recursions guarantee that they annihilate the state space for the model with arbitrarily long rows. In other words these operators are identically zero in any physical representation. We refer to these products as quadratic “zero-operators” [5], since they evaluate to zero on the basis of physical states. These relations establish the unique bialgebra structure compatible with the matrix coalgebra, and the given lowest dimensional representation of the coalgebra, namely the M-matrix, and are the familiar algebraic relations used in the algebraic Bethe ansatz. The algebraic Bethe ansatz begins with establishing a “vacuum” state Ф0
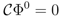
and from there building a collection of states
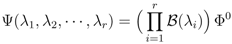
that are eigenvectors of the transfer matrix
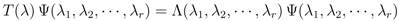
The set of parameters {λ1, λ2, …, λr} for which this can be done is determined by eliminating “unwanted” vectors using the zero-operator product rules.
For the eight-vertex model the  operator is non-singular, and one must perform local gauge transformations {
operator is non-singular, and one must perform local gauge transformations {  , …,
, …,  } → {
} → {  ', …,
', …,  '} so that
'} so that  ' has a zero-eigenvector in order to finish the program of quadrature by the algebraic Bethe ansatz [6]. For the simple dimer model, one can find two vacuum states (both
' has a zero-eigenvector in order to finish the program of quadrature by the algebraic Bethe ansatz [6]. For the simple dimer model, one can find two vacuum states (both  and
and  have kernels [7]) and modify the Bethe ansatz accordingly. It may be very difficult or impossible to select parameters that eliminate unwanted terms, but that is a separate issue.
have kernels [7]) and modify the Bethe ansatz accordingly. It may be very difficult or impossible to select parameters that eliminate unwanted terms, but that is a separate issue.
 operator is non-singular, and one must perform local gauge transformations {
operator is non-singular, and one must perform local gauge transformations {  , …,
, …,  } → {
} → {  ', …,
', …,  '} so that
'} so that  ' has a zero-eigenvector in order to finish the program of quadrature by the algebraic Bethe ansatz [6]. For the simple dimer model, one can find two vacuum states (both
' has a zero-eigenvector in order to finish the program of quadrature by the algebraic Bethe ansatz [6]. For the simple dimer model, one can find two vacuum states (both  and
and  have kernels [7]) and modify the Bethe ansatz accordingly. It may be very difficult or impossible to select parameters that eliminate unwanted terms, but that is a separate issue.
have kernels [7]) and modify the Bethe ansatz accordingly. It may be very difficult or impossible to select parameters that eliminate unwanted terms, but that is a separate issue.The plan of the article is to first establish those quadratic zero-operators that are compatible with the matrix coalgebra structure, and to show that this will require Equation 14 for closure, making it a necessary condition. The next step is to show that [  +
+  ,
,  ' +
' +  '] is also a quadratic zero-operator if Equation 14 holds true, so that it is a necessary condition for commutativity of the transfer matrix.
'] is also a quadratic zero-operator if Equation 14 holds true, so that it is a necessary condition for commutativity of the transfer matrix.
 +
+  ,
,  ' +
' +  '] is also a quadratic zero-operator if Equation 14 holds true, so that it is a necessary condition for commutativity of the transfer matrix.
'] is also a quadratic zero-operator if Equation 14 holds true, so that it is a necessary condition for commutativity of the transfer matrix.The motivation behind this work is the desire to have a way of attacking lattice models that may not satisfy the Yang–Baxter equation. Perhaps M is not invertible, or a suitable R matrix cannot be found. It may still be possible to apply the algebraic Bethe ansatz if the operator coalgebra can be extended to o bialgebra by the means described here.
2. Operator Bialgebra Relations Compatible with the Coalgebra
We seek out binary product relations of matrix representations (2n × 2n matrices) of the operators  ,
,  ,
,  ,
,  , which we denote by
, which we denote by  n,
n,  n,
n,  n,
n,  n of the coalgebra that are invariant under the coproduct operation of Equation 6 (Δ is an algebra homomorphism) by which higher-dimensional representations are constructed from the lower. We work in the vector space of physical states. For the lowest dimensional representation, the 2 × 2, these four matrices are
n of the coalgebra that are invariant under the coproduct operation of Equation 6 (Δ is an algebra homomorphism) by which higher-dimensional representations are constructed from the lower. We work in the vector space of physical states. For the lowest dimensional representation, the 2 × 2, these four matrices are  1 = A,
1 = A,  1 = B,
1 = B,  1 = C, and
1 = C, and  1 = D, and the basis for the vector space of physical states is
1 = D, and the basis for the vector space of physical states is
 ,
,  ,
,  ,
,  , which we denote by
, which we denote by  n,
n,  n,
n,  n,
n,  n of the coalgebra that are invariant under the coproduct operation of Equation 6 (Δ is an algebra homomorphism) by which higher-dimensional representations are constructed from the lower. We work in the vector space of physical states. For the lowest dimensional representation, the 2 × 2, these four matrices are
n of the coalgebra that are invariant under the coproduct operation of Equation 6 (Δ is an algebra homomorphism) by which higher-dimensional representations are constructed from the lower. We work in the vector space of physical states. For the lowest dimensional representation, the 2 × 2, these four matrices are  1 = A,
1 = A,  1 = B,
1 = B,  1 = C, and
1 = C, and  1 = D, and the basis for the vector space of physical states is
1 = D, and the basis for the vector space of physical states is 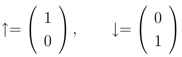
We will use notation A = A(λ), A' = A(λ') with λ, λ' being different parameter sets (a, b, c), (a', b', c'). The action of simple associative matrix products of these operators on the basis of physical states is
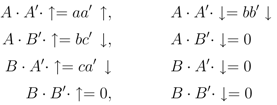
and so forth.
The coproducts (Equation 6)

give us another (the next higher dimensional) representation of the same coalgebra, the vector space of the representation is 2n+1-dimensional, and we can decompose a product of operators as
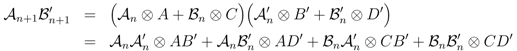
Let v be any basis vector of the vector space of the 2n-dimensional representation Фn, upon which  n,
n,  n,
n,  n,
n,  n act. Then the basis of the 2n+1-dimensional representation space Фn+1 upon which
n act. Then the basis of the 2n+1-dimensional representation space Фn+1 upon which  n+1,
n+1,  n+1,
n+1,  n+1,
n+1,  n+1 act is the set of all
n+1 act is the set of all
 n,
n,  n,
n,  n,
n,  n act. Then the basis of the 2n+1-dimensional representation space Фn+1 upon which
n act. Then the basis of the 2n+1-dimensional representation space Фn+1 upon which  n+1,
n+1,  n+1,
n+1,  n+1,
n+1,  n+1 act is the set of all
n+1 act is the set of all 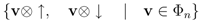
Apply the operator products Equation 21 to the basis of the vector space {v⊗ ↓, v⊗ ↑} of states for the model with n + 1 sites per row, in which v ∈ Фn is any n-site vector
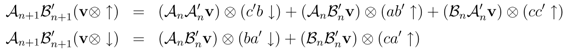
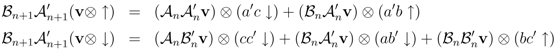
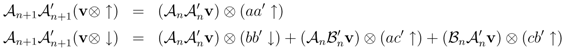
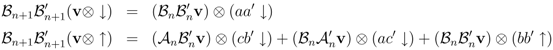
We can see that these binary products close in the sense that exactly the same set of binary products appear on both sides of each equation, a powerful constraint on the form of algebraic relations compatible with the coproduct.
The relations of Equations 25 and 26 can be written as
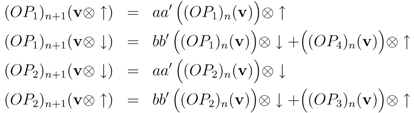
if the operator products OP1, …, OP4 are given by
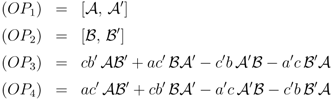
The operators given in Equation 28 annihilate the entire vector space of states for the n = 1 representation, {↑, ↓}. This is easy to verify using Equation 19. Therefore Equation 27 have all zeros on the right-hand side, and the operator products (OP1) and (OP2) annihilate the entire n = 2 vector space of states.
In the next section we will show that Equations 23 and 24 can also be written with right-hand sides expressed entirely in terms of (OPi) for i = 1, 2, 3, 4, and (OP3) and (OP4) also have recursion relations of the same form, making a complete set of recursions for the entire AB-subalgebra;
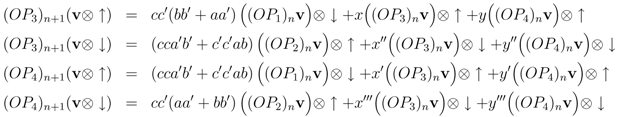
the action of (OP3)n+1 on a basis of the n + 1-vector space can be written entirely in terms of the actions of (OPi)n, i = 1, 2, 3, 4 on the basis of the n-vector space provided a, b, c and a', b', c' obey the star triangle equation, and the same for (OP4). This is the core of the method; in the matrix coalgebra structure, sets of operator products (here the AA', AB', BA', BB') have recursion relations for their actions on basis vectors that close within the set. A complete set of such recursion relations mean that these binary operator products annihilate the entire vector space for any n, since the recursions are single-step, and they annihilate the n = 1 vector space. Matrices that annihilate the entire basis of a vector space are identically zero. These operator combinations are the zero matrix on the spaces of physical states, and we have constructed those binary product laws (algebraic relations between  ,
,  preserved by the coproduct). From these we establish the product relations for the subalgebra spanned by
preserved by the coproduct). From these we establish the product relations for the subalgebra spanned by  and
and  compatible with the coalgebra structure.
compatible with the coalgebra structure.
 ,
,  preserved by the coproduct). From these we establish the product relations for the subalgebra spanned by
preserved by the coproduct). From these we establish the product relations for the subalgebra spanned by  and
and  compatible with the coalgebra structure.
compatible with the coalgebra structure.Equation 29 follow directly from Equation 28 by the fact that the coproduct is an algebra homomorphism in the bialgebra (for instance Δ( 
 ') = Δ(
') = Δ(  )Δ(
)Δ(  '), and the only question is closure—is the coproduct of (OPn) a linear combination of only (OP1), …, (OP4) for n = 1, 2, 3, 4. If so, then if each operator annihilates the physical basis, so does its coproduct, and the operator is zero on the basis of all physical representations. The coproduct is an algebra homomorphism requirement of compatibility of coalgebra and algebra structure in the bialgebra; it is what guarantees the existence of our basis-annihilating operator products.
'), and the only question is closure—is the coproduct of (OPn) a linear combination of only (OP1), …, (OP4) for n = 1, 2, 3, 4. If so, then if each operator annihilates the physical basis, so does its coproduct, and the operator is zero on the basis of all physical representations. The coproduct is an algebra homomorphism requirement of compatibility of coalgebra and algebra structure in the bialgebra; it is what guarantees the existence of our basis-annihilating operator products.

 ') = Δ(
') = Δ(  )Δ(
)Δ(  '), and the only question is closure—is the coproduct of (OPn) a linear combination of only (OP1), …, (OP4) for n = 1, 2, 3, 4. If so, then if each operator annihilates the physical basis, so does its coproduct, and the operator is zero on the basis of all physical representations. The coproduct is an algebra homomorphism requirement of compatibility of coalgebra and algebra structure in the bialgebra; it is what guarantees the existence of our basis-annihilating operator products.
'), and the only question is closure—is the coproduct of (OPn) a linear combination of only (OP1), …, (OP4) for n = 1, 2, 3, 4. If so, then if each operator annihilates the physical basis, so does its coproduct, and the operator is zero on the basis of all physical representations. The coproduct is an algebra homomorphism requirement of compatibility of coalgebra and algebra structure in the bialgebra; it is what guarantees the existence of our basis-annihilating operator products.We will also show that commutativity of the transfer matrix is one of the algebraic relations (a binary product that identically annihilates the entire vector space of states) if and only if this same constraint is imposed. The constraint is the star-triangle relation.
2.1. The AB Subalgebra and the Star-Triangle Relations
We prove that (OP3) and (OP4) have recursion relations of the form Equation 27, so that the operator products (OPi)n+1 for i = 1, 2, 3, 4 acting on any basis vector of the n + 1-vector space can be expressed entirely in terms of the operator products (OPi)n for i = 1, 2, 3, 4 acting on any basis vector of the n-vector space (the set is closed with a recursive action).
Let us explicitly calculate the action of (OP3)n+1 on the basis of the n + 1-site vector space. Let v be any basis vector of the n -site vector space Фn, then
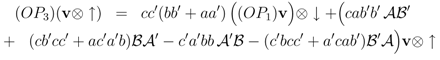
Force closure of the set of relations {OP1, OP2, OP3, OP4}; is there an x and y such that
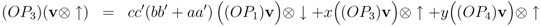
This requires that there be a solution to the equations
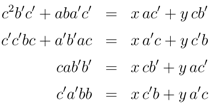
(and of course there might not be a solution) the first and third of these giving
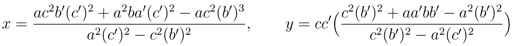
Note that the proposed zero-operators Equation 27 are unchanged by (a, b, c) ⇌ (a', b', c'), so the left-hand side of Equation 31 has this symmetry. Solution of the second and fourth requiring that for x to be symmetric under (a, b, c) ⇌ (a', b', c') leads to
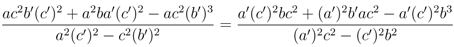
which can be factored into
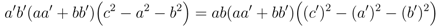
or
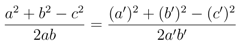
the familiar solution of the star-triangle relation for the six-vertex model. The (a, b, c) ⇌ (a', b', c') symmetry of y results in the same constraint
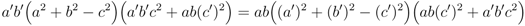
The second of Equation 29 results in
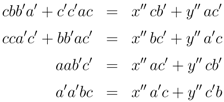
which are identical to Equation under interchange of a and b, and of a' with b', and also lead to Equation 35, and so to Equation 36.
Following the same set of steps, (which we do not repeat here) we discover that exactly the same condition gives us the desired recursion relation for the action of (OP4)n+1 on a basis of the n + 1 vector space decomposing into actions of (OP1)n, (OP2)n, (OP3)n and (OP4)n on a basis of the n-vector space. Since all four operator products annihilate the basis of the n = 1 space, the closure of these recursions forces the operator products to annihilate the bases of their vector spaces in their higher-dimensional representations. The product relations are universal (not representation dependent).
The star-triangle relations are a necessary condition for the operators Equation 28 to annihilate the entire vector space of physical states, a full set of recursions for the four zero-operators Equation 28 can be constructed in this way.
Combining OP3 and OP4 we obtain one of two important spectrum-generating relations used in the algebraic Bethe ansatz
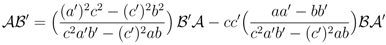
2.2. The BD Subalgebra and the Star-Triangle Relations
The other portion of the full bialgebra needed by the algebraic Bethe ansatz is the DB subalgebra, which we obtain by decomposing the coproducts as
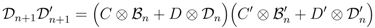
Let v be any basis of the n-site vector space, and apply the four possible binary products involving  and
and  to a basis of the n + 1 -site vector space
to a basis of the n + 1 -site vector space
 and
and  to a basis of the n + 1 -site vector space
to a basis of the n + 1 -site vector space 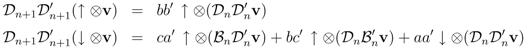
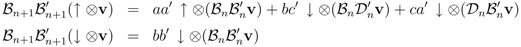
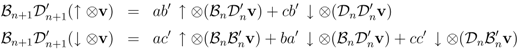
and finally
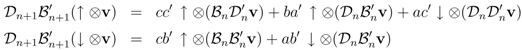
The first two sets of these identities suggest examining the combinations
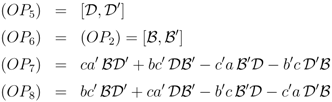
all of which annihilate the n = 1 vector space basis, and after following the same construction used to find the AB subalgebra relations, we discover that (OPi) for i = 5, 6, 7, 8 all have a set of one-step recursion relations that are closed among themselves if Equation 14 is true. Therefore each of these products annihilates the entire state-vector basis for any n, and are zero-operators. They constitute the algebraic relations of the BD subalgebra compatible with (preserved by) the matrix coalgebra structure. This pattern is repeated for all of the other subalgebras.
The second product law needed to complete the algebraic Bethe ansatz is made by combining (OP7) with (OP8)
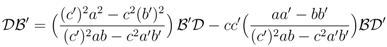
Relation Equation 14 imposed in the standard way by re-parameterization λ = (a, b, c) = (a(θ, γ), b(θ, γ), c(θ, γ)) with
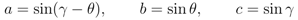
simplifies the coefficients of Equations 39 and 46
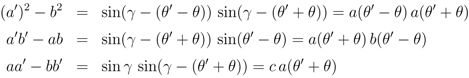
to the standard forms seen elsewhere
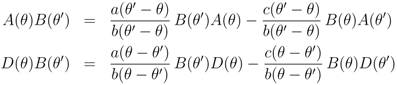
The analogous integrability condition for the five-vertex model found by constructing the zero-operators is much simpler [5,8]
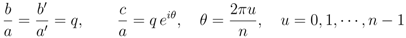
which is not a re-parameterization of the six-vertex model; the matrix of Boltzmann weights is singular;
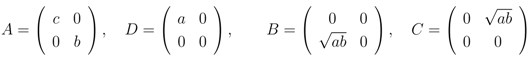
and so no invertible R-matrix can be constructed from it.
2.3. Commuting Transfer Matrices. The AD and BC Subalgebras
By building the binary product relations for each subalgebra that exhibits this closure inherent in the matrix coalgebra structure, we can complete the entire set of algebraic relations that make the operator coalgebra into a bialgebra. This is tedious, but each step is simply a repetition of what we have done for the AB and BD subalgebras. The AD and BC subalgebras have recursion relations that close among themselves, and one of these relations is the transfer matrix commutator.
From the relations
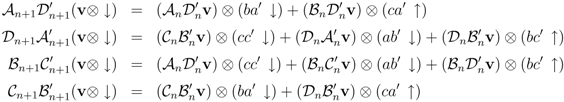
we find that (doing away with the subscripts; we know what these matrices act upon)
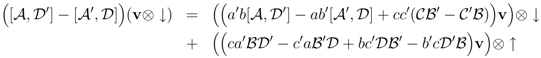
Calling
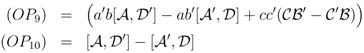
(OP9) and (OP10) could be zero-operators if for some x and y
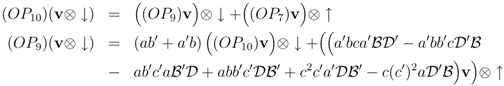
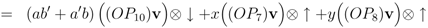
which requires that x and y be symmetric under (a, b, c) ⇌ (a', b', c')
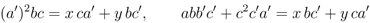
or
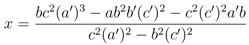
which is identical to Equation 33 with a ⇌ b, a' ⇌ b'. We conclude that in order for the condition of commuting transfer matrices (OP10 = 0) to hold, it is necessary for (a, b, c) and (a', b', c') to be related by the star-triangle relations Equation 14. Analysis of y in Equation 57 leads to the same conclusion. One still needs to show that (OP9) and (OP10) annihilate the other half of the basis, namely v⊗ ↑, and a short calculation verifies that they do. The same conclusion is drawn for the five-vertex model, (OP10) is a zero-operator and transfer matrices with different spectral parameters commute [7].
2.4. Generality of the Method
Despite the lack of elegance that other constructions of bialgebras utilizing a solution R of the Yang–Baxter equation may have (such as the RTT construction [3]), the methods used here appear to be quite general. Application to Sweedler’s Hopf algebra [9] generated by x, g with coproduct Δ(g) = g ⊗ g and Δ(x) = x ⊗ g + 1 ⊗ x leads uniquely to the algebraic relations g • g = 1 and x • x = 0 making the coalgebra a bialgebra (they are preserved by the coproduct), starting with a two-dimensional representation [8]. The less trivial example of the Hopf algebra Uq(  +) with generators K and X (the quantum deformation of the universal enveloping algebra of the upper Borel subalgebra of
+) with generators K and X (the quantum deformation of the universal enveloping algebra of the upper Borel subalgebra of 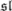 (2)) whose coproducts are
(2)) whose coproducts are
 +) with generators K and X (the quantum deformation of the universal enveloping algebra of the upper Borel subalgebra of
+) with generators K and X (the quantum deformation of the universal enveloping algebra of the upper Borel subalgebra of 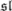 (2)) whose coproducts are
(2)) whose coproducts are 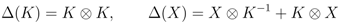
uniquely produces qX • K = K • X from such a representation [8]. The two-dimensional representation is the set of local Boltzmann weights, quantities that the model-builder would possess.
Starting with a two-dimensional representation of the Yangian Hopf algebra Y( 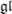 (2))
(2))
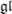 (2))
(2))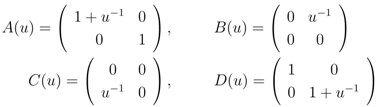
with matrix coproduct, analytical construction of the zero-operators leads to the well-known product rules [8]
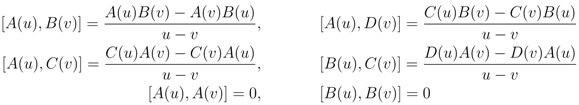
and finally when applied to the five-vertex or hexagonal lattice dimer model with spectral parameters a, b and c (using notation 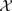 =
= 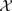 (a, c),
(a, c), 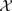 ' =
' = 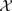 (a', c')) it results in a bialgebra structure
(a', c')) it results in a bialgebra structure
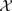 =
= 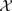 (a, c),
(a, c), 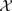 ' =
' = 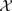 (a', c')) it results in a bialgebra structure
(a', c')) it results in a bialgebra structure 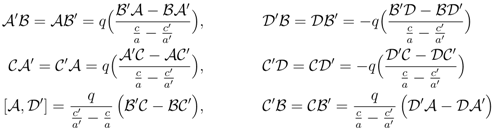
closely related to the Yangian, but which has no R-matrix or antipode [5,8]. It was for the purposes of studying such models that the technique was developed in the first place. Note that Sweedler’s algebra and the Yangian both possess R-matrices, but Uq(  +) and the five-vertex model do not, yet the methods of this article lead uniquely to their bialgebra structure equations.
+) and the five-vertex model do not, yet the methods of this article lead uniquely to their bialgebra structure equations.
 +) and the five-vertex model do not, yet the methods of this article lead uniquely to their bialgebra structure equations.
+) and the five-vertex model do not, yet the methods of this article lead uniquely to their bialgebra structure equations.3. The Algebraic Bethe Ansatz
Once the spectrum-generating relations Equation 49 have been established and a pseudo-vacuum state 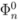 with
with 
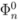 = 0 has been found, the eigenvalues of the transfer matrix can be found by the algebraic Bethe ansatz.
= 0 has been found, the eigenvalues of the transfer matrix can be found by the algebraic Bethe ansatz.
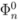 with
with 
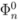 = 0 has been found, the eigenvalues of the transfer matrix can be found by the algebraic Bethe ansatz.
= 0 has been found, the eigenvalues of the transfer matrix can be found by the algebraic Bethe ansatz.The vector
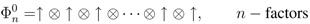
satisfies the requirements of the Bethe ground state (which we show inductively)
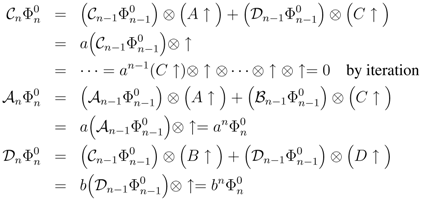
This state is an eigenstate of the transfer matrix
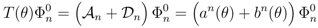
Products of the  operators applied to the vacuum state will produce vectors that are eigenvalues of the transfer matrix if the unwanted vectors in the expansion of T(θ)Ф have zero coefficients
operators applied to the vacuum state will produce vectors that are eigenvalues of the transfer matrix if the unwanted vectors in the expansion of T(θ)Ф have zero coefficients
 operators applied to the vacuum state will produce vectors that are eigenvalues of the transfer matrix if the unwanted vectors in the expansion of T(θ)Ф have zero coefficients
operators applied to the vacuum state will produce vectors that are eigenvalues of the transfer matrix if the unwanted vectors in the expansion of T(θ)Ф have zero coefficients 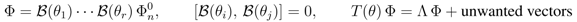
The eigenvalues are
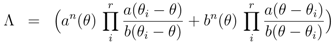
provided the set {θ1, θ2, …, θr} is chosen such that
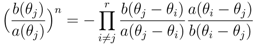
which eliminates the unwanted terms in the expansion of T(θ)Ф [6].
The conditions for elimination of the unwanted terms in the five-vertex model (hexagonal lattice dimer model) is far simpler [5,8], from
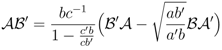
with a similar relation involving  and
and  , together with [
, together with [  ,
,  '] = 0.
'] = 0.
 and
and  , together with [
, together with [  ,
,  '] = 0.
'] = 0.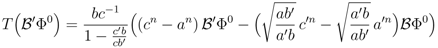
one is led to Equation 50, and this easily extends to the higher excitations [5,8].
4. Conclusions
The method of constructing zero-operators, quadratic operator products that annihilate the entire state-space which are preserved by the coproduct, can be used to deduce the conditions (on the model parameters) under which a lattice model has commuting transfer matrices. Coassociativity of the coproduct operation, which is the operation by which the transfer matrix is built up from local Boltzmann weights, is used to obtain recursion relations for a set of operators that in their lowest dimensional representation annihilate the state space. The recursions guarantee that they will annihilate all higher-dimensional state spaces. This promotes the operator coalgebra to a bialgebra. If the bialgebra can be shown to possess an antipode it may actually be a Hopf algebra, and the existence of an R-matrix would make it quasi-triangular, but these steps are not needed for a complete quadrature. Only two sub-algebras, the AB and DB, are required to construct Bethe vectors and perform the algebraic Bethe ansatz, assuming that the resulting equations for the elimination of unwanted terms can be solved. Simple possession of these subalgebras is no guarantee that this can be done.
In this article we have shown that a necessary condition for the zero-operator recursions to exist (for the six vertex model) is that the Boltzmann weights are constrained by
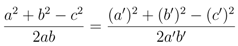
the star-triangle relations. One of these zero-operators is in fact [T, T'], T =  +
+  , and therefore a necessary condition for commutativity of transfer matrices with different Boltzmann weights is the star-triangle condition. This condition is well-known to be sufficient [1].
, and therefore a necessary condition for commutativity of transfer matrices with different Boltzmann weights is the star-triangle condition. This condition is well-known to be sufficient [1].
 +
+  , and therefore a necessary condition for commutativity of transfer matrices with different Boltzmann weights is the star-triangle condition. This condition is well-known to be sufficient [1].
, and therefore a necessary condition for commutativity of transfer matrices with different Boltzmann weights is the star-triangle condition. This condition is well-known to be sufficient [1].The zero-operator method does not make use of the Yang–Baxter equation or require the existence of an R-matrix. It is a direct determination of the spectrum-generating bialgebra of a lattice model, requiring only the lowest dimensional non-trivial representation of the bialgebra (the M matrix) and has been used to perform the algebraic Bethe ansatz for models with a singular M-matrix [5,8,7], in which the bialgebra is closest in structure to a Yangian quantum group, but possesses no antipode. This approach for constructing a bialgebra is complementary to the RTT method [3,10] which begins with a solution to the Yang–Baxter equation (an invertible R-matrix constructed from M) and produces a bialgebra with matrix coalgebra.
The zero-operators themselves are linear combinations of products of the  ,
,  ,
,  and
and  operators for pairs of spectral parameters. The commutator of the transfer matrices is just such an object, and so the method is particularly well-suited to the problem of establishing necessary spectral conditions under which the transfer matrices will commute.
operators for pairs of spectral parameters. The commutator of the transfer matrices is just such an object, and so the method is particularly well-suited to the problem of establishing necessary spectral conditions under which the transfer matrices will commute.
 ,
,  ,
,  and
and  operators for pairs of spectral parameters. The commutator of the transfer matrices is just such an object, and so the method is particularly well-suited to the problem of establishing necessary spectral conditions under which the transfer matrices will commute.
operators for pairs of spectral parameters. The commutator of the transfer matrices is just such an object, and so the method is particularly well-suited to the problem of establishing necessary spectral conditions under which the transfer matrices will commute.The methods used here are particularly amenable to the use of computer algebra systems. All of the calculations here were facilitated, and verified, by the use of REDUCE [11].
References
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: Waltham, MA, USA, 1982. [Google Scholar]
- Chari, V.; Pressley, A. A Guide to Quantum Groups; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Kauffman, L.H. Knots and Physics; World Scientific: Singapore, 1991. [Google Scholar]
- McCoy, B.M. Advanced Statistical Mechanics; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Schmidt, J.R. The algebraic Bethe Ansatz without the YangBaxter equation. Can. J. Phys. 2008, 86, 1177–1193. [Google Scholar]
- Takhtadzhan, L.A.; Faddeev, L.D. The quantum method of the inverse problem and the Heisenberg XYZ model. Uspekhi Mat. Nauk 1979, 34, 13–63. [Google Scholar]
- Schmidt, J.R. A modified Bethe Ansatz for the two-dimensional dimer problem. Can. J. Phys. 2007, 85, 745–762. [Google Scholar] [CrossRef]
- Schmidt, J.R. Spectrum-Generating bialgebra of the hexagonal-lattice dimer model. Can. J. Phys. 2009, 87, 1099–1125. [Google Scholar] [CrossRef]
- Sweedler, M.E. Hopf Algebras; W.A. Benjamin, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Faddeev, L.D.; Reshetikhin, N.Y.; Takhtajan, L.A. Quantization of Lie Groups and Lie Algebras. Leningrad Math. J. 1990, 1, 193–225. [Google Scholar]
- REDUCE is an open-source computer algebra system coded in Lisp. Available online: http://reduce-algebra.sourceforge.net/. Registered Dec 18, 2008.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).