The Duality between Corings and Ring Extensions
Abstract
:1. Introduction
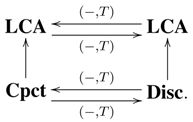
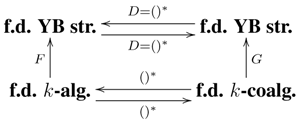
- (i) We propose as a research project the investigation of other connections between the duality of (co)algebras and the Pontryagin duality. (For example, one might try to endow the (co)algebra structures with some topological structures.)
- (ii) At the epistemologic level, the extension of the duality of (co)algebra structures seems to be a model for the relation between interdisciplinarity, pluridisciplinarity and transdisciplinarity (see [4]).
- (iii) This paper explains that taking the dual of some objects can be seen a “continuous” process. Let us visualize this statement by considering an example from geometry. We take a triangular prism: We can see it as two parallel triangles joint by 3 segments. In total it has 5 planar geometric figures, 9 edges and 6 vertices. The geometric dual of the triangular prism has 6 planar geometric figures, 9 edges and 5 vertices. Now, one can start with a triangular prism, “shave” its corners, and then continuously deform that figure in order to obtain the geometric dual of the triangular prism.
2. Notations and Preliminaries
 B, symbols M* , *M, *M* denote right dual, left dual and bidual of M, and A
B, symbols M* , *M, *M* denote right dual, left dual and bidual of M, and A  B (M, N) denotes the 𝕂-module of (A, B)-bimodule maps M → N. In what follows we shall concentrate on right dual of M but similar observations can be made for the left dual as well.
B (M, N) denotes the 𝕂-module of (A, B)-bimodule maps M → N. In what follows we shall concentrate on right dual of M but similar observations can be made for the left dual as well.  B (M, N), let ϕ* : N* → M* denote the right adjoint of ϕ i.e., ϕ* (g)(m) := g ◦ ϕ (m).
B (M, N), let ϕ* : N* → M* denote the right adjoint of ϕ i.e., ϕ* (g)(m) := g ◦ ϕ (m).  B then M* ∈ Aop
B then M* ∈ Aop  Bop with (aopfbop)(m) = bf(am).
Bop with (aopfbop)(m) = bf(am).  B is also finitely generated projective as a right B-module, i.e., there exists a dual basis
B is also finitely generated projective as a right B-module, i.e., there exists a dual basis 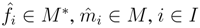 , such that for any m∈ M,
, such that for any m∈ M, 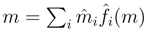 . Then
. Then  B, with the inverse
B, with the inverse 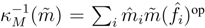 . In fact κ is a natural morphism between identity functor in A
. In fact κ is a natural morphism between identity functor in A  B and the functor ()** : A
B and the functor ()** : A  B → A
B → A  B.
B.  C then κM,N : M* ⊗ Bop N* → (M ⊗ B N)*, given by κM,N (f ⊗ Bop g)(m ⊗ n) = g(f(m)n), is an isomorphism in Aop
C then κM,N : M* ⊗ Bop N* → (M ⊗ B N)*, given by κM,N (f ⊗ Bop g)(m ⊗ n) = g(f(m)n), is an isomorphism in Aop  Cop with the inverse
Cop with the inverse 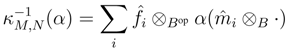
 B, N∈ B
B, N∈ B  C , P ∈C
C , P ∈C  D, where A, B, C, D are algebras. Then the following diagram is commutative:
D, where A, B, C, D are algebras. Then the following diagram is commutative: 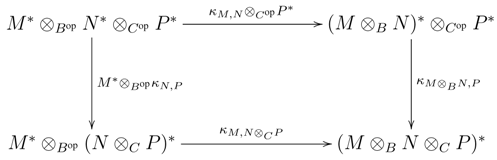
 B be finitely generated projective as B-module, with dual basis
B be finitely generated projective as B-module, with dual basis 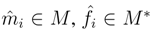 , i∈ I, and let N∈B
, i∈ I, and let N∈B  C be finitely generated projective as a C-module with dual basis
C be finitely generated projective as a C-module with dual basis 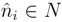 ,
, 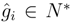 , i∈ J. Then M ⊗ B N∈A
, i∈ J. Then M ⊗ B N∈A  C is finitely generated projective as a C-module with a dual basis
C is finitely generated projective as a C-module with a dual basis 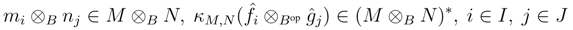
 B is called a B-coring if there exist morphisms ΔC, εC ∈B
B is called a B-coring if there exist morphisms ΔC, εC ∈B  B, ΔC : C→ C ⊗ B C, εC : C→ B such that
B, ΔC : C→ C ⊗ B C, εC : C→ B such that 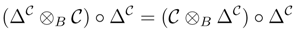
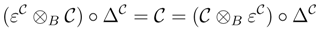
 B (C, D) is called a morphism of B-corings if (ϕ ⊗ Bϕ) ◦ ΔC = ΔD ◦ ϕ and εD ◦ ϕ = εC. The category of B-corings is denoted by CrgB.
B (C, D) is called a morphism of B-corings if (ϕ ⊗ Bϕ) ◦ ΔC = ΔD ◦ ϕ and εD ◦ ϕ = εC. The category of B-corings is denoted by CrgB.  is called an extension of a ring B if there exists an injective unital ring morphism
is called an extension of a ring B if there exists an injective unital ring morphism 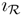 : B →
: B →  . Observe that
. Observe that  ∈B
∈B  B by
B by 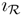 . Given ring extensions
. Given ring extensions 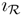 : B →
: B →  and
and 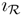 : B →P, a ring morphism α :
: B →P, a ring morphism α :  →P is called a morphism of ring extensions if α ◦
→P is called a morphism of ring extensions if α ◦ 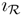 =
= 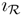 or, equivalently, if α ∈ B
or, equivalently, if α ∈ B  B (
B (  , P). The category of ring extensions of B is denoted by RgeB.
, P). The category of ring extensions of B is denoted by RgeB.  Bopis a ring extension of Bop with multiplication
Bopis a ring extension of Bop with multiplication 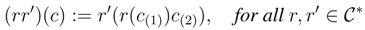
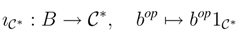
 ∈ r.f.g.pRgeB then
∈ r.f.g.pRgeB then  * is a Bop-coring with comultiplication and counit
* is a Bop-coring with comultiplication and counit 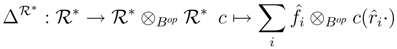
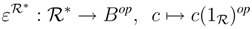
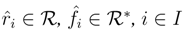 is a (finite) dual basis of
is a (finite) dual basis of  .
.  →S is a morphism of right finitely generated projective ring extensions of B, then
→S is a morphism of right finitely generated projective ring extensions of B, then  : S* →
: S* →  * is a morphism of Bop-corings.
* is a morphism of Bop-corings.  ∈ r.f.g.pRgeB, κR :
∈ r.f.g.pRgeB, κR :  →
→  ** is a ring extension isomorphism facilitating this equivalence.
** is a ring extension isomorphism facilitating this equivalence.  →S. Let
→S. Let 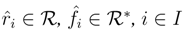 be any finite dual basis of
be any finite dual basis of  , and let
, and let 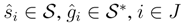 be any finite dual basis of S. For all s∈S*,
be any finite dual basis of S. For all s∈S*, 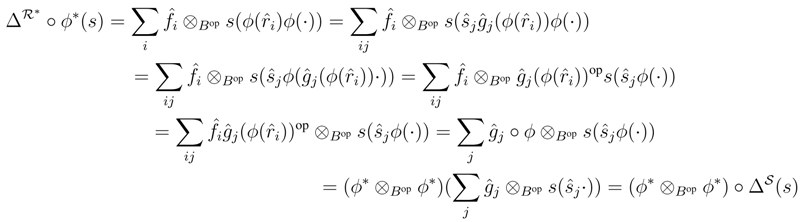
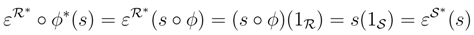
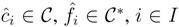 , be any finite dual basis of C. Observe that
, be any finite dual basis of C. Observe that 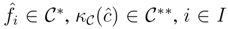 is a dual basis of C*. Indeed, for any g∈C*,
is a dual basis of C*. Indeed, for any g∈C*, 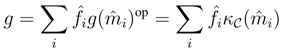
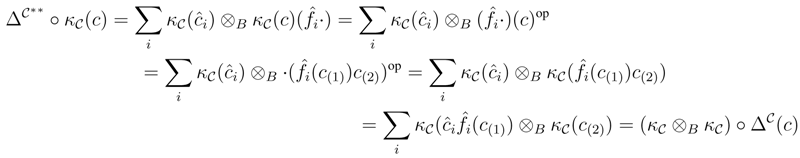
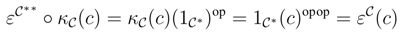

3. An Extension for the Duality between Corings and Ring Extensions
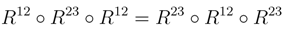
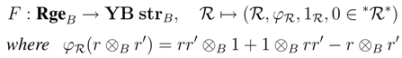
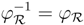 ). Furthermore
). Furthermore 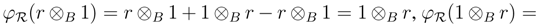
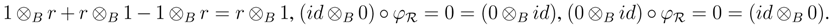 Hence (R, φR, 1R, 0) is an object in the category YB strB.
Hence (R, φR, 1R, 0) is an object in the category YB strB.  →S be a morphism of ring extensions. Then f(1R)= 1S and 0 ◦ f = 0. Moreover
→S be a morphism of ring extensions. Then f(1R)= 1S and 0 ◦ f = 0. Moreover 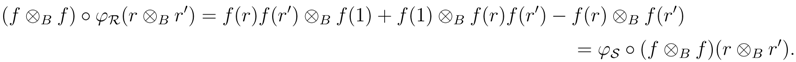
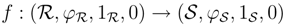 is a morphism in the category YB strB.
is a morphism in the category YB strB.  = F S, for some
= F S, for some  , S∈ RgeB, then obviously
, S∈ RgeB, then obviously  = S as (B, B)-bimodules, 1S = 1R, and the only thing which can differ is the multiplication. Denote by · the multiplication in
= S as (B, B)-bimodules, 1S = 1R, and the only thing which can differ is the multiplication. Denote by · the multiplication in  , and by ◦ the multiplication in S. Then, as φR = φS , for all r, r´∈
, and by ◦ the multiplication in S. Then, as φR = φS , for all r, r´∈  ,
,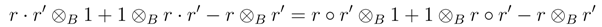
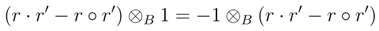
 or S is irrelevant) yields 2(r · r´− r ◦ r´) = 0, hence r · r = r ◦ r´, and so
or S is irrelevant) yields 2(r · r´− r ◦ r´) = 0, hence r · r = r ◦ r´, and so  = S as algebras. Therefore F is an embedding.
= S as algebras. Therefore F is an embedding. 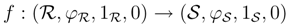 be a morphism in YB strB, where
be a morphism in YB strB, where  , S∈ RgeB. Then f is unital, and
, S∈ RgeB. Then f is unital, and 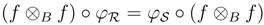 , hence, for all r, r´∈
, hence, for all r, r´∈  ,
, 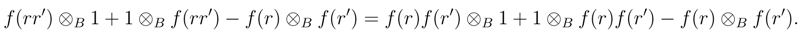
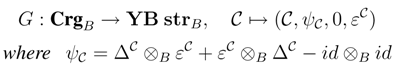
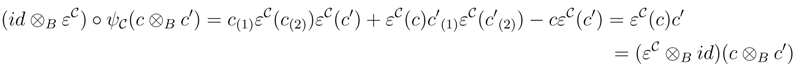
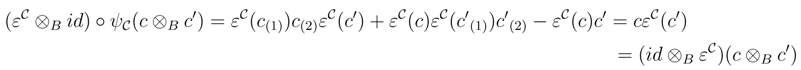
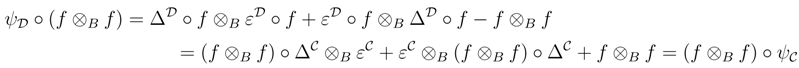
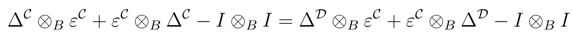
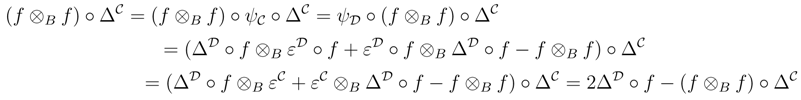
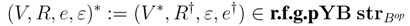
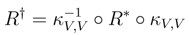
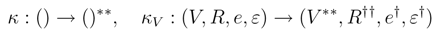
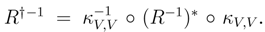 We shall prove that R† satisfies the Yang–Baxter equation. Observe that
We shall prove that R† satisfies the Yang–Baxter equation. Observe that 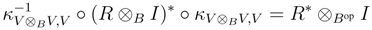
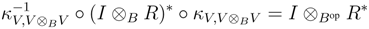
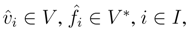 be a dual basis of V .
be a dual basis of V . 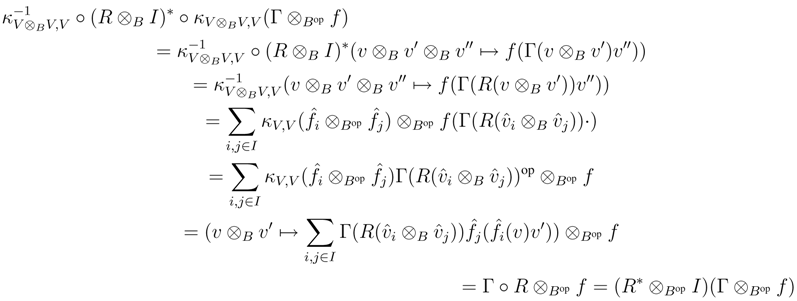
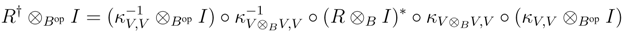
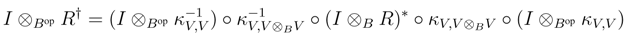
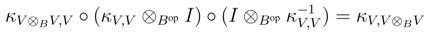
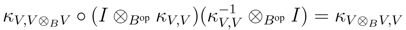
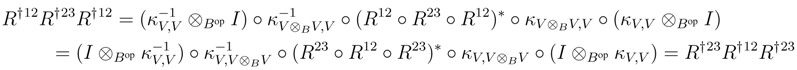
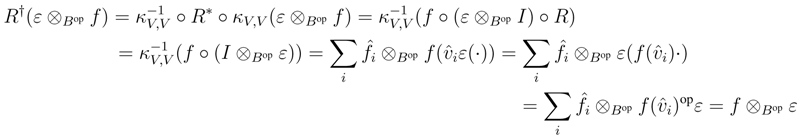
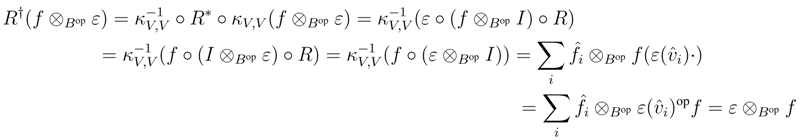
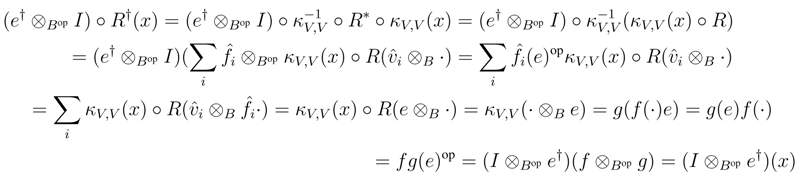
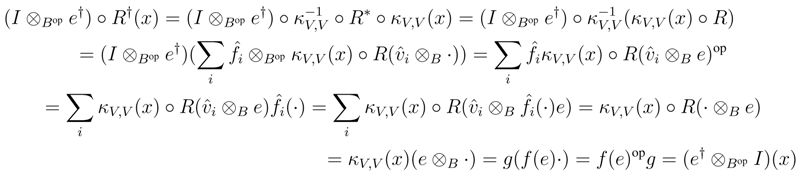
 B, and as V is finitely generated projective, κV is invertible. Therefore it suffices to prove that κV is a morphism in r.f.g.pYB strB. To this end, observe first that
B, and as V is finitely generated projective, κV is invertible. Therefore it suffices to prove that κV is a morphism in r.f.g.pYB strB. To this end, observe first that 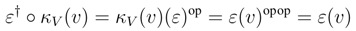
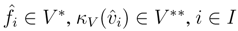 is a dual basis of V*. Therefore, for all Γ ∈ (V* ⊗ Bop V*)*,
is a dual basis of V*. Therefore, for all Γ ∈ (V* ⊗ Bop V*)*, 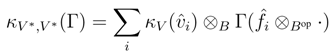
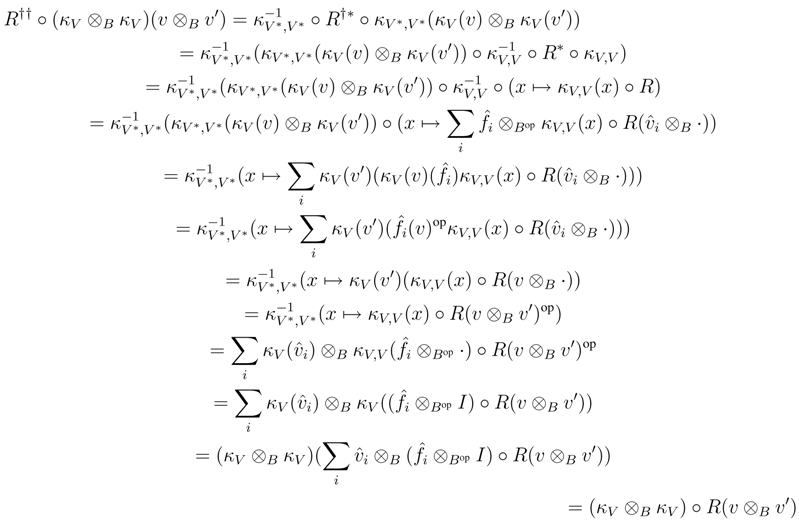
 ∈ r.f.g.pRgeB, C∈ r.f.g.pCrgB. Then
∈ r.f.g.pRgeB, C∈ r.f.g.pCrgB. Then 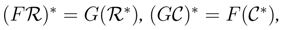 i.e.,
i.e.,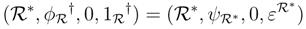
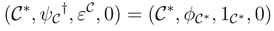
 *,
*, 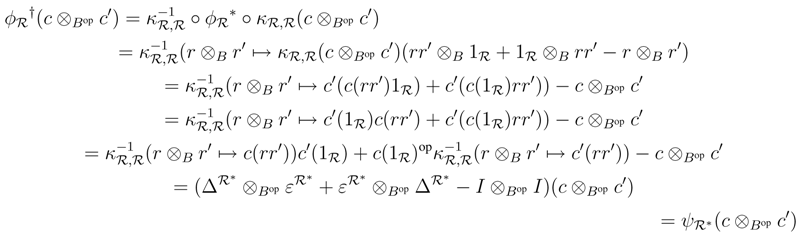
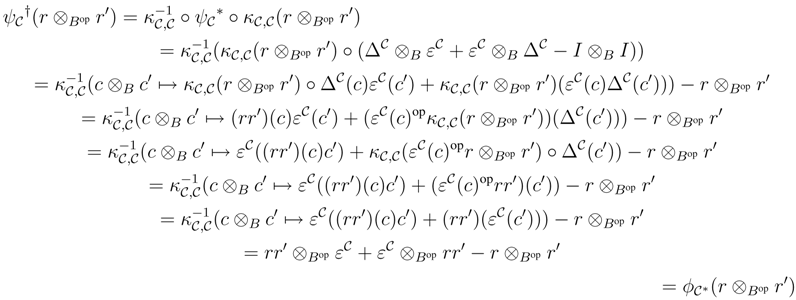
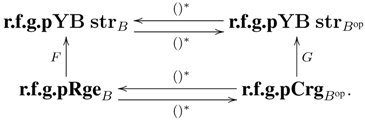
4. Conclusions
Acknowledgments
References
- Morris, S.A. Pontryagin Duality and the Structure of Locally Compact Abelian Groups; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Nichita, F.F.; Schack, S.D. The duality between algebras and coalgebras. Ann. Univ. Ferrara -Sez. VII -Sc. Mat. 2005, 51, 173–181. [Google Scholar]
- Brzeziński, T.; Wisbauer, R. Corings and Comodules; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nichita, F.F. Algebraic models for transdisciplinarity. Transdiscipl. J. Eng. Sci. 2011, 10, 42–46. [Google Scholar]
- Abe, E. Hopf Algebras; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Dăscălescu, S.; Năstăsescu, C.; Raianu, S. Hopf Algebras: An Introduction; Marcel Dekker, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Sweedler, M.E. Hopf Algebras; W.A.Benjamin, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Sweedler, M.E. The predual theorem to the Jacobson-Bourbaki theorem. Trans. Am. Math. Soc. 1975, 213, 391–406. [Google Scholar] [CrossRef]
- Kassel, C. Quantum Groups; Springer Verlag: New York, NY, USA, 1995. [Google Scholar]
- Lambe, L.; Radford, D. Introduction to the Quantum Yang-Baxter Equation and Quantum Groups: An Algebraic Approach; Kluwer Academic Publishers: Dordrecht, Germany, 1997. [Google Scholar]
- Nichita, F.F. Non-Linear Equation, Quantum Groups and Duality Theorems.
- Nichita, F.F. Self-inverse Yang-Baxter operators from (co)algebra structures. J. Algebra 1999, 218, 738–759. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nichita, F.F.; Zielinski, B. The Duality between Corings and Ring Extensions. Axioms 2012, 1, 173-185. https://doi.org/10.3390/axioms1020173
Nichita FF, Zielinski B. The Duality between Corings and Ring Extensions. Axioms. 2012; 1(2):173-185. https://doi.org/10.3390/axioms1020173
Chicago/Turabian StyleNichita, Florin F., and Bartosz Zielinski. 2012. "The Duality between Corings and Ring Extensions" Axioms 1, no. 2: 173-185. https://doi.org/10.3390/axioms1020173
APA StyleNichita, F. F., & Zielinski, B. (2012). The Duality between Corings and Ring Extensions. Axioms, 1(2), 173-185. https://doi.org/10.3390/axioms1020173




