Transforming Low-Value Quartz into Electronic-Grade Spherical SiO2 via a Morphology-Directed Hydrothermal Alkaline Process
Abstract
1. Introduction
2. Material and Experiment
2.1. Materials and Reagents
2.2. Experimental Procedures
2.2.1. Pretreatment of Powder Quartz Raw Ore
2.2.2. Preparation of High-Purity Sodium Silicate via Hydrothermal Impurity Removal from Quartz
2.2.3. Determination of Qn Distribution in Sodium Silicate Solution by Silicomolybdenum Yellow Method
2.2.4. Synthesis of Spherical Silica Dioxide
2.3. Characterization
3. Results and Discussion
3.1. Raw Material Analysis and Pretreatment
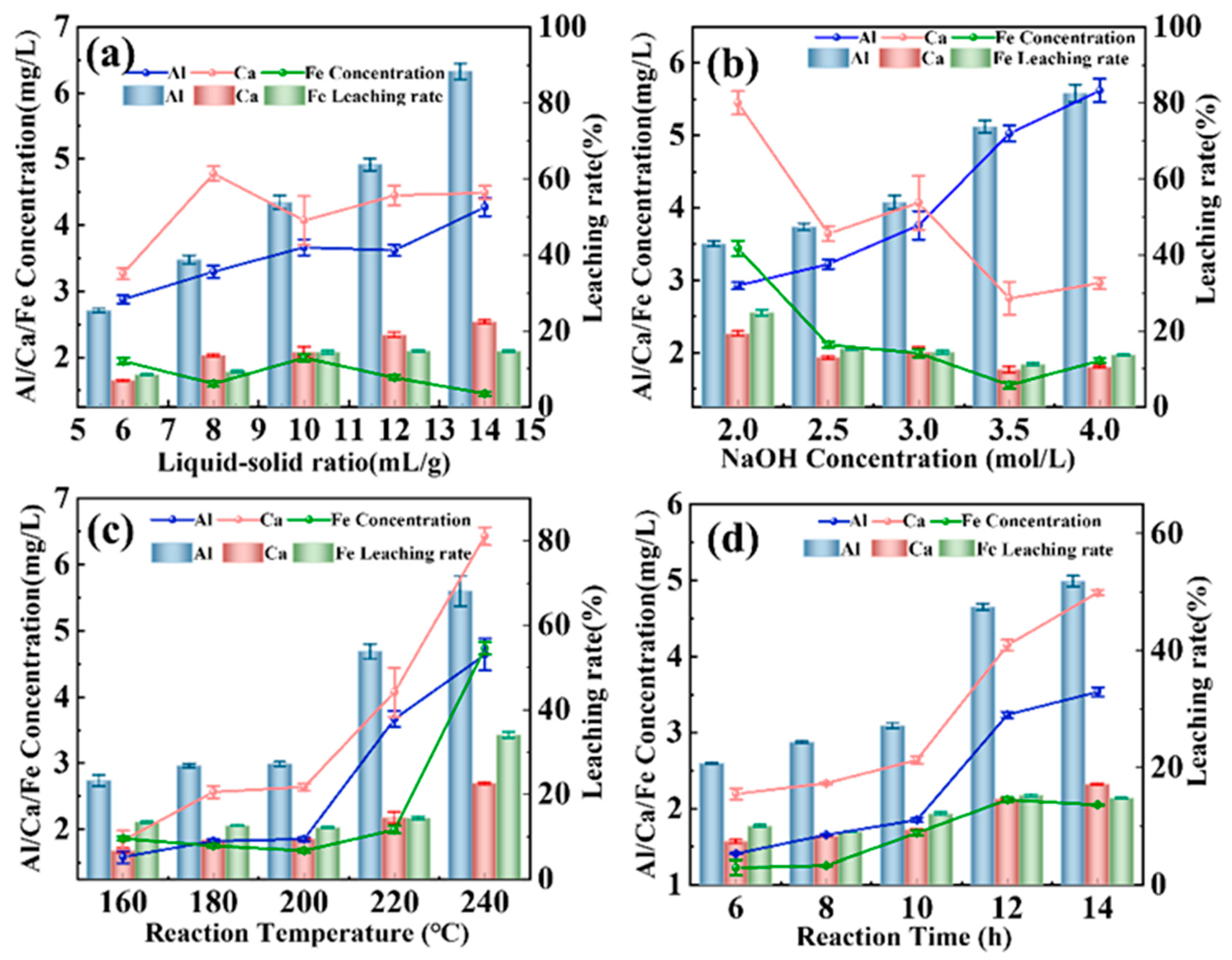
3.2. Effects of Hydrothermal Conditions on Leaching Behaviors of SiO2, Al3+, Ca2+, and Fe3+
3.2.1. Influence of Process Parameters on SiO2 Leaching Efficiency
3.2.2. Effects of Process Parameters on Leaching Efficiency of Al3+, Ca2+, and Fe3+
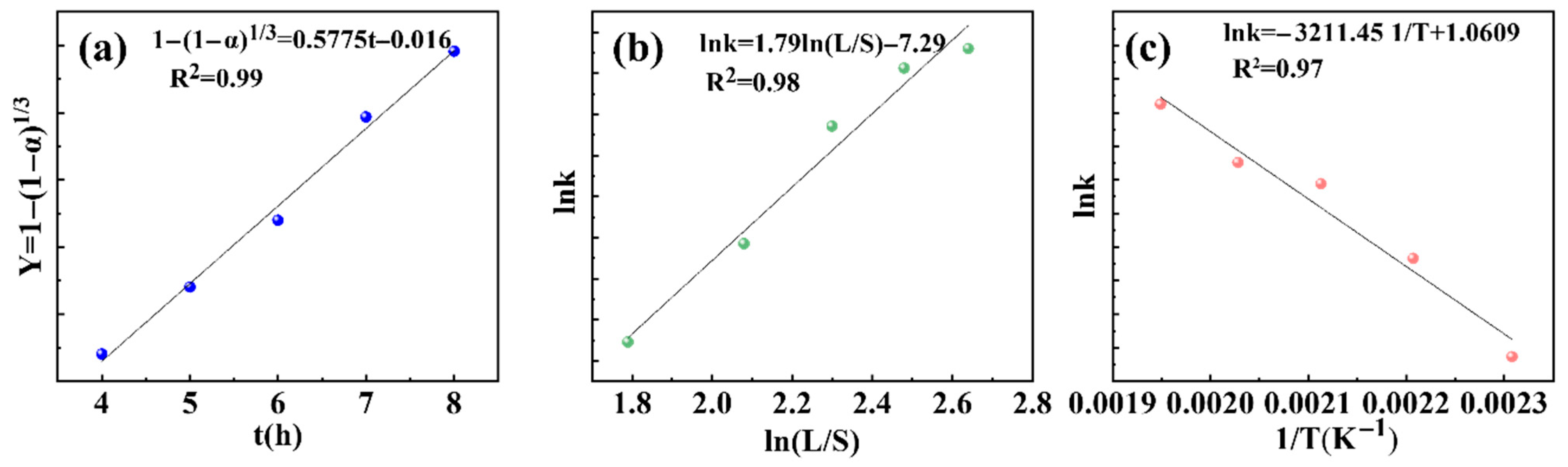
3.3. Leaching Kinetics of SiO2, Al3+, Ca2+, Fe3+, and Purification Mechanisms
3.3.1. Kinetic Characteristics of SiO2 Leaching
3.3.2. Kinetic Analysis of Al3+, Ca2+, and Fe3+ Leaching
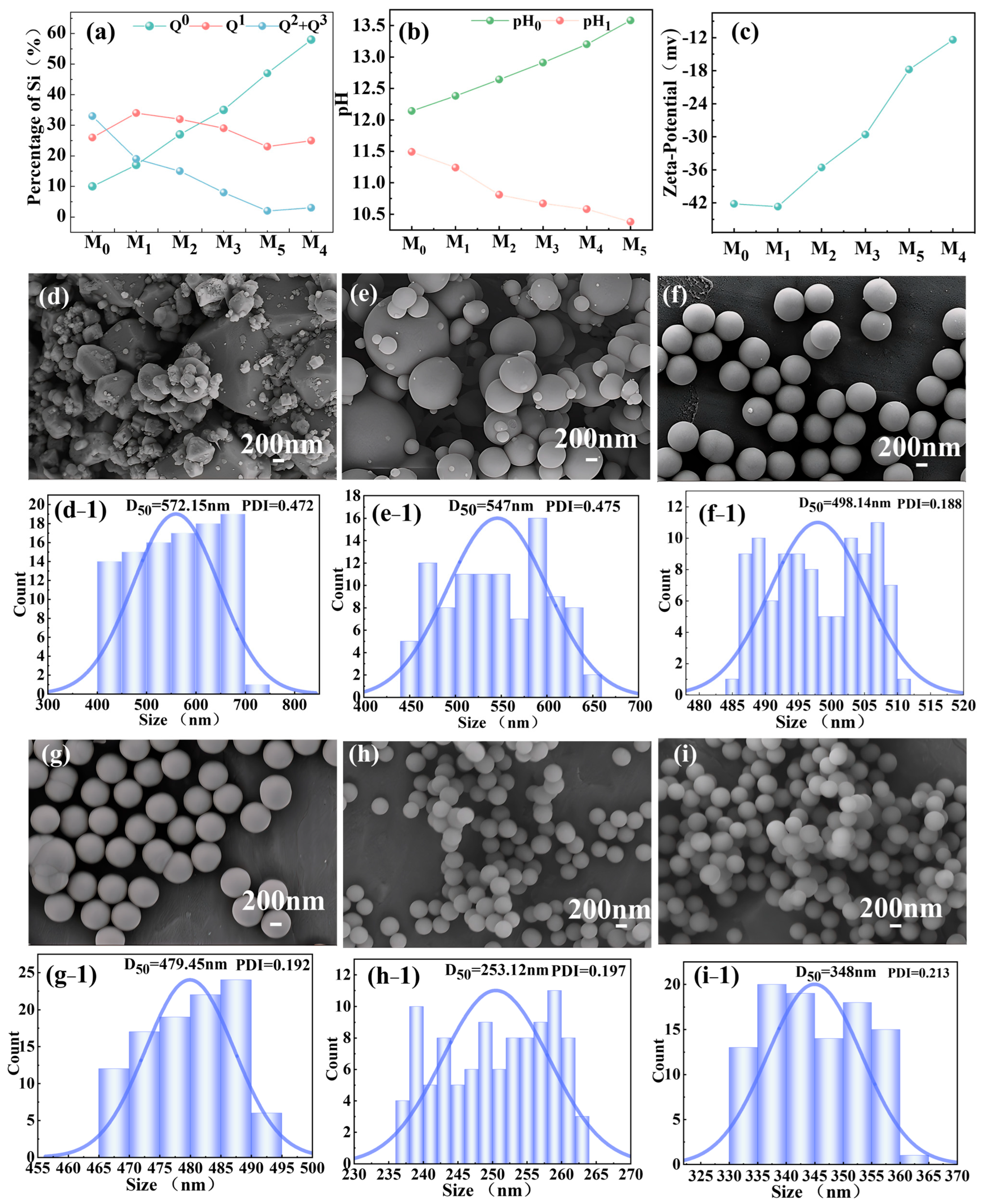
3.4. Effect of Silicate Anion Distribution (Qn) on Spherical SiO2 Morphology
3.5. Physicochemical Properties of Spherical SiO2 Prepared Under Optimal Hydrothermal Conditions
3.6. Spherical SiO2 Preliminary Analysis of Environmental and Economic Aspects
4. Conclusions
- Efficient purification was achieved under optimal hydrothermal conditions (L/S ratio: 10 mL/g and NaOH: 3 mol/L; 200 °C, 8 h), yielding 99.999% pure sodium silicate with 82.96% SiO2 leaching efficiency.
- Leaching kinetics revealed SiO2 dissolution followed the shrinking core model under mixed control (apparent activation energy: 26.70 kJ/mol). Differential impurity behaviors included Al3+ was diffusion controlled, Ca2+ was inhibited by chemical precipitation, and Fe3+ was governed by the dissolution–precipitation equilibrium, enabling selective SiO2 separation.
- Qn distribution of silicate anions critically regulated SiO2 sphericity and uniformity: modulus 0.9–1.1 (balanced Q0/Q1 ratio) enabled uniform nucleation, producing monodisperse spheres. Deviations from this (modulus <0.7 or >1.5) caused aggregation or irregular morphologies.
- Spherical SiO2 synthesized from modulus 1.08 precursor exhibited ultrahigh purity (99.996%), median size (D50: 498.74 nm), narrow PDI (0.178), and near-perfect sphericity (0.985), Surpassing electronic-grade standards (QYG-H Type 002), it demonstrated industrial viability for narrow size-distribution SiO2.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Zhang, H.; Liang, B.; Tian, M.; Li, X.; Ding, T.; Liu, P.; Yang, Y.; Niu, L.; Zhang, Z. Tri-functionally modified spherical silica for high-performance epoxy resin sealant. Compos. Commun. 2024, 51, 102081. [Google Scholar] [CrossRef]
- Jin, B.H.; Jang, J.; Kang, D.J.; Yoon, S.; Im, H.-G. Epoxy-based siloxane composites for electronic packaging: Effect of composition and molecular structure of siloxane matrix on their properties. Compos. Sci. Technol. 2022, 224, 109456. [Google Scholar] [CrossRef]
- Dong, T.; Liang, J.; Camayd-Muñoz, S.; Liu, Y.; Tang, H.; Kita, S.; Chen, P.; Wu, X.; Chu, W.; Mazur, E.; et al. Ultra-low-loss on-chip zero-index materials. Light Sci. Appl. 2021, 10, 10. [Google Scholar] [CrossRef] [PubMed]
- Sukhinina, N.S.; Masalov, V.M.; Yu, J.; Liu, Q.; Zhokhov, A.A.; Wang, J.; Emelchenko, G.A. A promising white pigment based on hollow spherical silica particles. Colloids Surf. A Physicochem. Eng. Asp. 2025, 726, 137909. [Google Scholar] [CrossRef]
- Hou, T.; Liu, X.; Ren, J.; Liu, Q.; Zhokhov, A.A.; Wang, J.; Emelchenko, G.A. Mesoporous hollow silica with controlled particle size for optimizing dielectric properties and coefficient of thermal expansion of polyimide packaging materials. J. Mater. Sci. Technol. 2025, 235, 122–132. [Google Scholar] [CrossRef]
- Malekzadeh, M.; Swihart, M.T. Vapor-phase production of nanomaterials. Chem. Soc. Rev. 2021, 50, 7132–7249. [Google Scholar] [CrossRef]
- Priyan, S.R.; Kumar, G.S.; Surendhiran, S.; Shkir, M. Size-controlled synthesis of mesoporous silica nanoparticles using rice husk by microwave-assisted sol–gel method. Int. J. Appl. Ceram. Technol. 2023, 20, 2807–2816. [Google Scholar] [CrossRef]
- Choi, J.; Lee, W.; Shim, T.; Park, J. Fumed silica-based ultra-high-purity synthetic quartz powder via sol–gel process for advanced semiconductor process beyond design rule of 3 nm. Nanomaterials 2023, 13, 390. [Google Scholar] [CrossRef]
- Kamila, R.; Ridwan Akhir, M.P.M.; Patriati, A.; Insani, A. Synthesis of silica particles through conventional sol-gel and sonochemistry methods and the effect of catalyst, water concentration and sample environment to the particle size. J. Phys. Conf. Ser. 2022, 2193, 12044. [Google Scholar] [CrossRef]
- Zhan, L.; Wang, Q.; Ku, J.; Shang, H.; Shen, Z. Purification technologies for high-purity quartz: From mineralogy to applications. Sep. Purif. Rev. 2025, 1–18. [Google Scholar] [CrossRef]
- Guo, W.; Lu, H.; Zhang, Z.; Jiang, L.; Wu, H.; Liu, D.; Chi, R. Crystal structure transformation and lattice impurities migration of quartz during chlorine roasting. Int. J. Min. Sci. Technol. 2024, 34, 1465–1474. [Google Scholar] [CrossRef]
- Lin, M.; Pei, Z.; Li, Y.; Liu, Y.; Wei, Z.; Lei, S. Separation mechanism of lattice-bound trace elements from quartz by KCl-doping calcination and pressure leaching. Miner. Eng. 2018, 125, 42–49. [Google Scholar] [CrossRef]
- Zhang, X.; Gong, P.; Zhang, Y.; Li, Y.; Zhou, G.; Yuan, F.; Li, C.; Sun, Z. Influence of inclusions with different morphological characteristic on the deep purification of vein quartz. Miner. Eng. 2025, 234, 109709. [Google Scholar] [CrossRef]
- Pan, X.; Li, S.; Li, Y.; Guo, P.; Zhao, X.; Cai, Y. Resource, characteristic, purification and application of quartz: A review. Miner. Eng. 2022, 183, 107600. [Google Scholar] [CrossRef]
- Zhao, X.; Zeng, L.; Guo, J.; Zhu, Q.; Huang, Z.; Lin, L.; Chen, X.; Cao, J.; Zhou, Z. Efficient separation and comprehensive extraction of aluminum, silicon, and iron from coal fly ash by a cascade extraction method. J. Clean. Prod. 2023, 406, 137090. [Google Scholar] [CrossRef]
- He, L.; Shi, L.; Huang, Q.; Hayat, W.; Shang, Z.; Ma, T.; Wang, M.; Yao, W.; Huang, H.; Chen, R. Extraction of alumina from aluminum dross by a non-hazardous alkaline sintering process: Dissolution kinetics of alumina and silica from calcined materials. Sci. Total Environ. 2021, 777, 146123. [Google Scholar] [CrossRef]
- Brinker, C.J. Hydrolysis and condensation of silicates: Effects on structure. J. Non-Cryst. Solids 1988, 100, 31–50. [Google Scholar] [CrossRef]
- Zou, H.; Wu, S.; Shen, J. Polymer/Silica nanocomposites: Preparation, characterization, properties, and applications. Chem. Rev. 2008, 108, 3893–3957. [Google Scholar] [CrossRef]
- Katoueizadeh, E.; Rasouli, M.; Zebarjad, S.M. A comprehensive study on the gelation process of silica gels from sodium silicate. J. Mater. Res. Technol. 2020, 9, 10157–10165. [Google Scholar] [CrossRef]
- GB/T 4209-2022; Sodium silicate for industrial use. Standards Press of China: Beijing, China, 2022.
- Zong, J.; Yue, J. Continuous solid particle flow in microreactors for efficient chemical conversion. Ind. Eng. Chem. Res. 2022, 61, 6269–6291. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, R.; Tang, X.; Sun, P.; Wang, T. Study on the mass transfer behavior of single CO2 bubbles in sodium silicate solution. Phys. Chem. Chem. Phys. 2025, 27, 13071–13082. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Lasaga, A.C. Ab initio quantum mechanical studies of the kinetics and mechanisms of quartz dissolution: OH− catalysis. Geochim. Cosmochim. Acta 1996, 60, 2283–2295. [Google Scholar] [CrossRef]
- Faraji, F.; Alizadeh, A.; Rashchi, F.; Mostoufi, N. Kinetics of leaching: A review. Rev. Chem. Eng. 2022, 38, 113–148. [Google Scholar] [CrossRef]
- Visser, J.H.M. Fundamentals of alkali-silica gel formation and swelling: Condensation under influence of dissolved salts. Cem. Concr. Res. 2018, 105, 18–30. [Google Scholar] [CrossRef]
- Dusselier, M.; Davis, M.E. Small-Pore Zeolites: Synthesis and Catalysis. Chem. Rev. 2018, 118, 5265–5329. [Google Scholar] [CrossRef]
- Maraghechi, H.; Rajabipour, F.; Pantano, C.G.; Burgos, W.D. Effect of calcium on dissolution and precipitation reactions of amorphous silica at high alkalinity. Cem. Concr. Res. 2016, 87, 1–13. [Google Scholar] [CrossRef]
- Carrasco, G.F.; Portillo, M.C.; Santiago, A.C.; Diaz, A.R.; Mora-Ramirez, M.; Moreno, O.P. Morphological and structural analysis of the Fe(OH)3 and CuS transitions to Fe2O3 and CuO. Optik 2021, 243, 167377. [Google Scholar] [CrossRef]
- Wu, J.; Xiao, Y.; Yang, X.; Xu, D.-H.; Zhang, Z.-Y.; Zhong, Y.-J.; Wang, X.-L. Leaching kinetics for magnesium extraction from phosphate rock in the nitric acid method. Miner. Eng. 2022, 189, 107894. [Google Scholar] [CrossRef]
- Yu, J.; Sun, H.; Sun, X.; Guo, Y.; Zhang, W.; Li, Y. Kinetic study on low-temperature reduction of hematite in a microfluidized bed: Effect of pore characteristics on reaction rate. Mater. Today Commun. 2025, 46, 112886. [Google Scholar] [CrossRef]
- Götze, J.; Pan, Y.; Müller, A. Mineralogy and mineral chemistry of quartz: A review. Mineral. Mag. 2021, 85, 639–664. [Google Scholar] [CrossRef]
- Azof, F.I.; Safarian, J. Leaching kinetics and mechanism of slag produced from smelting-reduction of bauxite for alumina recovery. Hydrometallurgy 2020, 195, 105388. [Google Scholar] [CrossRef]
- Matinfar, M.; Nychka, J.A. A Review of Sodium Silicate Solutions: Structure, Gelation, and Syneresis. Adv. Colloid. Interface Sci. 2023, 322, 103036. [Google Scholar] [CrossRef]
- Qiu, Y.; Ma, J.; Chen, Y. Ionic Behavior in Highly Concentrated Aqueous Solutions Nanoconfined between Discretely Charged Silicon Surfaces. Langmuir 2016, 32, 4806–4814. [Google Scholar] [CrossRef]
- Mahadevan, T.S.; Du, J. Hydration and reaction mechanisms on sodium silicate glass surfaces from molecular dynamics simulations with reactive force fields. J. Am. Ceram. Soc. 2020, 103, 3676–3690. [Google Scholar] [CrossRef]
- Maliavski, N.; Zhuravlova, O. Calculation of polycondensation equilibria in aqueous solutions of silica and silicates. East.-Eur. J. Enterp. Technol. 2018, 4, 48–55. [Google Scholar] [CrossRef]





| Evaluation Criterion | Vapor-Phase Method | Sol–Gel Method | Proposed Method (This Study) |
|---|---|---|---|
| Raw Material Cost | High (e.g., SiCl4) | Very High (relies on high-purity organosilicon alkoxides) | Low (uses natural powder quartz as the main feedstock, which is abundant and low in cost) |
| Process Energy Intensity | Very High (requires high-temperature vapor-phase reactions) | Low to Moderate (ambient/low-temperature solution reactions) | Moderate (core purification step requires hydrothermal conditions but avoids extreme high temperatures) |
| Environmental Impact | High (uses highly corrosive, toxic precursors; complex by-product handling) | Relatively High (involves substantial organic reagents and subsequent treatment) | Low (primarily an aqueous alkaline system, relatively greener reagents, and easier wastewater treatment) |
| Control over Particle Morphology | Good (can produce high-purity nano-spheres) | Excellent (allows precise control over size and morphology) | Excellent (effective control over sphericity, size, and monodispersity by modulating silicate solution modulus) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Sun, H.; Peng, T.; Rehman, S.; Chen, S.; Chu, L.; Chen, T. Transforming Low-Value Quartz into Electronic-Grade Spherical SiO2 via a Morphology-Directed Hydrothermal Alkaline Process. Minerals 2025, 15, 1296. https://doi.org/10.3390/min15121296
Zhang Y, Sun H, Peng T, Rehman S, Chen S, Chu L, Chen T. Transforming Low-Value Quartz into Electronic-Grade Spherical SiO2 via a Morphology-Directed Hydrothermal Alkaline Process. Minerals. 2025; 15(12):1296. https://doi.org/10.3390/min15121296
Chicago/Turabian StyleZhang, Yiqin, Hongjuan Sun, Tongjiang Peng, Saeed Rehman, Shize Chen, Lingyan Chu, and Tao Chen. 2025. "Transforming Low-Value Quartz into Electronic-Grade Spherical SiO2 via a Morphology-Directed Hydrothermal Alkaline Process" Minerals 15, no. 12: 1296. https://doi.org/10.3390/min15121296
APA StyleZhang, Y., Sun, H., Peng, T., Rehman, S., Chen, S., Chu, L., & Chen, T. (2025). Transforming Low-Value Quartz into Electronic-Grade Spherical SiO2 via a Morphology-Directed Hydrothermal Alkaline Process. Minerals, 15(12), 1296. https://doi.org/10.3390/min15121296








