4.2. Does Use of the 235U16O/238U16O Improve Precision and Accuracy at Low Count Rates?
For any isotope ratio determination, the total uncertainty is a combination of uncertainty associated with the count rate, the behavior of standards, the robustness of the mass fractionation correction regime, inter-detector calibration issues, as well as other factors. For SIMS, as with all mass spectrometric isotope ratio determinations, there are a variety of approaches to constraining and combining these uncertainties (see discussion by [
4]). However, it is indisputable that two major contributors to the precision and accuracy of any SIMS measurement are (1) the stability of the isotope ratio, as reflected by the standard deviation, during each analysis, and (2) the deviance of the raw (e.g., uncorrected) ratio relative to the ‘true’ value for the matrix in question. For the
235U/
238U ratio, both are known to vary proportionally with the count rate of
235U (when
235U is the minor isotope). For all the materials examined in this study, the secondary ion count rates of
235U
16O and
238U
16O were considerably higher than the
235U and
238U (exceptions are discussed in
Section 4.3).
As described in
Section 2, the UO
2 was analyzed using a variety of primary beam currents ranging from 200 pA down to 20 pA. This resulted in a wide range of total counts for
235U and
235U
16O that enable a robust assessment of the effect of using the
235U
16O/
238U
16O compared to the
235U/
238U ratio. In
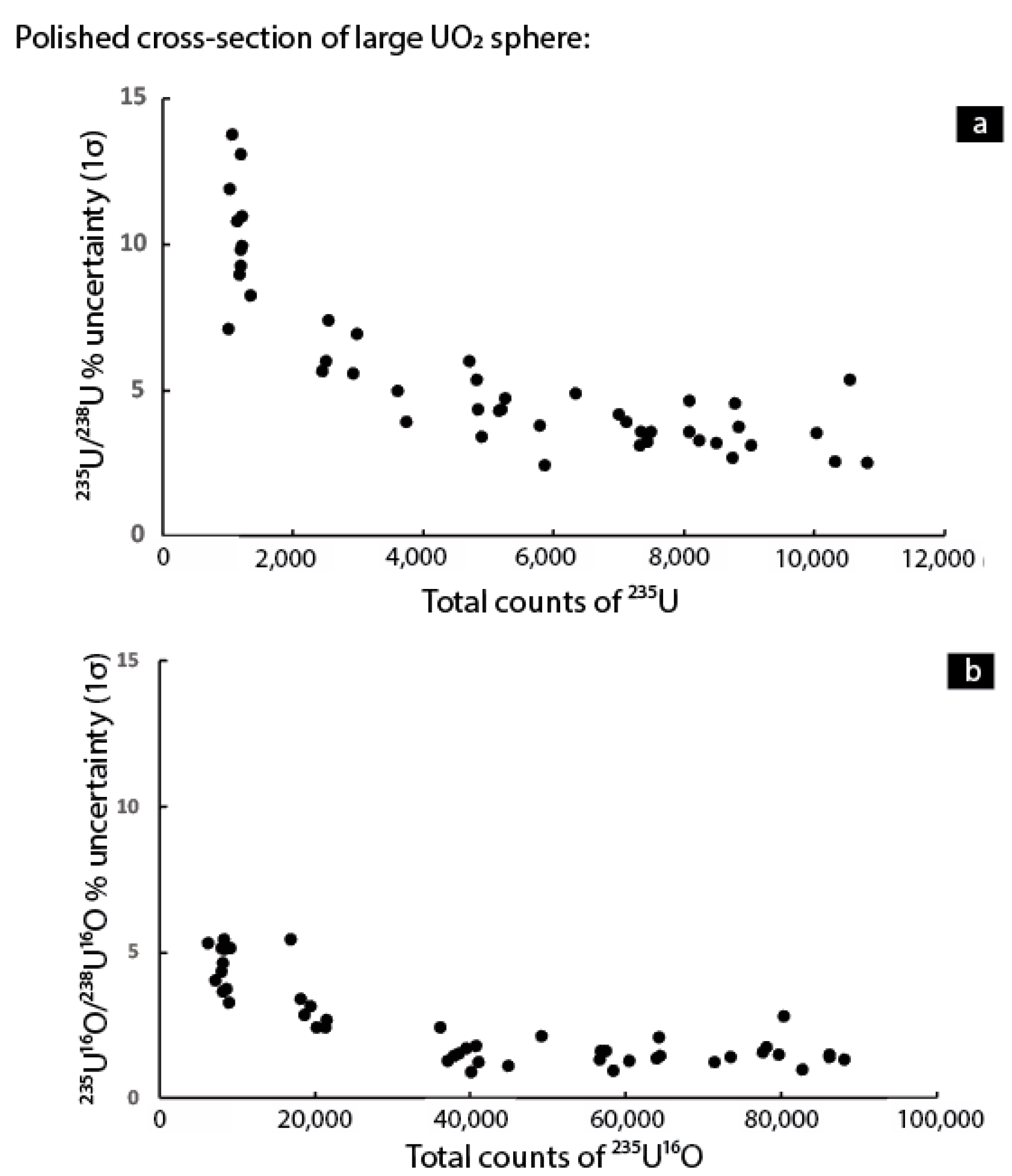
Figure 2, which is a plot of the percent uncertainty, calculated as 1σ associated with the average of the ratios observed at each cycle of data during each analysis, on the
235U/
238U (
Figure 2a) and
235U
16O/
238U
16O ratios (
Figure 2b) as a function of the total number of counts of
235U (
Figure 2a) and
235U
16O (
Figure 2b) observed during each analysis of the UO
2 sphere’s polished cross section, there is a clear improvement in the standard deviation associated with each individual measurement when the
235U
16O/
238U
16O ratio is used. This is also evident in
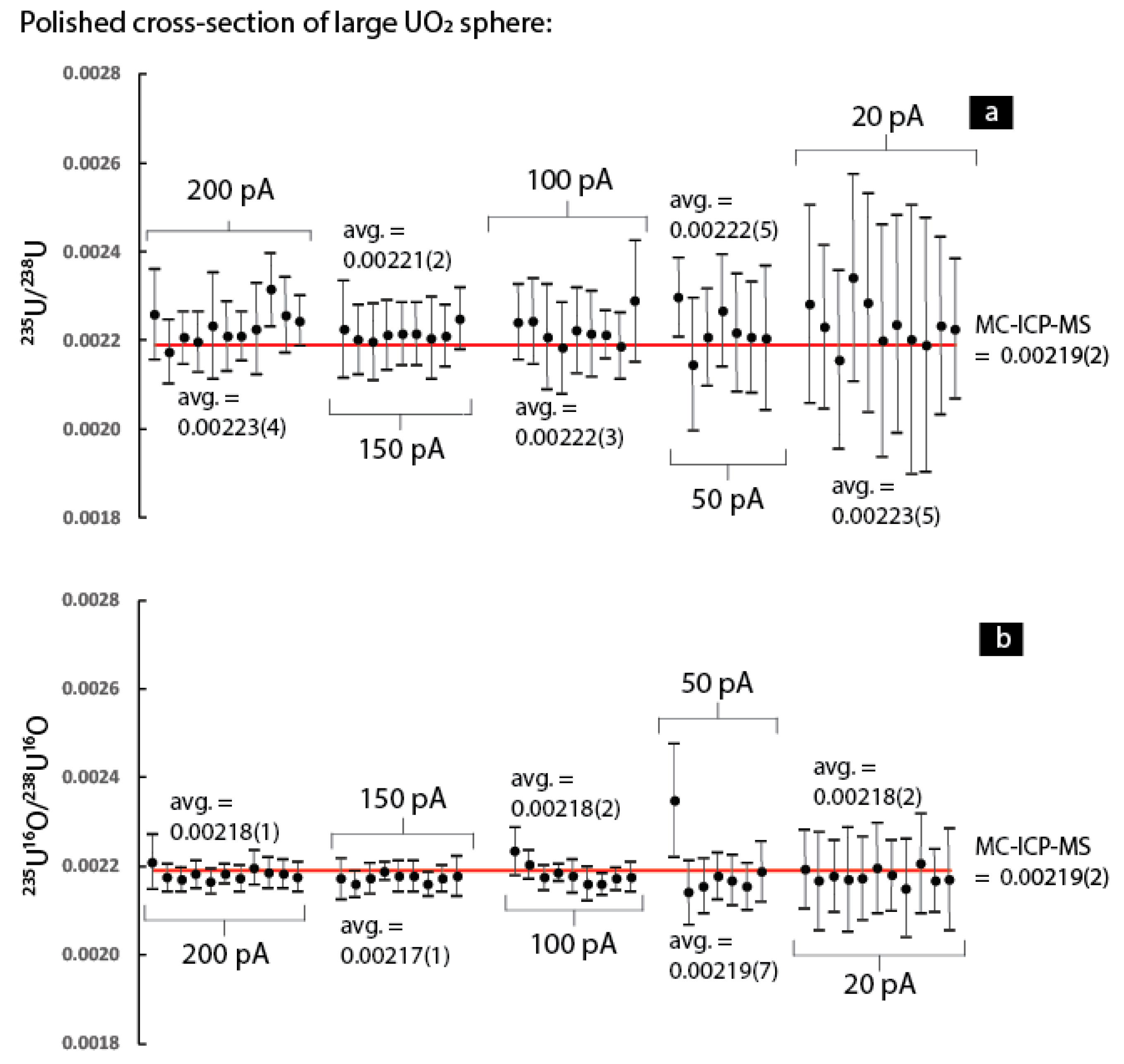
Figure 3, which plots each analysis’s
235U/
238U (
Figure 3a) and
235U
16O/
238U
16O ratios (
Figure 3b) and its associated 1σ uncertainty for the UO
2 sphere. In
Figure 3, the individual analyses are grouped according to the five primary beam currents (200 pA, 150 pA, 100 pA, 50 pA, and 20 pA) that were used to analyze the UO
2 sphere and are also shown relative to the solution MC-ICP-MS value. Clearly, there is a reduction in the standard deviation associated with each measurement. In
Figure 3, it is also evident that the raw isotope ratios fall closer to the solution MC-ICP-MS value when the
235U
16O/
238U
16O ratio is used. This observation is further bolstered by
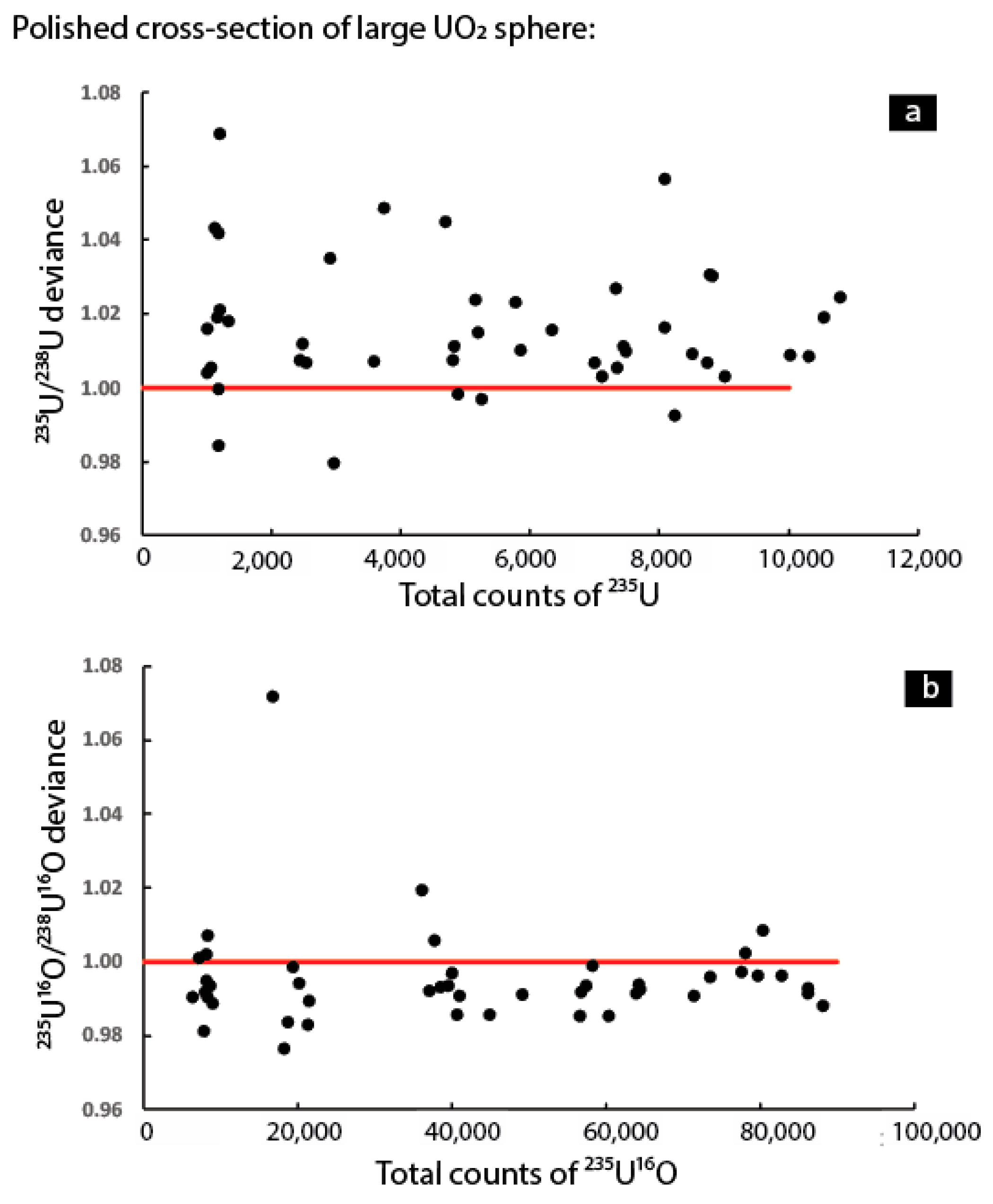
Figure 4, where each analysis’s deviance in the
235U/
238U (
Figure 4a) and
235U
16O/
238U
16O (
Figure 4b) ratios relative to the solution MC-ICP-MS value are plotted as a function of the total number of counts of
235U (
Figure 4a) and
235U
16O (
Figure 4b) observed during each analysis.
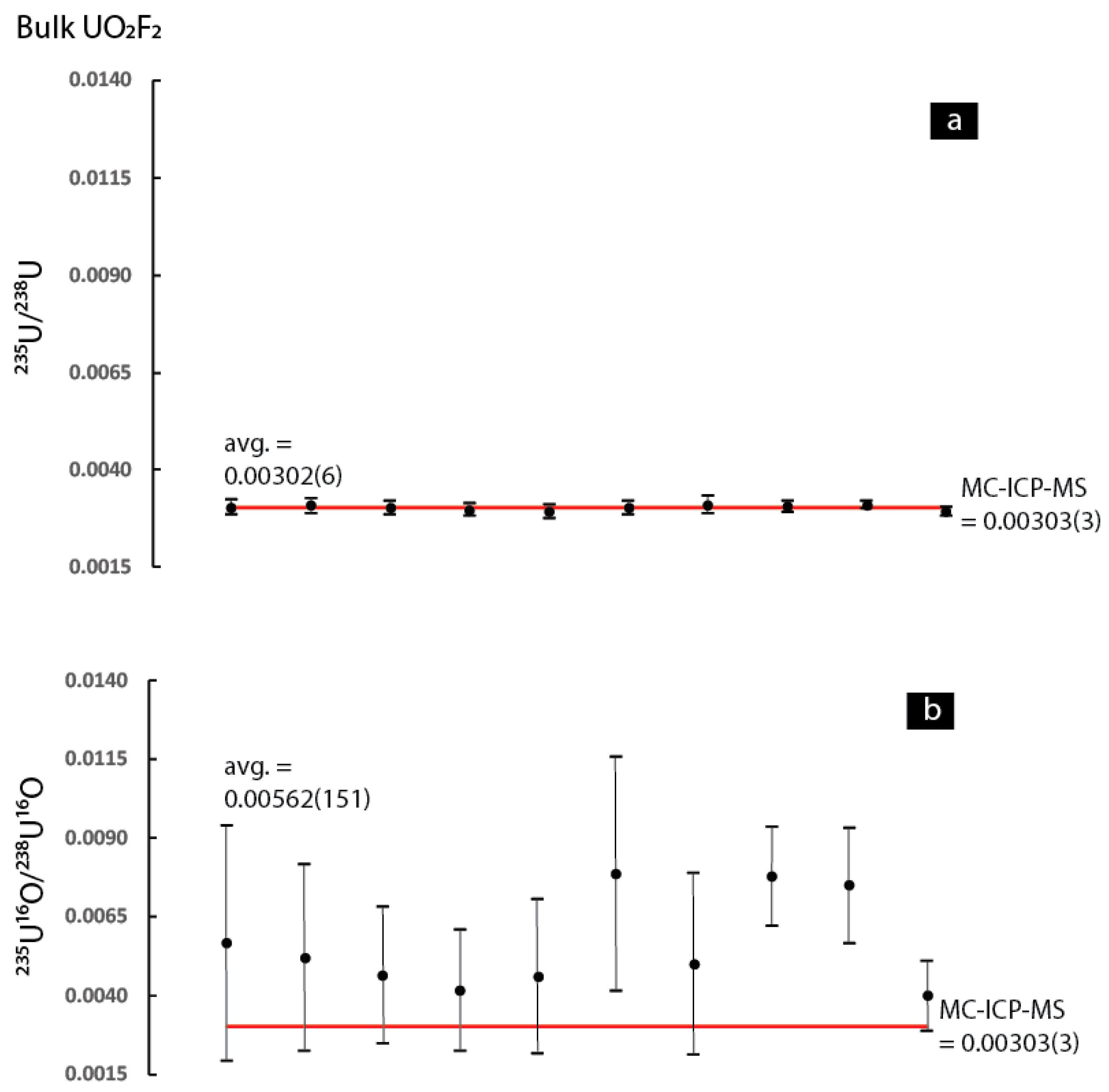
For the UO
2 analyzed in this study, use of the
235U
16O/
238U
16O ratio appears to result in improved accuracy and precision. However, because the atomic-to-molecular secondary ion formation rate and general behavior is matrix dependent, it is necessary to consider whether this behavior is present in the other matrices examined in this study. While the UO
2 was the only material that was investigated using multiple primary beam currents, the comparison of the
235U/
238U versus the
235U
16O/
238U
16O acquired using only a 200 pA beam current should still provide a preliminary indication of whether the observations made on UO
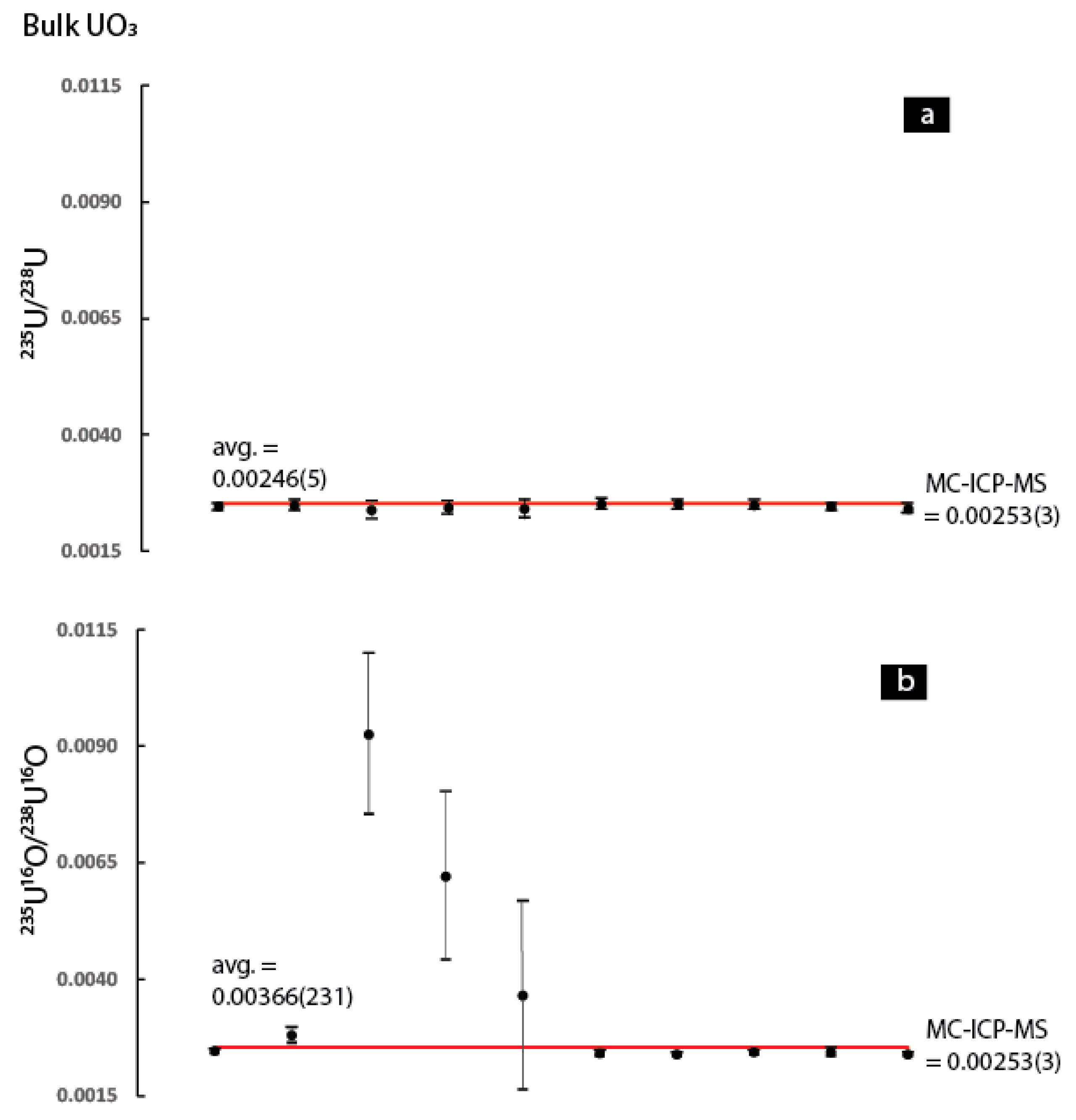
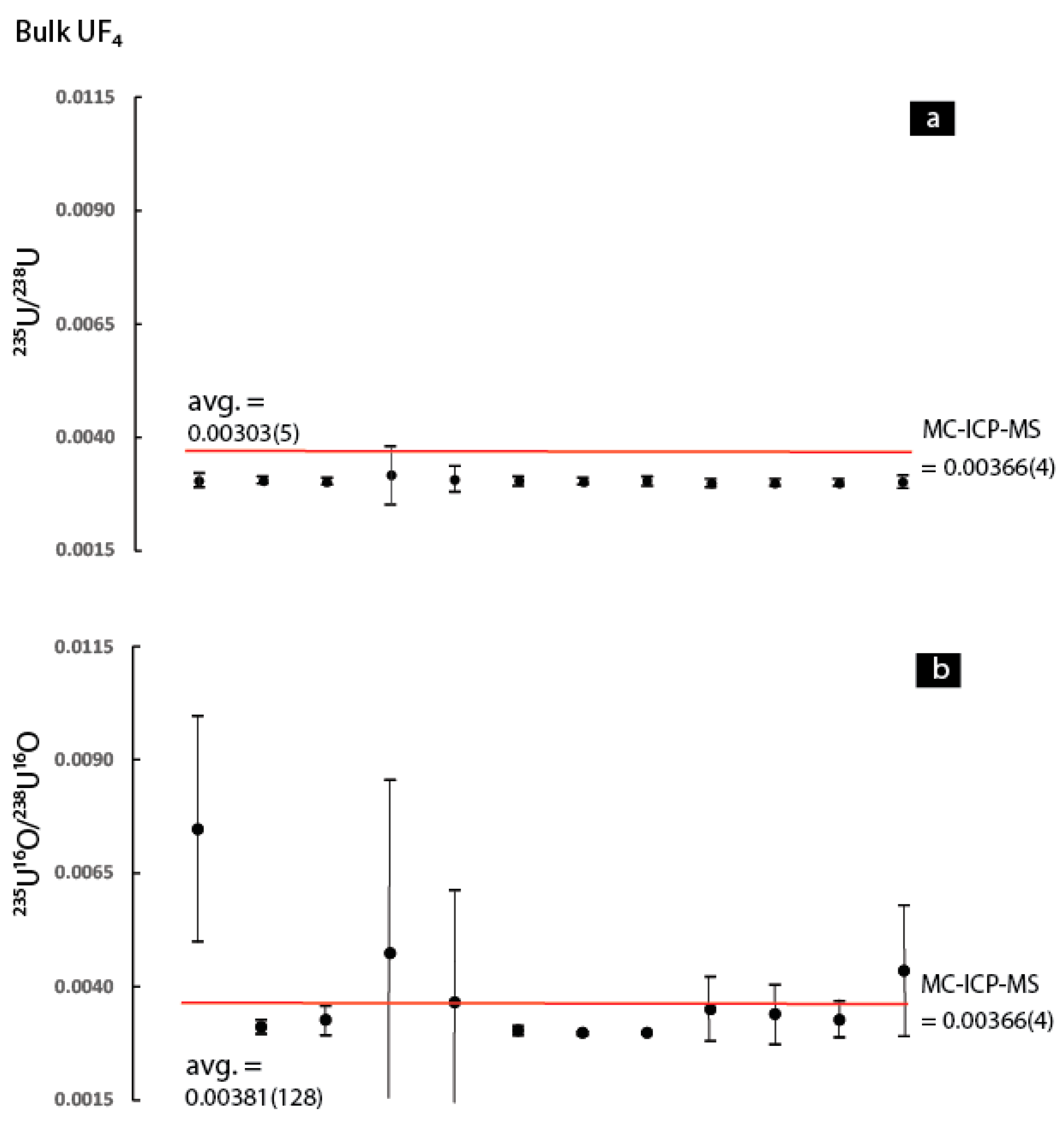
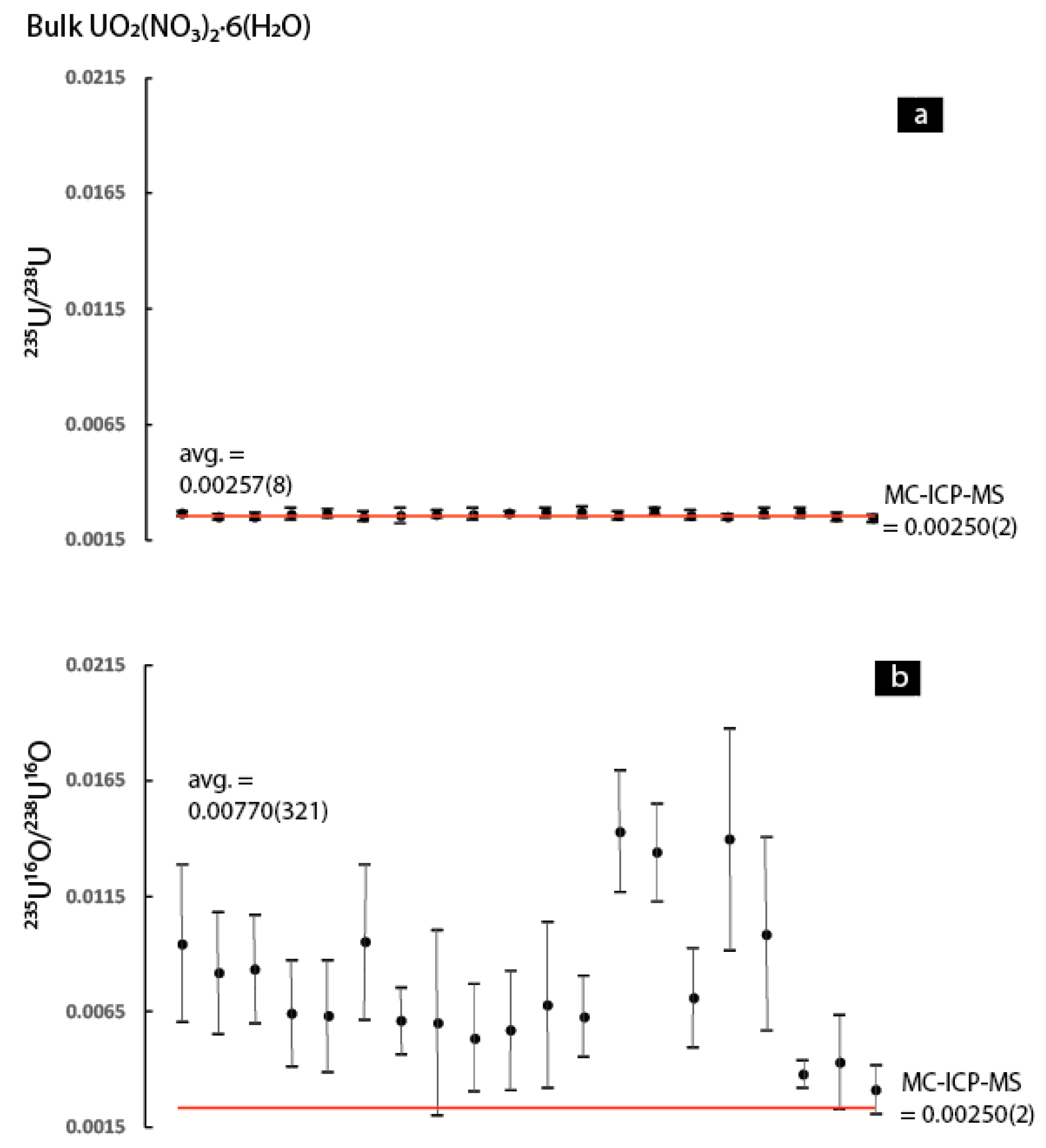
2 can be extended to the other uranium compounds. In
Figure 5,
Figure 6,
Figure 7 and
Figure 8, which are plots of each measured
235U/
238U and
235U
16O/
238U
16O ratio, and their associated 1σ uncertainty for the UO
2F
2 (
Figure 5a,b), UO
3 (
Figure 6a–b), UO
2(NO
3)
2·6(H
2O) (
Figure 7a,b), and UF
4 (
Figure 8a,b), it is clear that the observations made on UO
2 cannot be extended uniformly to the other uranium compounds. This is because for many of the analyses, there is considerably higher standard deviation when the
235U
16O/
238U
16O ratio is used. Additionally, when the NanoSIMS data is compared with the MC-ICP-MS
235U/
238U ratios (UO
2F
2 in
Figure 5, and UO
3 in
Figure 6, UO
2(NO
3)
2·6(H
2O) in
Figure 7, and UF
4 in
Figure 8), it is clear that there is considerably more scatter relative to the solution value when the
235U
16O/
238U
16O ratios are used for all of the uranium compounds except the UO
2. The scatter also appears decoupled from the
235U/
238U ratios (e.g., for some analyses, the
235U
16O/
238U
16O ratio deviates strongly from the solution value, but the
235U/
238U ratio remains stable).
Therefore, it appears that use of the
235U
16O/
238U
16O ratio would result in improved precision and accuracy for certain bulk chemistries (e.g., UO
2), but not others (e.g., UO
2F
2, UO
3, UO
2(NO
3)
2·6(H
2O), and UF
4). The reasons for this behavior will be discussed in the following section, but at this point it is also worth considering the behavior of matrices containing only trace levels of uranium. In
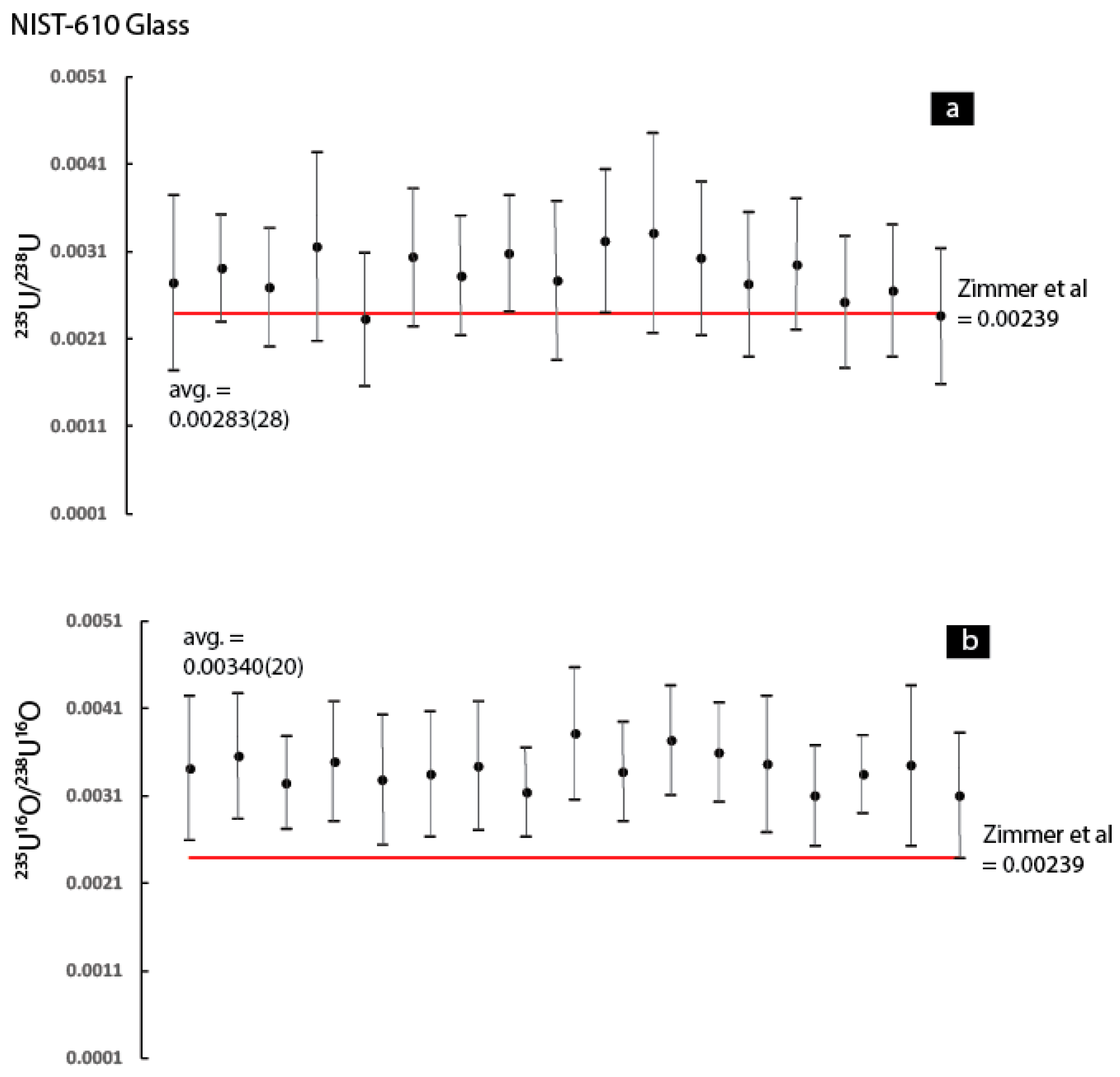
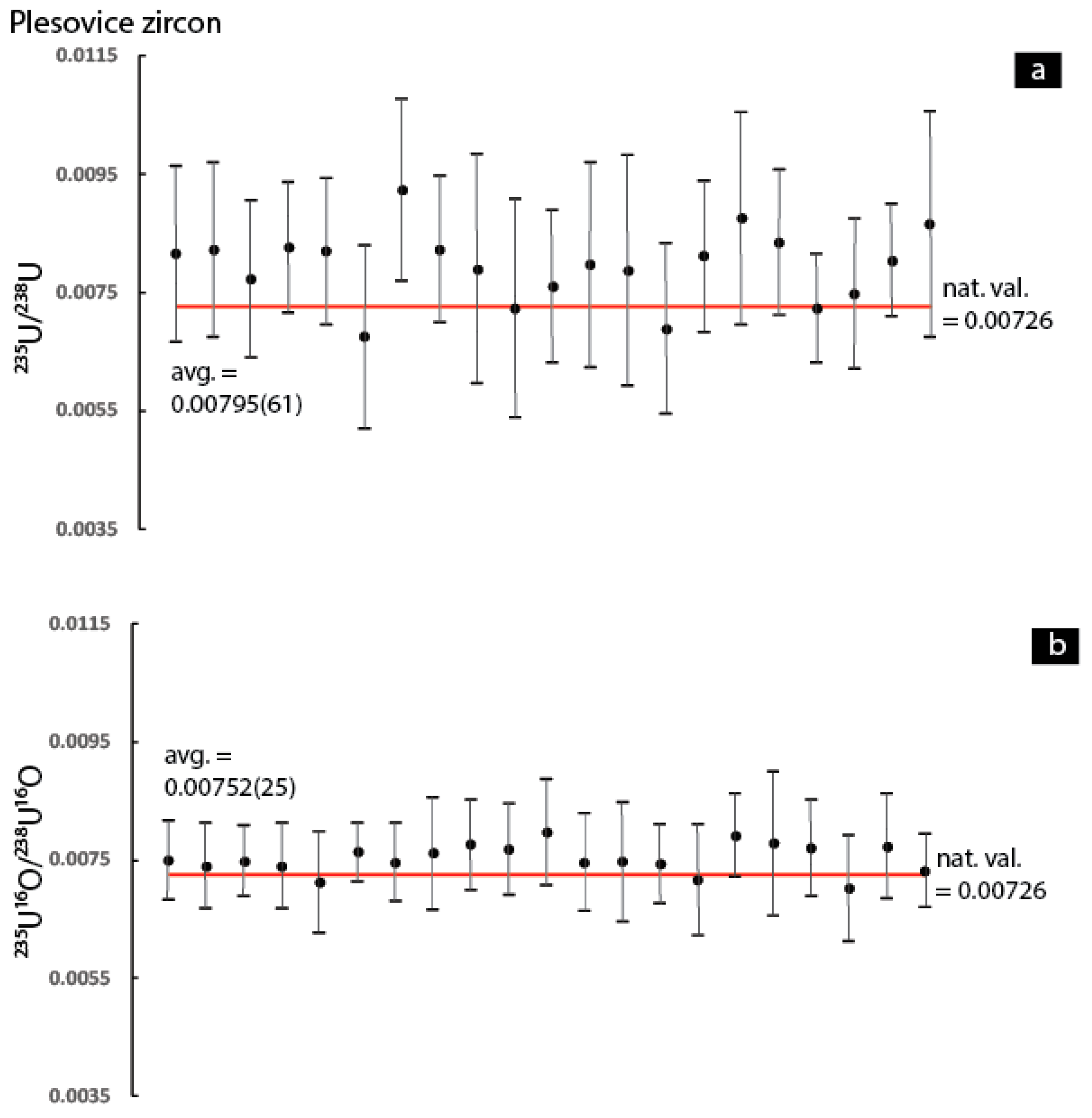
Figure 9 and
Figure 10, each analyses of
235U/
238U and
235U
16O/
238U
16O ratio, and their associated 1σ uncertainties, for the NIST-610 glass (
Figure 9a,b) and Plesovice zircon (
Figure 10a,b) are shown relative to the reference values (refer to figure captions) for these materials. For the NIST-610 glass, there is a slight improvement in the uncertainty of the individual measurements when the
235U
16O/
238U
16O ratio is used, but this is accompanied by a slight shift further away from the ‘true’
235U/
238U ratio reported in [
22]. In contrast, the data from the Plesovice zircon indicates a marked improvement in the uncertainty associated with the individual measurements as well as a decrease in the degree of deviance relative the natural
235U/
238U ratio used as the ‘true’ value. The observation that the
235U
16O/
238U
16O ratios have marked improvement for these two materials is an important observation considering that uranium is only present at a trace phase within these two matrices (ppm levels)—this is also evident by the considerably lower count rates for the atomic and molecular uranium secondary ion species relative to the uranium compounds (
Table S1).
In summary, the data indicates that use of the 235U16O/238U16O ratio results in higher precision and better accuracy for the UO2 as well as the two silicate reference materials. In contrast, for the UO2F2, UO3, UO2(NO3)2·6(H2O), and UF4 it is clear that the 235U16O/238U16O ratio is associated with considerably higher scatter (both within and between individual analyses) compared to the 235U/238U. The implications of this observation for SIMS isotope ratio measurements will be discussed in the final section of the discussion. Now, the discussion will shift to a discussion of the possible mechanisms responsible for producing the sporadic results regarding improvement in the accuracy and precision when the 235U16O/238U16O ratio is used.
4.3. Possible Origins of the Inconsistent Behavior Between the 235U/238U and 235U16O/238U16O Across the Various Compounds
As described in the preceding section, an observation from the dataset is that use of the 235U16O/238U16O compared to the 235U/238U ratio results in improved accuracy and internal precision for the UO2 and two silicate reference materials. In contrast, the accuracy and precision are considerably worse for the UO2F2, UO3, UO2(NO3)2·6(H2O), and UF4 when the 235U16O/238U16O is used. Three possible origins for this behavior will be explored in this discussion: (a) the SIMS ‘matrix effect’, (b) fluorine- and carbon-based interferences, and c) the effect of sample topography.
If only data from the uranium compounds were available, it would be reasonable to attribute the decrease in precision and accuracy to some type of matrix effect related to the presence of fluorine and nitrogen in the bulk matrices of the UO2F2, UO2(NO3)2·6(H2O), UO3, and UF4. The UO3 examined in this study was prepared by calcination of UO2(NO3)2·6(H2O), but no additional steps were taken to remove residual nitrogen. Therefore, there is presumably residual nitrogen present in the UO3 that was examined in this study. In such a scenario, it would be possible that nitrogen and fluorine contributed to scavenging of the oxygen ions available at the sputtering site, thus destabilizing the formation rate of the UO molecular ion. However, oxygen scavenging at the sputtering site does not explain why the results from the two silicate reference materials mirrored those from the UO2 in that the 235U16O/238U16O resulted in improved accuracy and precision relative to the 235U/238U ratio. In considering that uranium is only present as a trace phase within these two silicate reference materials, there would have been an abundance of reactive ions available at the sputtering site to scavenge oxygen ions.
For the two fluorine bearing uranium compounds, it is also possible that
19F
+ combined with
235U
+ to form the
235U
19F
+ molecular secondary ion (mass = 254.0423262) that would require an MRP of (defined as M/∆M) of 75,353, well above what as used in this study, to be separated from the
238U
16O
+ (mass = 254.045697622) molecular ion measured in this study. It is possible to assess whether
235U
19F contributed to the observed secondary ion signal of
238U
16O
+ by looking at the
235U
16O/
238U
16O ratios for the UO
2F
2 and UF
4 in
Figure 5b and
Figure 7b. The presence of
235U
19F
+ would be expected to enhance the secondary ion signal observed at
238U
16O
+, thus resulting in a lower
235U
16O/
238U
16O ratio. For the UO
2F
2 (
Figure 5b), the individual
235U
16O/
238U
16O ratios are consistently biased above the solution ICP-MS and NanoSIMS
235U/
238U ratios (
Figure 5a), whereas for the UF
4 (
Figure 7b), the
235U
16O/
238U
16O ratios are highly scattered but do tend to agree with the NanoSIMS
235U/
238U ratios (
Figure 7a), which are also biased below the solution ICP-MS value. Therefore, there does not appear to be a systematic or significant contribution from the
235U
19F
+ on the
238U
16O
+ signal.
It is also necessary to consider the possibility that
238U
13C
+ (mass = 251.054138) and
238U
12C
1H
+ (mass = 251.058608) molecular ions interfered with the observed
235U
16O
+ secondary ion signal (mass = 251.038837622). Because MRP values of 16,408 and 12,698 would be needed to separate the potential
238U
13C
+ and
238U
12C
1H
+ interferences on
235U
16O
+, respectively, and the fact that carbon from the epoxy or polishing compound may have contaminated, and then become trapped, in the uranium compounds with irregular surfaces, it is fully possible that a portion of the
235U
16O
+ signal was derived from carbon-based molecular interferences.
238U
13C
+ and
238U
12C
1H
+ would be expected to increase the observed
235U
16O
+ secondary ion signal, thus biasing the
235U
16O/
238U
16O ratio toward elevated values. Examination of the results from the UO
2F
2, UO
2(NO
3)
2·6(H
2O), UO
3, and UF
4 (
Figure 5,
Figure 6 and
Figure 7) reveals that some of the individual
235U
16O/
238U
16O ratios display a marked positive bias, suggesting that carbon-based molecular interferences may have contributed to the instability of the
235U
16O/
238U
16O ratios relative to the
235U/
238U ratios from these samples. However, it is important to note that the
235U
19F
+ molecular interference on
238U
16O would have an opposite effect to the carbon-based molecular interferences on the
235U
16O/
238U
16O ratio, so understanding the interplay between these two potential interferences is not straightforward.
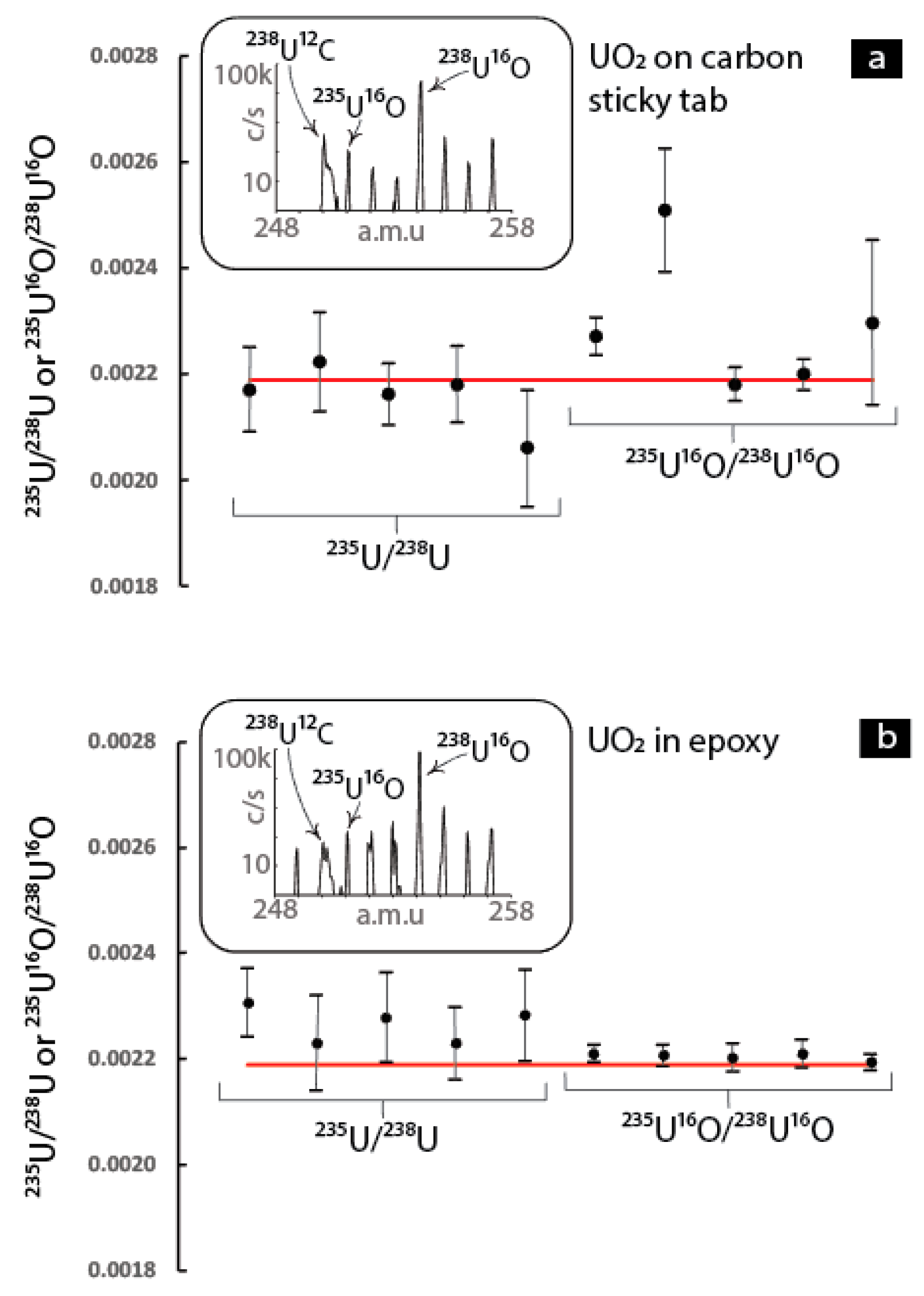
While the effects of fluorine- and carbon-based molecular interferences on the measured 235U16O/238U16O ratios cannot be ruled out, fully evaluating this potential mechanism as the cause of destabilization of the 235U16O/238U16O ratios is complicated by the fact that there are no data available to independently assess the rate at which these potential molecular interferences were formed. While it may theoretically be possible to monitor the intensity of the 238U12C molecular species, and then use this information to subtract the inferred 238U13C contribution to the 235U16O signal, this would require a different detector and magnetic field setup than what was used in this study, and therefore no such data are available. It would also be necessary to account for the 238U12C1H hydride formation rate. To more fully understand the magnitude of the 238U13C contribution to the 235U16O signal, an additional analytical session was conducted in March 2019 whereupon data collected from UO2 dispersed onto a sticky carbon tab could be compared with data collected from UO2 mounted in epoxy.
Examination of the insets on
Figure 11 reveals that the
238U
12C molecular species can be observed in both sample preparation approaches (the sticky carbon tab as well as the epoxy). Examination of a mass scan conducted on UO
2 pressed into Indium (provided in
Table S2) reveals no signal at the
238U
12C molecular species, suggesting that the source of carbon is indeed related to the sample preparation (e.g., contamination introduced during grinding/polishing) and sticky carbon Table For the UO
2 on the sticky carbon tab, the
238U
12C molecular species achieves a maximum of ~400 c/s (
Table S2), whereas for the UO
2 in epoxy, it achieves a maximum of ~65 c/s (
Table S2). Using the natural abundance of
13C (1.07%), the expected count rate for the
238U
13C interference on
235U
16O would be ~4.3 c/s for the UO
2 dispersed on the sticky carbon tab and ~0.7 c/s for the UO
2 in epoxy. For the UO
2 dispersed on the sticky carbon tab, this would account for ~3.7% of the signal at the
235U
16O mass position. For the UO
2 mounted in epoxy, the contribution is ~0.5%.
Based on these considerations, it does appear that if a significant amount of carbon is present within the analytical volume (as would be expected for the UO
2 dispersed onto the sticky carbon tab), the
235U
16O/
238U
16O ratio would be expected to exhibit a few % positive deviation relative to the
235U/
238U. In contrast, where only trace amounts of carbon are present (as would be expected for the UO
2 mounted in epoxy), the effect would be considerably less. This prediction is born out in
Figure 11, where it can be seen that some of the
235U
16O/
238U
16O values from the UO
2 dispersed onto the sticky carbon tab are positively deviated by anywhere from few % up to ~20% relative to the
235U/
238U, whereas for the UO
2 in epoxy, the
235U
16O/
238U
16O uniformly displays better precision and accuracy despite the fact that trace amounts of carbon are present. However, the fact that several of the analyses on the sticky carbon tab produce
235U
16O/
238U
16O with better precision and accuracy compared to the
235U/
238U suggests that the process of forming the U-C molecular species is not consistent from analysis to analysis despite having an abundance of carbon available at the sputtering site. Furthermore, the effect of this interference would be expected to be far worse on the carbon sticky tab in comparison to the epoxy, even under circumstances where an uneven sample surface may have trapped some epoxy and/or abrasive particles during preparation. Therefore, it is not clear whether the carbon-based molecular interferences can serve as the sole explanation for why the compounds shown in
Figure 5,
Figure 6,
Figure 7 and
Figure 8 exhibit highly scattered
235U
16O/
238U
16O in comparison to their
235U/
238U ratios.
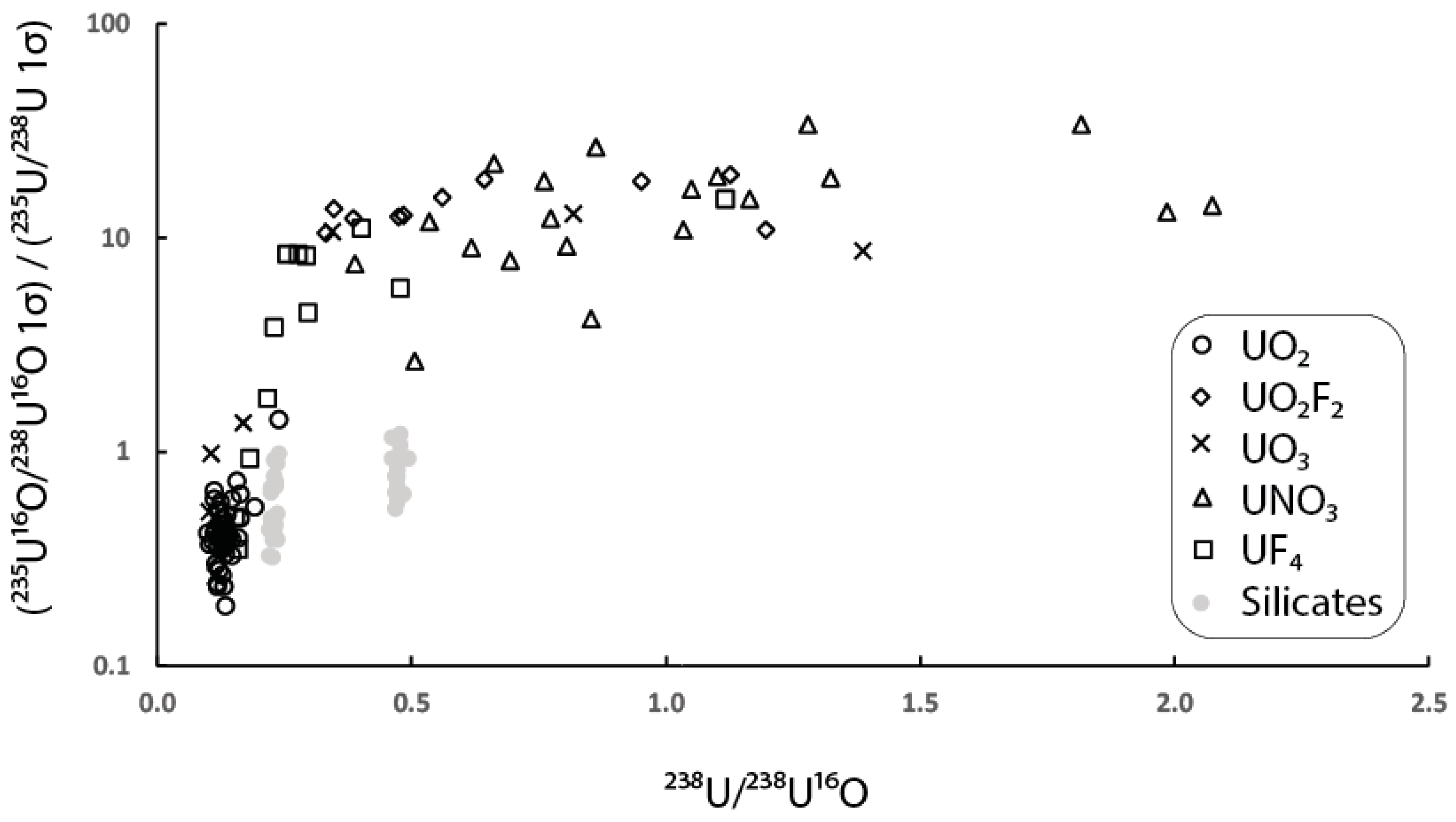
Therefore, it is still worthwhile to consider additional origins for the highly unsTable 235U
16O/
238U
16O ratios displayed by some of the uranium compounds. In
Figure 12, where the 1σ uncertainty of the
235U
16O/
238U
16O relative to that of the
235U/
238U ratios is plotted as a function of each analysis’s average
238U/
238U
16O ratio, there is a correlation between the results obtained from the
235U
16O/
238U
16O versus the
235U/
238U ratios and each analysis’s average
238U/
238U
16O. More specifically, analyses with a higher average elemental oxide abundance trend toward
235U
16O/
238U
16O ratios that are more precise than the
235U/
238U ratios. This observation might favor the scavenging scenario described at the start of this section, because it could be used to state that analyses where there was less available oxygen ions to form the U-O molecular ion display poorer precision and accuracy in the
235U
16O/
238U
16O ratio; however, this possibility is not supported by the fact that the two materials with the highest concentration of reactive ions and lowest uranium concentrations (the NIST 610 glass and the Plesovice zircon) align with the results from the UO
2, which is the only uranium compound not containing other elemental constituents.
Therefore, it is necessary to consider other reasons for worsening precision and accuracy at lower average uranium oxide molecular secondary ion formation rates. Another possibility that can be considered with the available data are the effects of topography. As discussed earlier regarding the potential for fluorine- and carbon-based molecular interferences, it is possible that carbon from the epoxy may have become trapped in the irregular surfaces of the some of the uranium compounds. However, it is also necessary to consider that topography can also have a direct effect on secondary ion yields [
35].
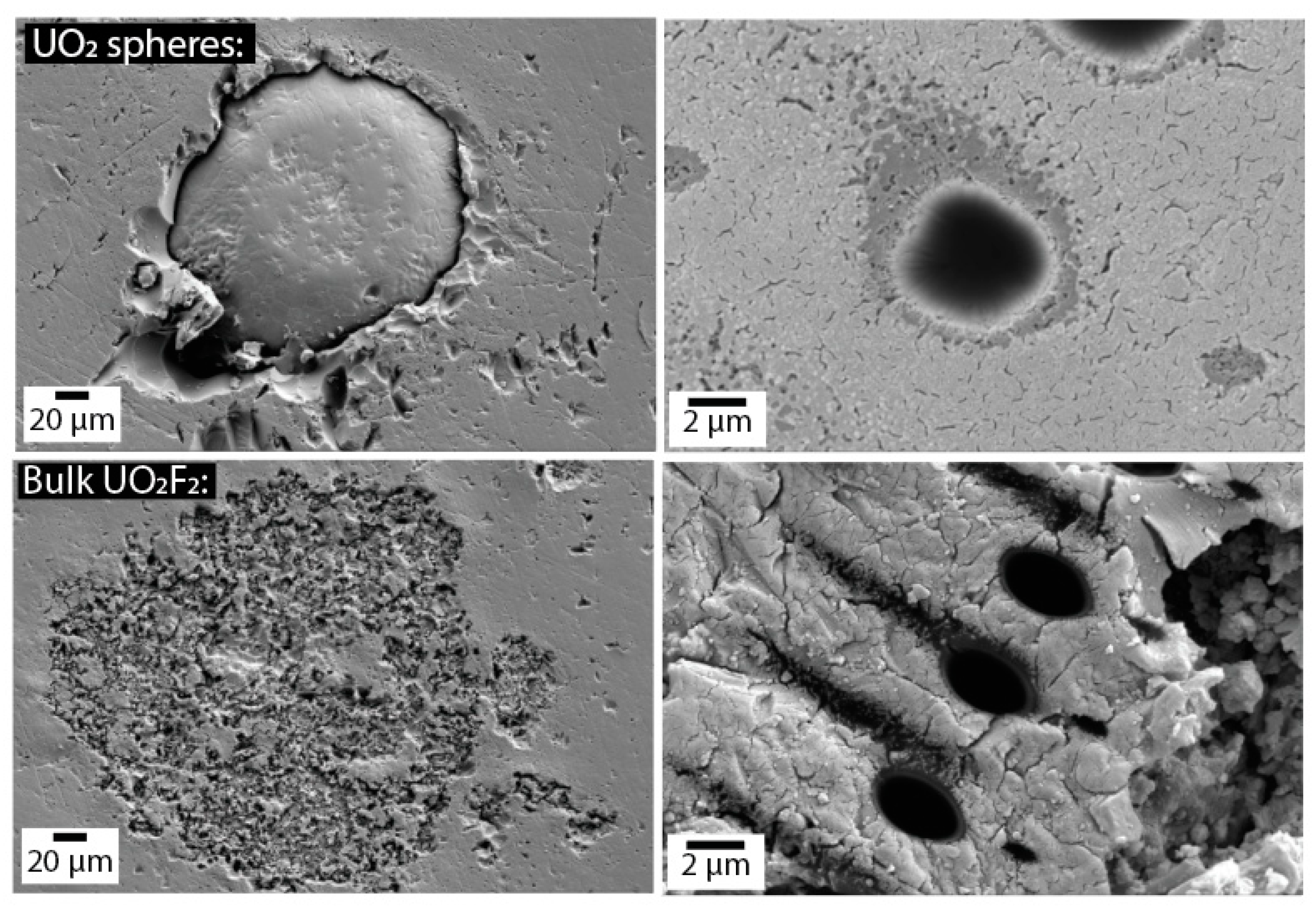
Examination of
Figure 1 reveals that the UO
2 produced a flat surface when the mount was polished, whereas the UO
2F
2 did not. Although SEM images of the two silicate reference materials were not acquired as part of this study, both materials are routinely analyzed by SIMS and are known to produce highly polished and flat surfaces when mounted in epoxy and polished. While SEM images of the UO
3, UO
2(NO
3)
2·6(H
2O), and UF
4 are not shown, their surfaces are more similar to the UO
2F
2 than the nicely polished and flat surface of the UO
2. Therefore, another basic observation from the data is the uranium compounds with poor surface preparation produced considerably worse
235U
16O/
238U
16O in comparison to the
235U/
238U ratios. The effect of topography on the precision and accuracy of isotope ratios determined by SIMS has been investigated by several authors (see discussion by [
35]), with the general consensus being that irregular surfaces can induce spot-to-spot variation at the per mil level. For the results of this study, it is important to note that the average levels of accuracy and precision associated with the
235U/
238U ratios of the UO
2F
2, UO
3, UO
2(NO
3)
2·6(H
2O), and UF
4 are not considerably worse than for the UO
2. Rather, the difference is seen in the
235U
16O/
238U
16O ratio. If sample topography is to blame for this behavior, then it would appear that the topographical influence on the
235U
16O/
238U
16O is an order of magnitude greater than for the
235U/
238U.
It is possible that the irregular surface produced by mounting and polishing the UO
2F
2, UO
3, UO
2(NO
3)
2·6(H
2O), and UF
4 results in irregular UO
+ production, whereas the effect on the U
+ ions is not as drastic. This lack of consistency in the UO
+ production rate is evident in
Figure 12, where it is clear that the materials for which use of the
235U
16O/
238U
16O ratio resulted in improved precision and accuracy (the UO
2 and silicate reference materials) display a relatively narrow range in their
235U/
235U
16O and
238U/
238U
16O ratios. In contrast, the materials with highly variable average
235U/
235U
16O and
238U/
238U
16O secondary ion ratios between the different analyses have
235U
16O/
238U
16O ratios with considerably poorer precision and accuracy in comparison to the
235U/
238U ratios. While there may be other factors that contributed to this variability, the only readily observable difference between these materials and those that yielded more precise and accurate
235U
16O/
238U
16O is the nature of the sample surface. Bulk chemistry or fluorine-based interferences may be factors, but the fact that the silicate reference materials yielded results such as the UO
2, as well as the results from the UO
2F
2 and UF
4, do not favor this possibility. For the individual analyses, whose
235U
16O/
238U
16O ratios are biased high relative to the
235U/
238U ratios, the effect of carbon-based interferences also cannot be ruled out. However, comparison of results from UO
2 in epoxy versus UO
2 dispersed onto a sticky carbon tab suggest that the effect of the carbon-based interferences may not be adequate to account for the extreme deviances in the
235U
16O/
238U
16O ratio displayed by some of the compounds. In the following section, the implications of these observations as well as a path to better understand this behavior are discussed.
4.4. Implications for SIMS Analysis and Need for Additional Studies
The results of this study indicate that use of the
235U
16O/
238U
16O ratio can result in improved precision and accuracy for UO
2 during SIMS analysis, baring significant contribution to the
235U
16O signal from
238U
13C. The most likely explanation for this effect is that the count rate of both the
235U
16O
+ and
238U
16O
+ consistently exceeds those of the
235U
+ and
238U
+ secondary ions by a factor of approximately 7.5 (
Table S1). A similar effect is observed for the two silicate reference materials that were examined, even though the other uranium compounds examined exhibit less consistency (e.g.,
Figure 12). Therefore, in a situation where low count rates are an anticipated issue (e.g., a small amount of material is available or a high spatial resolution measurement with a low primary beam current is needed) and there is limited information about the chemistry of the material, a prudent approach would be to collect both the
235U
16O
+ and
238U
16O
+ molecular and
235U
+ and
238U
+ atomic secondary ions. Based on the data collected in this study, it should be readily apparent whether the
235U
16O/
238U
16O or
235U/
238U ratios will yield the result with the highest precision and accuracy. This is because the materials that displayed considerably diminished accuracy on the
235U
16O/
238U
16O in comparison to the
235U/
238U ratio also displayed considerably worse internal precision (as reflected by the higher 1σ values associated with each analysis). Therefore, based on the available data, choosing the ratio (e.g.,
235U/
238U versus
235U
16O/
238U
16O) with the highest precision should also result in selecting the most accurate ratios. However, there are several caveats that must be considered.
The
235U/
238U and
235U
16O/
238U
16O ratios reported in this study have not been corrected for any type of mass fractionation or other instrument specific bias. Therefore, it is not possible to evaluate which ratio (e.g.,
235U/
238U versus
235U
16O/
238U
16O) is most amenable to the type of correction regimes that are typically used in isotope ratio mass spectrometry. The basic conclusion outlined in the preceding section will likely apply to any type of correction regime that is applied, but a logical next step is to further study the behavior of the
235U/
238U versus
235U
16O/
238U
16O ratio in a suite of uranium compounds with certified uranium isotope compositions. During such an approach, it would also be worthwhile to determine whether the observations made in this study hold true at different
235U/
238U ratios because all the materials examined in this study have depleted-to-natural
235U/
238U ratios. Other important variables to test would be the effects of different sample surface morphologies and substrates, in addition to a systematic assessment of the potential interference contributions outlined in
Section 4.3. In summary though, the basic observation that the raw
235U/
238U and
235U
16O/
238U
16O ratios are both quite close to the solution MC-ICP-MS results means that both ratios should be amenable to the application of a reference material-based correction scheme. Therefore, selection of the ratio with the lowest internal precision (e.g., 1σ value) should yield the ‘best’ result in count-rate-limited situations.
While this study was expressly focused on the
235U/
238U determination, the possibility of taking advantage of the greater U-O molecular generation in comparison to the U elemental secondary ion production to improve accuracy and precision may also extend to other uranium isotope ratios. For example, the
236U/
238U and
234U/
238U ratios are important indicator of whether samples from a variety of matrices contain anthropogenically perturbed U (see discussion by [
36,
37,
38]). Because the natural
234U/
238U is ~0.000055, and <10
−10 for
236U/
238U [
37], the issue of low secondary ion count rates for
235U that formed the basis of this investigation become much more severe for determination of the
234U/
238U and
236U/
238U by SIMS. Furthermore, the
236U/
238U determination is compounded by the formation of
235U
1H secondary ions (see discussion by [
4]). While it is likely that the secondary ion count rates of the
236U
16O (mass = 252.04077 amu) and
234U
16O (mass = 250.035861 amu) molecular species would exceed those of the
236U and
234U elemental secondary ions during SIMS analysis, MRPs (defined as M/∆M) of 18,836.6 and 16,755.8 would be needed to separate interferences from
238U
14N (mass = 252.053857 amu) and
238U
12C (mass = 250.050783), respectively. Furthermore, examination of the mass scans provided as insets in
Figure 12 reveals elevated secondary ion counts at masses ~250 and ~252, suggesting that a first step in exploring use of the elemental oxide ratios for the
236U/
238U and
234U/
238U determination would be to understand whether a suitable sample preparation route can be developed such that the contribution of nitrogen and carbon to the analytical volume is eliminated.