Effect of Carbon on the Volume of Solid Iron at High Pressure: Implications for Carbon Substitution in Iron Structures and Carbon Content in the Earth’s Inner Core
Abstract
1. Introduction
2. Experimental Method
2.1. Sample Synthesis
2.2. Carbon Analytical Procedure
2.3. Diamond Anvil Cell and Synchrotron X-ray Diffraction Experiements
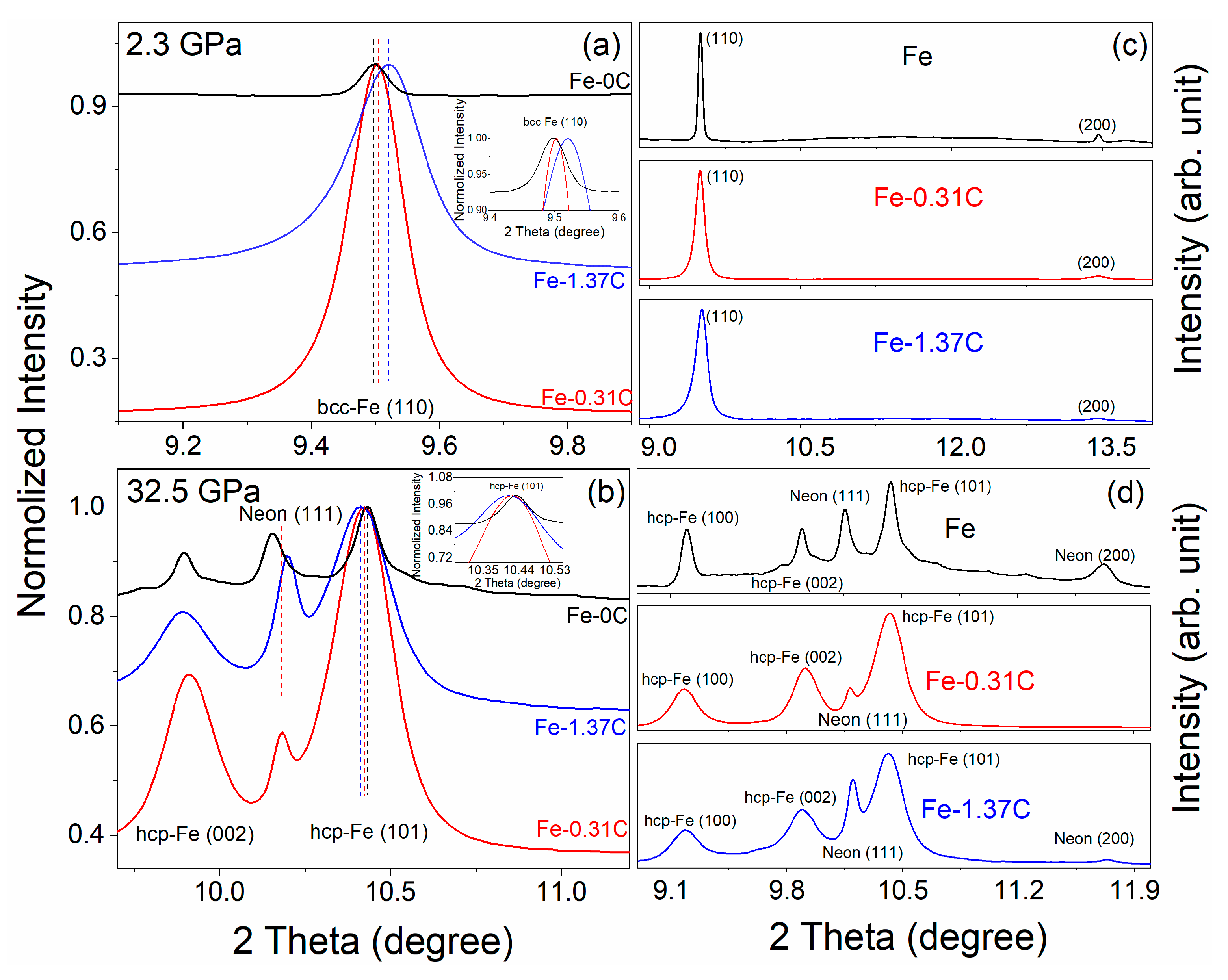
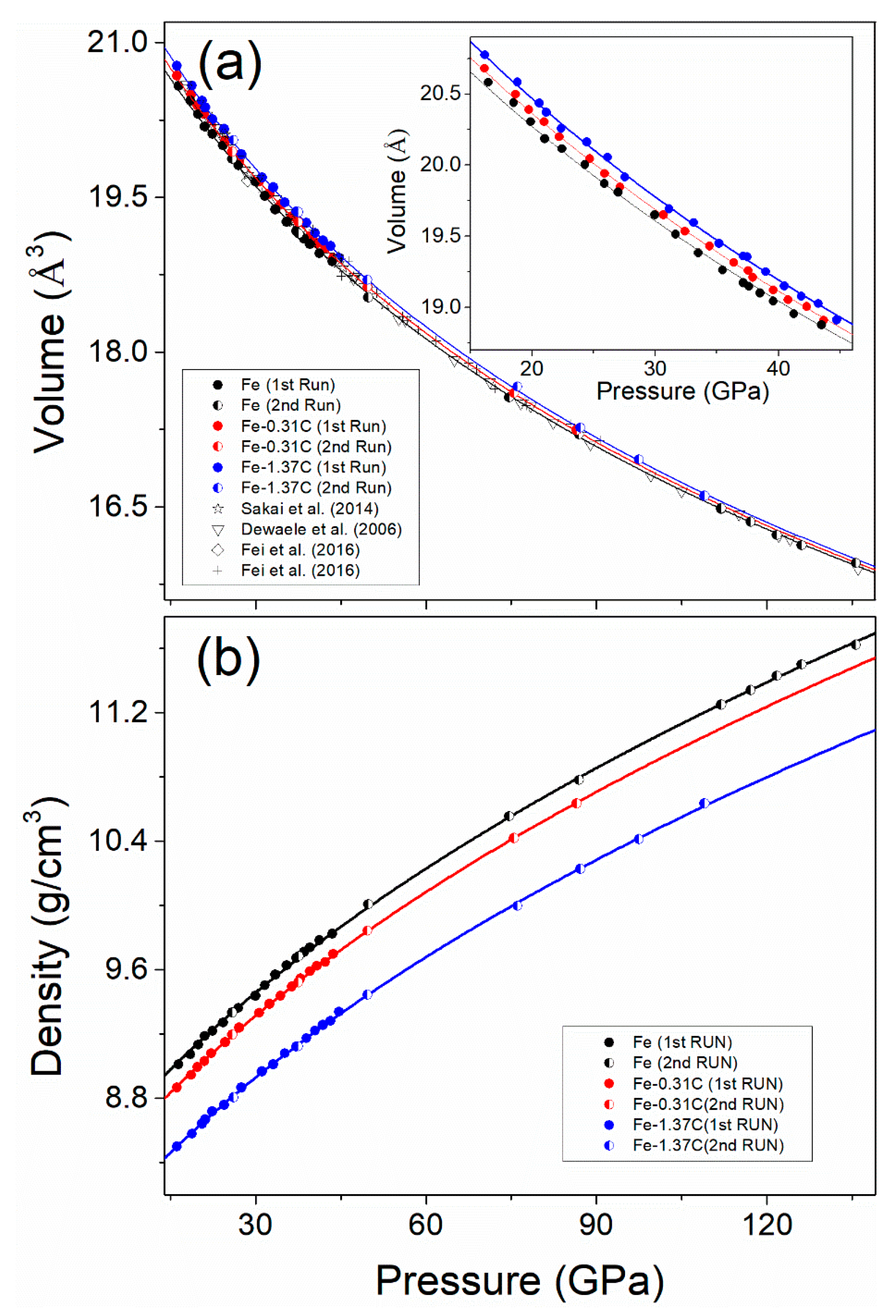
3. Results
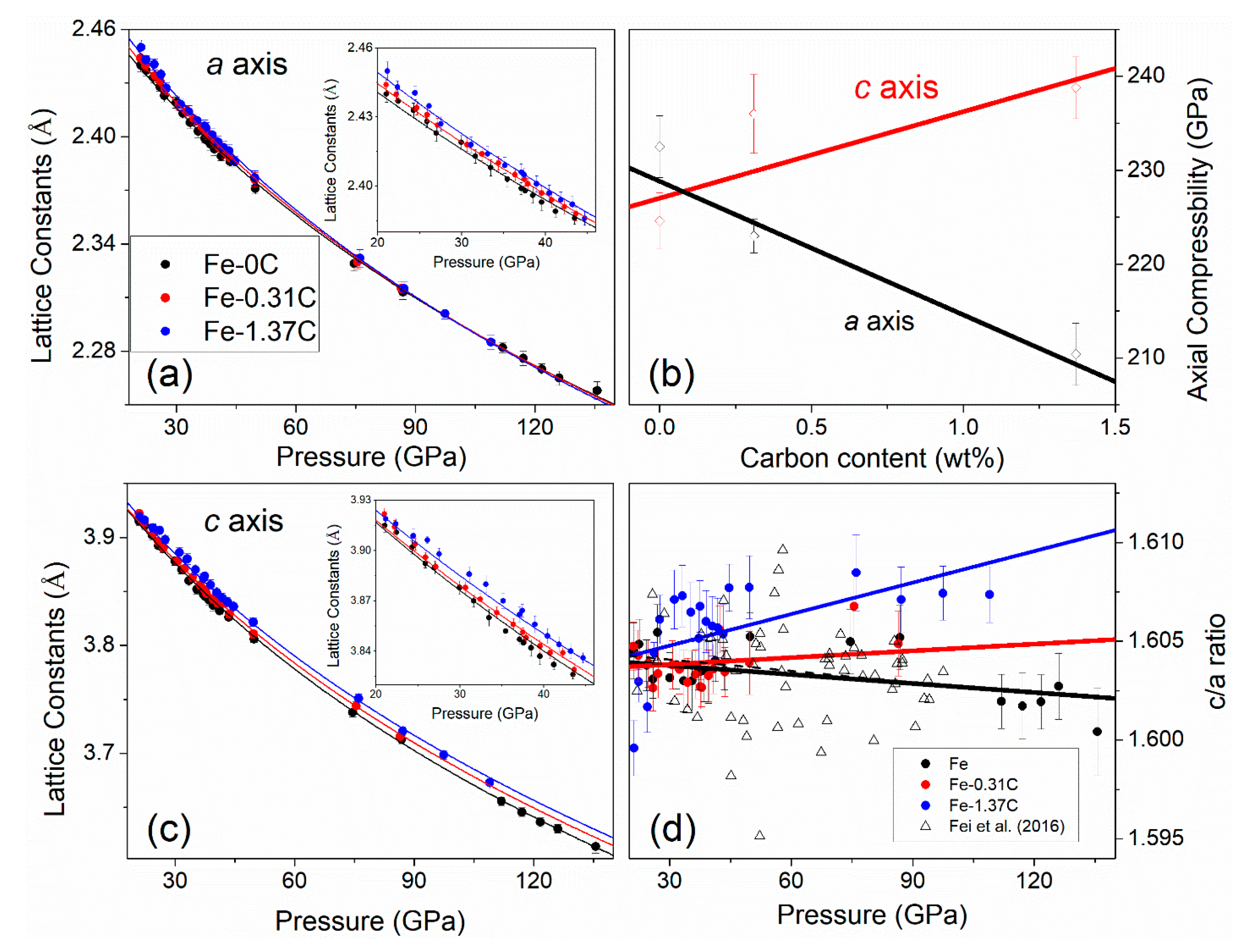
4. Discussion
4.1. Carbon Substitution Mechanism
4.2. Anisotropic Axial Compressibility in the hcp-Fe Phase
4.3. Density Deficit of Earth’s Inner Core
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buchwald, V.F. Handbook of Iron Meteorites: Their History, Distribution, Composition, and Structure; University of California Press: Berkeley, CA, USA, 1975. [Google Scholar]
- Fei, Y.; Brosh, E. Experimental study and thermodynamic calculations of phase relations in the Fe–C system at high pressure. Earth Planet. Sci. Lett. 2014, 408, 155–162. [Google Scholar] [CrossRef]
- Wood, B.J. Carbon in the core. Earth Planet. Sci. Lett. 1993, 117, 593–607. [Google Scholar] [CrossRef]
- Prescher, C.; Dubrovinsky, L.; Bykova, E.; Kupenko, I.; Glazyrin, K.; Kantor, A.; McCammon, C.; Mookherjee, M.; Nakajima, Y.; Miyajima, N. High Poisson’s ratio of Earth’s inner core explained by carbon alloying. Nat. Geosci. 2015, 8, 220. [Google Scholar] [CrossRef]
- Lord, O.; Walter, M.; Dasgupta, R.; Walker, D.; Clark, S. Melting in the Fe–C system to 70 GPa. Earth Planet. Sci. Lett. 2009, 284, 157–167. [Google Scholar] [CrossRef]
- Mashino, I.; Miozzi, F.; Hirose, K.; Morard, G.; Sinmyo, R. Melting experiments on the Fe–C binary system up to 255 GPa: Constraints on the carbon content in the Earth’s core. Earth Planet. Sci. Lett. 2019, 515, 135–144. [Google Scholar] [CrossRef]
- Chen, B.; Li, Z.; Zhang, D.; Liu, J.; Hu, M.Y.; Zhao, J.; Bi, W.; Alp, E.E.; Xiao, Y.; Chow, P. Hidden carbon in Earth’s inner core revealed by shear softening in dense Fe7C3. Proc. Natl. Acad. Sci. USA 2014, 111, 17755–17758. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Ikuta, D. Elastic softening in Fe7C3 with implications for Earth’s deep carbon reservoirs. J. Geophys. Res. Solid Earth 2016, 121, 1514–1524. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Ahuja, R.; Johansson, B. Stability of the body-centred-cubic phase of iron in the Earth’s inner core. Nature 2003, 424, 1032. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Lukinov, T.; Fu, J.; Zhao, J.; Davis, S.; Simak, S.I. Stabilization of body-centred cubic iron under inner-core conditions. Nat. Geosci. 2017, 10, 312. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Ohishi, Y.; Tatsumi, Y. The structure of iron in Earth’s inner core. Science 2010, 330, 359–361. [Google Scholar] [CrossRef]
- Mao, H.-k.; Shu, J.; Shen, G.; Hemley, R.J.; Li, B.; Singh, A.K. Elasticity and rheology of iron above 220 GPa and the nature of the Earth’s inner core. Nature 1998, 396, 741. [Google Scholar] [CrossRef]
- Stixrude, L.; Cohen, R. High-pressure elasticity of iron and anisotropy of Earth’s inner core. Science 1995, 267, 1972–1975. [Google Scholar] [CrossRef] [PubMed]
- Karato, S.-I. Inner core anisotropy due to the magnetic field—Induced preferred orientation of iron. Science 1993, 262, 1708–1711. [Google Scholar] [CrossRef] [PubMed]
- Song, X. Anisotropy of the Earth’s inner core. Rev. Geophys. 1997, 35, 297–313. [Google Scholar] [CrossRef]
- Caracas, R. The influence of carbon on the seismic properties of solid iron. Geophys. Res. Lett. 2017, 44, 128–134. [Google Scholar] [CrossRef]
- Dasgupta, R.; Walker, D. Carbon solubility in core melts in a shallow magma ocean environment and distribution of carbon between the Earth’s core and the mantle. Geochim. Cosmochim. Acta 2008, 72, 4627–4641. [Google Scholar] [CrossRef]
- Robaut, F.; Crisci, A.; Durand-Charre, M.; Jouanne, D. Practical aspects of carbon content determination in carburized steels by EPMA. Microsc. Microanal. 2006, 12, 331–334. [Google Scholar] [CrossRef]
- Fei, Y.; Ricolleau, A.; Frank, M.; Mibe, K.; Shen, G.; Prakapenka, V. Toward an internally consistent pressure scale. Proc. Natl. Acad. Sci. USA 2007, 104, 9182–9186. [Google Scholar] [CrossRef]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; John Wiley & Sons: New York, NY, USA, 2007; Volume 7. [Google Scholar]
- Walker, D.; Dasgupta, R.; Li, J.; Buono, A. Nonstoichiometry and growth of some Fe carbides. Contrib. Mineral. Petrol. 2013, 166, 935–957. [Google Scholar] [CrossRef]
- Lu, Y.; Yu, H.; Cai, X.; Rong, Y.; Sisson, R.D. Martensite lattice parameter measured by modern X-ray Diffraction in Fe-C alloy. In Proceedings of the 23rd International Federation of Heat Treatment and Surface Engineering Congress (IFHTSE 2016), Savannah, GA, USA, 18–21 April 2016. [Google Scholar]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Sakai, T.; Takahashi, S.; Nishitani, N.; Mashino, I.; Ohtani, E.; Hirao, N. Equation of state of pure iron and Fe0.9Ni0.1 alloy up to 3 Mbar. Phys. Earth Planet. Inter. 2014, 228, 114–126. [Google Scholar] [CrossRef]
- Fei, Y.; Murphy, C.; Shibazaki, Y.; Shahar, A.; Huang, H. Thermal equation of state of hcp-iron: Constraint on the density deficit of Earth’s solid inner core. Geophys. Res. Lett. 2016, 43, 6837–6843. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Occelli, F.; Mezouar, M.; Dorogokupets, P.I.; Torrent, M. Quasihydrostatic equation of state of iron above 2 Mbar. Phys. Rev. Lett. 2006, 97, 215504. [Google Scholar] [CrossRef] [PubMed]
- Boehler, R.; Santamaría-Pérez, D.; Errandonea, D.; Mezouar, M. Melting, density, and anisotropy of iron at core conditions: New X-ray measurements to 150 GPa. J. Phys. Conf. Ser. 2008, 121, 022018. [Google Scholar] [CrossRef]
- Dubrovinsky, L.; Saxena, S.; Tutti, F.; Rekhi, S.; LeBehan, T. In situ X-ray study of thermal expansion and phase transition of iron at multimegabar pressure. Phys. Rev. Lett 2000, 84, 1720. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ito, E.; Yoshino, T.; Yoneda, A.; Guo, X.; Zhang, B.; Sun, W.; Shimojuku, A.; Tsujino, N.; Kunimoto, T. P-V-T equation of state for ε-iron up to 80 GPa and 1900 K using the Kawai-type high pressure apparatus equipped with sintered diamond anvils. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Mao, H.; Wu, Y.; Chen, L.; Shu, J.; Jephcoat, A.P. Static compression of iron to 300 GPa and Fe0.8Ni0.2 alloy to 260 GPa: Implications for composition of the core. J. Geophys. Res. Solid Earth 1990, 95, 21737–21742. [Google Scholar] [CrossRef]
- Huang, L.; Skorodumova, N.; Belonoshko, A.B.; Johansson, B.; Ahuja, R. Carbon in iron phases under high pressure. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Li, Y.; Vočadlo, L.; Brodholt, J.P. The elastic properties of hcp-Fe alloys under the conditions of the Earth’s inner core. Earth Planet. Sci. Lett. 2018, 493, 118–127. [Google Scholar] [CrossRef]
- Steinle-Neumann, G.; Stixrude, L.; Cohen, R.E. First-principles elastic constants for the hcp transition metals Fe, Co, and Re at high pressure. Phys. Rev. B 1999, 60, 791. [Google Scholar] [CrossRef]
- Vočadlo, L.; Dobson, D.P.; Wood, I.G. Ab initio calculations of the elasticity of hcp-Fe as a function of temperature at inner-core pressure. Earth Planet. Sci. Lett. 2009, 288, 534–538. [Google Scholar] [CrossRef]
- Sha, X.; Cohen, R. First-principles thermal equation of state and thermoelasticity of hcp Fe at high pressures. Phys. Rev. B 2010, 81, 094105. [Google Scholar] [CrossRef]
- Williamson, G.; Smallman, R. X-ray evidence for the interstitial position of carbon in α-iron. Acta Crystallogr. 1953, 6, 361–362. [Google Scholar] [CrossRef]
- Komabayashi, T.; Pesce, G.; Morard, G.; Antonangeli, D.; Sinmyo, R.; Mezouar, M. Phase transition boundary between fcc and hcp structures in Fe-Si alloy and its implications for terrestrial planetary cores. Am. Mineral. J. Earth Planet. Mater. 2019, 104, 94–99. [Google Scholar] [CrossRef]
- Fischer, R.A.; Campbell, A.J.; Caracas, R.; Reaman, D.M.; Heinz, D.L.; Dera, P.; Prakapenka, V.B. Equations of state in the Fe-FeSi system at high pressures and temperatures. J. Geophys. Res. Solid Earth 2014, 119, 2810–2827. [Google Scholar] [CrossRef]
- Goldschmid, H.J. Interstitial Alloys; Springer: Berlin, Germany, 2013. [Google Scholar]
- Morelli, A.; Dziewonski, A.M.; Woodhouse, J.H. Anisotropy of the inner core inferred from PKIKP travel times. Geophys. Res. Lett. 1986, 13, 1545–1548. [Google Scholar] [CrossRef]
- Lincot, A.; Merkel, S.; Cardin, P. Is inner core seismic anisotropy a marker for plastic flow of cubic iron? Geophys. Res. Lett. 2015, 42, 1326–1333. [Google Scholar] [CrossRef]
- Antonangeli, D.; Merkel, S.; Farber, D.L. Elastic anisotropy in hcp metals at high pressure and the sound wave anisotropy of the Earth’s inner core. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Buffett, B.; Wenk, H.-R. Texturing of the Earth’s inner core by Maxwell stresses. Nature 2001, 413, 60. [Google Scholar] [CrossRef] [PubMed]
- Fischer, R.A.; Campbell, A.J. The axial ratio of hcp Fe and Fe–Ni–Si alloys to the conditions of Earth’s inner core. Am. Mineral. 2015, 100, 2718–2724. [Google Scholar] [CrossRef]
- Jephcoat, A.P.; Mao, H.; Bell, P.M. Static compression of iron to 78 GPa with rare gas solids as pressure-transmitting media. J. Geophys. Res. Solid Earth 1986, 91, 4677–4684. [Google Scholar] [CrossRef]
- Ma, Y.; Somayazulu, M.; Shen, G.; Mao, H.-K.; Shu, J.; Hemley, R.J. In situ X-ray diffraction studies of iron to Earth-core conditions. Phys. Earth Planet. Inter. 2004, 143, 455–467. [Google Scholar] [CrossRef]
- Ono, S.; Kikegawa, T.; Hirao, N.; Mibe, K. High-pressure magnetic transition in hcp-Fe. Am. Mineral. 2010, 95, 880–883. [Google Scholar] [CrossRef]
- Sakai, T.; Ohtani, E.; Kamada, S.; Terasaki, H.; Hirao, N. Compression of Fe88.1Ni9.1S2.8 alloy up to the pressure of Earth’s inner core. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Brown, J.; Fritz, J.; Hixson, R. Hugoniot data for iron. J. Appl. Phys. 2000, 88, 5496–5498. [Google Scholar] [CrossRef]
- Nakajima, Y.; Imada, S.; Hirose, K.; Komabayashi, T.; Ozawa, H.; Tateno, S.; Tsutsui, S.; Kuwayama, Y.; Baron, A.Q. Carbon-depleted outer core revealed by sound velocity measurements of liquid iron–carbon alloy. Nat. Commun. 2015, 6, 8942. [Google Scholar] [CrossRef]
- Morard, G.; Andrault, D.; Antonangeli, D.; Nakajima, Y.; Auzende, A.; Boulard, E.; Cervera, S.; Clark, A.; Lord, O.; Siebert, J. Fe–FeO and Fe–Fe3C melting relations at Earth’s core–mantle boundary conditions: Implications for a volatile-rich or oxygen-rich core. Earth Planet. Sci. Lett. 2017, 473, 94–103. [Google Scholar] [CrossRef]

| Compositions | V0 (Å3) | ρ (g/cm3) | K0 (GPa) | K0′ |
|---|---|---|---|---|
| This study | ||||
| Fe | 22.24(4) | 8.392 | 187.3(1.3) | 4.79(fixed) |
| Fe | 22.26(6) | 8.332 | 169.7(5.2) | 5.19(16) |
| Fe-0.31C | 22.26(3) | 8.242 | 182.8(1.0) | 4.79(fixed) |
| Fe-0.31C | 22.37(4) | 8.197 | 168.9(4.8) | 5.19(14) |
| Fe-1.37C | 22.44(3) | 7.881 | 177.6(1.2) | 4.79(fixed) |
| Fe-1.37C | 20.37(6) | 7.895 | 182.2(4.2) | 4.68(17) |
| Calculation (Fe) | ||||
| Non-magnetic, Steinle-Neumann et al., (1999) [35] | 20.45 | 9.069 | 292 | 4.4 |
| Steinle-Neumann et al., (1999) [35] | 21.10 | 8.790 | 209 | 5.2 |
| Vočadlo et al., (2009) [36] | 20.86(4) | 8.891 | 237.8(4) | 4.8 |
| Non-magnetic, Huang et al., (2005) [33] | 20.52 | 9.0385 | 289 | 4.46 |
| Non-magnetic, Sha and Cohen (2010) [37] | 20.18 | 9.191 | 296 | 4.4 |
| Calculation (Fe-1.3C) | ||||
| Huang et al., 2005 [33] | 21.46 | 8.254 | 291 | 4.34 |
| Experiments (Fe) | ||||
| Fei et al. (2016) [27] | 22.427(fixed) | 8.270(fixed) | 172.7(1.4) | 4.79 |
| Fei et al. (2016) [27] | 22.185 | 8.360(24) | 191.4(5.3) | 4.52(8) |
| Yamazaki et al. (2012) [31] | 22.15 | 8.373 | 202(7) | 4.5(2) |
| Mao et al. (1990) [32] | 22.35(2) | 8.298 | 165(4) | 5.33(90) |
| Dubrovinsky et al. (2000) [30] | 22.40 | 8.280 | 156(4) | 5.81 |
| Boehler et al. (2008) [29] | 22.46(4) | 8.258 | 160(6) | 5.6(2) |
| Dewaele et al. (2006) [28] | 22.43 | 8.269 | 165(fixed) | 4.97(4) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Fei, Y.; Hu, X.; Greenberg, E.; Prakapenka, V.B. Effect of Carbon on the Volume of Solid Iron at High Pressure: Implications for Carbon Substitution in Iron Structures and Carbon Content in the Earth’s Inner Core. Minerals 2019, 9, 720. https://doi.org/10.3390/min9120720
Yang J, Fei Y, Hu X, Greenberg E, Prakapenka VB. Effect of Carbon on the Volume of Solid Iron at High Pressure: Implications for Carbon Substitution in Iron Structures and Carbon Content in the Earth’s Inner Core. Minerals. 2019; 9(12):720. https://doi.org/10.3390/min9120720
Chicago/Turabian StyleYang, Jing, Yingwei Fei, Xiaojun Hu, Eran Greenberg, and Vitali B. Prakapenka. 2019. "Effect of Carbon on the Volume of Solid Iron at High Pressure: Implications for Carbon Substitution in Iron Structures and Carbon Content in the Earth’s Inner Core" Minerals 9, no. 12: 720. https://doi.org/10.3390/min9120720
APA StyleYang, J., Fei, Y., Hu, X., Greenberg, E., & Prakapenka, V. B. (2019). Effect of Carbon on the Volume of Solid Iron at High Pressure: Implications for Carbon Substitution in Iron Structures and Carbon Content in the Earth’s Inner Core. Minerals, 9(12), 720. https://doi.org/10.3390/min9120720






