Structural Controls on Copper Mineralization in the Tongling Ore District, Eastern China: Evidence from Spatial Analysis
Abstract
:1. Introduction
2. Materials and Methods
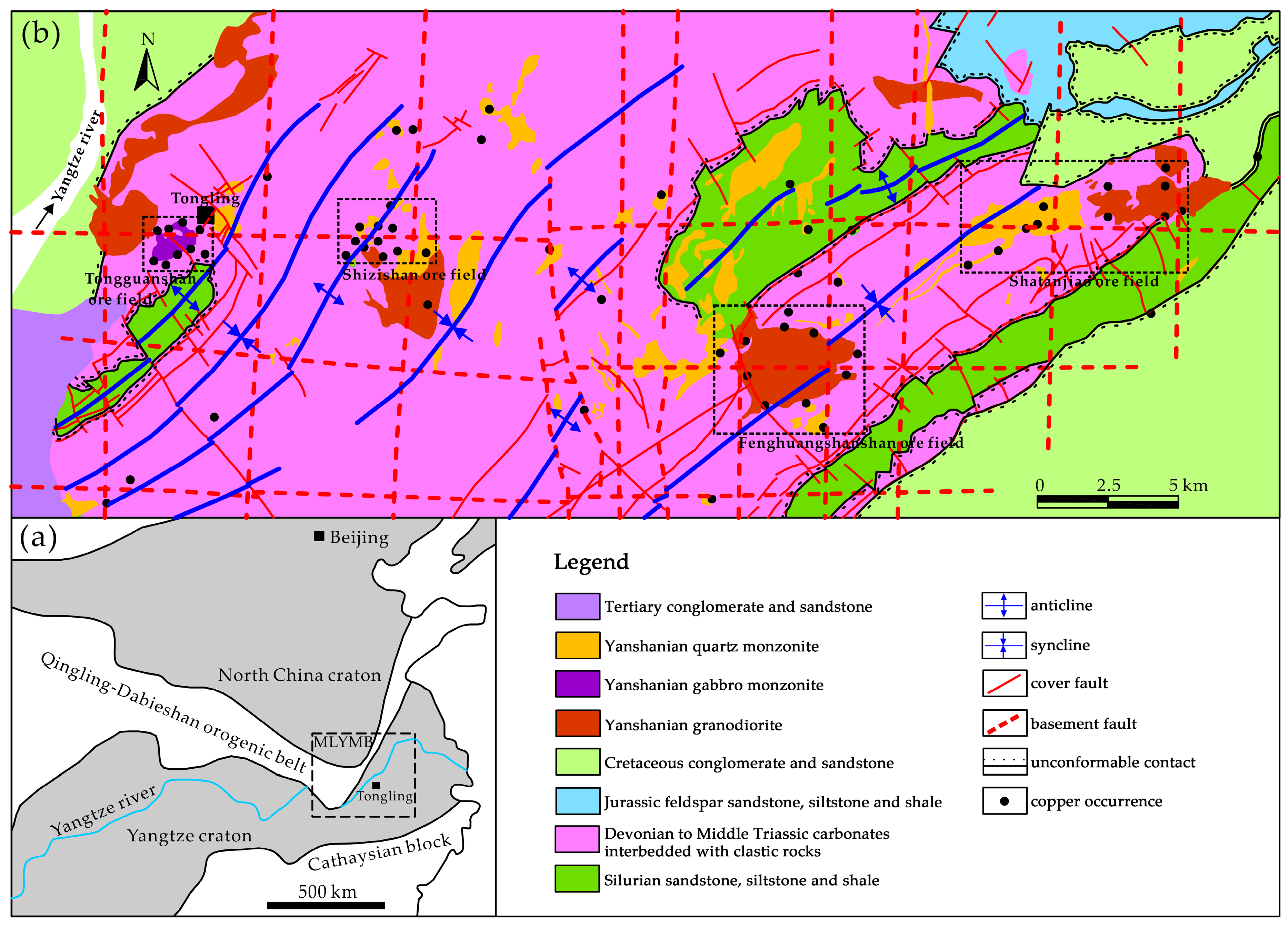
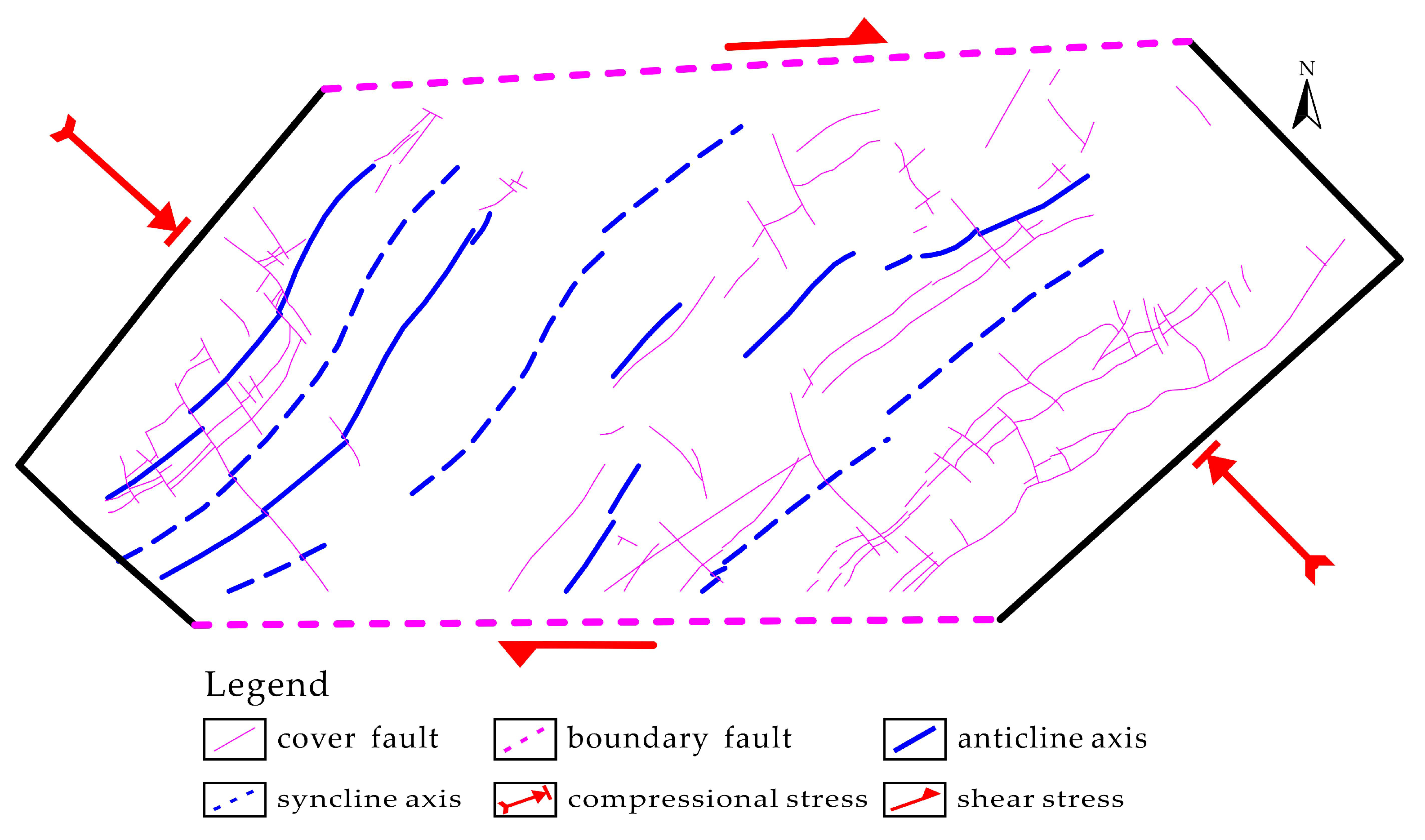
2.1. Study Area
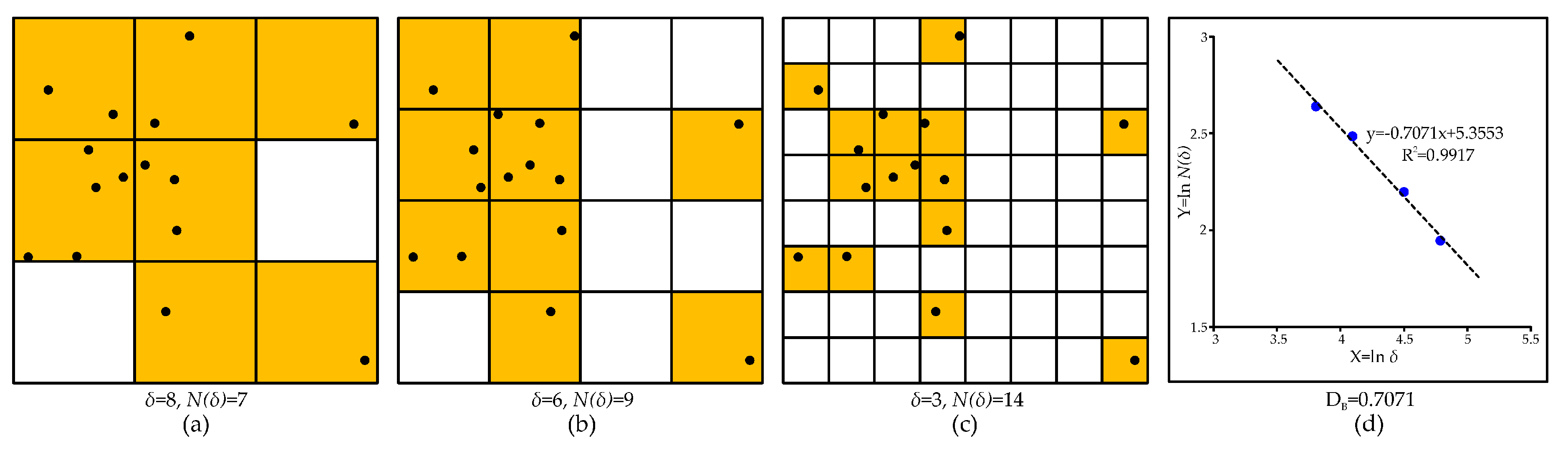
2.2. Fractal Analysis
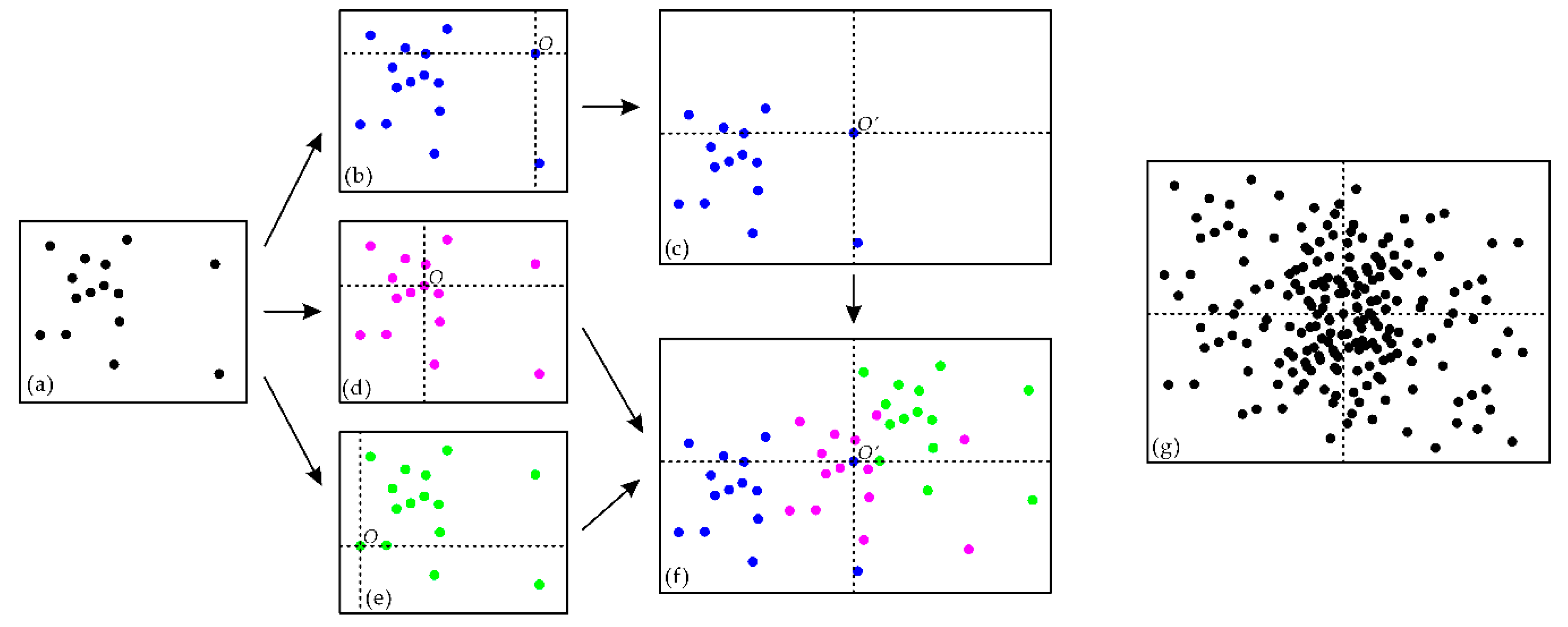
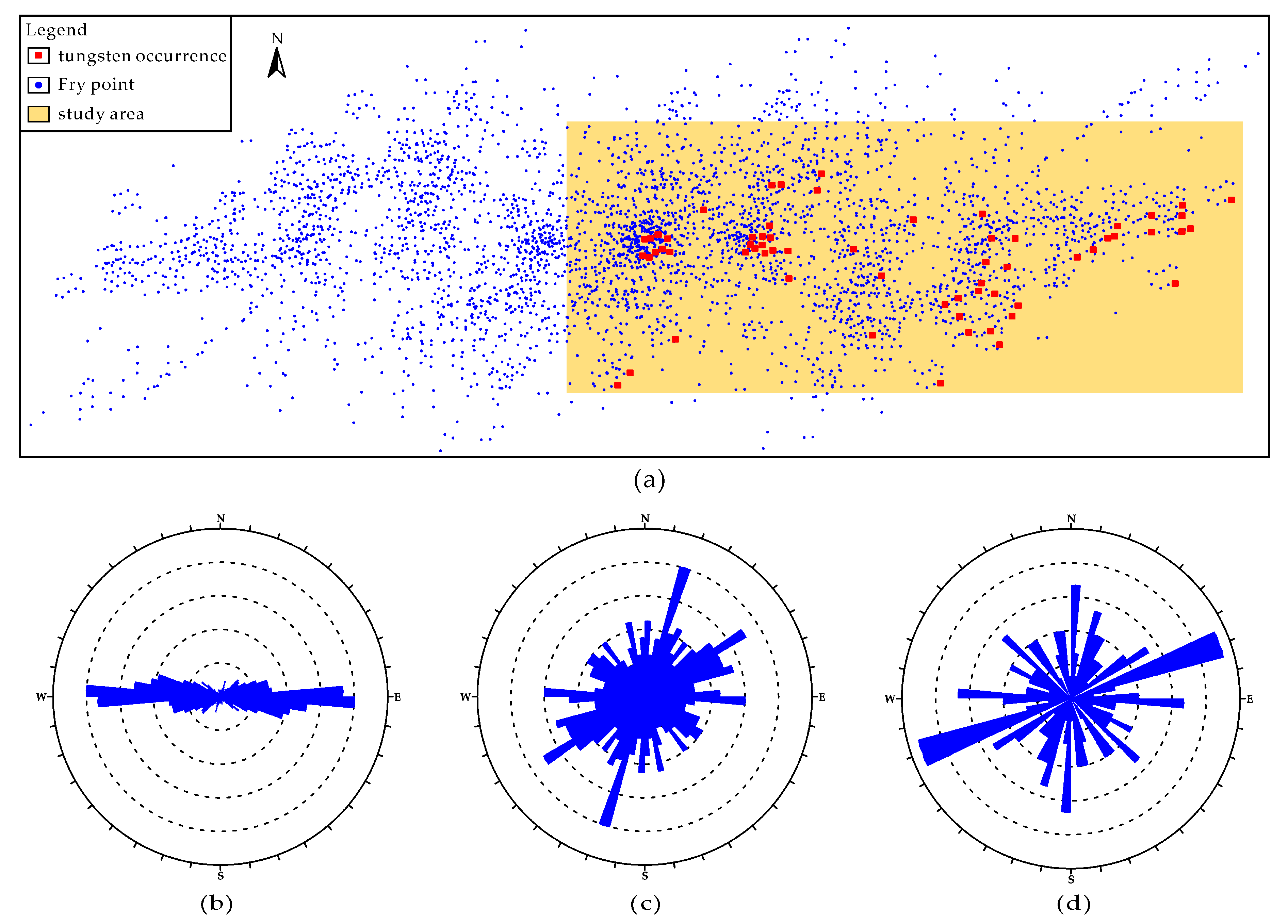
2.3. Fry Analysis
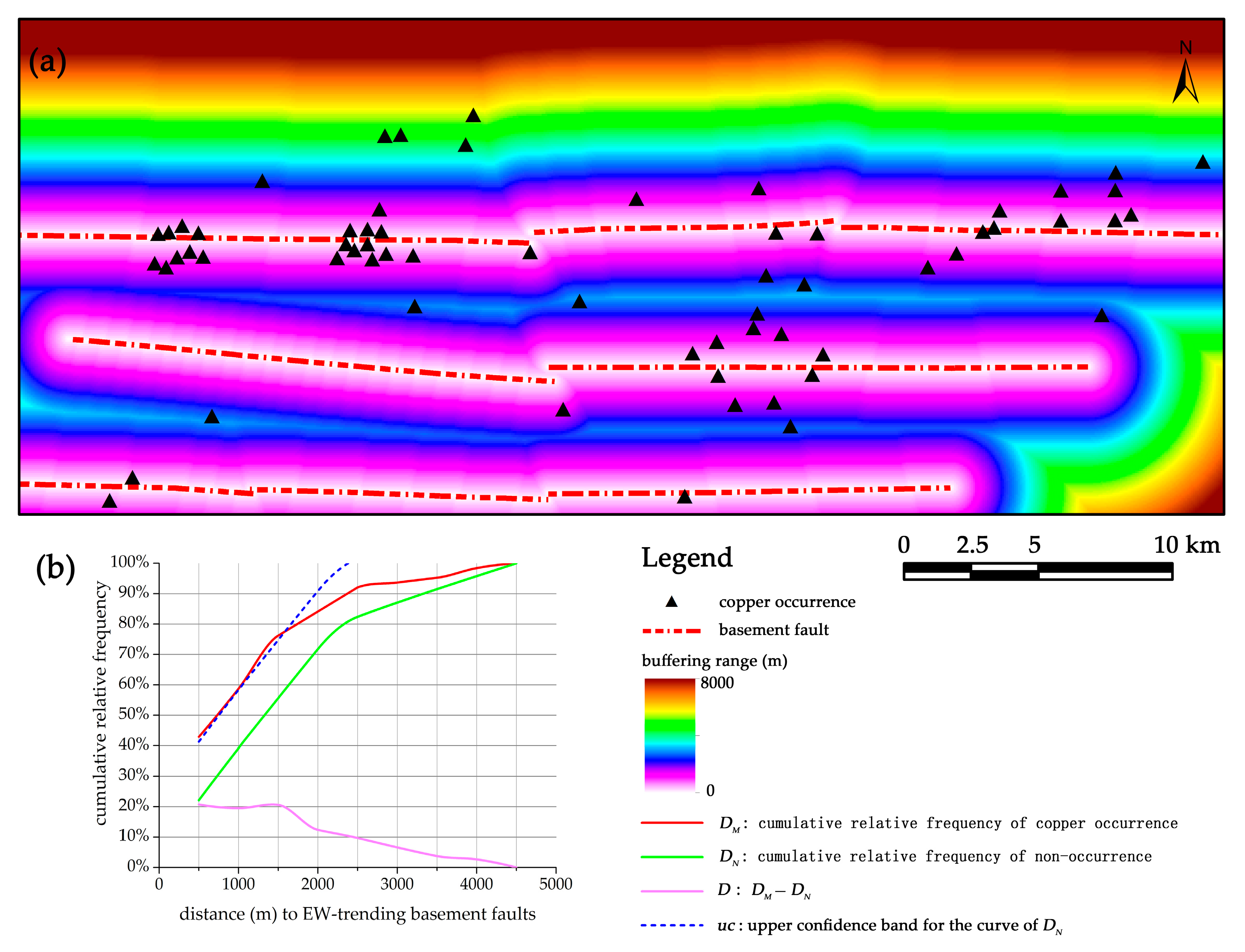
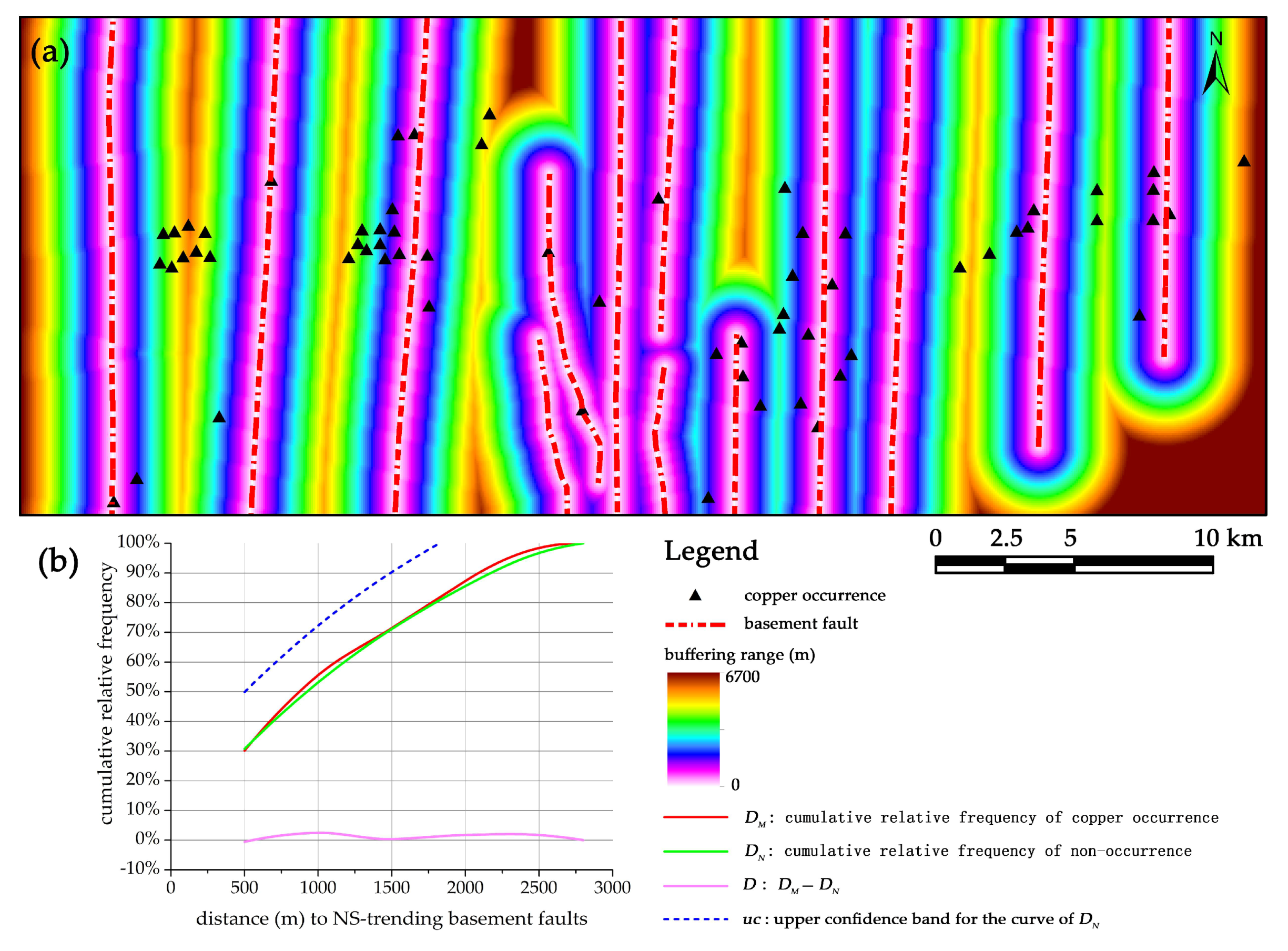
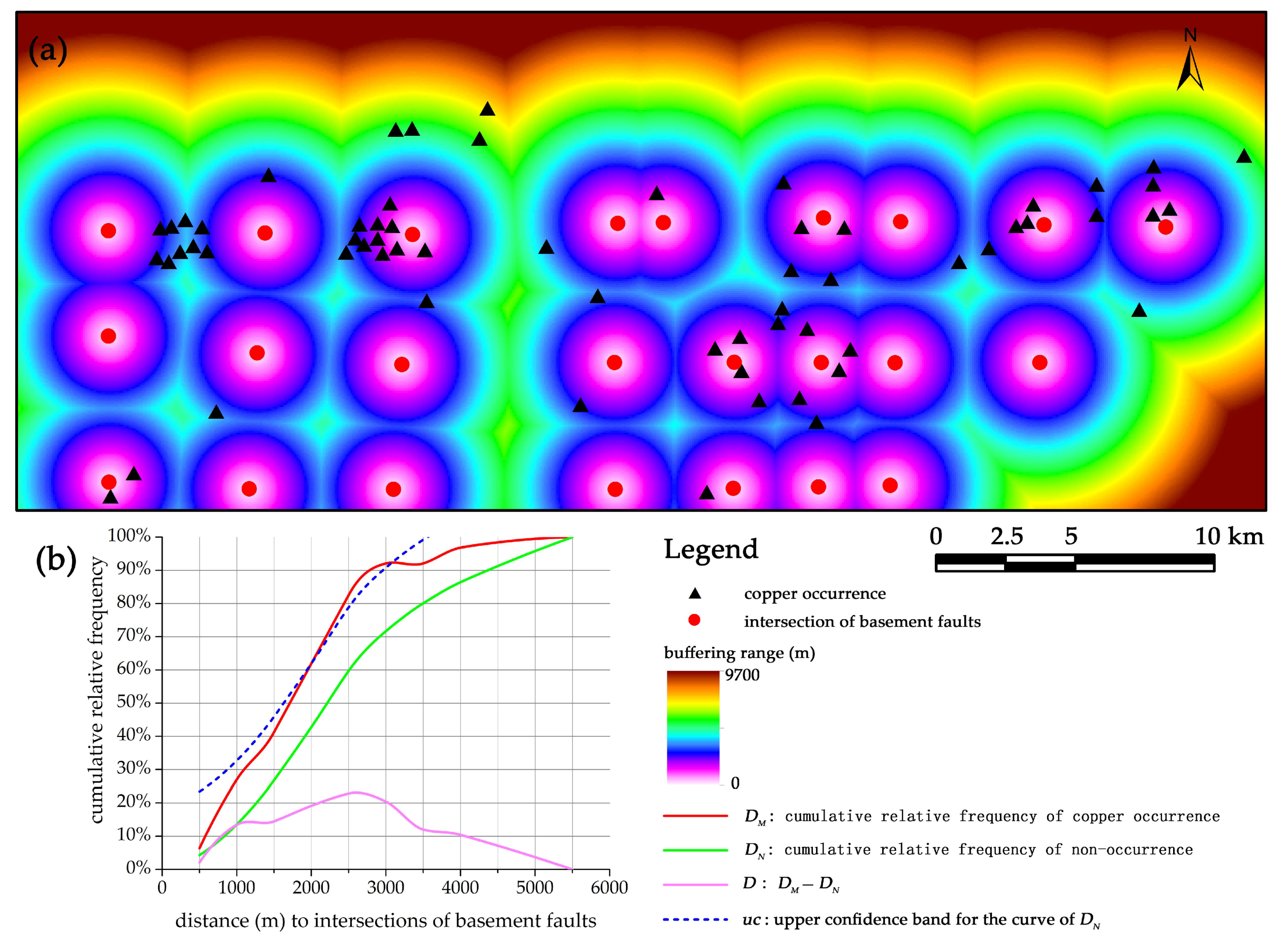
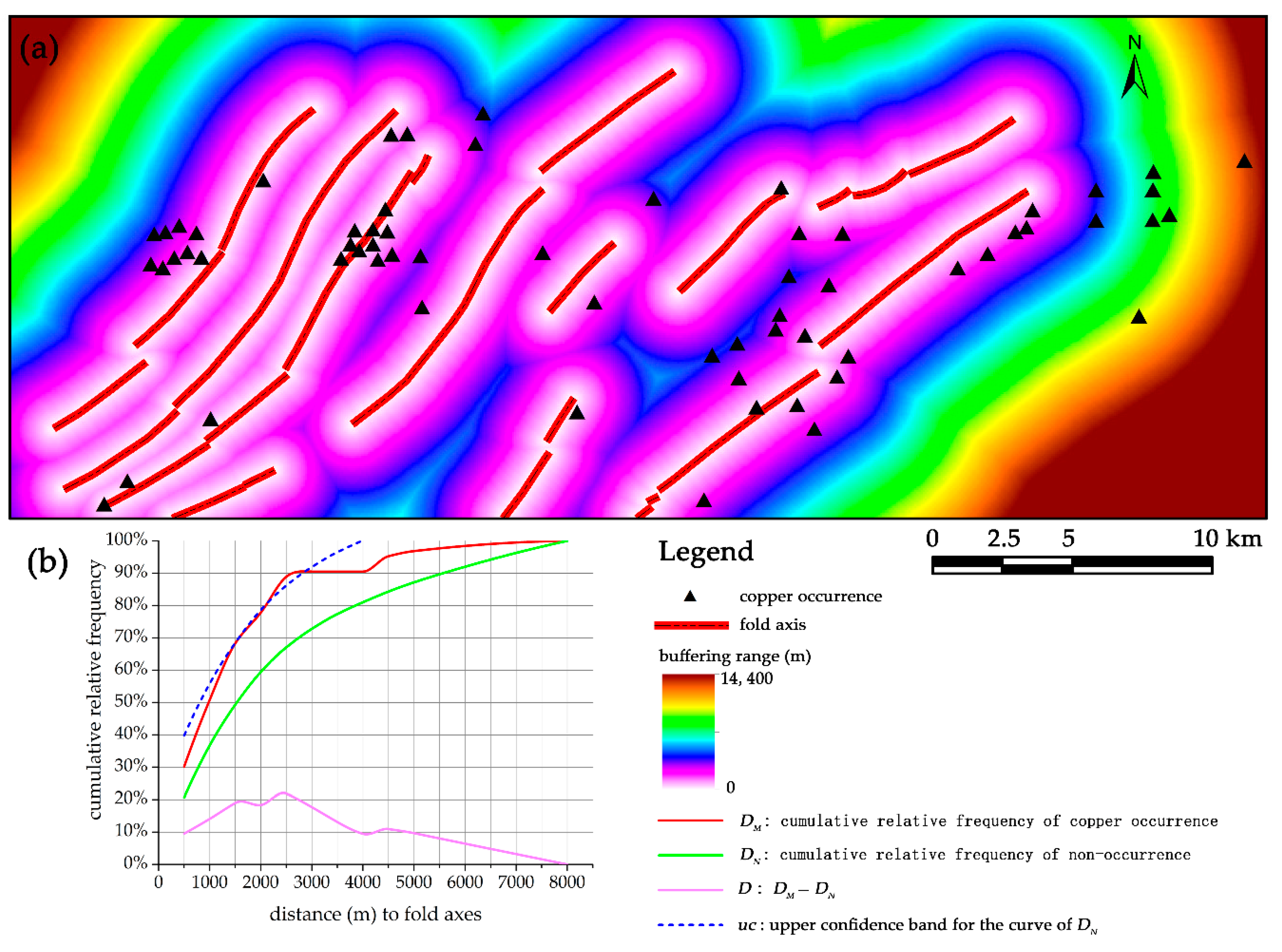
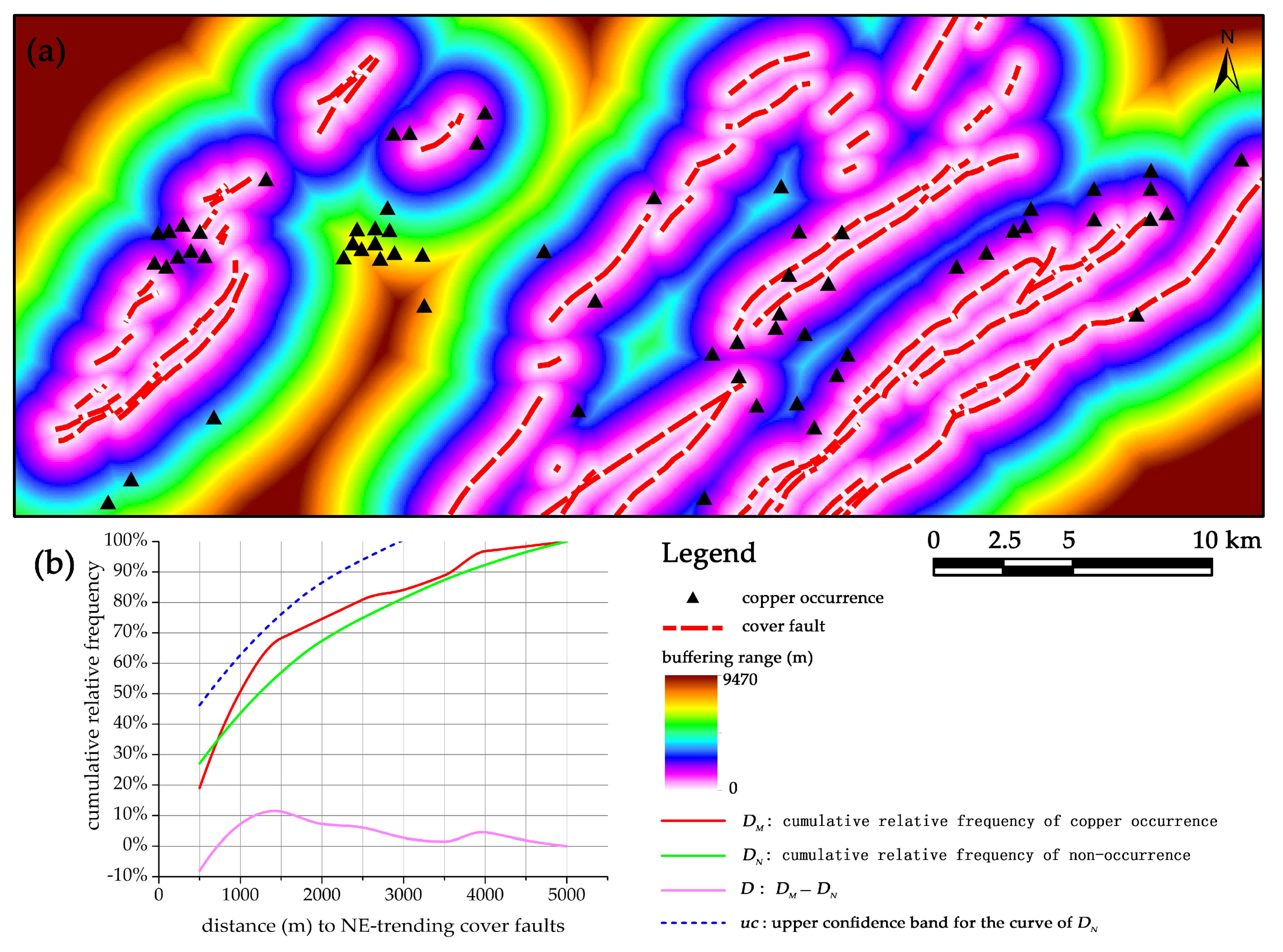
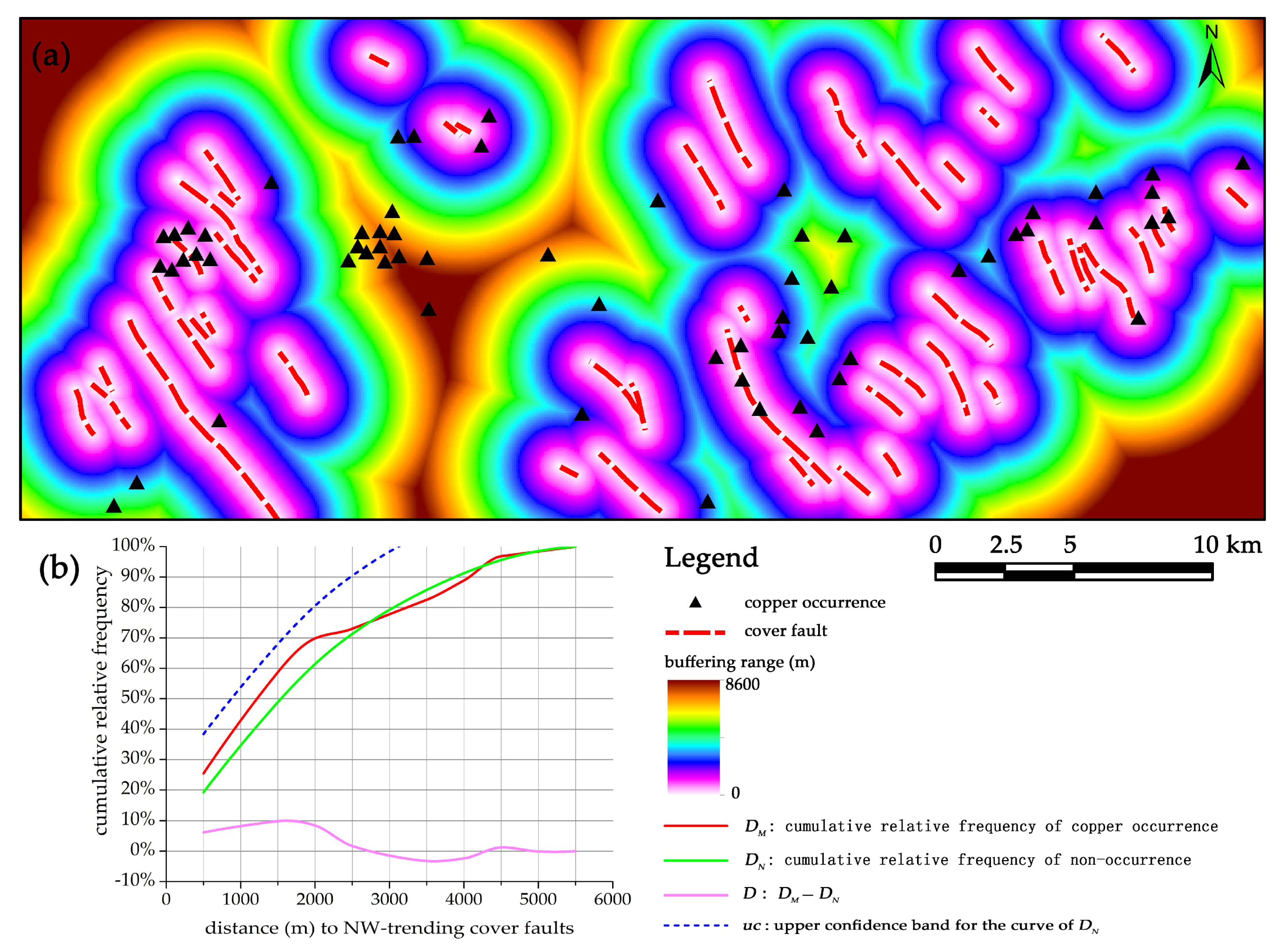
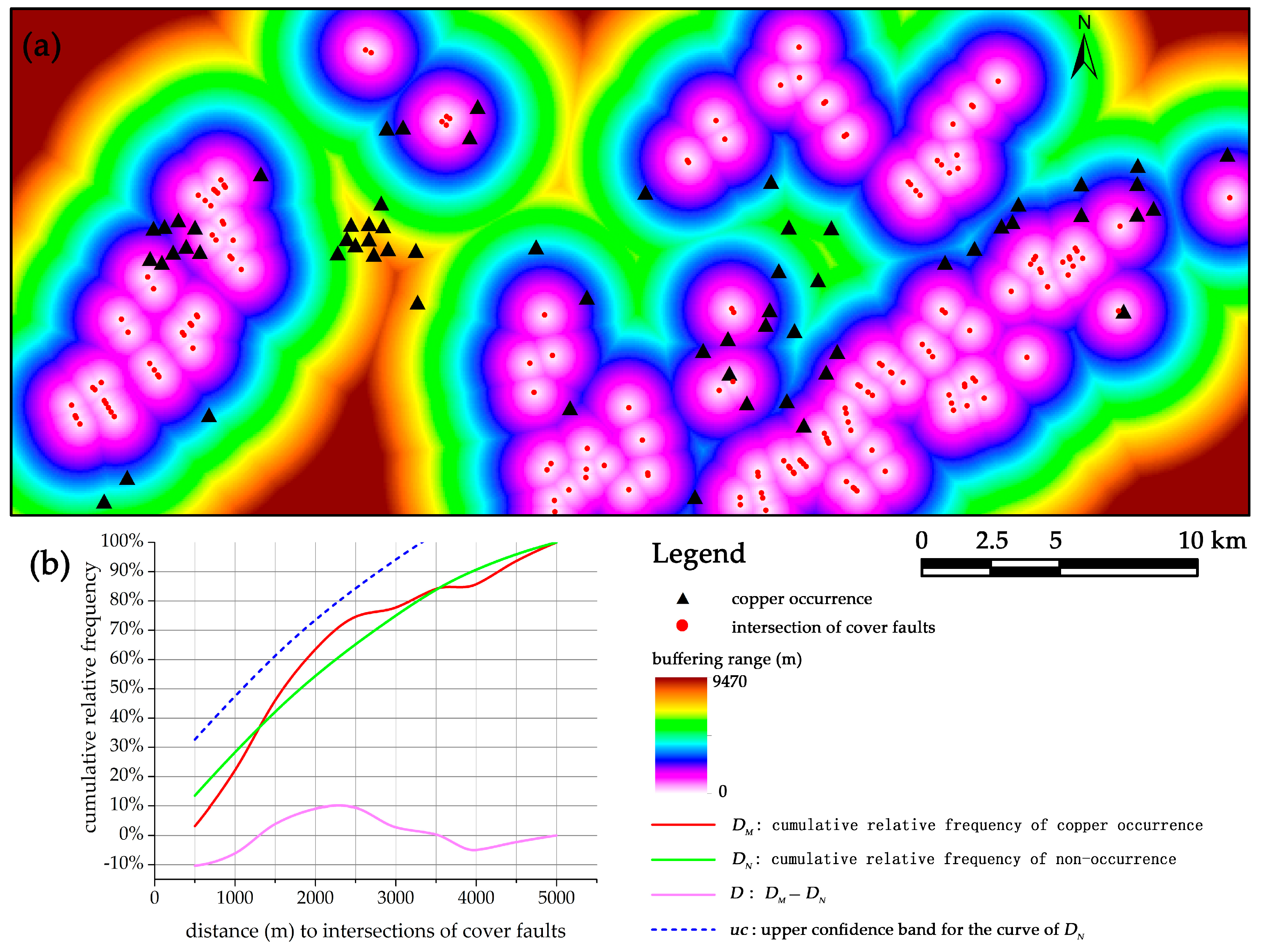
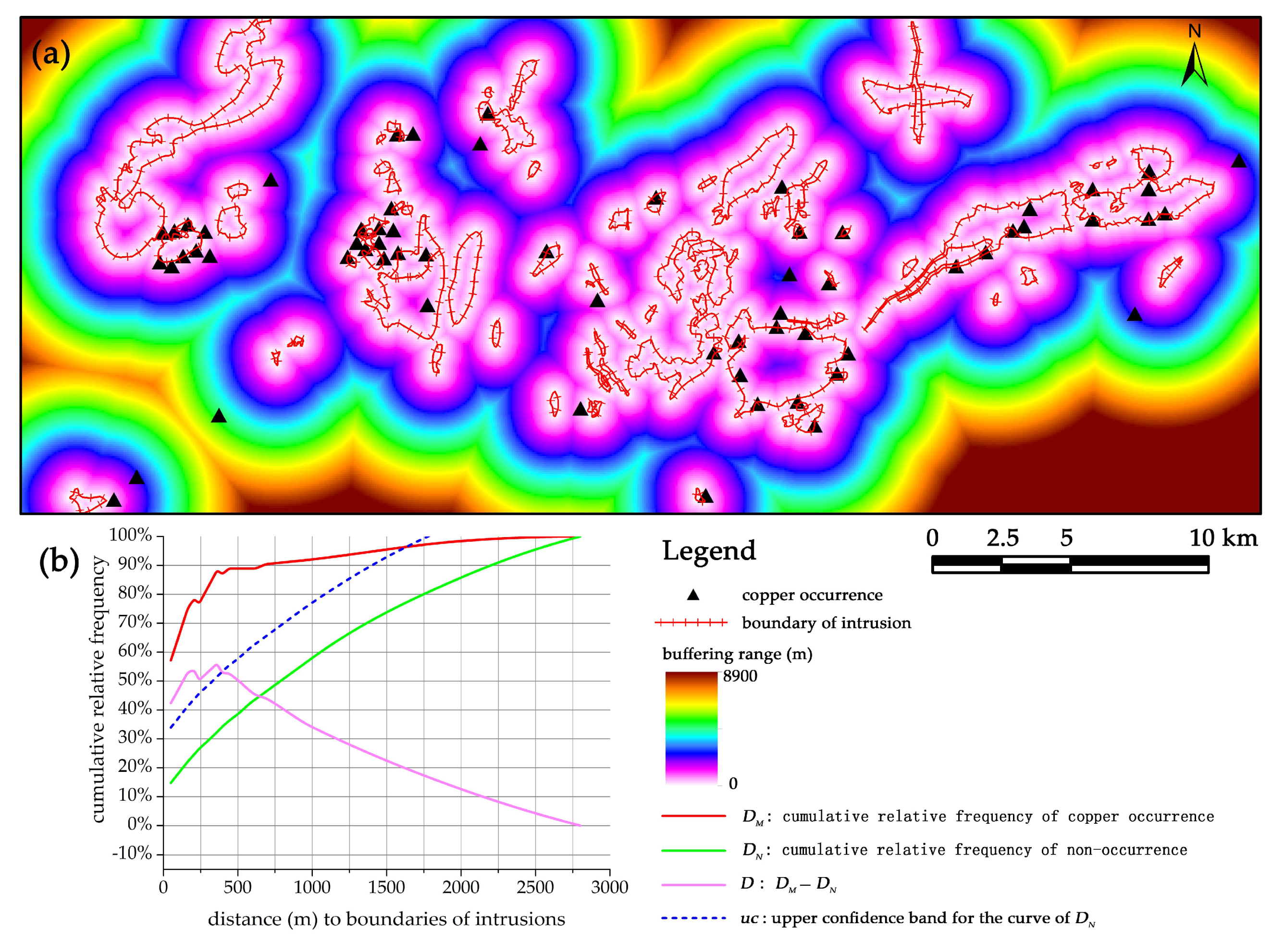
2.4. Distance Distribution Analysis
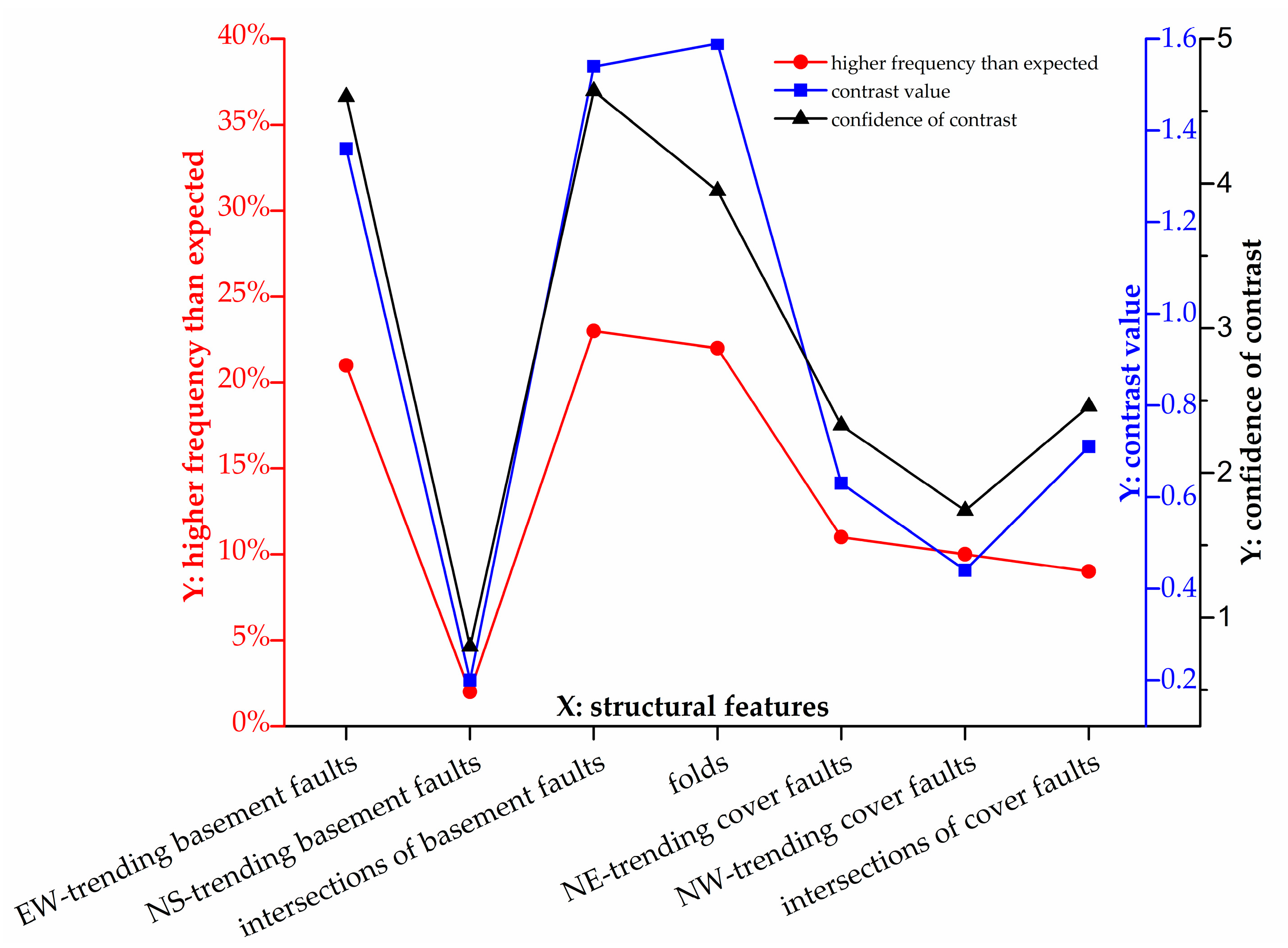
2.5. Weights of Evidence (WofE) Analysis
3. Results and Discussion
3.1. Spatial Patterns of Copper Occurrences
3.2. Spatial Correlation of Structural Features with Copper Mineralization
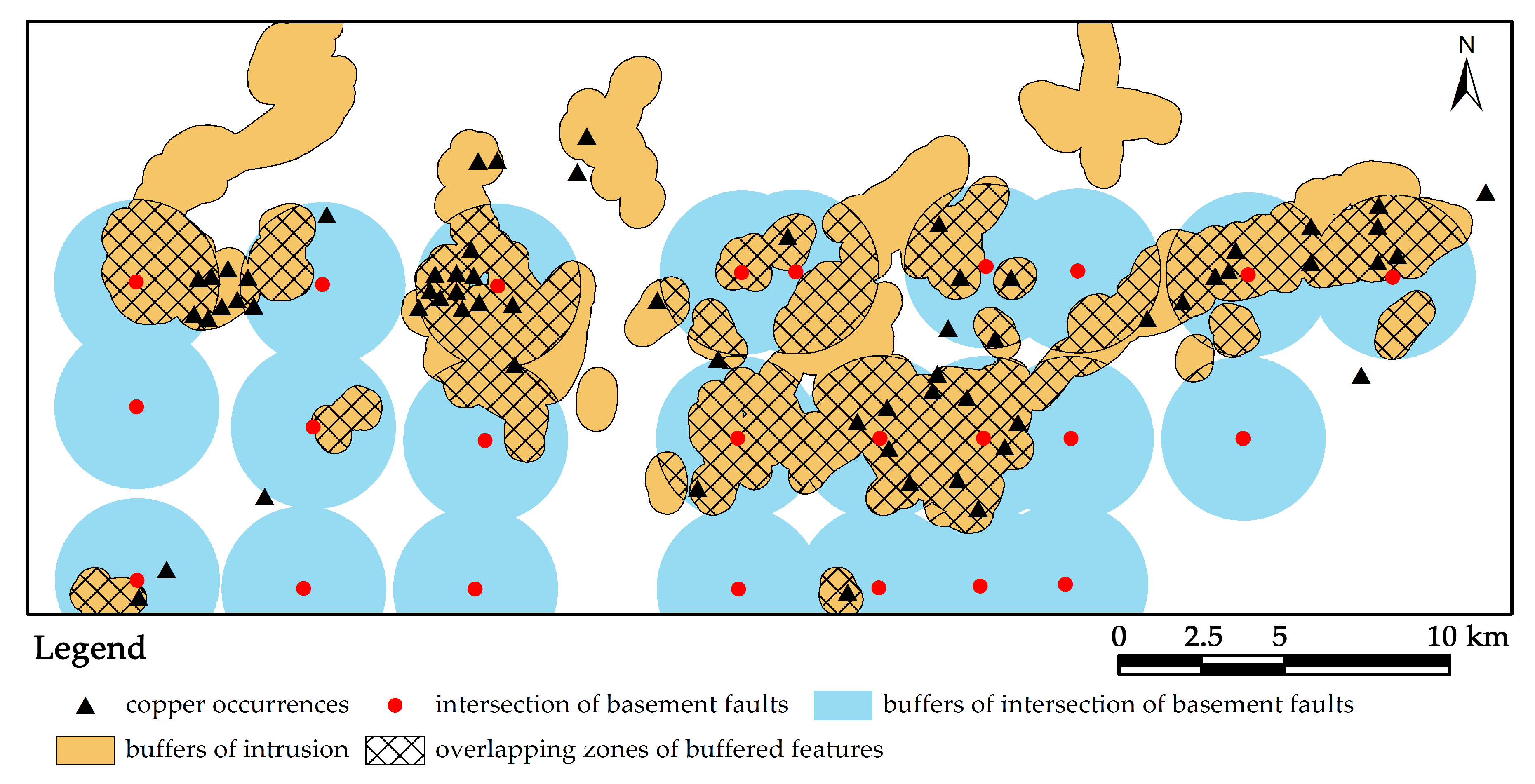
3.3. Spatial Correlation of Faults with Intrusions
3.4. Interpretation of Structural Controls on Copper Mineralization
4. Conclusions
- (i)
- Fractal dimensions obtained from box-counting and radial-density analyses suggest that different structural controls operate at diverse scales of <1.5 km, 1.5–4.5 km and >4.5 km. This scale-variable controlling behavior is supported and explored by the results of Fry analysis, which illustrates a dominant EW trend at regional scale (>4.5 km) and preferential NE-NNE-NEE trends at fine scale (<4.5 km).
- (ii)
- The spatial associations of detailed structural features with copper mineralization are further investigated by quantitative spatial analyses. The Yanshanian intrusions, EW-trending faults, intersections of basement faults, and folds have significant associations with copper mineralization, indicated by their high values of quantitative parameters in both distance distribution and WofE analyses.
- (iii)
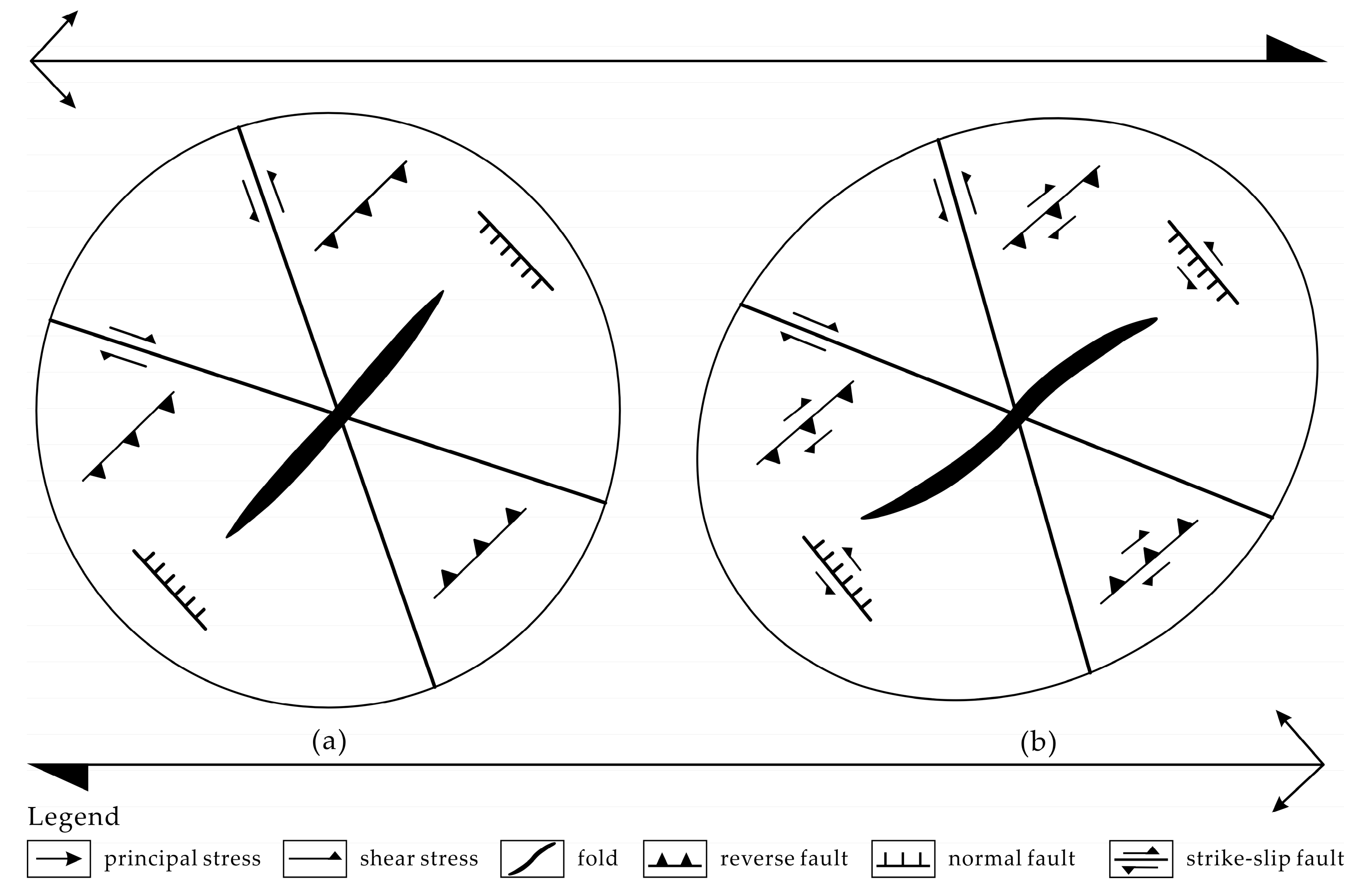
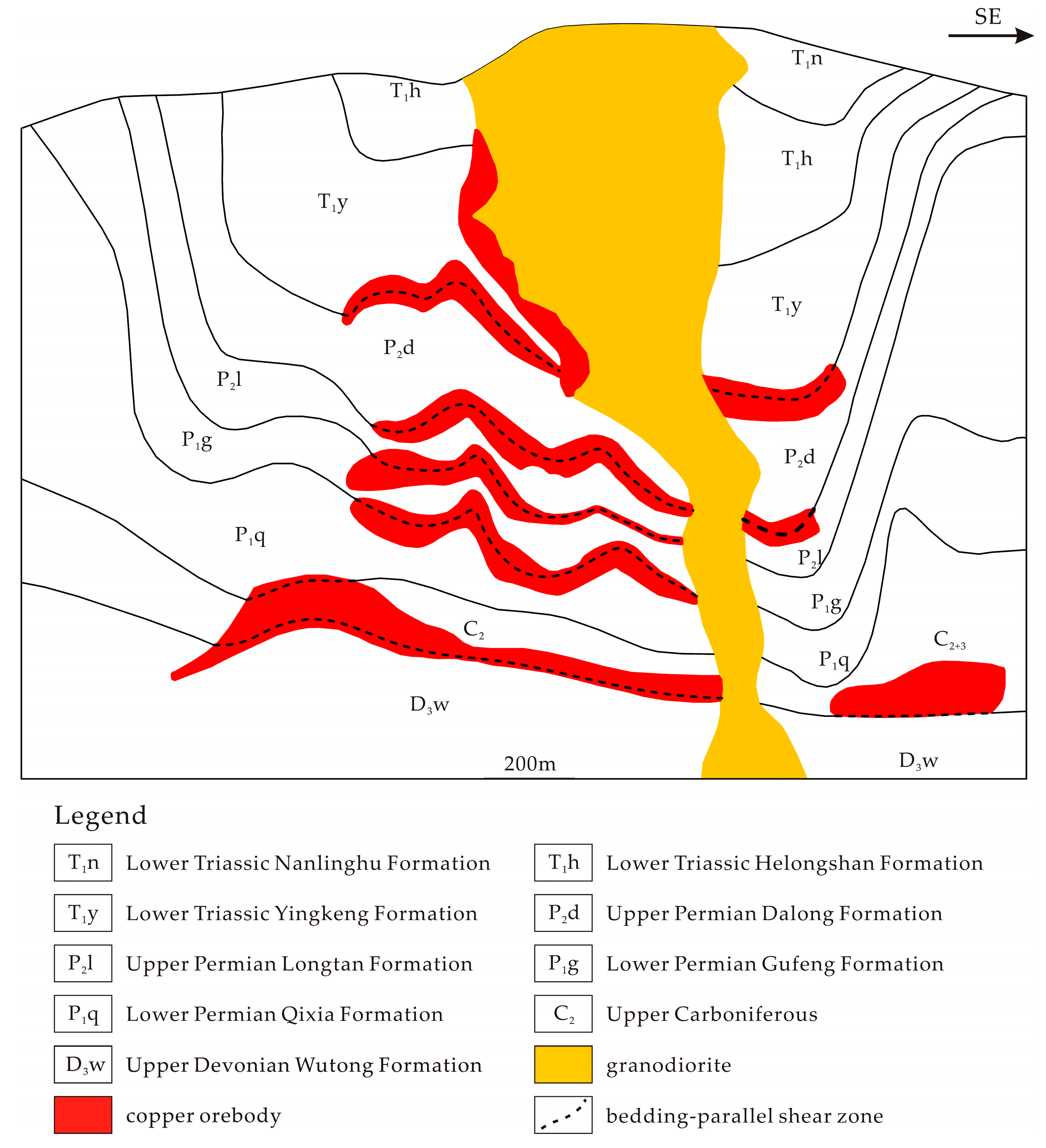
- The interpretation of structural controls on copper mineralization is made in combination of foregoing analytical results. The scale-variable patterns of mineral occurrences are attributed to the different structural controls operating in the basement and sedimentary cover. In the basement, the EW-trending faults serve as pathways for channeling magma from a magma chamber into trap zones in the caprocks during Yanshanian period. The significant control of the EW-trending faults on Yanshanian intrusion is fully responsible for the strong correlation between the EW-trending faults and copper mineralization. This inference is supported by the result of Fry analysis which shows a dominant EW trend at regional scale (>4.5 km). In the sedimentary cover, the bedding-parallel shear zones formed during Indosinian folding and shearing and overprinted by tensional deformation in Yanshanian period act as favorable sites for hosting, focusing and depositing the ore-bearing fluids, which is responsible for the dominance of NE-NNE-NEE trends at fine scale (<4.5 m) in the results of Fry analysis. Such bedding-parallel structures, together with the contact zones of intrusion, exert an important control on the formation of characteristic stratabound skarn deposits in the TOD.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sillitoe, R.H. A plate tectonic model for the origin of porphyry copper deposits. Econ. Geol. 1972, 67, 184–197. [Google Scholar] [CrossRef]
- Tosdal, R.M.; Richards, J.P. Magmatic and structural controls on the developments of porphyry Cu ± Mo ± Au deposits. Rev. Econ. Geol. 2001, 14, 157–181. [Google Scholar]
- Kwelwa, S.D.; Dirks, P.H.G.M.; Sanislav, I.V.; Blenkinsop, T.; Kolling, S.L. Archaean gold mineralization in an extensional setting: The structural history of the Kukuluma and Matandani Deposits, Geita Greenstone Belt, Tanzania. Minerals 2018, 8, 171. [Google Scholar] [CrossRef]
- Cox, S.F.; Knackstedt, M.A.; Braun, J. Principles of structural control on permeability and fluid flow in hydrothermal systems. Rev. Econ. Geol. 2001, 14, 1–24. [Google Scholar]
- Austin, J.R.; Blenkinsop, T.G. Local to regional scale structural controls on mineralisation and the importance of a major lineament in the eastern Mount Isa Inlier, Australia: Review and analysis with autocorrelation and weights of evidence. Ore Geol. Rev. 2009, 35, 298–316. [Google Scholar] [CrossRef]
- Sillito, R.H. Iron oxide-copper-gold deposits: An Andean view. Miner. Deposita 2003, 38, 787–812. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, D.; Zhang, Z.; Liu, T.; Li, C.; Wei, C. Structural controls on the Lala iron-copper deposit of the Kangdian metallogenic province, Southwestern China: Tectonic and metallogenic implications. Ore Geol. Rev. 2018, 97, 35–54. [Google Scholar] [CrossRef]
- Chauvet, A.; Piantone, P.; Barbanson, L.; Nehlig, P.; Pedroletti, I. Gold deposit formation during collapse tectonics: Structural, mineralogical, geochronological, and fluid inclusion constraints in the Ouro Preto Gold Mines, Quadrilátero Ferrífero, Brazil. Econ. Geol. 2001, 96, 25–48. [Google Scholar] [CrossRef]
- Bonham-Carter, G.F. Geographic Information System for Geoscientists, Modeling with GIS; Pergamon: Elmsford, NY, USA, 1994; pp. 238–333. [Google Scholar]
- Haddad-Martim, P.M.; Filho, C.R.D.S.; Carranza, E.J.M. Spatial analysis of mineral deposit distribution: A review of methods and implications for structural controls on iron oxide-copper-gold mineralization in Carajás, Brazil. Ore Geol. Rev. 2017, 81, 230–244. [Google Scholar] [CrossRef]
- Schetselaar, E.; Ames, D.; Grunsky, E. Integrated 3D geological modeling to gain insight in the effects of hydrothermal alteration on post-ore deformation style and strain localization in the Flin Flon Volcanogenic Massive Sulfide Ore System. Minerals 2018, 8, 3. [Google Scholar] [CrossRef]
- Sun, T.; Wu, K.X.; Chen, L.K.; Liu, W.M.; Wang, Y.; Zhang, C.S. Joint application of fractal analysis and weights-of-evidence method for revealing the geological controls on regional-scale tungsten mineralization in Southern Jiangxi Province, China. Minerals 2017, 7, 243. [Google Scholar] [CrossRef]
- Li, X.H.; Yuan, F.; Zhang, M.M.; Jia, C.; Jowitt, S.M.; Ord, A.; Zheng, T.K.; Hu, X.Y.; Li, Y. Three-dimensional mineral prospectivity modeling for targeting of concealed mineralization within the Zhonggu iron orefield, Ningwu Basin, China. Ore Geol. Rev. 2015, 71, 633–654. [Google Scholar] [CrossRef]
- Xie, J.Y.; Wang, G.W.; Sha, Y.Z.; Liu, J.J.; Wen, B.T.; Nie, M.; Zhang, S. GIS prospectivity mapping and 3D modeling validation for potential uranium deposit targets in Shangnan district, China. J. Afr. Earth Sci. 2017, 128, 161–175. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Developments in GIS-based mineral prospectivity mapping: An overview. In Proceedings of the Mineral Prospectivity, Current Approaches and Future Innovations, Orléans, France, 24–26 October 2017. [Google Scholar]
- Parsa, M.; Maghsoudi, A.; Yousefi, M. Spatial analyses of exploration evidence data to model skarn-type copper prospectivity in the Varzaghan district, NW Iran. Ore Geol. Rev. 2018, 92, 97–112. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chances and Dimension; W.H. Freeman: New York, NY, USA, 1977; pp. 1–23. [Google Scholar]
- Roberts, S.; Sanderson, D.J.; Gumiel, P. Fractal analysis of Sn-W mineralization from central Iberia; insights into the role of fracture connectivity in the formation of an ore deposit. Econ. Geol. 1998, 93, 360–365. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Owusu, E.A.; Hale, M. Mapping of prospectivity and estimation of number of undiscovered prospects for lode gold, Southwestern Ashanti Belt, Ghana. Miner. Deposita. 2009, 44, 915–938. [Google Scholar] [CrossRef]
- Mehrabi, B.; Ghasemi, S.M.; Tale, F.E. Structural control on epithermal mineralization in the Troud-Chah Shirin belt using point pattern and Fry analyses, North of Iran. Geotectonics 2015, 49, 320–331. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Bonham-Carter, G.F.; Wrigh, D.F. Statistical pattern integration for mineral exploration. In Computer Application in Resource Estimation Prediction and Assessment for Metals and Petroleum; Gaal, G., Merriam, D.F., Eds.; Pergamon: Elmsford, NY, USA, 1990; pp. 1–21. [Google Scholar]
- Cheng, Q.M.; Agterberg, F.P. Fuzzy weights of evidence method and its application in mineral potential mapping. Nat. Resour. Res. 1999, 8, 27–35. [Google Scholar] [CrossRef]
- Yuan, F.; Li, X.H.; Zhang, M.M.; Jowitt, S.M.; Jia, C.; Zheng, T.K.; Zhou, T.F. Three-dimensional weights of evidence-based prospectivity modeling: A case study of the Baixiangshan mining area, Ningwu Basin, Middle and Lower Yangtze Metallogenic Belt, China. J. Geochem. Explor. 2014, 145, 82–97. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Controls on mineral deposit occurrence inferred from analysis of their spatial pattern and spatial association with geological features. Ore Geol. Rev. 2009, 35, 383–400. [Google Scholar] [CrossRef]
- Cao, Y.; Zheng, Z.; Du, Y.; Gao, F.; Qin, X.; Yang, H.; Lu, Y.; Du, Y. Ore geology and fluid inclusions of the Hucunnan deposit, Tongling, Eastern China: Implications for the separation of copper and molybdenum in skarn deposits. Ore Geol. Rev. 2017, 81, 925–939. [Google Scholar] [CrossRef]
- Liu, L.M.; Zhao, Y.L.; Zhao, C.B. Coupled geodynamics in the formation of Cu skarn deposits in the Tongling–Anqing district, China: Computational modeling and implications for exploration. J. Geochem. Explor. 2010, 106, 146–155. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, Y.J.; Li, H.B.; Liu, Z.F. Genesis of the Xinqiao Cu–S–Fe–Au deposit in the Middle-Lower Yangtze River Valley metallogenic belt, Eastern China: Constraints from U–Pb–Hf, Rb–Sr, S, and Pb isotopes. Ore Geol. Rev. 2017, 86, 100–116. [Google Scholar] [CrossRef]
- Fu, S.G.; Yan, X.Y.; Yuan, C.X. Geologic feature of submarine volcanic eruption-sedimentary pyrite type deposit in Carboniferous in the Middle-Lower Yangtze River Valley metallogenic belt, Eastern China. J. Nanjing Univ. Nat. Sci. Ed. 1977, 4, 43–67. (In Chinese) [Google Scholar]
- Gu, L.X.; Xu, K.Q. On the carboniferous submarine massive sulfide deposit in the lower reaches of the Yangtze River. Acta Geol. Sin. 1986, 60, 176–188. (In Chinese) [Google Scholar]
- Gu, L.X.; Hu, W.X.; He, J.X. Regional variations in ore composition and fluid features of massive sulfide deposits in South China: Implications for genetic modeling. Episodes 2000, 23, 110–118. [Google Scholar]
- Yang, D.F.; Fu, D.X.; Wu, N.X. Genesis of pyrite type copper in Xinqiao and its neighboring region according to ore composition and structure. Issue Nanjing Inst. Geol. Miner. Resour. Chin. Acad. Geol. Sci. 1982, 3, 59–68. (In Chinese) [Google Scholar]
- Xie, H.G.; Wang, W.B.; Li, W.D. The genesis and metallogenetic of Xinqiao Cu–S–Fe deposit, Anhui Province. Volcanol. Miner. Resour. 1995, 16, 101–107. (In Chinese) [Google Scholar]
- Zhou, T.F.; Zhang, L.J.; Yuan, F.; Fang, Y.; Cooke, D.R. LA-ICP-MS in situ trace element analysis of pyrite from the Xinqiao Cu–Au–S Deposit in Tongling, Anhui, and its constrains on the ore genesis. Earth Sci. Front. 2010, 17, 306–319. (In Chinese) [Google Scholar]
- Chang, Y.F.; Liu, X.G. Layer control type skarn type deposit—Some deposits in the Middle-Lower Yangtze Depression in Anhui Province as an example. Miner. Depos. 1983, 2, 11–20. (In Chinese) [Google Scholar]
- Pan, Y.; Dong, P. The lower Changjiang (Yangtzi/Yangtze River) metallogenic belt, East-center China: Intrusion and wall rock hosted Cu–Fe–Au, Mo, Zn, Pb, Ag deposits. Ore. Geol. Rev. 1999, 15, 177–242. [Google Scholar] [CrossRef]
- Mao, J.W.; Shao, Y.J.; Xie, G.Q.; Zhang, J.D.; Chen, Y.C. Mineral deposit model for porphyry-skarn polymetallic copper deposits in Tongling ore dense district of Middle-Lower Yangtze Valley metallogenic belt. Miner. Depos. 2009, 28, 109–119. (In Chinese) [Google Scholar]
- Zhang, Y.; Shao, Y.; Zhang, R.; Li, D.; Liu, Z.; Chen, H. Dating ore deposit using garnet U–Pb geochronology: Example from the Xinqiao Cu–S–Fe–Au deposit, Eastern China. Minerals 2018, 8, 31. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, S.; Fan, Y.; Yuan, F.; Zhang, D.; White, N.C. A review of the intracontinental porphyry deposits in the Middle-Lower Yangtze River Valley metallogenic belt, Eastern China. Ore Geol. Rev. 2015, 65, 433–456. [Google Scholar] [CrossRef]
- Hu, R.Z.; Chen, W.T.; Xu, D.R.; Zhou, M.F. Reviews and new metallogenic models of mineral deposits in South China: An introduction. J. Asian Earth Sci. 2017, 137, 1–8. [Google Scholar] [CrossRef]
- Mertig, H.J.; Rubin, J.N.; Kyle, J.R. Skarn Cu–Au orebodies of the Gunung Bijih (Ertsberg) district, Irian Jaya, Indonesia. J. Geochem. Explor. 1994, 50, 179–202. [Google Scholar] [CrossRef]
- Sato, T. Manto type copper deposit in Chile—A review. Bull. Geo. Surv. Japan 1984, 35, 565–582. [Google Scholar]
- Wang, Q.F.; Deng, J.; Huang, D.H.; Xiao, C.H.; Yang, L.Q.; Wang, Y.R. Deformation model for the Tongling ore cluster region, East-Central China. Int. Geol. Rev. 2011, 53, 562–579. [Google Scholar] [CrossRef]
- Wu, G.G.; Zhang, D.; Zang, W.S. Study of tectonic layering motion and layering mineralization in the Tongling metallogenic cluster. Sci. China Ser. D Earth Sci. 2003, 46, 852–863. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.W.; Li, X.H.; Selby, D.; Huang, G.H.; Chen, L.J.; Zheng, K. A carbonate replacement origin for the Xinqiao stratabound massive sulfide deposit, middle-lower Yangtze Metallogenic Belt, China. Ore Geol. Rev. 2017, 80, 985–1003. [Google Scholar] [CrossRef]
- Chang, Y.F.; Liu, X.P.; Wu, Y.C. The Copper–Iron Belt of the Low and Middle Reaches of the Changjiang River; Geological Publish House: Beijing, China, 1991; pp. 1–359. (In Chinese) [Google Scholar]
- Liu, L.M.; Yang, G.Y.; Peng, S.L.; Zhao, C.B. Numerical modeling of coupled geodynamical processes and its role in facilitating predictive ore discovery: An example from Tongling, China. Resour. Geol. 2005, 55, 21–31. [Google Scholar] [CrossRef]
- Liu, W.C.; Li, D.X.; Gao, D.Z. Analysis on the time sequence of compounding of structural deformation systems and resulting effects in Tongling area. J. Geomech. 1996, 2, 42–48. (In Chinese) [Google Scholar]
- Lü, Q.T.; Hou, Z.Q.; Zhao, J.H.; Shi, D.N.; Wu, X.Z.; Chang, Y.F.; Pei, R.F.; Huang, D.D.; Kuang, C.Y. Complex crustal structure of Tongling ore district: Insights from deep seismic reflection profiling. Sci. China Ser. D 2003, 33, 442–449. (In Chinese) [Google Scholar]
- Liu, Z.F.; Shao, Y.J.; Wei, H.T.; Wang, C. Rock-forming mechanism of Qingshanjiao intrusion in Dongguashan copper (gold) deposit, Tongling area, Anhui province, China. Trans. Nonferr. Met. Soc. China 2016, 26, 2449–2461. [Google Scholar] [CrossRef]
- Xie, J.C.; Yang, X.Y.; Sun, W.D.; Du, J.G. Early Cretaceous dioritic rocks in the Tongling region, Eastern China: Implications for the tectonic settings. Lithos 2012, 150, 49–61. [Google Scholar] [CrossRef]
- Liu, L.M.; Peng, S.L. Prediction of hidden ore bodies by synthesis of geological, geophysical and geochemical information based on dynamic model in Fenghuangshan ore field, Tongling district, China. J. Geochem. Explor. 2004, 81, 81–98. [Google Scholar] [CrossRef]
- 321 Geological Team. Structural Maps of Tongling Area; Bureau of Geological and Mineral Resources of Anhui Province: Hefei, China, 1989; pp. 1–33. [Google Scholar]
- Du, Y.L. Ore-Controlling Factors and Metallogenic Model of Stratabound Skarn Deposits in Tongling Area, Anhui Province. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2013. (In Chinese). [Google Scholar]
- Zuo, R.G.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2016, 164, 33–41. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature: Updated and Augmented; W.H. Freeman: New York, NY, USA, 1983; pp. 1–31. [Google Scholar]
- Berman, M. Distance distributions associated with poisson processes of geometric figures. J. Appl. Probab. 1977, 14, 195–199. [Google Scholar] [CrossRef]
- Berman, M. Testing for spatial association between a point process and another stochastic process. J. R. Stat. Soc. C Appl. 1986, 35, 54–62. [Google Scholar] [CrossRef]
- Allek, K.; Boubaya, D.; Bouguern, A.; Hamoudi, M. Spatial association analysis between hydrocarbon fields and sedimentary residual magnetic anomalies using weights of evidence: An example from the Triassic Province of Algeria. J. Appl. Geophys. 2016, 135, 100–110. [Google Scholar] [CrossRef]
- Sang, X.J.; Xue, L.F.; Liu, J.W.; Zhan, L. A novel Workflow for geothermal prospectively mapping weights-of-evidence in Liaoning Province, Northeast China. Energies 2017, 10, 1069. [Google Scholar] [CrossRef]
- Deng, J.; Huang, D.H.; Wang, Q.F.; Hou, Z.Q.; Lü, Q.T.; Yao, L.Q.; Xin, H.B.; Zhang, Q.; Wei, Y.G. Formation mechanism of “drag depressions” and irregular boundaries in intraplate deformation. Acta Geol. Sin. 2004, 78, 267–272. [Google Scholar]
- Waldron, J.W.F. Extensional fault arrays in strike-slip and transtension. J. Struct. Geol. 2005, 27, 23–34. [Google Scholar] [CrossRef]
- David, G.H.; Reynolds, S.J.; Kluth, C.F. Structural Geology of Rocks and Regions, 3rd ed.; JohnWiley & Sons, Inc.: Westwood, MA, USA, 2011; pp. 336–338. [Google Scholar]
- Wang, Q.F. Model study of the tectonic-magmatic-metallogenical system in Tongling ore cluster area. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2005. (In Chinese). [Google Scholar]
- Liu, L.M.; Sun, T.; Zhou, R.C. Epigenetic genesis and magmatic intrusion’s control on the Dongguashan stratabound Cu-Au deposit, Tongling, China: Evidence from field geology and numerical modeling. J. Geochem. Explor. 2014, 144, 97–114. [Google Scholar] [CrossRef]




| Epoch | Lithostratigraphic Unit | Code | Lithological Description | Tectonic Activity |
|---|---|---|---|---|
| Upper Cretaceous | Xuannan Formation | K2x | Conglomerate and sandstone | Yanshanian movement (ca. 135 Ma) |
| Middle Jurassic | Luoling Formation | J2l | Feldspar sandstone, siltstone and shale | |
| Lower Jurassic | Moshan Formation | J1m | Feldspar sandstone with interlays of silty shale and coal, conglomerate at bottom | Indosinian movement (ca. 195 Ma) |
| Middle Triassic | Tongtoujian Formation | T2t | Siltstone with interlays of sandy shale | |
| Yueshan Formation | T2y | Limestone, dolomite in upper and siltstone in lower | ||
| Lower Triassic | Nanlinghu Formation | T1n | Limestone | |
| Helongshan Formation | T1h | Limestone | ||
| Yingkeng Formation | T1y | Limestone with interlays of silt shale | ||
| Upper Permian | Dalong Formation | P2d | Siliceous shale with interlays of limestone | |
| Longtan Formation | P2l | Fine sandstone and silt shale with interlays of coal | ||
| Lower Permian | Gufeng Formation | P1g | Siliceous slate and siliceous shale | |
| Qixia Formation | P1q | Bioclastic limestone in upper and carbonaceous shale in lower | ||
| Upper Carboniferous | Chuanshan Formation | C2c | Orbicular limestone and bioclastic limestone | |
| Huanglong Formation | C2h | Bioclastic limestone and dolomite | ||
| Upper Devonian | Wutong Formation | D3w | Quartz sandstone and silty shale | |
| Middle Silurian | Fentou Formation | S2f | Sandstone, siltstone and sandy shale | |
| Lower Silurian | Gaojiabian Formation | S1g | Black shale | |
| Upper Ordovician | Wufeng Formation | O3w | Black siliceous shale | |
| Tangtou Formation | O3t | Calcareous shale with interlayers of limestone | ||
| Middle Ordovician | Tangshan Formation | O2t | Limestone with interlayers of thin slate | |
| Lower Ordovician | Lunshan Formation | O1l | Limestone in upper and dolomite in lower | |
| Cambrian | Huangjiabang Formation | є | Limestone | |
| Precambrian | Dongling Group | Pt3d | Biotite quartz schist and gneiss | Jinning movement (ca. 850–800 Ma) |
| Structural Features | Optimal Buffer Distance (m) | Distance Distribution Analysis | WofE Analysis | ||||
|---|---|---|---|---|---|---|---|
| DM | DN | D | uc | C | Cs | ||
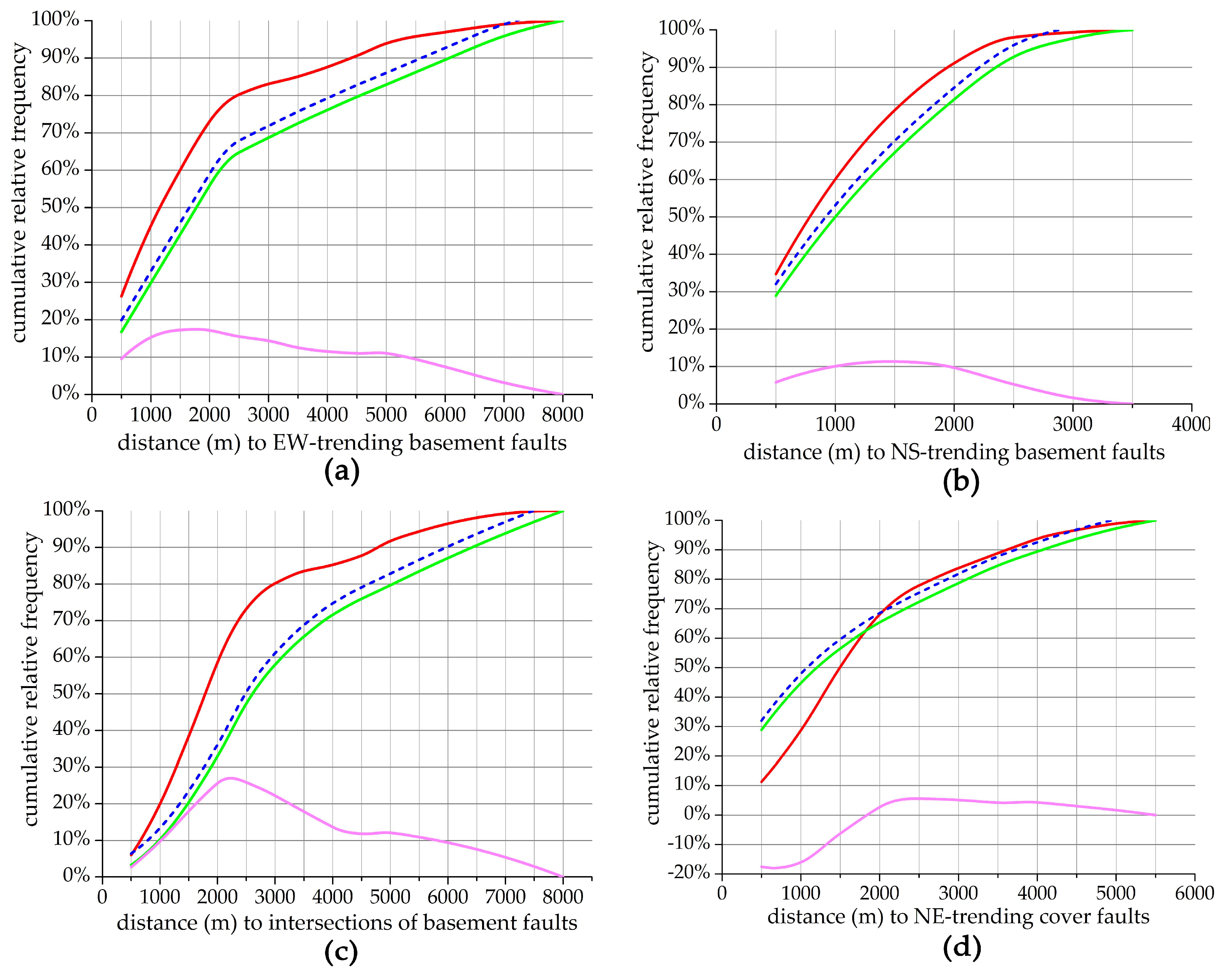
| EW-trending faults | 1500 | 76% | 55% | 21% | 75% | 1.36 | 4.6 |
| NS-trending faults | 1000 | 55% | 53% | 2% | 72% | 0.2 | 0.8 |
| intersections of basement faults | 2500 | 83% | 60% | 23% | 79% | 1.54 | 4.64 |
| folds | 2500 | 89% | 67% | 22% | 86% | 1.59 | 3.95 |
| NE-trending faults | 1500 | 68% | 57% | 11% | 76% | 0.63 | 2.33 |
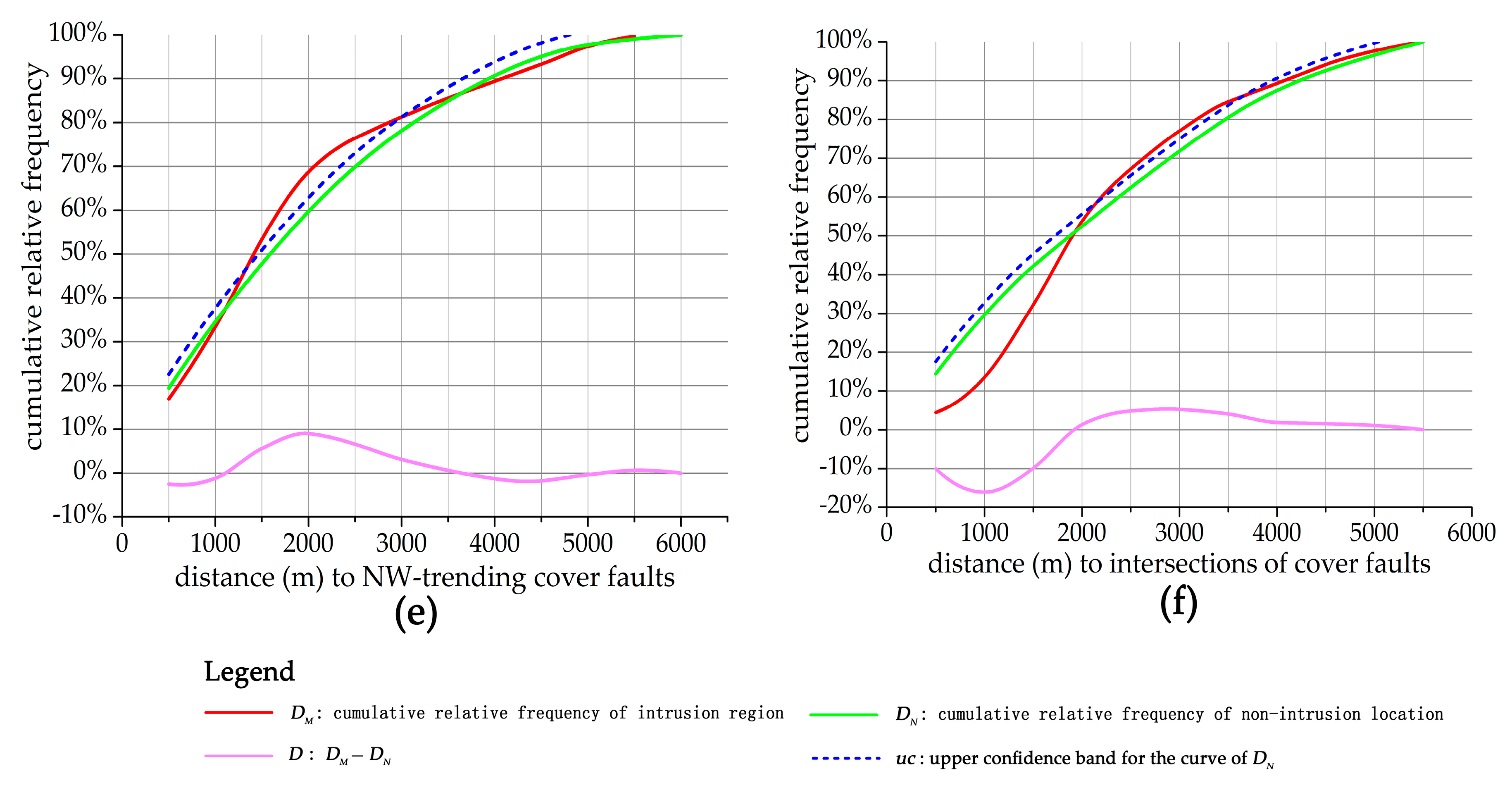
| NW-trending faults | 1500 | 59% | 49% | 10% | 68% | 0.44 | 1.74 |
| intersections of cover faults | 2500 | 74% | 65% | 9% | 84% | 0.71 | 2.46 |
| contact of Yanshanian intrusion | 350 | 87% | 21% | 55% | 52% | 3.04 | 8.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Xu, Y.; Yu, X.; Liu, W.; Li, R.; Hu, Z.; Wang, Y. Structural Controls on Copper Mineralization in the Tongling Ore District, Eastern China: Evidence from Spatial Analysis. Minerals 2018, 8, 254. https://doi.org/10.3390/min8060254
Sun T, Xu Y, Yu X, Liu W, Li R, Hu Z, Wang Y. Structural Controls on Copper Mineralization in the Tongling Ore District, Eastern China: Evidence from Spatial Analysis. Minerals. 2018; 8(6):254. https://doi.org/10.3390/min8060254
Chicago/Turabian StyleSun, Tao, Ying Xu, Xuhui Yu, Weiming Liu, Ruixue Li, Zijuan Hu, and Yun Wang. 2018. "Structural Controls on Copper Mineralization in the Tongling Ore District, Eastern China: Evidence from Spatial Analysis" Minerals 8, no. 6: 254. https://doi.org/10.3390/min8060254
APA StyleSun, T., Xu, Y., Yu, X., Liu, W., Li, R., Hu, Z., & Wang, Y. (2018). Structural Controls on Copper Mineralization in the Tongling Ore District, Eastern China: Evidence from Spatial Analysis. Minerals, 8(6), 254. https://doi.org/10.3390/min8060254





