Application of Depletion Attraction in Mineral Flotation: I. Theory
Abstract
1. Introduction
2. Theoretical Background
2.1. Probability for Particles to Attach to Bubbles Without Convective Flow
2.2. DLVO Interaction
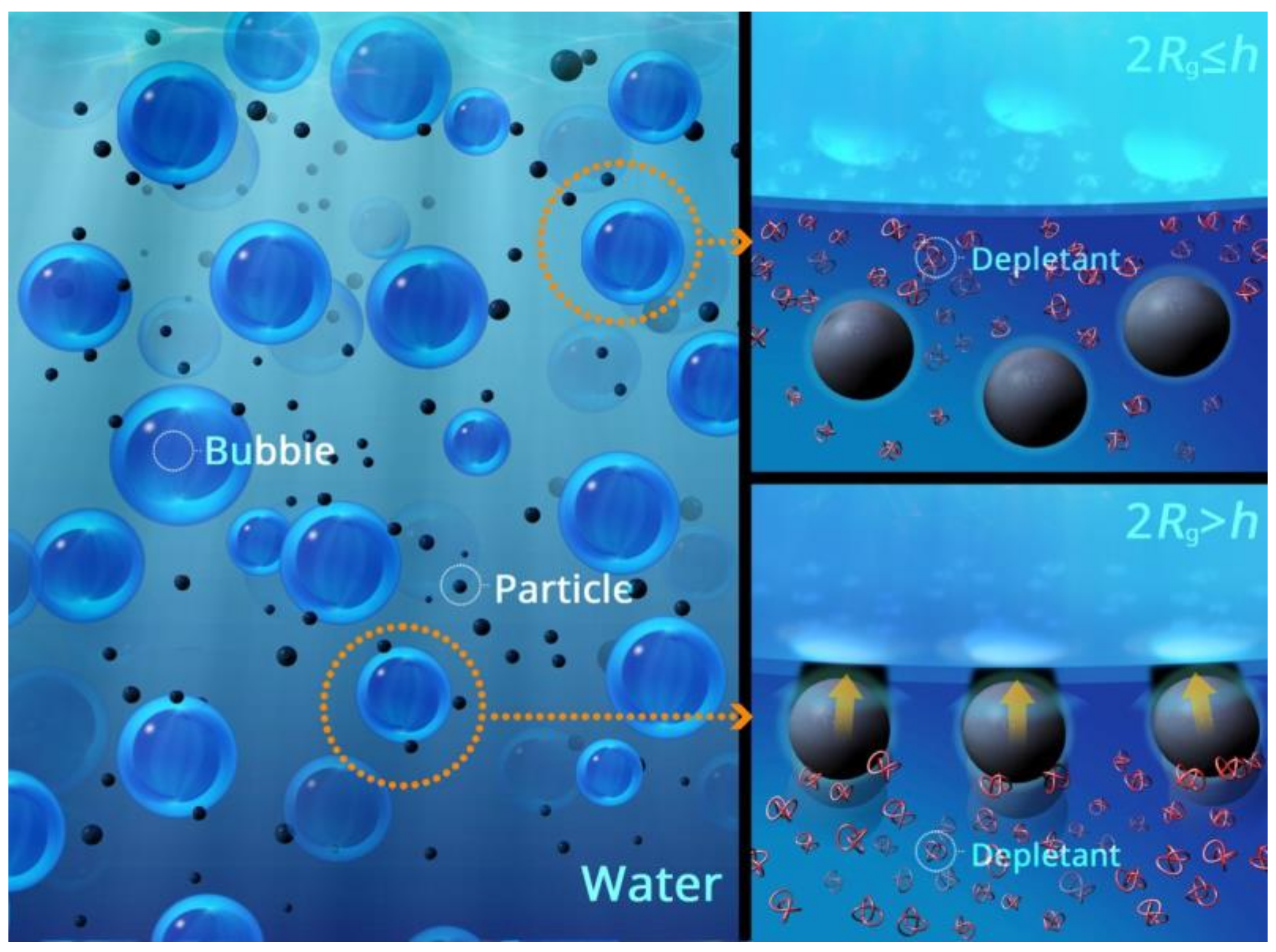
2.3. Depletion Interaction
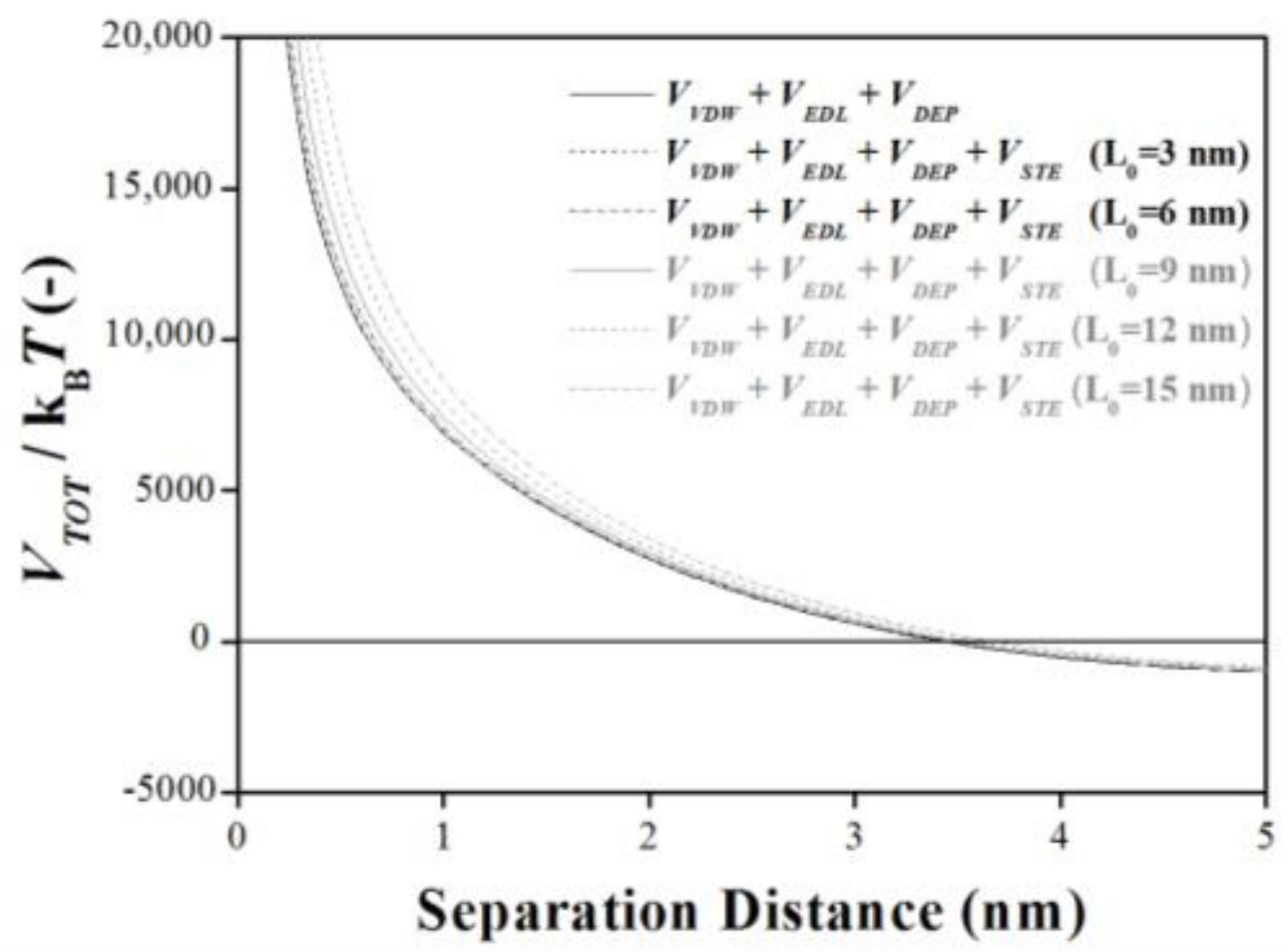
2.4. Steric Interaction
2.5. Other Possible Interaction (Surface Coverage)
3. Results and Discussion
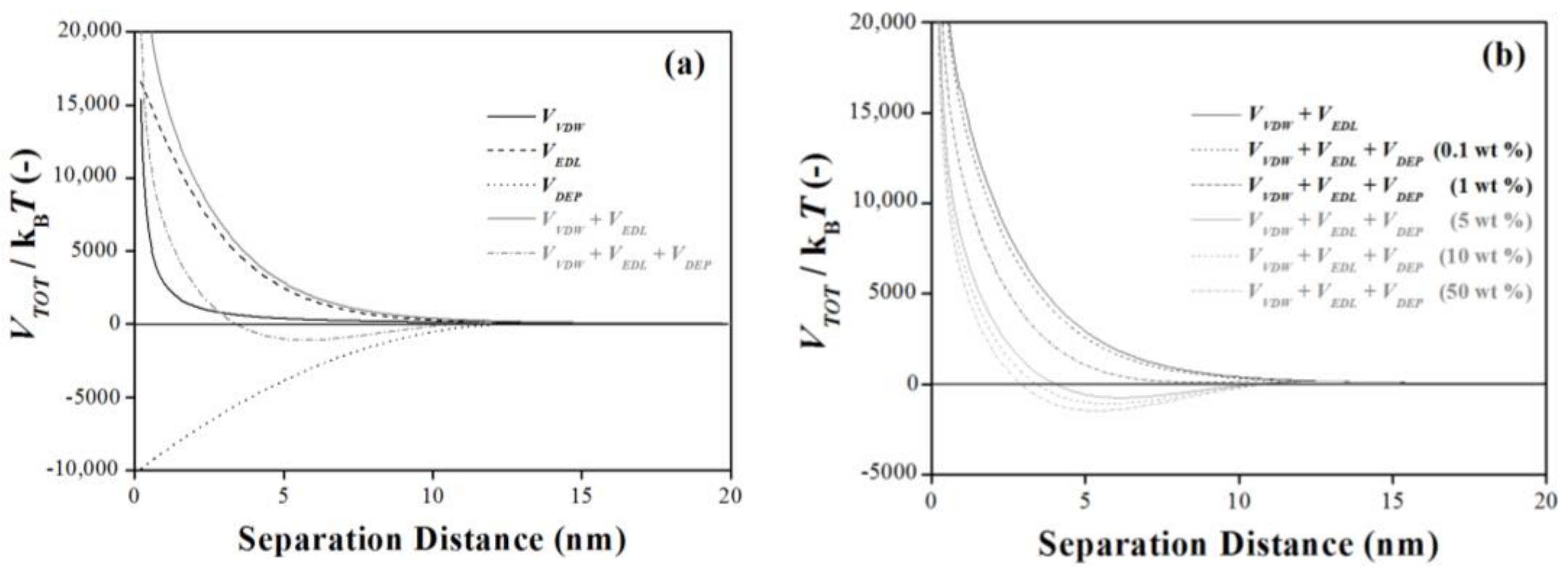
3.1. Depletion Interaction with DLVO Interactions
3.2. Concentration Dependent: Surface Activity of Depletion Agents (Steric Effects)
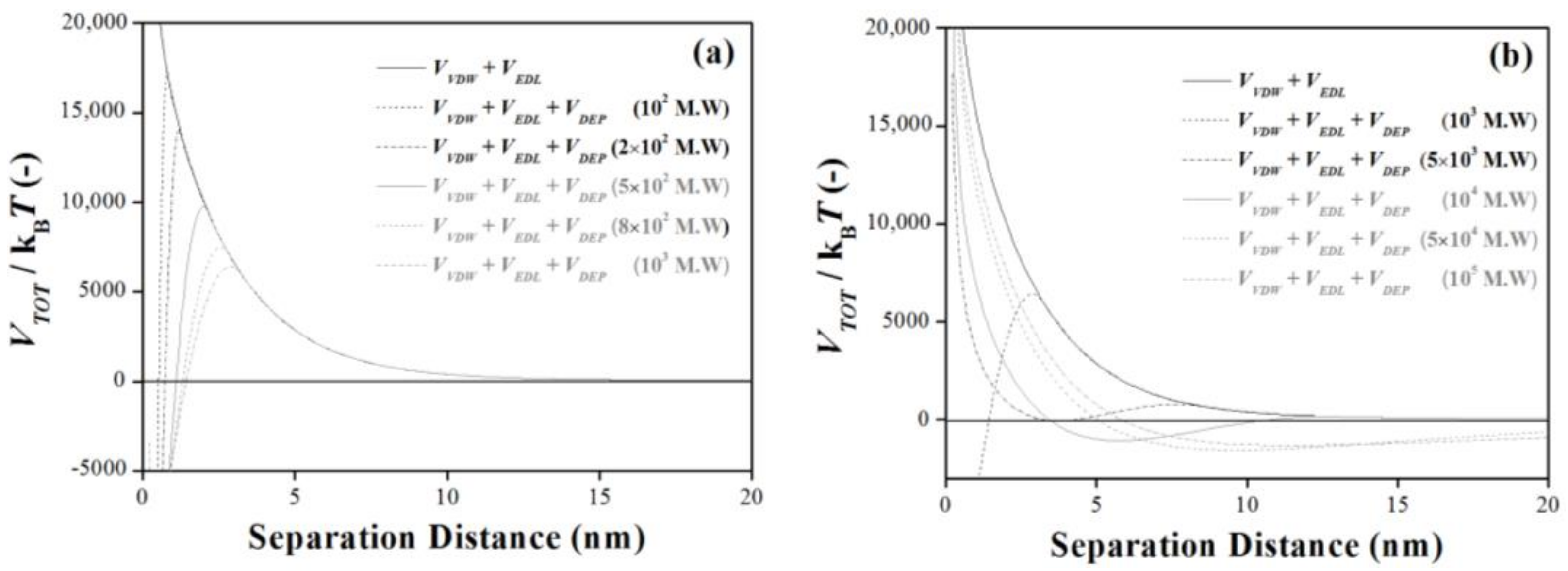
3.3. Molecular Weight Dependence: How Is the Energy Barrier Lowered?
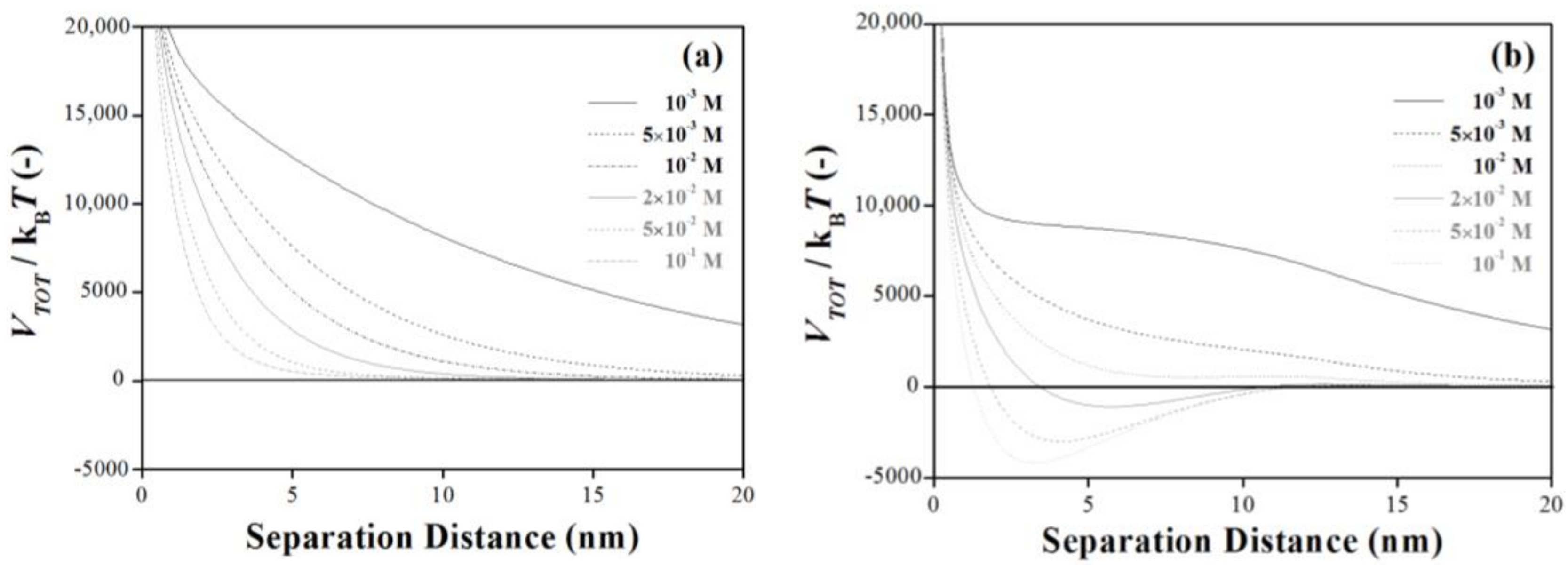
3.4. Ionic Strength Dependent: How Is the Energy Barrier Lowered?
3.5. Concentration Dependent: Gravity Versus Depletion (Particle Size Dependent)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fuerstenau, M.; Jameson, G.; Yoon, R.-H. Froth Flotation: A Century of Innovation; SME: Littleton, CO, USA, 2007. [Google Scholar]
- Choi, J.; Park, K.; Hong, J.; Park, J.; Kim, H. Arsenic removal from mine tailings for recycling via flotation. Mater. Trans. 2013, 54, 2291–2296. [Google Scholar] [CrossRef]
- Park, K.; Choi, J.; Gomez-Flores, A.; Kim, H. Flotation behavior of arsenopyrite and pyrite and their selective separation. Mater. Trans. 2015, 56, 435–440. [Google Scholar] [CrossRef]
- Park, K.; Park, S.; Choi, J.; Kim, G.; Tong, M.P.; Kim, H. Influence of excess sulfide ions on the malachite-bubble interaction in the presence of thiol-collector. Sep. Purif. Technol. 2016, 168, 1–7. [Google Scholar] [CrossRef]
- Choi, J.; Kim, W.; Chae, W.; Kim, S.B.; Kim, H. Electrostatically controlled enrichment of lepidolite via flotation. Mater. Trans. 2012, 53, 2191–2194. [Google Scholar] [CrossRef]
- Choi, J.; Choi, S.Q.; Park, K.; Han, Y.; Kim, H. Flotation behavior of malachite in mono- and di-valent salt solutions using sodium oleate as a collector. Int. J. Miner. Process. 2016, 146, 38–45. [Google Scholar] [CrossRef]
- Xing, Y.W.; Gui, X.H.; Cao, Y.J.; Wang, Y.W.; Xu, M.D.; Wang, D.Y.; Li, C.W. Effect of compound collector and blending frother on froth stability and flotation performance of oxidized coal. Powder Technol. 2017, 305, 166–173. [Google Scholar] [CrossRef]
- Espiritu, E.R.L.; da Silva, G.R.; Azizi, D.; Larachi, F.; Waters, K.E. The effect of dissolved mineral species on bastnäsite, monazite and dolomite flotation using benzohydroxamate collector. Colloids Surf. A-Physicochem. Eng. Asp. 2018, 539, 319–334. [Google Scholar] [CrossRef]
- Schubert, H.; Bischofberger, C. On the hydrodynamics of flotation machines. Int. J. Miner. Process. 1978, 5, 131–142. [Google Scholar] [CrossRef]
- Schubert, H. On the turbulence-controlled microprocesses in flotation machines. Int. J. Miner. Process. 1999, 56, 257–276. [Google Scholar] [CrossRef]
- Safari, M.; Deglon, D. An attachment-detachment kinetic model for the effect of energy input on flotation. Miner. Eng. 2018, 117, 8–13. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Nalaskowski, J.; Miller, J.D. A study of bubble-particle interaction using atomic force microscopy. Miner. Eng. 2003, 16, 1173–1181. [Google Scholar] [CrossRef]
- Hoseinian, F.S.; Rezai, B.; Kowsari, E. The main factors effecting the efficiency of Zn(ІІ) flotation: Optimum conditions and separation mechanism. J. Environ. Manag. 2018, 207, 169–179. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Jung, S.; Yoon, R.H. A fundamental study on the role of collector in the kinetics of bubble-particle interaction. Int. J. Miner. Process. 2012, 106, 37–41. [Google Scholar] [CrossRef]
- Hong, G.; Choi, J.; Han, Y.; Yoo, K.S.; Kim, K.; Kim, S.B.; Kim, H. Relationship between surface characteristics and floatability in representative sulfide minerals: Role of surface oxidation. Mater. Trans. 2017, 58, 1069–1075. [Google Scholar] [CrossRef]
- Phan, C.M.; Nguyen, A.V.; Miller, J.D.; Evans, G.M.; Jameson, G.J. Investigations of bubble-particle interactions. Int. J. Miner. Process. 2003, 72, 239–254. [Google Scholar] [CrossRef]
- Ralston, J.; Fornasiero, D.; Hayes, R. Bubble-particle attachment and detachment in flotation. Int. J. Miner. Process. 1999, 56, 133–164. [Google Scholar] [CrossRef]
- Verrelli, D.I.; Koh, P.T.L.; Nguyen, A.V. Particle-bubble interaction and attachment in flotation. Chem. Eng. Sci. 2011, 66, 5910–5921. [Google Scholar] [CrossRef]
- Kouachi, S.; Hassas, B.V.; Hassanzadeh, A.; Celik, M.S.; Bouhenguel, M. Effect of negative inertial forces on bubble-particle collision via implementation of schulze collision efficiency in general flotation rate constant equation. Colloids Surf. A-Physicochem. Eng. Asp. 2017, 517, 72–83. [Google Scholar] [CrossRef]
- Corin, K.C.; Reddy, A.; Miyen, L.; Wiese, J.G.; Harris, P.J. The effect of ionic strength of plant water on valuable mineral and gangue recovery in a platinum bearing ore from the merensky reef. Miner. Eng. 2011, 24, 131–137. [Google Scholar] [CrossRef]
- Ejtemaei, M.; Irannajad, M.; Gharabaghi, M. Influence of important factors on flotation of zinc oxide mineral using cationic, anionic and mixed (cationic/anionic) collectors. Miner. Eng. 2011, 24, 1402–1408. [Google Scholar] [CrossRef]
- Hu, Y.H.; Chen, P.; Sun, W. Study on quantitative structure-activity relationship of quaternary ammonium salt collectors for bauxite reverse flotation. Miner. Eng. 2012, 26, 24–33. [Google Scholar] [CrossRef]
- Jiang, H.; Sun, Z.C.; Xu, L.H.; Hu, Y.H.; Huang, K.; Zhu, S.S. A comparison study of the flotation and adsorption behaviors of diaspore and kaolinite with quaternary ammonium collectors. Miner. Eng. 2014, 65, 124–129. [Google Scholar] [CrossRef]
- Parker, G.K.; Buckley, A.N.; Woods, R.; Hope, G.A. The interaction of the flotation reagent, n-octanohydroxamate, with sulfide minerals. Miner. Eng. 2012, 36–38, 81–90. [Google Scholar] [CrossRef]
- Peng, Y.; Seaman, D. The flotation of slime-fine fractions of Mt. Keith pentlandite ore in de-ionised and saline water. Miner. Eng. 2011, 24, 479–481. [Google Scholar] [CrossRef]
- Shackleton, N.J.; Malysiak, V.; De Vaux, D.; Plint, N. Water quality—A comparative study between moncheite and pentlandite in mixture with pyroxene. Miner. Eng. 2012, 36–38, 53–64. [Google Scholar] [CrossRef]
- Vidyadhar, A.; Kumari, N.; Bhagat, R.P. Adsorption mechanism of mixed collector systems on hematite flotation. Miner. Eng. 2012, 26, 102–104. [Google Scholar] [CrossRef]
- Wang, B.; Peng, Y.J. The effect of saline water on mineral flotation—A critical review. Miner. Eng. 2014, 66–68, 13–24. [Google Scholar] [CrossRef]
- Zhang, M.; Peng, Y.J.; Xu, N. The effect of sea water on copper and gold flotation in the presence of bentonite. Miner. Eng. 2015, 77, 93–98. [Google Scholar] [CrossRef]
- Choi, J.; Lee, E.; Choi, S.Q.; Lee, S.; Han, Y.; Kim, H. Arsenic removal from contaminated soils for recycling via oil agglomerate flotation. Chem. Eng. J. 2016, 285, 207–217. [Google Scholar] [CrossRef]
- Kim, G.; Park, K.; Choi, J.; Gomez-Flores, A.; Han, Y.; Choi, S.Q.; Kim, H. Bioflotation of malachite using different growth phases of Rhodococcus opacus: Effect of bacterial shape on detachment by shear flow. Int. J. Miner. Process. 2015, 143, 98–104. [Google Scholar] [CrossRef]
- Kim, G.; Choi, J.; Silva, R.A.; Song, Y.; Kim, H. Feasibility of bench-scale selective bioflotation of copper oxide minerals using rhodococcus opacus. Hydrometallurgy 2017, 168, 94–102. [Google Scholar] [CrossRef]
- Liu, W.Y.; Moran, C.J.; Vink, S. A review of the effect of water quality on flotation. Miner. Eng. 2013, 53, 91–100. [Google Scholar] [CrossRef]
- Kim, H.N.; Walker, S.L. Escherichia coli transport in porous media: Influence of cell strain, solution chemistry and temperature. Colloids Surf. B-Biointerfaces 2009, 71, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Fielden, M.L.; Hayes, R.A.; Ralston, J. Surface and capillary forces affecting air bubble-particle interactions in aqueous electrolyte. Langmuir 1996, 12, 3721–3727. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Schulze, H.J.; Ralston, J. Elementary steps in particle-bubble attachment. Int. J. Miner. Process. 1997, 51, 183–195. [Google Scholar] [CrossRef]
- Asakura, S.; Oosawa, F. Interaction between particles suspended in solutions of macromolecules. J. Polym. Sci. 1958, 33, 183–192. [Google Scholar] [CrossRef]
- Mao, Y.; Cates, M.E.; Lekkerkerker, H.N.W. Depletion force in colloidal systems. Physica A 1995, 222, 10–24. [Google Scholar] [CrossRef]
- Walz, J.Y.; Sharma, A. Effect of long range interactions on the depletion force between colloidal particles. J. Colloid Interface Sci. 1994, 168, 485–496. [Google Scholar] [CrossRef]
- Lekkerkerker, H.N.W.; Tuinier, R. Colloids and the Depletion Interaction; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Kim, K.; Kim, S.; Ryu, J.; Jeon, J.; Jang, S.G.; Kim, H.; Gweon, D.G.; Im, W.B.; Han, Y.; Kim, H.; et al. Processable high internal phase pickering emulsions using depletion attraction. Nat. Commun. 2017, 8, 14305. [Google Scholar] [CrossRef] [PubMed]
- Zasadzinski, J.A.; Alig, T.F.; Alonso, C.; de la Serna, J.B.; Perez-Gil, J.; Taeusch, H.W. Inhibition of pulmonary surfactant adsorption by serum and the mechanisms of reversal by hydrophilic polymers: Theory. Biophys. J. 2005, 89, 1621–1629. [Google Scholar] [CrossRef] [PubMed]
- Biggs, S. Steric and bridging forces between surfaces fearing adsorbed polymer: An atomic-force microscopy study. Langmuir 1995, 11, 156–162. [Google Scholar] [CrossRef]
- Gotchev, G.; Kolarov, T.; Khristov, K.; Exerowa, D. Electrostatic and steric interactions in oil-in-water emulsion films from pluronic surfactants. Adv. Colloid Interface Sci. 2011, 168, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.U.; Matsen, M.W. Repulsion exerted on a spherical particle by a polymer brush. Macromolecules 2008, 41, 246–252. [Google Scholar] [CrossRef]
- Han, P.; Wang, X.T.; Cai, L.; Tong, M.P.; Kim, H. Transport and retention behaviors of titanium dioxide nanoparticles in iron oxide-coated quartz sand: Effects of pH, ionic strength and humic acid. Colloids Surf. A-Physicochem. Eng. Asp. 2014, 454, 119–127. [Google Scholar] [CrossRef]
- Han, Y.; Hwang, G.; Park, S.; Gomez-Flores, A.; Jo, E.; Eom, I.C.; Tong, M.P.; Kim, H.J.; Kim, H. Stability of carboxyl-functionalized carbon black nanoparticles: The role of solution chemistry and humic acid. Environ. Sci. Nano 2017, 4, 800–810. [Google Scholar] [CrossRef]
- Jiang, X.J.; Tong, M.P.; Kim, H. Influence of natural organic matter on the transport and deposition of zinc oxide nanoparticles in saturated porous media. J Colloid Interface Sci. 2012, 386, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.N.; Bradford, S.A.; Walker, S.L. Escherichia coli O157:H7 transport in saturated porous media: Role of solution chemistry and surface macromolecules. Environ. Sci. Technol. 2009, 43, 4340–4347. [Google Scholar] [CrossRef] [PubMed]
- Abrahamson, J. Collision rates of small particles in a vigorously turbulent fluid. Chem. Eng. Sci. 1975, 30, 1371–1379. [Google Scholar] [CrossRef]
- Schubert, H. On the optimization of hydrodynamics in fine particle flotation. Miner. Eng. 2008, 21, 930–936. [Google Scholar] [CrossRef]
- Hiemenz, P.C. Principles of Colloid and Surface Chemistry, 2nd ed.; M. Dekker: New York, NY, USA, 1986. [Google Scholar]
- Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged-particles in solutions of electrolytes. Prog. Surf. Sci. 1941, 14, 633–662. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Nes, K.V.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids: The Interaction of Sol Particles Having an Electric Double Layer; Elsevier: New York, NY, USA, 1948. [Google Scholar]
- Gregory, J. Approximate expressions for retarded vanderwaals interaction. J. Colloid Interface Sci. 1981, 83, 138–145. [Google Scholar] [CrossRef]
- Yoon, R.H. The role of hydrodynamic and surface forces in bubble-particle interaction. Int. J. Miner. Process. 2000, 58, 129–143. [Google Scholar] [CrossRef]
- Lu, S. Hydrophobic interaction in flocculation and flotation 3. Role of hydrophobic interaction in particle-bubble attachment. Colloid Surf. 1991, 57, 73–81. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Syngouna, V.I. Attachment of bacteriophages MS2 and ΦX174 onto kaolinite and montmorillonite: Extended-DLVO interactions. Colloids Surface. B Biointerfaces 2012, 92, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.N.; Walker, S.L.; Bradford, S.A. Macromolecule mediated transport and retention of Escherichia coli O157:H7 in saturated porous media. Water Res. 2010, 44, 1082–1093. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Hwang, G.; Kim, D.; Bradford, S.A.; Lee, B.; Eom, I.; Kim, P.J.; Choi, S.Q.; Kim, H. Transport, retention and long-term release behavior of ZnO nanoparticle aggregates in saturated quartz sand: Role of solution pH and biofilm coating. Water Res. 2016, 90, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Bickel, T. Depletion forces near a soft surface. J. Chem. Phys. 2003, 118, 8960–8968. [Google Scholar] [CrossRef]
- Reed, K.M.; Borovicka, J.; Horozov, T.S.; Paunov, V.N.; Thompson, K.L.; Walsh, A.; Armes, S.P. Adsorption of sterically stabilized latex particles at liquid surfaces: Effects of steric stabilizer surface coverage, particle size and chain length on particle wettability. Langmuir 2012, 28, 7291–7298. [Google Scholar] [CrossRef] [PubMed]
- Alexander, S. Adsorption of chain molecules with a polar head a-scaling description. J. Phys. 1977, 38, 983–987. [Google Scholar] [CrossRef]
- Degennes, P.G. Polymers at an interface; a simplified view. Adv. Colloid Interface Sci. 1987, 27, 189–209. [Google Scholar] [CrossRef]
- Helgason, T.; Awad, T.S.; Kristbergsson, K.; McClements, D.J.; Weiss, J. Effect of surfactant surface coverage on formation of solid lipid nanoparticles (SLN). J. Colloid Interface Sci. 2009, 334, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.-Y.; Tsay, R.-Y.; Lin, L.-W.; Chen, S.-I. Adsorption kinetics of C12E8 at the air-water interface: Adsorption onto a clean interface. Langmuir 1996, 12, 6530–6536. [Google Scholar] [CrossRef]
- Choi, S.Q.; Steltenkamp, S.; Zasadzinski, J.A.; Squires, T.M. Active microrheology and simultaneous visualization of sheared phospholipid monolayers. Nat. Commun. 2011, 2, 312. [Google Scholar] [CrossRef] [PubMed]
- Leal-Calderon, F.; Schmitt, V. Solid-stabilized emulsions. Curr. Opin. Colloid Interface Sci. 2008, 13, 217–227. [Google Scholar] [CrossRef]
- Stocco, A.; Rio, E.; Binks, B.P.; Langevin, D. Aqueous foams stabilized solely by particles. Soft Matter 2011, 7, 1260–1267. [Google Scholar] [CrossRef]
- Kim, G.; Choi, J.; Choi, S.; Kim, K.; Han, Y.; Bradford, S.A.; Choi, S.Q.; Kim, H. Application of depletion attraction in mineral flotation: II. Effects of depletant concentration. Minerals 2018. under review. [Google Scholar]
- Castro, S.H.; Baltierra, L. Study of the surface properties of enargite as a function of pH. Int. J. Miner. Process. 2005, 77, 104–115. [Google Scholar] [CrossRef]
- Elmallidy, A.M.; Mirnezami, M.; Finch, J.A. Zeta potential of air bubbles in presence of frothers. Int. J. Miner. Process. 2008, 89, 40–43. [Google Scholar]
- Ling, K.; Jiang, H.Y.; Zhang, Q.Q. A colorimetric method for the molecular weight determination of polyethylene glycol using gold nanoparticles. Nanoscale Res. Lett. 2013, 8, 538. [Google Scholar] [CrossRef] [PubMed]
- Gast, A.P.; Leibler, L. Interactions of sterically stabilized particles suspended in a polymer-solution. Macromolecules 1986, 19, 686–691. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Needham, D.; Kim, D.H. Peg-covered lipid surfaces: Bilayers and monolayers. Colloids Surf. B Biointerfaces 2000, 18, 183–195. [Google Scholar] [CrossRef]
- Herrmann, A.; Clague, M.J.; Blumenthal, R. Enhancement of viral fusion by nonadsorbing polymers. Biophys. J. 1993, 65, 528–534. [Google Scholar] [CrossRef]
- Unsworth, L.D.; Sheardown, H.; Brash, J.L. Protein-resistant poly(ethylene oxide)-grafted surfaces: Chain density-dependent multiple mechanisms of action. Langmuir 2008, 24, 1924–1929. [Google Scholar] [CrossRef] [PubMed]
- Gonzaleztello, P.; Camacho, F.; Blazquez, G. Density and viscosity of concentrated aqueous-solutions of polyethylene-glycol. J. Chem. Eng. Data 1994, 39, 611–614. [Google Scholar] [CrossRef]
- Levine, S.; Bowen, B.D.; Partridge, S.J. Stabilization of emulsions by fine particles І. Partitioning of particles between continuous phase and oil/water interface. Colloid Surf. 1989, 38, 325–343. [Google Scholar] [CrossRef]
- Binks, B.P.; Horozov, T. Colloidal Particles at Liquid Interfaces; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kim, K.; Park, K.; Kim, G.; Kim, H.; Choi, M.C.; Choi, S.Q. Surface charge regulation of carboxyl terminated polystyrene latex particles and their interactions at the oil/water interface. Langmuir 2014, 30, 12164–12170. [Google Scholar] [CrossRef] [PubMed]
| Parameters | Values | References |
|---|---|---|
| Relative Permittivity, εr | 78.5 a | |
| Permittivity of Free Space, ε0 | 8.85 × 10−12 C2/J m a | |
| Colloid Particle Radius, a | 2.5 × 10−5 m a | |
| Sphere Surface Potential, Ψp | −0.02 V a | [71] |
| Plate Surface Potential, Ψs | −0.025 V a | [72] |
| Elementary Charge, e | 1.60 × 10−19 C a | |
| Debye Length, ld | 2.15 × 10−9 m a | |
| 9.62 × 10−10–9.62 × 10−9 m b | ||
| Ionic Strength, IS | 2 × 10−2 mol/L a | |
| 10−3–10−1 mol/L b | ||
| Avogadro’s Number, NA | 6.02 × 1023 1/mol a | |
| Boltzman Constant, kB | 1.38 × 10−23 J/K a | |
| Absolute Temperature, T | 298 K a |
| Parameters | Values | References |
|---|---|---|
| Hamaker Constant, A132 | −3.12 × 10−21 J a | [56] |
| Colloid Particle Radius, a | 2.5 × 10−5 m a | |
| Directric Wavelength, λ | 10−7 m a | |
| Boltzman Constant, kB | 1.38 × 10−23 J/K a | |
| Absolute Temperature, T | 298 K a |
| Parameter | Values | References |
|---|---|---|
| Polymer Radius of Gyration, Rg | 6.48 × 10−9 m a | [73] |
| 4.09 × 10−10–2.58 × 10−8 m c | ||
| Polymer Volume Fraction, ϕp | 8.84 × 10−1 a (−) | |
| 6.44 × 10−2–9.86 × 10−1 b (−) | ||
| Colloid Particle Radius, a | 2.5 × 10−5 m a | |
| Polymer Weight Percent, Wtp | 10 wt % | |
| 0.1–50 wt % b | ||
| Polymer Molecular Weight, MW | 104 g/mol a | |
| 102–105 g/mol c | ||
| Boltzman Constant, kB | 1.38 × 10−23 J/K a | |
| Absolute Temperature, T | 298 K a |
| Parameters | Values | References |
|---|---|---|
| Areal Chain Density, σ | 1 nm−2 a | [78] |
| Brush Thickness, L0 | 3 × 10−9–1.5 × 10−8 m b |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Kim, G.; Choi, S.; Kim, K.; Han, Y.; Bradford, S.A.; Choi, S.Q.; Kim, H. Application of Depletion Attraction in Mineral Flotation: I. Theory. Minerals 2018, 8, 451. https://doi.org/10.3390/min8100451
Choi J, Kim G, Choi S, Kim K, Han Y, Bradford SA, Choi SQ, Kim H. Application of Depletion Attraction in Mineral Flotation: I. Theory. Minerals. 2018; 8(10):451. https://doi.org/10.3390/min8100451
Chicago/Turabian StyleChoi, Junhyun, Gahee Kim, Sowon Choi, KyuHan Kim, Yosep Han, Scott A. Bradford, Siyoung Q. Choi, and Hyunjung Kim. 2018. "Application of Depletion Attraction in Mineral Flotation: I. Theory" Minerals 8, no. 10: 451. https://doi.org/10.3390/min8100451
APA StyleChoi, J., Kim, G., Choi, S., Kim, K., Han, Y., Bradford, S. A., Choi, S. Q., & Kim, H. (2018). Application of Depletion Attraction in Mineral Flotation: I. Theory. Minerals, 8(10), 451. https://doi.org/10.3390/min8100451






