Numerical Simulations of Two-Phase Flow in a Self-Aerated Flotation Machine and Kinetics Modeling

Abstract

A new boundary condition treatment has been devised for two-phase flow numerical simulations in a self-aerated minerals flotation machine and applied to a Wemco 0.8 m³ pilot cell. Airflow rate is not specified a priori but is predicted by the simulations as well as power consumption. Time-dependent simulations of two-phase flow in flotation machines are essential to understanding flow behavior and physics in self-aerated machines such as the Wemco machines. In this paper, simulations have been conducted for three different uniform bubble sizes (d_b = 0.5, 0.7 and 1.0 mm) to study the effects of bubble size on air holdup and hydrodynamics in Wemco pilot cells. Moreover, a computational fluid dynamics (CFD)-based flotation model has been developed to predict the pulp recovery rate of minerals from a flotation cell for different bubble sizes, different particle sizes and particle size distribution. The model uses a first-order rate equation, where models for probabilities of collision, adhesion and stabilization and collisions frequency estimated by Zaitchik-2010 model are used for the calculation of rate constant. Spatial distributions of dissipation rate and air volume fraction (also called void fraction) determined by the two-phase simulations are the input for the flotation kinetics model. The average pulp recovery rate has been calculated locally for different uniform bubble and particle diameters. The CFD-based flotation kinetics model is also used to predict pulp recovery rate in the presence of particle size distribution. Particle number density pdf and the data generated for single particle size are used to compute the recovery rate for a specific mean particle diameter. Our computational model gives a figure of merit for the recovery rate of a flotation machine, and as such can be used to assess incremental design improvements as well as design of new machines.

1. Introduction

Mineral flotation machines are classified into two main types; forced air and self-aerated machines. Wemco machines are widely used self-aerated machines where no air pumping mechanism is required, which simplifies flotation plant design and operation. The rate of air flow and power consumption of Wemco machines depend on the flow structure and the hydrodynamics within the pulp volume. For a given machine, rate of airflow depends on the rotor speed (RPM) among other operating conditions such as rotor blades and disperser design. Instantaneous airflow rate in a Wemco machine is not known a priori and depends on machine design and operating conditions. Therefore, computational fluid dynamics (CFD) simulation of a Wemco machine is a challenging problem because airflow rate cannot be specified but it has to be an outcome of the simulation. Moreover, rate of air flow may vary significantly with time to the extent that air is temporarily “exhaled” by the standpipe instead of being “inhaled”. Computer simulations of such a machine should predict the time-history of the rate of air flow, and the average rate is an output. The unknown rate of air flow and the possibility of “breathing” require careful treatments of the standpipe and pulp–froth interface boundary conditions. Koh and Schwarz [1] conducted CFD simulation of the self-aerated flotation machine Denver-Metso Minerals. In that machine, air flow rate depends on suction pressure created by the impeller, the hydrostatic head of the pulp, and the frictional losses along the delivery shaft from the inlet valve to the impeller. The air motion was not simulated in the standpipe. They predicted the air flow rate iteratively during the simulation by applying pressure loss formula to find the pressure drop in the standpipe. An empirical constant in the formula was adjusted for CFD simulations to match the experimental data.

Computational domains of flotation machines are large, and flow physics are complex involving multi-phase flow turbulence. Even two-phase flow simulations of flotation machines are time consuming and require large computational resources. Some approaches have been used to reduce computational costs for two-phase flow; see, for example, the approach by Tiitinen et al. [2], where sector based simulations were used to reduce the number of grid nodes. Bubble size is one of the most important parameters that affect the air holdup of the pulp phase. A spectrum of bubble sizes exists in flotation machines depending on air flow rate and turbulence parameters. To predict such bubble size distribution, another set of equations that describes a population balance can be solved in the course of CFD simulation (Kerdouss et al. [3]). This approach increases the computational demands where transport equation for each size group has to be implemented. A more feasible approach is to conduct a parametric study for different uniform bubble sizes to study their effects on air holdup and rate constant.

One of the main characteristics of mechanical flotation machines is to agitate the slurry and disperse air bubbles throughout the pulp volume. In order to assess the performance of flotation machines, it is important to know the spatial distribution of dispersed bubbles within the tank which directly affects air hold up and rate constant. The current CFD simulations are parametric study of two-phase flow in Wemco 0.8 m³ that provide the hydrodynamic data and air volume fraction spatial distribution for uniform bubble size in the pulp phase. Three different bubble sizes—d_b = 0.5, 0.7 and 1.0 mm—are used to investigate the effects of the bubble size on air flow rate, air holdup and rate constant. The paper is organized as follow. Section 2 presents the governing equations for two-phase flow. Machine geometry is presented in Section 3, and simulation results are discussed in Section 4. Flotation model and results are presented and discussed in Section 5, and conclusions are summarized in Section 6.

2. Euler-Euler Two-Fluid Model

A practical approach for two-phase simulations is the Euler-Euler approach in which both phases are modeled by volume-averaged equations [4]. The motion of the two continuous phases is described by the unsteady Reynolds-averaged Navier–Stokes (RANS) equation:

Continuity equation:

$$\frac{\partial \left({\text{α}}_i{\text{ρ}}_i\right)}{\partial t}+\nabla .\left({\text{α}}_i{\text{ρ}}_{i }{\overrightarrow{V}}_{i }\right)=0$$

(1)

Momentum equation:

$$\frac{\partial \left({\text{α}}_i{\text{ρ}}_i{\overrightarrow{V}}_i\right)}{\partial t}+\nabla .\left({\text{α}}_i{\text{ρ}}_i{\overrightarrow{V}}_{i }{\overrightarrow{V}}_{i }\right)=-{\text{α}}_i\nabla P+\nabla .[{\text{μ}}_{i,\text{eff }}(\nabla {\overrightarrow{V}}_i+{\left(\nabla {\overrightarrow{V}}_i\right)}^T)]+S_i+M_i$$

(2)

where (i = 1) denotes water phase and (i = 2) denotes gas phase, $\nabla P$ is the modified pressure to include the gravity effects, S_i describes any external momentum source and $M_i$ is the interfacial force that acts on phase (i) due to the presence of other phases. In the present simulations, momentum exchanges between the two phases due to drag and buoyancy on bubbles are the only mechanisms that couple the motion of the two phases. Bubbles are deformable fluid particles when moving in high shear rate regions such as in minerals flotation machines. Schiller-Naumann drag model [5] has been used to estimate drag coefficient of air bubbles. Effects of bubbles deformations on the values of drag coefficient are neglected in Schiller-Naumann drag model [5].

Shear stress transport (SST) turbulence model has been used to model turbulence transport where two transport equations are solved. There is no such universal turbulence model for two-phase flow, particularly at high volume fraction [6]. Reynolds stress model is the most adequate model for swirling flows. However, Reynolds stress model (RSM) closes the RANS equations by solving six additional transport equations for averaged Reynolds stress terms, and that require large computational resources. Geometry and flow physics of minerals flotation machines are large and complex. Therefore, using RSM turbulence model is not feasible for such application and SST model has been used in our CFD study.

3. Cell Geometry and Simulations Parameters

The main components of Wemco-0.8 m³ machine (FLSmidth, Salt Lake City, UT, USA) as shown in Figure 1 include a six-blade rotor, a disperser, a draft tube, and a standpipe. Details of the different components are shown in Figure 2. The disperser has 34 holes arranged in two parallel rows. Seventeen semi-circular rods are attached to the inner surface of the disperser. Air is drawn into the machine through a hole in the top of standpipe. The machine is assembled in Figure 3. The simulated Wemco-0.8 m³ model does not have a disperser hood or tank baffles.

Figure 1. Core of the Wemco-0.8m³ machine: rotor, disperser, draft tube, and standpipe.

Figure 1. Core of the Wemco-0.8m³ machine: rotor, disperser, draft tube, and standpipe.

Figure 2. Details of Wemco-0.8m³ rotor, disperser, and standpipe; (a) relative vertical position of rotor and disperse; (b) rotor and disperser.

Figure 2. Details of Wemco-0.8m³ rotor, disperser, and standpipe; (a) relative vertical position of rotor and disperse; (b) rotor and disperser.

The boundary condition treatment at the air opening in top of the standpipe allows air to enter or exit from the standpipe above the rotor. There is no valve or any other device that obstructs air from flowing back to the ambient through the air inlet hole. If airflow reverses direction it may also carry a small amount of water with it. A container, which is connected to the standpipe only through the air inlet hole, is added. Its function is to retain any water that might be expelled and is to be retrieved when air flows back into the machine. Atmospheric pressure is prescribed at the top of that container. This treatment is unique to the present simulations of a self-aerated machine, and it allows the machine to “breath” for some operating conditions. An important operating assumption used in the present simulations is that the amount of water within the tank remains constant during operation. That is to say no water is allowed to flow over the weir. This condition may not be precisely satisfied in the actual machine operation; but it is a realizable situation. To guarantee that no water exits the tank, the tank wall is extended vertically above the weir edge thereby creating an overflow tank. The overflow tank is a mere vertical extension of the actual tank walls. Atmospheric pressure is prescribed at the top of the overflow tank. The actual tank is initialized with 100% water up to a certain level to be defined later, and the rest of the actual tank and overflow tank are initialized with 100% air.

Figure 3. Wemco-0.8 m³ assembly: tank, air-inlet and initial water level.

Figure 3. Wemco-0.8 m³ assembly: tank, air-inlet and initial water level.

The function of the overflow tank is to permit the water level to rise due to the accumulation of air in the pulp, and at the same time it does not allow water to exit the computational domain. No boundary conditions are needed at the interface between the actual tank and the overflow tank. The governing equations of the two-phase flow are solved in both tanks allowing air and water to flow back and forth between the tanks as required by the transport equations. The part of the computational domain below the initial water level is initialized (t = 0) with 100% water and the part above that level is initialized by 100% air. A multi block structured grid has been generated for the current simulations using ICEM CFD grid generator. The total number of nodes is around 2.4 × 10⁶. The size of the cells and number of nodes on rotor, disperser walls among other parts have been chosen to resolve boundary layer flow on these walls. Two phase flow simulations have been conducted using ANSYS CFX 12.0 commercial CFD software (ANSYS, Inc., Canonsburg, PA, USA). Governing equations are discretized in space using second order advection scheme and solved in time by using second order backward Euler method. The unsteady calculations have been performed on 10 parallel processors. The time step (∆t) is equal to 0.0007 s, at 620 rpm impeller speed that allows impeller volume to rotate (∆θ = 1.5) degrees per time step.

4. Two Phase Flow Results

4.1. Air Flow Rate and Power

The rate of air flow drawn into the machine varies with time as shown in Figure 4a for three assumed bubble diameters. It is evident that the airflow is unsteady and momentarily may reach zero or become slightly negative; air is flowing out of the standpipe. Little effects of the bubble diameter are observed. The power (the computed rotor torque is multiplied by angular velocity) as depicted in Figure 4b also varies with time; it also shows negligible effects of bubble diameter. Air flow rate fluctuates around 0.3 m³/min and power consumption fluctuate around 1.4 kW. Also, Figure 4a shows that simulations reach steady state after 8 s. The running average of air flow rate and power are defined by:

$${\tilde{Q}}_a\left(t\right)=\frac{1}{t}{\displaystyle {\int }_0^t}{Q}_a\left(\text{τ}\right)\text{ dτ}$$

(3)

$$\tilde{P}\left(t\right)=\frac{1}{t}{\displaystyle {\int }_0^t}P\left(\text{τ}\right)\text{ dτ}$$

(4)

Calculations of the running average include initial transient variations of air flow and power. As shown in Figure 5, the time running averaged air flow rate is converging to 0.35 m³/min and the power to 1.43 kW. The time-averaged air capacity coefficient C_a = Q_a/ND³ is 0.053 for Wemco 0.8 m³. Nelson et al. [7] reported measured values of C_a for large Wemco cells (for example, Wemco-160 m³ SmartCell) in the range of 0.13–0.17. Nelson’s et al. [7] work is the only available experimental study for Wemco machines that reports those values. It is notable that the experimental values are much greater than the present CFD prediction for the smaller pilot Wemco 0.8 m³ model. Values for capacity coefficient are machine dependent, and this discrepancy is due to the differences in machine design as well as operating conditions. In flotation process, air rise velocity in the tank is one of the important design parameters. It is used to determine tank diameter. Minerals flotation engineers usually consider air rise velocity to be around 1.0 m/min for efficient flotation process. This value does not depend on machine type or size. In the current CFD study, the predicted air rise velocity (Q_a/A_c) equals 0.92 m/min which is close to the recommended value. Moreover, predicted air rise velocity lies in the measured range of 0.80–1.24 m/min as reported by Nelson et al. for Wemco-160 m³.

Figure 4. Effects of assumed bubble diameter on airflow rate and power, d_b = 0.5, 0.7 and 1.0 mm; (a) Variation of air volume flow rate with time; (b) Variation of power with time.

Figure 4. Effects of assumed bubble diameter on airflow rate and power, d_b = 0.5, 0.7 and 1.0 mm; (a) Variation of air volume flow rate with time; (b) Variation of power with time.

Figure 5. Running average of air flow rate and power.

Figure 5. Running average of air flow rate and power.

4.2. Flow Pattern and Velocity Field.

The flow pattern in the Wemco rotor is very complex and unsteady. Analysis of the velocity field and air volume fraction in the rotor region will shed light on the principle of the Wemco machine operation. Water superficial radial velocity contours on horizontal planes that cut the rotor are depicted in Figure 6a–f at time t = 14.35 s. In Figure 6c, we see that the two blades at positions twelve-o’clock and six-o’clock have the strongest radial outflow, whereas the two blades in the positions four-o’clock and ten-o’clock have inward radial flow. The radial inward flow is entrained by the rotor from the secondary flow below the disperser. The pumping situation switches at higher elevations as shown in Figure 6e. Here, the radial flow at the blades at twelve-o’clock and six-o’clock is blocked whereas that at the blades at four-o’clock and ten-o’clock is strong and outward. Hence, water exits the rotor non-uniformly both circumferentially and vertically. Lack of flow periodicity in the Wemco rotor has also been predicted by CFD simulations of single-phase flow in Wemco 250 and 300 conducted by the present authors.

The velocity contours in the same planes are shown in Figure 7a–f at t = 15.4 s. At this instant, the maximum airflow has been observed and the water content in the rotor is a maximum. The important qualitative difference in the flow at this instant of time and the earlier one is the change in the direction of the vertical velocity at the rotor top. Water flows from the rotor into the standpipe mainly through the gap between rotor and disperser, and then falls down back from the standpipe mixed with air on rotor blades. Then rotor blades pump this mixture through the upper row of disperser holes to the tank. Figure 8a,b show the air volume fraction in a vertical mid plane that passes through the axis of the machine at two different times where the airflow rate is minimum and maximum, respectively. A vortex is formed in the standpipe, and water adheres to the standpipe walls under the effects of centrifugal forces (i.e., water flows up into the standpipe with high circumferential velocity component). Consequently, water head in the standpipe increases continuously until it reaches its maximum level. At this instant, water breaks away from the standpipe walls and falls under gravity to the rotor tips capturing air with it as a mixture as depicted in Figure 8a,b. Water velocity vectors in a mid-plane that passes through the axis of the machine at two different time levels are shown in Figure 9a,b. Figure 9a shows the water velocity vectors at the maximum airflow instant. Water is discharged radially through the upper holes of the disperser where some water falls down on the rotor tips. Water velocity vectors at minimum airflow rate instant are shown in Figure 9b. Secondary flow below the disperser has been noticed for both time instants.

Figure 6. Water superficial radial velocity contours in horizontal planes cutting rotor blades, t = 14.35 s, d_b = 0.7 mm; (a) y = 0.86 m; (b) y = 0.87 m; (c) y = 0.9 m; (d) y = 0.92 m; (e) y = 0.96 m; (f) y = 1.10 m.

Figure 6. Water superficial radial velocity contours in horizontal planes cutting rotor blades, t = 14.35 s, d_b = 0.7 mm; (a) y = 0.86 m; (b) y = 0.87 m; (c) y = 0.9 m; (d) y = 0.92 m; (e) y = 0.96 m; (f) y = 1.10 m.

Figure 7. Water superficial radial velocity contours in horizontal planes cutting rotor blades, t = 15.4 s, d_b = 0.7 mm; (a) y = 0.86 m; (b) y = 0.87 m; (c) y = 0.9 m; (d) y = 0.92 m; (e) y = 0.96 m; (f) y = 1.10 m.

Figure 7. Water superficial radial velocity contours in horizontal planes cutting rotor blades, t = 15.4 s, d_b = 0.7 mm; (a) y = 0.86 m; (b) y = 0.87 m; (c) y = 0.9 m; (d) y = 0.92 m; (e) y = 0.96 m; (f) y = 1.10 m.

Figure 8. Air volume fraction and velocity contours for, d_b = 0.7 mm (a) air volume fraction, t = 14.35 s; (b) air volume fraction, t = 15.4 s; (c) water superficial vertical velocity, t = 14.35 s; (d) water superficial vertical velocity, t = 15.4 s; (e) water superficial radial velocity, t = 14.35 s; (f) water superficial radial velocity, t = 15.4 s.

Figure 8. Air volume fraction and velocity contours for, d_b = 0.7 mm (a) air volume fraction, t = 14.35 s; (b) air volume fraction, t = 15.4 s; (c) water superficial vertical velocity, t = 14.35 s; (d) water superficial vertical velocity, t = 15.4 s; (e) water superficial radial velocity, t = 14.35 s; (f) water superficial radial velocity, t = 15.4 s.

Figure 9. (a) Water superficial velocity vectors at maximum rate of air flow, d_b = 0.7 mm; (b) water superficial velocity vectors at minimum rate of air flow, d_b = 0.7 mm.

Figure 9. (a) Water superficial velocity vectors at maximum rate of air flow, d_b = 0.7 mm; (b) water superficial velocity vectors at minimum rate of air flow, d_b = 0.7 mm.

Three uniform bubble diameters of 0.5, 0.7, and 1.0 mm have been used to study the effects of bubble size on air holdup. Air holdup is computed by integration of (local) air void fraction over the pulp volume and then divided by pulp volume. The computed air holdup for 0.5, 0.7, and 1.0 mm bubble diameters are 9.3%, 7.4%, and 5.7%, respectively. It is observed that air holdup increases as bubbles size decrease. In this study, drag and buoyancy are the only considered interfacial forces between air bubbles and the liquid phase. Drag on air bubbles depends on bubble cross sectional area (i.e., d_b²) while buoyancy depends on the bubble volume (i.e., d_b³). Therefore, drag is the dominant force for small bubbles while buoyancy is the dominant force for large bubbles. Small bubbles have negligible effective inertia and experience lower slip velocity to the liquid phase. They tend to penetrate deeper into the tank and take longer time (i.e., retention time) to escape out at the free surface of the pulp, which results in higher air holdup. Large bubbles experience higher slip velocity and escape quickly from the tank because of the larger buoyancy that results in lower air holdup.

5. CFD-Based Flotation Model

Collisions rate between particles and bubbles is a critical factor for minerals recovery by flotation machines. Collisions rate depends on the local turbulent dissipation rate in the pulp phase. Other factors such as attachment and detachment rate of particles-bubbles aggregates depend on turbulent dissipation rate as well as surface chemistry of particles and bubbles. Two-phase flow simulations of flotation machines provide spatial distribution of air void fraction and turbulent dissipation rate. A CFD-based flotation model has been developed in this work to predict pulp rate constant of Wemco 0.8 m³ pilot cell. The model provides local values of collisions rate between particles and bubbles as well as probabilities of attachment, collisions and stabilization. Abrahamson collision [8] model is commonly used in estimation for collisions rate in flotation modeling. This paper provides an alternative more accurate model for collisions rate developed by Zaichik et al. [9]. In this paper, we present flotation model as a first rate equation. The rate constant in this equation depends on the local collisions frequency, probability of collision, probability of attachment, and probability of stabilization.

Yoon and Lutrell [10], Pyke et al. [11], Bloom and Heindel [12] among others developed theoretical flotation models to predict pulp recovery rate. In these models, flotation process is represented mathematically by a first order kinetic ODE Ordinary Differential Equation). These theoretical models depend on the average air void fraction and dissipation rate for a given flotation cell. However, distributions of turbulent dissipation rates and air volume fraction are not uniform and depend on the design of the machine. Distribution of turbulent dissipation rate is the key factor in computing recovery rate. Koh and Schwarz [13] developed a 3D CFD flotation model for a forced air Rushton’s impeller flotation tank. Collisions frequency and flotation probabilities have been computed locally. CFD simulations of flotation machines provide the spatial distribution of the rate of turbulent kinetic energy dissipation and air void fraction throughout the cell. Flotation model is based on estimating local recovery rate. Local recovery rate is the multiplication of collision kernel and probabilities of collision, attachment and stabilization. These parameters depend mainly on dissipation rate throughout the machine in addition to particles and bubbles sizes, surface tension and contact angle. The model has been applied to a self-aerated flotation machine (Wemco 0.8) to predict pulp recovery rate. In this paper, a range of particle sizes (10 μm ≤ d_p ≤ 500 μm) have been used with three different bubble sizes d_b = 0.5 mm, d_b = 0.7 mm, d_b = 1.0 mm to investigate the effects of particles and bubbles sizes on pulp rate constant. Effects of feed particles size distribution has been studied also in this work.

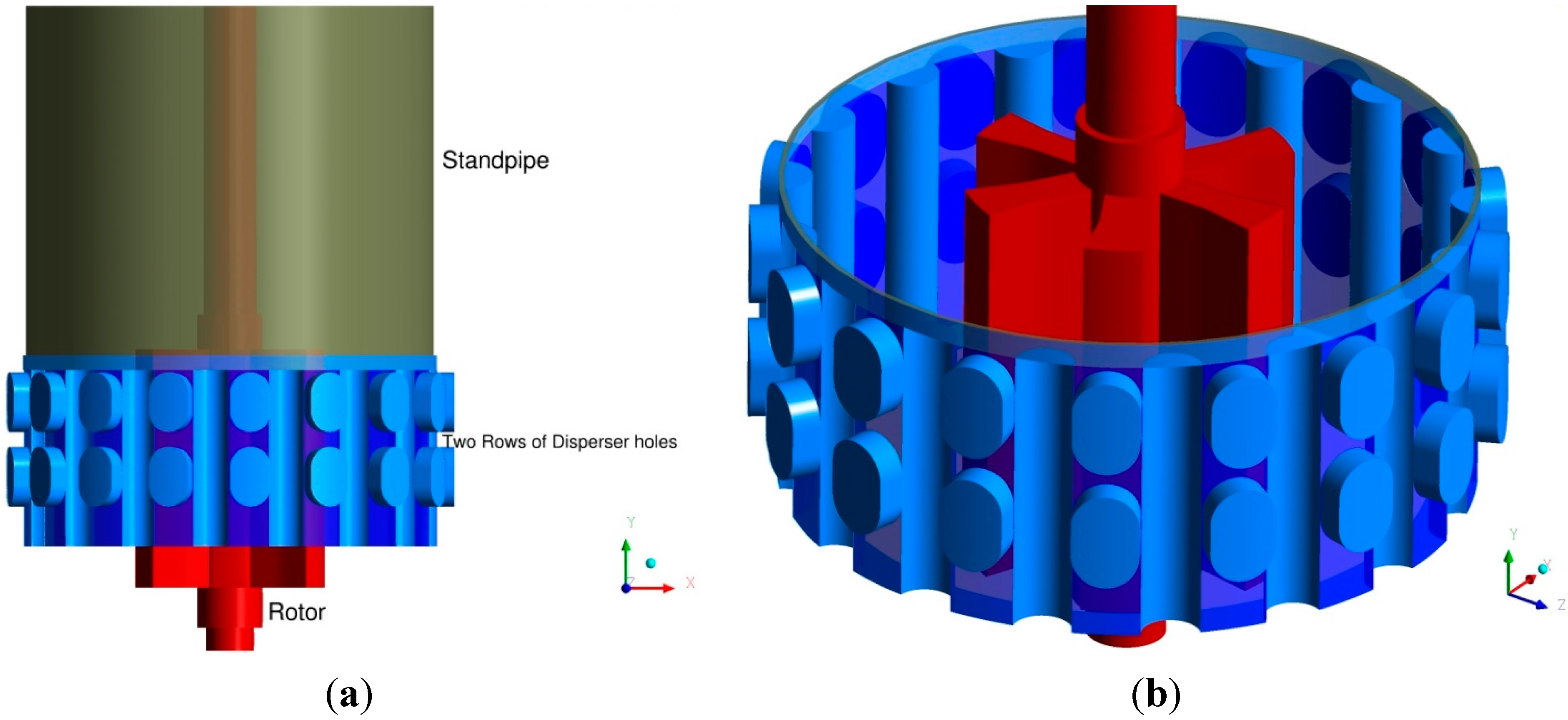
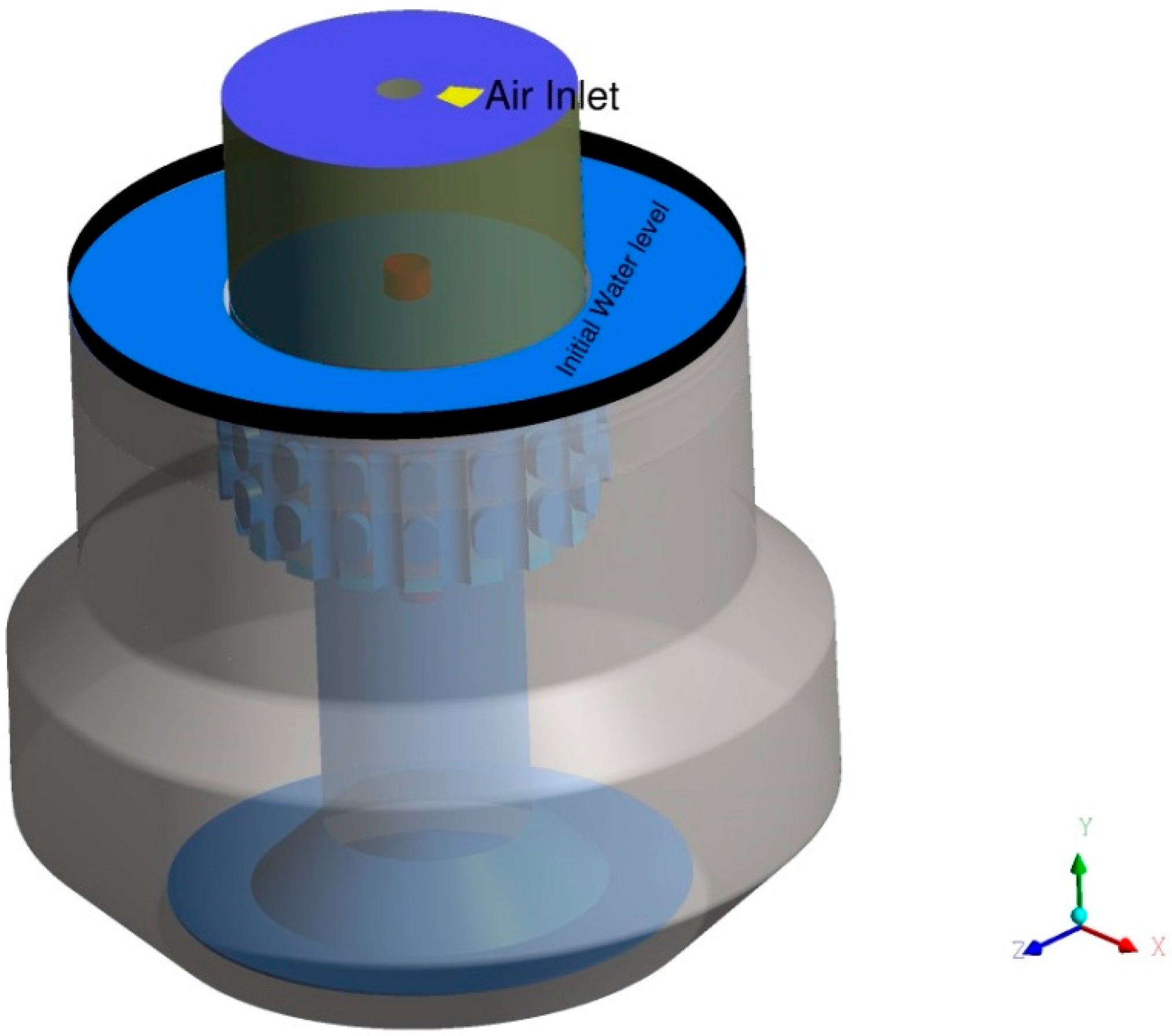
5.1. Flotation Model: First-Order Rate Equation

The objective of a flotation model is to predict the recovery rate (rate of mass flow of useful minerals collected from a flotation cell). Following Koh and Schwarz [13], we model the flotation kinetics as a first-order rate process, which is given by the fundamental equation:

$$\frac{d{N}_{\text{p}1}}{dt}=-K_1{N}_{\text{p}1}{N}_{\text{b}}+K_2{N}_{\text{a}}$$

(5)

where $N_{\text{p}1}$ is the particle number concentration (number of particles per unit volume) of free particles (not attached to bubbles), $N_{\text{b}}$ is the number concentration of bubbles available for attachment (not fully loaded bubbles), $N_{\text{a}}$ is the number of particle-bubble aggregates (bubbles that cannot accept more particles but can lose particles), $K_1$ is the average particle-bubble attachment rate constant, and $K_2$ is the average particle-bubble detachment rate constant. We note the difference in the dimensions (units) of $K_1$ (m³/s) and $K_2$ (1/s). The total particle number concentration $N_{\text{PT}}$ is:

$$N_{PT}=N_{\text{p}1}+N_{\text{p}2}$$

(6)

where $N_{\text{p}2}$ is the number concentration of particles attached to bubbles. All number concentrations are functions of time and location in a flotation cell. A bubble is either fully loaded (cannot accept more particles) or clean (no particles attached). The number of particle-bubble aggregates is proportional to the total number of bubbles,

$$N_{\text{a}}=b N_{bT}$$

(7)

where $b$ is an average loading parameter, which varies with time and position. The number of clean bubbles (those available for attachment) is

$$N_{\text{b}}=\left(1-b\right)N_{bT}$$

(8)

The rate equation can now be written as:

$$\frac{d{N}_{\text{p}1}}{dt}=-k_1\left(1-b\right)N_{\text{p}1}{N}_{bT}+k_{2}b{N}_{bT}$$

(9)

The number of particles (S) that can be attached to a bubble is given by the ratio of surface area of the bubble to the projected area of the particle.

$$S=4{\left(\frac{d_b}{d_p}\right)}^2$$

(10)

Such an estimation is not realistic. In Koh and Schwarz [13] work, only half of that number is assumed as a first approximation.

$$S_{max}=0.5 S=2{\left(\frac{d_b}{d_p}\right)}^2=\frac{N_{\text{p}2}}{\text{β} N_{bT}}$$

(11)

Rearranging, we obtain:

$$b=\frac{N_{\text{p}2}}{S_{max} N_{bT}}=\frac{N_{\text{p}2}}{2 N_{bT}}{\left(\frac{d_b}{d_p}\right)}^2$$

(12)

5.2. Attachment Model

Collisions frequency (${\text{Z}}_{pb}$) of two groups of dispersed species (e.g., particles and bubbles) is the number of collisions per unit volume per unit time (m⁻³·s⁻¹). It is proportional to the product of the number densities N_b and N_p of bubbles and particles (${\text{Z}}_{pb}=\text{β} N_p N_b$), where $\text{β}$ is called the collisions kernel (${\text{m}}^3/\text{s}$). The attachment rate constant ($k_1, {\text{m}}^3/\text{s}$) is defined as the product of particle-bubble collisions kernel times probabilities (or efficiencies). This is because not every collision event leads to successful attachment of a particle to a bubble. Following Koh and Schwarz [13], the attachment rate constant is written as:

$$k_1= \text{β } P_c P_a P_s$$

(13)

where P_c, P_a, and P_s are probabilities of particle-bubble collision, adhesion, and stabilization. Multiplication by P_c is questionable since it should be considered as a part of the collisions kernel. Apparently including P_c is a remnant of the original model that was developed under quiescent conditions. This collisions probability P_c should be eliminated because collisions kernel is modeled under turbulent conditions, and the assumption of laminar flow is irrelevant. When turbulence is the mechanism of collisions of particles and bubbles, “quiescent” conditions should be defined as the turbulent fluctuations $u\prime$ and turbulent dissipation rate that maximizes the attachment rate and minimizes detachment.

5.3. Collision Kernel

The collision kernel $\text{β}$ is perhaps the most important ingredient of the attachment rate constant $k_1$. For turbulent flows, two classical models are in use. The first is Saffman and Turner model [14], which is applicable in the limit of zero Stokes particle number. The second is Abrahamson model [8] which is applicable in the limit of infinite particle Stokes number. The form of the later model is usually written (Schubert and Bischofberger 1979) [15] as:

$$\text{β}=5{\left(\frac{d_p+d_b}{2}\right)}^2\sqrt{U_p^2+U_b^2}$$

(14)

where $U_{\text{p}}$ and $U_{\text{b}}$ are the turbulent ($rms$) fluctuating velocities of the particles and bubbles relative to the carrier liquid, respectively. Leipe and Mockel’s [16] formula (not the original formula by Abrahamson) is used for these velocities,

$$U_i=\frac{0.4 {ϵ}^{4/9}{d}^{7/9}}{{\nu }^{1/3}}{\left(\frac{\left|{\text{ρ}}_i-{\text{ρ}}_f\right|}{{\text{ρ}}_f}\right)}^{2/3}$$

(15)

where $ϵ$ is dissipation rate of the turbulent kinetic energy per unit mass (w/kg), $\nu$ and ${\text{ρ}}_{\text{f}}$ are the kinematic viscosity and density of the liquid, respectively. ${\text{ρ}}_i$ and ${\text{d}}_i$ are the density and diameter of the colliding particles, $i = p$ for particles and $i = b$ for bubbles. The mass density for a bubble is assumed to be equal 0.5${\text{ρ}}_{\text{f}}$, as if the bubble mass is the virtual mass of a spherical bubble. This equation implies that high dissipation results in higher collisions rates between bubbles and particles, and in this regard high dissipation has favorable effects on flotation. Schubert [15] model have been developed for very high inertia particles. In minerals, flotation particles have a wide spectrum of inertia. Therefore, application of Schubert collisions model results in over prediction of collision kernel as discussed by Fayed [17].

Zaichik et al. [9] developed another statistical model for the collisions kernel for particles and bubbles. The model applies to arbitrary values of density ratio and particle sizes. This model has been validated by Fayed and Ragab [18] to study its limitation and it provides more accurate prediction for collisions kernel than Schubert model [15]. The model is not presented here because of the space and interested reader is referred to Zaichik et al. [9] and Fayed [17] where the model has been presented and discussed extensively. In this paper, comparison between Schubert model [15] and Zaichik et al. model [9] is presented to show the over-estimation of collision kernel by the former model. Hence, Zaichik et al. model [9] has been used herein for more accurate prediction of collision kernel.

5.4. Flotation Probabilities

Process of minerals flotation involves two main events which are collisions of particles with bubbles and attachment of the colliding particles with bubbles. The first event happens under turbulent flow conditions where particles and bubbles sizes and turbulent velocity rms fluctuations are the main variables that control this event. Upon collision, useful minerals particles have to attach to the bubble and then transported to the froth phase by buoyancy of bubbles. The attachment process is due to the adhesive forces between particles and bubbles and then stabilization of the particle-bubble aggregates. An accurate model for collisions frequency of particles and bubbles has been used in this work [9] to estimate kernel collisions. The second step is to model for the probability of particles’ attachment to a bubble. In the literature, considerable efforts have been made to model for the probabilities of collisions, adhesion and stabilization. The concept of probability of collisions has been developed under laminar flow conditions which do not exist in minerals flotation. In this section, we summarize and present models for probabilities of collisions, adhesion and stabilization developed by other authors. These models have been used in our CFD-flotation model to predict pulp recovery rate of a flotation cell. Hopefully, some validation work will be completed on a fundamental level in future to study the limitations of these models and their accuracy.

The probability (efficiency) of collision P_c is given by a formula due to Yoon and Luttrell [10],

$$P_c=\left(\frac{3}{2}+\frac{4}{15} R{e_b}^{0.72}\right)\frac{{{\text{d}}_p}^2}{{{\text{d}}_b}^2}$$

(16)

where the bubble Reynolds number is defined by $R{e}_b =\frac{ d_{b }{U}_b}{\upsilon }$. In the actual calculations $P_c$ is limited to a maximum of 1.

The expression for probability of adhesion P_a is also derived by Yoon and Luttrell [10],

$$P_a={\text{sin}}^2\left(2{\text{tan}}^{-1}\exp \left[\frac{-\left(45+8R{e_b}^{0.72}\right)U_b{t}_{\text{ind}}}{15{\text{ d}}_{b }\left(\frac{{\text{d}}_{b }}{{\text{d}}_{p }}+1\right)}\right]\right)$$

(17)

where $t_{\text{ind}}$ is the induction time, which is determined by an empirical formula due to Dai et al. [19]:

$$t_{\text{ind}}=\frac{75}{\text{θ}}{\text{ d}}_p^{0.6}$$

(18)

where $t_{\text{ind}}$ is measured in seconds, $\text{θ}$ is particle-bubble contact angle in degrees, and $d_p$ is the particle diameter in meters.

The formula proposed by Schulze [20] and modified by Bloom and Heindel [12] for the probability of stabilization $P_s$ is used:

$$P_s=1-\text{exp}\left[A_{\text{s}}\left(1-\frac{1}{\min (1,{\text{Bo}}^{\text{*}})}\right)\right]$$

(19)

where the modified Bond number is defined by:

$${\text{Bo}}^{\text{*}}=\frac{{\text{d}}_{\text{p}}^2\left[\text{Δρg}+1.9{\text{ ρ}}_p{ϵ}^{\frac{2}{3}}{(\frac{{\text{d}}_p}{2}+\frac{{\text{d}}_b}{2})}^{\frac{-1}{3}}\right]+1.5{\text{ d}}_p\left(\frac{4\text{ σ}}{{\text{d}}_b}-{\text{d}}_b\text{ρg}\right){\text{ sin}}^2(\text{π}-\frac{\text{θ}}{2})}{\left|6\text{σ sin}\left(\text{π}-\frac{\text{θ}}{2}\right)\sin \left(\text{π}+\frac{\text{θ}}{2}\right)\right|}$$

(20)

where A_s = 0.5 is an empirical constant suggested by Bloom and Heindel [12], where $\text{σ}$ is the surface tension (N/m), $\text{Δρ}={\text{ρ}}_{\text{p}}-{\text{ρ}}_{\text{f}}$, and g is the gravitational acceleration.

5.5. Detachment Model

The particle-bubble detachment rate constant ($k_2$) is defined by:

$$k_2=Z_2{P}_{\text{d}}={\text{ Z}}_2\left(1-P_{\text{s}}\right)$$

(21)

The probability of detachment $P_{\text{d}}$ is assumed to be equal to $(1-P_{\text{s}})$. Koh and Schwarz [13] justified the inclusion of $P_{\text{s}}$ in both $k_1$ and $k_2$ because the processes involve different turbulent eddies acting independently of each other. The detachment frequency $Z_2$ is given by Bloom and Heindel [12] as:

$$Z_2=\frac{\sqrt{{\text{C}}_1}{\text{ ε}}^{\frac{1}{3}}}{{\left({\text{d}}_p+{\text{d}}_b\right)}^{\frac{2}{3}}}$$

(22)

where $C_1=2.0$ is an the empirical constant. We note in this equation the unfavorable effects of dissipation that high dissipation results in destabilization of particle-bubble aggregates.

5.6. Particle Size Distribution

Particles in the feed slurry to a flotation machine have a particle size distribution. Several models in the literature have been developed to account for different particles properties in the feed slurry. These models predict the global rate constant of a flotation cell and classified into three groups—discrete rate constant distribution, continuous rate constant distribution and mean rate constant. Several discrete rate constant models have been developed but they differ in the number of fractions (Morris [21], Kelsall [22], Cutting [23], Jowett [24], Imaizumi [25]). Two fraction discrete models developed by (Kelsall [22]) are named as fast float and slow float fractions. Continuous rate constant models assume that rate constants are distributed as a continuous distribution represented by a Gamma-distribution function (Harris [26], Woodburn [27], Loveday [28], Kappur [29]). The mean rate constant model has been proposed by Chen (Chen Z.M. [30,31]). However, prediction of rate constant in all flotation models is strongly affected by operating conditions as well as particles and bubbles properties on a local basis. Flotation modeling using CFD enables more accurate prediction of rate constant and helps to assess the performance of a flotation cell.

The attachment rate $k_1$ as given above is mainly a function of bubble size, particle size, air/water surface tension and contact angle. An effective pulp recovery rate constant proposed here is defined by:

$$k_1^{\text{*}}=k_1\frac{\text{α}}{v_{\text{b}}}\left(1-\text{α}\right)$$

(23)

We recognize the factor $\frac{\text{α}}{v_{\text{b}}}$ as the local number concentration of bubbles, and the factor $\left(1-\text{α}\right)$ is included so that in a region of high air volume fraction ($\text{α}\approx 1 )$ the recovery rate should drop to zero. The local number concentration of particles $N_{\text{p}}$ depends on slurry loading, and we expect it to be proportional to the local water volume fraction, ($1-\text{α}$). We believe that including the factor ($1-\text{α}$) gives a better figure of merit that can be used to evaluate different designs in the absence of $N_{\text{p}}$ distribution. The machine average rate constant is obtained by integration over the machine volume,

$$K_1^{*}=\frac{R_f}{V}{\displaystyle {\int }_V^{\hspace{1em}}}{k}_1^{*} (1-b)dV$$

(24)

where $R_f$ is a froth recovery factor.

Minerals particles in the feed slurry have a size distribution and this distribution has great impact on recovery rate. Let $P(dp)$ denote the pdf of particle size distribution. Particle size distribution depends on the grinding process and metallurgical properties of the minerals particles. The current CFD-based flotation kinetic model can be used to determine pulp recovery rate for both bubble size and particle size distributions. We assume a Gamma-distribution for the particles number density function.

$$P\left(d_p\right)=\frac{{\left(d_p-{\mu }_p\right)}^{\gamma -1}}{B^{\gamma }\text{ Γ}(\gamma )}\text{exp}\left(-\frac{d_p-{\mu }_p}{B}\right)$$

(25)

where ${\text{μ}}_p$ is the minimum possible particle diameter and $\text{Γ}$ is the Gamma function. In this paper, we used ${\text{μ}}_p=0$ and $B = 30$. To obtain different particles number distributions, we assign different values for $\text{γ}$ starting from 1.0–15, incremented by one. This also changes the mean diameter. The pseudo rate constant for particle size distribution $\overline{K_1^{*}}$ is computed:

$$\overline{K_1^{*}}={\displaystyle {\int }_{d_{p,min}}^{d_{p,max}}}P\left(\text{λ}\right)K_1^{\text{*}}\left(\text{λ}\right) d\text{λ}$$

(26)

and $d_{p,min} ,d_{p,max}$ are the minimum and maximum particle diameters present in the feed slurry.

5.7. Flotation Results

In this section, we demonstrate the viability of CFD-based flotation model as a tool to evaluate the performance of flotation machines and provide detailed hydrodynamic and kinetics data that can help improve the design of such machines. Ragab and Fayed [32] developed a CFD-based flotation model, and used it to determine the effects of particle size on the rate constant. We use particle specific gravity $\text{ρ}=4.1$, contact angle $\text{θ}=40°$, and surface tension $\text{σ}=0.06 N/m$ as input parameters to the flotation model. Two-phase hydrodynamic simulations provided spatial distributions of dissipation rate, $ϵ$, and air volume fraction, $\text{α}$ (also called void fraction). The number concentration of bubbles is $N_{bT}=\text{α}/v_b$, where $v_b$ is the bubble volume and spherical bubbles are assumed. Particles-bubbles collisions rate has been estimated using Zaichik et al.’s model [9]. Zaichik et al.’s model and probabilities models rely on velocity fluctuations, bubble diameter, particle diameter, particle density, air void fraction, contact angle and air-water surface tension coefficient. Velocity fluctuation, $u\prime$ has been estimated from the local eddy viscosity and dissipation rate. Local air void fraction is obtained from the CFD results of the two-phase flow. Other parameters are user input. CFD-based flotation kinetics model is a post processing program to the two-phase simulations runs of flotation cells such as Wemco 0.8 m³. Effects of particles size distribution on pulp recovery rate are presented here.

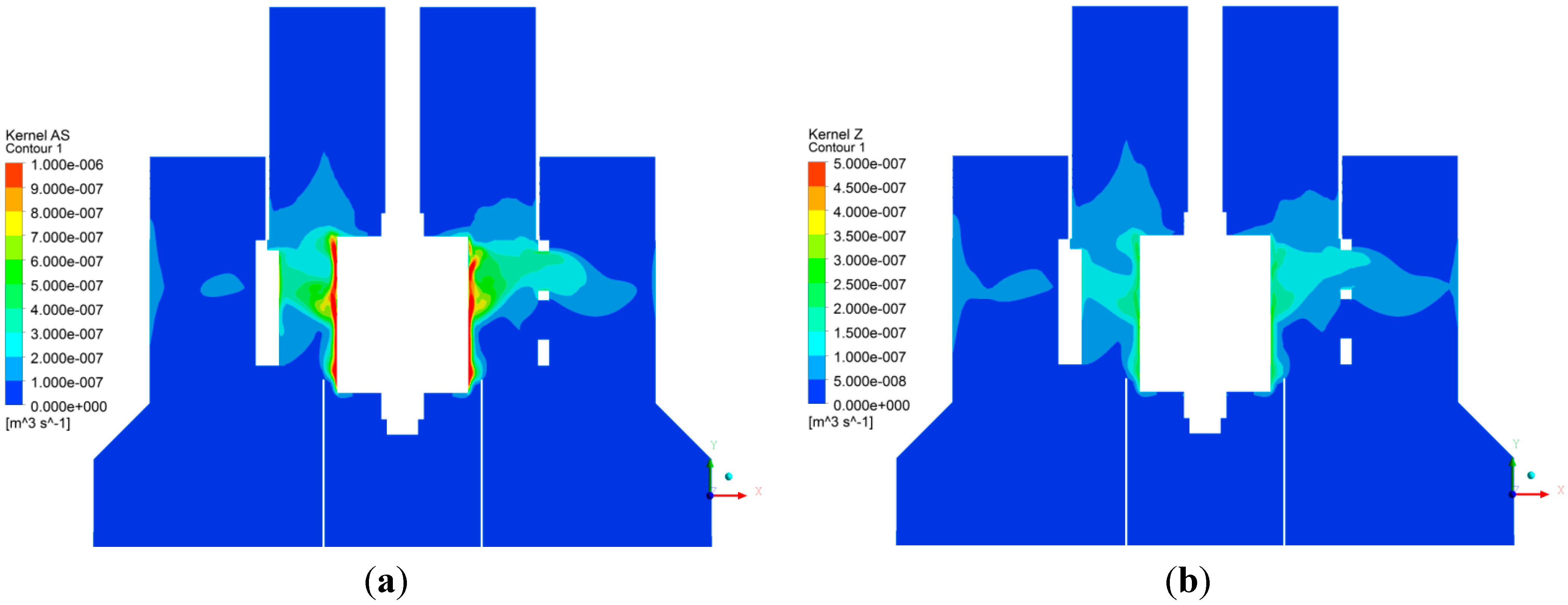
As described above, accurate estimation of particle-bubble collision rate is essential for accurate modeling of rate constant. Fayed and Ragab [18] validated Zaichik et al. model [9] and recommended it for use in flotation modeling. A comparison between collisions kernel by Schubert model [15] and Zaichik et al. model [9] are shown in Figure 10a,b. Schubert model overestimates the collisions kernel by an order of magnitude when compared to that of Zaichik et al. model. Based on these results, we recommend Zaichik et al. model in flotation kinetics. 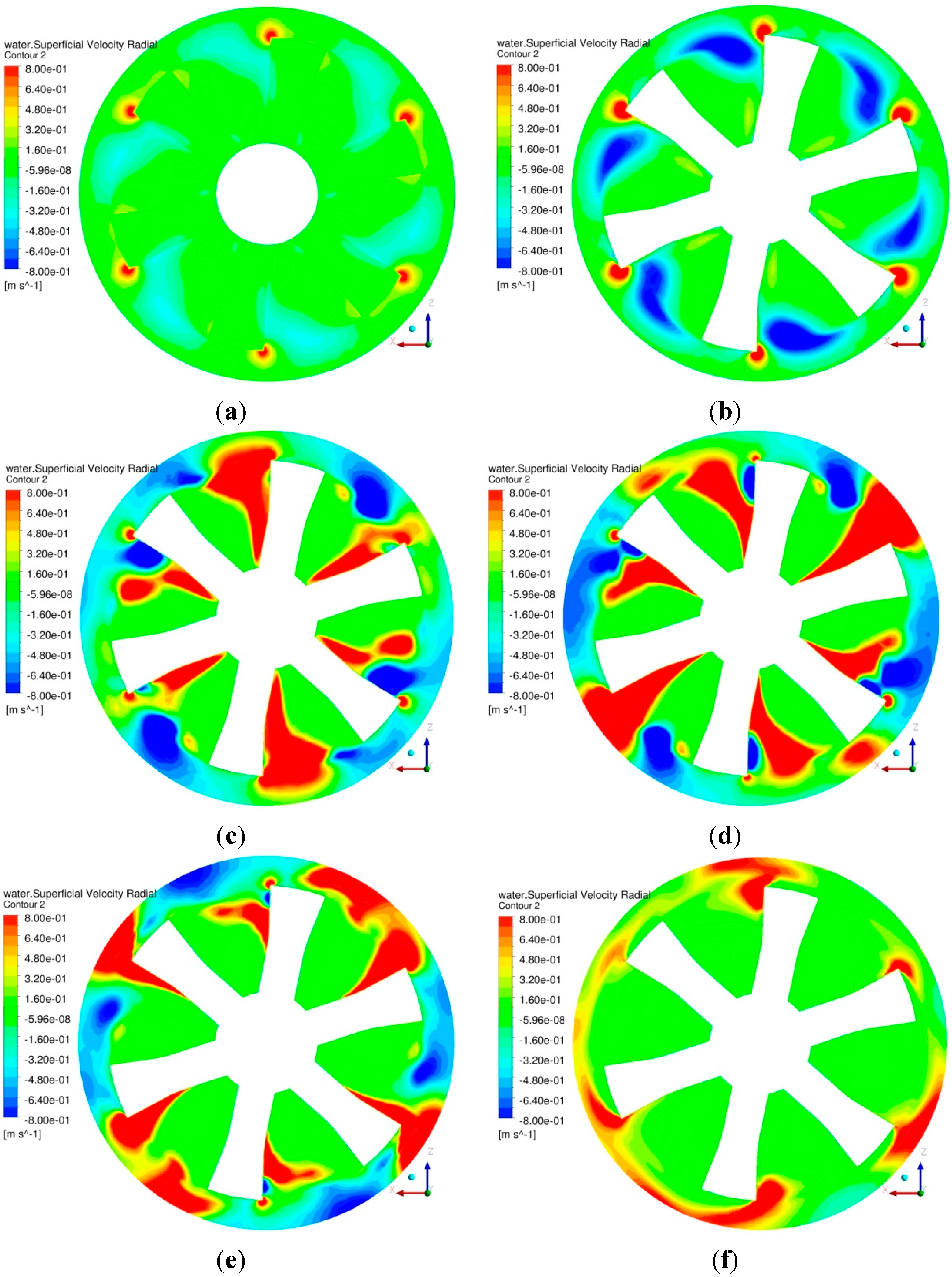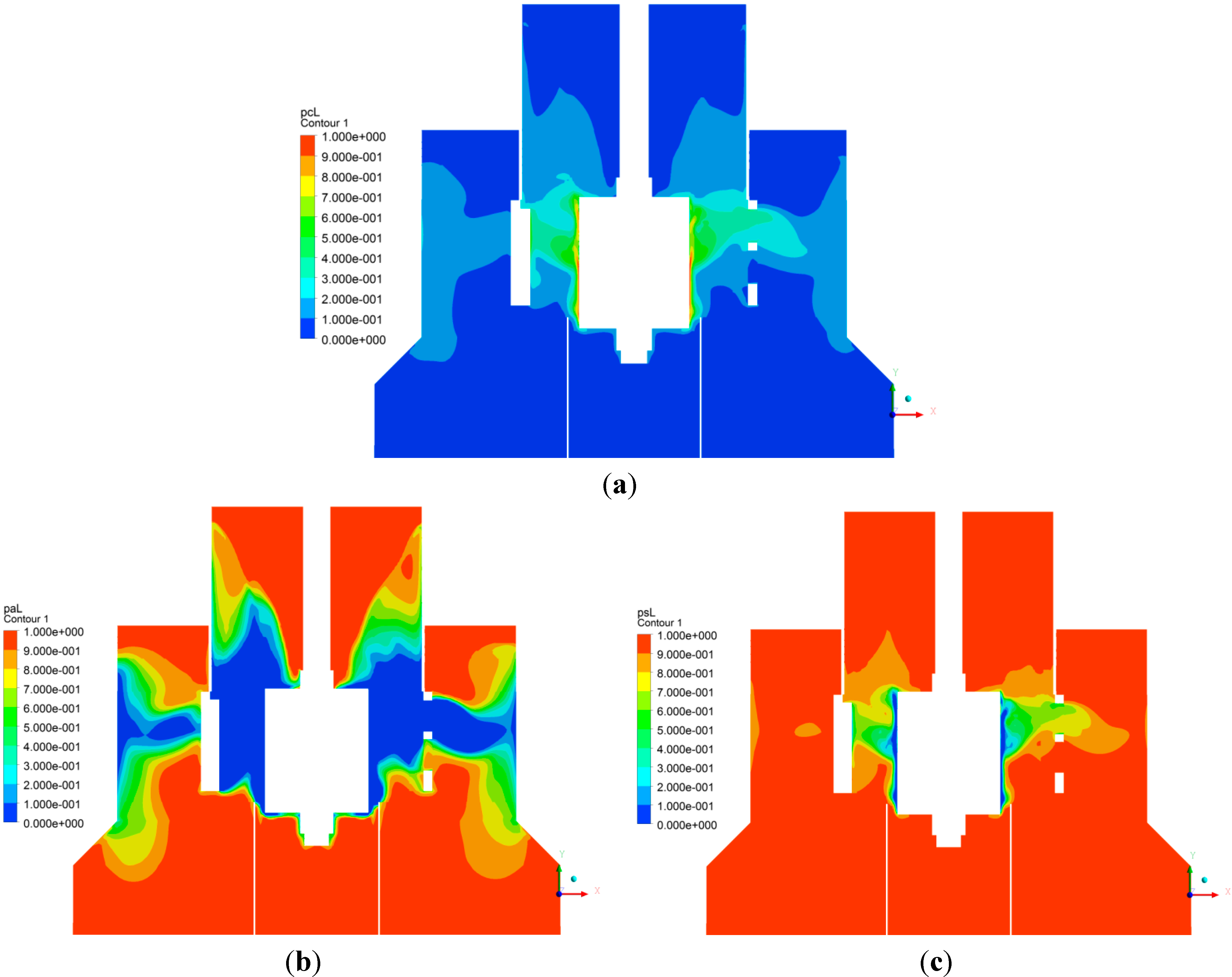Figure 11a–c shows the spatial distribution of probabilities of collision, adhesion and stabilization in a vertical plane that passes through the machine axis. Figure 11a,b shows the favorable effects of turbulent dissipation rate where higher collisions rate and higher probability of collisions in the region between rotor and disperser and within the jet region. However, high local dissipation rates have adverse effects on the probabilities of adhesion and stabilization where low values are observed in the regions between rotor and disperser and within the jet. As described above, flotation process is mainly due to two events—collisions of particles and bubbles and particles attachment to a bubble. That is to say, we can achieve high dissipation rate regions that cause a high collisions rate but lower rates of attachment are obtained which results in a lower rate constant. Therefore, the presented CFD-based flotation model in this paper is a useful tool to optimize for rate constant in flotation machines.

Figure 10. (a) Abrahmson-Schubert [6] collisions kernel for d_p = 100 micron; (b) Zaichik et al. [9] collisions kernel for d_p = 100 micron.

Figure 10. (a) Abrahmson-Schubert [6] collisions kernel for d_p = 100 micron; (b) Zaichik et al. [9] collisions kernel for d_p = 100 micron.

Figure 11. (a) Probability of collisions for d_p = 100 micron; (b) Probability of adhesion for d_p = 100 micron; (c) Probability of stabilization for d_p = 100 micron.

Figure 11. (a) Probability of collisions for d_p = 100 micron; (b) Probability of adhesion for d_p = 100 micron; (c) Probability of stabilization for d_p = 100 micron.

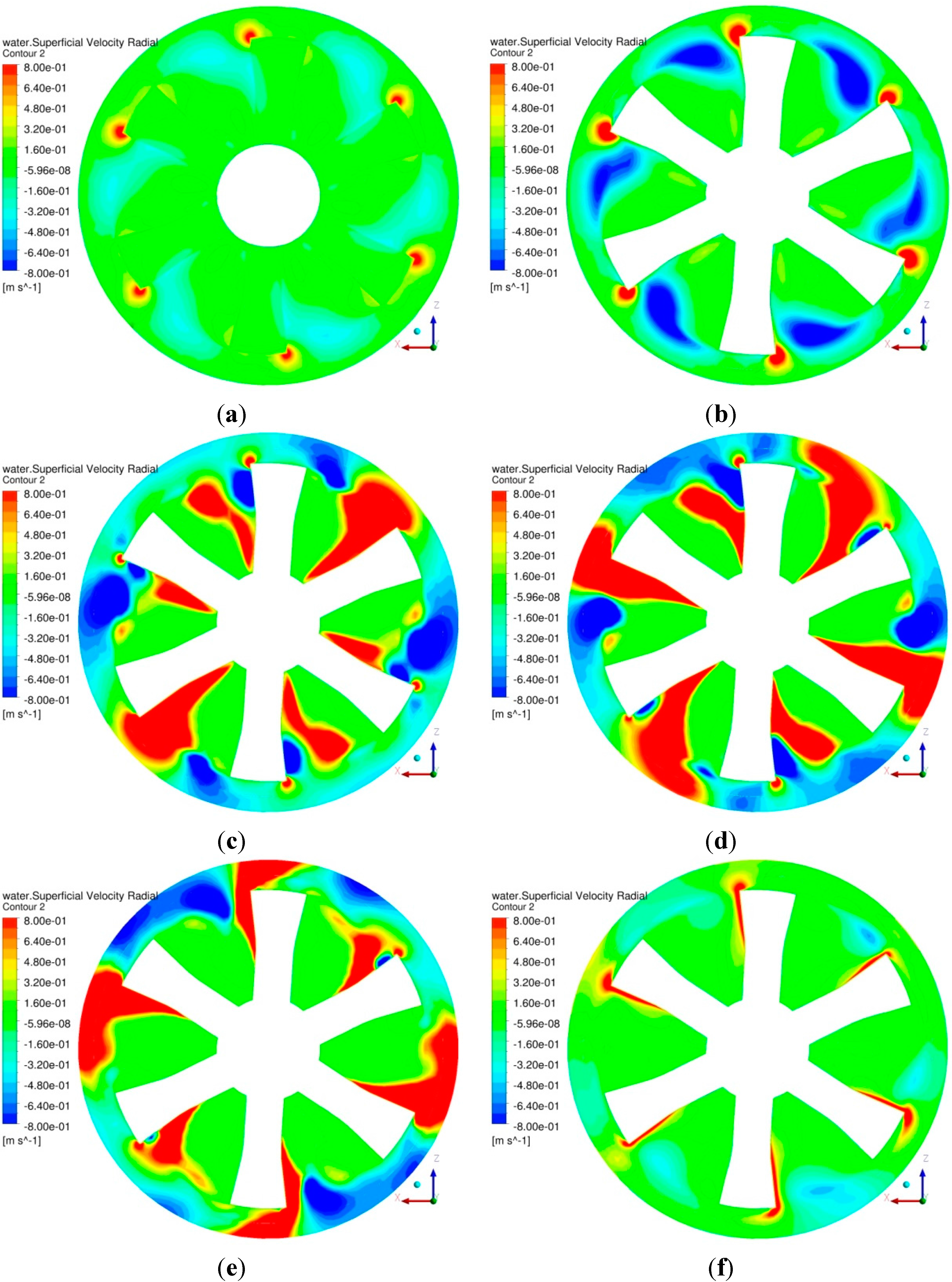
The product of collision kernel and probabilities of collision, adhesion and stabilization gives the local attachment rate $k_1$. An effective pulp recovery rate constant (in the absence of detachment) is defined here by $k_1\text{α} \left(1-\text{α}\right)/v_b$, and corresponding contours are depicted in Figure 12a–d. The factor $\left(1-\text{α}\right)$ is included in this definition so that in a region of 100% air ($\text{α}=1.0$) the local recovery rate should be zero. The spatial distribution of $\text{α}\left(1-\text{α}\right)$, which is zero if $\text{α}=0.0$ or $\text{α}=1.0$ and maximum if $\text{α}=0.5$ (50% void fraction), implies that the local recovery rate is maximized when the air is well dispersed throughout the machine. The actual recovery rate will depend on the balance between the favorable effects of dissipation rate $ϵ$ in increasing the collision frequency against its adverse effects on reducing the attachment rate and increasing detachment rate. Therefore, knowing the spatial distributions of both $\text{α}$ and $ϵ$ throughout the machine is essential in understanding the effectiveness of different components (rotor, stator or disperser, jets) on the flotation efficiency. Only through CFD of two-phase simulations (or elaborate experimental measurements) one can determine those spatial distributions. This is a clear advantage of CFD-based flotation models in comparison with models that treat the entire cell as one unit which assumes a single value for $ϵ$ determined by the consumed power and single value for $\text{α}$ that is equal to the gas holdup.

Figure 12. (a) Pulp recovery rate $k_1^{*}$ for 40 μm particle diameter; (b) Pulp recovery rate $k_1^{*}$ for 100 μm particle diameter; (c) Pulp recovery rate $k_1^{*}$ for 200 μm particle diameter; (d) Pulp recovery rate $k_1^{*}$ for 300 μm particle diameter.

Figure 12. (a) Pulp recovery rate $k_1^{*}$ for 40 μm particle diameter; (b) Pulp recovery rate $k_1^{*}$ for 100 μm particle diameter; (c) Pulp recovery rate $k_1^{*}$ for 200 μm particle diameter; (d) Pulp recovery rate $k_1^{*}$ for 300 μm particle diameter.

Particle diameter has significant effects on distribution of the pulp rate constant $k_1^{*}$ throughout the Wemco machine. Contours of $k_1^{*}$ in a vertical mid plane are shown in Figure 12a–d, for particle diameters of 40, 100, 200, and 300 $\text{μ}$m. Fine particles $d_p< 50 \text{μm}$ are efficiently recovered in the high dissipation region between the rotor and disperser. For a medium particle diameter of $100 \text{μm}\le d_p\le 200 \text{μm}$, recovery happens in the jets out of the disperser. For coarse particles $d_p\ge 300 \text{μm}$ pulp recovery is more efficient in the moderate dissipation regions outside the disperser below, above and between the disperser jets. In the present work, the pseudo rate constant is computed as a function of particle diameter for two values of contact angle ($\text{θ}=40°$ and $\text{θ}=50°$). Values for rate constant are obtained for different uniform bubble size and different uniform particle size. Average flotation rate constant $k_1^{*}$ can be defined according to the Equation (24) where $R_f$ is a froth recovery factor. We assumed $R_f=1.0$ and $\text{β}=0.0$ for a fully unloaded bubble and studied the effects of bubble diameter, particle diameter, and contact angle on $k_1^{*}$. The results are shown in Figure 13a–c. As expected, rate constant increases with the increase of contact angle. Also, higher rate constant is observed for smaller bubble size ($d_b=0.5 \text{mm}$) because air holdup increases for smaller bubble diameter, and hence higher bubble concentration number, as well as a lower rate constant for larger bubble diameter due to the decreases in the air holdup (i.e., local bubbles number concentration). The maximum recovery rate shifts to higher particle diameter with the increase in bubble diameter. The recovery rate shown in these figures is very high relative to experimental data reported in literature because of the assumed values of $R_f$ and $\text{β}$. Maximum rate constant for bubble sizes of 0.5, 0.7 and 1.0 mm occur at particle size of 125, 150 and 175 μm, respectively. This reveals that fact that smaller bubbles sizes (d_b < 0.5 mm) are needed to float very tiny particles (d_p < 100 μm).

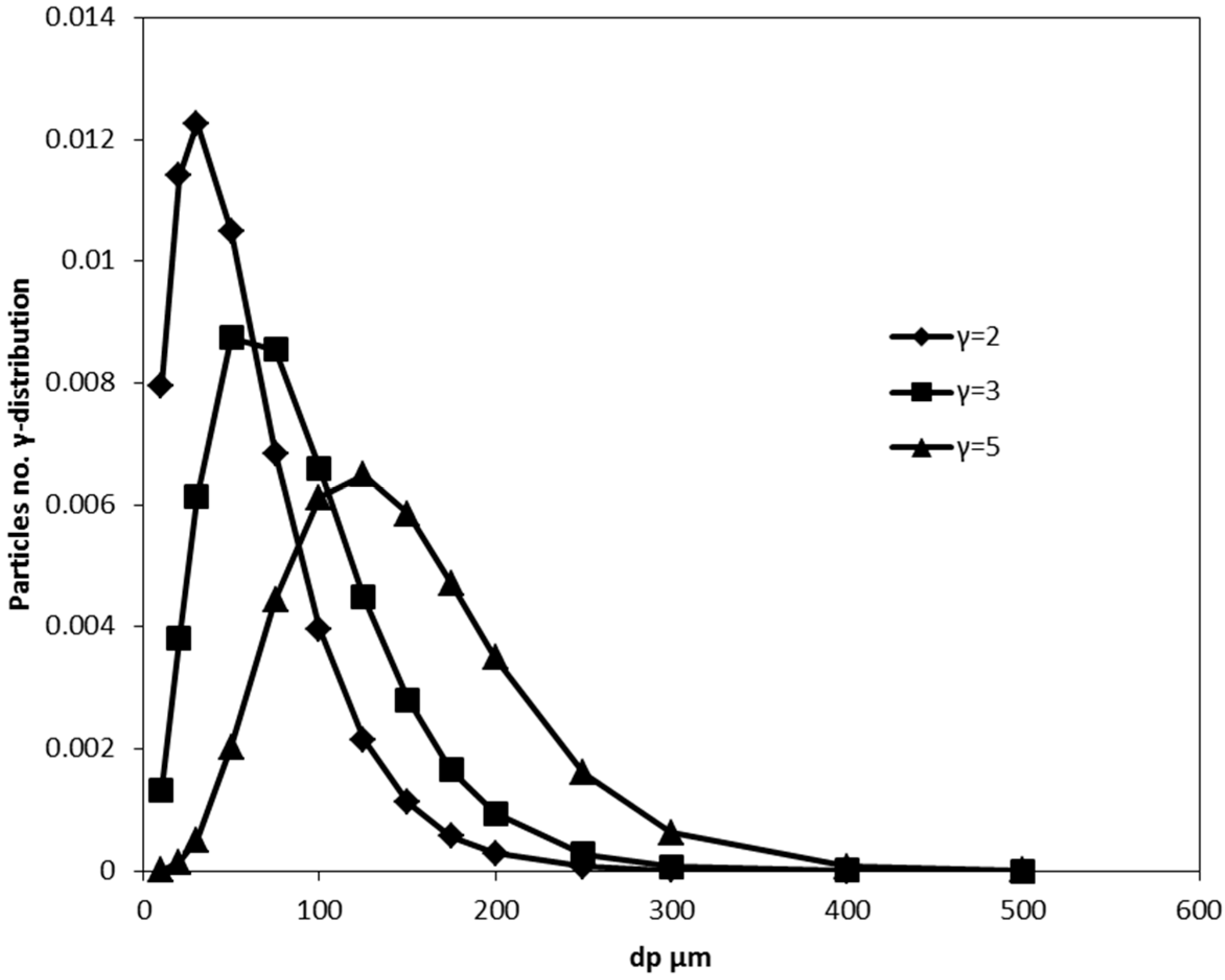
Next, we study the effects of particles size distribution on the mean flotation rate constant. As shown in Figure 13a–c, rate constant is dramatically affected by particle sizes and the feed slurry to a flotation cell contains a wide spectrum of particles sizes. Therefore, modeling for rate constant with particle size distribution is more realistic and useful. Samples of assumed particles’ number distribution are shown in Figure 14 for B = 30 and three different values for γ (γ = 2, 3 and 5). Changing values for γ changes the size distribution and mean diameter of the particles. In real samples, this distribution depends on the grinding process as well as metallurgical properties of the ore. The procedure herein is to apply the present CFD flotation model for a single particle size and uniform bubble diameter in the postprocessor of the used CFD package (CFX). Using Equation (23), we obtain the local rate constant for a specific particle size. We used particles sizes ranging from 10–500 μm to be within the practical particle sizes. We used Equation (24) to obtain the average rate constant over the pulp volume and from Equation (26) we calculate the average pulp rate constant for a specific distribution. This process yields a single value for the rate constant that we attribute to the mean value of the proposed particle size. Different particle number distributions pdfs are used (each has different mean diameter) to plot rate constant versus particles mean diameter. This deterministic method in the calculation of rate constant for certain particle size distribution is more robust than the other probabilistic models [26,27,28,29]. This is because the effects of all variables such as surface tension, contact angle, bubbles size and particles size are explicitly included in the model.

Figure 13. (a) Average rate constant for 0.5 mm bubble diameter and for single particle sizes; (b) average rate constant for 0.7 mm bubble diameter and for single particle sizes; (c) average rate constant for 1.0 mm bubble diameter and for single particle sizes.

Figure 13. (a) Average rate constant for 0.5 mm bubble diameter and for single particle sizes; (b) average rate constant for 0.7 mm bubble diameter and for single particle sizes; (c) average rate constant for 1.0 mm bubble diameter and for single particle sizes.

Figure 14. Assumed particles number distribution, B = 30.

Figure 14. Assumed particles number distribution, B = 30.

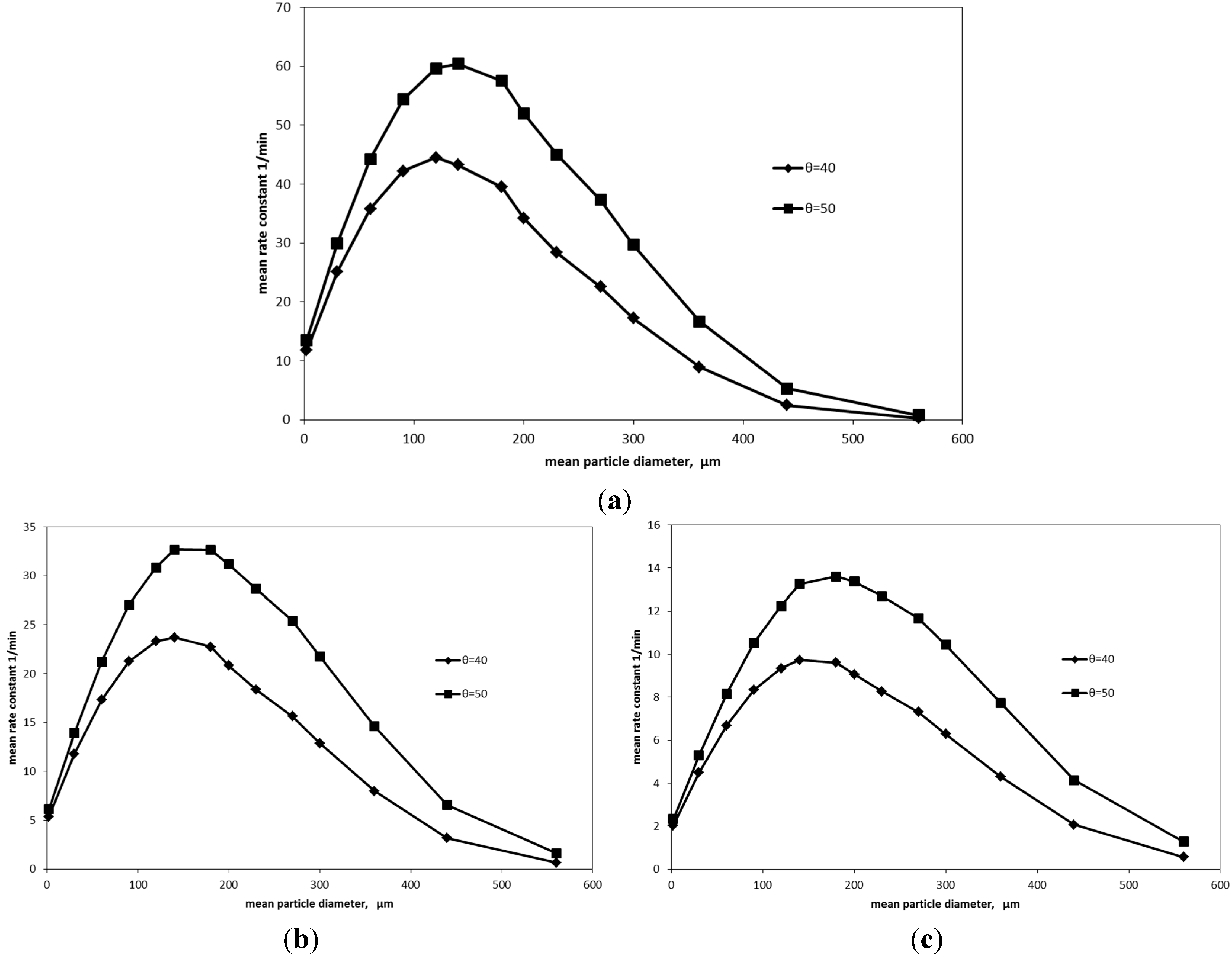
The effect of particles size distribution on the rate constant has been studied also by an assumed γ-particle number distribution. Effects of different size distribution on mean rate constant are depicted in Figure 15a–c for different bubbles sizes. Figure 15a shows that the maximum rate constant is around the mean particle diameter of 140 μm for a contact angle of 50°, and the particle diameter of 120 μm for a contact angle of 40° where, increasing contact angle increases the possibilities of floating larger particles. A considerable mean rate constant for very small mean diameter (d_mean = 5 μm) is observed for bubble size of 0.5 mm while very low rate constant exists for the larger bubble size (d_mean = 0.7 and 1.0 mm) at the same particle mean diameter. Maximum mean rate constant for bubble size (d_mean = 0.7 mm) is also observed to be around particle mean diameter 140 and 180 μm for bubble size (d_mean = 1.0 mm) as shown in Figure 15b,c.

Figure 15. (a) Average rate constant for 0.5 mm bubble diameter and for particle no. γ-distribution; (b) average rate constant for 0.7 mm bubble diameter and for particle no. γ-distribution; (c) average rate constant for 1.0 mm bubble and diameter for particle no. γ-distribution.

Figure 15. (a) Average rate constant for 0.5 mm bubble diameter and for particle no. γ-distribution; (b) average rate constant for 0.7 mm bubble diameter and for particle no. γ-distribution; (c) average rate constant for 1.0 mm bubble and diameter for particle no. γ-distribution.

6. Conclusions

Two phase simulations of self-aerated flotation Wemco 0.8 m³ pilot cells have been conducted to study the transient flow structures and predict air flow rate and power consumption as a function of time. The newly devised overflow tank on top of the pulp volume and constant static pressure at the top boundary of this tank and the standpipe opening allowed us to predict the airflow rate and the transient position of the pulp–air interface until it reached a steady position. Also, investigating dynamical behavior of two-phase flow in the standpipe provides us with a detailed picture of the mixing of air and water and pumping this mixture into the tank. The two-phase simulations provide us with essential parameters for flotation modeling such as local turbulent dissipation rate, velocity rms fluctuations and air void fraction throughout the whole machine. These parameters have been used to develop a CFD-based flotation model. This model predicts pulp rate constant for an arbitrary particle size and bubble size. It uses a first-order rate equation, where processes of collision, attachment and detachments are described by well-known theoretical and empirical formulae. The model uses local values of the rate of turbulent energy dissipation and air volume fraction. Not only the average pulp recovery rate can be estimated but also the regions of high/low recovery rate can be identified. The CFD-based flotation model presented here is also used to determine the dependence of recovery rate constant at any locality within the pulp on bubble diameter, particle diameter, particle specific gravity, contact angle, and surface tension. Furthermore, we have updated our CFD-based flotation kinetics model to predict pulp recovery rate in the presence of both particles size distributions. The calculations are repeated for many particle diameters selected from a range that covers the anticipated minimum and maximum diameters in the slurry. The particles number density pdf and the data generated for single particle size are used to compute the recovery rate for a specific mean particle diameter. Our computational model gives a figure of merit for the recovery rate of a flotation machine, and as such can be used to assess incremental design improvements and design of new machines. The model is a very useful design tool because it can be used to establish the effects of different components (rotor, stator, or disperser jets) on the pulp recovery.