Dehydroxylation of Kaolinite: Evaluation of Activation Energy by Thermogravimetric Analysis and Density Functional Theory Insights
Abstract
1. Introduction
2. Materials and Methods
2.1. Studied Samples
2.2. Kinetic Analyses
2.3. DFT Calculations
3. Results
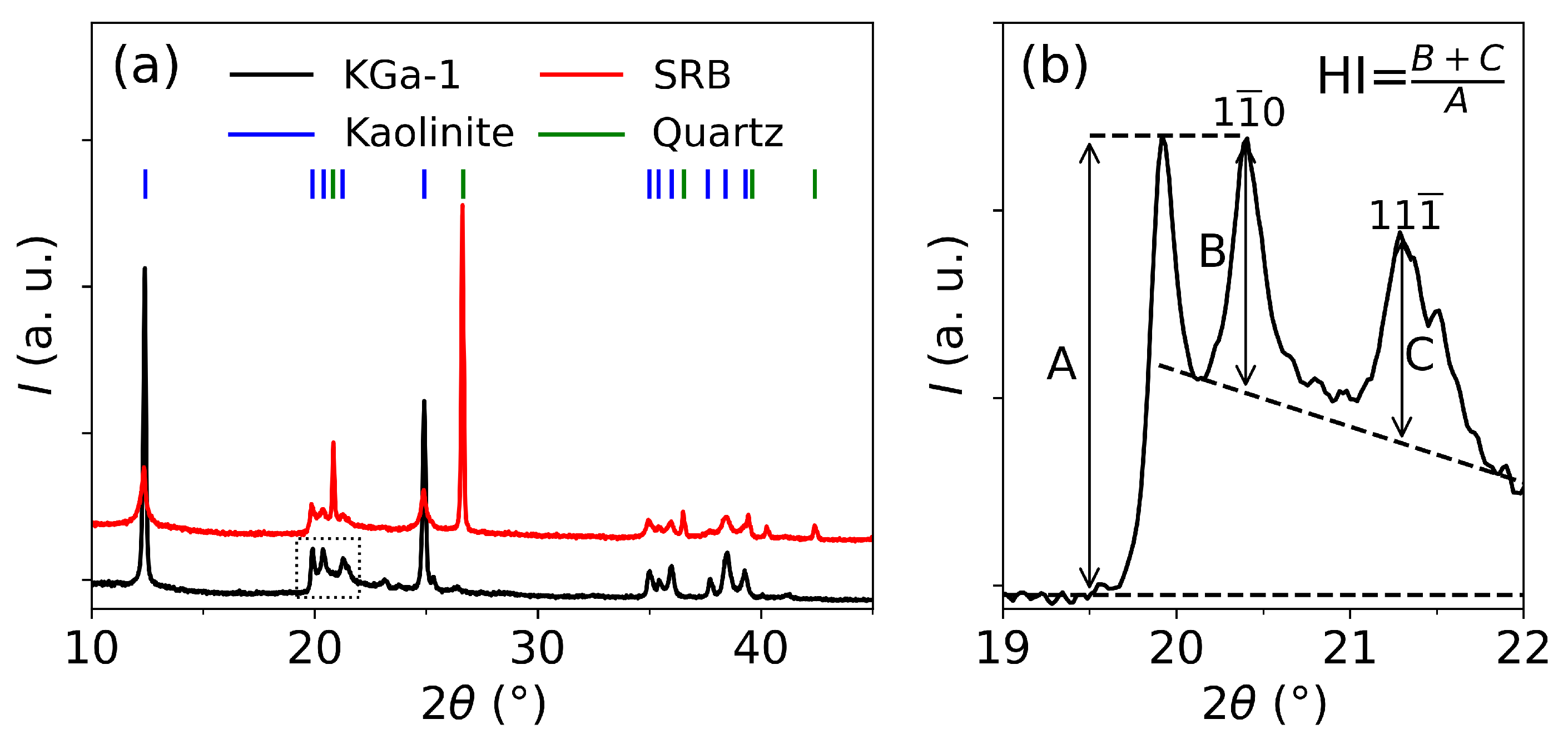
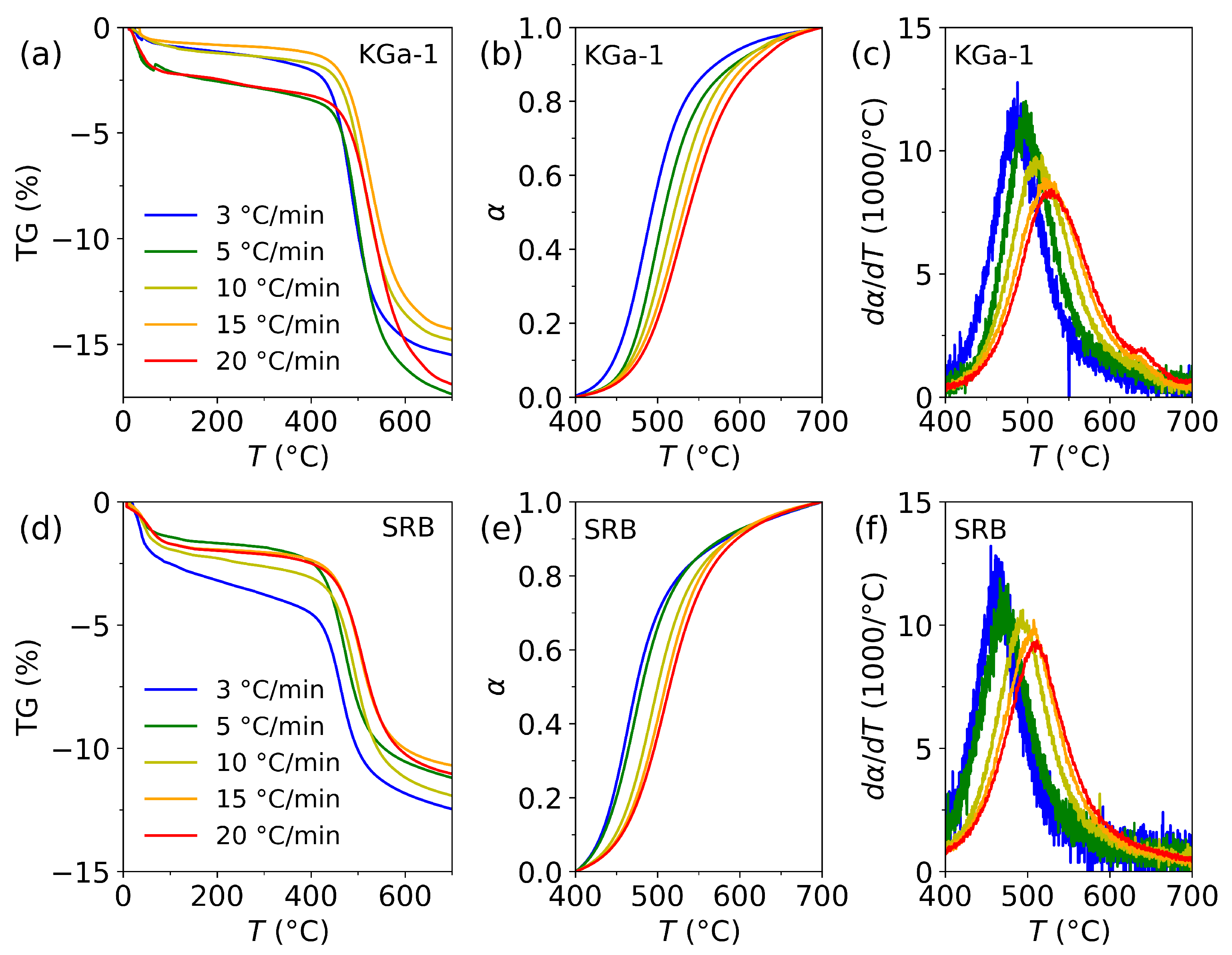
3.1. Dehydroxylation in KGa-1 and SRB
3.2. Search for the Kinetic Reaction Mechanism
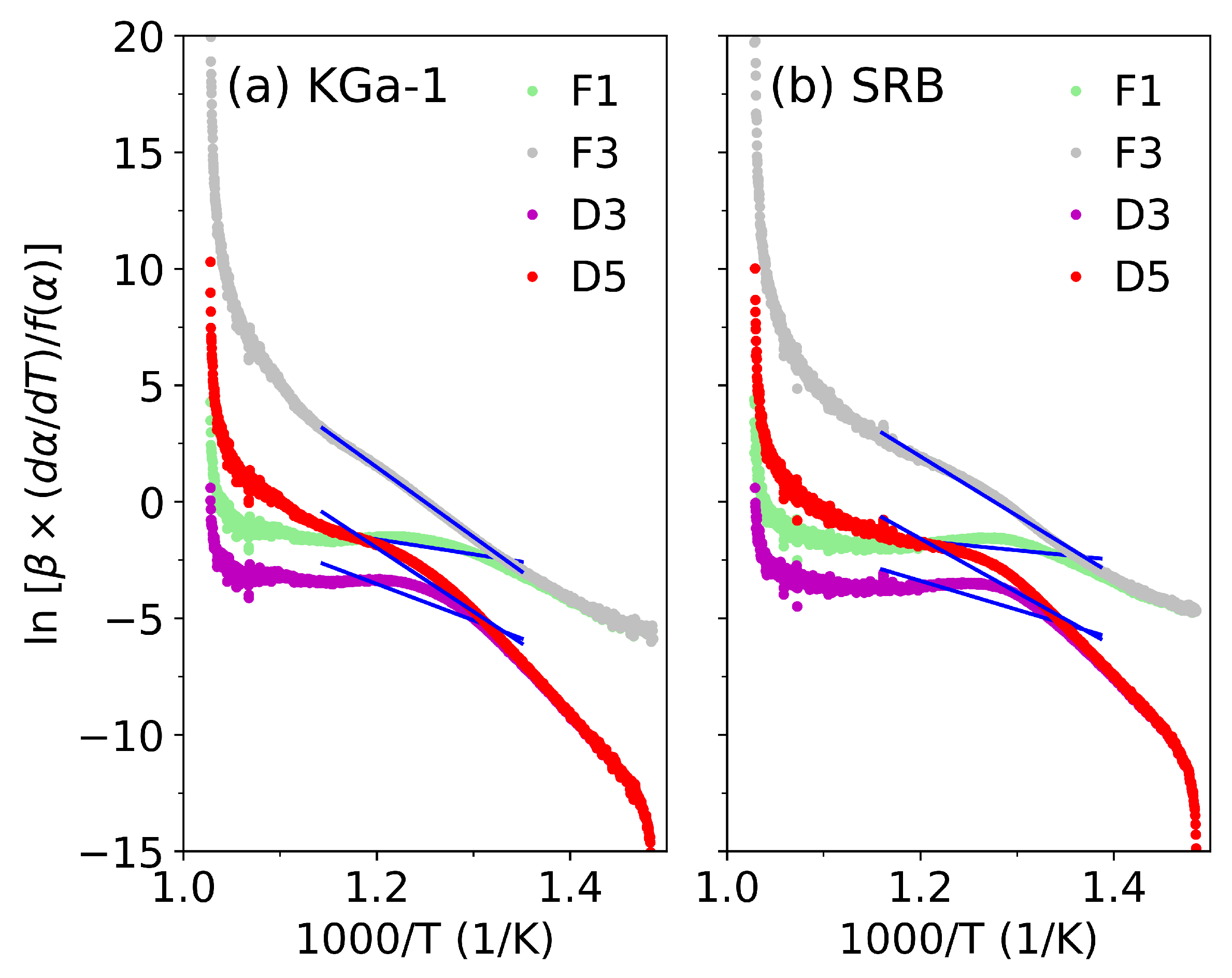
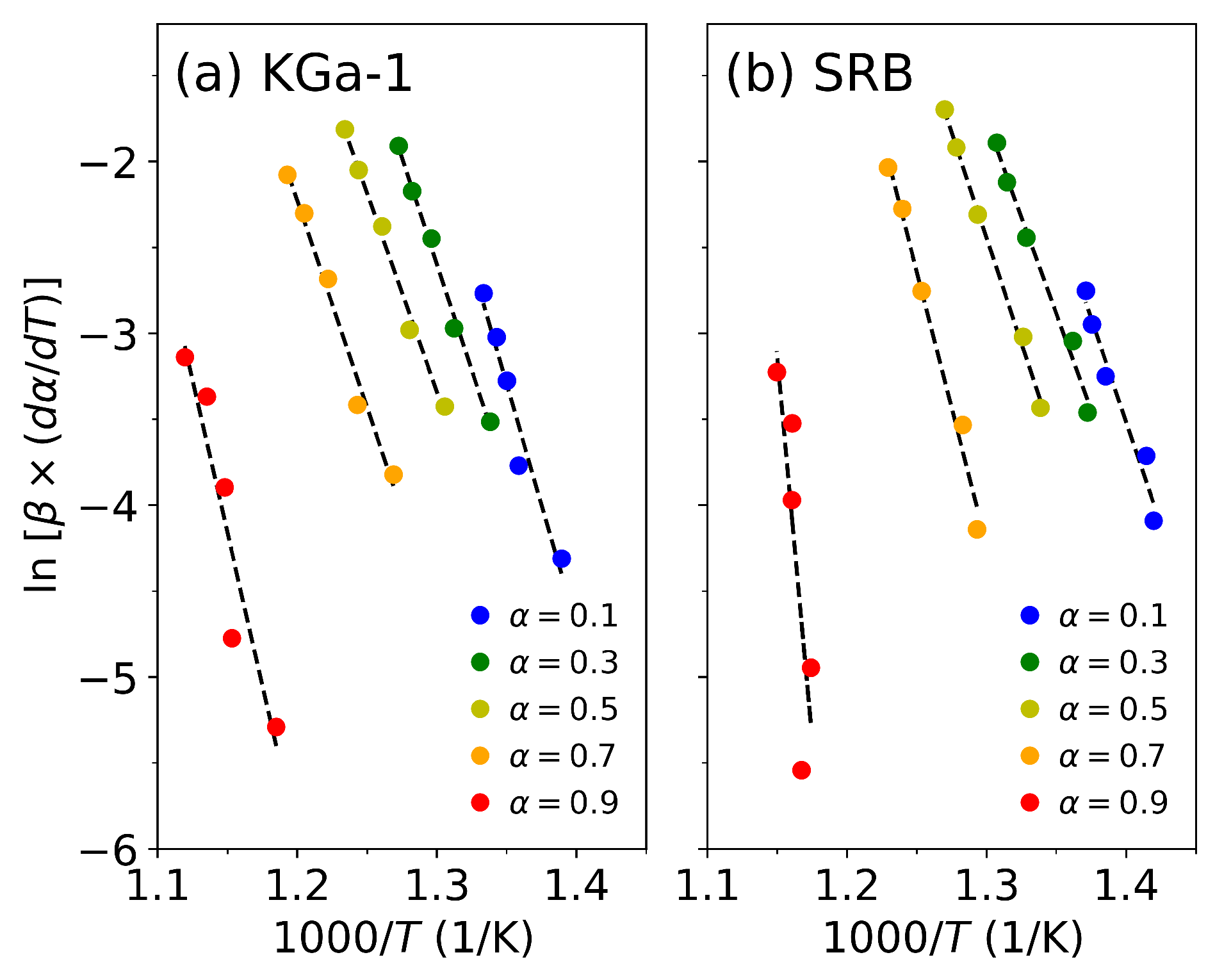
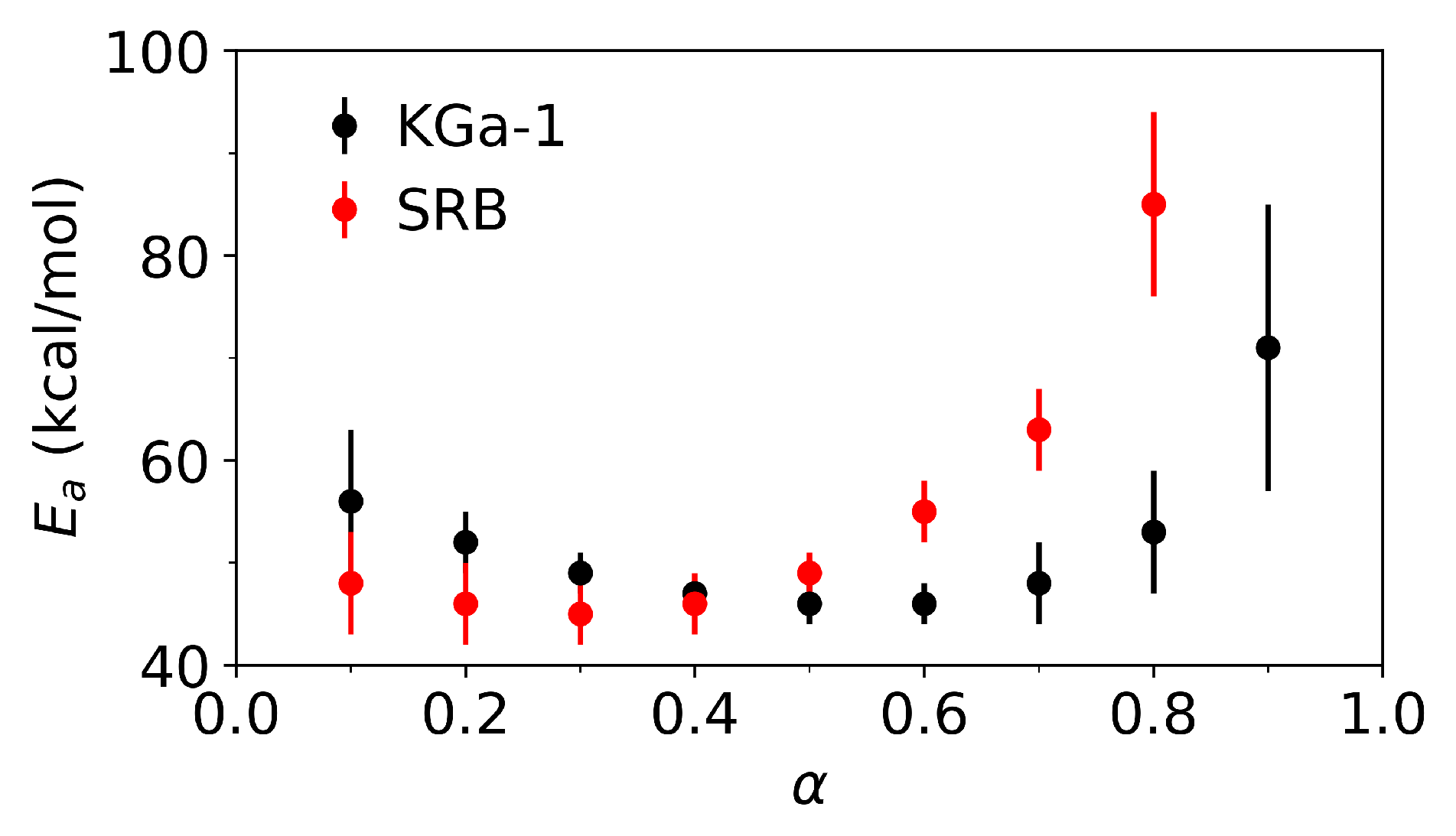
3.3. Isoconversional Method Results
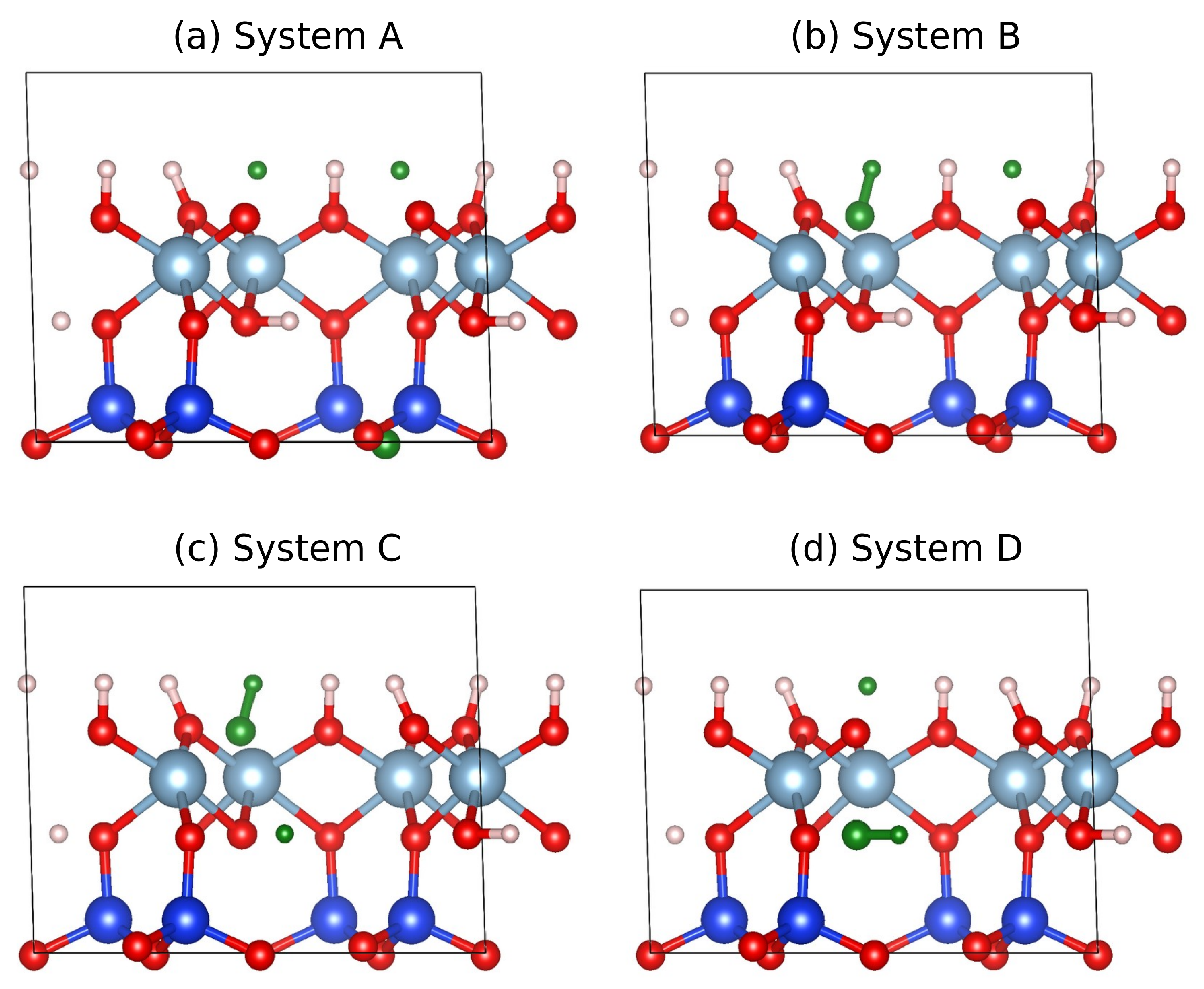
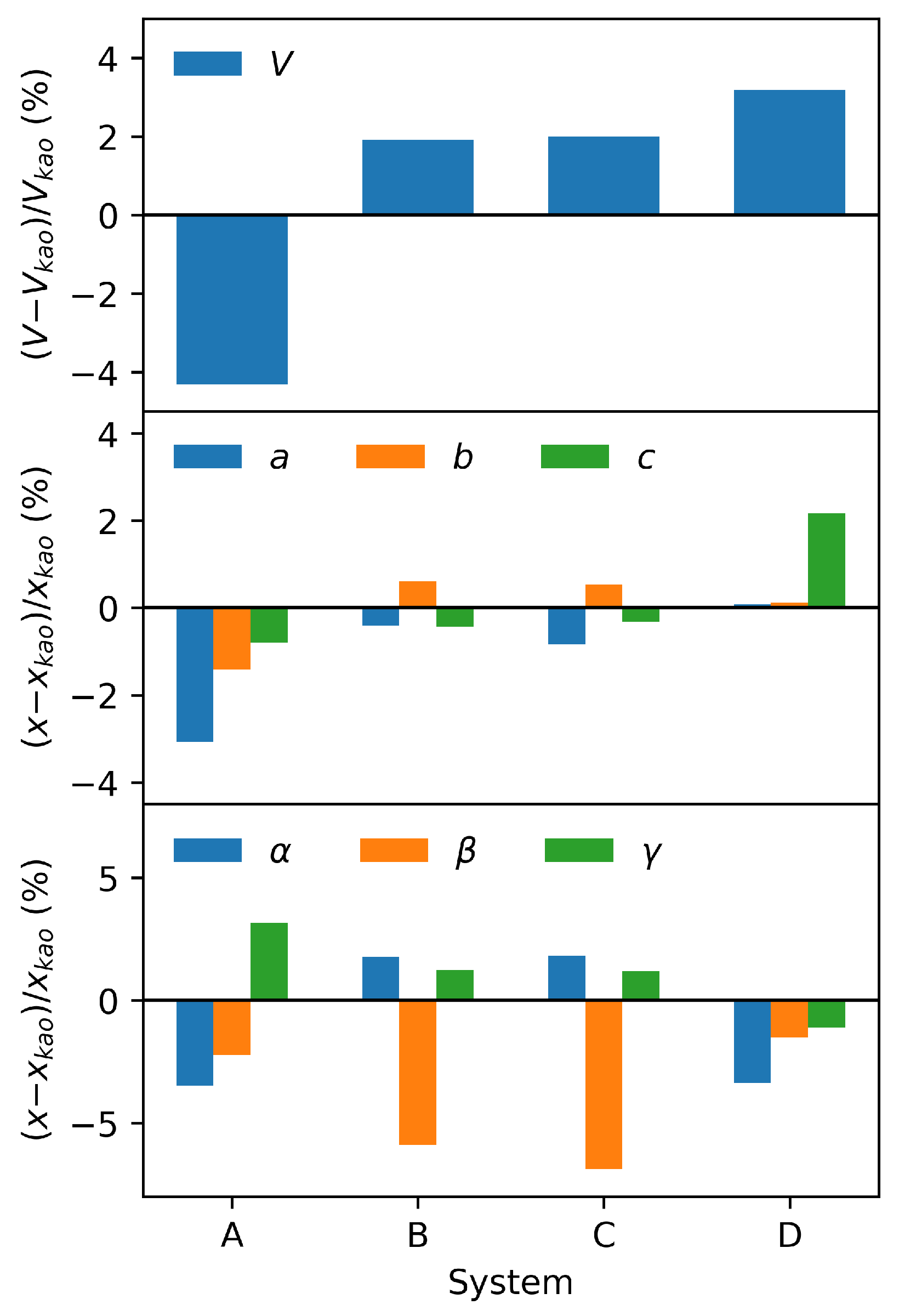
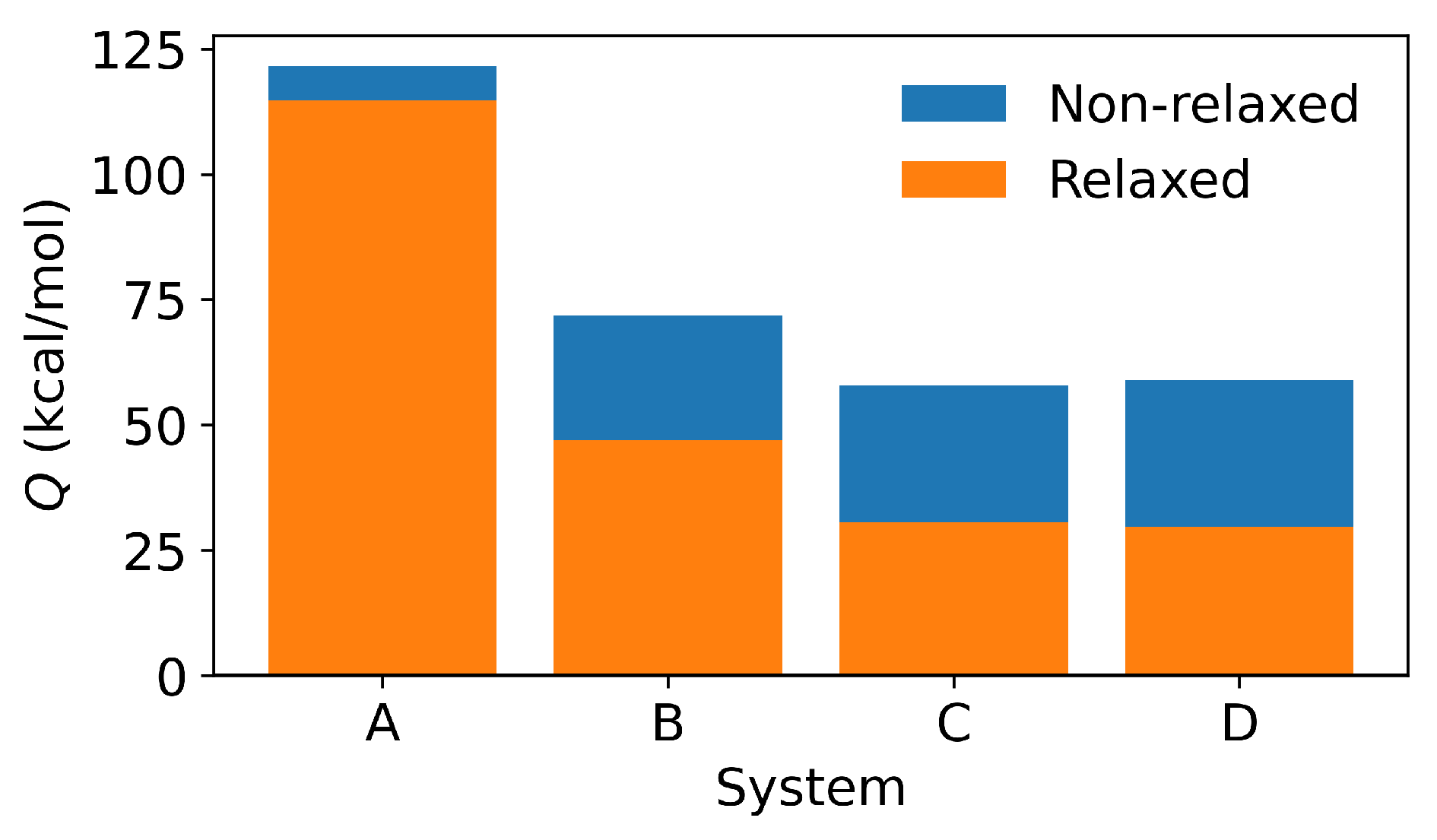
3.4. DFT Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| HI | Hinckley index |
| TG | thermogravimetric analysis |
| XRD | X-ray diffraction |
References
- Gillespie, S.D. Clay: The entanglement of Earth in the Age of Clay. In Impact of Materials on Society; Krzys Acord, S., Jones, K.S., Bryant, M., Dauphin-Jones, D., Hupp, P.S., Gillespie, S.D., Sassaman, K.E., Eaverly, M.A., Curta, F., Adams, S., et al., Eds.; Pressbooks: Gainesville, FL, USA, 2001; pp. 15–43. [Google Scholar]
- Murray, H.H. Kaolin Applications. In Developments in Clay Science; Murray, H.H., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2006; Volume 2, pp. 85–109. [Google Scholar] [CrossRef]
- Schroeder, P.A.; Erickson, G. Kaolin: From ancient porcelains to nanocomposites. Elements 2014, 10, 177–182. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Y.; Zhang, Z.; Ma, Y.; Wang, H. Recent progress of utilization of activated kaolinitic clay in cementitious construction materials. Compos. B Eng. 2021, 211, 108636. [Google Scholar] [CrossRef]
- Ece, Ö.I.; Ercan, H.Ü. Global occurrence, geology and characteristics of hydrothermal-origin kaolin deposits. Minerals 2024, 14, 353. [Google Scholar] [CrossRef]
- Al-Ameri, O.B.; Alzuhairi, M.; Bailón-Gercía, O.; Carrasco-Marín, F.; Amaro-Gahete, J. Transforming petrochemical processes: Cutting-edge advances in kaolin catalyst fabrication. Appl. Sci. 2024, 14, 9080. [Google Scholar] [CrossRef]
- Brigatti, M.F.; Galán, E.; Theng, B.K.G. Structure and mineralogy of clay minerals. Dev. Clay Sci. 2013, 5, 21–81. [Google Scholar] [CrossRef]
- Carty, W.M.; Senapati, U. Porcelain–Raw Materials, Processing, Phase Evolution, and Mechanical Behavior. J. Am. Ceram. Soc. 2005, 81, 3–20. [Google Scholar] [CrossRef]
- Arikan, M.; Sobolev, K.; Ertün, T.; Yeğinobali, A.; Turker, P. Properties of blended cements with thermally activated kaolin. Constr. Build. Mater. 2009, 23, 62–70. [Google Scholar] [CrossRef]
- Shafiq, N.; Nuruddin, M.F.; Ullah Khan, S.; Ayub, T. Calcined kaolin as cement replacing material and its use in high strength concrete. Constr. Build. Mater. 2015, 81, 313–323. [Google Scholar] [CrossRef]
- Liew, Y.M.; Kamarudin, H.; Al Bakri, A.M.; Luqman, M.; Nizar, I.K.; Ruzaidi, C.M.; Heah, C.Y. Processing and characterization of calcined kaolin cement powder. Constr. Build. Mater. 2012, 30, 794–802. [Google Scholar] [CrossRef]
- Mocciaro, A.; Conconi, M.S.; Rendtorff, N.M.; Scian, A.N. Ceramic properties of kaolinitic clay with monoaluminum phosphate (Al(H2PO4)3) addition. J. Therm. Anal. Calorim. 2021, 144, 1083–1093. [Google Scholar] [CrossRef]
- Cordoba, G.; Sposito, R.; Köberl, M.; Zito, S.; Beuntner, N.; Tironi, A.; Thienel, K.C.; Irassar, E.F. Chloride migration and long-term natural carbonation on concretes with calcined clays: A study of calcined clays in Argentina. Case Stud. Constr. Mater. 2022, 17, e01190. [Google Scholar] [CrossRef]
- Hernández, M.F.; López, P.V.; Conconi, M.S.; Rendtorff, N.M. Effect of boron sources in the thermal behavior of a clay-based ceramics. Open Ceram. 2022, 9, 100227. [Google Scholar] [CrossRef]
- Anaya, R.; Hernández, M.F.; Mocciaro, A.; Richard, D.; Rendtorff, N.M. Reused green glass for the production of low-density ceramic proppants. Open Ceram. 2024, 19, 100659. [Google Scholar] [CrossRef]
- Anaya, R.; Carranza, M.B.; Booth, F.; Hernández, M.F.; Mocciaro, A.; Richard, D.; Rendtorff, N.M. Low-density kaolinitic ceramic proppants based on rice husk ash. Ceram. Int. 2025. [Google Scholar] [CrossRef]
- Torres, C.I.; Miquelarena, C.P.; Bianchi, G.L. Optimization of ceramic proppant properties through an innovative coating approach. Bol. Soc. Esp. Ceram. Vidr. 2025, 64, 2–11. [Google Scholar] [CrossRef]
- Chakraborty, A.K. Phase Transformation of Kaolinite Clay; Springer: New Delhi, India, 2014. [Google Scholar] [CrossRef]
- Ptáček, P.; Frajkorová, F.; Šoukal, F.; Opravil, T. Kinetics and mechanism of three stages of thermal transformation of kaolinite to metakaolinite. Powder Technol. 2014, 264, 439–445. [Google Scholar] [CrossRef]
- Drits, V.A.; Derkowski, A. Kinetic behavior of partially dehydroxylated kaolinite. Am. Mineral. 2015, 100, 883–896. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, J.L.; Pascual, J.; Franco, F.; de Haro, M.C.J.; Duran, A.; del Valle, V.R.; Pérez-Maqueda, L.A. The influence of ultrasound on the thermal behaviour of clay minerals. J. Eur. Ceram. Soc. 2006, 26, 747–753. [Google Scholar] [CrossRef]
- Temuujin, J.; Okada, K.; MacKenzie, K.J.D.; Jadambaa, T. The effect of water vapour atmospheres on the thermal transformation of kaolinite investigated by XRD, FTIR and solid state MAS NMR. J. Eur. Ceram. Soc. 1998, 19, 105–112. [Google Scholar] [CrossRef]
- Nahdi, K.; Llewellyn, P.; Rouquérol, F.; Rouquérol, J.; Ariguib, N.K.; Ayedi, M.T. Controlled rate thermal analysis of kaolinite dehydroxylation: Effect of water vapour pressure on the mechanism. Thermochim. Acta 2002, 390, 123–132. [Google Scholar] [CrossRef]
- Ptáček, P.; Kubátová, D.; Havlica, J.; Brandštetr, J.; Šoukal, F.; Opravil, T. The non-isothermal kinetic analysis of the thermal decomposition of kaolinite by thermogravimetric analysis. Powder Technol. 2010, 204, 222–227. [Google Scholar] [CrossRef]
- Adesina, O.C.; Volaity, S.S.; Aylas-Paredes, B.K.; Qi, C.; Kumar, A.; Neithalath, N. Dehydroxylation kinetics of kaolinite and montmorillonite examined using isoconversional methods. Appl. Clay Sci. 2025, 270, 107776. [Google Scholar] [CrossRef]
- Ortega, A.; Macías, M.; Gotor, F.J. The multistep nature of the kaolinite dehydroxylation: Kinetics and mechanism. J. Am. Ceram. Soc. 2010, 93, 197–203. [Google Scholar] [CrossRef]
- De Aza, A.H.; Turrillas, X.; Rodriguez, M.A.; Duran, T.; Peña, P. Time-resolved powder neutron diffraction study of the phase transformation sequence of kaolinite to mullite. J. Eur. Ceram. Soc. 2014, 34, 1409–1421. [Google Scholar] [CrossRef]
- Ondro, T.; Húlan, T.; Vitázek, I. Non-isothermal kinetic analysis of the dehydroxilation of kaolinite in dynamic air atmosphere. Acta Technol. Agric. 2017, 2, 52–56. [Google Scholar] [CrossRef][Green Version]
- Jones, R.O. Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 2015, 87, 897. [Google Scholar] [CrossRef]
- Marzari, N.; Ferretti, A.; Wolverton, C. Electronic-structure methods for materials design. Nat. Mater. 2021, 20, 736–749. [Google Scholar] [CrossRef]
- White, C.E.; Provis, J.L.; Riley, D.P.; Kearley, G.J.; van Deventer, J.S.J. What is the structure of kaolinite? Reconciling theory and experiment. J. Phys. Chem. B 2009, 113, 6756–6765. [Google Scholar] [CrossRef]
- Nisar, J.; Århammar, C.; Jämstorp, E.; Ahuja, R. Optical gap and native point defects in kaolinite studied by the GGA-PBE, HSE functional, and GW approaches. Phys. Rev. B 2011, 84, 075120. [Google Scholar] [CrossRef]
- Tunega, D.; Bučko, T.; Zaoui, A. Assessment of ten DFT methods in predicting structures of sheet silicates: Importance of dispersion corrections. J. Chem. Phys. 2012, 137, 114105. [Google Scholar] [CrossRef]
- Richard, D.; Rendtorff, N.M. First principles study of structural properties and electric field gradients in kaolinite. Appl. Clay Sci. 2019, 169, 67–73. [Google Scholar] [CrossRef]
- Richard, D.; Rendtorff, N.M. Local Environments in Iron-Bearing Clay Minerals by DFT Approaches: The Case of Structural Fe in Kaolinite. Appl. Clay Sci. 2021, 213, 106251. [Google Scholar] [CrossRef]
- Richard, D.; Rendtorff, N.M. Kaolin group minerals under pressure: The study of their structural and electronic properties by DFT methods. Appl. Clay Sci. 2022, 219, 106444. [Google Scholar] [CrossRef]
- Shafei, L.; Adhikari, P.; Ching, W.Y. DFT study of electronic structure and optical properties of kaolinite, muscovite, and montmorillonite. Crystals 2021, 11, 618. [Google Scholar] [CrossRef]
- White, C.E.; Provis, J.L.; Proffen, T.; Riley, D.P.; van Deventer, J.S.J. Density functional modeling of the local structure of kaolinite subjected to thermal dehydroxylation. J. Phys. Chem. A 2010, 114, 4988–4996. [Google Scholar] [CrossRef]
- Sperinck, S.; Raiteri, P.; Marks, N.; Wright, K. Dehydroxylation of kaolinite to metakaolin—A molecular dynamics study. J. Mater. Chem. 2011, 21, 2118–2125. [Google Scholar] [CrossRef]
- Izadifar, M.; Thissen, P.; Steudel, A.; Kleeberg, R.; Kaufhold, S.; Kaltenbach, J.; Schuhmann, R.; Dehn, F.; Emmerich, K. Comprehensive examination of dehydroxylation of kaolinite, disordered kaolinite, and dickite: Experimental studies and density functional theory. Clays Clay Miner. 2020, 68, 319–333. [Google Scholar] [CrossRef]
- Zeng, Q.; Xie, J.; Zhou, W.; Zhu, J.; Liu, L.; Yin, J.; Zhu, W. Study of the crystallographic distortion mechanism during the annealing of kaolinite. Minerals 2022, 12, 994. [Google Scholar] [CrossRef]
- Mermut, A.R.; Faz Cano, A. Baseline studies of the Clay Minerals Society source clays: Chemical analyses of major elements. Clays Clay Miner. 2001, 49, 381–386. [Google Scholar] [CrossRef]
- López, P.V.; Mocciaro, A.; Hernández, M.F.; Richard, D.; Rendtorff, N.M. Microstructure and mechanical properties of a porous ceramic composite with needle-like mullite and zirconia. Int. J. Appl. Ceram. Technol. 2024, 21, 4081–4090. [Google Scholar] [CrossRef]
- Chipera, S.J.; Bish, D.L. Baseline studies of the Clay Minerals Society source clays: Powder X-ray diffraction analyses. Clays Clay Miner. 2001, 49, 398–409. [Google Scholar] [CrossRef]
- Hinckley, D. Variability in ‘crystallinity’ values among the kaolin deposits of the Coastal Plain of Georgia and South Carolina. In Clays and Clay Minerals (National Conference on Clays and Clay Minerals); Cambridge University Press & Assessment: Cambridge, UK, 1962; Volume 11, pp. 229–235. [Google Scholar]
- Bastida, J.; Pardo-Ibañez, P. Applications of X-ray powder diffraction microstructural analysis in applied clay mineralogy. Minerals 2024, 14, 584. [Google Scholar] [CrossRef]
- Richard, D.; Martínez, J.M.; Mizrahi, M.; Andrini, L.; Rendtorff, N.M. Assessment of structural order indices in kaolinites: A multi-technique study including EXAFS. J. Electron Spectrosc. Relat. Phenom. 2022, 254, 147128. [Google Scholar] [CrossRef]
- Bish, L. Rietveld refinement of the kaolinite structure at 1.5 K. Clays Clay Miner. 1993, 41, 738–744. [Google Scholar] [CrossRef]
- Kroll, P.; Milko, M. Theoretical investigation of the solid state reaction of silicon nitride and silicon dioxide forming silicon oxynitride (Si2N2O) under pressure. Z. Anorg. Allg. Chem. 2003, 629, 1737–1750. [Google Scholar] [CrossRef]
- Wendlandt, W. Thermal Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 1986. [Google Scholar]
- Belloto, M.; Gualtieri, A.; Artioli, G.; Clark, S.M. Kinetic study of the kaolinite-mullite reaction sequence. Part I: Kaolinite dehydroxylation. Phys. Chem. Minerals 1995, 22, 207–214. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry: Application to a phenolic plastic. J. Polym. Sci. C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116. [Google Scholar] [CrossRef]
- Hirsch, T.K.; Ojamäe, L. Quantum-chemical and force-field investigations of ice Ih: Computation of proton-ordered structures and prediction of their lattice energies. J. Phys. Chem. B 2004, 108, 15856–15864. [Google Scholar] [CrossRef]
- Zamiatina, D.A.; Zamyatin, D.A.; Mikhalevskii, G.B.; Chebikin, N.S. Silica polymorphs formation in the Jänisjärvi impact structure: Tridymite, Cristobalite, Quartz, Trace Stishovite and Coesite. Minerals 2023, 13, 686. [Google Scholar] [CrossRef]
- Baldo, J.B.; dos Santos, W.N. Phase transitions and their effects on the thermal diffusivity behaviour of some SiO2 polymorphs. Cerâmica 2002, 48, 172–177. [Google Scholar] [CrossRef]
- Suárez, M.P.; Palermo, A.; Aldao, C.M. The compensation effect revisited. J. Therm. Anal. 1994, 41, 807–816. [Google Scholar] [CrossRef]
- Barrie, P.J. The mathematical origins of the kinetic compensation effect: 1. The effect of random experimental errors. Phys. Chem. Chem. Phys. 2012, 14, 318–326. [Google Scholar] [CrossRef]
- Xu, X.; Goddard, W.A. Bonding properties of the water dimer: A comparative study of density functional theories. J. Phys. Chem. A 2004, 108, 2305–2313. [Google Scholar] [CrossRef]
- Molina-Montes, E.; Timón, V.; Hernández-laguna, A.; Sainz-díaz, C.I. Dehydroxylation mechanisms in Al3+/Fe3+ dioctahedral phyllosilicates by quantum mechanical methods with cluster models. Geochim. Cosmochim. Acta 2008, 72, 3929–3938. [Google Scholar] [CrossRef]
- Molina-Montes, E.; Donadio, D.; Hernández-laguna, A.; Parrinello, M.; Sainz-díaz, C.I. Water release from pyrophyllite during the dehydroxylation process explored by quantum mechanical simulations. J. Phys. Chem. C 2013, 117, 7526–7532. [Google Scholar] [CrossRef]
- Dean, J.A. Lange’s Handbook of Chemistry; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]


| Chemical composition | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | Fe2O3 | CaO | MgO | Na2O | K2O | TiO2 | LOI * | Ref. | |
| KGa-1 | 43.36 | 38.58 | 0.35 | 0.04 | 0.04 | 0.05 | 0.00 | 1.67 | 13.6 | [42] |
| SRB | 60.00 | 26.40 | 1.03 | 0.16 | 0.18 | 0.12 | 0.64 | 0.37 | 11.1 | [43] |
| Mineralogical composition | ||||||||||
| Kaolinite | Quartz | Potassum felspar | Anatase | Ref. | ||||||
| KGa-1 | 96 | Traces | - | Traces | [44] | |||||
| SRB | 76.6 | 22.0 | 1.4 | Traces | [43] | |||||
| Symbol | Name | Rate-Controlling Process | Ref. | |
|---|---|---|---|---|
| F1 | First-order | Interface-controlled reaction | [23,51] | |
| F3 | Third-order | Nucleation-growth chemical reaction | [24,28] | |
| D3 | Jander equation | 3D diffusion, spherical symmetry | [27,28,51] | |
| D5 | Zhuravlev equation | Diffusion process with additional transport effects | [24,28] |
| Sample | (°C/min) | F1 | F3 | D3 | D5 |
|---|---|---|---|---|---|
| KGa-1 | 3 | 0.4034 | 0.9898 | 0.6818 | 0.9134 |
| 5 | 0.2732 | 0.9882 | 0.6270 | 0.8968 | |
| 10 | 0.6960 | 0.9992 | 0.7945 | 0.9534 | |
| 15 | 0.8100 | 0.9989 | 0.8515 | 0.9721 | |
| 20 | 0.8030 | 0.9994 | 0.8501 | 0.9700 | |
| SRB | 3 | 0.0217 | 0.9475 | 0.3439 | 0.7945 |
| 5 | 0.1115 | 0.9794 | 0.5518 | 0.8722 | |
| 10 | 0.4164 | 0.9890 | 0.6824 | 0.9107 | |
| 15 | 0.6854 | 0.9976 | 0.7976 | 0.9511 | |
| 20 | 0.7219 | 0.9983 | 0.8152 | 0.9568 |
| Kaolinite | System A | System B | System C | System D | |
|---|---|---|---|---|---|
| V (Å3) | 329.79 | 315.57 | 336.11 | 336.39 | 340.31 |
| a (Å) | 5.1739 | 5.0151 | 5.1525 | 5.1310 | 5.1781 |
| b (Å) | 8.9851 | 8.8579 | 9.0398 | 9.0334 | 8.9952 |
| c (Å) | 7.3518 | 7.2928 | 7.3194 | 7.3288 | 7.5110 |
| () | 91.686 | 88.509 | 93.305 | 93.361 | 88.602 |
| () | 105.126 | 102.789 | 98.941 | 97.901 | 103.530 |
| () | 89.757 | 92.590 | 90.870 | 90.842 | 88.758 |
| (Ry) | −1053.5443 | −1053.8612 | −1053.9503 | −1053.9438 | |
| (Ry) | −1098.0593 | −1053.5872 | −1054.0197 | −1054.1245 | −1054.1305 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polcowñuk Iriarte, I.A.; Mocciaro, A.; Rendtorff, N.M.; Richard, D. Dehydroxylation of Kaolinite: Evaluation of Activation Energy by Thermogravimetric Analysis and Density Functional Theory Insights. Minerals 2025, 15, 607. https://doi.org/10.3390/min15060607
Polcowñuk Iriarte IA, Mocciaro A, Rendtorff NM, Richard D. Dehydroxylation of Kaolinite: Evaluation of Activation Energy by Thermogravimetric Analysis and Density Functional Theory Insights. Minerals. 2025; 15(6):607. https://doi.org/10.3390/min15060607
Chicago/Turabian StylePolcowñuk Iriarte, Iván Aitor, Anabella Mocciaro, Nicolás Maximiliano Rendtorff, and Diego Richard. 2025. "Dehydroxylation of Kaolinite: Evaluation of Activation Energy by Thermogravimetric Analysis and Density Functional Theory Insights" Minerals 15, no. 6: 607. https://doi.org/10.3390/min15060607
APA StylePolcowñuk Iriarte, I. A., Mocciaro, A., Rendtorff, N. M., & Richard, D. (2025). Dehydroxylation of Kaolinite: Evaluation of Activation Energy by Thermogravimetric Analysis and Density Functional Theory Insights. Minerals, 15(6), 607. https://doi.org/10.3390/min15060607









