1. Introduction
Metallurgical plants are central to the mineral value chain, significantly affecting a mine’s operating costs and revenue. A critical example is the comminution process—encompassing crushing and grinding—which liberates valuable minerals for subsequent flotation or leaching. This stage alone often consumes over 30% of a mine’s total energy usage, and as much as 50% of a mine’s electrical energy [
1,
2,
3] and is influenced by ore characteristics such as hardness and liberation size [
4]. Consequently, optimizing comminution is crucial for increasing metal recovery while reducing both energy consumption and operational costs [
5].
Beyond comminution, additional factors limit the full recovery of valuable metals. For instance, the presence of cyanide-consuming elements—like gold and silver—necessitates higher reagent dosages, driving up operating costs [
6]. Inevitably, some fraction of the valuable minerals is lost to tailings [
7]. Striking an optimal balance between the final product sold and the material sent to tailings thus becomes essential. This ratio depends on the natural variability of the incoming feed and the extent to which the plant can adapt to these fluctuations, directly impacting both costs and revenues.
Adapting to feed variability often involves reconfiguring the plant to ensure efficient processing. For example, switching from a coarse to a fine grind may require emptying the semi-autogenous grinding (SAG) mill and substituting the existing steel ball load—a procedure that can force the plant to halt or operate below capacity. While such changes can improve recovery, frequent reconfigurations are impractical. Instead, metallurgical plants typically operate within predefined operational modes—sets of parameters (e.g., blending proportions, feed rates, and grinding conditions) specifically suited to certain ore characteristics or production targets [
8]. These modes help maintain efficiency and throughput during substantial or prolonged changes in the feed. Additionally, introducing new equipment or sensors may prompt the creation of further operational modes [
9,
10].
Importantly, these operational decisions also carry significant long-term financial consequences. Choices around reconfiguration, energy consumption, metal recovery, and maintenance can accumulate over the life of a mine, making it essential to capture their effects in strategic mine-planning frameworks. However, despite the importance of operational modes, relatively few models integrate them at a detailed level within long-term mine planning. For instance, Ref. [
7] extended stochastic mine-planning algorithms to evaluate net present value (NPV) by incorporating alternative operational modes under geological uncertainty. Lamghari’s variable neighborhood descent (VND) approach [
10] provided a statistical foundation to compare plant designs and justify expansions. Ref. [
11] observed that, while current long-term mine-planning methods often handle geological uncertainty effectively, they frequently lack robust representations of alternate processing modes. They responded by proposing a computational framework that integrates geometallurgical models, enabling the evaluation of multiple operational modes more accurately.
Production control for mineral processing has been addressed by developing a digital twin framework that combines discrete event simulation (DES) with a customized machine learning (ML) model [
12]. The work identifies trigger points for switching operational modes, improving short- and long-term outcomes. However, because this framework relies on simulation rather than a formal optimization model, it does not guarantee a mathematically optimal solution. In contrast, Ref. [
8] focused on enhancing stochastic mine-planning algorithms to implement mode changes in greater detail, proposing a two-stage optimization model. In the second stage—representing the metallurgical plant—they introduced a Dantzig–Wolfe decomposition [
13] with a linear programming formulation, nested within the stochastic mine-planning algorithm. Ref. [
14] then built on that work by applying the ultimate pit limit (UPL) to reduce the number of blocks and parallelizing the VND algorithm. Although these improvements lowered execution times to around 41 min for a case with 13,000 blocks, 2 rock types, and 2 operational modes, such a runtime remains impractical for real open-pit mines containing millions of blocks. Because the Dantzig–Wolfe decomposition is iterated thousands of times within the optimization, even modest per-iteration improvements can significantly reduce the overall runtime. Consequently, further improving this computationally intensive step remains a priority.
Against this backdrop, the present study introduces a matheuristic that balances two objectives: maximizing mineral-processing performance and minimizing deviation from the exact optimal solution. By matheuristics, we refer to heuristic algorithms that integrate metaheuristic and mathematical programming techniques [
15]. The proposed approach combines a greedy algorithm with a continuous knapsack subproblem to address efficiently the unique challenges of multi-mode mineral processing, where variations in ore grade and textural characteristics demand adaptive strategies. While the underlying computational framework is essential, our method is grounded in metallurgical principles captured by the operational modes, ensuring that decisions related to ore blending, comminution, and flotation process are informed by the geological and mineralogical properties of the deposit.
This paper begins by reviewing the knapsack problem and its main variants, then discusses how the unique constraints of multi-mode mineral processing depart from standard formulations. Next, we describe the metaheuristic aspects of our approach, underscoring the elements essential for flexible mode selection. We then illustrate the potential of this method through a detailed case study, showcasing its efficacy in maintaining near-optimal solutions within reduced computational times. Finally, we draw conclusions regarding the broader implications of incorporating multiple operational modes into strategic mine planning and suggest possible avenues for future research.
2. Knapsack Problem
The knapsack problem is a well-known combinatorial optimization model that seeks to maximize value while respecting a capacity constraint [
16]. Two common variants are as follows:
s.t.
where
vi is the value of item
i,
wi is its weight, and
K is the knapsack capacity.
This enables a fraction of each item i to be included. In the standard fractional knapsack, a simple greedy algorithm that sorts items by their value-to-weight ratio solves the problem optimally in time.
2.1. From Knapsack to Mineral Processing
Mineral processing can be conceptually framed as a fractional knapsack problem, especially when an orebody is divided into discrete blocks that can be partially processed. If we draw an analogy, we have the following:
Items Blocks of ore b , each with a specific mas, mb.
Value vi Potential revenue vb from extracting minerals in block b.
Weight wi Mass mb, which contributes to a plant’s capacity usage.
Capacity K A limit on how much the plant can process over a given scheduling period.
Therefore, in the simplest case, a metallurgical plant has a fixed capacity K, and each block can be processed either fully or partially, depending on whether it is beneficial to do so. However, real-world mineral-processing scenarios seldom adhere strictly to the basic 0–1 knapsack or fractional assumptions. In practice, operational modes enter the picture. Each operational mode may be viewed as a specific plant configuration or setting, designed to process different blends of the varying rock types, at varying rates. Consequently, multiple constraints arise as follows:
Multiple rock types: Blocks can belong to distinct rock types, each with unique metallurgical properties.
Blending requirements: Certain modes may demand specific ratios of rock types to ensure stable metallurgical performance.
Partial processing across modes: A single block may be partially processed under one mode and partially under another, if this yields higher overall returns and meets blending constraints.
Time-based capacity: Instead of a simple tonnage limit, the capacity may be measured in hours of plant operation, which must be allocated efficiently among modes and blocks.
2.2. Mathematical Formulation
The mathematical formulation that incorporates the aforementioned aspects is a mixed-integer linear program (MILP) presented in [
8].
Table 1 summarizes the notation used throughout.
The objective function and constraints are as follows:
This formulation maximizes the total recoverable value across all blocks and modes using vbo/mb to represent the value per unit mass (Equation (5)). Constraint 6 ensures that the cumulative processing time does not exceed the available hours q. Since (1/ro) xbo denotes the time required to process mass xbo of block b under mode o, the sum of these terms must be less than or equal to q. Constraint 7 limits the total processed mass of each block b to at most mb. Constraint 8 enforces the blending ratios for rock types within each mode o. Because wop1 and wop2 represent the fractional requirements for rock types p1 and p2, respectively, their processed masses must reflect the specified ratio. Finally, Constraint 9 ensures the non-negativity of the decision variables.
As mentioned previously, this formulation was implemented in [
8] and further refined in [
14]. However, the runtime reaches almost 41 min for 13,000 blocks, 2 operational modes, and 2 rock types. Although the Dantzig–Wolfe implementation in these works is highly efficient, the fact that this part of the code is executed thousands of times means that even a minor improvement in the implementation could significantly reduce the overall execution time, especially when scaling to scenarios involving millions of blocks.
3. Matheuristic
We proposed a matheuristic to solve the MILP formulation efficiently to determine the amount of mass of each block b to be processed under a specific operational mode, o , which maximizes the recoverable value vbo of the set of blocks .
The matheuristic consists of the following two phases: the benefit calculation phase and the fraction assignment phase. The benefit calculation phase computes the potential benefit of processing blocks for each operational mode. Once the operational mode with the highest benefit is selected, the fraction assignment phase determines the percentage of the blocks to be processed.
The main algorithm and its two phases are described in the following subsections. Additionally,
Appendix A presents a supplementary numerical example that further illustrates how the algorithm operates.
3.1. Main Algorithm
Algorithm 1 describes the main procedure of the matheuristic. It begins with a set of blocks,
; a set of rock types,
; a set of operational modes,
, of the plant; parameters related to the available time of the plant,
q; the mass
mb of each block
b ; the tonnage processing rate
ro by mode
o ; the value,
vbo, of each block
b processed by mode
o and the proportion requirement,
wop, for each block of rock type
p processed by mode
o. Then, the best benefit, σ, is initialized as zero, and lists related to the problem information for each iteration of the algorithm—
,
,
,
,
, and
—are initialized.
| Algorithm 1 Main Algorithm | |
| 1: | Inputs: , , , q, mb, ro, vbo, wop | |
| 2: | Output: Processed blocks and their assigned fraction () | |
| 3: | | |
| 4: | Initialization: | |
| 5: | σ 0 | ◊ best benefit |
| 6: | , , , , , | |
| 7: | | |
| 8: | Sort all lists according to non-increasing order of their OR. | |
| 9: | while , q > 0, σ ≥ 0 do | |
| 10: | Call o*, σ BENEFIT_CALCULATION(, , , ) | |
| 11: | if σ ≥ 0 then | |
| 12: | Call FRACTION_ASSIGNMENT() | |
| 13: |
end if | |
| 14: | end while | |
, , and remain unchanged at every iteration of the algorithm and are only updated with a new instance of the problem. stores the recoverable value of each block classified by rock type. It is initialized with the recoverable value, vbo, of each block b of rock type p when it is processed by mode o. stores the processing time information for each block classified by rock type p when a specific operational mode, o, is selected. It is initialized with the quotient between the mass, mb, of the block and the processing ratio, ro, for each mode o. saves the proportion requirement information to ensure the correct mix of rock types for each processing mode. It is initialized with the proportion requirement wop for each rock type p when it is processed by mode o.
, and are updated at every iteration of the algorithm and allow us to determine a decision path to process blocks in the best operational mode with the correct tonnage quantity, respectively.
stores the order ratios (ORs) of the blocks to determine which are potentially more attractive to process, considering different operational modes. These ratios are calculated using the quotient of the values of and for each block b of rock type p when processed by mode o. The list is computed once at the algorithm’s beginning and sorted in a non-increasing order. In every iteration, when a block is completely processed, it is eliminated.
stores the feasible fractions assigned (FAs) for each block b of rock type p that is processed under different operational modes, o (xbo/mb). At each iteration, the FA value for each block is updated to ensure a feasible mix of rock types for each processing mode. The list is initialized with a fraction assignment of zero for each block.
stores 1 − to track the remaining portion of each block b that has not yet been processed. Unlike , this list is initialized with a value of 1.
After initialization, the list of blocks is sorted in non-increasing order based on their ORs. Then the benefit calculation phase and the fraction assignment phase are called until some of the following stop criteria are met: (i) there are no remaining unprocessed blocks, (ii) the processing capacity is fully occupied, or (iii) the best potential benefit offered by a next iteration is negative.
The algorithm concludes by returning a list of processed blocks of rock type p in mode o, along with their assigned fractions . The total value of ore processing is calculated as the product of each block’s value and its corresponding FA. The following subsections, the benefit calculation phase and the fraction assignment phase, are described in detail.
3.2. Benefit Calculation
Algorithm 2 describes the
benefit calculation phase, which computes the best potential benefit of processing blocks considering different operational modes. It begins with a set of operational modes,
, of the plant, a set of rock types,
, the proportion requirement,
, and the order ratios,
. The function outputs the best operational mode
o* and the best benefit σ generated by the block of rock type
p processed by the best operational mode
o*.
| Algorithm 2 Benefit Calculation Function | |
| 1: | function BENEFIT_CALCULATION(, , , ) | |
| 2: |
Initialization: | |
| 3: | o* none | ◊ best operational mode |
| 4: | σ −∞ | ◊ best benefit in mode o* |
| 5: |
total_benefit[o]
| |
| 6: | | |
| 7: | for all o do | |
| 8: | Determine rock type p* with the maximum value wop, p | |
| 9: | total_benefit[o] × | |
| 10: | if total_benefit[o] > σ then | |
| 11: | σ total_benefit[o] | |
| 12: |
o*
o | ◊ Update best operational mode |
| 13: |
end if | |
| 14: |
end for | |
| 15: | | |
| 16: | return o*, σ | |
| 17: | end function | |
First, we initialize the best mode as none, the best benefit as −∞, and the total benefit at each mode as 0. Then, for each mode, o , we determine the rock type p* with the maximum wop in to compute the relation factor concerning all the other blocks of rock type p in order to determine the total benefit in mode o , considering only feasible rock type mixes.
In the final evaluation of all operational modes, we obtain the best operational mode o* and the best benefit σ.
3.3. Fraction Assignment
Once the best operational mode
o* with the highest benefit σ is selected, the
fraction assignment phase determines the proportion of the rock type block that must be processed in the selected mode. This procedure is described in Algorithm 3.
| Algorithm 3 Fraction Assignment Function | |
| 1: | function FRACTION_ASSIGNMENT(, , , , , , mb, q, o*) | |
| 2: | TP ∞ | ◊ Total tonnage to be processed |
| 3: | for all p do | |
| 4: | Get block b of rock type p with the highest value in | |
| 5: | ATp mb × (−)/ | ◊ Available tonnage to be processed |
| 6: | if TP > ATp then | ◊ min(TP, ATp) |
| 7: | pmin p | |
| 8: | TP ATp | |
| 9: |
end if | |
| 10: |
end for | |
| 11: | | |
| 12: | for all p do | |
| 13: | TRTp × TP | ◊ Tonnage of each rock type to be processed |
| 14: | + TRTp/mb | ◊ Update FA for each block |
| 15: | for all o \ {o*} do | |
| 16: | 1 − | ◊ Update FA for the same blocks in other modes |
| 17: |
end for | |
| 18: | q q − TRTp/ ro* | ◊ Update available plant capacity |
| 19: |
end for | |
| 20: | end function | |
The fraction assignment phase begins with a set of operational modes of the plant, a set of rock types, ; the order ratios, ; the fraction assignments, ; the mass of each block, mb; the proportion requirement, ; the available time of the plant, q; and the best mode, o*. At the end, this procedure updates the fraction assignments, , to be processed for the following iterations.
First, for all rock type p , we determine the available tonnage (ATp) to be processed in the best mode o*, and we set up the total tonnage to be processed, TP, as the min (TP, ATp), for all p . Then, we compute the tonnage of each rock type to be processed (TRTp) in order to determine their respective fraction assignment, updating . In this process, we ensure that the required fractions of each rock type p must be processed according to the proportion requirement . Also, we update the fraction assignment for each block in the other operational modes for the following iterations . Finally, we update the available plant capacity.
3.4. Advantages of the Matheuristic Approach
The matheuristic approach described in this section is particularly advantageous for complex problems where multiple constraints must be satisfied, such as maintaining specific proportions of rock types in different modes while considering plant capacity limitations. By modularizing the key phases of the algorithm, the approach remains flexible and can be adapted to a wide variety of real-world scenarios. The use of separate functions for benefit calculation, fraction assignment, and termination checking ensures that the algorithm remains computationally efficient, even as the number of rock types and operational modes increases.
5. Conclusions
This study introduced a novel matheuristic approach to optimize mineral processing in metallurgical plants, formulated as a variant of the fractional knapsack problem. The proposed method integrates plant operational modes, blending constraints, and capacity limitations to maximize the recoverable value of mineral blocks. By leveraging a greedy strategy within a heuristic framework, the algorithm significantly reduces computational time while maintaining near-optimal solutions. Validation through a case study demonstrated its ability to effectively manage complex constraints, reinforcing its practical applicability in real-world mining operations.
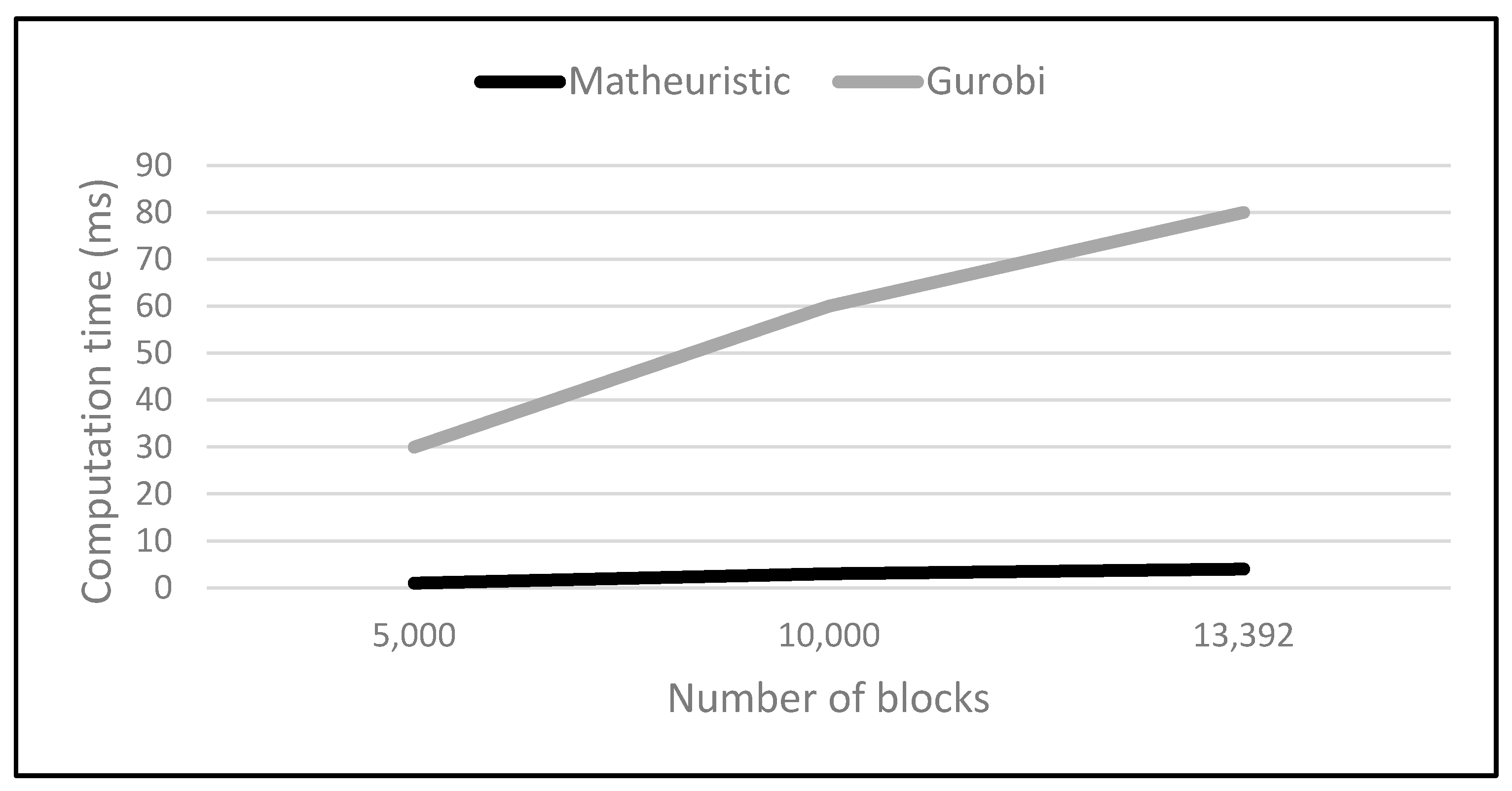
Despite minor deviations from the optimal solution in the case study—less than 0.1% in total value—the proposed algorithm drastically reduces computation time, highlighting its superior efficiency in comparison to exact methods implemented in the Gurobi solver. Additionally, in the case study, the matheuristic successfully maintains blending requirements and operational constraints, ensuring feasible and efficient processing strategies. The preference for operational Mode A over Mode B in the results suggests an inherent flexibility in adapting to different mineralogical compositions and plant configurations, consistent with previous studies that consider multiple processing modes [
6,
7,
8,
9,
11,
12,
14].
Given that the current implementation achieves near-optimal results, future research will focus on analyzing whether fine-tuning specific algorithmic components can further enhance performance. In addition, we plan to explore the integration of additional elements—such as accounting for variations in valuable component content across the block and addressing challenges related to geological sampling—to improve the reliability of our forecasting approach. Moreover, while cyanide consumption is currently incorporated indirectly within the processing cost and recovery parameters, future work will investigate modeling the direct costs and usage of reagents like cyanide, further refining the representation of processing economics. On the other hand, this matheuristic is intended to replace the existing Dantzig–Wolfe decomposition-based implementation described by [
14], providing a more computationally efficient alternative implementation for the second stage of a formulation relating to a stochastic long-term open-pit mine planning optimization.
Finally, further investigations will explore strategies to ensure that the matheuristic consistently achieves optimal solutions. This includes integrating additional heuristics or hybrid optimization techniques to enhance solution precision while maintaining computational efficiency. The findings of this study pave the way for broader applications of heuristic-based optimization in the mining industry, offering a balance between accuracy and scalability in decision-support frameworks.