Joint Modeling of Floor Elevations and Thickness of a Bauxite Unit Considering Trend, Histogram and Variogram Uncertainty

Abstract

Laterite-type bauxite deposits typically exhibit a highly irregular boundary between the bauxite and underlying ferricrete units. This irregularity cannot be accurately modeled using data collected from sparsely spaced drillholes (e.g., $76.2\times 76.2$ m or $250\times 250$ ft). Geological models that assume a sharp and nearly horizontal bauxite/ferricrete contact can result in significant errors when calculating the in situ bauxite resource (in volume) and in misclassifying ore and waste during mining operations. Two primary sources of uncertainty must be addressed when modeling lateritic bauxite deposits: (1) grade uncertainty associated with variations in Al₂O₃ and SiO₂% concentrations, and (2) geometric uncertainty related to lateral variations in the bauxite/ferricrete contact. Among these, geometric uncertainty is more critical, as accurately estimating bauxite ore tonnage depends on the precise modeling of the lateral variation in the boundary between the bauxite and underlying ferricrete units. This study evaluates the uncertainty of the bauxite resource within a selected mine area in northern Queensland, Australia, particularly in cases where experimental data are sparse and limited. To address this, the position variable (bauxite floor elevations) and the thickness of the bauxite unit are jointly simulated under two scenarios. In the first scenario, the histograms, variogram model parameters, and the estimated trend of the variables of interest are assumed to be known with certainty; that is, parameter uncertainty is not considered in the modeling process. In the second scenario, the histograms, variogram model parameters, and the estimated trend are considered uncertain, and parameter uncertainty is explicitly incorporated into the modeling process using the multivariate spatial bootstrap procedure. The methodology is applied to both scenarios, showing that incorporating parameter uncertainty in geostatistical modeling results in greater dispersion of the uncertainty associated with the in situ bauxite resource. The results show that the $95\%$ confidence intervals for the in situ bauxite ore volume, derived from bauxite thickness realizations, vary depending on whether parameter uncertainty is considered. When parameter uncertainty is incorporated, the interval is (390,123 ${\mathrm{m}}^3$ and 393,223 ${\mathrm{m}}^3$), whereas without parameter uncertainty, it is (382,332 ${\mathrm{m}}^3$ and 384,373 m³). This comparison highlights that incorporating parameter uncertainty provides a more realistic assessment of resource risk in the modeling process.

1. Introduction

1.1. General Issues and Problem Description

Geostatistical modeling of lateritic bauxite deposits presents several challenges due to the undulating contact between the bauxite ore unit, which is rich in aluminous minerals, and the underlying ferricrete unit, which contains high silica-bearing mineral content [1]. In a typical pre-feasibility study, key variables are modeled to assess the economic viability of the deposit. These include Al₂O₃%, which determines the economic value of the bauxite ore; SiO₂%, the primary deleterious component that specifies the product type; bauxite ore thickness, which controls the estimated ore volume and tonnage; and bauxite floor elevations, which are essential for modeling the bauxite/ferricrete contact topography [2].

Of these variables, the concentrations of Al₂O₃% and SiO₂% can be accurately estimated by ordinary kriging (OK) using the equally sampled data from the sparsely spaced drillholes (e.g., $76.2\times 76.2$ m or $250\times 250$ ft) [3,4]. However, accurately estimating bauxite thickness and bauxite/ferricrete contact topography using sparse drillhole data is challenging due to the high spatial variability of these variables, even between adjacent drillholes. From a geostatistical modeling perspective, OK is a data-driven approach, that is, unless there are sufficient hard data, the bauxite/ferricrete contact topography cannot be accurately estimated due to the smoothing effect inherent to the estimator (i.e., there is not as much variability in the estimates as there is in the true values). The degree of smoothing in a kriging estimator is the kriging variance. The higher the kriging variance, the smoother the estimates [5].

A straightforward solution is in-fill drilling, which provides additional data for modeling; however, this approach can significantly increase drilling costs. Alternatively, geophysical surveying techniques, such as ground-penetrating radar, offer a cost-effective and complementary means of acquiring data for modeling the bauxite/ferricrete contact topography [1,6]. While geophysical data are not as precise as drillhole data due to the noninvasive nature of the survey and the assumptions required during data processing, their interpretability and accuracy can be enhanced by integrating geological interpretations with machine learning techniques [7].

The kriging estimates, which are locally accurate and smooth, may be appropriate for visualizing trends but inappropriate for assessing the global uncertainty associated with the bauxite thickness and bauxite/ferricrete contact topography. Additionally, the kriging errors (square root of the kriging error variance) cannot be used for resource risk assessment, as they are spatially correlated. Geostatistical simulation, on the other hand, fairly samples the uncertainty by generating a set of realizations that match the histogram and experimental variogram of the original data with statistical fluctuations. Using the set of realizations, a distribution of uncertainty in the response variable (e.g., resource volume) can be calculated [8,9,10]. The structural information used in the geostatistical simulation is a two-point statistic; however, a set of realizations of the bauxite/ferricrete contact topography can also be generated using a multiple-point statistics framework where a training image is used as structural information [11,12].

The hanging wall topography (bauxite top elevations) of the deposit is relatively flat. The values of the bauxite thickness and bauxite/ferricrete contact topography are negatively correlated; therefore, they must be jointly simulated. In addition, the bauxite/ferricrete contact topography generally exhibit a large-scale trend that needs to be considered in the simulation procedure. In the case where the experimental data are sparse and limited, the uncertainty associated with the trend, histogram, and the variogram model parameters should also be assessed and propagated to the uncertainty in the realizations. The spatial bootstrap [13], which is a traditional bootstrap [14] applied to the spatially correlated data, is used to assess the parameter uncertainty associated with the limited data. This study documents a workflow for jointly simulating the correlated thickness and bauxite floor elevations considering the parameter uncertainty.

1.2. The Weipa Bauxite Deposit

The Weipa bauxite deposit, located in northern Queensland, Australia, is a laterite-type deposit covering approximately 11,000 km², making it the world’s largest proven bauxite resource [15]. The mine, operated by Rio Tinto since 1963, plays a crucial role in global aluminium production. With an annual output exceeding 34 million tonnes, Weipa is a significant contributor to the aluminium industry. In 2023, the mine produced approximately 35.13 million tonnes of bauxite, accounting for about 8.8% of the estimated 400 million tonnes of global bauxite production and around 35% of Australia’s total output [16,17].

The deposit consists of pisolitic bauxite ore, characterized by a loose texture and a thickness ranging from zero to approximately 10 meters. The formation of the bauxite resulted from the in situ weathering (or intensive leaching) of kaolinite, quartz, and iron oxide minerals. The development of alumina-rich soil is primarily influenced by aluminous bedrock, high rainfall, effective vertical drainage, and a generally flat topography [18]. Groundwater movement plays a critical role in controlling alumina concentration and the dissolution of deleterious rock components [19]. A comprehensive review of the geology, landscape, and geochemistry of the Weipa bauxite deposit is available in [15,18,20,21].

The typical regolith profile at Weipa consists of sandy and silty topsoil, which is underlain by a fine-grained bauxite (locally termed as redsoil) unit. The redsoil unit overlies a pisolitic bauxite unit, which varies in thickness from a few meters to as much as 10 m, and this unit is underlain by a ferricrete unit [15]. The pisolitic bauxite unit, which is the main source of bauxite ore, is rich in alumina, whereas the underlying ferricrete unit has a much lower alumina content and is rich in iron and kaolin [20]. The nature of the contact between the bauxite and the underlying ferricrete units is strongly influenced by the position of the groundwater table during bauxite formation. In zones where the groundwater table fluctuated significantly throughout the weathering profile, the contact exhibits a transitional and complex spatial structure. Conversely, in areas where the groundwater table remained stable, the contact is typically more uniform and nearly horizontal [22].

2. Methodology

2.1. Geostatistical Simulation in the Presence of a Deterministic Trend

Let Z denote a variable sampled at n locations $\{z\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$ with ${\mathbf{u}}_i=[x_i,y_i]$ being a vector of orthogonal coordinates (i.e., easting and northing). Z exhibits a large-scale deterministic trend when its values tend to systematically increase or decrease with the coordinates.

As the presence of a trend violates the second-order stationary assumption (where the mean of the random function $Z\left(\mathbf{u}\right)$, $\left\{Z\right(\mathbf{u}),\mathbf{u}\in D\}$ is, on average, constant throughout the domain D, $E\left[Z\right(\mathbf{u}\left)\right]=m,\forall \mathbf{u}\in D$, and the covariance depends solely on the separation distance $\mathbf{h}$, $E[Z\left(\mathbf{u}\right)·Z(\mathbf{u}+\mathbf{h})]-m^2=\mathrm{C}\left(\mathbf{h}\right),\forall \mathbf{u},\mathbf{u}+\mathbf{h}\in D$), the normal score transformation of the data $\{z\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$ conditional to their estimated trend values at the collocated locations $\{m^{\ast }\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$ is performed using the stepwise conditional transform (SCT) [23] along with the Gaussian mixture model (GMM) [24,25]. The resulting SCT scores are modeled using a second-order stationary random function, and the back-transformation restores the large-scale deterministic trend in each realization of Z. The implementation steps of the algorithm proposed by [26] are given as follows:

i.

Define a representative empirical CDF of the variable Z, $F_Z\left(z\right)$.

ii.

Transform the samples of the variable Z into normal scores

$$y_i=G_Y^{-1}\left(F_Z\left(z_i\right)\right),i=1,\dots ,n,$$

(1)

where $G_Y^{-1}$ is the inverse CDF (quantile function) of the standard Gaussian distribution.

• Estimate the deterministic trend $m^{\ast }\left(\mathbf{u}\right)\forall \mathbf{u}\in D$ at N grid nodes using the normal scores $\{y\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$.
• Transform the estimated trend values available at N grid nodes into normal scores

  $$y_{m_i^{\ast }}=G_Y^{-1}\left(F_{m^{\ast }}\left(m_i^{\ast }\right)\right),i=1,\dots ,N,$$

  (2)

  where $F_{m^{\ast }}\left(m_i^{\ast }\right)$ is the CDF of the estimated trend values at N grid nodes.
• Fit a GMM to the bivariate distribution of the normal scores of the original data $\{y\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$ and the co-located normal scores of the estimated trend values $\{y_{m^{\ast }}\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$.
• Transform the normal scores of the original data $\{y\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$ conditional to the normal scores of the estimated trend values $\{y_{m^{\ast }}\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$ using SCT along with the GMM fitted in Step v

  $$y_i^{\prime }=G^{-1}\left(F_{Y|Y_{m^{\ast }}}\left(y_i\right|y_{m_i^{\ast }})\right),i=1,\dots ,n,$$

  (3)

  where $G^{-1}$ is the inverse CDF of the standard Gaussian distribution and $F_{Y|Y_{m^{\ast }}}\left(y_i\right|y_{m_i^{\ast }})$ denotes the CDF of the normal scores of the original data given the normal scores of the estimated trend values.
• Compute the experimental variogram of the stepwise conditionally transformed data $\{y^{\prime }\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$ and fit an analytical model to it.
• Generate simulated realizations $Y^{\prime ,l}\left(\mathbf{u}\right)\forall \mathbf{u}\in D$ with $l=1,\dots ,L$ using the conditioning data $\{y^{\prime }\left({\mathbf{u}}_i\right),i=1,\dots ,n\}$.
• Back-transform the simulated realizations by reversing SCT and normal score transform to obtain the realizations in the original data unit $Z^l\left(\mathbf{u}\right)\forall \mathbf{u}\in D$ with $l=1,\dots ,L$.

The aforementioned implementation steps of the algorithm generate L simulated realizations of a geological variable exhibiting a large-scale deterministic trend. In Step i, a representative CDF of the variable is defined, and the samples of this variable are transformed to normal scores (Step ii). In Step iii, the deterministic trend evident in the normal scored data is estimated on each grid node, and in Step iv, the estimated trend values available at N grid nodes are transformed to the normal scores. In Step v, the GMM is fitted to the bivariate distribution of the normal scores of the estimated trend values and the normal scores of the original data. In Step vi, the normal scores of the original data conditional to the normal scores of the estimated trend values are transformed using SCT, which use the fitted GMM values in the transformation procedure. In Step vii, the experimental variogram of the resulting transformed data (or SCT scores) is computed and modeled. In Step viii, a set of realizations are generated using the SCT scores as conditioning data, and in Step ix, the resulting realizations are back-transformed to the original data unit by inverting SCT and normal score transformation.

2.2. Multivariate Spatial Bootstrap

To assess the parameter uncertainty associated with K variables $\{Z_k,k=1,\dots ,K\}$ sampled at n locations, the multivariate spatial bootstrap (MVSB) procedure is used to generate the correlated bootstrap realizations (or resamples) by sampling the original data $\{z_{k,i},k=1,\dots ,K;i=1,\dots ,n\}$ with replacement [27]. The resulting M realizations $\{z_{k,i}^{\left(m\right)},k=1,\dots ,K;i=1,\dots ,n;m=1,\dots ,M\}$ have the same spatial structure as the original data and honor the existing pairwise correlation between the variables. The implementation steps of the MVSB procedure are given as follows:

• Define a representative empirical CDF of the variables, $F_Z\left(z_k\right)$, $\{Z_k,k=1,\dots ,K\}$ that are equally sampled at n locations.
• Transform the samples of each variable into corresponding normal scores:

  $$y_{k,i}=G_Y^{-1}\left(F_Z\left(z_{k,i}\right)\right),i=1,\dots ,n,$$

  (4)

  where $G_Y^{-1}$ is the inverse CDF of the standard Gaussian distribution.
• Fit a linear model of coregionalization (LMC) to the experimental direct and cross variograms of the normal scored variables $\{Y_k,k=1,\dots ,K\}$.
• Calculate the spatial data-to-data covariance matrix $\mathbf{C}$ using the variogram model from Step 3. Considering a second-order stationary assumption, the covariance and variogram functions are related:

  $$C\left(\mathbf{h}\right)=C\left(0\right)-\gamma \left(\mathbf{h}\right).$$

  (5)
• Calculate the lower and upper triangular matrices of the covariance matrix $\mathbf{C}$ using the Cholesky decomposition [28]:

  $$\mathbf{C}=\mathbf{L}{\mathbf{L}}^T,$$

  (6)

  where $\mathbf{L}$ is $(nK\times nK)$ lower triangular matrix and ${\mathbf{L}}^T$ is $(nK\times nK)$ upper triangular matrix.
• Generate $(nK\times 1)$ vector $\mathbf{w}$ of independent Gaussian deviates using Monte Carlo simulation, and impose the correlation by multiplying the lower triangle matrix $\mathbf{L}$ by $\mathbf{w}$:

  $${\mathbf{y}}^{\left(m\right)}=\mathbf{L}{\mathbf{w}}^{\left(m\right)},m=1,\dots ,M,$$

  (7)

  where $(nK\times 1)$ vector ${\mathbf{y}}^{\left(m\right)}$ is the $m^{\mathrm{th}}$ bootstrap realization with the correct correlation.
• Back-transform each bootstrap realization ${\mathbf{y}}^{\left(m\right)},m=1,\dots ,M$ to the original data unit:

  $$z_{k,i}^{\left(m\right)}=F_Z^{-1}\left(G_Y\left(y_{k,i}^{\left(m\right)}\right)\right),i=1,\dots ,n.$$

  (8)

The steps given above generate M bootstrap realizations of the K geological variables that are correlated. In Step i, a representative CDF of each variable is defined, and in Step ii, the samples of each variable are transformed to the normal scores. In Step iii, instead of an LMC fitting, the experimental direct and cross variograms of the normal scored variables are fitted by assuming intrinsic (or proportional) cross-correlation functions and the Markov model approximations [29,30]. In Step iv, the data-to-data covariance matrix is constructed using the variogram model fitted in the previous step, and in Step v, this matrix is decomposed into lower and upper triangular matrices using Cholesky decomposition. In Step vi, M correlated bootstrap realizations are generated, and in Step vii, each realization set is back-transformed to the original data unit using the global back-transformation tables generated in Step ii.

2.3. Kriging with a Trend Model

In the presence of a large-scale trend, the kriging with a trend model (KT) approach [31] is employed to estimate the unknown values of the variable Z. This estimation is achieved through a linear combination of sample values collected from $n\left(\mathbf{u}\right)$ locations within a specified neighborhood. The estimator is expressed as

$$Z_{KT}^{\ast }\left(\mathbf{u}\right)=\sum _{i=1}^{n\left(\mathbf{u}\right)}{\lambda }_i^{KT}\left(\mathbf{u}\right)Z\left({\mathbf{u}}_i\right),$$

(9)

where ${\lambda }_i^{KT}\left(\mathbf{u}\right)$ is the weight assigned to the $i^{\mathrm{th}}$ datum $Z\left({\mathbf{u}}_i\right)$ and $n\left(\mathbf{u}\right)$ is the number conditioning data used to estimate the unknown value $Z_{KT}^{\ast }\left(\mathbf{u}\right)$. In the KT approach, the mean is modeled as a linear combination of the unknown coefficients and known basis functions (i.e., monomials of the coordinates, $\mathbf{u}=[x,y]$$\forall \mathbf{u}\in D$), that is,

$$m\left(\mathbf{u}\right)=\sum _{l=0}^L{a}_l{f}_l\left(\mathbf{u}\right),$$

(10)

where $a_l$ are the coefficients to be estimated and $f_l\left(\mathbf{u}\right)$ are the basis functions, both of which are considered to be constant within each local neighborhood. Considering the case where the data (i.e., bauxite floor elevations) are defined in the two-dimensional space, the trends of order one (linear trend, $f_0\left(\mathbf{u}\right)=1$, $f_1\left(\mathbf{u}\right)=x$, $f_2\left(\mathbf{u}\right)=y$) or order two (quadratic trend, $f_0\left(\mathbf{u}\right)=1$, $f_1\left(\mathbf{u}\right)=x$, $f_2\left(\mathbf{u}\right)=y$, $f_3\left(\mathbf{u}\right)=x^2$, $f_4\left(\mathbf{u}\right)=y^2$, $f_5\left(\mathbf{u}\right)=xy$) generally suffice for a plausible model. The KT weights are calculated by the following system of equations:

$$\begin{array}{cc}\hfill & \sum _{j=1}^{n\left(\mathbf{u}\right)}{\lambda }_j^{KT}\left(\mathbf{u}\right)C({\mathbf{u}}_i-{\mathbf{u}}_j)+\sum _{l=0}^L{\mu }_l{f}_l\left({\mathbf{u}}_i\right)=C({\mathbf{u}}_i-\mathbf{u}),i=1,\dots ,n\left(\mathbf{u}\right)\hfill \\ \hfill & \sum _{j=1}^{n\left(\mathbf{u}\right)}{\lambda }_j^{KT}\left(\mathbf{u}\right)f_l\left({\mathbf{u}}_j\right)=f_l\left(\mathbf{u}\right),l=0,\dots ,L\hfill \end{array},$$

(11)

where $C({\mathbf{u}}_i-{\mathbf{u}}_j)$ are the covariance values between the residuals; $f_l\left({\mathbf{u}}_i\right)$ is the $l\mathrm{th}$ trend function; ${\mu }_l$ is the $l\mathrm{th}$ Lagrange multiplier; and $C({\mathbf{u}}_i-\mathbf{u})$ is the covariance values between the residuals and variable at the location being estimated. It can be seen from Equation (11) that for $L=0$, the KT system reverts to the OK system. The error (or estimation) variance is calculated by

$${\sigma }_{KT}^2\left(\mathbf{u}\right)=C\left(0\right)-\sum _{i=1}^{n\left(\mathbf{u}\right)}{\lambda }_i^{KT}\left(\mathbf{u}\right)C({\mathbf{u}}_i-\mathbf{u})-\sum _{l=0}^L{\mu }_l{f}_l\left(\mathbf{u}\right)=C({\mathbf{u}}_i-\mathbf{u}).$$

(12)

It can be seen from Equation (12) that considering only the first trend function ($f_0\left(\mathbf{u}\right)=1$), the error variance ${\sigma }_{KT}^2\left(\mathbf{u}\right)$ is equal to the OK estimation variance.

The general steps of the joint geostatistical modeling of the bauxite floor elevation and bauxite thickness variables are given as a flowchart in Figure 1 for clarity.

3. Case Study

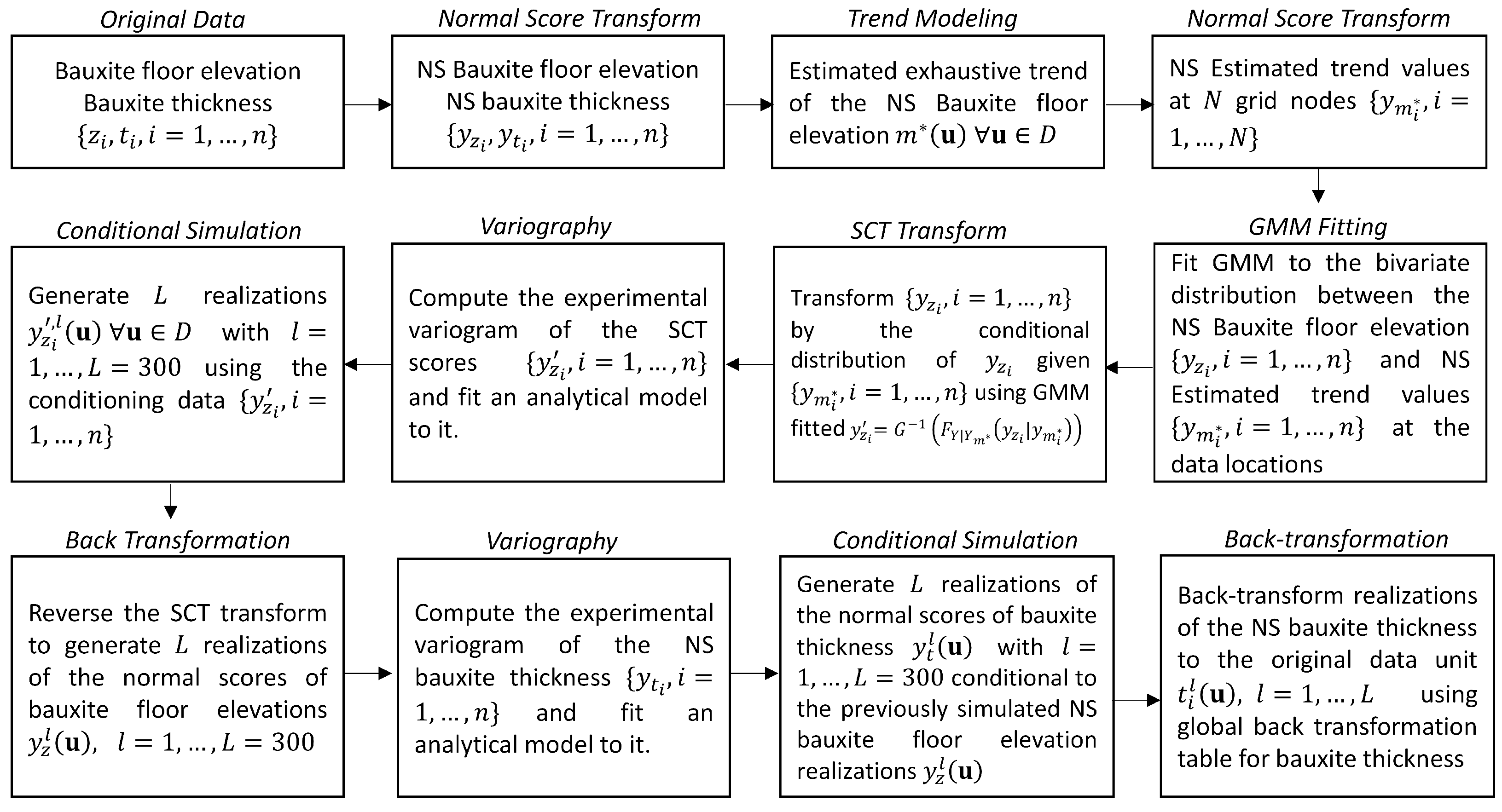
3.1. The Data

Two types of datasets are available in this study: (1) the exploration drillhole data and (2) the post-mining survey data. The provenance of these datasets is detailed in previous studies [1,10], which describe the methods used for estimating the lateral variability between the bauxite and underlying ferricrete sections, as well as the uncertainty associated with the bauxite ore volume.

The first type of dataset is from 33 vertical drillholes on a regular grid of $76.2\times 76.2$ m $(250\times 250\mathrm{ft})$ at a lateritic bauxite mine site covering an area of approximately 288,000 ${\mathrm{m}}^2$. The samples, assayed mainly for alumina (Al₂O₃%) and silica (SiO₂%) grades, were collected from each drillhole with a sampling interval of $0.25$ m. These data are used to create the bauxite ore’s thickness intercepts, which are then converted into a two-dimensional point dataset, the variables of which include bauxite floor elevation and bauxite thickness.

The second type of dataset was acquired by surveying the mine floor topography after the mining activity (i.e., extraction of the loose bauxite pisolites by a large front-end loader) was completed at the mine site. The total number of surveying points is 10,934, and the average surveying distance is approximately eight meters. The available drillhole data are used to demonstrate the methodology, while the post-mining survey data are used to compare the results. The sampling locations of both datasets are shown in Figure 2.

As it can be noticed from Figure 2a, there appears to be a systematic decrease in the values of the bauxite floor elevations along the north–west to south–east directions, indicating the presence of a large-scale trend in the data. The bauxite thickness values (Figure 2b), on the other hand, exhibit a stationary behavior throughout the mine site. The survey points (Figure 2c), which provide a high-resolution representation of the mine floor topography after mining, cover a larger area than the available drillholes. To compare the results, the polygon defining the mine site, excluding the non-surveyed areas, is used to clip the estimated and simulated models (Figure 2c).

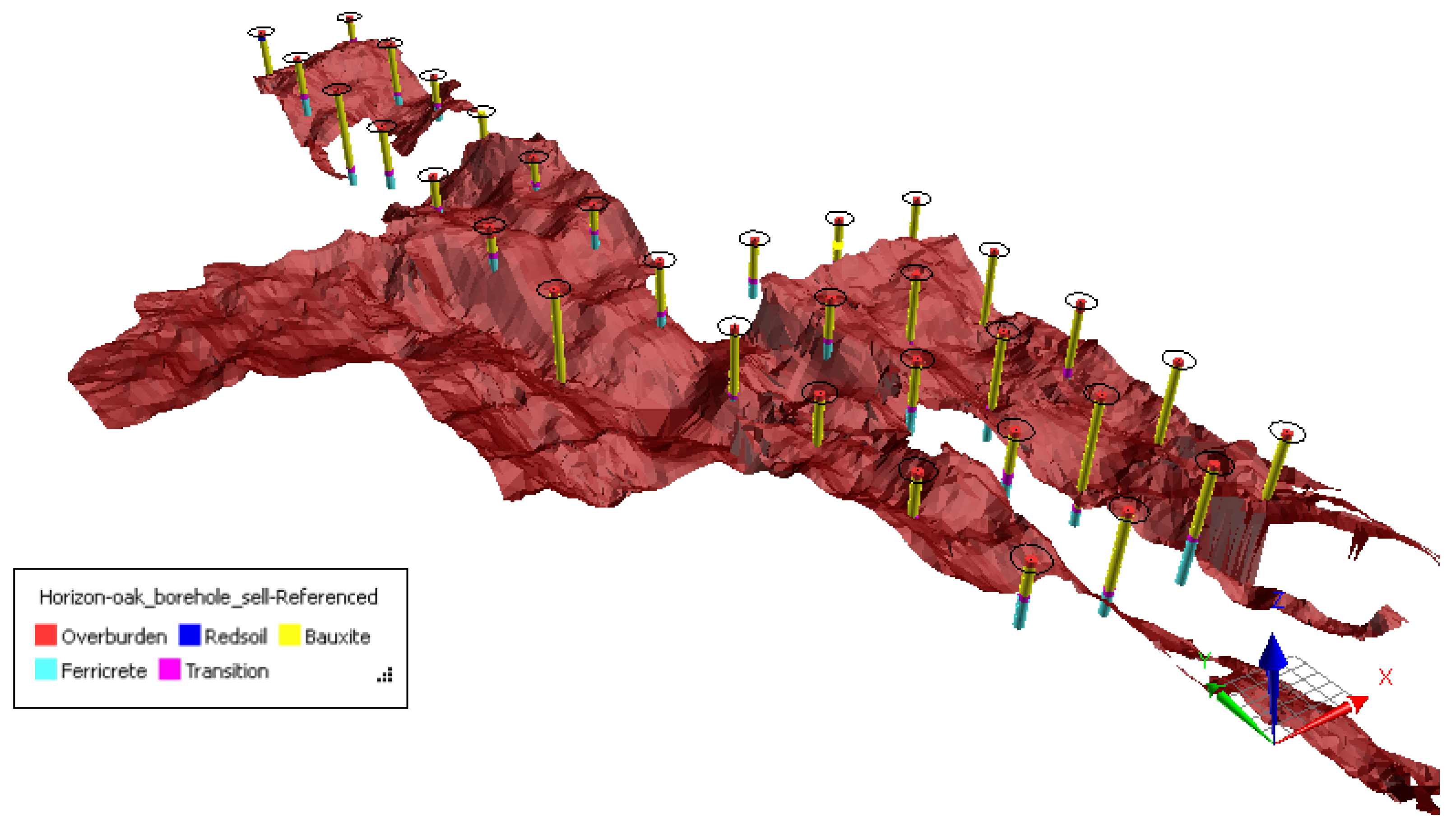
At the time of mining, the determination of the interface between the bauxite ore and underlying ferricrete (or locally known as ironstone) units is based—to a larger extent—on the experience of the front-end loader operator. In other words, there is additional uncertainty associated with the shape of the bauxite/ferricrete contact due to the operator’s skill and experience. Figure 3 presents the surface of the final mine floor topography along with the drillholes, visualized using the free software Geoscience Analyst (version: 4.5.1) provided by Mira Geoscience.

As shown in Figure 3, the final mine floor is highly irregular, characterized by random undulations. The deposit is stratified into five lithological units, including overburden, redsoil, bauxite, transition, and ferricrete. It is evident from Figure 3 that the mine floor elevations determined by the front-end loader operation do not always align with the bauxite floor elevations observed at the drillholes. Therefore, before calculating the bauxite ore volume, the final mine floor elevations must be calibrated based on the bauxite floor elevations observed at the drillholes. The histograms and summary statistics of the variables are shown in Figure 4.

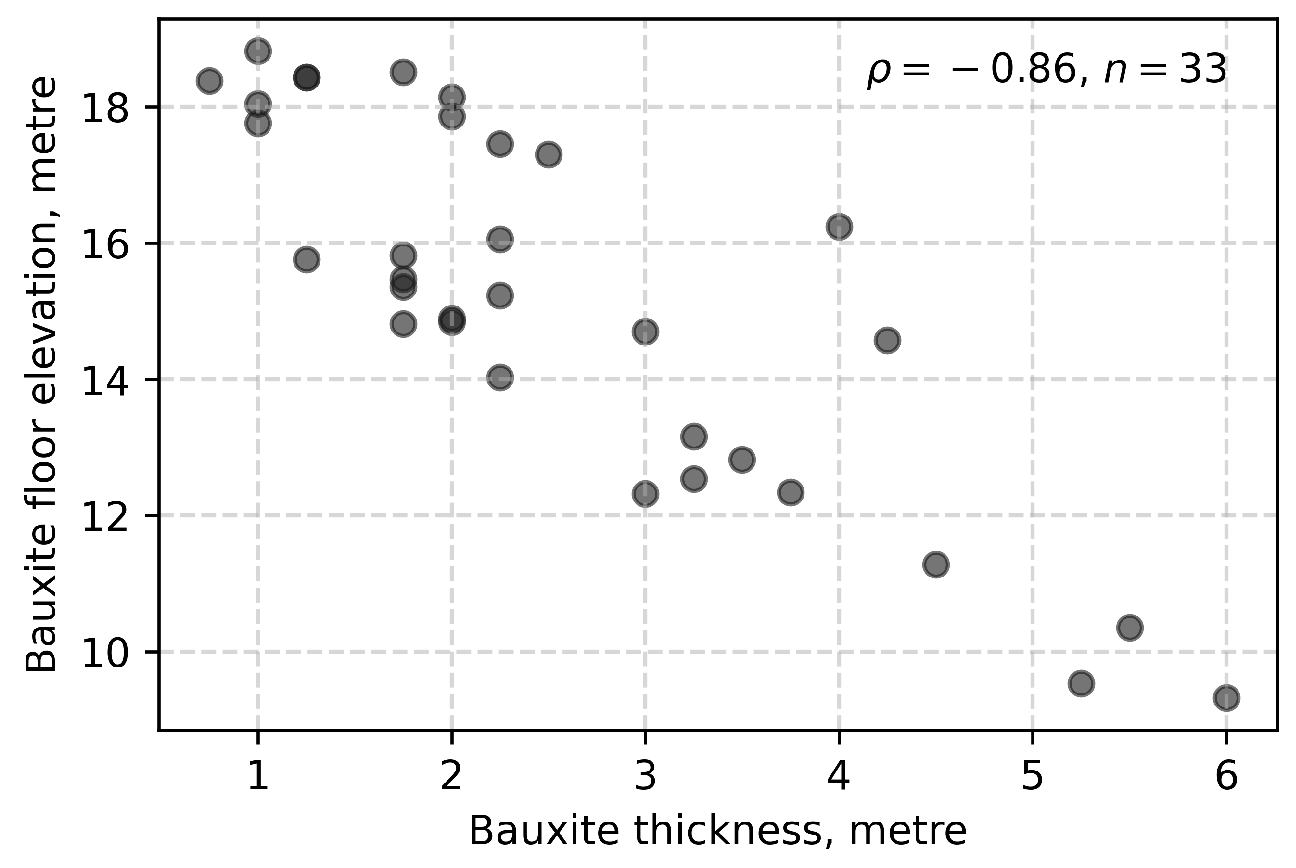
It is clear from Figure 2a,b and Figure 4a,b that bauxite ore unit tends to become thicker at the topographically low areas and is generally in the form of a thin layer at the topographically high areas, indicating a negative correlation between the values of the bauxite floor elevation and bauxite thickness variables, which is further illustrated in the crossplot presented in Figure 5.

The scatter plot shown in Figure 5 reveals a strong negative correlation between bauxite thickness and floor elevation, indicating that thicker bauxite deposits tend to occur at lower elevations.

3.2. Estimation of Bauxite Floor Elevation, Bauxite Thickness, and Mine Floor Topography

To compare the overall bauxite ore volume calculated from the estimated and simulated models against the mined (or actual) bauxite ore volume, the bauxite thickness and the bauxite floor elevations from the drillhole data and mine floor elevations from the post-mining survey data are first interpolated at each grid node $(2.38\times 2.38\mathrm{m})$ in the mine area. Due to the large-scale trend that exists in the bauxite floor elevations, the local mean cannot be assumed to be constant throughout the entire area; therefore, the KT approach (refer to Section 2.3) is used to estimate the values of the bauxite floor elevations at all grid nodes.

The trend of order one (i.e., linear trend) is selected to model the trend evident in the bauxite floor elevations. The coefficients of the trend are estimated using the maximum likelihood approach [32,33]. The estimated coefficients are as follows: ${\widehat{a}}_0=-36.79$ with $\mathrm{SE}=3.90$ m, ${\widehat{a}}_1=-0.0082$ with $\mathrm{SE}=0.0007$ m, and ${\widehat{a}}_2=0.0038$ with $\mathrm{SE}=0.0004$ m, where SE denotes the standard error. The aforementioned coefficients are, in fact, not used in the KT system, but they are still needed to calculate the residuals. The parameters of the standardized variogram model fitted to the experimental omni-directional variogram of the residuals, ${\gamma }_R\left(\mathbf{h}\right)$, are given by

$${\gamma }_R\left(\mathbf{h}\right)=1.0·\mathrm{Sph}(\mathbf{h};180\mathrm{m}).$$

(13)

The values of the bauxite floor elevations are then estimated at all grid nodes by KT using the variogram model given in Equation (13).

The bauxite thickness values are estimated at all grid nodes by OK using the standardized spherical variogram model fitted to the experimental omni-directional variogram of the bauxite thickness values:

$$\gamma \left(\mathbf{h}\right)=1.0·\mathrm{Sph}(\mathbf{h};220\mathrm{m}).$$

(14)

Considering the abundant post-mining survey data, the mine floor elevations are interpolated at all grid nodes using the inverse distance squared weighting algorithm. Figure 6 shows the estimation maps of the bauxite floor elevations, bauxite thickness, and the mine floor elevations, which are clipped to the polygon created.

To compare the mined and estimated bauxite ore volumes, the estimates of the bauxite top elevations $Z_{BTop}^{\ast }\left(\mathbf{u}\right)=Z_{BTh}^{\ast }\left(\mathbf{u}\right)+Z_{BFl}^{\ast }\left(\mathbf{u}\right)$ are calculated by adding the estimates of the bauxite thickness $Z_{BTh}^{\ast }\left(\mathbf{u}\right)$ to the estimates of the bauxite floor elevation $Z_{BFl}^{\ast }\left(\mathbf{u}\right)$. The estimates of the mined bauxite thickness $Z_{MBTh}^{\ast }\left(\mathbf{u}\right)$ are then calculated by subtracting the estimates of the bauxite top elevations $Z_{BTop}^{\ast }\left(\mathbf{u}\right)$ from the estimates of the mine floor elevations $Z_{MBFl}^{\ast }\left(\mathbf{u}\right)$ (Figure 6c). It is noted that the estimates of the mine floor elevations are calibrated according to the bauxite floor elevations at the drillholes and that any negative values of the mined bauxite thickness variable is set to zero before calculating the in situ bauxite ore volume.

The bauxite resource calculated from the estimates of the bauxite thickness (Figure 6b) and from the estimates of the mined bauxite thickness are 395,649 ${\mathrm{m}}^3$ and 418,432 ${\mathrm{m}}^3$, respectively. The uncertainty associated with the estimated bauxite thickness model (Figure 6b) cannot be evaluated by the kriging error, as the kriging errors are spatially correlated and cannot be used jointly for the entire mine area. For example, kriging error at one location is related to errors at neighboring locations due to spatial dependence in the data; as a result, these errors cannot be used jointly to characterize uncertainty across the entire domain. Geostatistical simulation is therefore used for assessing the uncertainty associated with the bauxite thickness and bauxite floor elevation variables first by assuming that the trend, histograms, and variogram model parameters are known with certainty and then assuming that the trend, histograms, and variogram model parameters are uncertain.

3.3. Simulation of Bauxite Floor Elevation and Bauxite Thickness Without Parameter Uncertainty

In this case, the joint simulation of the bauxite floor elevation and bauxite thickness variables is carried out, assuming that the large-scale trend evident in the bauxite floor elevations, histograms, and variogram model parameters of both variables are known with certainty.

As the drillholes are on a regular grid, declustering is not considered before the transformation of the bauxite floor elevation and bauxite thickness values into the corresponding normal scores. The normal scores of the bauxite floor elevation are used to estimate the trend, indicating only the large-scale variability of the data in the mine area, that is, the trend model should not under- or over-fit the data. The estimated trend values at all grid nodes are then transformed to the normal scores, and the values retained at the data locations are plotted against the normal scores of the bauxite floor elevation, as shown in Figure 7a.

It can be seen from Figure 7a that the normal scores of the estimated trend values are highly correlated $(\rho =0.93)$ with the normal scores of the bauxite floor elevation. The high correlation is explained by the fact that the bauxite floor elevation variable represents position values which are expected to be continuous and closer to the ones estimated by the trend modeling. Because the shape of the crossplot, shown in Figure 7a, does not exhibit any complexity, a GMM with one component, essentially a single Gaussian distribution, is used to fit the bivariate distribution. A 2D probability density plot representing this bivariate distribution is shown in Figure 7a. The normal scores of the bauxite floor elevation variable are then transformed by the conditional distribution of the normal scores of the bauxite floor elevation given the normal scores of the estimated trend values. The resulting transformed values (or SCT scores) do not show any correlation with the normal scores of the estimated trend values, as shown in Figure 7b. It is worth mentioning that in SCT, the order of the variables is important to avoid possible mismatch between the variograms of the simulated realizations and variogram model fitted to the original data. Ref. [23] suggests that the more continuous variable be selected as the primary variable to minimize the aforementioned mismatch. In this case, the primary variable is represented by the normal scores of the estimated trend values (as this variable is more continuous), and the secondary variable is represented by the normal scores of the bauxite floor elevation variable. The experimental omni-directional variogram of the SCT scores ${\gamma }_{SCT}\left(\mathbf{h}\right)$ is then computed and modeled by a standardized spherical (Sph) structure:

$${\gamma }_{SCT}\left(\mathbf{h}\right)=1.0·\mathrm{Sph}(\mathbf{h};103\mathrm{m}).$$

(15)

The variogram model given in Equation (15) is used as structural information in the turning bands’ simulation algorithm [34,35], which generates unconditionally simulated 300 realizations of the SCT scores on the point support at a grid of $2.38\times 2.38$ m. The number of turning bands used in the simulation is set to 1000, and the number of simulated points in the domain of the mine area is 25,452. The resulting realizations are conditioned, as a separate step, using simple kriging (SK) [36].

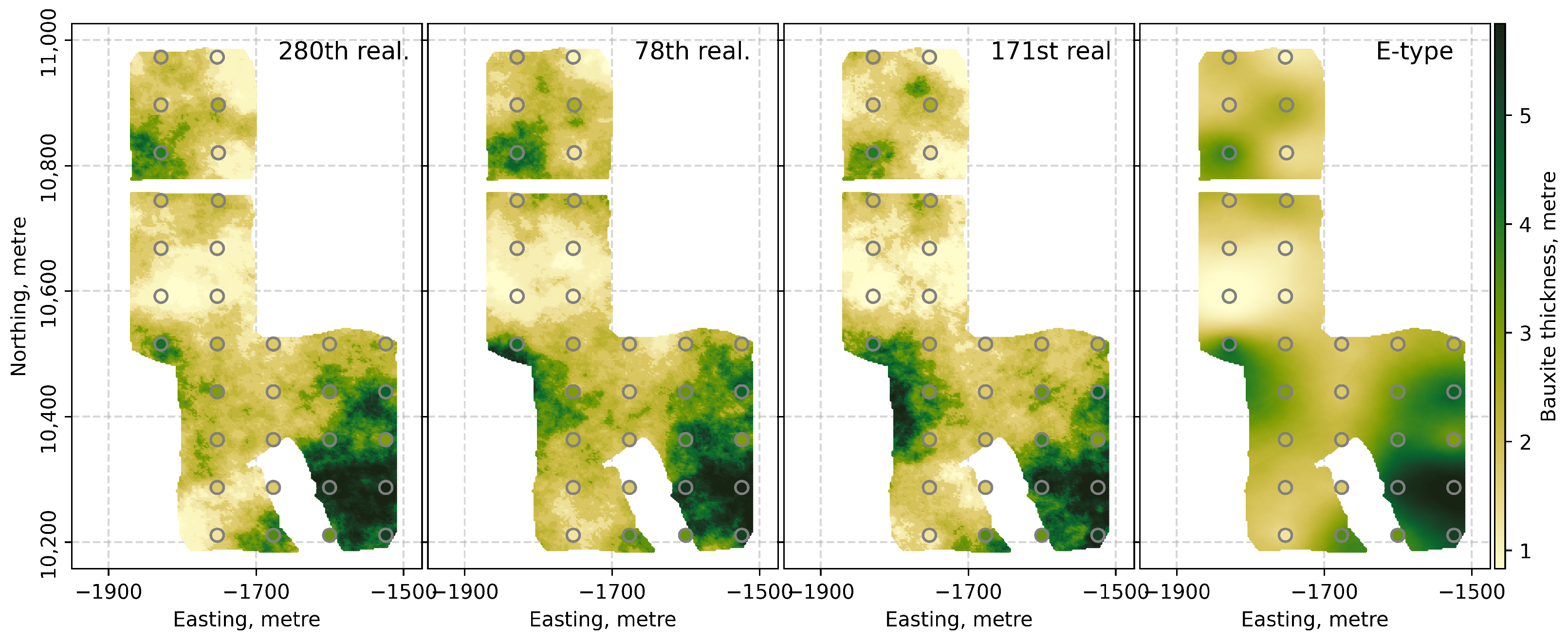
The back-transformation of the realizations is carried out in the reverse order of the forward transformation, that is, the realizations of the SCT scores are first back-transformed to the realizations of the normal scores of the bauxite floor elevations, and these realizations are then back-transformed to the realizations in the original data unit using the global back-transformation table for the bauxite floor elevations. The randomly selected three realizations of the bauxite floor elevation variable and the E-type model of the bauxite floor elevation variable, calculated by averaging the realizations of the bauxite floor elevation variable in a node-by-node basis, are shown in Figure 8.

It is clear from Figure 8 that the large-scale trend evident in the bauxite floor elevations is restored in each realization and that the co-located simulated values honor the original data superimposed on the realizations. It is also clear from Figure 8 that the trend along the north–west to south–east directions in the original data is restored in the E-type model as well.

The realizations of the bauxite floor elevation variable in the Gaussian unit are then inputted, as exhaustive secondary information, in the turning bands’ simulation algorithm to generate unconditionally simulated 300 realizations of the normal scores of the bauxite thickness variable (refer to Figure 1 for the implementation steps of the methodology). The structural input required for the simulation is the variogram model fitted to the experimental omni-directional variogram of the normal scores of the bauxite thickness:

$$\gamma \left(\mathbf{h}\right)=1.0·\mathrm{Sph}(\mathbf{h};219.8\mathrm{m}).$$

(16)

The conditioning of the realizations is achieved by the simple intrinsic co-located cokriging (SICCK) approach [37], where the values of the previously simulated normal scores of the bauxite floor elevation are retained both at the bauxite thickness data locations and at the grid node to be simulated in each local neighborhood. Considering a Markov assumption of conditional independence, i.e., Markov model 1 [29], the implementation requirements of the SICCK approach are the variogram model given in Equation (16) and the correlation coefficient $(\rho =-0.83)$, indicating the strength of the linear relationship between the co-located normal scores of the bauxite thickness and normal scores of the bauxite floor elevation variables. The resulting realizations of the normal scores of the bauxite thickness are then back-transformed to the realizations in the original data unit using the global back-transformation table for the bauxite thickness variable.

The plausibility of the resulting realizations is validated by comparing their CDFs and variograms with the empirical CDF and the experimental variogram of the bauxite thickness variable, as illustrated in Figure 9.

It is clear from Figure 9 that the realizations satisfactorily reproduce the empirical CDF and experimental variogram of the bauxite thickness variable, and that considering the crossplot (Figure 9c) between the randomly selected realizations of the bauxite thickness and bauxite floor elevation variables, the original bivariate statistic ($\rho =-0.86$) is also reproduced well. The kernel density estimate overlaid on the crossplot in Figure 9c highlights variations in the values of the bauxite thickness and bauxite floor elevation realizations that are randomly selected. The darker regions indicate higher-density areas, suggesting that the pairwise realization values are more concentrated where thickness is relatively low and elevation is high. It is, however, noted that the banding effect is visible in the crossplot given in Figure 9c, which is the result of back-transforming the values using insufficient data for robust inference of all conditional distributions. The randomly selected three realizations of the bauxite thickness variable and the E-type model are shown in Figure 10.

It can be seen from Figure 10 that the simulated bauxite thickness values honor the original bauxite thickness data at the co-located locations. The total bauxite resource from the E-type model (or expected resource) shown in Figure 10 is calculated to be 383,352 m³.

3.4. Simulation of Bauxite Floor Elevation and Bauxite Thickness with Parameter Uncertainty

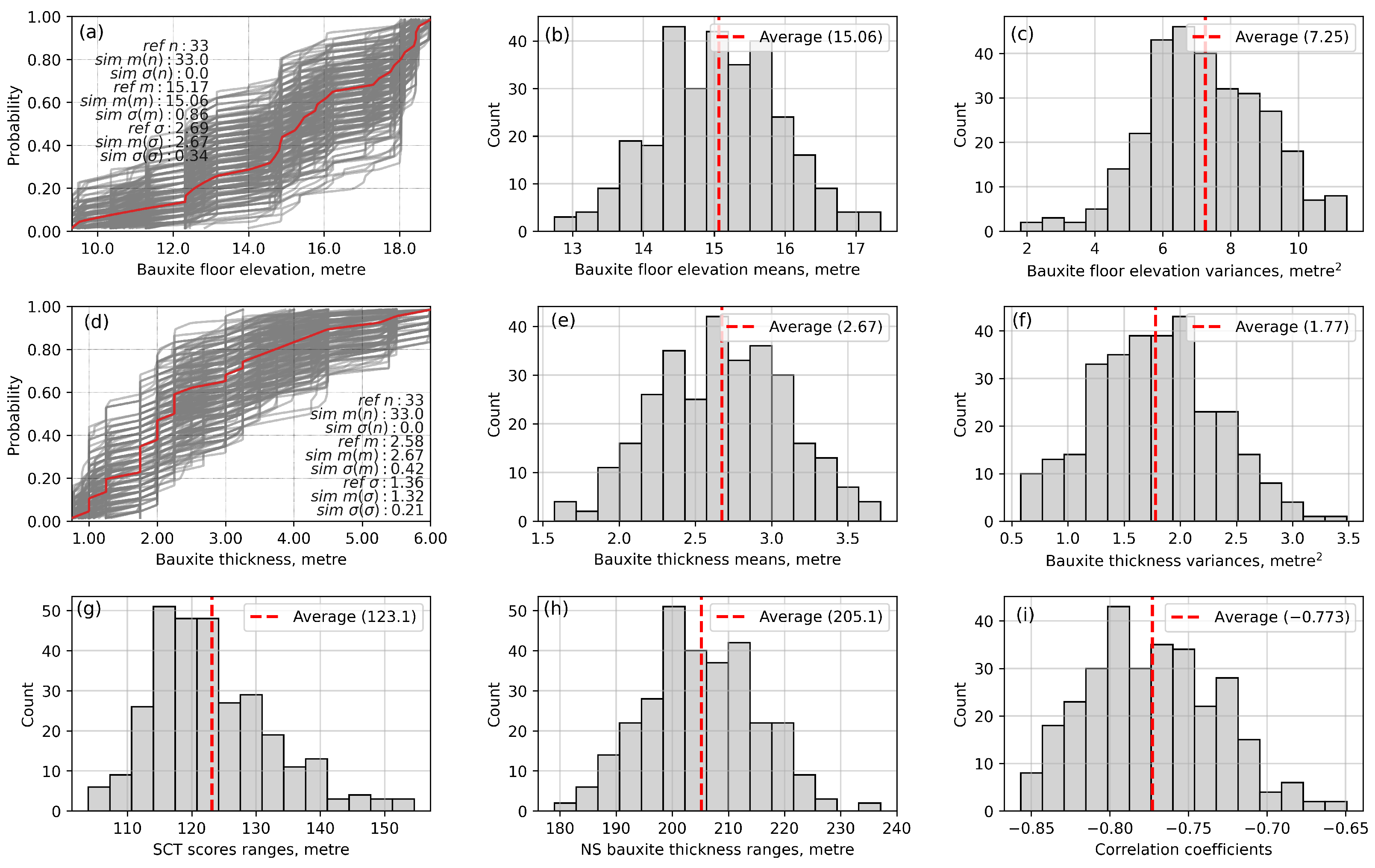
In this case, before the joint modeling of the bauxite floor elevation and bauxite thickness variables, the parameter uncertainty is assessed by the MVSB procedure, the steps of which are given in Section 2.2. Figure 11a,d show the CDFs of the 300 correlated bootstrap realizations of the bauxite floor elevation and bauxite thickness variables.

It can be seen from Figure 11a,d that the bootstrap realizations, which indicate the prior uncertainty, are closely mimicking the empirical CDFs (shown in red color) of the original data variables. The 95% confidence intervals for the true means of the bauxite floor elevations and bauxite thickness are $[13.42,16.75]$ m and $[1.90,3.45]$ m, respectively, and for the true variances of the bauxite floor elevations and bauxite thickness are $[3.85,10.76]$${\mathrm{m}}^2$ and $[0.74,2.87]$${\mathrm{m}}^2$, respectively (Figure 11b,c,e,f). The means and medians $(m,M)$ of the bootstrap distributions of the bauxite floor elevation and bauxite thickness are $(15.06,15.08)$ m and $(2.67,2.66)$ m, respectively. The similarity between the aforementioned means and medians indicates that the bootstrap distributions are symmetrical. The correlation coefficient between the original bauxite floor elevation and bauxite thickness values is $\rho =-0.86$, while the mean of the correlation coefficients calculated from each set of the bootstrap realizations of the bauxite floor elevation and bauxite thickness is $\overline{\rho }=-0.84$. Therefore, the bootstrap realizations are considered plausible.

To propagate the prior uncertainty assessed by the MVSB procedure into the uncertainty in the simulated realizations, the original values of the bauxite floor elevation and bauxite thickness variables are first transformed into the corresponding normal scores by considering each set of the bootstrap realizations of these variables as reference distributions. This procedure generates 300 unique back-transformation tables for each variable that need to be used in the correct order when each simulated realization is back-transformed to the original data unit. As explained in Section 2.1 and shown in Figure 1, a large-scale trend is estimated from each set of the normal scores of the bauxite floor elevations, and the resulting estimated trend values are transformed into normal scores. 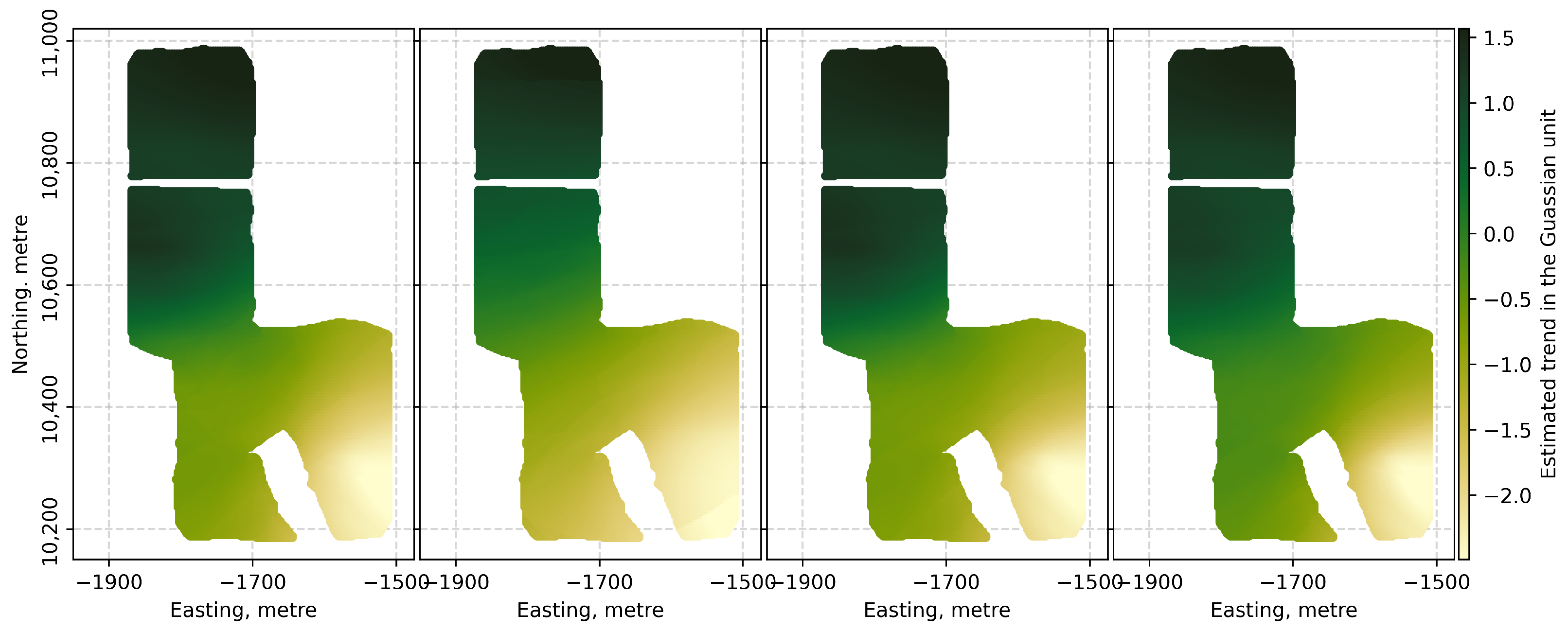Figure 12 shows the randomly selected four normal scores of the estimated trend models.

It can be noticed from Figure 12 that the estimated large-scale trends differ slightly. This is because each set of normal scores of the bauxite floor elevation is generated by using a different reference distribution (i.e., a CDF of a bootstrap realization) in the normal score transformation procedure. For each trend model estimated, a 2D probability density representing the bivariate distribution between the pairwise normal scores of the estimated trend values and the normal scores of the bauxite floor elevations is fitted by a GMM, which uses a single Gaussian distribution. The normal scores of the bauxite floor elevations are then transformed conditional to the normal scores of the estimated trend values by SCT using the fitted GMM values.

Experimental omni-directional variogram of each set of the SCT scores is computed and modeled using a standardized spherical structure. It is noted that no nugget variance is considered, and the only variogram model parameter that varies among the sets of the models fitted is the range (Figure 11g). Each set of the SCT scores is unconditionally simulated by the turning bands’ simulation approach using the corresponding variogram model. After conditioning of the realizations using SK, each realization is back-transformed by reversing the SCT and normal score transformation. However, it is worth mentioning that unlike the first case (i.e., without considering the parameter uncertainty) where only the global back-transformation table is used to back-transform all of the simulated realizations, a unique back-transformation table is used for the values of each realization to be back-transformed to the original data unit. Figure 13 shows the randomly selected three realizations of the bauxite floor elevation variable in the original data unit and the E-type model of the bauxite floor elevation variable calculated from 300 realizations.

It can be seen from Figure 13 that the large-scale trend evident in the bauxite floor elevations is restored in each realization and in the resulting E-type model.

Each set of the normal scores of the bauxite thickness variable is then simulated conditional to the previously simulated realizations of the normal scores of the bauxite floor elevation variable by the turning bands’ simulation approach (refer to Figure 1 for the implementation steps of the methodology). Each realization is conditioned using ICCK by considering the Markov assumption of conditional independence. The inputs required for the simulation and conditioning are the correlation coefficients between each set of the normal scores of the bauxite thickness and bauxite floor elevation variables (Figure 11i) and the standardized spherical variogram models fitted to the experimental omni-directional variograms of each set of the normal scores of the bauxite thickness. The nugget variance is not considered in any of the variogram models fitted, and the only model parameter that varies is the range (Figure 11h).

The resulting realizations are back-transformed to the realizations in the original data unit using the unique back-transformation tables in the correct order. The reproductions of the first- and second-order moments are checked by superimposing the CDF and variogram of each realization of the bauxite thickness variable on the empirical CDF and experimental variogram of the bauxite thickness data, as shown in Figure 14.

It can be seen from Figure 14 that both first- and second-order moments (mean and experimental variogram) of the original data are reproduced satisfactorily by the simulated realizations of the bauxite thickness variable. A randomly selected realization of the bauxite floor elevation and bauxite thickness variables indicates that the bivariate statistic between the original data variables is also reproduced well. As in the crossplot given in the first scenario, a banding effect is visible in the crossplot given in Figure 14c. 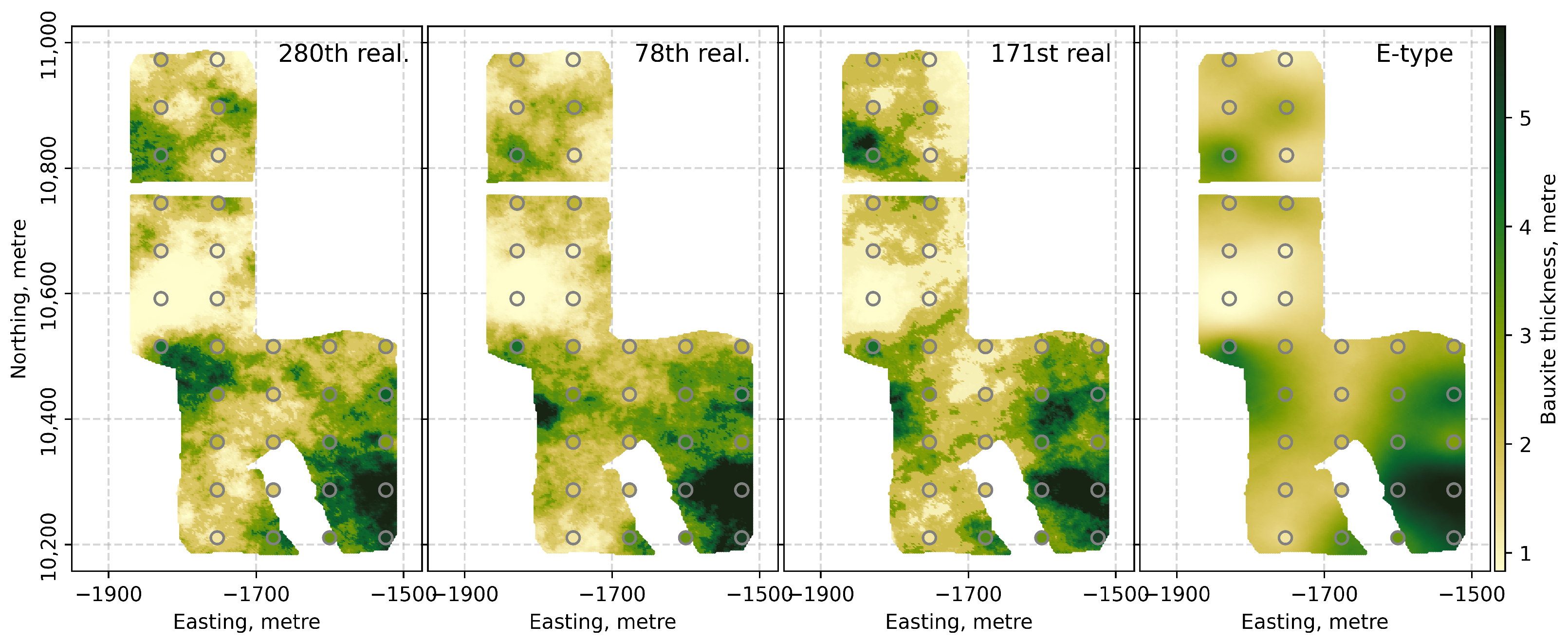Figure 15 shows the randomly selected three realizations of the bauxite thickness variable in the original data unit and the resulting E-type model.

It is clear from Figure 15 that the original bauxite thickness data are honored at the co-located locations in each realization. The total bauxite resource calculated from the E-type model is 391,673 m³.

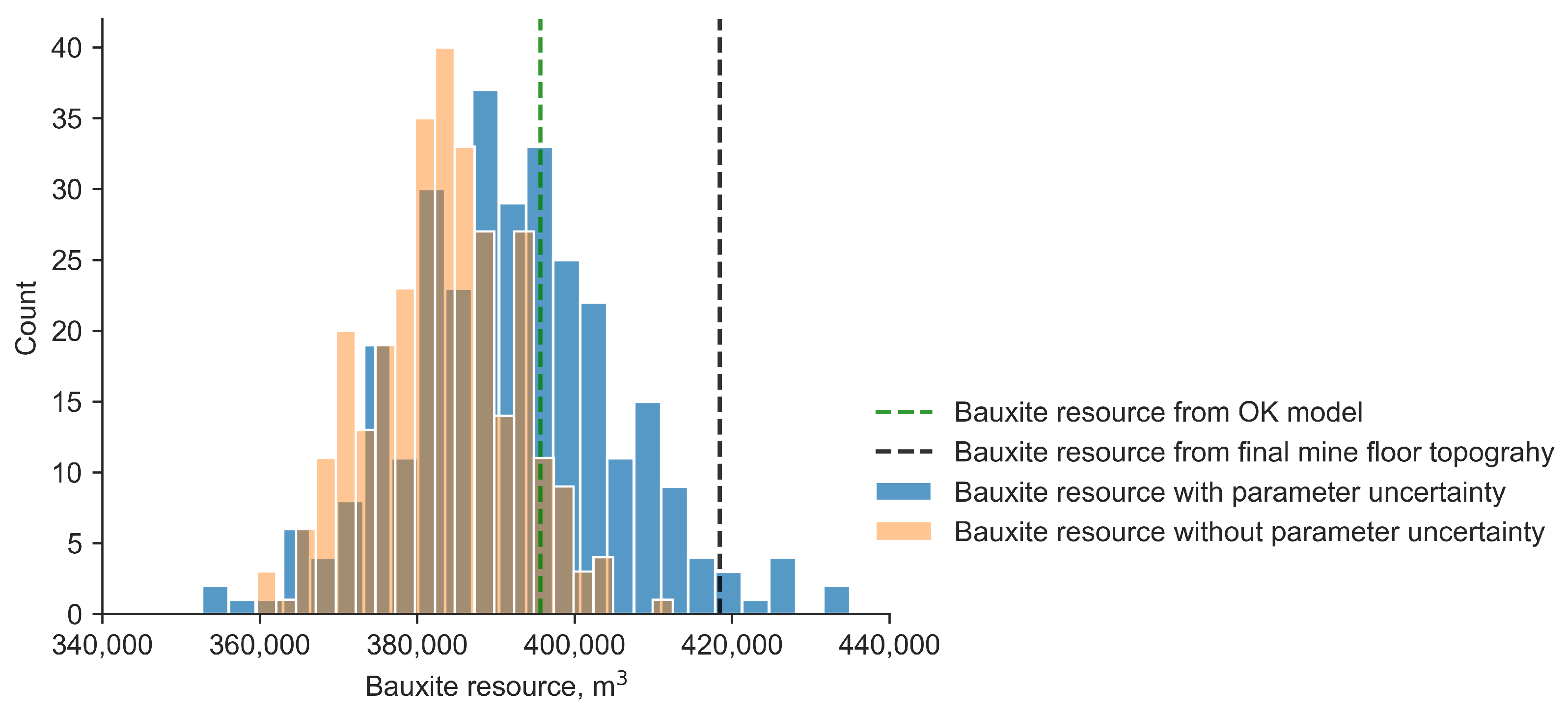
To assess the uncertainty associated with the in situ bauxite resource (in volume) within the selected mine area, the ore volume is calculated from each realization generated for both scenarios. In other words, the uncertainty in the bauxite thickness variable is transferred to the resource uncertainty (i.e., a response variable of uncertainty). The histogram in Figure 16 illustrates the distributions of the bauxite ore volume calculated from the resulting bauxite thickness realizations without and with parameter uncertainty (Figure 10 and Figure 15).

The incorporation of the parameter uncertainty (blue bars) results in more dispersed distribution of the bauxite ore volumes compared to the distribution without parameter uncertainty (orange bars). The $95\%$ confidence intervals for the in situ bauxite ore volume calculated from the bauxite thickness realizations with and without parameter uncertainty are (390,123 ${\mathrm{m}}^3$ and 393,223 ${\mathrm{m}}^3$) and (382,332 ${\mathrm{m}}^3$ and 384,373 m³), respectively. When incorporating the parameter uncertainty into the geological modeling process, the $95\%$ confidence interval for the total bauxite resource is slightly wider than the same interval calculated in the case where no parameter uncertainty is considered.

The mean values of two distributions, which are approximately the midpoints of the confidence intervals under the assumption that the distributions are symmetric, are close but appear to be slightly less than the bauxite ore volume (395,649 m³, green dashed line) calculated from the OK model (Figure 6b). This difference can be explained by the fact that the average behavior of the bauxite thickness realizations is slightly different from that of the kriged model, although the realizations of the bauxite thickness variable locally average to the model generated by OK (E-type model). Although there is not much difference in the mean resource for the two distributions, each distribution indicates different in situ bauxite ore volumes above the selected resource volume. For example, the probability that the total bauxite resource is greater than 390,000 m³ is 0.226 when the parameter uncertainty is not incorporated and 0.543 when the parameter uncertainty is considered in the modeling process.

It is also clear from Figure 16 that the distribution of the calculated bauxite ore volumes considering parameter uncertainty tends to include the bauxite resource calculated from the final mine floor topography (black dashed line, 418,432 m³). The high value of the bauxite resource calculated from the final mine floor topography is due to the operational factors (e.g., dilution and ore loss occurring during the mining activity) that are not reflected in the simulated realizations. However, there is no smoothing in the realizations, and when the parameter uncertainty is propagated to the geological uncertainty through geostatistical simulation, the fluctuations among the realizations increase even more, which may reflect the uncertainty occurring due to the operational factors at the time of mining.

4. Discussion and Conclusions

In laterite-type bauxite deposits, the lateral variability of bauxite/ferricrete contact (i.e., bauxite floor elevations) typically exceeds the variability of the ore grade (i.e., Al₂O₃%). When utilizing a conventional drilling grid (e.g., $76.2\times 76.2$ m), accurately delineating the undulating interface between the bauxite and underlying ferricrete units is challenging due to the sparsity of drillhole data. Kriging, a probabilistic approach incorporating spatial variability through a variogram model, generates locally accurate estimates. However, due to the smoothing effect as a consequence of the minimization of error variance, the estimates result in a surface representing an oversimplified interface between the bauxite and underlying ferricrete units. Additionally, the kriging errors are spatially correlated, which makes them unsuitable for quantifying global uncertainty in these estimates. Geostatistical simulation, on the other hand, provides a robust alternative to assess the global uncertainty by generating multiple realizations of the variable of interest using the variogram model fitted to the experimental variogram computed from the available data. However, in the case where the experimental data are limited, the estimated trend, histogram, and the variogram model parameters are also uncertain. Therefore, for the realistic assessment of global uncertainty, the parameter uncertainty should be propagated to the geological uncertainty assessed by the realizations.

In this study, a geostatistical workflow for assessing the uncertainty associated with the in situ bauxite resource at a selected mine area is documented. Given the fact that the available drillhole data are sparse and limited, two scenarios are considered. In the first scenario, the correlated bauxite floor elevation and bauxite thickness variables are jointly simulated by assuming that there is no uncertainty associated with the estimated trend, histogram, and variogram model parameters of the variables of interest. In the second scenario, the aforementioned variables are jointly simulated by taking into account the parameter uncertainty. The results indicate that incorporating parameter uncertainty into the modeling process leads to a more realistic assessment of resource in a lateritic bauxite mine area.