The Joint Bayesian Inversion of CSAMT and DC Data for the Jinba Gold Mine in Xinjiang Using Physical Property Priors
Abstract
1. Introduction
2. Bayesian Inversion for CSAMT and DC
2.1. Controlled-Source Audio-Frequency Magnetotelluric (CSAMT) Forward Modeling
2.2. Direct Current (DC) Forward Modeling
2.3. Bayesian Inversion
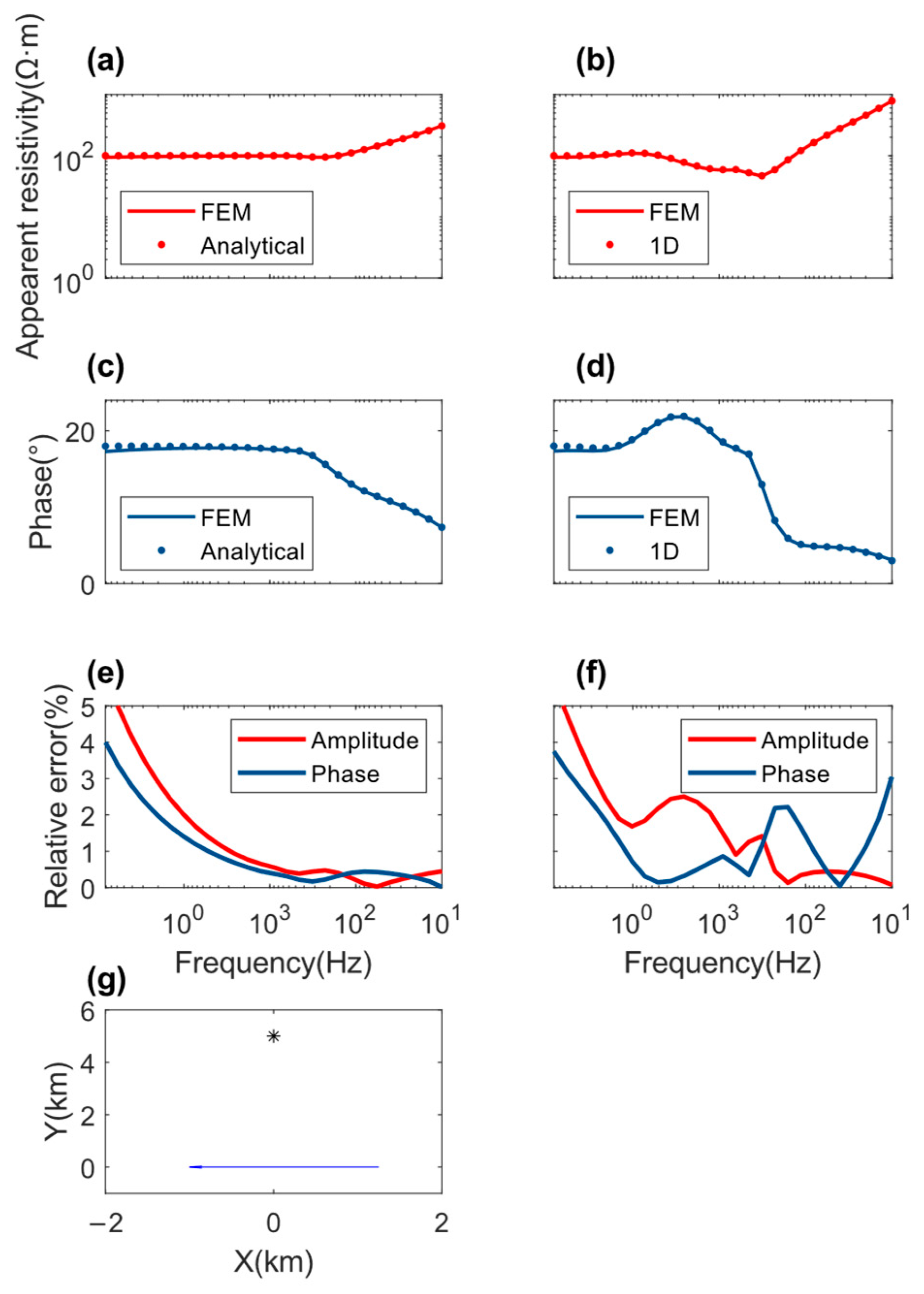
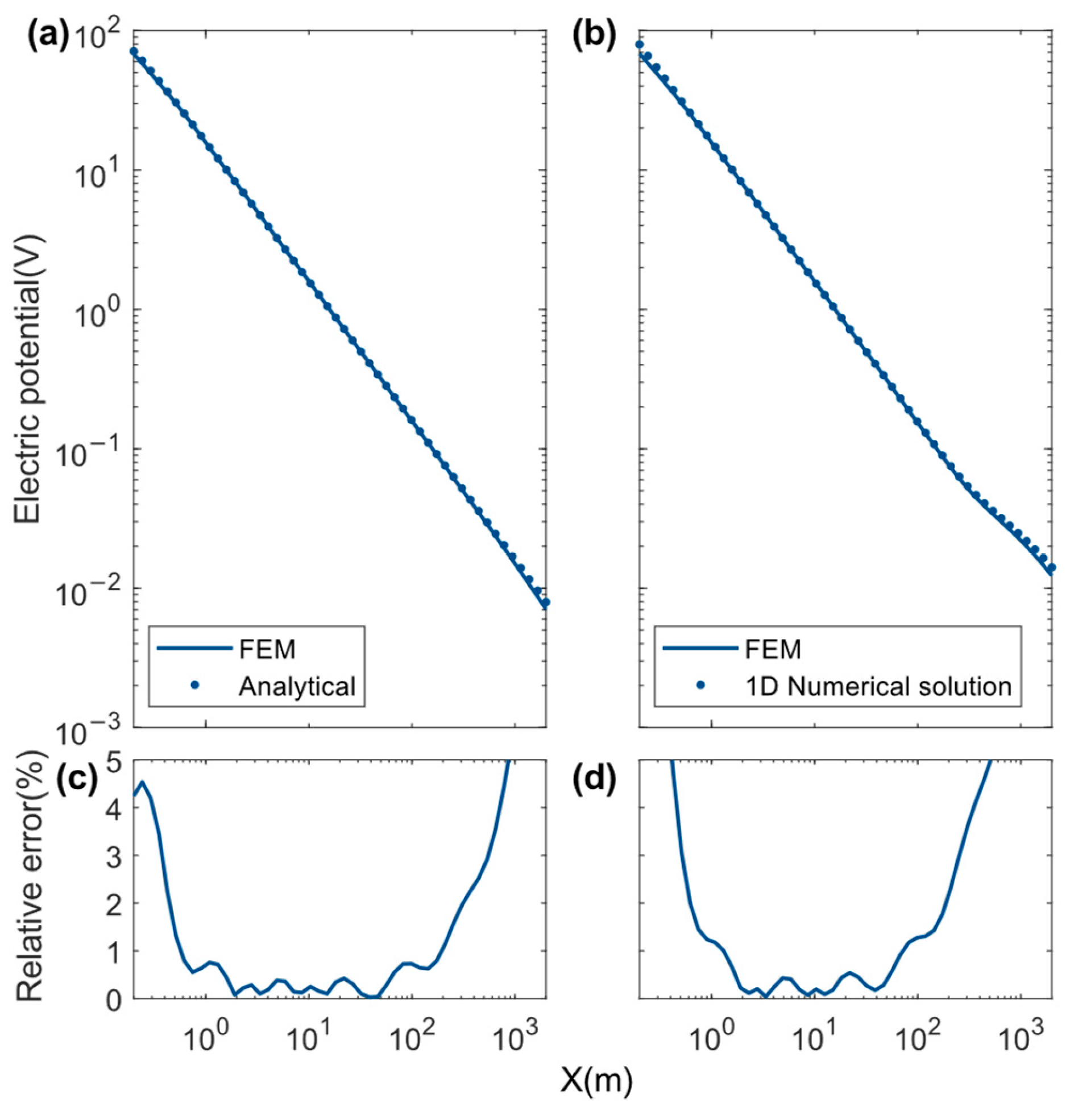
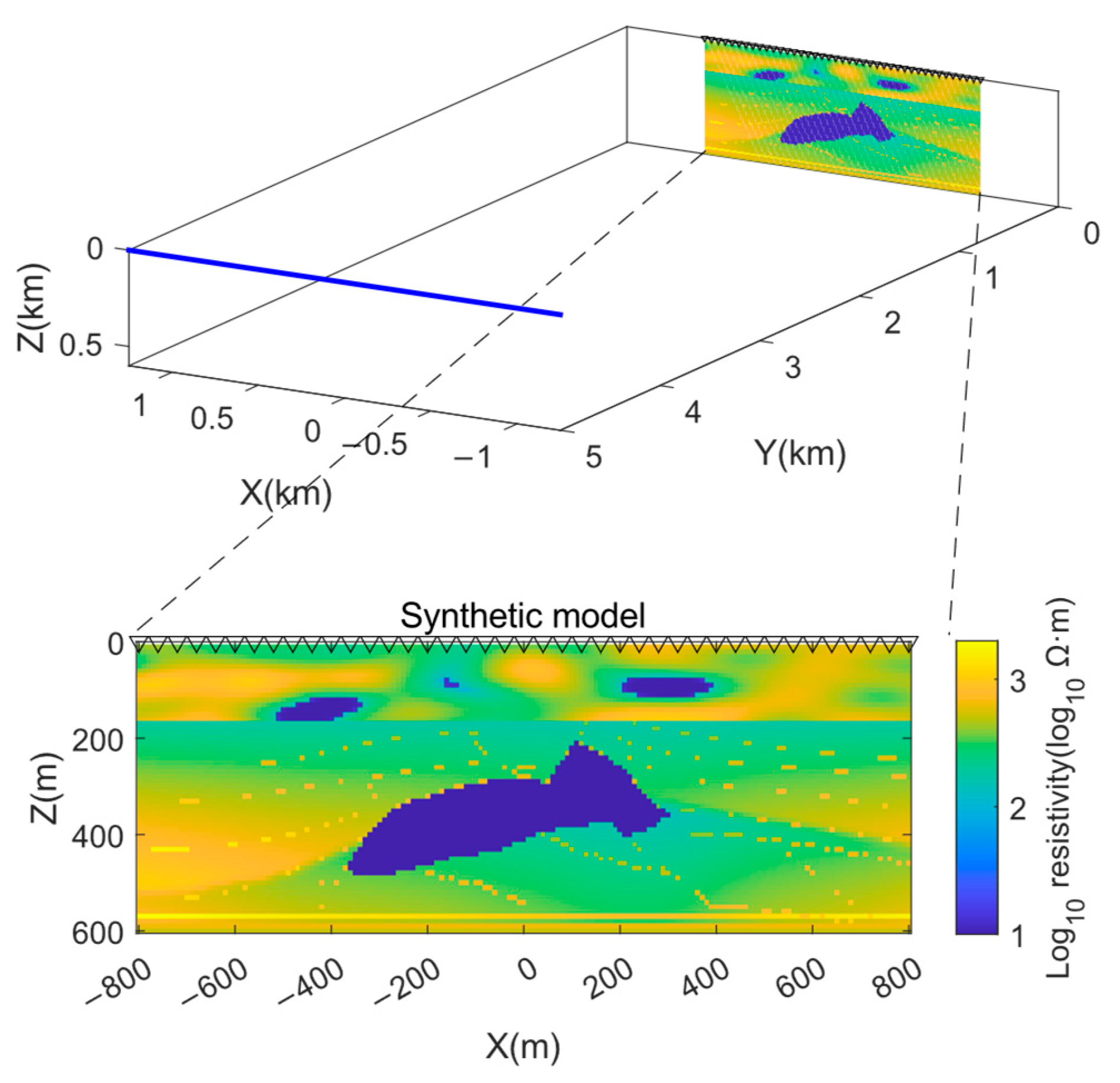
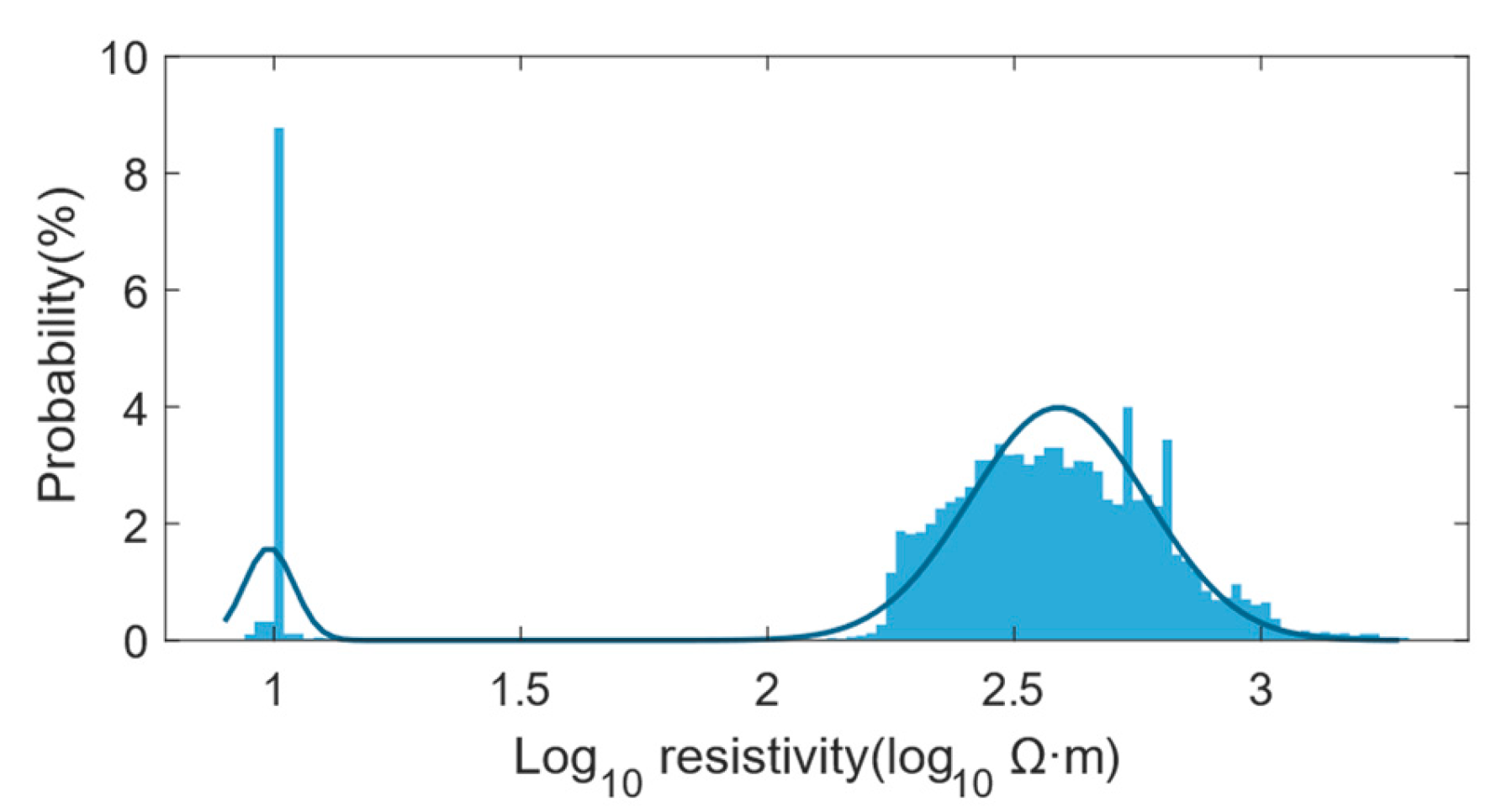
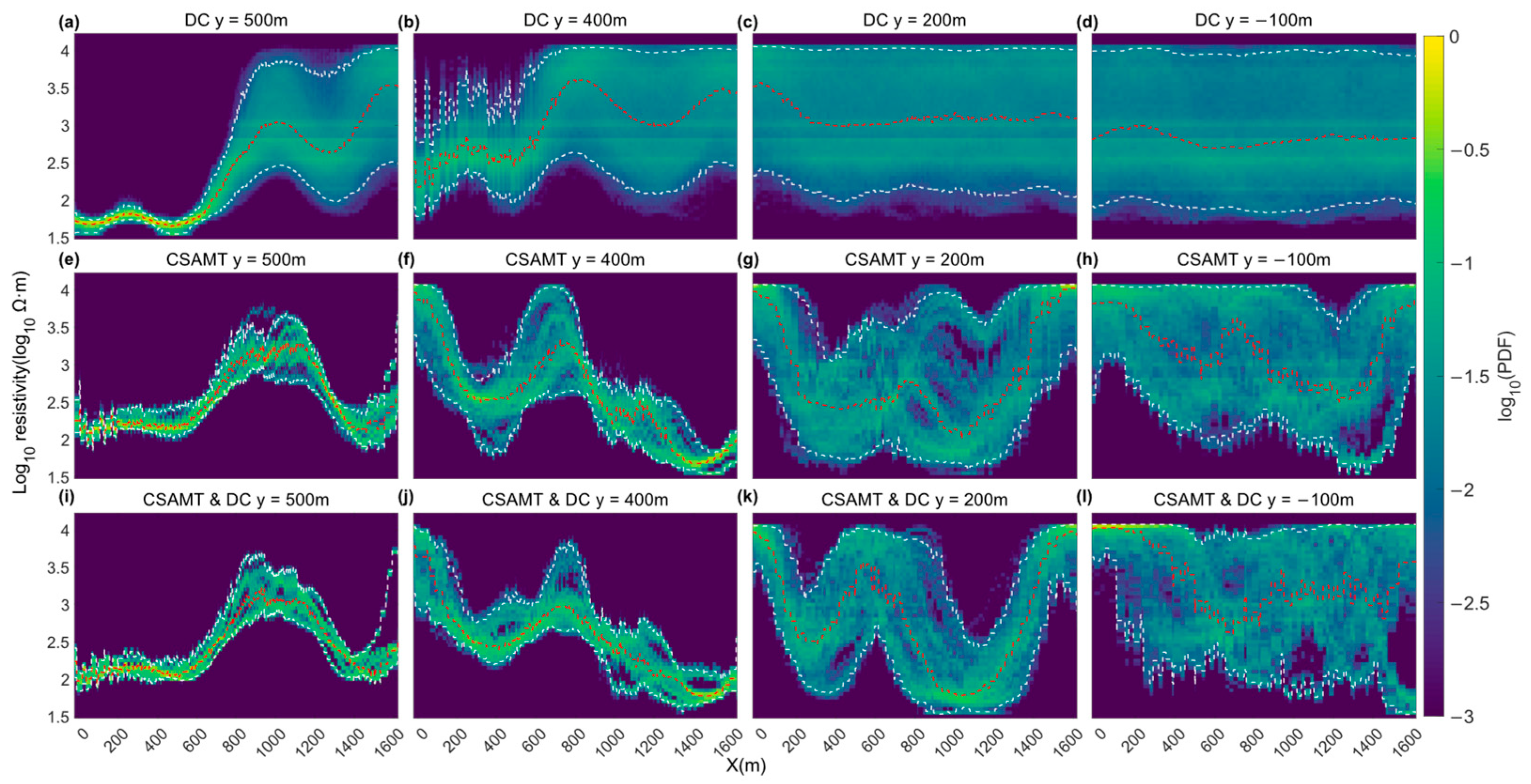
3. Synthetic Results
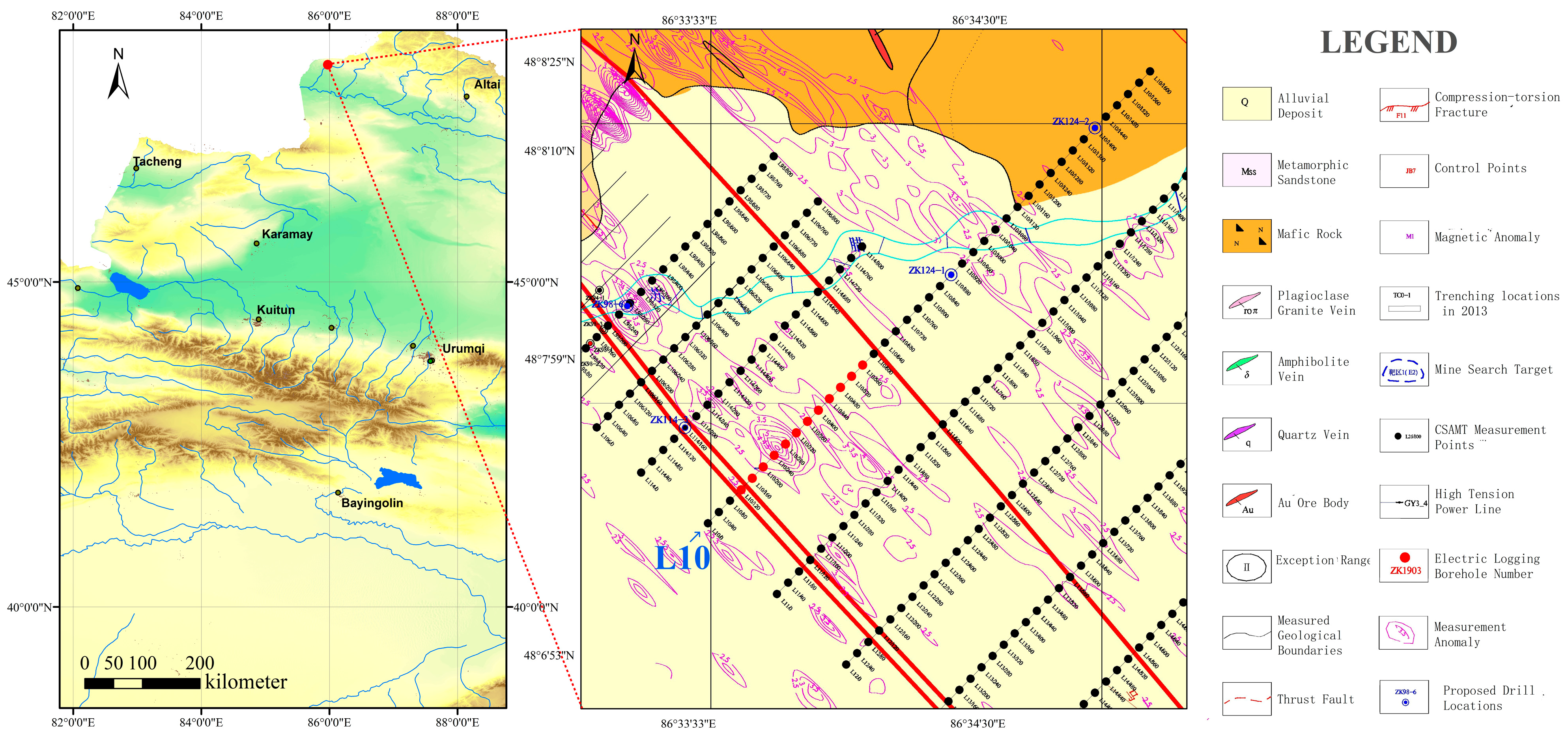
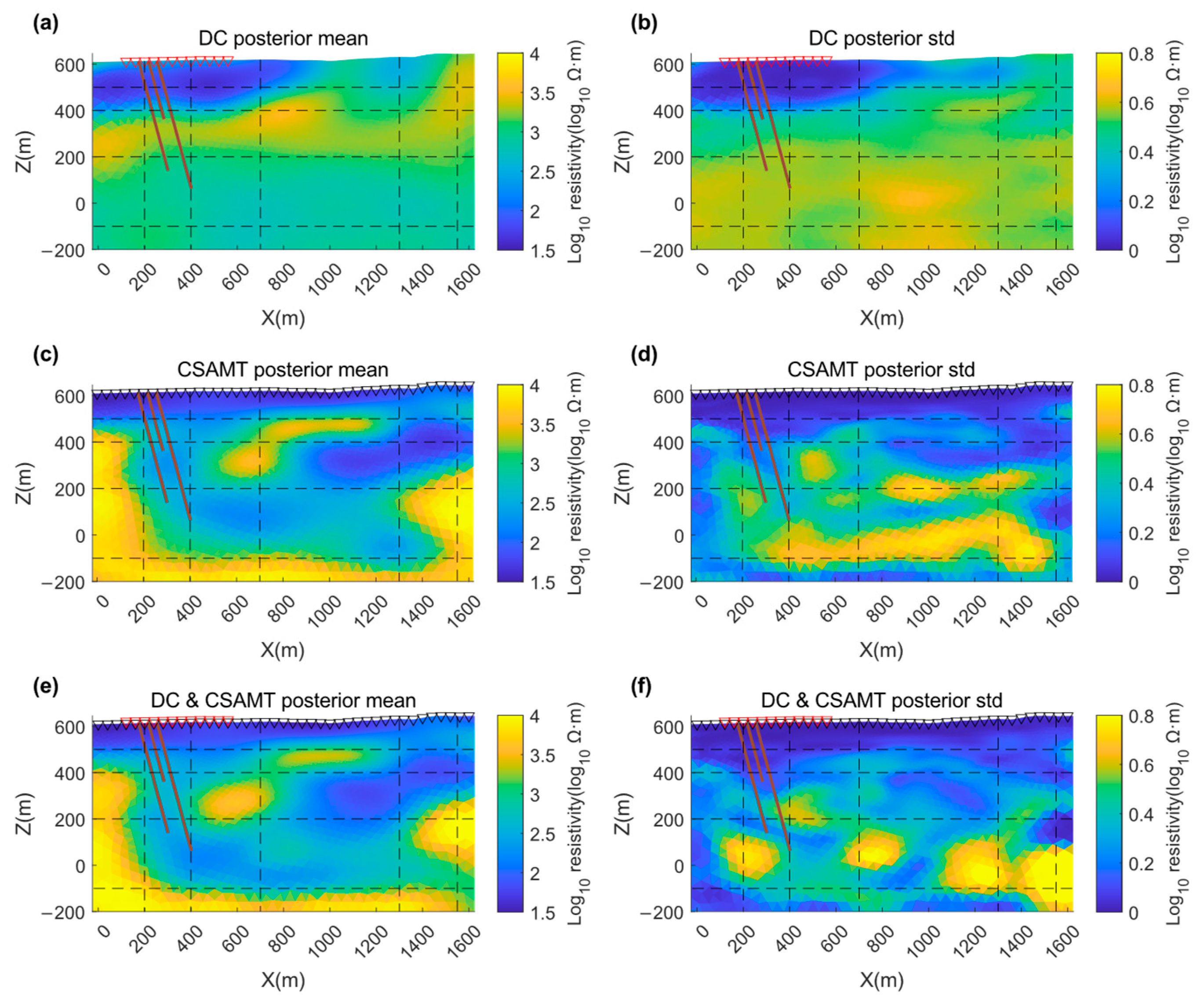
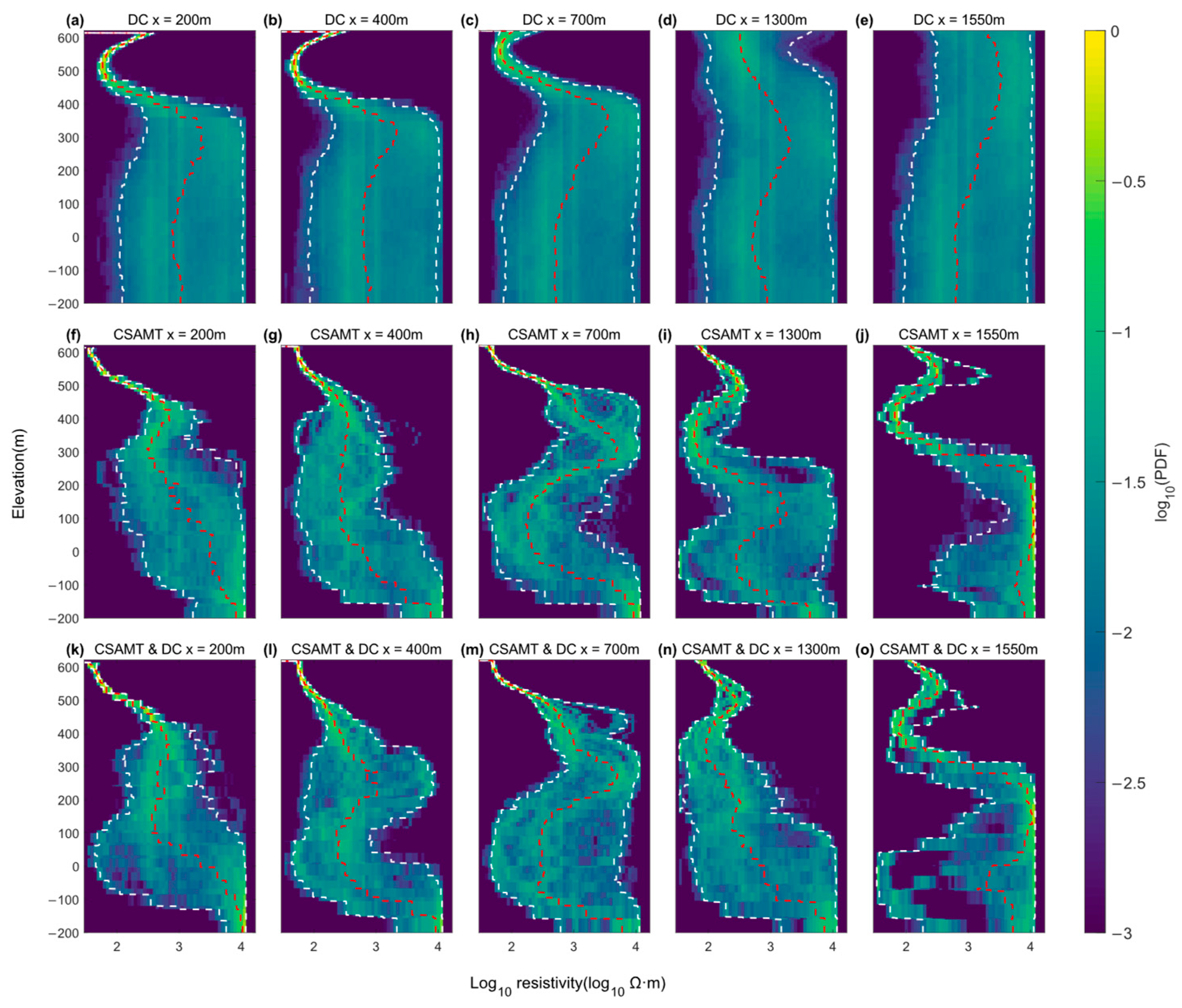
4. Field Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Løseth, L.O.; Pedersen, H.M.; Ursin, B.; Amundsen, L.; Ellingsrud, S. Low-frequency electromagnetic fields in applied geophysics: Waves or diffusion? Geophysics 2006, 71, W29–W40. [Google Scholar] [CrossRef]
- An, Z.; Di, Q. Application of the CSAMT method for exploring deep coal mines in Fujian Province, Southeastern China. J. Environ. Eng. Geophys. 2010, 15, 243–249. [Google Scholar] [CrossRef]
- Yang, D.; Oldenburg, D.W. Survey decomposition: A scalable framework for 3D controlled-source electromagnetic inversion. Geophysics 2016, 81, E69–E87. [Google Scholar] [CrossRef]
- Dai, Q.-w.; Dan, D.; Biao, L.; Wu, Q.-H.; Yan, J.-B.; Hua, K.; Chen, S.-F.; Qi, Z.; Tang, Y.-Y. Deep exploration of W-Sn and Cu polymetallic deposits in middle Qin-Hang metallogenic belt, South China. Trans. Nonferrous Met. Soc. China 2023, 33, 231–253. [Google Scholar] [CrossRef]
- Thorkildsen, V.S.; Gelius, L.-J. Electromagnetic resolution—A CSEM study based on the Wisting oil field. Geophys. J. Int. 2023, 233, 2124–2141. [Google Scholar] [CrossRef]
- Ray, A.; Key, K.; Bodin, T.; Myer, D.; Constable, S. Bayesian inversion of marine CSEM data from the Scarborough gas field using a transdimensional 2-D parametrization. Geophys. J. Int. 2014, 199, 1847–1860. [Google Scholar] [CrossRef]
- Wang, K.; Queralt, P.; Ledo, J.; Meqbel, N. CSEM and MT Inversion at the Hontomín CO2 Storage Site in Burgos, Spain. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5922316. [Google Scholar] [CrossRef]
- Escalas, M.; Queralt, P.; Ledo, J.; Marcuello, A. Polarisation analysis of magnetotelluric time series using a wavelet-based scheme: A method for detection and characterisation of cultural noise sources. Phys. Earth Planet. Inter. 2013, 218, 31–50. [Google Scholar] [CrossRef]
- Yang, H.; Li, T.; Zhang, R.; Dong, X.; Zhuang, Y. 3D joint inversion of DC resistivity and time domain induced polarization with structural constraints in undulating topography. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5920412. [Google Scholar] [CrossRef]
- Bouchedda, A.; Bernard, G.; Gloaguen, E. Constrained electrical resistivity tomography Bayesian inversion using inverse Matérn covariance matrix. Geophysics 2017, 82, E129–E141. [Google Scholar] [CrossRef]
- Loke, M.; Chambers, J.; Rucker, D.; Kuras, O.; Wilkinson, P. Recent developments in the direct-current geoelectrical imaging method. J. Appl. Geophys. 2013, 95, 135–156. [Google Scholar] [CrossRef]
- Bortolozo, C.A.; Campaña, J.D.R.; Santos, F.A.M.D.; De Oliveira, G.S.; Porsani, J.L.; Pryer, T.; Sialounas, G. Joint Inversion of DC and TEM Methods for Geological Imaging. Pure Appl. Geophys. 2024, 181, 2541–2560. [Google Scholar] [CrossRef]
- Sharma, R.; Vashisth, D.; Sarkar, K.; Singh, U.K. Joint Inversion of DC Resistivity and MT Data using Multi-Objective Grey Wolf Optimization. In Proceedings of the NSG 2024 30th European Meeting of Environmental and Engineering Geophysics, Helsinki, Finland, 8–12 September 2024; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2024; pp. 1–5. [Google Scholar]
- Liu, M.; Vashisth, D.; Grana, D.; Mukerji, T. Joint inversion of geophysical data for geologic carbon sequestration monitoring: A differentiable physics-informed neural network model. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025372. [Google Scholar] [CrossRef]
- Cheng, J.; Li, F.; Peng, S.; Sun, X.; Zheng, J.; Jia, J. Joint inversion of TEM and DC in roadway advanced detection based on particle swarm optimization. J. Appl. Geophys. 2015, 123, 30–35. [Google Scholar] [CrossRef]
- Massoud, U.; Kenawy, A.A.; Ragab, E.-S.A.; Abbas, A.M.; El-Kosery, H.M. Characterization of the groundwater aquifers at El Sadat City by joint inversion of VES and TEM data. NRIAG J. Astron. Geophys. 2014, 3, 137–149. [Google Scholar] [CrossRef]
- Bortolozo, C.A.; Couto, M.A., Jr.; Porsani, J.L.; Almeida, E.R.; dos Santos, F.A.M. Geoelectrical characterization using joint inversion of VES/TEM data: A case study in Paraná Sedimentary Basin, São Paulo State, Brazil. J. Appl. Geophys. 2014, 111, 33–46. [Google Scholar] [CrossRef]
- Meqbel, N.; Ritter, O. New Advances for a joint 3D inversion of multiple EM methods. In Proceedings of the 76th EAGE Conference and Exhibition-Workshops, Amsterdam, The Netherlands, 16–19 June 2014; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2014; p. cp-401-00065. [Google Scholar]
- Rovetta, D.; Lovatini, A.; Watts, M. Probabilistic joint inversion of TD-CSEM, MT and DC data for hydrocarbon exploration. In Proceedings of the SEG International Exposition and Annual Meeting, 2008, Las Vegas, NV, USA, 9–14 November 2008; SEG: Littleton, CO, USA, 2008; p. SEG-2008-0599. [Google Scholar]
- Li, G.; Zhang, L.; Goswami, B.K. Complex frequency-shifted perfectly matched layers for 2.5 D frequency-domain marine controlled-source EM field simulations. Surv. Geophys. 2022, 43, 1055–1084. [Google Scholar] [CrossRef]
- Cai, H.; Liu, M.; Zhou, J.; Li, J.; Hu, X. Effective 3D-transient electromagnetic inversion using finite-element method with a parallel direct solver. Geophysics 2022, 87, E377–E392. [Google Scholar] [CrossRef]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- Gribenko, A.; Zhdanov, M. Rigorous 3D inversion of marine CSEM data based on the integral equation method. Geophysics 2007, 72, WA73–WA84. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G.A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int. 2008, 172, 513–535. [Google Scholar] [CrossRef]
- Hawkins, R.; Brodie, R.C.; Sambridge, M. Trans-dimensional Bayesian inversion of airborne electromagnetic data for 2D conductivity profiles. Explor. Geophys. 2018, 49, 134–147. [Google Scholar] [CrossRef]
- Ren, Z.; Kalscheuer, T. Uncertainty and resolution analysis of 2D and 3D inversion models computed from geophysical electromagnetic data. Surv. Geophys. 2020, 41, 47–112. [Google Scholar] [CrossRef]
- Dai, Q.; Wu, Y.; Yue, J. 2.5 D transient electromagnetic inversion based on the unstructured quadrilateral finite-element method and a geologic statistics-driven Bayesian framework. Geophysics 2025, 90, WA1–WA16. [Google Scholar] [CrossRef]
- Mosegaard, K.; Tarantola, A. Monte Carlo sampling of solutions to inverse problems. J. Geophys. Res. Solid Earth 1995, 100, 12431–12447. [Google Scholar] [CrossRef]
- Dosso, S.E.; Holland, C.W.; Sambridge, M. Parallel tempering for strongly nonlinear geoacoustic inversion. J. Acoust. Soc. Am. 2012, 132, 3030–3040. [Google Scholar] [CrossRef]
- Faghih, Z.; Haroon, A.; Jegen, M.; Gehrmann, R.; Schwalenberg, K.; Micallef, A.; Dettmer, J.; Berndt, C.; Mountjoy, J.; Weymer, B.A. Characterizing offshore freshened groundwater salinity patterns using trans-dimensional Bayesian inversion of controlled source electromagnetic data: A case study from the Canterbury Bight, New Zealand. Water Resour. Res. 2024, 60, e2023WR035714. [Google Scholar] [CrossRef]
- Buland, A.; Kolbjørnsen, O. Bayesian inversion of CSEM and magnetotelluric data. Geophysics 2012, 77, E33–E42. [Google Scholar] [CrossRef]
- Chen, J.; Hoversten, G.M.; Vasco, D.; Rubin, Y.; Hou, Z. A Bayesian model for gas saturation estimation using marine seismic AVA and CSEM data. Geophysics 2007, 72, WA85–WA95. [Google Scholar] [CrossRef]
- Blatter, D.; Morzfeld, M.; Key, K.; Constable, S. Uncertainty quantification for regularized inversion of electromagnetic geophysical data—Part I: Motivation and theory. Geophys. J. Int. 2022, 231, 1057–1074. [Google Scholar] [CrossRef]
- Blatter, D.; Key, K.; Ray, A.; Gustafson, C.; Evans, R. Bayesian joint inversion of controlled source electromagnetic and magnetotelluric data to image freshwater aquifer offshore New Jersey. Geophys. J. Int. 2019, 218, 1822–1837. [Google Scholar] [CrossRef]
- Blatter, D.; Morzfeld, M.; Key, K.; Constable, S. Uncertainty quantification for regularized inversion of electromagnetic geophysical data–part II: Application in 1-D and 2-D problems. Geophys. J. Int. 2022, 231, 1075–1095. [Google Scholar] [CrossRef]
- Key, K. MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophys. J. Int. 2016, 207, 571–588. [Google Scholar] [CrossRef]
- Mitsuhata, Y. 2-D electromagnetic modeling by finite-element method with a dipole source and topography. Geophysics 2000, 65, 465–475. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Constable, S.; Weiss, C.J. Mapping thin resistors and hydrocarbons with marine EM methods: Insights from 1D modeling. Geophysics 2006, 71, G43–G51. [Google Scholar] [CrossRef]
- Xu, S.Z.; Duan, B.C.; Zhang, D.H. Selection of the wavenumbers k using an optimization method for the inverse Fourier transform in 2.5 D electrical modelling. Geophys. Prospect. 2000, 48, 789–796. [Google Scholar] [CrossRef]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Guptasarma, D.; Singh, B. New digital linear filters for Hankel J0 and J1 transforms [link]. Geophys. Prospect. 1997, 45, 745–762. [Google Scholar] [CrossRef]
- Pidlisecky, A.; Knight, R. FW2_5D: A MATLAB 2.5-D electrical resistivity modeling code. Comput. Geosci. 2008, 34, 1645–1654. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer: New York, NY, USA, 1999. [Google Scholar]
- Long, Z.; Cai, H.; Hu, X.; Zhou, J.; Yang, X. 3D inversion of CSEM data using finite element method in data space. IEEE Trans. Geosci. Remote Sens. 2024, 62, 2001711. [Google Scholar] [CrossRef]
- Sambridge, M. A parallel tempering algorithm for probabilistic sampling and multimodal optimization. Geophys. J. Int. 2014, 196, 357–374. [Google Scholar] [CrossRef]
- Hansen, T.M.; Cordua, K.S.; Looms, M.C.; Mosegaard, K. SIPPI: A Matlab toolbox for sampling the solution to inverse problems with complex prior information: Part 2—Application to crosshole GPR tomography. Comput. Geosci. 2013, 52, 481–492. [Google Scholar] [CrossRef]
- Aminzadeh, F. 3-D salt and overthrust seismic models. In Applications of 3-D Seismic Data to Exploration and Production; American Association of Petroleum Geologists: Tulsa, OK, USA, 1996. [Google Scholar]
- Mulder, W. A robust solver for CSEM modelling on stretched grids. In Proceedings of the 69th EAGE Conference and Exhibition incorporating SPE EUROPEC 2007, London, UK, 1–14 June 2007; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2007; p. cp-27-00149. [Google Scholar]
- Hansen, T.M.; Cordua, K.S.; Jacobsen, B.H.; Mosegaard, K. Accounting for imperfect forward modeling in geophysical inverse problems—Exemplified for crosshole tomography. Geophysics 2014, 79, H1–H21. [Google Scholar] [CrossRef]
- Hansen, T.M.; Cordua, K.S.; Looms, M.C.; Mosegaard, K. SIPPI: A Matlab toolbox for sampling the solution to inverse problems with complex prior information: Part 1—Methodology. Comput. Geosci. 2013, 52, 470–480. [Google Scholar] [CrossRef]
- Blatter, D.; Naif, S.; Key, K.; Ray, A. A plume origin for hydrous melt at the lithosphere–asthenosphere boundary. Nature 2022, 604, 491–494. [Google Scholar] [CrossRef]



| Serial Number | Rock Name | Measurement Location | Number of Measurements | Resistivity (log10 Ω·m) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Minimum Value | Maximum Value | Measurement Time | ||||
| 1 | Altered Sandstone | Tunnel Wall | 15 | 2.8048 | 2.4183 | 3.4064 | 2020 | |
| 2 | Pyrite-Quartz Vein | Tunnel Wall | 23 | 3.9729 | 2.9996 | 4.5013 | ||
| 3 | Altered Sandstone | Pit Wall | 5 | 1.3617 | 1.2788 | 1.4314 | ||
| 4 | Diorite | Surface Exposure | 5 | 2.1614 | 2.0792 | 2.2355 | ||
| 5 | Granite | Surface Exposure | 6 | 3.1326 | 2.2068 | 3.6479 | ||
| 6 | Phyllite | Surface Exposure | 5 | 1.5563 | 1.1461 | 1.8633 | ||
| 7 | Ore-bearing Diorite | Pit Wall | 5 | 2.4346 | 2.3222 | 2.5490 | ||
| 8 | Altered Sandstone | Tunnel Wall and Borehole | 6 | 4.1105 | 2.8609 | 4.4044 | 2021 | |
| 9 | Granite | Tunnel Wall and Borehole | 5 | 4.2560 | 3.4982 | 4.6711 | ||
| 10 | Pyritized Altered Sandstone | Tunnel Wall | 5 | 3.6950 | 3.2068 | 4.1164 | ||
| 11 | Pyritized Granite | Tunnel Wall | 5 | 4.1525 | 3.8223 | 4.4017 | ||
| 12 | Pyritized Phyllite | Tunnel Wall | 5 | 3.9982 | 2.6884 | 4.3557 | ||
| 13 | Pyritized Diorite | Tunnel Wall | 5 | 3.5344 | 1.6990 | 3.7301 | ||
| 14 | Pyritized Quartz Vein | Tunnel Wall | 5 | 3.4089 | 2.8531 | 3.8182 | ||
| 15 | Amphibolite | Borehole | 4 | 3.2310 | 3.0849 | 3.4173 | ||
| 16 | Phyllite | Tunnel Wall | 5 | 4.2262 | 3.3955 | 4.5936 | ||
| 17 | Diorite | Tunnel Wall | 5 | 3.5359 | 2.7752 | 3.7877 | ||
| 18 | Quartz Vein | Tunnel Wall | 6 | 3.5660 | 3.0924 | 3.9687 | ||
| 19 | Monzonite | Borehole | 8 | 4.0683 | 3.5532 | 4.4537 | ||
| 20 | Altered Sandstone | 28 | 3.0911 | 2.0043 | 3.9283 | 2021 | ||
| 21 | Biotite Quartz Schist | 83 | 3.2020 | 2.1553 | 3.9258 | |||
| 22 | Ore-bearing Diorite | Ore | 33 | 3.4261 | 2.7364 | 4.7516 | ||
| 23 | Diorite | Borehole | 15 | 3.0479 | 1.6628 | 4.3136 | ||
| 24 | Granite | 86 | 3.5928 | 2.1004 | 5.0541 | |||
| 25 | Monzonite | 23 | 3.7907 | 3.3066 | 4.2302 | |||
| 26 | Quartz Vein-bearing Altered Sandstone | Surface Exposure | 7 | 3.8736 | 2.5211 | 5.0086 | ||
| 27 | Pyrite-Quartz Vein | 5 | 3.9729 | 2.9996 | 4.5013 | |||
| 28 | Metamorphic Sandstone | Surface Exposure and Borehole | 21 | 2.9600 | 1.9494 | 3.3300 | 2022 | |
| 29 | Biotite Schist | Surface Exposure and Borehole | 4 | 2.9832 | 2.6590 | 3.2230 | ||
| 30 | Pyritized Diorite | Surface Exposure and Borehole | 6 | 2.7340 | 2.4983 | 3.0004 | ||
| 31 | Sericite Green Clay Phyllite | Surface Exposure and Borehole | 6 | 2.7275 | 2.2672 | 2.9513 | ||
| 32 | Phyllite | Surface Exposure and Borehole | 26 | 2.8241 | 2.1959 | 3.1998 | ||
| 33 | Diorite | Surface Exposure and Borehole | 17 | 2.6928 | 1.9956 | 3.1096 | ||
| 34 | Altered Diorite | Surface Exposure and Borehole | 14 | 2.7910 | 2.2989 | 3.1735 | ||
| 35 | Carbonatized Metamorphic Rock | Surface Exposure and Borehole | 3 | 2.9154 | 2.2175 | 3.1316 | ||
| 36 | Granite | Surface Exposure and Borehole | 16 | 3.1556 | 0.2295 | 2.8831 | 3.7067 | 2024 |
| 37 | Coarse-grained Granite | Surface Exposure and Borehole | 22 | 3.1308 | 0.2464 | 2.6812 | 3.5562 | |
| 38 | Phyllite | Surface Exposure and Borehole | 17 | 3.3762 | 0.2962 | 2.7419 | 3.9645 | |
| 39 | Silicified Phyllite | Surface Exposure and Borehole | 7 | 3.4736 | 0.4196 | 3.0945 | 4.1859 | |
| 40 | Diorite | Surface Exposure and Borehole | 31 | 3.1261 | 0.2931 | 2.6395 | 3.8289 | |
| 41 | Pyrite-bearing Diorite A | Surface Exposure and Borehole | 21 | 2.5146 | 0.1673 | 2.1820 | 2.8301 | |
| 42 | Pyrite-bearing Diorite B | Surface Exposure and Borehole | 11 | 3.1886 | 0.1885 | 3.0001 | 3.4656 | |
| 43 | Quartzite | Surface Exposure and Borehole | 22 | 3.0927 | 0.4125 | 2.4518 | 3.8254 | |
| 44 | Pyrite-bearing Quartzite | Surface Exposure and Borehole | 5 | 2.6091 | 0.2806 | 2.1128 | 2.9737 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Q.; Duan, D.; Wu, Y.; Xiong, Z.; Guo, L. The Joint Bayesian Inversion of CSAMT and DC Data for the Jinba Gold Mine in Xinjiang Using Physical Property Priors. Minerals 2025, 15, 299. https://doi.org/10.3390/min15030299
Dai Q, Duan D, Wu Y, Xiong Z, Guo L. The Joint Bayesian Inversion of CSAMT and DC Data for the Jinba Gold Mine in Xinjiang Using Physical Property Priors. Minerals. 2025; 15(3):299. https://doi.org/10.3390/min15030299
Chicago/Turabian StyleDai, Qianwei, Dan Duan, Yun Wu, Zhexian Xiong, and Luyao Guo. 2025. "The Joint Bayesian Inversion of CSAMT and DC Data for the Jinba Gold Mine in Xinjiang Using Physical Property Priors" Minerals 15, no. 3: 299. https://doi.org/10.3390/min15030299
APA StyleDai, Q., Duan, D., Wu, Y., Xiong, Z., & Guo, L. (2025). The Joint Bayesian Inversion of CSAMT and DC Data for the Jinba Gold Mine in Xinjiang Using Physical Property Priors. Minerals, 15(3), 299. https://doi.org/10.3390/min15030299






