On the Initial Fabric of Naturally Occurring and Reconstituted Weakly Cemented Geomaterials
Abstract
1. Introduction
2. Materials and Methods
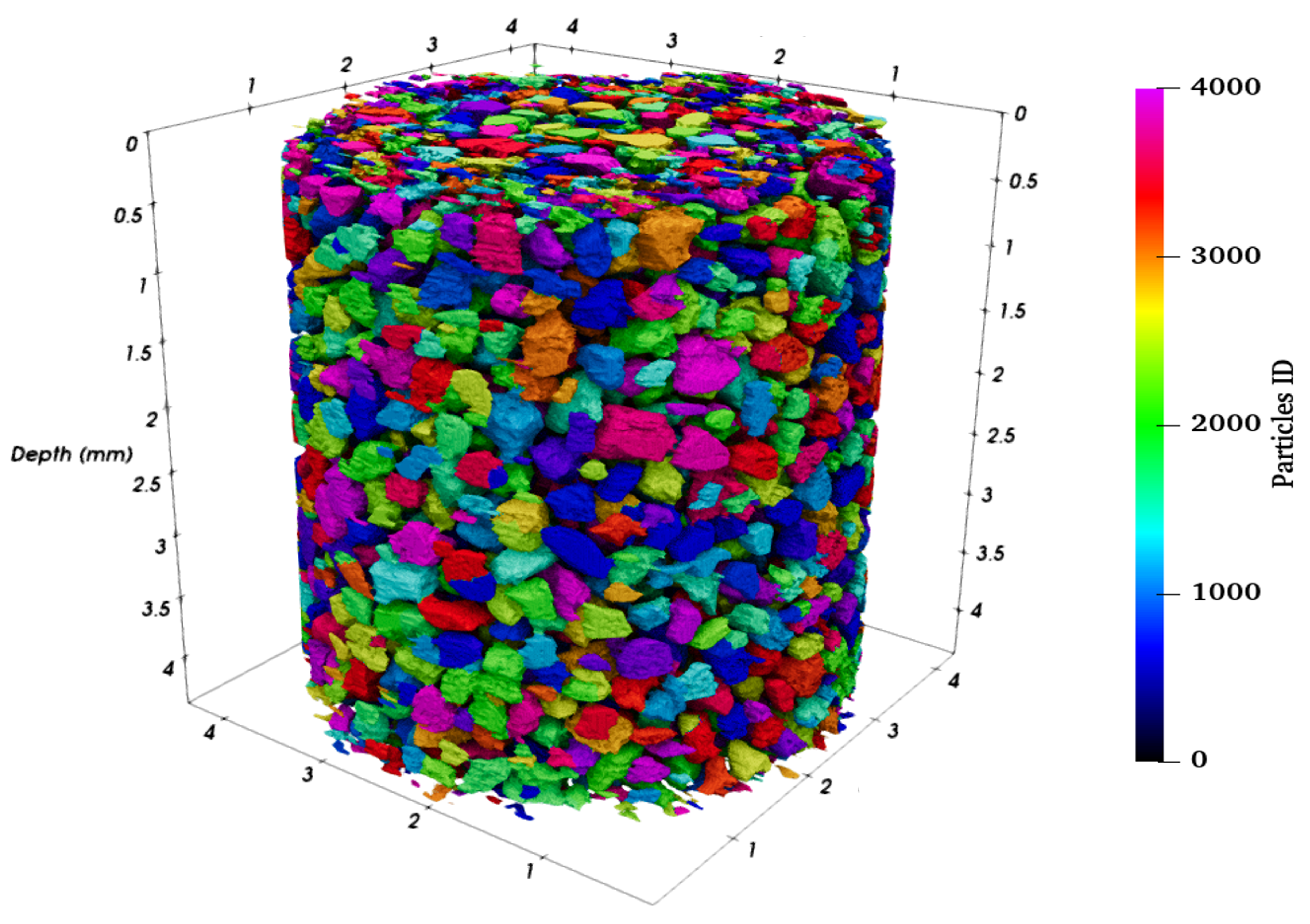
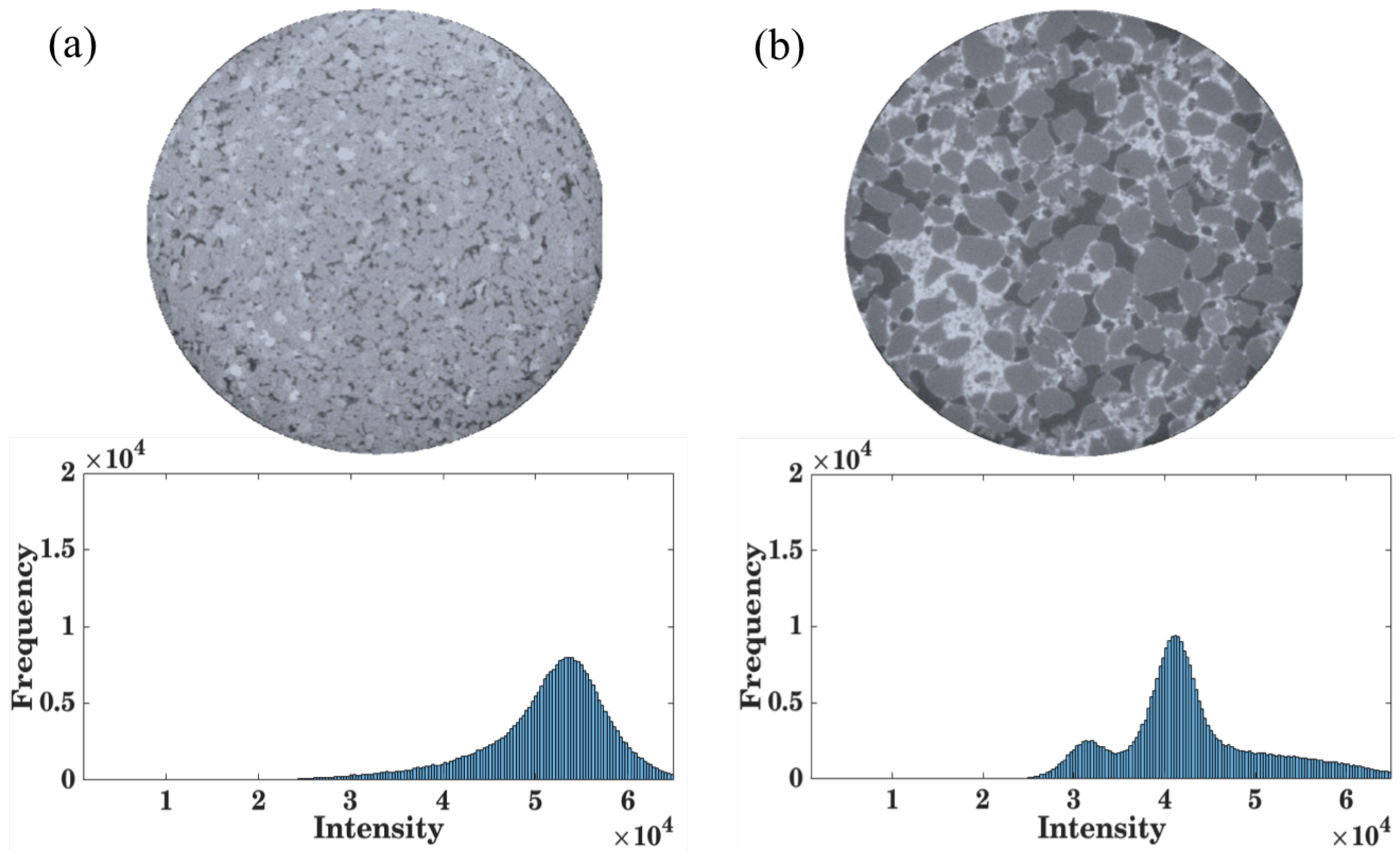
2.1. Experiments
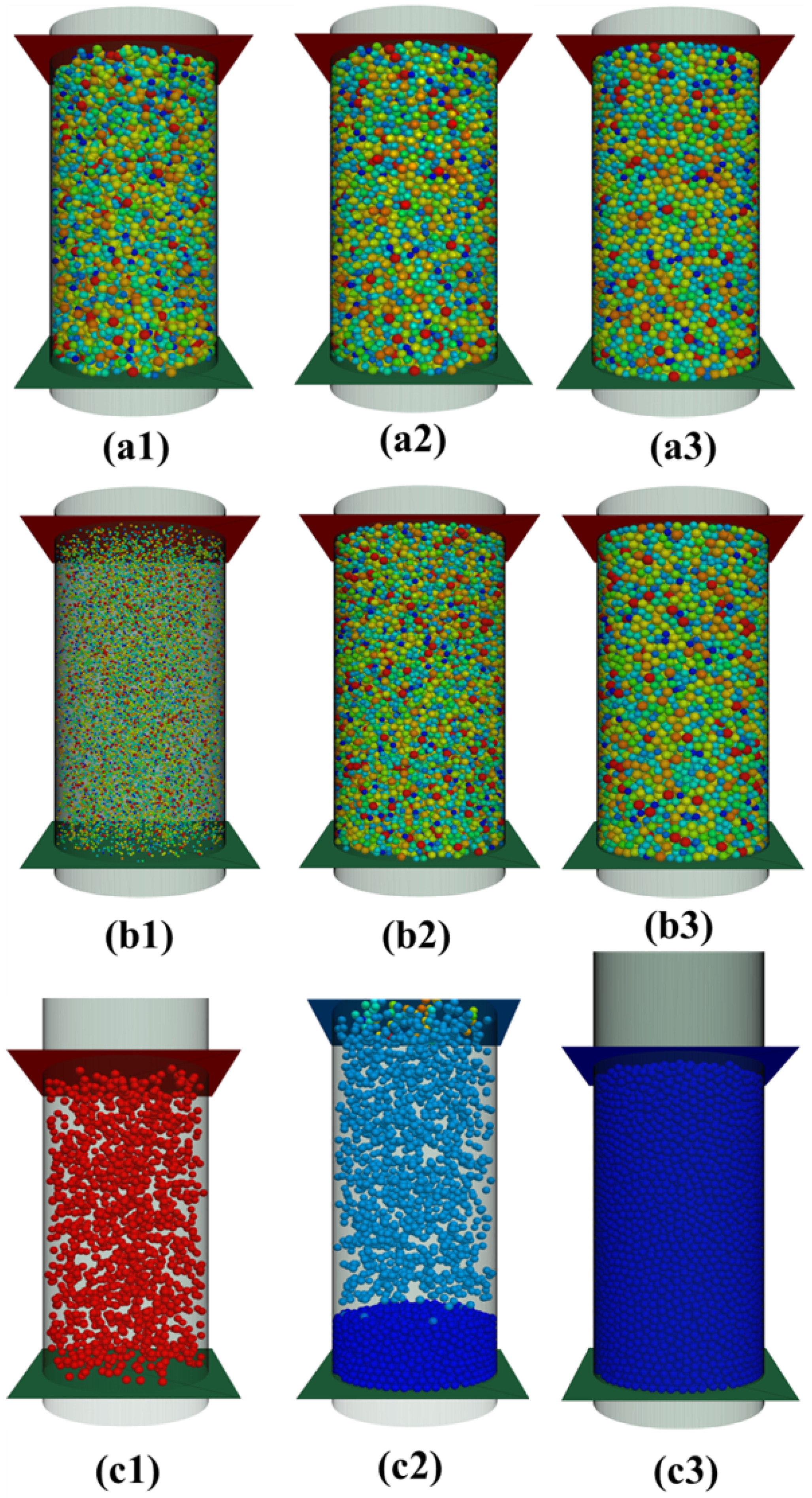
2.2. DEM Simulations
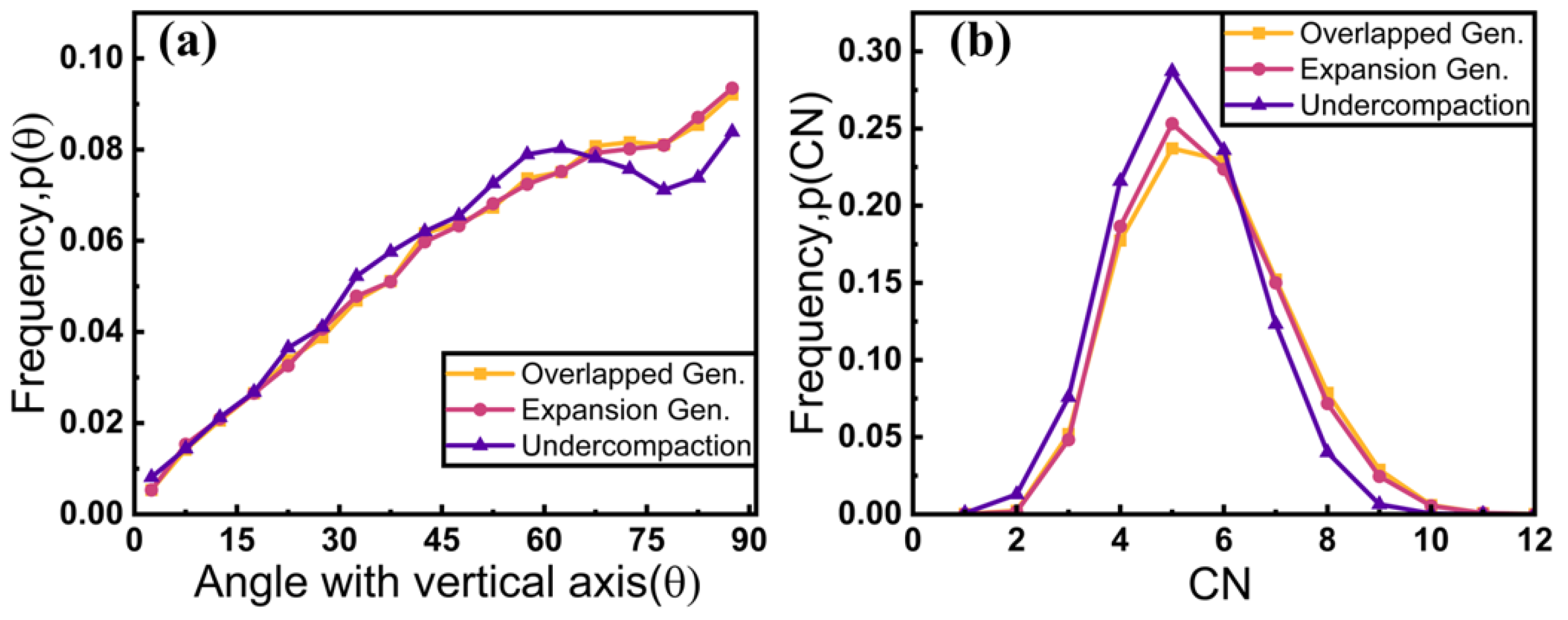
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leroueil, S.; Vaughan, P. The general and congruent effects of structure in natural soils and weak rocks. Géotechnique 1990, 40, 467–488. [Google Scholar] [CrossRef]
- Gens, A. Conceptual bases for a constitutive model for bonded soils and weak rocks. In Proceedings of the Geotechnical Engineering of Hard Soils-Soft Rocks: Proceedings of International Symposium under the auspices of the ISSMFE, Athens, Greece, 20–23 September 1993; pp. 485–494. [Google Scholar]
- Cuccovillo, T.; Coop, M. On the mechanics of structured sands. Géotechnique 1999, 49, 741–760. [Google Scholar] [CrossRef]
- Wang, Y.H.; Leung, S.C. A particulate-scale investigation of cemented sand behavior. Can. Geotech. J. 2008, 45, 29–44. [Google Scholar] [CrossRef]
- Cheng, L.; Cord-Ruwisch, R.; Shahin, M.A. Cementation of sand soil by microbially induced calcite precipitation at various degrees of saturation. Can. Geotech. J. 2013, 50, 81–90. [Google Scholar] [CrossRef]
- Haeri, S.M.; Hamidi, A.; Tabatabaee, N. The effect of gypsum cementation on the mechanical behavior of gravely sands. Geotech. Test. J. 2005, 28, 380–390. [Google Scholar] [CrossRef]
- Jawad, T.; Baqir, A. Improvement of sandy soil properties by using bentonite. Kufa J. Eng. 2009, 1, 29–39. [Google Scholar] [CrossRef]
- Najjar, S.; Yaghi, K.; Adwan, M.; Jaoude, A. Drained shear strength of compacted sand with clayey fines. Int. J. Geotech. Eng. 2015, 9, 513–520. [Google Scholar] [CrossRef]
- Alvarado, G.; COOP, M.R.; Willson, S. On the role of bond breakage due to unloading in the behaviour of weak sandstones. Géotechnique 2012, 62, 303–316. [Google Scholar] [CrossRef]
- Mackenzie, F.T.; Garrels, R. Evolution of Sedimentary Rocks; Norton: New York, NY, USA, 1971. [Google Scholar]
- Jeng, F.S.; Weng, M.C.; Huang, T.H.; Lin, M.L. Deformational characteristics of weak sandstone and impact to tunnel deformation. Tunn. Undergr. Space Technol. 2002, 17, 263–274. [Google Scholar] [CrossRef]
- Maynard, J.B. Geochemistry of Sedimentary Ore Deposits; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hunt, J.M. Distribution of hydrocarbons in sedimentary rocks. Geochim. Cosmochim. Acta 1961, 22, 37–49. [Google Scholar] [CrossRef]
- Quinteros, V.S.; Carraro, J.A.H. The initial fabric of undisturbed and reconstituted fluvial sand. Géotechnique 2023, 73, 1–15. [Google Scholar] [CrossRef]
- Gao, Z.; Zhao, J. Constitutive modeling of artificially cemented sand by considering fabric anisotropy. Comput. Geotech. 2012, 41, 57–69. [Google Scholar] [CrossRef]
- Singh, S.; Miers, J.; Saldana, C.; Murthy, T. Quantification of fabric in cemented granular materials. Comput. Geotech. 2020, 125, 103644. [Google Scholar] [CrossRef]
- Alvarado, G.; Lui, N.; Coop, M.R. Effect of fabric on the behaviour of reservoir sandstones. Can. Geotech. J. 2012, 49, 1036–1051. [Google Scholar] [CrossRef]
- Brewer, R.; Sleeman, J. Soil structure and fabric: Their definition and description. J. Soil Sci. 1960, 11, 172–185. [Google Scholar] [CrossRef]
- Tucker, M.E.; Jones, S.J. Sedimentary Petrology; John Wiley & Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Shrock, R.R. A classification of sedimentary rocks. J. Geol. 1948, 56, 118–129. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Yang, K.; Guo, P.; Tao, Z. Model test study on large deformation mechanism of thin-bedded metamorphic sandstone tunnel. Bull. Eng. Geol. Environ. 2022, 81, 436. [Google Scholar] [CrossRef]
- Liu, X.; Chen, H.; Liu, K.; He, C. Model test and stress distribution law of unsymmetrical loading tunnel in bedding rock mass. Arab. J. Geosci. 2017, 10, 1–11. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, D.; Han, Z.; Li, X.; Zhou, Z. Mechanical properties and fracture evolution of sandstone specimens containing different inclusions under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2019, 115, 33–47. [Google Scholar] [CrossRef]
- Fakhimi, A.; Hemami, B. Rock uniaxial compression test and axial splitting. Procedia Eng. 2017, 191, 623–630. [Google Scholar] [CrossRef]
- Zong, Y.; Han, L.; Wei, J.; Wen, S. Mechanical and damage evolution properties of sandstone under triaxial compression. Int. J. Min. Sci. Technol. 2016, 26, 601–607. [Google Scholar] [CrossRef]
- Corfdir, A.; Sulem, J. Comparison of extension and compression triaxial tests for dense sand and sandstone. Acta Geotech. 2008, 3, 241–246. [Google Scholar] [CrossRef]
- Tsesarsky, M.; Gal, E.; Machlav, E. 3-D global–local finite element analysis of shallow underground caverns in soft sedimentary rock. Int. J. Rock Mech. Min. Sci. 2013, 57, 89–99. [Google Scholar] [CrossRef]
- Fazio, N.L.; Perrotti, M.; Lollino, P.; Parise, M.; Vattano, M.; Madonia, G.; Di Maggio, C. A three-dimensional back-analysis of the collapse of an underground cavity in soft rocks. Eng. Geol. 2017, 228, 301–311. [Google Scholar] [CrossRef]
- Adachi, T.; Oka, F. An elasto-plastic constitutive model for soft rock with strain softening. Int. J. Numer. Anal. Methods Geomech. 1995, 19, 233–247. [Google Scholar] [CrossRef]
- Cao, P.; Youdao, W.; Yixian, W.; Haiping, Y.; Bingxiang, Y. Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ. Earth Sci. 2016, 75, 1–8. [Google Scholar] [CrossRef]
- Baudet, B.; Stallebrass, S. A constitutive model for structured clays. Géotechnique 2004, 54, 269–278. [Google Scholar] [CrossRef]
- Zimbardo, M.; Nocilla, A.; Coop, M.R. Influence of Destructuration on the Compression Behaviour of a Weak Rock. Geosciences 2022, 12, 249. [Google Scholar] [CrossRef]
- Coop, M.; Willson, S. Behavior of hydrocarbon reservoir sands and sandstones. J. Geotech. Geoenviron. Eng. 2003, 129, 1010–1019. [Google Scholar] [CrossRef]
- Aversa, S.; Evangelista, A. The mechanical behaviour of a pyroclastic rock: Yield strength and “destructuration” effects. Rock Mech. Rock Eng. 1998, 31, 25–42. [Google Scholar] [CrossRef]
- Burland, J.; Rampello, S.; Georgiannou, V.; Calabresi, G. A laboratory study of the strength of four stiff clays. Géotechnique 1996, 46, 491–514. [Google Scholar] [CrossRef]
- Burland, J.B. On the compressibility and shear strength of natural clays. Géotechnique 1990, 40, 329–378. [Google Scholar] [CrossRef]
- Clough, G.W.; Sitar, N.; Bachus, R.C.; Rad, N.S. Cemented sands under static loading. J. Geotech. Eng. Div. 1981, 107, 799–817. [Google Scholar] [CrossRef]
- Schnaid, F.; Prietto, P.D.; Consoli, N.C. Characterization of cemented sand in triaxial compression. J. Geotech. Geoenviron. Eng. 2001, 127, 857–868. [Google Scholar] [CrossRef]
- Consoli, N.C.; Viana da Fonseca, A.; Cruz, R.C.; Heineck, K.S. Fundamental parameters for the stiffness and strength control of artificially cemented sand. J. Geotech. Geoenviron. Eng. 2009, 135, 1347–1353. [Google Scholar] [CrossRef]
- Abdulla, A.A.; Kiousis, P.D. Behavior of cemented sands—I. Testing. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 533–547. [Google Scholar] [CrossRef]
- Veloso Marques, S.F.; Consoli, N.C.; Almeida e Sousa, J. Testing cement improved residual soil layers. J. Mater. Civ. Eng. 2014, 26, 544–550. [Google Scholar] [CrossRef]
- Cabalar, A.F.; Karabash, Z. Influence of cement type and sample preparation on the small-strain behaviour of sands. Arab. J. Sci. Eng. 2019, 44, 8835–8848. [Google Scholar] [CrossRef]
- Ismail, M.; Joer, H.; Randolph, M.; Meritt, A. Cementation of porous materials using calcite. Geotechnique 2002, 52, 313–324. [Google Scholar] [CrossRef]
- Fearon, R.; Coop, M. Reconstitution: What makes an appropriate reference material? Géotechnique 2000, 50, 471–477. [Google Scholar] [CrossRef]
- Coop, M. On the mechanics of reconstituted and natural sands. In Deformation Characteristics of Geomaterials; CRC Press: Boca Raton, FL, USA, 2005; pp. 36–65. [Google Scholar]
- Cuccovillo, T.; Coop, M. Yielding and pre-failure deformation of structured sands. Géotechnique 1997, 47, 491–508. [Google Scholar] [CrossRef]
- Rahimi, M.; Chan, D.; Nouri, A.; Rasouli, R. Effects of inherent fabric anisotropy and intermediate principal stress on constitutive behavior of uncemented and cemented sands. Comput. Geotech. 2016, 80, 237–247. [Google Scholar] [CrossRef]
- Cnudde, V.; Boone, M.; Dewanckele, J.; Dierick, M.; Van Hoorebeke, L.; Jacobs, P. 3D characterization of sandstone by means of X-ray computed tomography. Geosphere 2011, 7, 54–61. [Google Scholar] [CrossRef]
- Wang, L.; Frost, J.; Lai, J. Three-dimensional digital representation of granular material microstructure from X-ray tomography imaging. J. Comput. Civ. Eng. 2004, 18, 28–35. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Sowers, G.F. Strength Testing of Soils; ASTM International: West Conshohocken, PA, USA, 1964. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Pandey, K.; Bin Masood, T.; Singh, S.; Hotz, I.; Natarajan, V.; Murthy, T.G. Morse theory-based segmentation and fabric quantification of granular materials. Granul. Matter 2022, 24, 1–20. [Google Scholar] [CrossRef]
- O’Sullivan, C. Particulate Discrete Element Modelling: A Geomechanics Perspective; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Bagi, K. An algorithm to generate random dense arrangements for discrete element simulations of granular assemblies. Granul. Matter 2005, 7, 31–43. [Google Scholar] [CrossRef]
- Jiang, M.; Konrad, J.; Leroueil, S. An efficient technique for generating homogeneous specimens for DEM studies. Comput. Geotech. 2003, 30, 579–597. [Google Scholar] [CrossRef]
- Cui, L.; O’Sullivan, C. Analysis of a triangulation based approach for specimen generation for discrete element simulations. Granul. Matter 2003, 5, 135–145. [Google Scholar] [CrossRef]
- Cheng, Y.; Nakata, Y.; Bolton, M.D. Discrete element simulation of crushable soil. Geotechnique 2003, 53, 633–641. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Cundall, P. Computer simulations of dense sphere assemblies. In Studies in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1988; Volume 20, pp. 113–123. [Google Scholar]
- Ladd, R. Preparing test specimens using undercompaction. Geotech. Test. J. 1978, 1, 16–23. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P.; Maxwell, S. Micromechanical modeling of cracking and failure in brittle rocks. J. Geophys. Res. Solid Earth 2000, 105, 16683–16697. [Google Scholar] [CrossRef]
- Shen, Z.; Jiang, M.; Thornton, C. DEM simulation of bonded granular material. Part I: Contact model and application to cemented sand. Comput. Geotech. 2016, 75, 192–209. [Google Scholar] [CrossRef]
- Satake, M. Fabric tensor in granular materials. In Proceedings of the IUTAM-Conference on Deformation and Failure of Granular Materials, Delft, The Netherlands, 31 August–3 September 1982; pp. 63–68. [Google Scholar]
- Oda, M. Fabric tensor for discontinuous geological materials. Soils Found. 1982, 22, 96–108. [Google Scholar] [CrossRef]
- Thornton, C. Numerical simulations of deviatoric shear deformation of granular media. Géotechnique 2000, 50, 43–53. [Google Scholar] [CrossRef]
- Maeda, K. Critical State-based Geo-micromechanics on Granular Flow. In Proceedings of the AIP Conference Proceedings. American Institute of Physics, Golden, CO, USA, 28 June–1 July 2009; Volume 1145, pp. 17–24. [Google Scholar]
- Bhat KI, M.; Hurley, R.C.; Murthy, T.G. Micromechanics of contact-bound cohesive granular materials in confined compression. Phys. Rev. E 2024, 109, 054903. [Google Scholar] [CrossRef]
- Chand, B.; Bhat, M.; Kumar Agrawal, A.; Murthy, T.G. Experimental Measurements of Degradation of Cementation in Contact-Bound and Void-Bound Cemented Sands. In Proceedings of the Geo-Congress, Vancouver, BC, Canada, 25–28 February 2024; pp. 108–117. [Google Scholar]
- Singh, S.; Murthy, T.G. Evolution of structure of cohesive granular ensembles in compression. Int. J. Solids Struct. 2022, 238, 111359. [Google Scholar] [CrossRef]

| Model Parameter | Value |
|---|---|
| Normal contact stiffness () | N/m |
| Shear contact stiffness () | N/m |
| Damping factor () | 0.2 |
| Sliding friction coefficient () | 0.25 |
| Rolling friction coefficient () | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhat, M.I.; Chand, B.; Murthy, T.G. On the Initial Fabric of Naturally Occurring and Reconstituted Weakly Cemented Geomaterials. Minerals 2024, 14, 1000. https://doi.org/10.3390/min14101000
Bhat MI, Chand B, Murthy TG. On the Initial Fabric of Naturally Occurring and Reconstituted Weakly Cemented Geomaterials. Minerals. 2024; 14(10):1000. https://doi.org/10.3390/min14101000
Chicago/Turabian StyleBhat, Mohd Ilyas, Bhupendra Chand, and Tejas Gorur Murthy. 2024. "On the Initial Fabric of Naturally Occurring and Reconstituted Weakly Cemented Geomaterials" Minerals 14, no. 10: 1000. https://doi.org/10.3390/min14101000
APA StyleBhat, M. I., Chand, B., & Murthy, T. G. (2024). On the Initial Fabric of Naturally Occurring and Reconstituted Weakly Cemented Geomaterials. Minerals, 14(10), 1000. https://doi.org/10.3390/min14101000





