A Prediction Method of Compacted Rock Hydraulic Permeability Based on the MGEMTIP Model
Abstract
1. Introduction
2. Methods
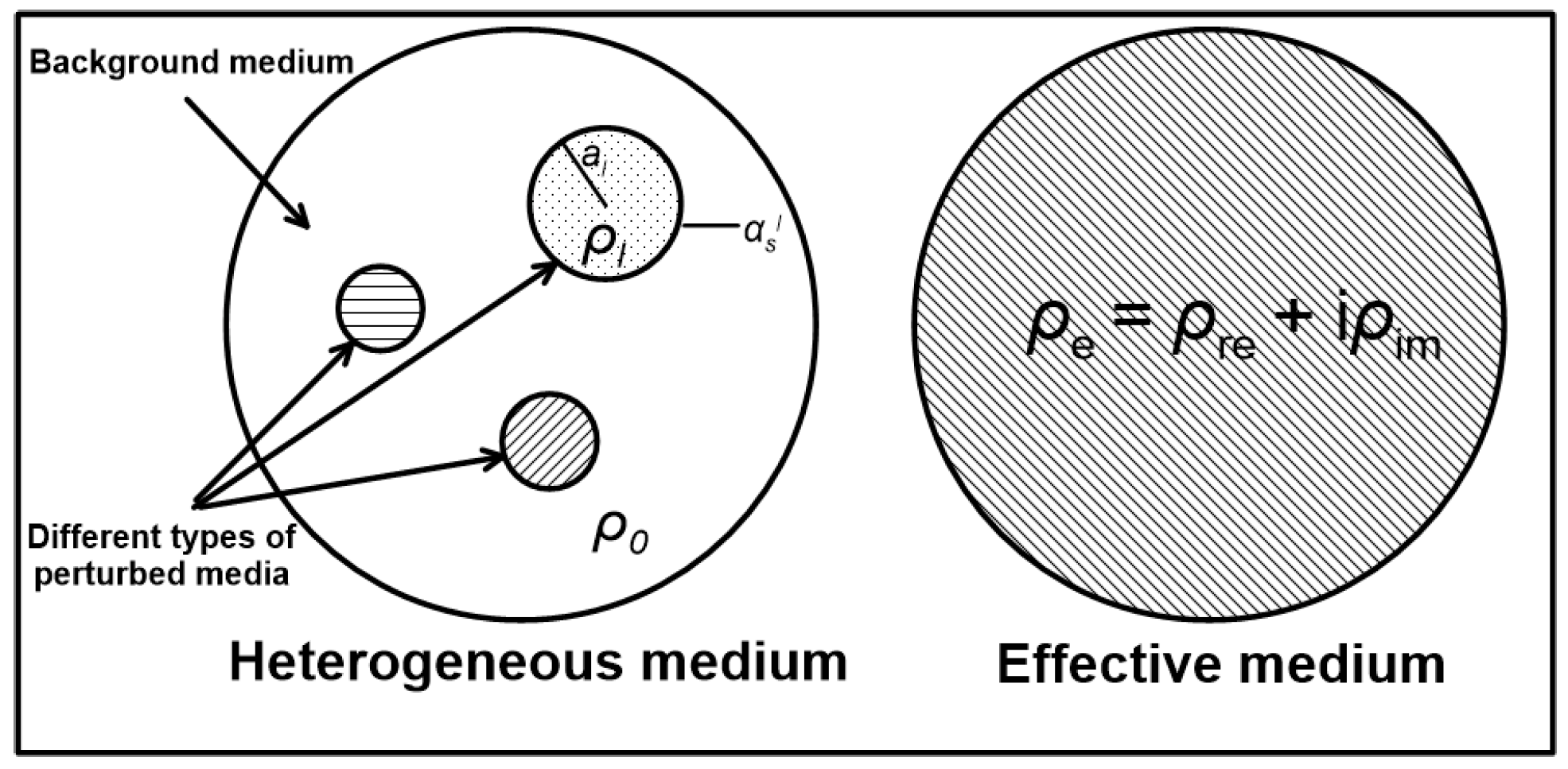
2.1. MGEMTIP Model
2.2. Relationship between Permeability and Chargeability in the MGEMTIP Model
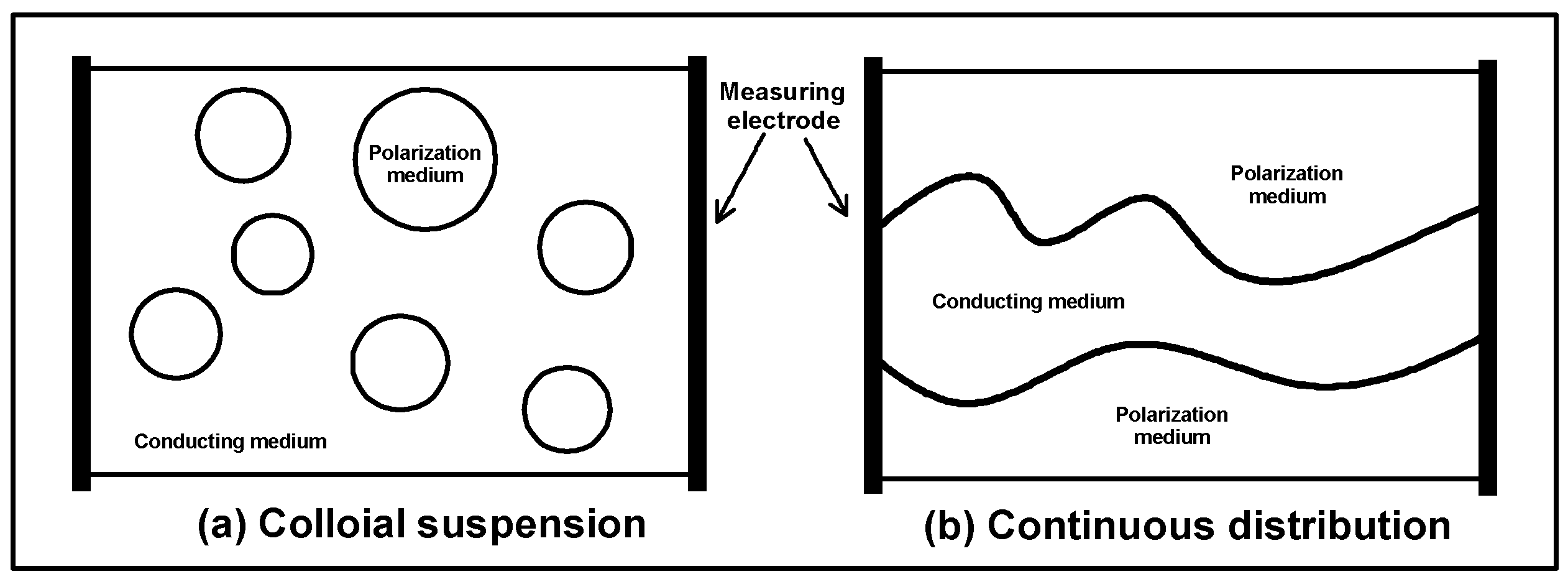
- (a)
- Part of the boundary does not provide polarization. Since the finite volume of the actual rock sample is different from that in the open-domain model of the actual exploration object, the boundary formed by part of the perturbation is in direct contact with the insulating material (air or rubber sleeve) during the test process, and no complete boundary of the perturbation is provided. According to Appendix A, the chargeability difference between the infinite boundary MGEMTIP and the finite boundary MGEMTIP iswhere is the outer surface of the first perturbation, is the surface area of the first perturbation, is the ratio of the surface area and the outer surface, is the total volume of the rock, and the total surface area of all perturbations is determined by the size of the core, so in determining the volume of the perturbed medium, the bigger , the bigger will be.
- (b)
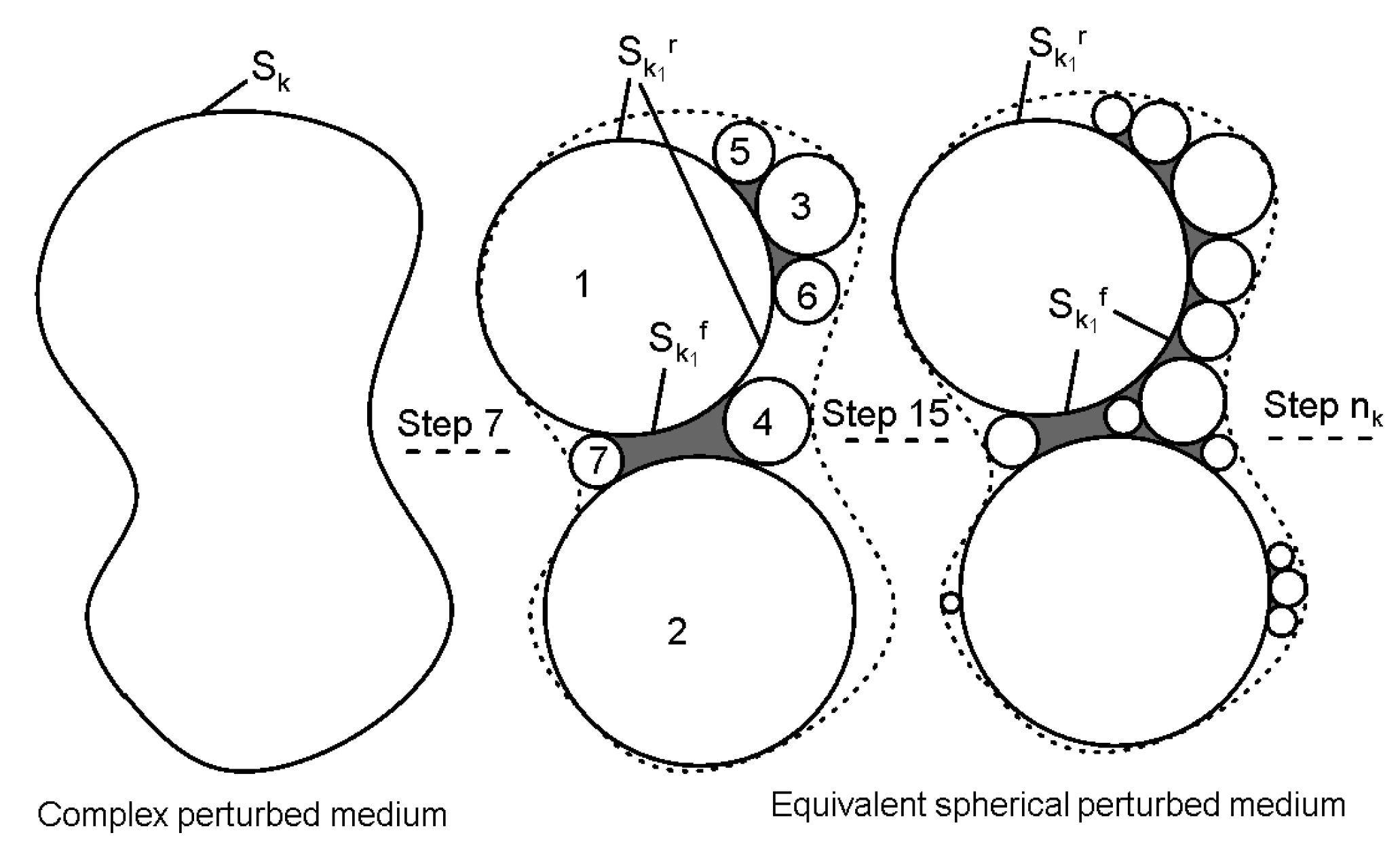
- By approximating the rock structure, the effective boundary decreases and the equivalent radius of perturbations increases. According to Appendix B, the difference between the chargeability of the MGEMTIP of the complex perturbations and the chargeability of the finite boundary MGEMTIP iswhere is the imaginary boundary area of the first perturbation, and the polarization difference is mainly caused by and . When there is a large-scale perturbation and the boundary is complex, the gets bigger.
- (c)
- Limitation of the measured frequency band. According to the logarithmic form of the time constant in Formula (2)
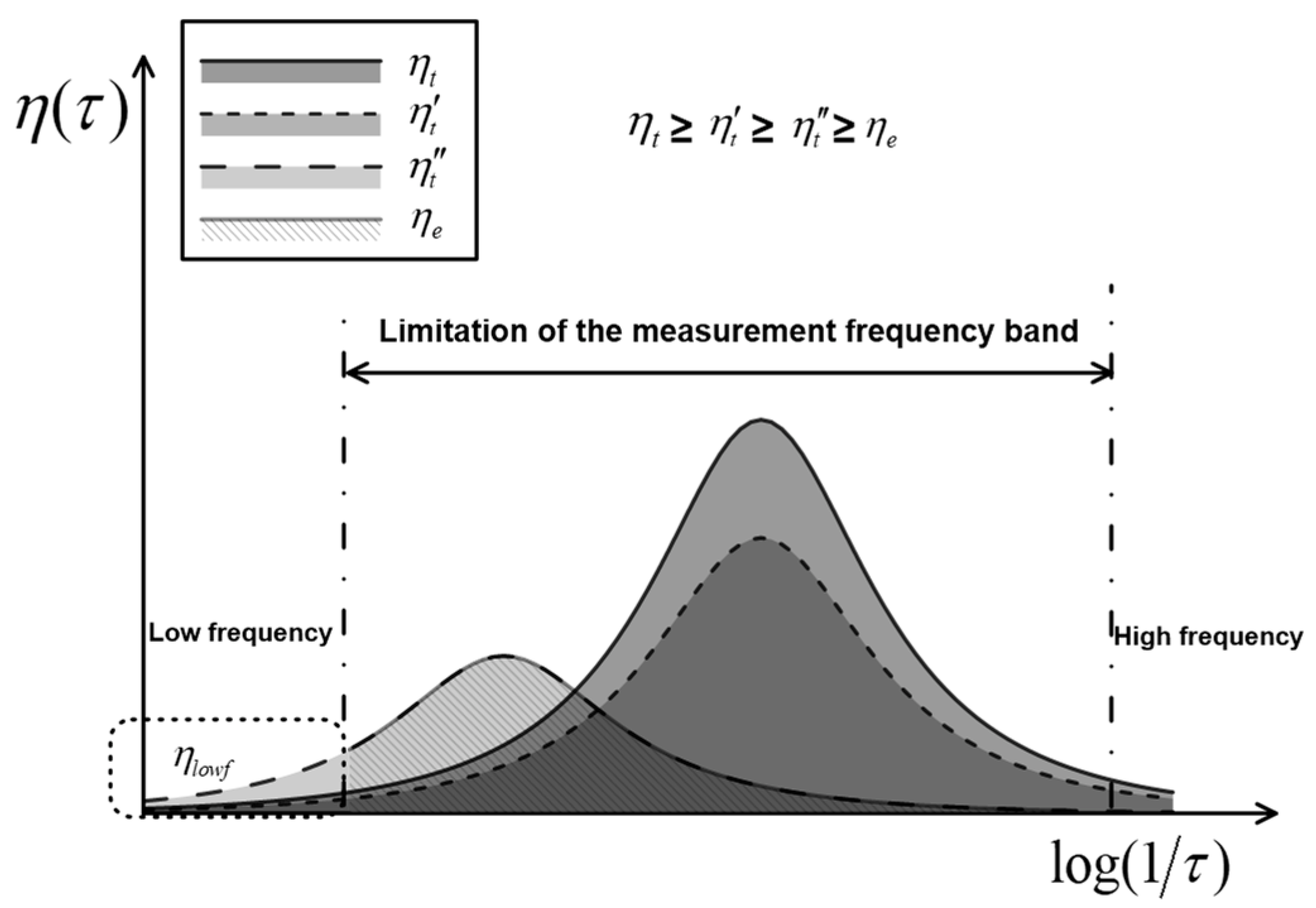
2.3. Permeability Prediction Model
2.4. Applicability Analysis of the Permeability Prediction Model
3. Physics Experiment
3.1. Experimental Sample Information
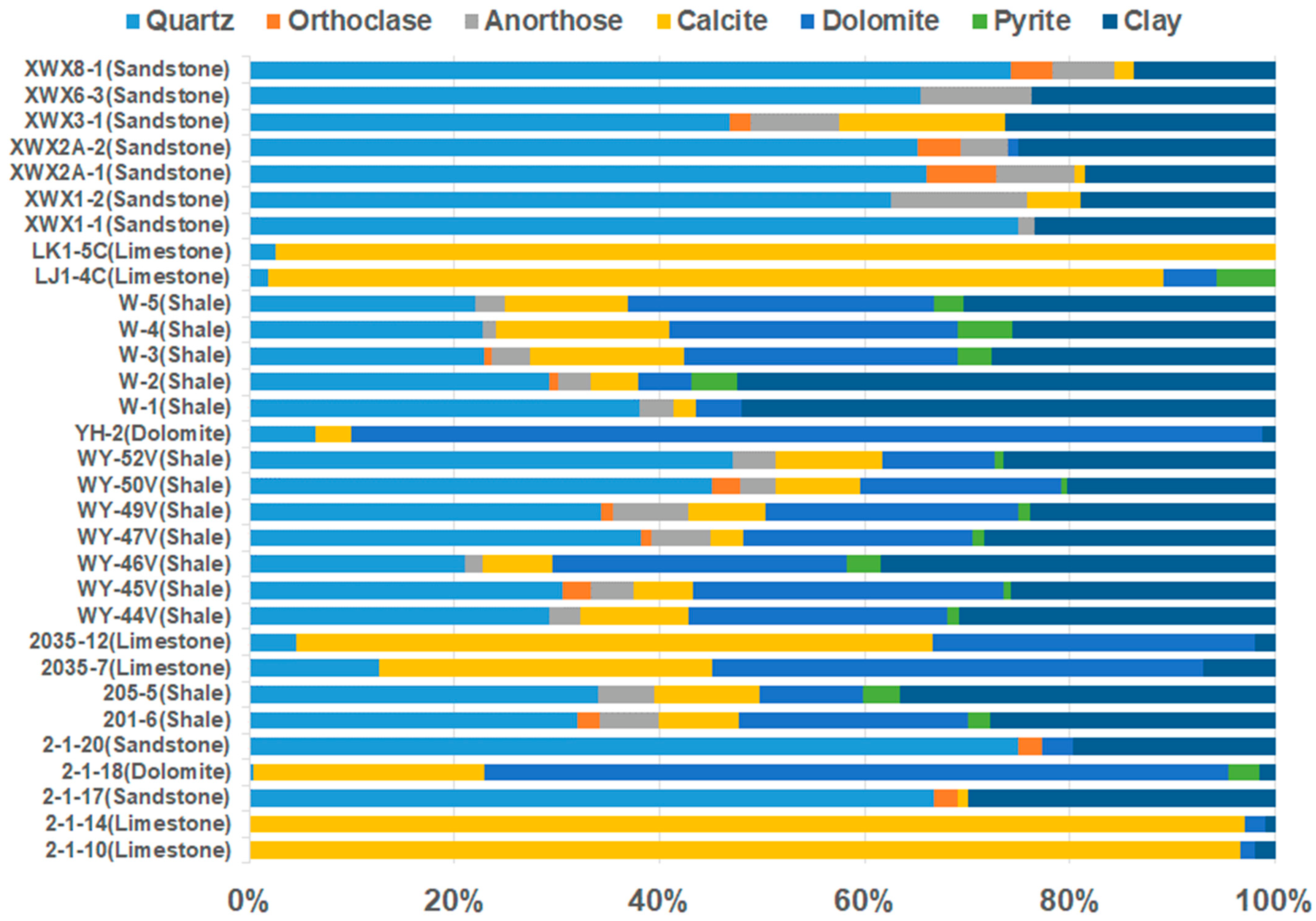
| No. | Lithology | Porosity/% | Permeability | Dry Resistivity | Conductive Mineral | Experimental Project | |
|---|---|---|---|---|---|---|---|
| /mD | /ohm-m | Clay/% | Pyrite/% | ||||
| 2-1-17 | Sandstone | 3.50 | 0.0230 | 5.70 × 102 | 30 | 0 | Fitting samples with high clay |
| 2-1-20 | Sandstone | 2.20 | 0.0750 | 2.50 × 103 | 19.7 | 0 | |
| 201-6 | Shale | 5.40 | 0.4850 | 5.90 × 102 | 27.8 | 2.2 | |
| 205-5 | Shale | 5.90 | 0.3810 | 9.40 × 102 | 36.5 | 3.7 | |
| WY-44V | Shale | 3.80 | 0.0400 | 8.50 × 102 | 30.8 | 0.9 | |
| WY-45V | Shale | 1.50 | 0.0350 | 8.30 × 103 | 25.7 | 0.8 | |
| WY-46V | Shale | 2.10 | 0.0300 | 7.80 × 102 | 38.5 | 3.1 | |
| WY-47V | Shale | 1.30 | 0.0500 | 1.00 × 104 | 28.4 | 0.8 | |
| WY-49V | Shale | 1.20 | 0.0580 | 2.30 × 104 | 23.9 | 1 | |
| WY-50V | Shale | 1.00 | 0.0660 | 3.40 × 104 | 20.3 | 0.8 | |
| WY-52V | Shale | 2.40 | 0.0270 | 1.10 × 103 | 26.5 | 0.7 | |
| 2-1-10 | Limestone | 0.33 | 0.0420 | 3.10 × 106 | 2 | 0 | Fitting samples with low clay |
| 2-1-14 | Limestone | 0.57 | 0.0300 | 1.40 × 106 | 1 | 0 | |
| 2-1-18 | Dolomite | 1.40 | 0.1100 | 1.30 × 106 | 1.5 | 3.1 | |
| 2035-7 | Limestone | 4.00 | 0.5440 | 7.30 × 103 | 7 | 0 | |
| 2035-12 | Limestone | 5.40 | 0.1180 | 2.30 × 107 | 2 | 0 | |
| YH-2 | Dolomite | 2.97 | 1.2100 | 2.20 × 105 | 1.3 | ||
| AS-2 | Sandstone | 7.75 | 3.4500 | 8.16 × 106 | 0 | 0 | |
| AS-4 | Sandstone | 12.84 | 87.5000 | 1.08 × 107 | 0 | 0 | |
| AS-5 | Sandstone | 18.36 | 326.0000 | 1.11 × 107 | 0 | 0 | |
| W1 | Shale | 4.84 | 0.1100 | 1.80 × 103 | 52 | 0 | Predicted samples with high clay |
| W2 | Shale | 5.42 | 0.3160 | 1.28 × 103 | 52.4 | 4.5 | |
| W3 | Shale | 5.26 | 0.6260 | 3.61 × 103 | 27.6 | 3.4 | |
| W4 | Shale | 4.36 | 3.9900 | 2.24 × 103 | 25.6 | 5.4 | |
| W5 | Shale | 4.21 | 0.1310 | 4.39 × 103 | 30.3 | 2.9 | |
| XWX1-1 | Sandstone | 9.93 | 0.8019 | 4.23 × 102 | 23.5 | 0 | |
| XWX1-2 | Sandstone | 2.22 | 0.0712 | 1.26 × 104 | 19 | 0 | |
| XWX2A-1 | Sandstone | 7.88 | 0.2643 | 1.44 × 104 | 18.6 | 2.3 | |
| XWX2A-2 | Sandstone | 5.53 | 0.3578 | 4.22 × 102 | 25 | 0 | |
| XWX3-1 | Sandstone | 0.86 | 0.0045 | 9.91 × 104 | 26.3 | 0 | |
| XWX6-3 | Sandstone | 6.72 | 0.8354 | 8.31 × 102 | 23.7 | 0 | |
| XWX8-1 | Sandstone | 8.74 | 0.9193 | 1.45 × 104 | 13.8 | 0 | |
| LJ1-4C | Limestone | 0.18 | 0.0010 | 1.36 × 105 | 0 | 5.7 | Predicted samples with low clay |
| AS-6 | Sandstone | 15.80 | 247.0000 | 9.57 × 106 | 0 | 0 | |
| AS-7 | Sandstone | 16.50 | 331.4000 | 1.25 × 107 | 0 | 0 | |
| AS-8 | Sandstone | 9.70 | 12.6000 | 7.64 × 106 | 0 | 0 | |
3.2. Theoretical Chargeability and Measured Chargeability
4. Results and Discussion
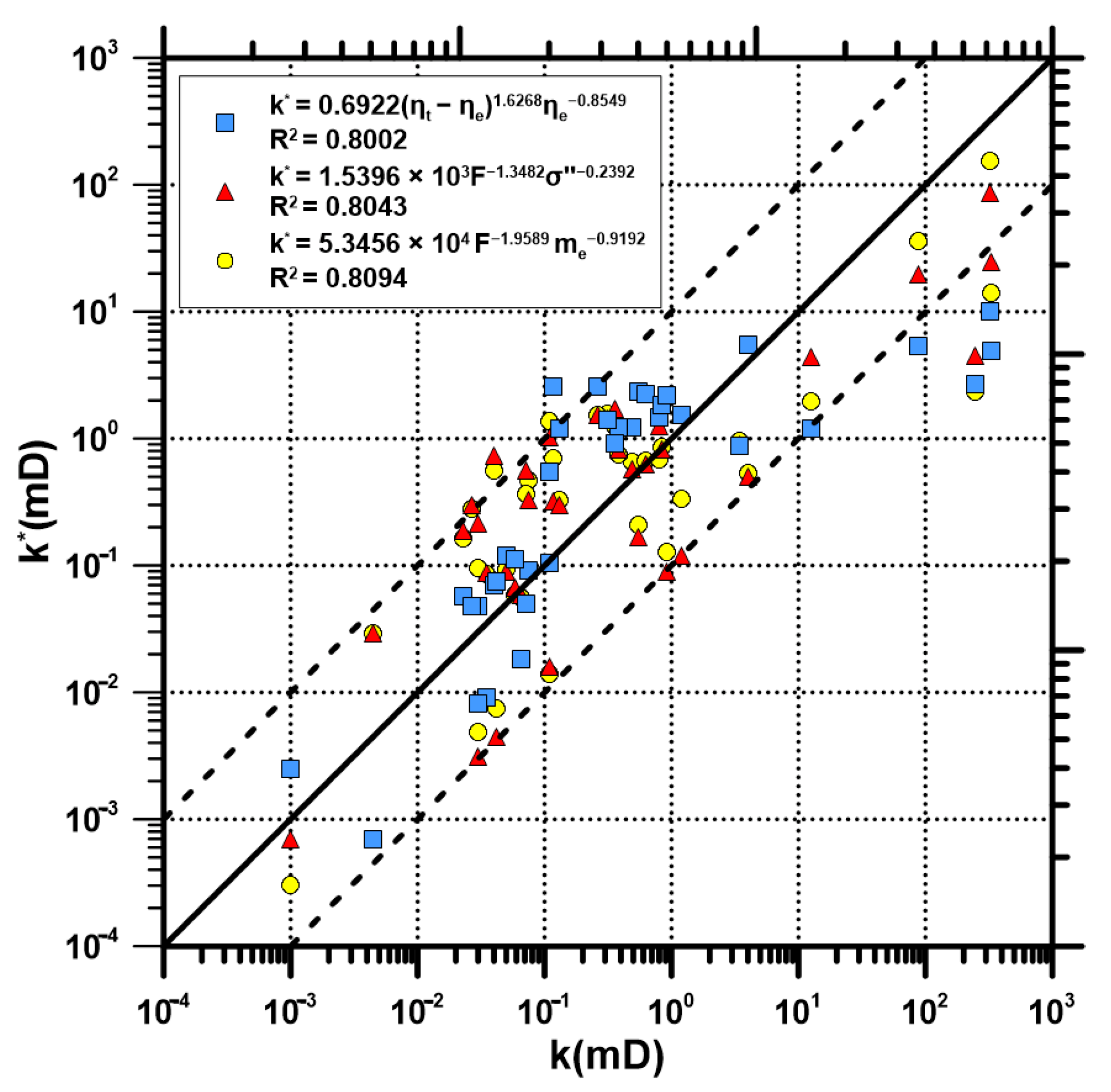
4.1. Fitting Relationship
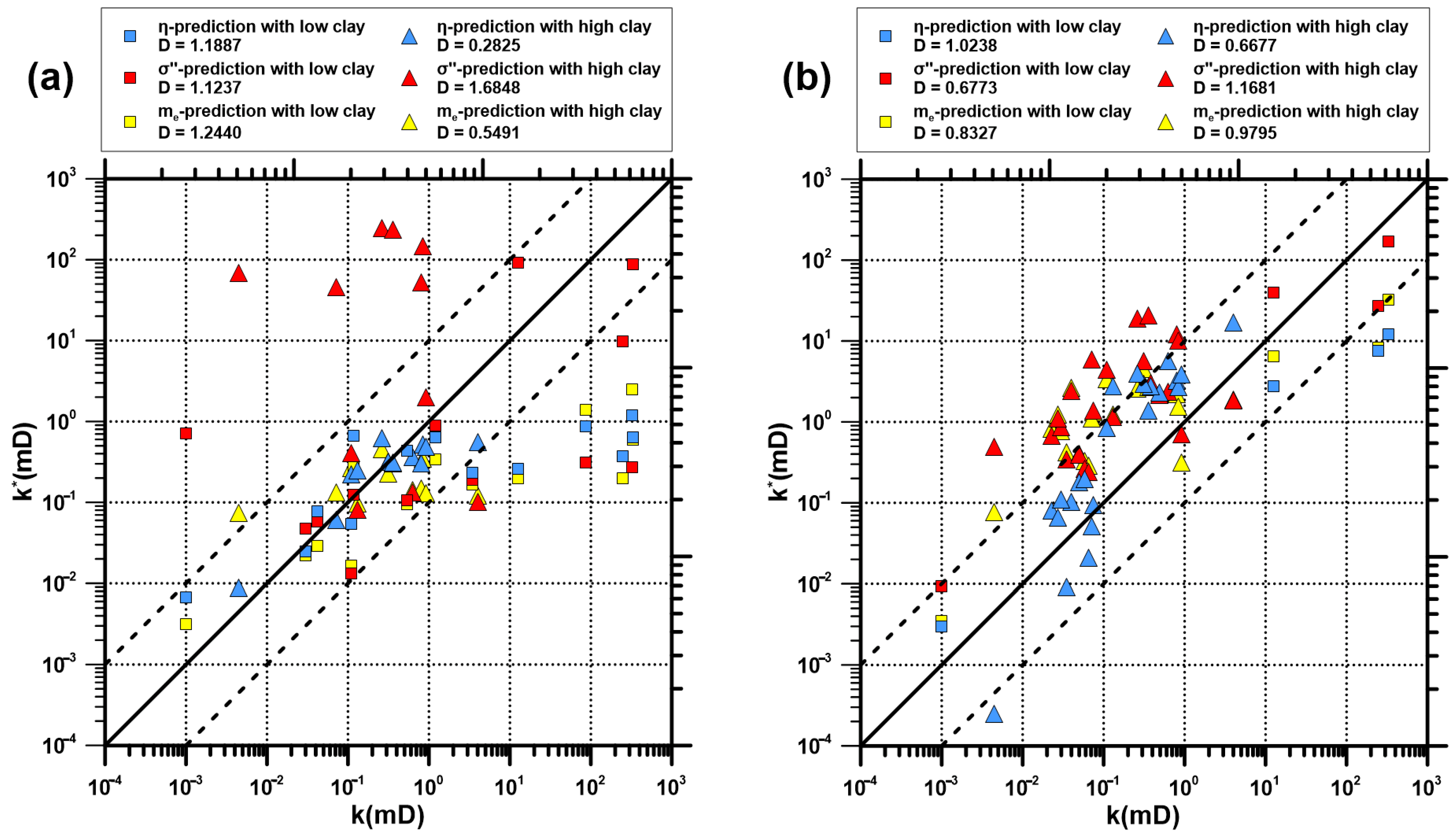
4.2. Prediction Results
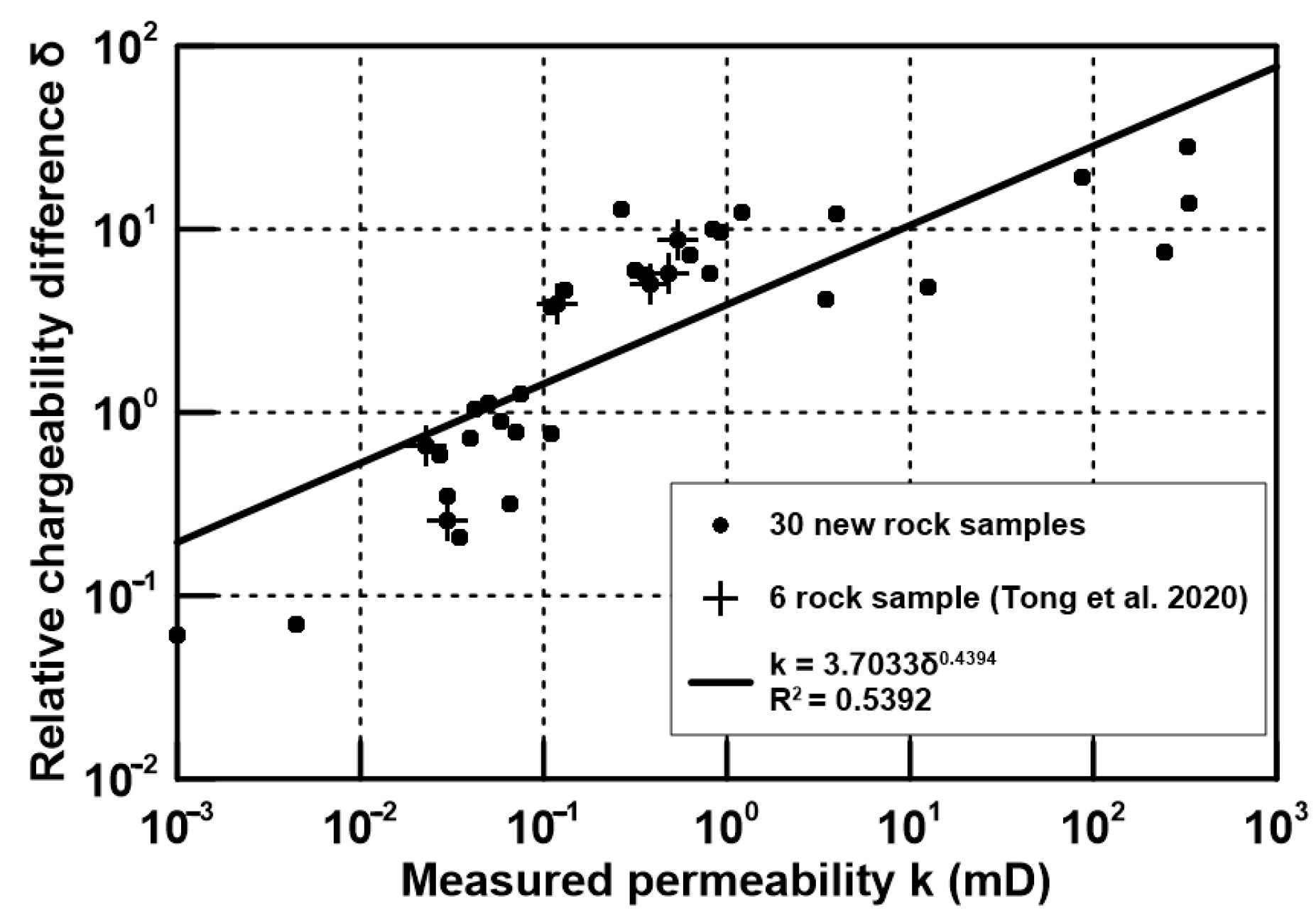
4.3. Relationship with K-C Model
4.4. Application of the Permeability Prediction Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Zhang, R.; Yan, L.; Sun, S.; Jiang, X.; Xie, X.; Jin, G. IP parameter extraction from TFEM data in the time domain. Oil Geophys. Prospect. 2016, 51, 1227–1232. [Google Scholar]
- Feng, L.; Li, Q.; Cameron, S.D.; He, K.; Colby, R.; Walker, K.M.; Deckman, H.W.; Ertaş, D. Quantifying induced polarization of conductive inclusions in porous media and implications for geophysical measurements. Sci. Rep. 2020, 10, 1669. [Google Scholar] [CrossRef] [PubMed]
- Revil, A.; Vaudelet, P.; Su, Z.; Chen, R. Induced Polarization as a Tool to Assess Mineral Deposits: A Review. Minerals 2022, 12, 571. [Google Scholar] [CrossRef]
- Linde, N.; Chen, J.; Kowalsky, M.B.; Hubbard, S. Applied Hydrogeophysics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 9–44. [Google Scholar]
- Slater, L. Near surface electrical characterization of hydraulic conductivity: From petrophysical properties to aquifer geometries—A review. Surv. Geophys. 2007, 28, 169–197. [Google Scholar] [CrossRef]
- Revil, A.; Eppehimer, J.; Skold, M.; Karaoulis, M.; Godinez, L.; Prasad, M. Low-frequency complex conductivity of sandy and clayey materials. J. Colloid Interface Sci. 2013, 398, 193–209. [Google Scholar] [CrossRef] [PubMed]
- Kozeny, J. Uber kapillare leitung der wasser in boden. R. Acad. Sci. Vienna Proc. Class I 1927, 136, 271–306. [Google Scholar]
- Guéguen, Y.; Palciauskas, V. Introduction to the Physics of Rocks; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Katz, A.; Thompson, A. Quantitative prediction of permeability in porous rock. Phys. Rev. B 1986, 34, 8179. [Google Scholar] [CrossRef]
- Kostek, S.; Schwartz, L.M.; Johnson, D.L. Fluid permeability in porous media: Comparison of electrical estimates with hydrodynamical calculations. Phys. Rev. B 1992, 45, 186. [Google Scholar] [CrossRef]
- Vinegar, H.J.; Waxman, M.H. Induced polarization of shaly sands. Geophysics 1984, 49, 1267–1287. [Google Scholar] [CrossRef]
- de Lima, O.A. Water saturation and permeability from resistivity, dielectric, and porosity Logs. Geophysics 1995, 60, 1756–1764. [Google Scholar] [CrossRef]
- Börner, F.; Schopper, J.; Weller, A. Evaluation of transport and storage properties in the soil and groundwater zone from induced polarization measurements1. Geophys. Prospect. 1996, 44, 583–601. [Google Scholar] [CrossRef]
- Weller, A.; Slater, L. Permeability estimation from induced polarization: An evaluation of geophysical length scales using an effective hydraulic radius concept. Near Surface Geophys. 2019, 17, 581–594. [Google Scholar] [CrossRef]
- Schwarz, G. A theory of the low-frequency dielectric dispersion of colloidal particles in electrolyte solution1,2. J. Phys. Chem. 1962, 66, 2636–2642. [Google Scholar] [CrossRef]
- Revil, A.; Florsch, N. Determination of permeability from spectral induced polarization in granular media. Geophys. J. Int. 2010, 181, 1480–1498. [Google Scholar] [CrossRef]
- Binley, A.; Slater, L.D.; Fukes, M.; Cassiani, G. Relationship between spectral induced polarization and hydraulic properties of saturated and unsaturated sandstone. Water Resour. Res. 2005, 41, 1–13. [Google Scholar]
- Tong, M.; Li, L.; Wang, W.; Jiang, Y. Determining capillary-pressure curve, pore-size distribution, and permeability from induced polarization of shaley sand. Geophysics 2006, 71, N33–N40. [Google Scholar] [CrossRef]
- Weller, A.; Slater, L.; Binley, A.; Nordsiek, S.; Xu, S. Permeability prediction based on induced polarization: Insights from measurements on sandstone and unconsolidated samples spanning a wide permeability range. Geophysics 2015, 80, D161–D173. [Google Scholar] [CrossRef]
- Fiandaca, G.; Maurya, P.; Balbarini, N.; Hördt, A.; Christiansen, A.; Foged, N.; Bjerg, P.L.; Auken, E. Permeability estimation directly from logging-while-drilling induced polarization data. Water Resour. Res. 2018, 54, 2851–2870. [Google Scholar] [CrossRef]
- Maurya, P.K.; Balbarini, N.; Møller, I.; Rønde, V.; Christiansen, A.; Bjerg, P.L.; Auken, E.; Fiandaca, G. Subsurface imaging of water electrical conductivity, hydraulic permeability and lithology at contaminated sites by induced polarization. Geophys. J. Int. 2018, 213, 770–785. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Javadpour, F. Upscaling pore pressure-dependent gas permeability in shales. J. Geophys. Res. Solid Earth 2017, 122, 2541–2552. [Google Scholar] [CrossRef]
- Revil, A.; Binley, A.; Mejus, L.; Kessouri, P. Predicting permeability from the characteristic relaxation time and intrinsic formation factor of complex conductivity spectra. Water Resour. Res. 2015, 51, 6672–6700. [Google Scholar] [CrossRef]
- Revil, A.; Leroy, P. Constitutive equations for ionic transport in porous shales. J. Geophys. Res. Solid Earth 2004, 109, 1–19. [Google Scholar] [CrossRef]
- Weller, A.; Zhang, Z.; Slater, L. High-salinity polarization of sandstones. Geophysics 2015, 80, D309–D318. [Google Scholar] [CrossRef]
- Revil, A.; Florsch, N.; Mao, D. Induced polarization response of porous media with metallic particles—Part 1: A theory for disseminated semiconductors. Geophysics 2015, 80, D525–D538. [Google Scholar] [CrossRef]
- Wong, J. An electrochemical model of the induced-polarization phenomenon in disseminated sulfide ores. Geophysics 1979, 44, 1245–1265. [Google Scholar] [CrossRef]
- Zhdanov, M. Generalized effective-medium theory of induced polarization. Geophysics 2008, 73, F197–F211. [Google Scholar] [CrossRef]
- Lin, W.; Zhdanov, M.S.; Burtman, V.; Gribenko, A. GEMTIP inversion of complex resistivity data using a hybrid method based on a genetic algorithm with simulated annealing and regularized conjugate gradient method. In SEG Technical Program Expanded Abstracts 2015; Society of Exploration Geophysicists: Tulsa, OK, USA, 2015; pp. 952–956. [Google Scholar]
- Tong, X.; Yan, L.; Xiang, K. Modifying the Generalized Effective-medium Theory of Induced Polarization Model in Compacted Rocks. Geophysics 2020, 85, 1–44. [Google Scholar]
- Latt, K.M.; Giao, P. Prediction of permeability of cement-admixed soft clay using resistivity and time-domain IP measurements. J. Appl. Geophys. 2017, 137, 92–103. [Google Scholar] [CrossRef]
- Revil, A.; Cosenza, P. Comment on “Generalized effective-medium theory of induced polarization”. Geophysics 2010, 75, X7–X9. [Google Scholar] [CrossRef]
- Weigand, M.; Kemna, A. Relationship between Cole–Cole model parameters and spectral decomposition parameters derived from SIP data. Geophys. J. Int. 2016, 205, 1414–1419. [Google Scholar] [CrossRef]
- Revil, A. Ionic diffusivity, electrical conductivity, membrane and thermoelectric potentials in colloids and granular porous media: A unified model. J. Colloid Interface Sci. 1999, 212, 503–522. [Google Scholar] [CrossRef] [PubMed]
- Nordsiek, S.; Weller, A. A new approach to fitting induced-polarization spectra. Geophysics 2008, 73, F235–F245. [Google Scholar] [CrossRef]

| No. | Main Conductive Medium | Main Polarization Medium | Spatial Correlation | |||||
|---|---|---|---|---|---|---|---|---|
| Medium | Medium | |||||||
| 2-1-17 | 66.42 | 9.49% | Clay | 28.95% | Solution | 3.50% | 0 | 15.75% |
| 2-1-20 | 44.02 | 4.37% | Clay | 19.27% | Solution | 2.20% | 0 | 9.90% |
| 201-6 | 25.79 | 5.33% | Clay | 26.30% | Pyrite | 2.08% | 1 | 35.61% |
| 205-5 | 19.24 | 7.20% | Clay | 36.50% | Pyrite | 3.48% | 1 | 42.93% |
| WY-44V | 20.37 | 10.22% | Clay | 29.63% | Pyrite | 1.15% | 1 | 17.53% |
| WY-45V | 132.24 | 10.15% | Clay | 25.31% | Pyrite | 0.69% | 1 | 12.26% |
| WY-46V | 69.52 | 28.61% | Clay | 37.69% | Pyrite | 3.23% | 1 | 38.57% |
| WY-47V | 138.89 | 8.23% | Clay | 28.03% | Pyrite | 1.09% | 1 | 17.43% |
| WY-49V | 168.93 | 11.95% | Clay | 23.61% | Pyrite | 1.19% | 1 | 22.59% |
| WY-50V | 194.76 | 10.08% | Clay | 20.10% | Pyrite | 0.59% | 1 | 13.30% |
| WY-52V | 44.18 | 9.61% | Clay | 25.86% | Pyrite | 0.88% | 1 | 15.28% |
| 2-1-10 | 2134.65 | 5.13% | HRM | 97.68% | Solution/Clay | 2.32% | 0 | 10.46% |
| 2-1-14 | 2878.45 | 5.60% | HRM | 98.44% | Solution/Clay | 1.56% | 0 | 7.04% |
| 2-1-18 | 594.43 | 15.18% | HRM | 94.06% | Solution/Clay/ Pyrite | 5.94% | 0 | 26.71% |
| 2035-7 | 78.65 | 4.94% | HRM | 89.28% | Solution/Clay | 10.72% | 0 | 48.24% |
| 2035-12 | 42.77 | 2.29% | HRM | 92.71% | Solution/Clay | 7.29% | 0 | 32.81% |
| YH-2 | 131.18 | 1.44% | HRM | 95.77% | Solution/Clay | 4.23% | 0 | 19.04% |
| AS-2 | 18.06 | 6.77% | HRM | 92.25% | Solution | 7.75% | 0 | 34.88% |
| AS-4 | 1.04 | 2.89% | HRM | 87.16% | Solution | 12.84% | 0 | 57.77% |
| AS-5 | 0.26 | 2.83% | HRM | 81.64% | Solution | 18.36% | 0 | 82.64% |
| W1 | 16.99 | 4.57% | Clay | 49.48% | Solution | 4.84% | 0 | 21.78% |
| W2 | 12.27 | 5.89% | Clay | 49.56% | Pyrite | 4.50% | 1 | 40.86% |
| W3 | 24.17 | 7.09% | Clay | 26.15% | Pyrite | 3.40% | 1 | 58.51% |
| W4 | 28.94 | 7.56% | Clay | 24.48% | Pyrite | 5.40% | 1 | 99.25% |
| W5 | 45.09 | 7.97% | Clay | 29.02% | Pyrite | 2.90% | 1 | 44.96% |
| XWX1-1 | 25.01 | 6.61% | Clay | 23.50% | Solution | 9.93% | 0 | 44.69% |
| XWX1-2 | 51.57 | 5.63% | Clay | 19.00% | Solution | 2.22% | 0 | 9.99% |
| XWX2A-1 | 23.69 | 2.58% | Clay | 18.60% | Solution | 7.88% | 0 | 35.46% |
| XWX2A-2 | 21.44 | 3.76% | Clay | 25.00% | Solution | 5.53% | 0 | 24.89% |
| XWX3-1 | 818.59 | 3.62% | Clay | 26.30% | Solution | 0.86% | 0 | 3.87% |
| XWX6-3 | 39.84 | 2.74% | Clay | 23.70% | Solution | 6.72% | 0 | 30.24% |
| XWX8-1 | 193.20 | 3.68% | Clay | 13.80% | Solution | 8.74% | 0 | 39.33% |
| LJ1-4C | 16946.92 | 24.90% | HRM | 94.13% | Solution/Pyrite | 5.87% | 0 | 26.41% |
| AS-6 | 6.46 | 8.36% | HRM | 84.20% | Solution | 15.80% | 0 | 71.10% |
| AS-7 | 1.66 | 5.05% | HRM | 83.50% | Solution | 16.50% | 0 | 74.25% |
| AS-8 | 8.34 | 7.54% | HRM | 90.30% | Solution | 9.70% | 0 | 43.65% |
| No. | F | ||
|---|---|---|---|
| 2-1-17 | 517.55 | 11.5221 | 1.6323 |
| 2-1-20 | 366.77 | 8.1300 | 1.0921 |
| 201-6 | 211.22 | 17.2002 | 2.4788 |
| 205-5 | 155.18 | 22.1860 | 4.0711 |
| WY-44V | 158.51 | 31.5545 | 5.4056 |
| WY-45V | 1041.73 | 5.5821 | 0.7590 |
| WY-46V | 502.12 | 7.9912 | 3.1579 |
| WY-47V | 1118.21 | 3.5422 | 0.5801 |
| WY-49V | 1305.63 | 4.7706 | 0.6958 |
| WY-50V | 1530.63 | 3.5658 | 0.5247 |
| WY-52V | 351.57 | 14.2435 | 2.0736 |
| 2-1-10 | 17659.59 | 0.1741 | 0.0257 |
| 2-1-14 | 23601.09 | 0.1397 | 0.0219 |
| 2-1-18 | 4471.45 | 1.7568 | 0.2402 |
| 2035-7 | 645.38 | 5.2304 | 0.7891 |
| 2035-12 | 362.71 | 9.1927 | 0.7271 |
| YH-2 | 1126.95 | 0.9363 | 0.1428 |
| AS-2 | 148.17 | 20.2161 | 3.4935 |
| AS-4 | 8.86 | 371.2225 | 26.9525 |
| AS-5 | 2.23 | 1867.0926 | 104.8977 |
| W1 | 142.32 | 14.3595 | 2.5664 |
| W2 | 101.51 | 23.6047 | 4.5197 |
| W3 | 197.77 | 17.5357 | 2.7247 |
| W4 | 235.79 | 16.7108 | 2.4150 |
| W5 | 366.06 | 11.4582 | 1.6260 |
| XWX1-1 | 205.90 | 0.7644 | 2.4675 |
| XWX1-2 | 428.40 | 0.3601 | 1.0310 |
| XWX2A-1 | 202.57 | 0.3506 | 1.0630 |
| XWX2A-2 | 181.25 | 0.4065 | 1.6862 |
| XWX3-1 | 6930.47 | 0.0128 | 0.0426 |
| XWX6-3 | 340.21 | 0.2538 | 0.6682 |
| XWX8-1 | 1634.67 | 0.4037 | 0.1837 |
| LJ1-4C | 125430.11 | 0.0052 | 0.0110 |
| AS-6 | 52.37 | 8.4709 | 11.8593 |
| AS-7 | 13.87 | 12.0579 | 28.8854 |
| AS-8 | 68.09 | 1.9752 | 8.3591 |
| Prediction Model | Fitted Samples | Model Parameters | Coefficient of Determination R2 | Geometric Mean Error D | |||
|---|---|---|---|---|---|---|---|
| a | b | c | Low-Clay | High-Clay | |||
| High-clay | 0.0580 | 0.8136 | 0.8983 | 0.8613 | 1.1887 | 0.2825 | |
| Low-clay | 5.1725 | 1.9503 | 0.5212 | 0.7915 | 1.0238 | 0.6677 | |
| High-clay | 3.27 × 106 | 2.1705 | 1.9321 | 0.6015 | 1.1237 | 1.6848 | |
| Low-clay | 3.72 × 104 | 1.5361 | 0.5382 | 0.9581 | 0.6773 | 1.1681 | |
| High-clay | 4.12 × 103 | 1.6994 | 1.2995 | 0.6180 | 1.2440 | 0.5491 | |
| Low-clay | 1.14 × 103 | 1.1445 | 0.1652 | 0.9547 | 0.8327 | 0.9795 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, X.; Yan, L.; Xiang, K. A Prediction Method of Compacted Rock Hydraulic Permeability Based on the MGEMTIP Model. Minerals 2023, 13, 281. https://doi.org/10.3390/min13020281
Tong X, Yan L, Xiang K. A Prediction Method of Compacted Rock Hydraulic Permeability Based on the MGEMTIP Model. Minerals. 2023; 13(2):281. https://doi.org/10.3390/min13020281
Chicago/Turabian StyleTong, Xiaolong, Liangjun Yan, and Kui Xiang. 2023. "A Prediction Method of Compacted Rock Hydraulic Permeability Based on the MGEMTIP Model" Minerals 13, no. 2: 281. https://doi.org/10.3390/min13020281
APA StyleTong, X., Yan, L., & Xiang, K. (2023). A Prediction Method of Compacted Rock Hydraulic Permeability Based on the MGEMTIP Model. Minerals, 13(2), 281. https://doi.org/10.3390/min13020281







