Abstract
The ferricrete units (Fe oxide cemented colluvial-alluvial sediment) of the Yilgarn Craton in Western Australia formed during the humid tropical and sub-tropical climates of the Cenozoic. Ferricretes are generally developed on long-lived paleodrainage systems and are products of the ferruginisation of detritus provided by the continuous erosion of upslopes. These iron-rich accumulations can become Au-enriched, as is the case in several locations previously discovered in the Yilgarn Craton; many of these host economic secondary gold deposits (e.g., Moolart Well, Mt Gibson, and Bulchina), typically occurring downslope of low saprolite hills and near paleovalleys (i.e., inset-valleys). Inset-valleys are a common paleotopographic feature buried under Quaternary alluvial and colluvial sedimentary cover. Maps of these ancient channel networks can be used as a proxy for targeting ferricrete gold deposits. These inset-valley systems generally form dendritic and noisy patterns in high-resolution aeromagnetic data due to the presence of maghemite-rich nodules and detrital magnetic pisoliths on their flanks. The main aim of this study was to use high-resolution aeromagnetic data to target ferricrete units related to inset-valleys systems across the Yilgarn Craton. A spatial predictive model was used to learn and predict the geological units of interest from pre-processed aeromagnetic data. The predicted inset-valleys systems were able to confine the exploration space and define a new exploration frontier for ferricrete gold deposits.
1. Introduction
The ferricrete units of the Yilgarn Craton are Fe oxide-cemented colluvial-alluvial sediments [1] that are generally developed on long-lived drainage systems of paleovalleys. These units are formed during the humid tropical and sub-tropical climates of the early to mid-Cenozoic [2]. Ferricretes are generated through the ferruginisation of nodules and pisoliths supplied by the continuous erosion of older duricrust and lithic fragments of less-weathered materials from upslope saprock and saprolite [3,4]. Pisoliths and nodules are mainly hematite-, goethite- and kaolinite-rich. Ferricretes have been overprinted continuously through the re-weathering of sediments by groundwater in the presence of organic matter [3,4].
Au-enriched ferricretes have been discovered in multiple locations of the Yilgarn Craton and some of them host economic secondary gold mineralisation (e.g., Moolart Well, Mt Gibson, and Bulchina). Ferricrete gold deposits are typically small (<500,000 ounces) and low grade (<1–5 g/t Au). This type of deposit generally consists of flat-lying zones (a few hundred metres to several kilometres long, less than a kilometre wide, and 2–10 m thick) of Au enrichment within the upper ferruginous zone of lateritic profiles [3,4]. They can be efficiently mined because they are generally located near the surface [4,5,6,7]. The physical and chemical behaviour of Au during the formation and evolution of ferricretes are not fully known [3]. For instance, significant unweathered mineralisation beneath Au-enriched ferricretes cannot be located easily. This is because the ferricrete deposits are mechanically transported from the upper ferruginous zone of lateritic profiles and form an extensive blanket compared to unweathered mineralisation. Anand et al. [3] thoroughly investigated the ferricrete Au deposits of the Yilgarn Craton and identified the possible mechanisms of dispersion and enrichment of Au during their formation. The evolution of the ferricrete Au deposits generally consists of multiple stages of mechanical, chemical, and biological mobilisation and reprecipitation of Au in a paleodrainage environment. Au enrichment in ferricretes is likely sourced from underlying or near upslope-located primary Au-enriched rocks. The Fe oxide-rich paleodrainage systems of the Yilgarn Craton indicate that significant subterranean lateral influx and groundwater migration have transported dissolved Fe and Au along and above an unconformity during an extended period of biological and chemical weathering [8].
Au-enriched ferricretes typically occur downslope of the low saprolite hills and proximal to inset-valleys (i.e., buried paleovalleys). The predicted map of inset-valleys [9] can be used as a proxy for targeting ferricrete gold deposits as they are developed along the flanks of inset-valleys. Ferricretes are generally covered by 2–10 m of younger transported sediments (Figure 1). Inset-valleys are a common feature of regolith in the Yilgarn Craton [2,10,11,12,13]. Large-scale structures such as faults and shears may have influenced the position of paleovalleys; however, these structures may not be associated with Au mineralisation [14].
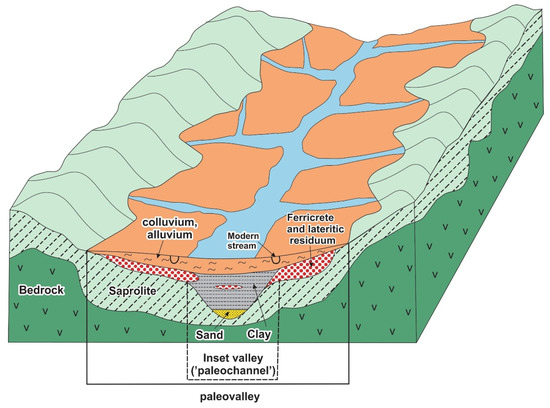
Figure 1.
Location of Au-enriched ferricrete units in paleovalley systems (adapted with permission from Ref. [3]. Copyright 2022 Elsevier).
Maghemite-rich nodules and pisoliths in inset-valley systems form dendritic and noisy patterns in high-resolution aeromagnetic data. Aeromagnetic data are often used to map paleovalleys [15,16], and resolution permitting, are accompanied with radiometric or different types of electromagnetic data [17,18]. Maghemite is a common mineral in ferricretes overlying saprolite units; however, its levels decrease sharply down the weathering profile [2]. The heating of goethite during bush fires may be a reason for maghemite formation [19]. High-resolution aeromagnetic data can be used efficiently to identify maghemite-rich ferruginous nodules and pisoliths in paleovalley systems. These maghemite-rich units form noisy and dendritic patterns visible in imaged aeromagnetic data [2,14]. Periodic accumulation or the reworking of maghemite-rich ferruginous nodules and pisoliths from higher elevations in the paleodrainage system likely have generated more than one magnetic edge feature in inset-valleys. Inset-valleys with magnetic features vary in width from 100 m to 1.5 km and are up to 30 km in length.
Applied machine learning is considered an established tool in the geosciences, including solid Earth geoscience [20,21], geochemistry [22], mineral potential mapping [23,24,25], remote sensing [26], and seismic interpretation [27]. However, it is important to acknowledge the shortcomings of machine learning in geoscience applications [28,29]. The particularities of geosystems and geoscience data (e.g., multi-source, multi-scale, spatial and temporal heterogeneity, auto- and cross-correlations) must be fully understood before any implementation of machine learning models. Suitable machine learning algorithms for geoscience applications should be accurate, interpretable, and physically realistic.
The geological features of interest in this study are the paleovalley-related ferricrete units with unique magnetic characteristics. These units form noisy and dendritic patterns in gridded aeromagnetic data. Capturing such complex spatial patterns is not possible via classical machine learning algorithms because these techniques only use the information available at single points. Spatially-aware machine learning algorithms, such as convolutional neural networks [30,31] and spatial random forests [32], can be used to predict such complex spatial patterns automatically.
The main aim of this study is to use high-resolution aeromagnetic data and spatial machine learning to automatically target paleovalley-related ferricrete units with magnetic characteristics. High-resolution aeromagnetic data are pre-processed to enhance the short-wavelength features produced by shallow sources and suppress long-wavelength magnetic features. A spatial predictive model (i.e., spatial random forests, Talebi, et al. [32]) is subsequently used to learn paleovalley-related ferricrete units with magnetic characteristics from pre-processed aeromagnetic data. The trained spatial random forests model is finally used to predict ferricrete units in other areas across the Yilgarn craton where high-resolution aeromagnetic data are available. The predicted ferricrete units can be used later to confine the exploration space and define new exploration targets for ferricrete gold deposits.
2. Study Areas
Three areas in the Yilgarn craton (Figure 2) were selected for the proposed experiment. There are publicly available high-resolution aeromagnetic data for Tarmoola, Bronzewing, and Moolart Well in Western Australia, collected by the various exploration companies over the last few decades. The following sub-sections discuss the geological settings of these three areas.
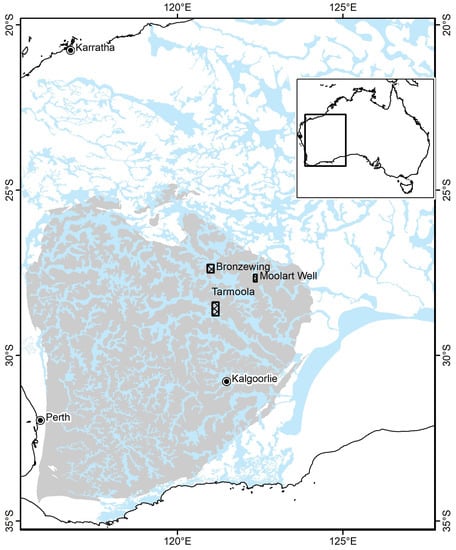
Figure 2.
Location of three case study areas (black rectangles crosshatched) within the Yilgarn Craton in grey colour. The regional extent of the known mapped paleovalleys in blue after Bell, et al. [33].
2.1. Tarmoola
The Tarmoola gold deposit is located 30 km to the north-west of Leonora in the Eastern Goldfields and is 265 km north of Kalgoorlie (Figure 2). It is the largest granitoid-hosted gold deposit in the Yilgarn Craton and produces ~28 Mt of ore with an average grade of 1.8 g/t Au; secondary mineralisation occurs in multiple styles including shallow ferricrete gold and supergene-enriched saprolite.
2.2. Bronzewing
The Bronzewing ferricrete Au deposit is located in the Yandal greenstone belt, 375 km north of the Kalgoorlie gold mine. No primary mineralisation has been reported beneath the deposit [5]. In total, 19,000 ounces of gold (average ore grade of 1.49 g/t Au) have been mined at this location. This deposit is located on alluvial systems that are underlain by 30–50 m deep inset-valleys. Variably indurated yellowish-brown ferricrete at the flanks of the inset-valley hosts the Au mineralisation. The ferricrete units are overlain by about 7 m of younger transported cover. The lower part of the younger transported cover is significantly Au-enriched (up to 600 ppb). The Au contained in the ferricrete is probably derived from nearby deposits [5].
2.3. Moolart Well
The Moolart Well is the largest ferricrete Au deposit of the Yilgarn Craton, located 400 km NE of Kalgoorlie in the Duketon greenstone belt. Intermediate and tholeiitic dolerite sills (up to 200 m thick) have intruded the interflow sedimentary horizons [4,34] and formed the bedrock of the area. Low-grade primary mineralisation (0.3–0.5 g/t Au; 103,000 oz Au) is predominantly hosted within diorite intrusives and a north-trending shear zone. The economic Au mineralisation is of a secondary nature and confined to the upper flat-laying ferricrete units (i.e., yellowish-brown and reddish-brown ferricretes extend over 4 km N-S and up to 1 km E-W) within the paleovalley sediments. The ferricrete deposit has an average thickness of 4 m. In addition, the underlying Au-bearing saprolite is derived from the weathering of primary mineralisation [4]. The Moolart Well Au deposit is situated in a paleovalley system bounded by low hills of saprolite and saprock.
3. Materials and Methods
The high-resolution aeromagnetic data were pre-processed to enhance the characteristic patterns of the inset-valley’s ferricrete units and to prepare the input raster layers for analysis through the spatial random forest predictive model workflow. The implemented pre-processing steps and the spatial random forests algorithm are discussed in the following subsections.
3.1. High-Resolution Aeromagnetic Data
The high-resolution aeromagnetic data used in this study were sourced from the Western Australia Department of Mining, Industrial Regulation and Safety (DMIRS) data portal (dasc.dmirs.wa.gov.au, accessed on 10 June 2021). Data was extracted from various company surveys recorded between 1996 and 2003. Details of these surveys are available in Table 1.

Table 1.
Aeromagnetic surveys specifications.
The first step in the preparation of a consistent aeromagnetic input layer for all three areas involved generating total magnetic intensity (TMI) grids of consistent resolution, using line data from the surveys listed in Table 1. The upward and downward continuation transformations [35] were used to reproduce the aeromagnetic data at the designated height (25 m).
The aeromagnetic dataset for the Moolart Well area was firstly upward-continued for 5 m and then gridded by the use of a 25 m grid cell size. The aeromagnetic data for the Tarmoola were downward-continued for 25 m and then gridded with a 25 m grid cell size. The individual surveys in the Bronzewing area were upward/downward-continued to reproduce a signal at the same height of 25 m prior to gridding. The same gridding algorithm (i.e., minimum curvature [36]) was used for all areas. These TMI grids of consistent resolution were used as a basis for the reduction to pole transformation, as described below.
The texture and amplitude variation of the magnetic signal strongly depend on various structural elements (e.g., faults, folds, and lithological factors) and the variable distribution of the magnetic minerals among different units. In order to enhance features of interest, a few transformation techniques were applied to the aeromagnetic data. The main goal was to emphasise shallow inset-valley-related ferricrete units. In addition, long-wavelength magnetic features should have been suppressed. Since the available data is of high resolution with considerable high-frequency content, applying almost any type of high and low pass filters would cause Gibb’s ringing, a common artifact with this type of processing.
Firstly, the reduction to pole transformation (RTP) was applied to the TMI data. To avoid processing artifacts, the upward-continued version of the RTP data were generated at the height of an additional 50 m on top of the flying height (25 m). This upward-continued data were subtracted from the original RTP data, suppressing long-wavelength magnetic content and producing a data set with high frequency (HF) features. The short-wavelength features of shallow sources were further enhanced by applying the first vertical derivative transformation (1VD) to the HF content data. This final transformed data set was used as an input for SRF. All these transformations are further described in Table 2. The processing of the aeromagnetic data was undertaken in Seequent Oasis Montaj. Figure 3 shows the pre-processing sequence for the high-resolution aeromagnetic data in the Tarmoola area.

Table 2.
Transformations applied to the aeromagnetic data.
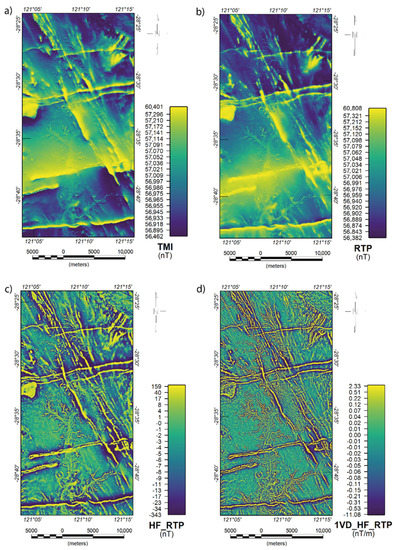
Figure 3.
Pre-processed high-resolution aeromagnetic data in the Tarmoola area. (a) Total magnetic intensity (TMI) grid. (b) Reduced to pole (RTP) grid. (c) Accentuated high frequency (HF) content of the RTP grid. (d) First vertical derivative (1VD) of the HF grid. All grids are histogram-equalised and presented in a perceptually uniform colour scale.
3.2. Spatial Machine Learning
The spatial random forests technique [32] is a spatially-aware machine learning algorithm [28] on the basis of higher-order spatial statistics and is used for the analysis and modelling of geospatial data. Unlike non-spatial machine learning techniques that use the spectral information in a single pixel as input predictors, the SRF technique uses local spatial-spectral information to learn heterogeneity, auto- and cross-correlations, and complex spatial patterns. This study used an SRF classifier to target inset-valley-related ferricrete units.
The most important parameters for the SRF technique are the size of the local patterns, the number of spatial trees in the forest, and the number of randomly selected predictors at each split. More information regarding the details of the SRF technique and suitable strategies used for tuning hyperparameters can be found in Probst, et al. [39] and Talebi, et al. [32].
3.3. Model Training
The processed (i.e., RTP, HF, and 1VD-filtered) high-resolution aeromagnetic layer for the Tarmoola area was used to train the SRF classifier. A balanced dataset was selected manually from this area, including 850 samples from the dendritic and noisy patterns associated with the inset-valley-related ferricrete units (blue dots in Figure 4) and 850 randomly selected samples from the rest of the area (red dots in Figure 4). In addition, validation datasets (500 samples from each class) were selected from the three study areas to assess the overall performance and generalisation capability of the SRF classifier.
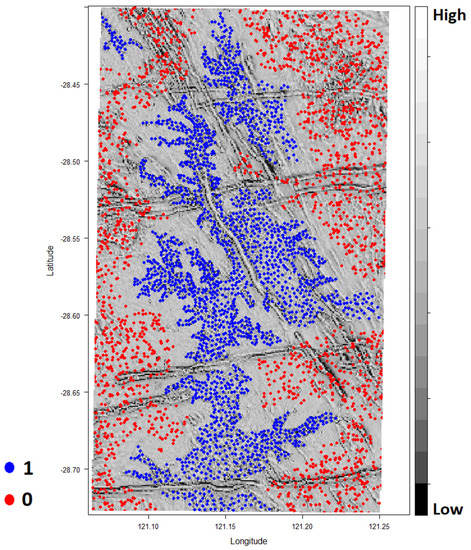
Figure 4.
Processed high--resolution aeromagnetic layer for the Tarmoola area overlain by the training samples. Blue dots represent the positive samples from the area of interest, whereas the red dots represent the random negative samples from the rest of the area.
A grid-search was used to find the optimal hyperparameters of the SRF model, which resulted in 400 pixels (i.e., 20 pixels × 20 pixels) as the optimum size of local patterns, 1000 spatial trees in the forest, and the default value, , for the number of randomly selected predictors at each split. This trained SRF classifier was used to predict the dendritic and noisy patterns associated with the inset-valley-related ferricrete units in the Tarmoola, Bronzewing, and Moolart Well areas.
4. Results
4.1. Tarmoola
The processed high-resolution aeromagnetic layer for the Tarmoola area is shown in Figure 5. The predicted results of the SRF classifier were draped over the high-resolution aeromagnetic data. The blue colour represents areas predicted as the positive class—mapping the extent of the magnetic gravels—and the red colour represents the areas predicted as the negative class, devoid of these gravels. The majority of the dendritic and noisy patterns related to the inset-valley ferricretes units are accurately predicted. Table 3 shows the confusion matrix for the SRF classifier on the basis of the validation dataset from the Tarmoola area. The overall accuracy of the SRF model in this area was 91.9%.

Figure 5.
Processed high-resolution aeromagnetic layer for the Tarmoola area overlain by the predicted results via the SRF classifier. The blue colour represents the areas predicted as the positive class whereas the red colour represents the areas predicted as the negative class. The yellow marker shows the point location of the main deposit, with a yellow outline giving the approximate envelope of the mineralised ferricrete unit.

Table 3.
Confusion matrix for the SRF classifier—Tarmoola area.
4.2. Bronzewing
The processed high-resolution aeromagnetic layer for the Bronzewing area is shown in Figure 6. Although the majority of the dendritic and noisy patterns related to the inset-valley ferricrete units were accurately predicted, the proportion of misclassified areas was higher than the Tarmoola area. This was expected because the SRF model was trained via the use of a dataset from the Tarmoola area. Table 4 shows the confusion matrix for the SRF classifier on the basis of the validation dataset from the Bronzewing area. The overall accuracy of the SRF model in this area was 82.5%.
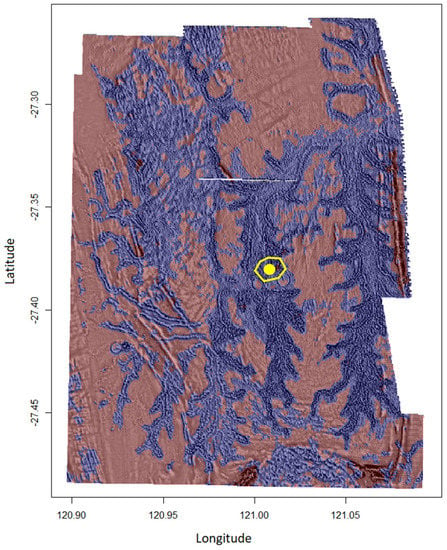
Figure 6.
Processed high-resolution aeromagnetic layer for the Bronzewing area overlain by the predicted results via the SRF classifier. The blue colour represents the areas predicted as the positive class whereas the red colour represents the areas predicted as the negative class. The yellow marker shows the point location of the main deposit, with a yellow outline giving the approximate envelope of the mineralised ferricrete unit.

Table 4.
Confusion matrix for the SRF classifier—Bronzewing area.
4.3. Moolart Well
Even though the SRF classifier was trained on the basis of the dataset from the Tarmoola area, the extent of the ferricrete units hosting the Moolart Well Au deposit was accurately predicted (yellow dot in Figure 7). This is partly related to the implementation of a consistent pre-processing step for the high-resolution aeromagnetic data and the generalisation capability of the SRF model. Table 5 shows the confusion matrix for the SRF classifier based on the validation dataset from the Moolart Well area. The overall accuracy of the SRF model in this area was 92%.

Figure 7.
Processed high-resolution aeromagnetic layer for the Moolart Well area overlain by the predicted results via SRF classifier. The blue colour represents the areas predicted as the positive class, whereas the red colour represents the areas predicted as the negative class. The yellow marker shows the point location of the main deposit, with a yellow outline the approximate envelope of the mineralised ferricrete unit.

Table 5.
Confusion matrix for the SRF classifier—Moolart Well area.
5. Discussion
Aeromagnetic data are often used to map paleovalley systems. However, the mapping process is a time-consuming manual task [33]. Manually delineated potential paleovalley system maps are subjective and depend on the operator’s experience and familiarity with the study area. The use of spatial machine learning to detect paleovalley systems is more objective and faster, potentially allowing for the large-scale analysis of extensive areas—provided the appropriate resolution of the geophysical data.
This study used high-resolution aeromagnetic data and spatial machine learning to predict inset-valley-related ferricrete units. Implementing a consistent approach to the pre-processing of the aeromagnetic data was necessary to improve the generalisation capability of the predictive model. A sequence of transformations (e.g., RTP, multiple upward continuations and 1VD) was used to enhance the dendritic and noisy patterns associated with the inset-valley-related ferricrete units and suppress the long-wavelength magnetic content. The resolution of the magnetic data was crucial; while the presented method worked well with detailed surveys flown between 20–50 m above ground at 50–100 m line spacing (Table 1), it will fail to detect patterns in regional-scale data. The patterns became non-apparent in the regional data due to higher ground separation, which attenuated the high-frequency signal and the additional along- and across-flight line signal smoothing inherently present in most gridding algorithms. The overall accuracy of the SRF classifier in the Bronzewing area was lower than in the other two study areas. The lower prediction accuracy might be related to the fact that the Bronzewing dataset was composed of multiple surveys and the slightly different near-surface geological setting in this area.
Ferricrete units form complex spatial patterns (i.e., dendritic and noisy patterns) in processed aeromagnetic layers. These patterns cannot be detected via classical non-spatial machine learning algorithms. A spatially aware machine learning algorithm such as SRF or convolutional neural networks (CNN) is needed to detect such complex spatial patterns. The SRF classifier predicted the location of the host regolith units, i.e., the magnetic ferricretes and gravels, successfully. The model could be extended to target the ferricrete Au deposits directly. For this purpose, more pre-processed geophysical, geochemical, geological, and paleotopographic layers could be added to provide additional information that would further constrain the search space. However, the SRF model is computationally demanding, and for the prediction of larger areas such as the entire Yilgarn craton or using many input layers, access to fast computers would be necessary.
Aeromagnetic mapping of the ferricrete deposits in inset-valleys is relevant to gold exploration in the Yilgarn Craton. These ferricretes are dominated by ferruginous pisoliths and nodules, which represent the coarser fraction (>2 mm in diameter)—compared to the finer fractions (<2 mm)—of the ferricrete. Maghemite only occurs in the coarse fraction, which displays the highest content of Fe2O3, Au, and As, as compared to the fine fractions. Anand et al. (2019) [3] separated the magnetic (hematite-maghemite-rich) from the non-magnetic (hematite-goethite-rich) ferruginous nodules and pisoliths of the coarse fraction and found that both magnetic and non-magnetic fractions occur in the ferricrete at Moolart Well; the non-magnetic fraction is more abundant than the magnetic fraction, and both are highly anomalous in Au. However, Au is much more abundant in the magnetic fraction compared to the non-magnetic fraction. Therefore, mapping inset-valley systems can confine the exploration space and define the exploration frontier for ferricrete gold deposits. The proposed predictive model for mapping inset-valley systems uses high-resolution aeromagnetic data which are generally available for brownfield exploration.
6. Conclusions
This study used high-resolution aeromagnetic data and spatial machine learning to target ferricrete units that are related to inset-valley systems across the Yilgarn Craton. The high-resolution aeromagnetic data were pre-processed by implementing a sequence of transformations (e.g., RTP, multiple upward continuations, and 1VD) to enhance the dendritic and noisy patterns associated with the inset-valley-related ferricrete units and to suppress the long wavelength magnetic content. A spatial random forest predictive model was trained by the use of the pre-processed aeromagnetic layer in the Tarmoola area. The trained SRF model was used to efficiently predict the ferricrete units in the Tarmoola, Bronzewing, and Moolart Well areas in Western Australia. The predicted map of the inset-valley-related ferricrete units can be used as a proxy for targeting ferricrete gold deposits.
Author Contributions
Conceptualization, H.T., W.S., A.O., V.M. and R.A.; methodology, H.T., J.M. and D.C.; data curation, H.T. and J.M.; writing—original draft preparation, H.T., W.S., J.M. and V.M.; writing—review and editing, H.T., J.M., W.S., V.M., A.O., R.A. and D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deep Earth Imaging Future Science Platform and Mineral Resources Discovery Program at CSIRO.
Data Availability Statement
The high-resolution aeromagnetic surveys stated in Table 1 are freely available from the Western Australia Department of Mining, Industrial Regulation and Safety (DMIRS) data portal (dasc.dmirs.wa.gov.au). The final processed aeromagnetic data used as the input to the SRF model are available from the authors upon request.
Acknowledgments
We acknowledge the CSIRO colleagues who reviewed the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lamplugh, G.W. Calcrete. Geol. Mag. 1902, 9, 575. [Google Scholar] [CrossRef] [Green Version]
- Anand, R.R.; Paine, M. Regolith Geology of the Yilgarn Craton, Western Australia: Implications for Exploration. Aust. J. Earth Sci. 2002, 49, 3–162. [Google Scholar] [CrossRef]
- Anand, R.R.; Hough, R.M.; Salama, W.; Aspandiar, M.F.; Butt, C.R.M.; González-Álvarez, I.; Metelka, V. Gold and Pathfinder Elements in Ferricrete Gold Deposits of the Yilgarn Craton of Western Australia: A Review with New Concepts. Ore Geol. Rev. 2019, 104, 294–355. [Google Scholar] [CrossRef]
- Anand, R.R.; Lintern, M.; Hough, R.; Noble, R.; Verrall, M.; Salama, W.; Balkau, J.; Radford, N. The Dynamics of Gold in Regolith Change with Differing Environmental Conditions over Time. Geology 2017, 45, 127–130. [Google Scholar] [CrossRef]
- Galloway Warland, N.; Phang, C. Laterite Gold Deposits-Southern Yandal Belt. In Yandal Greenstone Belt Regolith, Geology and Mineralisation; AIG Bulletin No. 32; Phillips, G.N., Anand, R.R., Eds.; Australian Institute of Geoscientists Bulletin: Perth, Australia, 2000; pp. 179–186. [Google Scholar]
- Paine, M.D.; Foo, M.F.P.; Phang, C.; Cox, A. Description and Evolution of the Gourdis and Empire Laterite Gold Deposits, Northern Yandal Belt. In Proceedings of the Yandal Greenstone Belt, Perth, Australia, 10–11 July 2000; Phillips, G.N., Anand, R.R., Eds.; AIG Bulletin No. 32. Australian Institute of Geoscientists: Perth, Australia, 2000; pp. 165–177. [Google Scholar]
- Anand, R.R. Regolith and Geochemical Synthesis of the Yandal Greenstone Belt. In Proceedings of the Yandal Greenstone Belt, Perth, Australia, 10–11 July 2000; Phillips, G.N., Anand, R.R., Eds.; AIG Bulletin No. 32. Australian Institute of Geoscientists: Perth, Australia; 2000; pp. 79–111. [Google Scholar]
- Jones, M.; Lidbury, R. Unconformity-Related Weathered Laterite Profiles at Mt Gibson Gold Mine, Yilgarn Craton, Western Australia. In New Approaches to an Old Continent, Proceedings of the 3rd Australian Regolith Conference, Kalgoorlie, Australia, 2–9 May 1998; Britt, A.F., Bettenay, L., Eds.; CRC Leme: Glen Osmond, Australia, 1998. [Google Scholar]
- De Broekert, P. Origin of Tertiary Inset-Valleys and Their Fills, Kalgoorlie, Western Australia. Ph.D. Thesis, Australian National University, Canberra, Australia, 2002. [Google Scholar]
- Kern, A.M.; Commander, D.P. Cainozoic Stratigraphy in the Roe Palaeodrainage of the Kalgoorlie Region, Western Australia. Geol. Surv. West. Aust. Rep. 1993, 34, 85–95. [Google Scholar]
- Clarke, J.D.A. Stratigraphy of the Lefroy and Cowan Palaeodrainages, Western Australia. J. R. Soc. West. Aust. 1993, 76, 15–22. [Google Scholar]
- De Broekert, P.; Sandiford, M. Buried Inset-Valleys in the Eastern Yilgarn Craton, Western Australia: Geomorphology, Age, and Allogenic Control. J. Geol. 2005, 113, 471–493. [Google Scholar] [CrossRef] [Green Version]
- Thorne, R.; Anand, R.; Suvorova, A. The Formation of Fluvio-Lacustrine Ferruginous Pisoliths in the Extensive Palaeochannels of the Yilgarn Craton, Western Australia. Sediment. Geol. 2014, 313, 32–44. [Google Scholar] [CrossRef]
- Wildman, J.E.; Compston, D. Magnetic Expression of Palaeodrainage Systems in the Yandal Greenstone Belt: Implications for Exploration. In Yandal Greenstone Belt, Regolith, Geology and Mineralisation; AIG Bulletin No. 32; Australian Institute of Geoscientists: Perth, Australia, 2000; pp. 157–164. [Google Scholar]
- Foss, C.; Reed, G.; Keeping, T.; Davies, M. Magnetic Mapping of River Channel and Palaeochannel Deposits—An Example from Teetulpa, South Australia. ASEG Ext. Abstr. 2015, 2015, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Mackey, T.; Lawrie, K.; Wilkes, P.; Munday, T.; de Souza Kovacs, N.; Chan, R.; Gibson, D.; Chartres, C.; Evans, R. Palaeochannels near West Wyalong, New South Wales: A Case Study in Delineation and Modelling Using Aeromagnetics. Explor. Geophys. 2000, 31, 1–7. [Google Scholar] [CrossRef]
- Jessell, M.; Boamah, K.; Duodu, J.A.; Ley-Cooper, Y. Geophysical Evidence for a Major Palaeochannel within the Obosum Group of the Volta Basin, Northern Region, Ghana. J. Afr. Earth Sci. 2015, 112, 586–596. [Google Scholar] [CrossRef]
- Wilford, J. Using Airborne Geophysics to Define the 3D Distribution and Landscape Evolution of Quaternary Valley-Fill Deposits around the Jamestown Area, South Australia. Aust. J. Earth Sci. 2009, 56, S67–S88. [Google Scholar] [CrossRef]
- Anand, R.R.; Gilkes, R.J. The Association of Maghemite and Corundum in Darling Range Laterites, Western Australia. Soil Res. 1987, 25, 303–311. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine Learning for Data-Driven Discovery in Solid Earth Geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Talebi, H.; Mueller, U.; Tolosana-Delgado, R.; Grunsky, E.C.; McKinley, J.M.; Caritat, P. Surficial and Deep Earth Material Prediction from Geochemical Compositions. Nat. Resour. Res. 2019, 28, 869–891. [Google Scholar] [CrossRef] [Green Version]
- Zuo, R.; Xiong, Y.; Wang, J.; Carranza, E.J.M. Deep Learning and Its Application in Geochemical Mapping. Earth-Sci. Rev. 2019, 192, 1–14. [Google Scholar] [CrossRef]
- Talebi, H.; Mueller, U.; Peeters, L.J.M.; Otto, A.; de Caritat, P.; Tolosana-Delgado, R.; van den Boogaart, K.G. Stochastic Modelling of Mineral Exploration Targets. Math. Geosci. 2022, 54, 593–621. [Google Scholar] [CrossRef]
- Schaeben, H.; Kost, S.; Semmler, G. Popular Raster-Based Methods of Prospectivity Modeling and Their Relationships. Math. Geosci. 2019. [Google Scholar] [CrossRef]
- Sun, T.; Li, H.; Wu, K.; Chen, F.; Zhu, Z.; Hu, Z. Data-Driven Predictive Modelling of Mineral Prospectivity Using Machine Learning and Deep Learning Methods: A Case Study from Southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef] [Green Version]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine Learning in Geosciences and Remote Sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Di, H.; Shafiq, M.A.; Alaudah, Y.; AlRegib, G. Successful Leveraging of Image Processing and Machine Learning in Seismic Structural Interpretation: A Review. Lead. Edge 2018, 37, 451–461. [Google Scholar] [CrossRef]
- Talebi, H.; Peeters, L.J.M.; Mueller, U.; Tolosana-Delgado, R.; van den Boogaart, K.G. Towards Geostatistical Learning for the Geosciences: A Case Study in Improving the Spatial Awareness of Spectral Clustering. Math. Geosci. 2020, 52, 1035–1048. [Google Scholar] [CrossRef]
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine Learning for the Geosciences: Challenges and Opportunities. IEEE Trans. Knowl. Data Eng. 2019, 31, 1544–1554. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Talebi, H.; Peeters, L.J.M.; Otto, A.; Tolosana-Delgado, R. A Truly Spatial Random Forests Algorithm for Geoscience Data Analysis and Modelling. Math. Geosci. 2022, 54, 1–22. [Google Scholar] [CrossRef]
- Bell, J.; Kilgour, P.; English, P.; Woodgate, M.; Lewis, S.; Wischusen, J. WASANT Palaeovalley Map—Distribution of Palaeovalleys in Arid and Semi-Arid WA-SA-NT (First Edition), Scale: 1:4 500 000. Geoscientific Thematic Map (Geocat No 73980); Geoscience Australia: Canberra, Australia, 2012. [Google Scholar]
- Balkau, J.; Walker, D.; McCracken, S.; Hawker, A.; Carver, R.; Taylor, T.; Ion, J. The discovery and resource development of the Moolart Well gold deposit, Western Australia. In Proceedings of the New Generation of Gold Mines Conference, Perth, Australia, 15–16 November 2007; Paydirt Media Pty. Ltd.: Perth, Australia, 2007; pp. 833–855. [Google Scholar]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Briggs, I.C. Machine Contouring Using Minimum Curvature. Geophysics 1974, 39, 39–48. [Google Scholar] [CrossRef]
- Nabighian, M.N. The Analytic Signal of Two-Dimensional Magnetic Bodies with Polygonal Cross-Section: Its Properties and Use for Automated Anomaly Interpretation. Geophysics 1972, 37, 507–517. [Google Scholar] [CrossRef]
- Dentith, M.; Mudge, S.T. Geophysics for the Mineral Exploration Geoscientist; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and Tuning Strategies for Random Forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).