Automated Hyperparameter Optimization of Gradient Boosting Decision Tree Approach for Gold Mineral Prospectivity Mapping in the Xiong’ershan Area
Abstract
1. Introduction
2. Methodology
2.1. GBDT Algorithm
2.2. Hyperparameter Optimization Method
2.2.1. Random Grid Search Optimization
2.2.2. Tree Parzen Estimator in Bayesian Optimization
- (1)
- Define the objective function to be estimated and the definition domain of ;
- (2)
- Take out the values on finite , and solve the of these (solve the observed values);
- (3)
- According to the limited observations, the function is estimated (this assumption is called the prior knowledge in Bayesian Optimization), and the target value (maximum or minimum) on the estimated is obtained;
- (4)
- Define a rule to determine the next observation point to be calculated.
2.3. GBDT Modeling
3. Study area and Geological Data
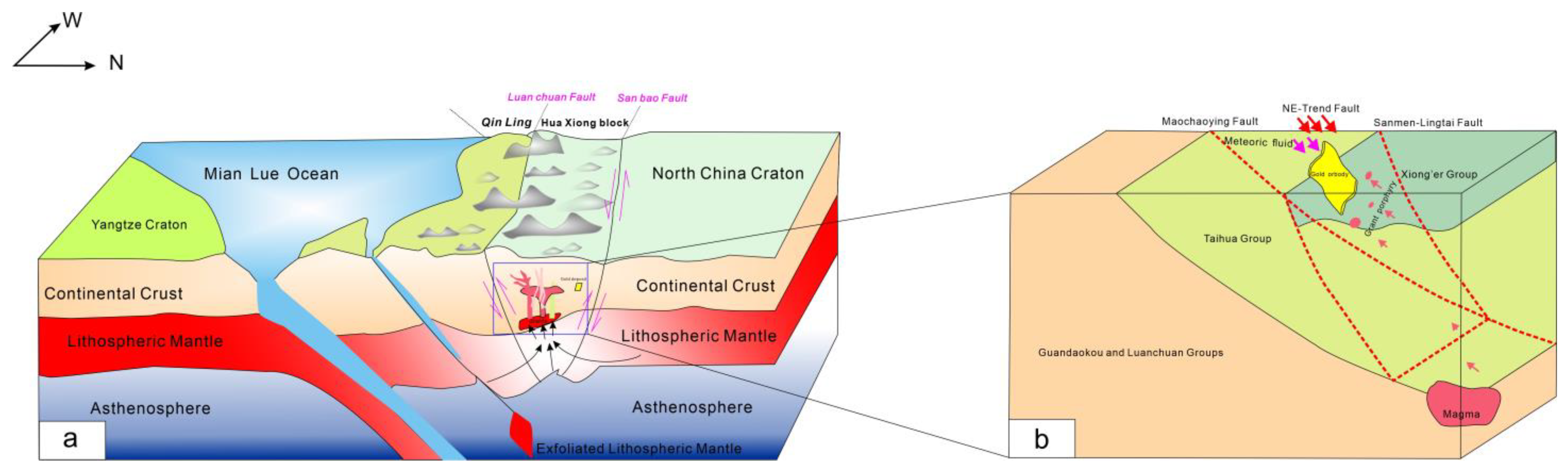
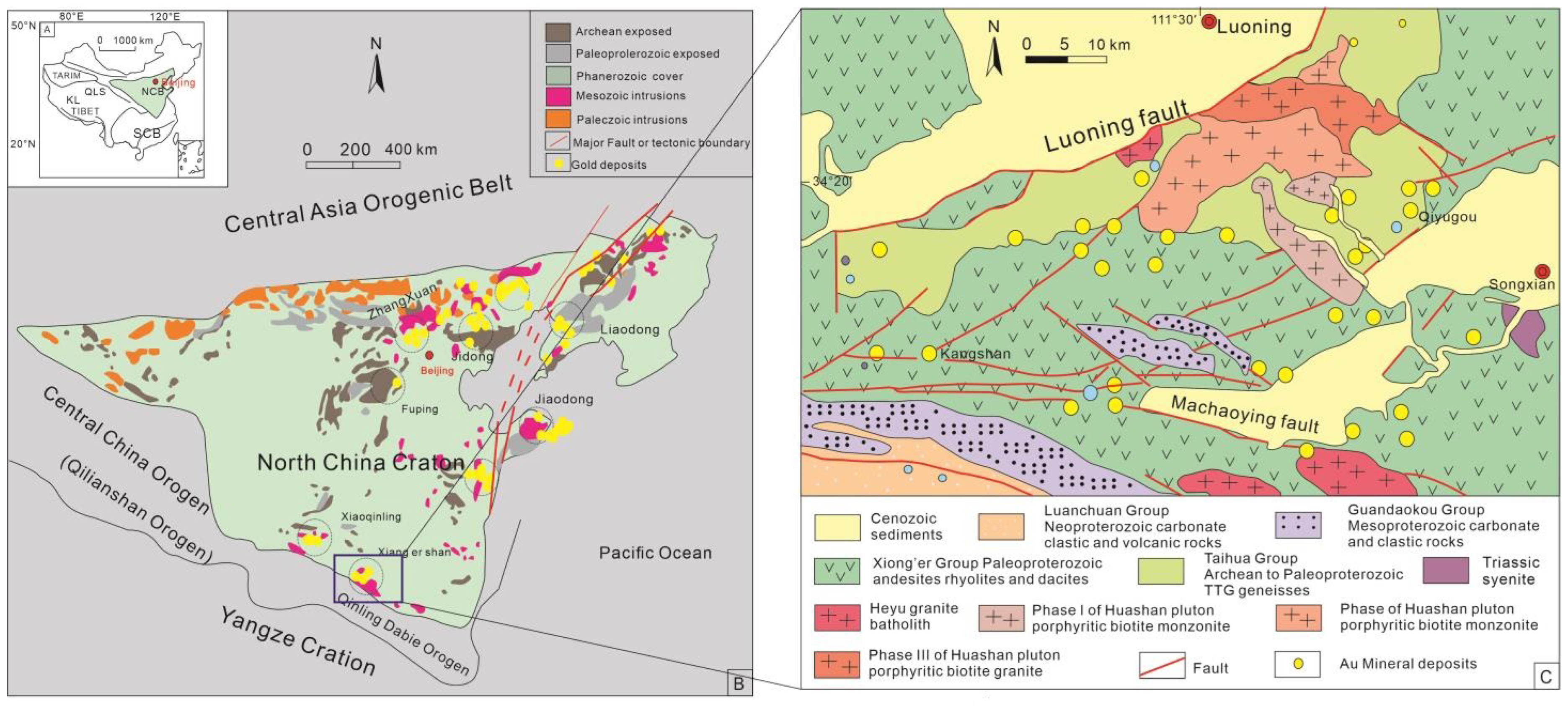
3.1. Geological Setting
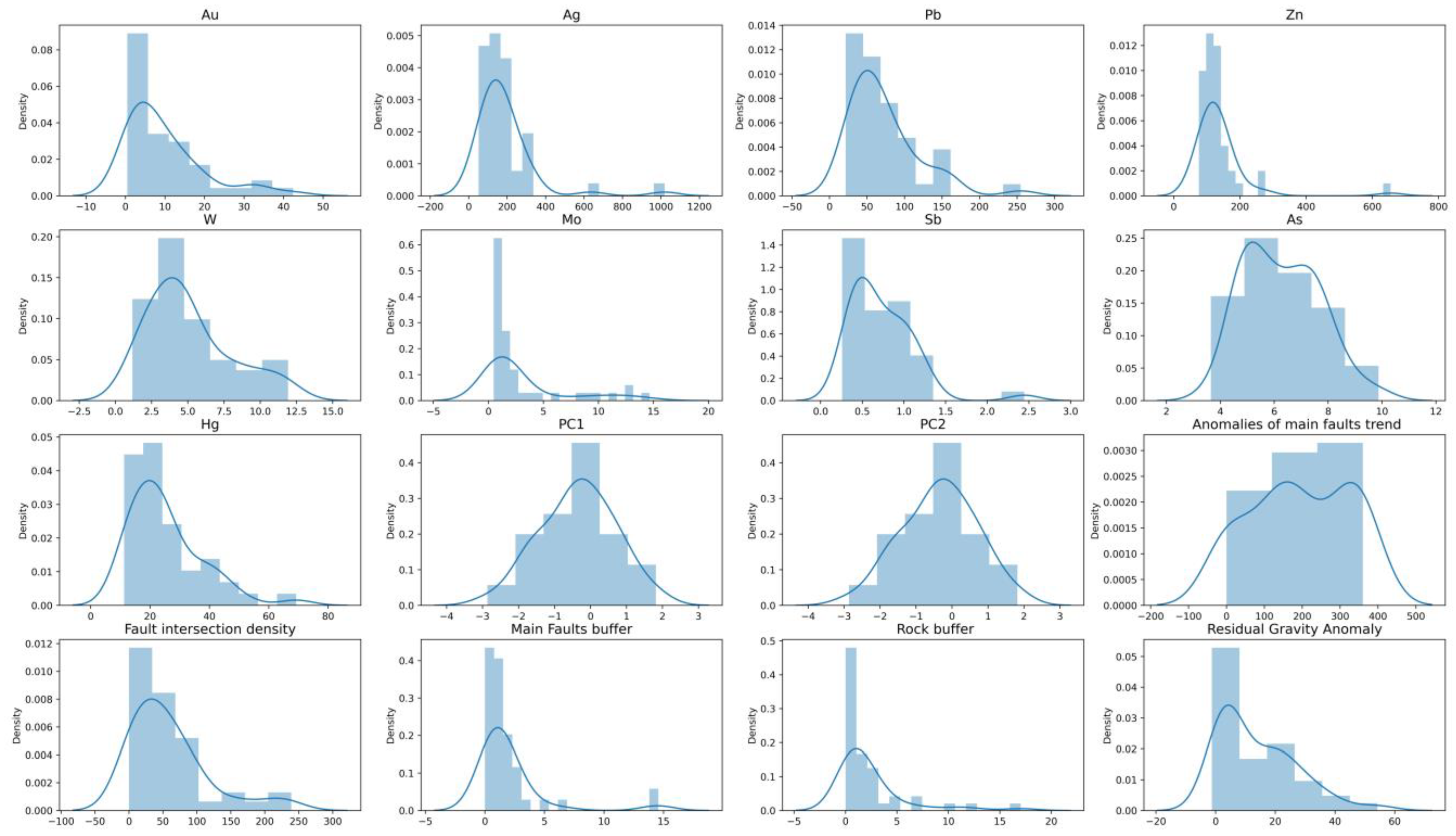
3.2. Geological Exploration Datasets
3.2.1. Source
3.2.2. Transport and Deposition
3.2.3. Training and Validation Data
4. Results and Discussion
4.1. Parameters Optimization
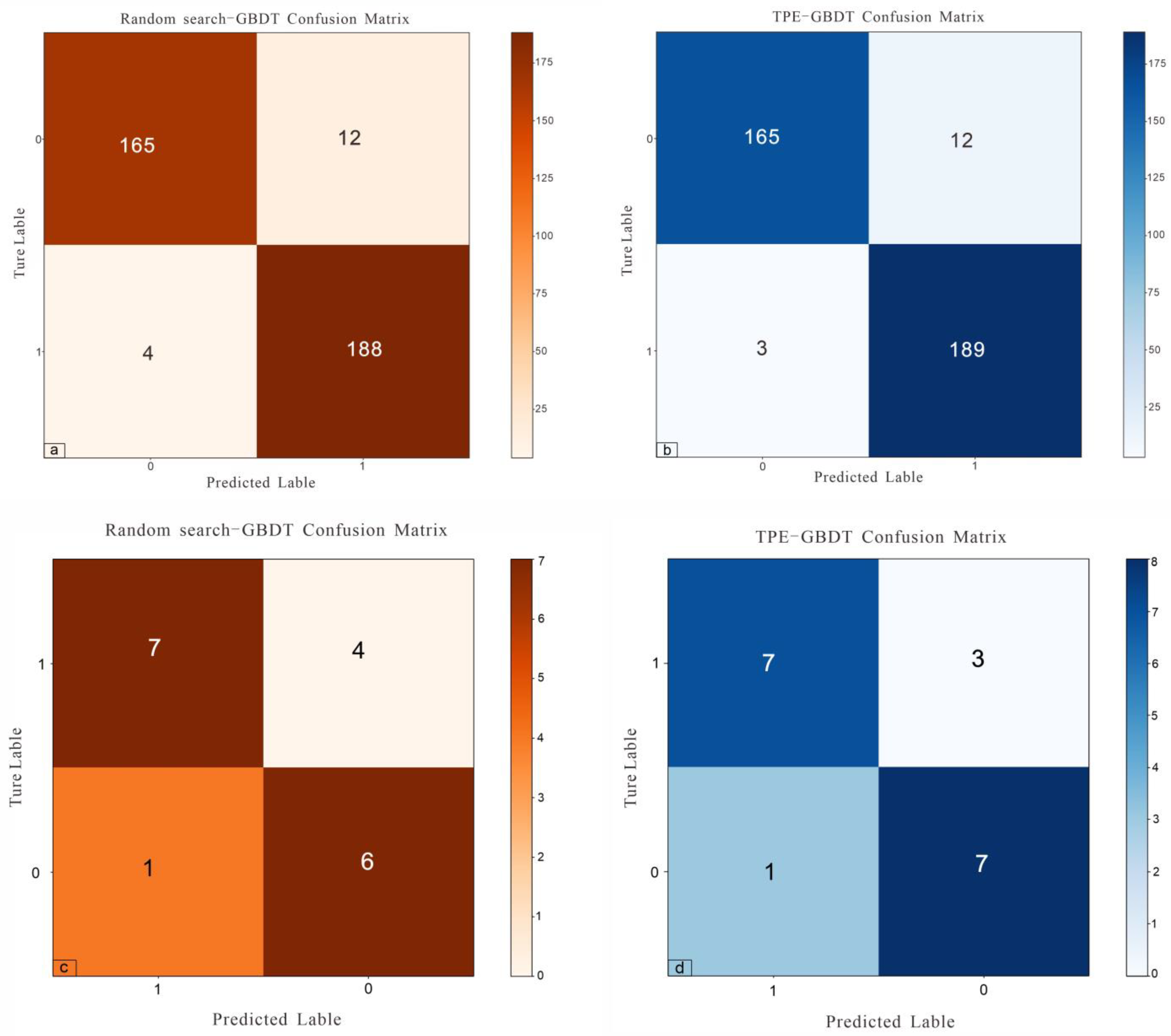
4.2. Performance Evaluation
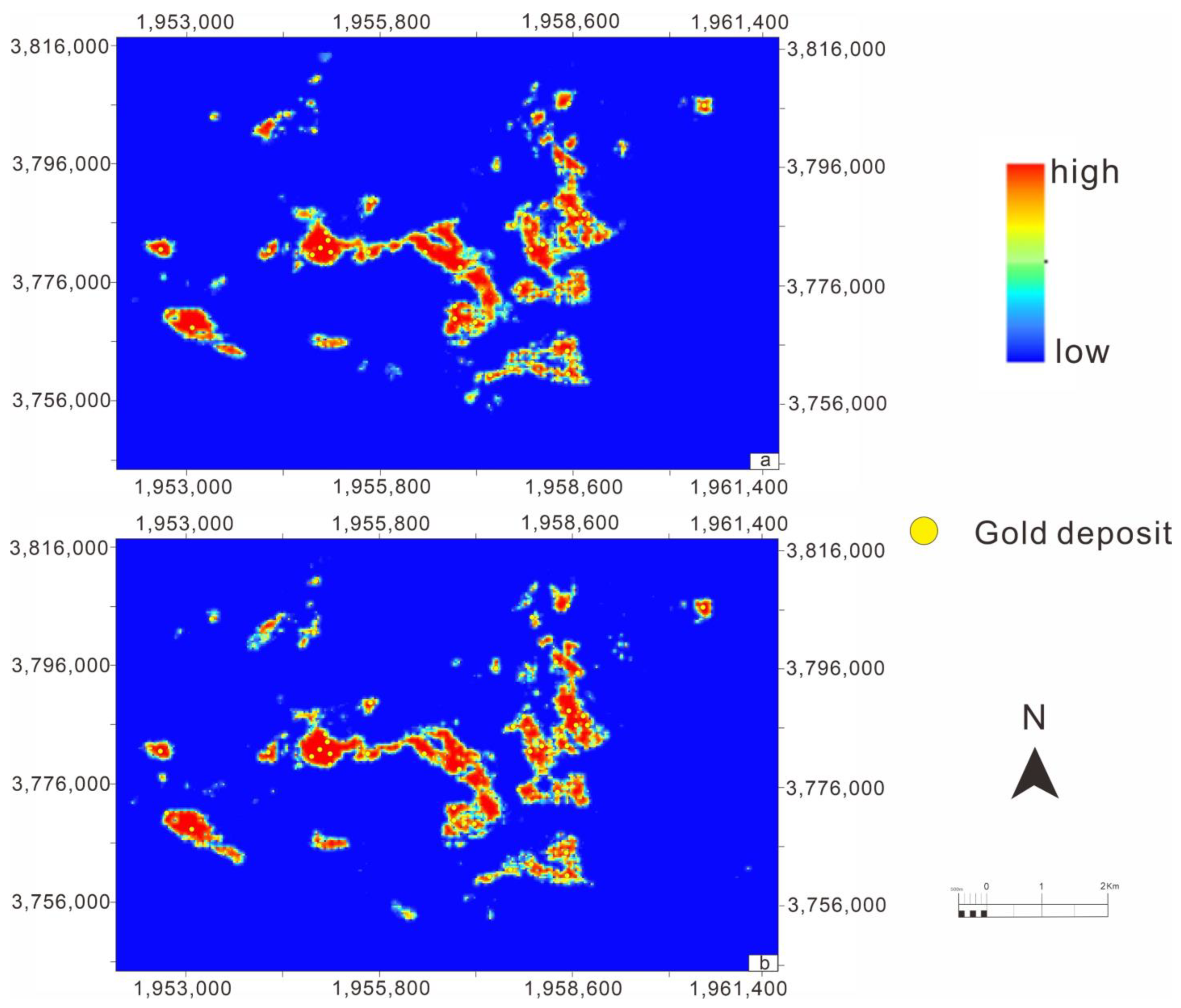
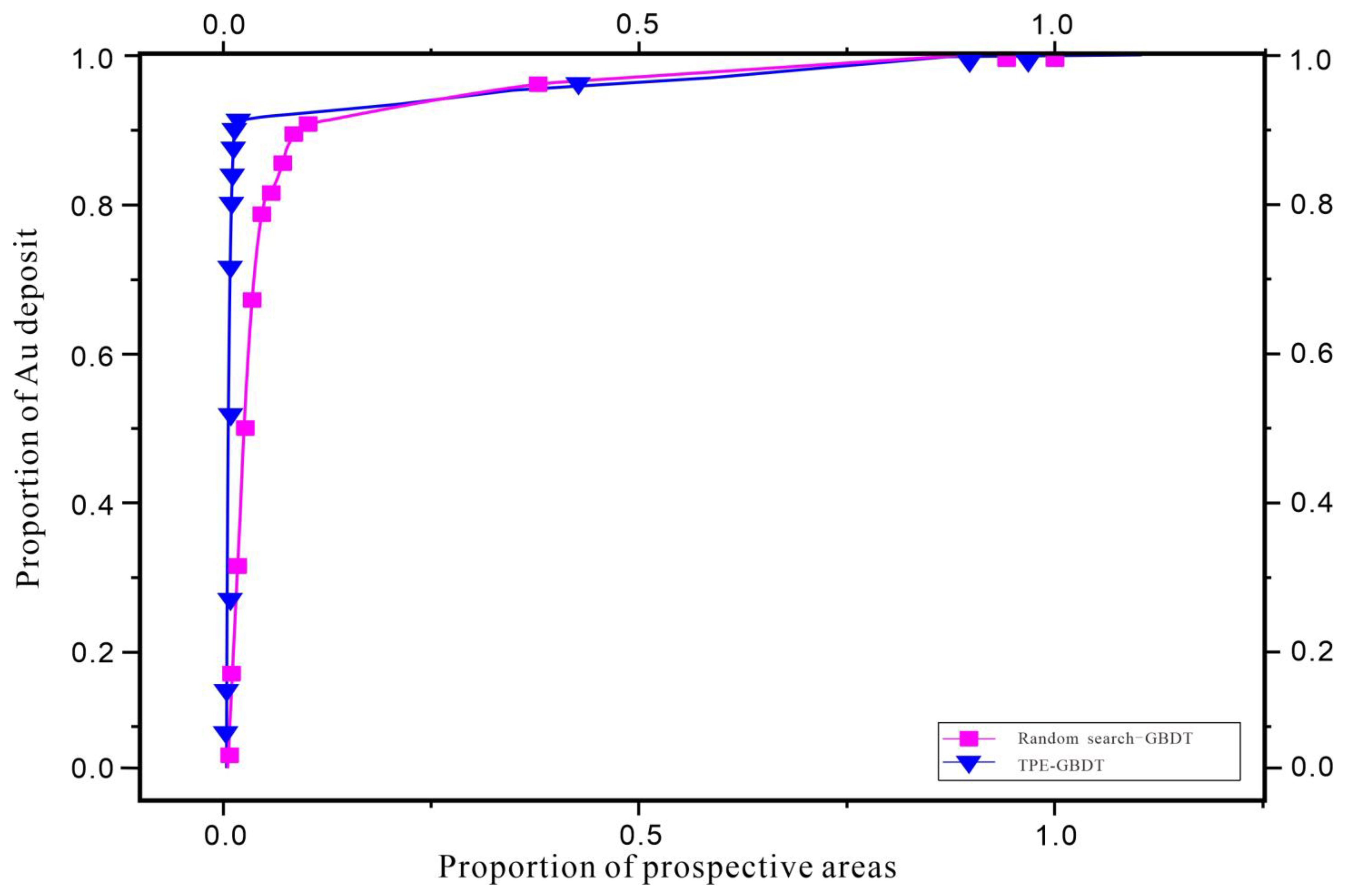
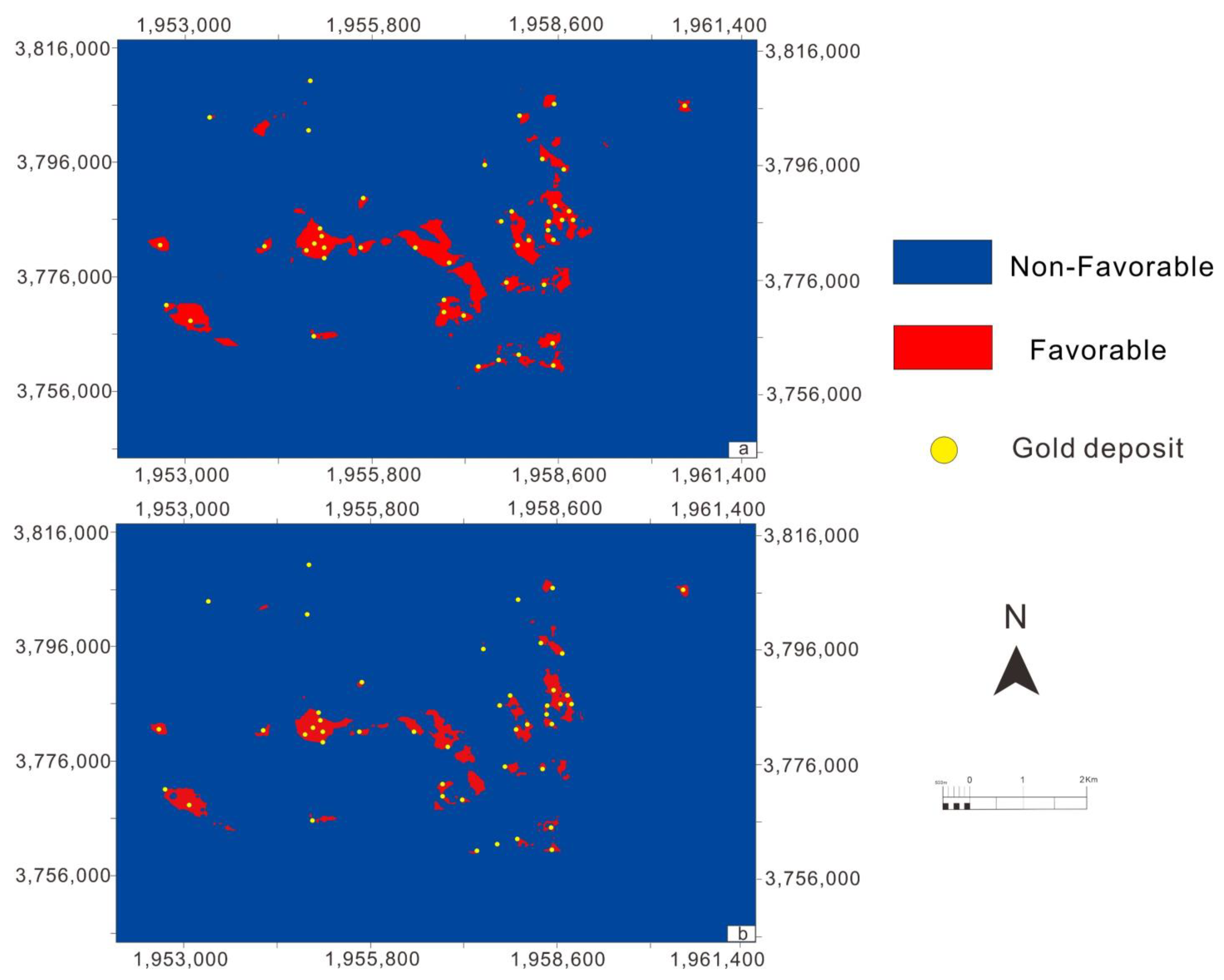
4.3. Mapping of Mineral Prospectivity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Payne, C.E.; Cunningham, F.; Peters, K.J.; Nielsen, S.; Puccioni, E.; Wildman, C.; Partington, G.A. From 2D to 3D: Prospectivity modelling in the Taupo volcanic zone, New Zealand. Ore Geol. Rev. 2015, 71, 558–577. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Wang, G.; Carranza, E.J.M.; Pang, Z.; Wang, H. From 2D to 3D modeling of mineral prospectivity using multi-source geoscience datasets, Wulong Gold District, China. Nat. Resour. Res. 2020, 29, 345–364. [Google Scholar] [CrossRef]
- Joly, A.; Porwal, A.; McCuaig, T.C.; Chudasama, B.; Dentith, M.C.; Aitken, A.R. Mineral systems approach applied to GIS-based 2D-prospectivity modelling of geological regions: Insights from Western Australia. Ore Geol. Rev. 2015, 71, 673–702. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Prediction–area (P–A) plot and C–A fractal analysis to classify and evaluate evidential maps for mineral prospectivity modeling. Comput. Geosci. 2015, 79, 69–81. [Google Scholar] [CrossRef]
- Jiang, W.; Korsch, R.J.; Doublier, M.P.; Duan, J.; Costelloe, R. Mapping deep electrical conductivity structure in the mount isa region, northern australia: Implications for mineral prospectivity. J. Geophys. Res. Solid Earth 2019, 124, 10655–10671. [Google Scholar] [CrossRef]
- Li, T.; Zuo, R.; Xiong, Y.; Peng, Y. Random-drop data augmentation of deep convolutional neural network for mineral prospectivity mapping. Nat. Resour. Res. 2021, 30, 27–38. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Yang, J.; Hong, Z.; Shi, J. A convolutional neural network of GoogLeNet applied in mineral prospectivity prediction based on multi-source geoinformation. Nat. Resour. Res. 2021, 30, 3905–3923. [Google Scholar] [CrossRef]
- Wang, Z.; Zuo, R. Mineral prospectivity mapping using a joint singularity-based weighting method and long short-term memory network. Comput. Geosci. 2022, 158, 104974. [Google Scholar] [CrossRef]
- Xiao, K.; Li, N.; Porwal, A.; Holden, E.J.; Bagas, L.; Lu, Y. GIS-based 3D prospectivity mapping: A case study of Jiama copper-polymetallic deposit in Tibet, China. Ore Geol. Rev. 2015, 71, 611–632. [Google Scholar] [CrossRef]
- Li, X.; Yuan, F.; Zhang, M.; Jia, C.; Jowitt, S.M.; Ord, A.; Zheng, T.; Hu, X.; Li, Y. Three-dimensional mineral prospectivity modeling for targeting of concealed mineralization within the Zhonggu iron orefield, Ningwu Basin, China. Ore Geol. Rev. 2015, 71, 633–654. [Google Scholar] [CrossRef]
- Li, X.; Yuan, F.; Zhang, M.; Jowitt, S.M.; Ord, A.; Zhou, T.; Dai, W. 3D computational simulation-based mineral prospectivity modeling for exploration for concealed Fe–Cu skarn-type mineralization within the Yueshan orefield, Anqing district, Anhui Province, China. Ore Geol. Rev. 2019, 105, 1–17. [Google Scholar] [CrossRef]
- Xiang, J.; Xiao, K.; Carranza, E.J.M.; Chen, J.; Li, S. 3D mineral prospectivity mapping with random forests: A case study of Tongling, Anhui, China. Nat. Resour. Res. 2020, 29, 395–414. [Google Scholar] [CrossRef]
- Mao, X.; Zhang, W.; Liu, Z.; Ren, J.; Bayless, R.C.; Deng, H. 3D mineral prospectivity modeling for the low-sulfidation epithermal gold deposit: A case study of the axi gold deposit, western Tianshan, NW China. Minerals 2020, 10, 233. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, L.; Wu, W. Machine learning-based 3D modeling of mineral prospectivity mapping in the Anqing Orefield, Eastern China. Nat. Resour. Res. 2021, 30, 3099–3120. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Bahroudi, A.; Abedi, M. Three dimensional mineral prospectivity modeling by evidential belief functions, a case study from Kahang porphyry Cu deposit. J. Afr. Earth Sci. 2021, 174, 104098. [Google Scholar] [CrossRef]
- Xiao, K.; Xiang, J.; Fan, M.; Xu, Y. 3D mineral prospectivity mapping based on deep metallogenic prediction theory: A case study of the Lala Copper Mine, Sichuan, China. J. Earth Sci. 2021, 32, 348–357. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M.; Hale, M. Knowledge-driven and data-driven fuzzy models for predictive mineral potential mapping. Nat. Resour. Res. 2003, 12, 1–25. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Van Ruitenbeek, F.J.A.; Hecker, C.; van der Meijde, M.; van der Meer, F.D. Knowledge-guided data-driven evidential belief modeling of mineral prospectivity in Cabo de Gata, SE Spain. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 374–387. [Google Scholar] [CrossRef]
- Abedi, M.; Torabi, S.A.; Norouzi, G.H.; Hamzeh, M. ELECTRE III: A knowledge-driven method for integration of geophysical data with geological and geochemical data in mineral prospectivity mapping. J. Appl. Geophys. 2012, 87, 9–18. [Google Scholar] [CrossRef]
- Harris, J.R.; Grunsky, E.; Behnia, P.; Corrigan, D. Data-and knowledge-driven mineral prospectivity maps for Canada’s North. Ore Geol. Rev. 2015, 71, 788–803. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Abedi, M. Data envelopment analysis: A knowledge-driven method for mineral prospectivity mapping. Comput. Geosci. 2015, 82, 111–119. [Google Scholar] [CrossRef]
- Abedi, M.; Kashani, S.B.M.; Norouzi, G.H.; Yousefi, M. A deposit scale mineral prospectivity analysis: A comparison of various knowledge-driven approaches for porphyry copper targeting in Seridune, Iran. J. Afr. Earth Sci. 2017, 128, 127–146. [Google Scholar] [CrossRef]
- Skirrow, R.G.; Murr, J.; Schofield, A.; Huston, D.L.; van der Wielen, S.; Czarnota, K.; Coghlan, R.; Highet, L.M.; Connolly, D.; Doublier, M.; et al. Mapping iron oxide Cu-Au (IOCG) mineral potential in Australia using a knowledge-driven mineral systems-based approach. Ore Geol. Rev. 2019, 113, 103011. [Google Scholar] [CrossRef]
- Daviran, M.; Parsa, M.; Maghsoudi, A.; Ghezelbash, R. Quantifying uncertainties linked to the diversity of mathematical frameworks in knowledge-driven mineral prospectivity mapping. Nat. Resour. Res. 2022, 31, 2271–2287. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Hale, M.; Faassen, C. Selection of coherent deposit-type locations and their application in data-driven mineral prospectivity mapping. Ore Geol. Rev. 2008, 33, 536–558. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Objective selection of suitable unit cell size in data-driven modeling of mineral prospectivity. Comput. Geosci. 2009, 35, 2032–2046. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Data-driven predictive mapping of gold prospectivity, Baguio district, Philippines: Application of Random Forests algorithm. Ore Geol. Rev. 2015, 71, 777–787. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Data-driven predictive modeling of mineral prospectivity using random forests: A case study in Catanduanes Island (Philippines). Nat. Resour. Res. 2016, 25, 35–50. [Google Scholar] [CrossRef]
- Yousefi, M.; Nykänen, V. Data-driven logistic-based weighting of geochemical and geological evidence layers in mineral prospectivity mapping. J. Geochem. Explor. 2016, 164, 94–106. [Google Scholar] [CrossRef]
- Yousefi, M.; Carranza, E.J.M. Data-driven index overlay and Boolean logic mineral prospectivity modeling in greenfields exploration. Nat. Resour. Res. 2016, 25, 3–18. [Google Scholar] [CrossRef]
- McKay, G.; Harris, J.R. Comparison of the data-driven random forests model and a knowledge-driven method for mineral prospectivity mapping: A case study for gold deposits around the Huritz Group and Nueltin Suite, Nunavut, Canada. Nat. Resour. Res. 2016, 25, 125–143. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. Isolation forest as an alternative data-driven mineral prospectivity mapping method with a higher data-processing efficiency. Nat. Resour. Res. 2019, 28, 31–46. [Google Scholar] [CrossRef]
- Sun, T.; Li, H.; Wu, K.; Chen, F.; Zhu, Z.; Hu, Z. Data-driven predictive modelling of mineral prospectivity using machine learning and deep learning methods: A case study from southern Jiangxi Province, China. Minerals 2020, 10, 102. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Wei, H.; Xiao, K.; Yang, F.; Xiang, J.; Zhang, S.; Xu, Y. Data-driven Mineral Prospectivity Mapping by Joint Application of Unsupervised Convolutional Auto-encoder Network and Supervised Convolutional Neural Network. Nat. Resour. Res. 2021, 30, 1011–1031. [Google Scholar] [CrossRef]
- Parsa, M.; Carranza, E.J.M. Modulating the impacts of stochastic uncertainties linked to deposit locations in data-driven predictive mapping of mineral prospectivity. Nat. Resour. Res. 2021, 30, 3081–3097. [Google Scholar] [CrossRef]
- Bacardit, J.; Llorà, X. Large scale data mining using genetics-based machine learning. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference, Montréal, Canada, 8–12 July 2009; pp. 3381–3412. [Google Scholar]
- Najafabadi, M.M.; Villanustre, F.; Khoshgoftaar, T.M.; Seliya, N.; Wald, R.; Muharemagic, E. Deep learning applications and challenges in big data analytics. J. Big Data 2015, 2, 1. [Google Scholar] [CrossRef]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef]
- Sun, C.; Shrivastava, A.; Singh, S.; Gupta, A. Revisiting unreasonable effectiveness of data in deep learning era. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 843–852. [Google Scholar]
- Rusk, N. Deep learning. Nat. Methods 2016, 13, 35. [Google Scholar] [CrossRef]
- Nguyen, G.; Dlugolinsky, S.; Bobák, M.; Tran, V.; López García, Á.; Heredia, I.; Malík, P.; Hluchý, L. Machine learning and deep learning frameworks and libraries for large-scale data mining: A survey. Artif. Intell. Rev. 2019, 52, 77–124. [Google Scholar] [CrossRef]
- Zuo, R. Geodata science-based mineral prospectivity mapping: A review. Nat. Resour. Res. 2020, 29, 3415–3424. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the International Conference on Intelligent Computing, Hefei China, 23–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. Safe-level-smote: Safe-level-synthetic minority over-sampling technique for handling the class imbalanced problem. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Bangkok, Thailand, 27–30 April 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 475–482. [Google Scholar]
- Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. DBSMOTE: Density-based synthetic minority over-sampling technique. Appl. Intell. 2012, 36, 664–684. [Google Scholar] [CrossRef]
- Guzmán-Ponce, A.; Sánchez, J.S.; Valdovinos, R.M.; Marcial-Romero, J.R. DBIG-US: A two-stage under-sampling algorithm to face the class imbalance problem. Expert Syst. Appl. 2021, 168, 114301. [Google Scholar] [CrossRef]
- Soltanzadeh, P.; Hashemzadeh, M. RCSMOTE: Range-Controlled synthetic minority over-sampling technique for handling the class imbalance problem. Inf. Sci. 2021, 542, 92–111. [Google Scholar] [CrossRef]
- Peng, C.Y.; Park, Y.J. A New Hybrid Under-sampling Approach to Imbalanced Classification Problems. Appl. Artif. Intell. 2022, 36, 1975393. [Google Scholar] [CrossRef]
- Lenka, S.R.; Bisoy, S.K.; Priyadarshini, R.; Nayak, B. Representative-based cluster undersampling technique for imbalanced credit scoring datasets. In Innovations in Computational Intelligence and Computer Vision; Springer: Singapore, 2022; pp. 119–129. [Google Scholar]
- Amirruddin, A.D.; Muharam, F.M.; Ismail, M.H.; Tan, N.P.; Ismail, M.F. Synthetic Minority Over-sampling TEchnique (SMOTE) and Logistic Model Tree (LMT)-Adaptive Boosting algorithms for classifying imbalanced datasets of nutrient and chlorophyll sufficiency levels of oil palm (Elaeis guineensis) using spectroradiometers and unmanned aerial vehicles. Comput. Electron. Agric. 2022, 193, 106646. [Google Scholar]
- Perez, L.; Wang, J. The effectiveness of data augmentation in image classification using deep learning. arXiv 2017, arXiv:1712.04621. Preprint. [Google Scholar]
- Abbaszadeh, M.; Soltani-Mohammadi, S.; Ahmed, A.N. Optimization of support vector machine parameters in modeling of Iju deposit mineralization and alteration zones using particle swarm optimization algorithm and grid search method. Comput. Geosci. 2022, 165, 105140. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Inoue, H. Data augmentation by pairing samples for images classification. arXiv 2018, arXiv:1801.02929; Preprint. [Google Scholar]
- Jackson, P.T.; Abarghouei, A.A.; Bonner, S.; Breckon, T.P.; Obara, B. Style augmentation: Data augmentation via style randomization. CVPR Workshops 2019, 6, 10–11. [Google Scholar]
- Raj, R.; Mathew, J.; Kannath, S.K.; Rajan, J. Crossover based technique for data augmentation. Comput. Methods Programs Biomed. 2022, 218, 106716. [Google Scholar] [CrossRef] [PubMed]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. Preprint. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. Autoaugment: Learning augmentation policies from data. arXiv 2018, arXiv:1805.09501. Preprint. [Google Scholar]
- Lim, S.; Kim, I.; Kim, T.; Kim, C.; Kim, S. Fast autoaugment. Adv. Neural Inf. Process. Syst. 2019, 32, 1–11. [Google Scholar]
- Xiong, Y.; Zuo, R. Effects of misclassification costs on mapping mineral prospectivity. Ore Geol. Rev. 2017, 82, 1–9. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R. GIS-based rare events logistic regression for mineral prospectivity mapping. Comput. Geosci. 2018, 111, 18–25. [Google Scholar] [CrossRef]
- Lin, C.F.; Wang, S.D. Fuzzy support vector machines. IEEE Trans. Neural Netw. 2002, 13, 464–471. [Google Scholar]
- Min, R.; Cheng, H.D. Effective image retrieval using dominant color descriptor and fuzzy support vector machine. Pattern Recognit. 2009, 42, 147–157. [Google Scholar] [CrossRef]
- Batuwita, R.; Palade, V. FSVM-CIL: Fuzzy support vector machines for class imbalance learning. IEEE Trans. Fuzzy Syst. 2010, 18, 558–571. [Google Scholar] [CrossRef]
- Yu, H.; Sun, C.; Yang, X.; Zheng, S.; Zou, H. Fuzzy support vector machine with relative density information for classifying imbalanced data. IEEE Trans. Fuzzy Syst. 2019, 27, 2353–2367. [Google Scholar] [CrossRef]
- Maldonado, S.; López, J.; Vairetti, C. Time-weighted Fuzzy Support Vector Machines for classification in changing environments. Inf. Sci. 2021, 559, 97–110. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X. Imbalanced data classification algorithm based on hybrid model. In Proceedings of the International Conference on Machine Learning and Cybernetics, Xi’an, China, 15–17 July 2012; IEEE: New York, NY, USA, 2012; Volume 2, pp. 735–740. [Google Scholar]
- Zhang, M.; Wu, M. Efficient super greedy boosting for classification. In Proceedings of the 2020 10th Institute of Electrical and Electronics Engineers International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Xi’an, China, 10–13 October 2020; IEEE: New York, NY, USA, 2020; pp. 192–197. [Google Scholar]
- Ding, J.; Wang, S.; Jia, L.; You, J.; Jiang, Y. Spark-based Ensemble Learning for Imbalanced Data Classification. Int. J. Perform. Eng. 2018, 14, 955. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, X.; Lin, S. Rescaled boosting in classification. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2598–2610. [Google Scholar] [CrossRef]
- Lim, S.K.; Loo, Y.; Tran, N.T.; Cheung, N.M.; Roig, G.; Elovici, Y. Doping: Generative data augmentation for unsupervised anomaly detection with gan. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; IEEE: New York, NY, USA, 2018; pp. 1122–1127. [Google Scholar]
- Wen, Q.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time series data augmentation for deep learning: A survey. arXiv 2002, arXiv:2002.12478. Preprint. [Google Scholar]
- Al Olaimat, M.; Lee, D.; Kim, Y.; Kim, J.; Kim, J. A learning-based data augmentation for network anomaly detection. In Proceedings of the 2020 29th International Conference on Computer Communications and Networks (ICCCN), Honolulu, HI, USA, 3–6 August 2020; IEEE: New York, NY, USA, 2020; pp. 1–10. [Google Scholar]
- Sinha, A.; Ayush, K.; Song, J.; Uzkent, B.; Jin, H.; Ermon, S. Negative data augmentation. arXiv 2021, arXiv:2102.05113. Preprint. [Google Scholar]
- Chen, R.T.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural ordinary differential equations. In Advances in Neural Information Processing Systems; NeurIPS: New Orleans, LA, USA, 2018; p. 31. [Google Scholar]
- Song, L.; Gong, D.; Li, Z.; Liu, C.; Liu, W. Occlusion robust face recognition based on mask learning with pairwise differential siamese network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seould, Republic of Korea, 27 October–2 November 2019; pp. 773–782. [Google Scholar]
- Meldo, A.A.; Utkin, L.V. A new approach to differential lung diagnosis with ct scans based on the siamese neural network. J. Phys. 2019, 1236, 12–58. [Google Scholar] [CrossRef]
- Ruthotto, L.; Haber, E. Deep neural networks motivated by partial differential equations. J. Math. Imaging Vis. 2020, 62, 352–364. [Google Scholar] [CrossRef]
- Soleymani, S.; Chaudhary, B.; Dabouei, A.; Dawson, J.; Nasrabadi, N.M. Differential morphed face detection using deep siamese networks. In International Conference on Pattern Recognition; Springer: Cham, Switzerland, 2021; pp. 560–572. [Google Scholar]
- Booth, A.; Gerding, E.; McGroarty, F. Automated trading with performance weighted random forests and seasonality. Expert Syst. Appl. 2014, 41, 3651–3661. [Google Scholar] [CrossRef]
- Li, H.B.; Wang, W.; Ding, H.W.; Dong, J. Trees weighting random forest method for classifying high-dimensional noisy data. In Proceedings of the 2010 IEEE 7th International Conference on e-Business Engineering, Shanghai, China, 10–12 November 2010; IEEE: New York, NY, USA, 2010; pp. 160–163. [Google Scholar]
- Gajowniczek, K.; Grzegorczyk, I.; Ząbkowski, T.; Bajaj, C. Weighted random forests to improve arrhythmia classification. Electronics 2020, 9, 99. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, M.M.U.; Hammond, F.; Konowicz, G.; Xin, C.; Wu, H.; Li, J. A few-shot deep learning approach for improved intrusion detection. In Proceedings of the 2017 IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 19–21 October 2017; IEEE: New York, NY, USA, 2017; pp. 456–462. [Google Scholar]
- Wang, A.; Zhang, Y.; Wu, H.; Jiang, K.; Wang, M. Few-shot learning based balanced distribution adaptation for heterogeneous defect prediction. IEEE Access 2020, 8, 32989–33001. [Google Scholar] [CrossRef]
- Zhang, B.; Jiang, H.; Li, X.; Feng, S.; Ye, Y.; Ye, R. MetaDT: Meta Decision Tree for Interpretable Few-Shot Learning. arXiv 2022, arXiv:2203.01482. Preprint. [Google Scholar]
- Bishop, C.M. Model-based machine learning. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120222. [Google Scholar] [CrossRef]
- Singh, A.; Thakur, N.; Sharma, A. A review of supervised machine learning algorithms. In Proceedings of the 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016; IEEE: New York, NY, USA, 2016; pp. 1310–1315. [Google Scholar]
- Kern, C.; Klausch, T.; Kreuter, F. Tree-based machine learning methods for survey research. Surv. Res. Methods 2019, 13, 73. [Google Scholar]
- Mahesh, B. Machine learning algorithms-a review. Int. J. Sci. Res. 2020, 9, 381–386. [Google Scholar]
- Charbuty, B.; Abdulazeez, A. Classification based on decision tree algorithm for machine learning. J. Appl. Sci. Technol. Trends 2021, 2, 20–28. [Google Scholar] [CrossRef]
- Flores, V.; Keith, B.; Leiva, C. Using artificial intelligence techniques to improve the prediction of copper recovery by leaching. J. Sens. 2020, 2020, 2454875. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, Y.; Deng, H. Gradient boosting decision tree for lithology identification with well logs: A case study of zhaoxian gold deposit, shandong peninsula, China. Nat. Resour. Res. 2021, 30, 3197–3217. [Google Scholar] [CrossRef]
- Kotthoff, L.; Thornton, C.; Hoos, H.H.; Hutter, F.; Leyton-Brown, K. Auto-WEKA: Automatic model selection and hyperparameter optimization in WEKA. In Automated Machine Learning; Springer: Cham, Switzerland, 2019; pp. 81–95. [Google Scholar]
- Wong, J.; Manderson, T.; Abrahamowicz, M.; Buckeridge, D.L.; Tamblyn, R. Can hyperparameter tuning improve the performance of a super learner? A case study. Epidemiology 2019, 30, 521. [Google Scholar] [CrossRef]
- Rafique, D.; Velasco, L. Machine Learning for Network Automation: Overview, Architecture, and Applications [Invited Tutorial]. J. Opt. Commun. Netw. 2018, 10, D126–D143. [Google Scholar] [CrossRef]
- Marshall, I.J.; Wallace, B.C. Toward systematic review automation: A practical guide to using machine learning tools in research synthesis. Syst. Rev. 2019, 8, 163. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Siau, K. Artificial intelligence, machine learning, automation, robotics, future of work and future of humanity: A review and research agenda. J. Database Manag. 2019, 30, 61–79. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst.24. 2011, 2546–2554. [Google Scholar]
- Feurer, M.; Hutter, F. Hyperparameter optimization. In Automated Machine Learning; Springer: Cham, Switzerland, 2019; pp. 3–33. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Maclaurin, D.; Duvenaud, D.; Adams, R. Gradient-based hyperparameter optimization through reversible learning. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2113–2122. [Google Scholar]
- Nalçakan, Y.; Ensari, T. Decision of neural networks hyperparameters with a population-based algorithm. In Proceedings of the International Conference on Machine Learning, Optimization, and Data Science, Volterra, Italy, 13–16 September 2018; Springer: Cham, Switzerland, 2018; pp. 276–281. [Google Scholar]
- Bakhteev, O.Y.; Strijov, V.V. Comprehensive analysis of gradient-based hyperparameter optimization algorithms. Ann. Oper. Res. 2019, 289, 51–65. [Google Scholar] [CrossRef]
- Li, W.; Wang, T.; Ng, W.W.Y. Population-Based Hyperparameter Tuning With Multitask Collaboration. IEEE Trans. Neural Networks Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ll, M.; Baxter, J. Boosting Algorithms as Gradient Descent in Function Space; NIPS: New Orleans, LA, USA, 1999. [Google Scholar]
- Bhat, P.C.; Prosper, H.B.; Sekmen, S.; Stewart, C. Optimizing event selection with the random grid search. Comput. Phys. Commun. 2018, 228, 245–257. [Google Scholar] [CrossRef]
- Nguyen, D.A.; Kong, J.; Wang, H.; Menzel, S.; Sendhoff, B.; Kononova, A.V.; Bäck, T. Improved automated cash optimization with tree parzen estimators for class imbalance problems. In Proceedings of the 2021 IEEE 8th international conference on data science and advanced analytics (DSAA), Porto, Portugal, 6–9 October 2021; IEEE: New York, NY, USA, 2021; pp. 1–9. [Google Scholar]
- Zhai, M.G.; Peng, P. Paleoproterozoic tectonic events in North China Craton. Acta Petrol. Sin. 2007, 11, 2665–2682, (In Chinese with English abstract). [Google Scholar]
- Wan, Y.S.; Dong, C.Y.; Ren, P. A Review of the Temporal and Spatial Distribution, Composition and Evolution of Archean TTG Rocks in the North China Craton. Acta Petrol. Sin. 2017, 33, 1405–1419. [Google Scholar]
- Jia, X.; Zhai, M.; Xiao, W.; Li, L.; Ratheesh-Kumar, R.; Wu, J.; Liu, Y. Mesoarchean to Paleoproterozoic crustal evolution of the Taihua Complex in the southern North China Craton. Precambrian Res. 2019, 337, 105451. [Google Scholar] [CrossRef]
- Zhao, G.; He, Y.; Sun, M. The Xiong’er volcanic belt at the southern margin of the North China Craton: Petrographic and geochemical evidence for its outboard position in the Paleo-Mesoproterozoic Columbia Supercontinent. Gondwana Res. 2009, 16, 170–181. [Google Scholar] [CrossRef]
- He, Y.; Zhao, G.; Sun, M. Geochemical and Isotopic Study of the Xiong’er Volcanic Rocks at the Southern Margin of the North China Craton: Petrogenesis and Tectonic Implications. J. Geol. 2010, 118, 417–433. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Carranza, E.J.M.; Cui, C. Paleoproterozoic volcanic rocks in the southern margin of the North China Craton, central China: Implications for the Columbia supercontinent. Geosci. Front. 2019, 10, 1543–1560. [Google Scholar] [CrossRef]
- Li, Y.F. The Temporal-Spital Evolution of Mesozoid Granitoids in the Xiong’ershan Area and Their Relationships to Molybdenum-Gold Mineralization; China University of Geosciences: Beijing, China, 2005; pp. 1–122, (In Chinese with English abstract). [Google Scholar]
- Wenxiang, X.; Fang, P.; Guangjin, B. Rock Strata in Henan Province; China University of Geosciences: Wuhan, China, 1997; pp. 1–209, (In Chinese with English abstract). [Google Scholar]
- Hu, X.-K.; Tang, L.; Zhang, S.-T.; Santosh, M.; Spencer, C.J.; Zhao, Y.; Cao, H.-W.; Pei, Q.-M. In situ trace element and sulfur isotope of pyrite constrain ore genesis in the Shapoling molybdenum deposit, East Qinling Orogen, China. Ore Geol. Rev. 2018, 105, 123–136. [Google Scholar] [CrossRef]
- Zhai, M.-G.; Santosh, M. The early Precambrian odyssey of the North China Craton: A synoptic overview. Gondwana Res. 2011, 20, 6–25. [Google Scholar] [CrossRef]
- Li, S.-R.; Santosh, M. Geodynamics of heterogeneous gold mineralization in the North China Craton and its relationship to lithospheric destruction. Gondwana Res. 2017, 50, 267–292. [Google Scholar] [CrossRef]
- Li, L.; Li, C.; Li, Q.; Yuan, M.-W.; Zhang, J.-Q.; Li, S.-R.; Santosh, M.; Shen, J.-F.; Zhang, H.-F. Indicators of decratonic gold mineralization in the North China Craton. Earth Sci. Rev. 2022, 228, 103995. [Google Scholar] [CrossRef]
- Mao, J.; Goldfarb, R.J.; Zhang, Z.; Xu, W.; Qiu, Y.; Deng, J. Gold deposits in the Xiaoqinling–Xiong’ershan region, Qinling Mountains, central China. Miner. Depos. 2002, 37, 306–325. [Google Scholar] [CrossRef]
- Cao, M.; Yao, J.; Deng, X.; Yang, F.; Mao, G.; Mathur, R. Diverse and multistage Mo, Au, Ag–Pb–Zn and Cu deposits in the Xiong’er Terrane, East Qinling: From Triassic Cu mineralization. Ore Geol. Rev. 2017, 81, 565–574. [Google Scholar] [CrossRef]
- Deng, J.; Gong, Q.; Wang, C.; Carranza, E.J.M.; Santosh, M. Sequence of Late Jurassic–Early Cretaceous magmatic–hydrothermal events in the Xiong’ershan region, Central China: An overview with new zircon U–Pb geochronology data on quartz porphyries. J. Asian Earth Sci. 2014, 79, 161–172. [Google Scholar] [CrossRef]
- Yan, J.S.; Wang, M.S.; Yang, J.C. Tectonic evolution of the Machaoying fault zone in western Henan and its relationship with Au-polymetallic mineralization. Reg. Geol. China 2000, 19, 166–171, (In Chinese with English abstract). [Google Scholar]
- Kefei, T. Characteristics, Genesis, and Geodynamic Setting of Representative Gold Deposits in the Xiong’ershan District, Southern Margin of the North China Craton; China University of Geosciences: Wuhan, China, 2014; pp. 1–131, (In Chinese with English abstract). [Google Scholar]
- Tang, L.; Zhang, S.T.; Yang, F.; Santosh, M.; Li, J.J.; Kim, S.W.; Hu, X.K.; Zhao, Y.; Cao, H.W. Triassic alkaline magmatism and mineralization in the Xiong’ershan area, East Qinling, China. Geol. J. 2019, 54, 143–156. [Google Scholar] [CrossRef]
- McCuaig, T.C.; Hronsky, J.M. The Mineral System Concept: The Key to Exploration Targeting; Society of Economic Geologists, Inc.: Littleton, CO, USA, 2014; Volume 18, pp. 153–175. [Google Scholar]
- McCuaig, T.C.; Beresford, S.; Hronsky, J. Translating the mineral systems approach into an effective exploration targeting system. Ore Geol. Rev. 2010, 38, 128–138. [Google Scholar] [CrossRef]
- Ni, S.J.; Li, C.Y.; Zhang, C.; Gao, R.D.; Liu, C.F. Contribution of Meso-basic dykerocks to gold deposits—An example from gold deposits in Xiaoqinling area. J. Chengdu Inst. Technol. 1994, 21, 70–78. [Google Scholar]
- Li, S.M.; Huang, J.J.; Wang, X.S.; Zhai, L.Q. The Geology of Xiaoqinling Gold Deposits and Metallogenetic Prospecting; Beijing, Geological Publishing House: Beijing, China, 1996; pp. 1–250, (In Chinese with English abstract). [Google Scholar]
- Xu, J.H.; Xie, Y.L.; Liu, J.M.; Zhu, H.P. Trace elements in fluid inclusions of Wenyu-Dongchuang gold deposits in the Xiaoqinling area, China. Geol. Prospect. 2004, 40, 1–6, (In Chinese with English abstract). [Google Scholar]
- Wang, T.H.; Xie, G.Q.; Ye, A.W.; Li, Z.Y. Material sources of gold deposits in Xiaoqinling–Xiong’ershan area of Western Henan Province as well as the relationship between gold deposits and intermediate-basic dykes. Acta Geosci. Sin. 2009, 30, 27–38. [Google Scholar]
- Yanjing, C.; Jigu, F.; Bing, L. Classification of genetic types and series of gold deposits. Adv. Earth Sci. 1992, 3, 73–79, (In Chinese with English abstract). [Google Scholar]
- Chen, Y.J.; Santosh, M. Triassic tectonics and mineral systems in the Qinling Orogen, central China. Geol. J. 2014, 49, 338–358. [Google Scholar] [CrossRef]
- Deng, X.H.; Chen, Y.J.; Santosh, M.; Yao, J.M.; Sun, Y.L. Re–Os and Sr–Nd–Pb isotope constraints on source of fluids in the Zhifang Mo deposit, Qinling Orogen, China. Gondwana Res. 2016, 30, 132–143. [Google Scholar] [CrossRef]
- Aitchison, J. The statistical analysis of compositional data. J. R. Stat. Soc. Ser. B Methodol. 1982, 44, 139–160. [Google Scholar] [CrossRef]
- Van den Boogaart, K.G.; Tolosana-Delgado, R. Analyzing Compositional Data with R; Springer: Berlin, Germany, 2013; Volume 122, pp. 1–200. [Google Scholar]
- Galletti, A.; Maratea, A. Numerical stability analysis of the centered log-ratio transformation. In Proceedings of the 2016 12th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Naples, Italy, 28 November–1 December 2016; IEEE: New York, NY, USA, 2016; pp. 713–716. [Google Scholar]
- Brodersen, K.H.; Ong, C.S.; Stephan, K.E.; Buhmann, J.M. The balanced accuracy and its posterior distribution. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: New York, NY, USA, 2010; pp. 3121–3124. [Google Scholar]
- Wei, Q.; Dunbrack, R.L., Jr. The role of balanced training and testing data sets for binary classifiers in bioinformatics. PLoS ONE 2013, 8, e67863. [Google Scholar] [CrossRef]
- Velez, D.R.; White, B.C.; Motsinger, A.A.; Bush, W.S.; Ritchie, M.D.; Williams, S.M.; Moore, J.H. A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction. Genet. Epidemiol. 2007, 31, 306–315. [Google Scholar] [CrossRef]
- Weng, C.G.; Poon, J. A new evaluation measure for imbalanced datasets. In Proceedings of the 7th Australasian Data Mining Conference, Glenelg, Australia, 27–28 November 2008; Volume 87, pp. 27–32. [Google Scholar]
- Chuang, C.L.; Chang, P.C.; Lin, R.H. An efficiency data envelopment analysis model reinforced by classification and regression tree for hospital performance evaluation. J. Med. Syst. 2011, 35, 1075–1083. [Google Scholar] [CrossRef]
- Gu, Q.; Zhu, L.; Cai, Z. Evaluation measures of the classification performance of imbalanced data sets. In Proceedings of the International Symposium on Intelligence Computation and Applications, Guangzhou, China, 20–21 November 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 461–471. [Google Scholar]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]

| Type | Parameter |
|---|---|
| boosting | n_estimators, learning_rate, loss, alpha, init |
| Weak evaluator structure | criterion, max_depth, min_samples_split, min_samples_leaf, min_weight_fraction_leaf, max_leaf_nodes, min_impurity_decrease |
| early stop | validation_fraction, n_iter_no_change, tol, n_estimators_ |
| Weak evaluator training data | subsample, max_features, random_state |
| others | ccp_alpha, warm_start |
| Parameter | Function of Parameters | Default Value |
|---|---|---|
| loss | loss function | “deviance” |
| criterion | Impurity measurement index of weak estimate when branching | “friedman_mse” |
| n_estimators | The Actual number of iterations | 100 |
| learning_rate | Weighted summation process affecting weak estimator results | 0.1 |
| max_features | Maximum number of features considered in constructing optimal CART tree model | None |
| subsample | The Proportion of random samples released from the full dataset before each CART tree is built | 1.0 |
| max_depth | Maximum allowable depth of weak estimator | 3 |
| min_impurity_decrease | The minimum reduction in impurity is allowed when the weak evaluator branches | 0.0 |
| Parameter | Initial Parameter Space | Final Parameter Space |
|---|---|---|
| loss | [“deviance”,”exponential”] | [“deviance”,”exponential”] |
| criterion | [“friedman_mse”, “squared_error”] | [“friedman_mse”, “squared_error”] |
| n_estimators | (25,200,25) | (55,200,1) |
| learning_rate | (0.1,2.1,0.1) | (0.05,1,0.005) |
| max_features | (4,20,2) | (1,16,1) |
| subsample | (0.1,0.8,0.1) | (0.5,1.0,0.05) |
| max_depth | (2,30,2) | (10,35,1) |
| min_impurity_decrease | (0,5,1) | (0,5,0.1) |
| Parameter | Parameter Value Based on the Random Search | Parameter Value Based on the TPE |
|---|---|---|
| loss | “deviance” | “deviance” |
| criterion | “friedman_mse” | “friedman_mse” |
| n_estimators | 186 | 69 |
| learning_rate | 0.09 | 0.7 |
| max_features | 9 | 12 |
| subsample | 0.95 | 0.8 |
| max_depth | 12 | 10 |
| min_impurity_decrease | 0.1 | 0.1 |
| Model | Train Accuracy | Test Accuracy | Five-Fold Cross-Validation Time | Datasets |
|---|---|---|---|---|
| GBDT | 0.981 | 0.940 | 0.55 s | MS |
| GBDT-Random | 1.000 | 0.963 | 3.16 s | |
| GBDT-TPE | 1.000 | 0.966 | 0.71 s | |
| GBDT | 1.000 | 0.754 | 0.07 s | OS |
| GBDT-Random | 1.000 | 0.764 | 0.33 s | |
| GBDT-TPE | 1.000 | 0.786 | 0.09 s |
| Model | Accuracy | Recall | Precision | Specificity | Datasets |
|---|---|---|---|---|---|
| GBDT-Random | 0.9566 | 0.9791 | 0.940 | 0.9322 | MS |
| GBDT-TPE | 0.9593 | 0.9844 | 0.941 | 0.9322 | |
| GBDT-Random | 0.777 | 0.636 | 0.875 | 0.857 | OS |
| GBDT-TPE | 0.833 | 0.727 | 0.875 | 0.875 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, M.; Xiao, K.; Sun, L.; Zhang, S.; Xu, Y. Automated Hyperparameter Optimization of Gradient Boosting Decision Tree Approach for Gold Mineral Prospectivity Mapping in the Xiong’ershan Area. Minerals 2022, 12, 1621. https://doi.org/10.3390/min12121621
Fan M, Xiao K, Sun L, Zhang S, Xu Y. Automated Hyperparameter Optimization of Gradient Boosting Decision Tree Approach for Gold Mineral Prospectivity Mapping in the Xiong’ershan Area. Minerals. 2022; 12(12):1621. https://doi.org/10.3390/min12121621
Chicago/Turabian StyleFan, Mingjing, Keyan Xiao, Li Sun, Shuai Zhang, and Yang Xu. 2022. "Automated Hyperparameter Optimization of Gradient Boosting Decision Tree Approach for Gold Mineral Prospectivity Mapping in the Xiong’ershan Area" Minerals 12, no. 12: 1621. https://doi.org/10.3390/min12121621
APA StyleFan, M., Xiao, K., Sun, L., Zhang, S., & Xu, Y. (2022). Automated Hyperparameter Optimization of Gradient Boosting Decision Tree Approach for Gold Mineral Prospectivity Mapping in the Xiong’ershan Area. Minerals, 12(12), 1621. https://doi.org/10.3390/min12121621