Oxygen Isotopes in Carbonate and Phosphate of Modern Mammal Bioapatite: New Data and Critical Revision after about 25 Years from the First Recognitions

Abstract

Oxygen and carbon isotopes of well-preserved skeletal remains give relevant support to archaeological and environmental reconstructions. However, the preservation of the skeletal remains must be preliminarily checked. About twenty-five years ago, a diagnostic method based on the oxygen isotope ratio in the phosphate, $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}},$ and carbonate, $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}},$ of bioapatite of modern mammals was proposed: for well-preserved samples, the $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$should plot near the regression line $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ on $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$ obtained for modern mammals. In the last twenty years, techniques of analysis have changed. In the past, ${\mathrm{BiPO}}_4$or ${\mathrm{Ag}}_3{\mathrm{PO}}_4$were precipitated from dissolved bioapatite and analysed with the fluorination technique, whereas at present, temperature reduction (HTR) in a glassy carbon reactor with $\mathrm{CO}$release is commonly used. Taking into account the HTR technique, for some modern mammals, we report a new$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ + 1 on $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$ + 1 regression line, and related dispersion of the data that, in addition to mineralogical and structural methods, may be used to select samples reliable for archaeological use. In the past, other similar regression lines on modern mammals were defined by several authors. However, statistical results indicate that data used for these regression lines cannot be pooled because the hypothesis of a similar elevation is rejected.

1. Introduction

In this paper, the parameter delta (δ) is defined according to IUPAC (International Union of Pure and Applied Chemistry):

$$\mathsf{\delta }{({}_{}{}^a\mathrm{E}/{}_{}{}^b\mathrm{E})}_{\mathrm{i}/\mathrm{RM}}=\frac{\mathrm{R}{({}_{}{}^{\mathrm{a}}\mathrm{E}/{}_{}{}^{\mathrm{b}}\mathrm{E})}_{\mathrm{i}}}{\mathrm{R}{({}_{}{}^{\mathrm{a}}\mathrm{E}/{}_{}{}^{\mathrm{b}}\mathrm{E})}_{\mathrm{RM}}}-1=\left(\frac{\mathrm{R}{({}_{}{}^{\mathrm{a}}\mathrm{E}/{}_{}{}^{\mathrm{b}}\mathrm{E})}_{\mathrm{i}}}{\mathrm{R}{({}_{}{}^{\mathrm{a}}\mathrm{E}/{}_{}{}^{\mathrm{b}}\mathrm{E})}_{\mathrm{RM}}}-1\right){10}^3‰,$$

where R is the ratio between the abundances of the isotope ${}_{}{}^{\mathrm{a}}\mathrm{E}$ and of the isotope ${}_{}{}^{\mathrm{b}}\mathrm{E}$ present in a chemical species of the material i or of the reference material RM, and ‰ = ${10}^{-3}$.

The inorganic portion of bones and teeth of animals and humans mostly consists of bioapatite. Bioapatite ([1,2,3,4] and references therein) is a calcium phosphate with the general formula:

$${(\mathrm{M}☐,)}_{10}{\mathrm{Z}}_6{(\mathrm{X},☐)}_2$$

where: M = ${\mathrm{Ca}}^{2+},$ ${\mathrm{Na}}^{+},{\mathrm{Mg}}^{2+},{\mathrm{Ba}}^{2+}$, ${\mathrm{Sr}}^{2+}$, …; $\mathrm{Z}={\mathrm{PO}}_4^{3-},{\mathrm{HPO}}_4^{2-},{\mathrm{CO}}_3^{2-}$; X = ${\mathrm{OH}}^{-},{\mathrm{F}}^{-},{\mathrm{Cl}}^{-},$ ${\mathrm{O}}^{2-}$, ${\mathrm{CO}}_3^{2-};$ ⎕ = lattice vacancy. Substitution of ${\mathrm{CO}}_3^{2-}$ for ${\mathrm{PO}}_4^{3-}$ and ${\mathrm{CO}}_3^{2-}$ for ${\mathrm{OH}}^{-}$ are called B and A substitutions, respectively, the latter being much lower than the former. Moreover, the total ${\mathrm{CO}}_3^{2-}$substitution is less than about 4–5% weight as ${\mathrm{CO}}_2$ ([2] and references therein).

In archaeology and environmental reconstruction, carbon isotopes of the carbonate (${\mathrm{CO}}_3^{2-},\mathrm{here}\mathrm{indicated}\mathrm{as}\mathrm{Carb})$ of bone and tooth (enamel and dentine) of bioapatite are commonly used for defining the palaeodiet of ancient populations (e.g.,: [5,6,7]). Moreover, the oxygen isotopes of the phosphate (${\mathrm{PO}}_4^{3-}$ and ${\mathrm{HPO}}_4^{2-}$, here indicated as Ph) of apatite are used by archaeologists, in particular, to reconstruct the average isotope values of drinking water ingested directly or indirectly by humans or other animals, and thus, indirectly, the climatic condition of their living area (e.g.,: ([8,9,10,11]). A relationship between the ratio of the ${}_{}{}^{18}\mathrm{O}$ and ${}_{}{}^{16}\mathrm{O}$ abundances in phosphate and drinking water (W) ingested by modern mammals was demonstrated starting from about four decades by several authors (e.g.,: [12,13,14]). The uncertainty on the δ${({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{W}}$ evaluation from experimental $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ values is high to very high (for the water ingested by humans the uncertainty is about 2.5‰ [15]). In spite of it, this correlation and similar correlations for animals (e.g.,: [16]) are still in use for palaeclimate and archaeological reconstructions.

Bioapatite, however, may suffer post mortem low-temperature transformations (diagenetic processes), that may change its$\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)$ value both in phosphate and carbonate and the $\mathsf{\delta }({}_{}{}^{13}\mathrm{C}/{}_{}{}^{12}\mathrm{C})$ value in carbonate. Therefore, before using these data, an investigation of the possible diagenetic changes is necessary. In particular, bioapatite recrystallization may lead to loss of the carbonate group of bioapatite (e.g.,: [4]); thus, an evaluation of its structural features may be useful. A control of apatite crystallinity for the assessment of bone integrity has been recently proposed by Del Sasso [4] combining vibrational spectroscopies and X-ray diffraction methods. It is noteworthy, however, that recrystallization of apatite does not furnish direct evidence of variation in the isotopic distribution (e.g.,: [17,18,19] and references therein), but only suggests that possible changes in the isotopic values could have occurred.

Using the fluorination technique, Bryant et al. [20] and Iacumin et al. [21] analysed oxygen of the phosphate of bone and tooth bioapatite from different species of modern mammals that lived in different climatic conditions. These authors found a very good correlation between $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$ that, together with structural evidence, has been largely used to evaluate the diagenetic conditions of bone apatite. Actually, post mortem diagenetic processes may lead to increasing scattering around and/or systematic deviation of the isotope data from the $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$on the $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$ regression line. If the oxygen of carbonate undergoes an exchange with the environment, this, reasonably, could also occur for carbon. Thus, $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$vs. $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$ distribution also assumes relevance as a potential indicator of reliability of $\mathsf{\delta }\left({}_{}{}^{13}\mathrm{C}/{}_{}{}^{12}\mathrm{C}\right)$ values.

Standard enthalpies of the formation of carbonate and phosphate (−677.1 and −1277.4 kJ mole⁻¹, respectively [22]) suggest that carbonate is less stable in a solution than phosphate, and thus, that an oxygen exchange is easier for carbonate than for phosphate. This is in agreement with kinetic considerations for inorganic water-mineral interaction. Experiments demonstrated that oxygen exchange between phosphate and the environment is extremely slow in inorganic conditions [23] but is very rapid in enzyme-catalysed reactions [24]. If the exchange reaction is bacteria-mediated, the behaviour of the phosphate and carbonate is apparently inverted, the oxygen of phosphate reacting faster than the oxygen of carbonate [25].

Taking into account the present common use of the high-temperature reduction technique (HTR) ([26,27]), in this paper, (1) we report a new $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$+ 1 vs. $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$+ 1 regression line for modern mammals, for which the $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ data were obtained by HTR using international easily available standards and a defined procedure; (2) we compare the regression lines obtained for modern mammals by different authors; we did not consider ancient remains of mammals since they may be affected by diagenesis; (3) staring from this new regression line, we give an indication for selecting samples used for archaeological and palaeoclimatic inferences.

The scarce number of data at disposal in this paper is a limit for deep theoretical considerations. It is noteworthy, however, that the aim of this paper (point 3) is merely practical, not theoretical.

2. Significance of the Measured $\delta {({}_{}{}^{18}O/{}_{}{}^{16}O)}_{Carb}$

The $\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)$for carbonate of minerals (in our case bioapatite and low-Mg calcite) is not directly determined but obtained by measuring the isotope ratios of gaseous carbon dioxide, ${\mathrm{CO}}_{2\mathrm{gas}}$, produced, at the defined temperature T, by the dissolution of the mineral in orthophosphoric acid with the defined concentration of the ${\mathrm{H}}_3{\mathrm{PO}}_4$ component. The definition of “oxygen isotope phosphoric acid fractionation factor”, ${\mathsf{\alpha }}_{\mathrm{ACID}\left(\mathrm{Ap}\right)}^{\mathrm{T}}$, between ${\mathrm{CO}}_{2\mathrm{gas}}$, produced by dissolution of bioapatite, and the carbonate of bioapatite at temperature T allows us to understand the significance of the measured $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$. The ${\alpha }_{ACID\left(Ap\right)}^T$ definition is the following:

$$\begin{gathered} {\mathsf{\alpha }}_{\mathrm{ACID}\left(\mathrm{Ap}\right)}^{\mathrm{T}}=\frac{\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{CO}2\left(\mathrm{Ap}\right)}^{\mathrm{T}}+1}{\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}+1}\to \\ \mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}+1=\frac{1}{{\mathsf{\alpha }}_{\mathrm{ACID}\left(\mathrm{Ap}\right)}^{\mathrm{T}}}(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{CO}2\left(\mathrm{Ap}\right)}^{\mathrm{T}}+1) \end{gathered}$$

where $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{CO}2\left(\mathrm{Ap}\right)}^{\mathrm{T}}$ and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$ are the delta values for the ${\mathrm{CO}}_{2\mathrm{gas}}$ generated from apatite and for the ${\mathrm{CO}}_3^{2-}$ of apatite, respectively. Since ${\mathsf{\alpha }}_{\mathrm{ACID}\left(\mathrm{Ap}\right)}^{\mathrm{T}}$ is unknown, $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}$ cannot be correctly evaluated. Only an “apparent” value $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}$ is determined. This value is obtained assuming that during the acid dissolution at the temperature T, bioapatite behaves as low-Mg calcite (Cal) used as the standard for the isotope analysis (see Appendix A); i.e.,:

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1=\frac{1}{{\mathsf{\alpha }}_{\mathrm{ACID}\left(\mathrm{Cal}\right)}^{\mathrm{T}}}\left(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{CO}2\left(\mathrm{Ap}\right)}^{\mathrm{T}}+1\right)$$

where

${\mathsf{\alpha }}_{\mathrm{ACID}\left(\mathrm{Cal}\right)}^{\mathrm{T}}$ = $\frac{\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{CO}2\left(\mathrm{Cal}\right)}^{\mathrm{T}}+1}{\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Cal}}+1}$, $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{CO}2\left(\mathrm{Cal}\right)}^{\mathrm{T}}$ is the value for the ${\mathrm{CO}}_{2\mathrm{gas}}$ produced by dissolution of low-Mg calcite and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Cal}}$ is the value for carbonate of low-Mg calcite.

The oxygen isotopic composition of ${\mathrm{CO}}_{2\mathrm{gas}}$ produced depends on several important factors (e.g., [28,29,30,31,32,33,34,35,36,37,38,39,40]). Among these factors, we emphasize the following: (1) pre-treatment of the sample; (2) temperature of reaction of the sample with H₃PO₄; (3) concentration of the H₃PO₄ chemical component in the acid; (4) composition of bioapatite; (5) interaction of the new-formed ${\mathrm{CO}}_2$ with endogenic water that is generated by the reaction producing ${\mathrm{CO}}_2$; (6) solution species that formed with phosphorous-bearing anions and cations liberated by the mineral dissolution.

3. Methods and Materials

3.1. Materials

The $\mathsf{\delta }({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})$ values for carbonate and phosphate have been determined on tooth (enamel) and bone bioapatite from several modern mammals (Canis aureus, Vulpes vulpes, Vulpes zerda, Vulpes lagopus, Alces alces) that lived in different localities under variable climatic conditions. Only one portion of bone or tooth for each individual was analysed. The data reported are the average of two experimental values obtained during the same analytical run.

3.2. Calibration for Sample Analysis

Calibration is generally done using several international or in-house standards. In the case that the linearity of the final instrumental response is verified, matrix effect, errors on the isotopic measurements and errors on the isotopic values of the standards used for the regression are absent, the standards will be perfectly aligned along the regression line of the form

$$\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{st},\mathrm{m}/\mathrm{w}}+1=\mathrm{B}(\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{st}/\mathrm{WSMOW}}+1)$$

(1a)

where $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{st},\mathrm{m}/\mathrm{w}}$ is the measured value of a generic standard st referred to the laboratory working standard w (${\mathrm{CO}}_2\mathrm{of}\mathrm{the}\tan \mathrm{k})$, $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{st}/\mathrm{WSMOW}}$ is the “true” values, and B is the slope. From Equation (1a) we obtain the calibration line which gives the estimate:

$$\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{i}/\mathrm{WSMOW}}+1=\frac{1}{\mathrm{B}}(\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{i},\mathrm{m}/\mathrm{w}}+1)$$

(1b)

for the material i in analysis. We prefer Equation (1b) in place of the usual expression $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{i}/\mathrm{WSMOW}}$ = $b$ $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{i},\mathrm{m}/\mathrm{w}}$ + a because (1b) may give direct information on instrumental linearity. Linearity of the final instrumental response may be defined as proportionality between the measured (m) isotope abundance ratio, R(¹⁸O/¹⁶O)_i,m, and the “true” value R(¹⁸O/¹⁶O)_i, i.e.,

R(¹⁸O/¹⁶O)_i,m = c R(¹⁸O/¹⁶O)_i

(2)

where R(¹⁸O/¹⁶O) is referred to the chemical species of interest (e.g.,: C${\mathrm{O}}_3^{2-}$, P${\mathrm{O}}_4^{3-}$), present in generic substance i, and c is a constant. In terms of δ + 1 values referred to the laboratory working standard w, relation (2) is written as:

$$\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{i},\mathrm{m}/\mathrm{w}}+1=c(\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{i},/\mathrm{w}}+1)$$

which represents a straight line passing through the origin.

Systematic errors and random errors in the measurements of the standards occur; matrix effect for standards of different material may be present; in general, the instrument response is not perfectly linear. Thus, the scattering of data around the calibration line and the intercept significantly different from zero are frequent. Note that, in this case, intercept is significantly different from zero, only new values of the analysed samples that fall in the range of the delta values of standards may be accepted; practically, only very small extrapolation is allowed.

3.3. Analytical Methods

Since the results obtained in this paper may be compared with data obtained from archaeological and palaeontological samples, in agreement with the Criterion of Identity Treatment, the modern samples of this study were chemically treated as ancient samples.

3.3.1. Oxygen of the Carbonate

Initial considerations. Different procedures of sample preparation frequently give different isotopic results not only on ancient, but also on modern samples. This argument has been widely discussed in the literature (e.g.,: [35,36,39,41,42,43,44,45]). In particular, Crowley and Wheatley [43] suggest that pre-treatment with NaClO or H₂O₂ and Ca-buffered acetic acid solution produces similar results for enamel carbonate, whereas NaClO is not recommended for tissues with higher organic content, such as bone and dentine. Our experience, however, suggests that it is difficult to obtain complete elimination of high content of organic components using H₂O₂ and that, on bones, a very low concentration of NaClO (2% solution) allows results that, in the limit of the analytical uncertainty of our analyses, are comparable with those obtained using H₂O₂. Thus, also for a better comparison with data produced in our laboratory in the past, we preferred to follow our routine procedure with the use of NaClO.

Analysis of our samples. Powdered bioapatite samples were previously treated with 2%wt. NaClO solution for one day to eliminate organic material, later repeatedly rinsed with distilled water, and, finally, treated with Ca-acetic buffer (1 N). About 2 mg of the treated apatite and 0.1 mg of the international standards NBS 18 (low-Mg calcite, $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{NBS}18/\mathrm{WSMOW}}$ = 7.20‰ ± 0.10‰) and NBS 19 (low-Mg calcite, $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{NBS}19/\mathrm{WSMOW}}$ = 28.64‰ by definition) were loaded into reaction vessels of a Finnigan GasBench II automatic sampling system. Reaction vessels were flushed with helium and, later, the samples were reacted at 50 °C for 7–8 h with 0.2 cm³ of H₃PO₄ acid solution (concentration of the H₃PO₄ component ≥ 100%, density ≅ 1.90 g cm⁻³). The CO_2gas produced was analysed by a mass spectrometer Finnigan Delta Plus.

3.3.2. Oxygen of the Phosphate

Initial considerations. In the past, $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{Ph}}$ was usually determined by conventional fluorination ([20] and references therein) of BiPO₄ or Ag₃PO₄ precipitated from dissolved bioapatite. At present, however, $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{Ph}}$is frequently measured by online high-temperature reduction (HTR) in a glassy carbon reactor with CO release ([27] and references therein). According to the Identical Treatment Principle [46], the HTR method would require standards used for calibration and samples in analysis to be reduced to the same material, namely Ag₃PO₄. Unfortunately, however, this is not always possible.

Vennemann et al. [27], together with other laboratories, prepared several Ag₃PO₄ samples precipitated from natural or synthetic materials and analysed their oxygen isotopes by fluorination. The accuracy of the obtained results (referred to as VSMOW) was guaranteed by replicate analyses of the quartz standard NBS-28 (9.56‰ ± 0.07‰, standard deviation, 12 data, against the expected value of 9.58‰ ± 0.09‰, [47]) and of the in-house quartz standard NCSU (11.62‰ ± 0.17‰, 20 data, against the expected value 11.67‰). In addition, the standard NIST SRM 120c (Florida Phosphate Rock) gave a value of 22.58‰ ± 0.05‰. Five of the samples analysed (namely TU-1, 21.11‰ ± 0.07‰, standard error on the average; TU-2, 5.45‰ ± 0.04‰; YR-1, −5.19‰ ± 0.09‰; YR-2, 13.06‰ ± 0.11‰; YR-3, 34.03‰ ± 0.13‰) were considered as standards to be distributed worldwide. The same Ag₃PO₄ samples were also analysed by HTR and the obtained raw values normalised to the data for the samples GW-1, 130-9, and 130-1 previously analysed by fluorination (TU-1, 21.11‰ ± 0.12‰; TU-2, 5.35‰ ± 0.17‰; YR-1, −5.77‰ ± 0.08‰; YR-2, 13.05‰ ± 0.07‰; YR-3, 33.54 ‰ ± 0.24‰). Fluorination and HTR data for TU-1, TU-2, YR-1, YR-2, and YR-3.1 are very well correlated according to a line passing for the origin (p_{(slope =1)} = 0.86 and p_{(intercept =0)} = 0.29, s(yx) = standard error of estimate = 0.32, p_{(homoscedastic)} = 0.85) suggesting that not significant bias occurs in the HTR analysis. Unfortunately, these samples are no longer available.

Halas et al. [48] prepared three new samples of Ag₃PO₄ (UMCS-1, UMCS-2, and AGPO-SCRI) for inter-laboratory comparison. These samples were analysed in two different laboratories together with the standards NIST SRM 120c and the samples TU-1 and TU-2 mentioned above. The data were normalised to IAEA-601 (benzoic acid), IAEA-602 (benzoic acid), IAEA-CH6 (sucrose), and IAEA-C3 (cellulose) or to IAEA-601 and IAEA-602. In spite of the use of these standards does not match the Principle of the Identical Treatment [46]; for the standards TU-1 and TU-2, the agreement between data reported by Vennemann et al. [27] and by Halas et al. [48] (Dundee Laboratory data) was very good (p_{(same average)} ≈ 1) whereas the agreement for the standard NIST SRM 120c, was not so good (p_{(same average)} ≈ 0.10), but still acceptable.

More recently, Watzinger et al. [49] reported oxygen isotope analyses carried out in four different laboratories on a new silver phosphate sample (BOKU Ag₃PO₄) with 13.71‰ ± 0.34‰ (combined standard uncertainty). Calibration was done using the standards IAEA-601, IAEA-602, and NBS 127 (barium sulphate) and the “quality control” using the standard AGPO-SCRI (14.6‰ ± 0.2‰, standard deviation, against 14.58‰ ± 0.13‰ [48]) and NIST SRM 120c (22.9‰ ± 0.2‰ against 21.79‰ ± 0.15‰, [48]). The values obtained by Halas et al. [49] and by Watzinger et al. [49] for NIST SRM 120c are apparently significantly different (p_{(same average)} < 0.005); it is noteworthy, however, that analyses reported in literature for NIST SRM 120c are largely variable ([48] and references therein).

Based on the results reported above, we emphasize the following points:

(1)

The matrix effect apparently is not largely relevant for calibration; this makes the use of silver phosphate standards not strictly necessary.

(2)

Practically, the new phosphate BOKU cannot substitute the use of the standards listed above because calibration with only one standard is risky. Sample BOKU could be used only for “quality control”.

Analysis of our samples. The chemical treatment of the samples to obtain silver phosphate followed the protocol by Stephan [50]. About 50 mg of powdered sample was placed in 2.5%wt. NaClO solution for 24 h to eliminate organic material. After that, the supernatant was removed and the pellet was washed several times to neutralise it. Then, a 0.125 M NaOH solution was added (this is frequently used to dissolve humic substances possibly present in archaeological samples) and samples were left for 48 h for reacting. After the dissolution of the sample in 2M HF at 25 °C for 24 h, the precipitated CaF₂ was separated from the phosphate solution by centrifugation and the solution was neutralized with 3 mL of 2M KOH solution in a 250 cm³ beaker. Doubly distilled water was added to make up the apatite solution to a total volume of 200 cm³. Later, 30 cm³ of buffered silver nitrate solution (AgNO₃ 0.2 M, NH₄NO₃ 0.3 M, NH₃ 0.7 M) was added and the solution was gradually warmed to 70 °C for 3 h. The crystals of silver phosphate were collected on a millipore filter, and then washed and air-dried overnight at 50 °C. A total of 0.3 mg of sample was weighed in silver capsules together with 0.3 mg of glassy carbon and 0.5 mg of AgCl (the latter two act as catalysts for the combustion reaction). The oxygen isotope composition was analysed using a thermal conversion-elemental analyser unit (1420 °C) online with a mass spectrometer (Finnigan TC/EA-Delta Plus XP, Thermo Fisher Scientific, Bremen, Germany). The yield for oxygen was checked for all samples.

As discussed above, apparently the matrix effect is not relevant for calibration. Thus, standards IAEA-601 (benzoic acid, $\mathsf{\delta }({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})$= 23.14‰ ± 0.10‰ VSMOW, approximate standard error of the mean better than 0.1‰, [51]), IAEA-CH-6 (sucrose, $\mathsf{\delta }({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})$ = 36.4‰ ± 0.15‰ VSMOW, [52]) and IAEA-600 (caffeine, $\mathsf{\delta }({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})$= −3.48‰ ± 0.53‰ VSMOW, [51]) were used for calibration in this paper. Sulphate standards were disregarded because the yield of these substances was generally lower than 100% (down to 80%). As far as the Ag₃PO₄ from the samples is concerned, we disregarded two samples that gave a yield for oxygen of less than 100%. Unfortunately, the calibration with these three standards did not exactly match the Equation (1). A regression line in the form:

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{st},\mathrm{m}/\mathrm{w}}+1=\mathrm{B}(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{st}/\mathrm{WSMOW}}+1)+\mathrm{A}$$

(3a)

with A ≠ 0 was established. Thus, the calibration line is:

$$(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{i}/\mathrm{WSMOW}}+1=\frac{1}{\mathrm{B}}(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{i},\mathrm{m}/\mathrm{w}}+1)-\frac{\mathrm{A}}{\mathrm{B}}$$

(3b)

Equation (3) may be due to the absence of linearity of the spectrometric response (actual absence of linearity is not rare, [15,53]). If linearity is not perfect, the calibration line obtained with more than one standard is not a straight line but a curve. It is noteworthy, however, that the standards used in this paper cover a narrow range of values and, thus, in this range, the calibration curve approaches a straight line. Moreover, the samples of this paper fall in the delta interval of standards, and thus, no extrapolation was done.

3.4. Analytical Uncertainty

Usually, papers only report repeatability and reproducibility, and very rarely the prediction uncertainty related to the calibration line [54]. This is surprising because prediction uncertainty is the only value which is relevant for the comparison of data obtained in the same laboratory or in different laboratories.

Repeatability and reproducibility. During our routine analysis of carbonate, repeatability for $\mathsf{\delta }({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})$ analysis was about 0.15‰ and reproducibility (a different portion of the same sample at different times) was about 0.20‰. For phosphate, repeatability was about 0.20‰ and reproducibility was about 0.30‰ (different portions of different Ag₃PO₄ precipitates from the same sample, measured at different times).

Prediction uncertainty. Given the OLS (Ordinary Least Square Regression) $\mathrm{Y}$ = $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{st},\mathrm{m}/\mathrm{w}}$ + 1 on $\mathrm{X}$ = ($\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{st}/\mathrm{WSMOW}}$ + 1 for the standards, st, the prediction uncertainty u(${\mathrm{X}}_{\mathrm{i}}$) on the estimate value ${\mathrm{X}}_{\mathrm{i}}$ corresponding to a new Y_j value was calculated as follows [54]:

$$\mathrm{u}({\mathrm{X}}_{\mathrm{i}})\cong {\mathrm{t}}_{\left(\mathsf{\alpha }\right(2),\mathsf{\upsilon })}\frac{\mathrm{s}\left(\mathrm{yx}\right)}{\mathrm{B}}\sqrt{\frac{1}{\mathrm{g}}+\frac{1}{\mathrm{n}}+\frac{{({\overline{\mathrm{Y}}}_{\mathrm{i}}-{\overline{\mathrm{Y}}}_{\mathrm{st}})}^2/{\mathrm{B}}^2}{{\displaystyle \sum }{({\mathrm{X}}_{\mathrm{st}}-{\overline{\mathrm{X}}}_{\mathrm{st}})}^2}}$$

(4)

where ${\overline{\mathrm{Y}}}_{\mathrm{st}}$ and ${\overline{\mathrm{X}}}_{\mathrm{st}}$ are average values for the standard; ${\mathrm{X}}_{\mathrm{st}}$ refers to each standard;${\mathrm{t}}_{\left(\mathsf{\alpha }\left(2\right),\mathsf{\nu }\right)}$is the Student’s t-value (two-tailed test); α is the significance level; g, for each individual i, it is the number of experimental values with average value ${\overline{\mathrm{Y}}}_{\mathrm{i}}$ (in our case, two experimental values); n is the number of experimental values for the standards; $\mathrm{s}\left(\mathrm{yx}\right)$is the standard error of regression; υ the degree of freedom (υ = n − 2). However, in our case, ${\mathrm{X}}_{\mathrm{st}}$ is affected by some uncertainty, $\mathrm{s}\left({\mathrm{X}}_{\mathrm{st}}\right)$. In this case, Taylor ([55], pp. 188–190) suggests adding uncertainty $\mathrm{s}\left({\mathrm{X}}_{\mathrm{st}}\right)$ to $\mathrm{s}\left(\mathrm{yx}\right)$, i.e., $\mathrm{s}{\left(\mathrm{yx}\right)}_{\mathrm{tot}}^2$ = $\mathrm{s}{\left(\mathrm{yx}\right)}^2$ + B² $\mathrm{s}{\left({\mathrm{X}}_{\mathrm{st}}\right)}^2$. For the standards used is, on average, $\mathrm{s}\left({\mathrm{X}}_{\mathrm{st}}\right)$ ≈ 0.25‰ for $\mathsf{\delta }({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})$. Thus, in Equation (4), $\mathrm{s}{\left(\mathrm{yx}\right)}_{\mathrm{tot}}$ may be introduced in place of $\mathrm{s}\left(\mathrm{yx}\right)$to have a better evaluation of the uncertainty. From several calibration lines, we estimated the analytical prediction uncertainty, u(${\mathrm{X}}_{\mathrm{i}}$) for $\mathsf{\delta }({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})$: it is about 0.25‰ for carbonate and 0.35‰ for phosphate.

Accuracy. The accuracy of the data was checked using the standard BOKU for which we obtained 13.90‰ ± 0.35‰ (average of two experimental values, ± prediction uncertainty, [54]) against the declared value of 13.71‰ ± 0.34‰.

4. Results and Discussion

4.1. Results

Table 1 and Figure 1 report the obtained results. The range of delta values is a little bit narrower than the ranges obtained by Bryant et al. [20] and Iacumin et al. [21] (Table 2).

Table 1. Oxygen isotope analyses of phosphate, Ph, and carbonate, Carb, from bone and tooth (enamel) bioapatite of modern mammals of different provenance.

Provenance	Species	${10}^3\times \mathsf{\delta }{\left({}_{}{}^{18}\mathbf{O}/{}_{}{}^{16}\mathbf{O}\right)}_{\mathbf{P}\mathbf{h}}$ VSMOW	$\mathsf{\delta }{\left({}_{}{}^{18}\mathbf{O}/{}_{}{}^{16}\mathbf{O}\right)}_{\mathbf{P}\mathbf{h}}$ + 1	103× $\mathsf{\delta }{\left({}_{}{}^{18}\mathbf{O}/{}_{}{}^{16}\mathbf{O}\right)}_{\mathbf{C}\mathbf{a}\mathbf{r}\mathbf{b}}$ VSMOW	$\mathsf{\delta }{\left({}_{}{}^{18}\mathbf{O}/{}_{}{}^{16}\mathbf{O}\right)}_{\mathbf{C}\mathbf{a}\mathbf{r}\mathbf{b}}$ + 1
Spanish Sahara	Canis aureus 1	21.5	1.0215	30.1	1.0301
Southern Spain	Vulpes vulpes 1	18.3	1.0183	25.6	1.0256
Southern Spain	Vulpes vulpes 1	20.6	1.0206	27.6	1.0276
Marocco	Vulpes zerda 1	24.6	1.0246	32.5	1.0325
Southern Spain	Vulpes vulpes 1	19.7	1.0197	26.4	1.0264
Central Spain	Vulpes vulpes 1	17.7	1.0177	24.6	1.0246
Central Italy	Vulpes vulpes 1	18.9	1.0189	25.9	1.0259
Central Italy	Vulpes vulpes 1	18.0	1.0180	26.6	1.0266
Siberia	Vulpes lagopus 2	8.7	1.0087	16.0	1.0160
Siberia	Alces alces 2	17.5	1.0175	25.3	1.0253
Siberia	Alces alces 2	16.0	1.0160	24.2	1.0242
Siberia	Alces alces 2	13.8	1.0138	21.3	1.0213
Siberia	Alces alces 2	11.1	1.0111	19.5	1.0195
Siberia	Alces alces 2	14.6	1.0146	21.9	1.0219
Siberia	Alces alces 2	11.8	1.0118	19.0	1.0190
Siberia	Alces alces 2	13.5	1.0135	21.6	1.0216

¹ = enamel, ² = bone. The values are averages of two different experimental values obtained during the same analytical run on the same individual. The δ + 1 values will be used in the calculations.

Figure 1. $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{Ph}}$ + 1 on ${(\mathsf{\delta }{}_{}{}^{18}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#}$ + 1. The regression lines have the same slope but different elevations [20,21,56,57].

Table 2. Statistical data.

	Iacumin et al. (1996) [20]	Bryant et al. (1996) [21]	Zazzo et al. (2004b) [56]	Miller et al. (2019) [57]	This Work
s(Carb), s(Ph) u(Carb), u(Ph)	0.2‰, 0.2‰ nd	0.1‰, 0.1‰ nd	0.2‰, 0.2‰ nd	0.08‰, 0.23‰ (?) nd	0.15‰, 0.20‰ 0.25‰, 0.35‰
Number of data	17	42	7	55	16
Interval of X	1.0132–1.0354	1.0180–1.0347	1.0270–1.0340	1.0204–1.0288	1.0160–1.0325
Interval of Y	1.0048–1.0254	1.0093–1.0254	1.0170–1.0238	1.0109–1.0217	1.0087–1.0246
Normality test for X and Y
W, A for X	0.830, 0.797	0.002, < 0.001	0.733, 0.787	0.003, 0.001	0.984, 0.850
W, A for Y	0.344, 0.428	0.008, 0.007	0.607, 0.604	0.271, 0.101	0.995, 0.928
Regression line OLS, Y = B X + A
A ± s(A)	0.0164 ± 0.0314	0.0297 ± 0.0189	0.0230 ± 0.0502	0.0708 ± 0.0541	0.0142 ± 0.0399
B ± s(B)	0.9751 ± 0.0306	0.9625 ± 0.0184	0.9681 ± 0.0487	0.9227 ± 0.0527	0.9787 ± 0.0390
s(yx)	0.00073	0.00061	0.00031	0.00085	0.00064
R2	0.985	0.986	0.987	0.853	0.978
p(A = 0)	0.61	0.12	0.46	0.20	0.73
Normality test for residuals
Shapiro-Wilk test	0.26	0.82	0.26	0.001	0.33
Anderson-Darling test	0.12	0.74	0.27	< 0.001	0.45
Autocorrelation Durbin-Watson test	0.99	0.03	0.74	0.73	0.43
Homoscedasticity Breusch-Pagan test	0.13	0.03	0.35	0.17	0.28

Data was obtained under routine conditions of analysis. All δ values are referred to VSMOW; $\mathrm{X}$ = $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1$, $\mathrm{Y}$ = $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1$; $\mathrm{p}$ = probability; $\mathrm{OLS}$, Ordinary Least-Square regression; for Bryant et al. [20] and Miller et al. [58], $\mathrm{X}$ values have been reduced to 50°C; $\mathrm{s}\left(\mathrm{Carb}\right),$ $\mathrm{s}\left(\mathrm{Ph}\right)$ = repeatability of $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}$ and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ measurements; $\mathrm{u}\left(\mathrm{Carb}\right),$ $\mathrm{u}\left(\mathrm{Ph}\right)$ = prediction uncertainty for $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}$ and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ for a new measure; $\mathrm{nd}$: not determined (assumed equal to 0.3‰ in the statistical calculation); s(yx) = standard error of regression. Investigated genera: Bryant et al. [20], Equus: the data refer prevalently to teeth of 8 different individuals; data for bones are only 5. Iacumin et al. [21], Cervus, Rangifer, Ursus, Canis, Bos, Ovis, Capra, Alcephalus, Camelus, Syncerus, Kobus, Ichneumon: the data are averages of different experimental values obtained on different individuals of the same genus from the same area (31 experimental values). Zazzo et al. [56], Hippopotamus. Miller et al. [57], Dama; This work, Canis, Vulpes, Alces: the data are average of two experimental values.

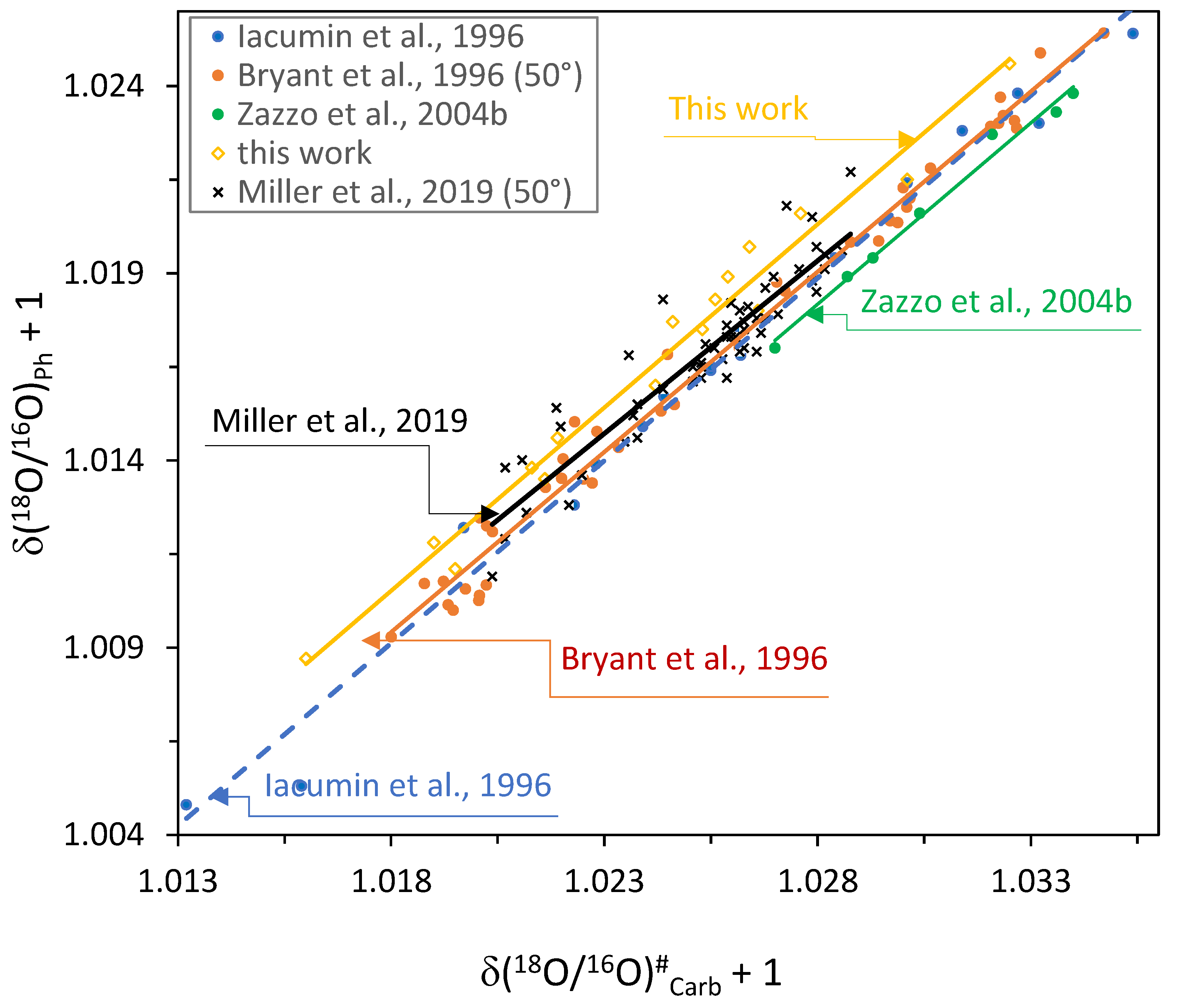
4.2. Comparison of $\delta {\left({}_{}{}^{18}O/{}_{}{}^{16}O\right)}_{Ph}$ + 1 on $\delta {\left({}_{}{}^{18}O/{}_{}{}^{16}O\right)}_{Carb}^{\#}$ + 1 Regression Lines for Modern Samples

4.2.1. Data Used for Comparison

We considered data from Bryant et al. [20], Iacumin et al. [21], Zazzo et al. [56], and Miller et al. [57]. Different authors used different standards and analytical techniques. Bryant et al. [20] used laboratory standards; Iacumin et al. [21] used a laboratory standard for the analysis of ${\mathrm{CO}}_{2\mathrm{gas}}$ and quartz NBS28 for the oxygen of phosphate analysis; Zazzo et al. [56] used international standards NBS18 and NBS19 for the oxygen analysis of ${\mathrm{CO}}_{2\mathrm{gas}}$. Iacumin et al. [21] analysed the oxygen isotope of phosphate by fluorination of BiPO₄ precipitated from dissolved bioapatite and Bryant et al. [20] by fluorination of Ag₃PO₄. Zazzo et al. [56] analysed Ag₃PO₄ by graphite method (since with this method the oxygen yield in only 25%, they corrected the data using a constant offset of +0.5‰). Miller et al. [57] analysed Ag₃PO₄ by HTR.

4.2.2. Data Obtained at Different Temperatures

The temperature of the acid dissolution is a critical parameter for the $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{{\mathrm{CO}}_2\left(\mathrm{Ap}\right)}$ value of the ${\mathrm{CO}}_{2\mathrm{gas}}$ produced by the dissolution of apatite. For instance, using GasBench (Thermo-Finnigan, Bremen, Germany) as a preliminary test, we determined the delta raw values $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{{\mathrm{CO}}_2\left(\mathrm{Ap}\right)/\mathrm{w}}$at 50 °C and 72 °C on 46 portions of the same sample of bone bioapatite. The result was the following: Δ = $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{{\mathrm{CO}}_2\left(\mathrm{Ap}\right)/\mathrm{w}}^{50°\mathrm{C}}$ − $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{{\mathrm{CO}}_2\left(\mathrm{Ap}\right)/\mathrm{w}}^{72°\mathrm{C}}$ = (1.0 ± 0.2‰, standard deviation). This suggests an important role of temperature. Obviously, the use of phosphate standards with known values of $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ would eliminate the offset due to the different temperatures. Unfortunately, however, the standards commonly used (this is also our case) are low-Mg calcites, not phosphates. Thus, data obtained at different temperatures must be corrected, as indicated in the Appendix A. The oxygen isotope analyses on the carbonate reported by Iacumin et al. [21] and by Zazzo et al. [56] refer to ${\mathrm{CO}}_2$ produced at 50 °C, whereas the data reported by Bryant et al. [20] and Miller et al. [57] was of ${\mathrm{CO}}_2$ produced at 90 °C. Thus, the $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#}$ values obtained by Bryant et al. [20] and Miller et al. [57] were reduced to 50 °C. The systematic differences calculated between the estimated $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}/\mathrm{VSMOW}}^{\#}$ values at 50 °C and at 90 °C (about 0.10–0.15‰) are similar to, or lower than, the uncertainty of the data.

4.2.3. The Regression Lines

For the oxygen isotopes present in phosphate and carbonate of bioapatite, the apparent equilibrium isotope fractionation factor between phosphate and carbonate at a defined temperature is expressed as:

$${\mathsf{\alpha }}_{\mathrm{Ph}-\mathrm{Carb}}^{\mathrm{T},\#}=(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Ph}}+1\right)/\left(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)=\mathrm{constant}$$

(5)

from which we obtain:

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1={\mathsf{\alpha }}_{\mathrm{Ph}-\mathrm{Carb}}^{\mathrm{T},\#}\left(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)$$

(6a)

Consider the linear equation:

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1=b(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1)+a$$

(6b)

The regression line obtained using the experimental data allows us to verify immediately the agreement of our data with Equation (5) if the obtained regression line has an intercept a not significantly different from zero ($p_{A=0}$ exhibits a very high value). The b value is an estimate of ${\mathsf{\alpha }}_{\mathrm{Ph}-\mathrm{Carb}}^{\mathrm{T},\#}$ and the uncertainty on ${\mathsf{\alpha }}_{\mathrm{Ph}-\mathrm{Carb}}^{\mathrm{T},\#}$ is given by the standard error on the slope b. In case the intercept a is significantly different from zero, dividing by $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1$, Equation (6b) becomes $\frac{\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1}{\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1}$ = $\frac{a}{\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1}$ + b. The ratio $(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1)$/$(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1)$ is not independent of the carbonate delta value, that disagrees with the Equation (5): the ratio is not a correct estimate of ${\mathsf{\alpha }}_{\mathrm{Ph}-\mathrm{Carb}}^{\mathrm{T},\#}$. Usually, in the literature, the relationship between $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}$ is expressed as linear function $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ = $\mathrm{b}$ $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+\mathrm{a}$. Using this function, however, we cannot immediately evaluate the independence of $\left(\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1\right)$/$(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)$ from $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1$. Therefore, we preferred to use the regression $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1$on $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1$ in place of the regression $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ on $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}$ commonly used in the literature.

The regression lines for the data obtained by the different authors on modern bioapatite are reported below and in Figure 1, whereas the related statistics are summarised in Table 2. The regression lines are the following (Equations (7)–(10) [20,21,56,57], respectively, and Equation (11) (This work)):

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1=0.9624(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)+0.0297 (\mathrm{values} \mathrm{at} 50 °\mathrm{C})$$

(7)

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1=0.9751(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)+0.0164$$

(8)

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1=0.9681(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)+0.0229$$

(9)

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1=0.9227(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)+0.0708 (\mathrm{values} \mathrm{at} 50 °\mathrm{C})$$

(10)

$$\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1=0.9787(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1\right)+0.0142$$

(11)

The null hypothesis for the intercept, H_o: A = 0, cannot be rejected at α = 0.1 for all the data groups considered. However, for the data from Bryant et al. [20], we obtained a low value for p(homoscedasticity) (0.03); moreover, both for the data from Bryant et al. [20] and Miller et al. [57], for residuals the value p(normal) is low to very low (0.03 and <0.001, respectively). Thus, the hypotheses reported below (such as differences between slopes and elevation of straight lines) are only tentative. Finally, always in the limit of the analytical uncertainty, we obtained $p_{\mathrm{A}=0}$ ≥ 0.2 (except for [20]). The high probability for A = 0 is not in contrast with the hypothesis of equilibrium of oxygen isotope in carbonate and phosphate of bioapatite, this, of course, is within the limit of the analytical errors.

Comparison of slopes and elevations for regression Equations (7)–(11) were done according to Zar [58] the different lines exhibit high probability for the same slope (p_{same slope} ≅ 0.9), whereas the null hypothesis for the same elevation is rejected (p_{same elevation} << 0.001). Therefore, theoretically, the data would not be pooled altogether for obtaining a common regression line.

4.2.4. The Role of Different Species and of Tooth (Enamel)/Bone Bioapatite on the Regressions

In the regressions reported in Section 4.2.3, we pooled the data for different genus/species and for bones and teeth. Now the question is: in the limit of our approach, was it correct? The following points must be taken into account in the discussion: (a) The body temperature of the investigated modern mammals is very similar (approximately in the range 35–39 °C, [59]). (b) Bioapatite is a mineral, its crystallization is a slow process; thus, as commonly occurs for minerals, intra-lattice equilibrium is very probably reached. (c) Material commonly used for isotope determination of modern, recent (Holocene) and fossil mammals is enamel and bone bioapatite. Enamel bioapatite and bone bioapatite have similar crystal lattice and chemical composition; only crystal size and content of organic matter are significantly different. Thus, for a given temperature, teeth and bones are expected to behave similarly as far as the oxygen isotope fractionation between carbonate and phosphate is concerned.

Before comparing genus/species and bones and teeth, we note, that the standard error of the regression, s(yx), for the regression lines (7)–(11) is up to more than twice the prediction uncertainty for $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{Ph}}$(0.00031–0.00085 against 0.00035). This indicates that the scattering of the data around the regression lines is not only due to analytical uncertainty, but also to other reasons, not excluding a priori genus/species and teeth/bones effect. In this work, however, we are not interested in comparing regressions on teeth and bones and on different genus/species, but only to verify if data from teeth and bones and for different genus/species may be pooled to obtain single regression lines. This was tested using data from Iacumin et al. [21]. The distribution of data for the different genus are so chaotic that we cannot recognize systematic differences between the different genus. As far as the role of bones and teeth are concerned, the two independent regression lines $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{Ph}}$ + 1 on $\mathsf{\delta }{\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}\right)}_{\mathrm{Carb}}^{\#}$ + 1, calculated separately for teeth enamel (t) and bones (b), estimate the same statistical population (p_{(same regression)} = 0.84). Therefore, there is a very high probability that regression lines obtained on teeth and bones do not differ significantly and, thus, the data may be pooled.

4.2.5. Final Considerations

The differences among the regression lines obtained using samples dissolved at the same temperature could be prevalently due to the following reasons:

(a)

Different standard materials used for calibration.

(b)

Difference in technical procedures.

(c)

Although the role of standard materials and procedures would need a separate approach, the effect of materials and procedures on the slope and elevation cannot be identified separately. As far as phosphate is concerned, there is no unequivocal answer because different authors frequently used different techniques and did not use international standards, or they did not always indicate the international standards to which the in-house standards used were referred. For instance, Iacumin et al. [21] determined oxygen of carbonate using in-house standards and Bryant et al. [20] used in-house standards for both carbonate and phosphate. Miller et al. [57] used in-house standards for determining the oxygen isotope ratio in precipitated Ag₃PO₄. (b) For phosphate, this point has been approached and discussed by several authors (e.g.,: [27,60] and references therein) to which we address the attention of the reader. For carbonate, point (b) has been briefly discussed above (Section 2 and Section 3.3.1).

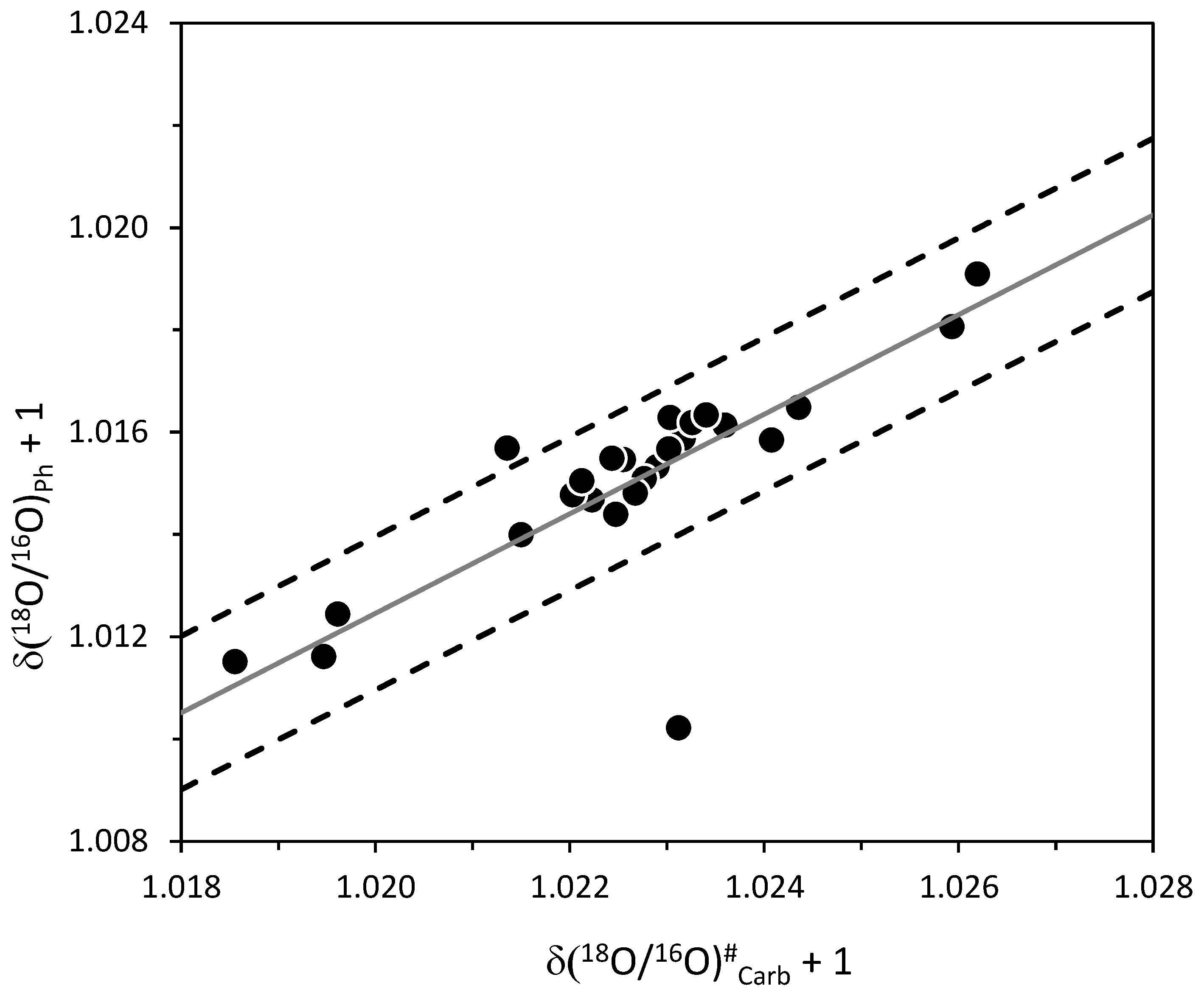
4.3. Identification of Potential Diagenetic Processes

If diagenetic processes affect bioapatite, two different types of deviations from the $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{P}}+1$ on $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{C}}^{\#,\mathrm{T}}+1$ regression line (11) should occur: (a) increase in scattering around the line, (b) systematic deviation from the line. Thus, the comparison of new values with our regression line (11) allows us to recognise samples that possibly underwent diagenesis. This may give support to other mineralogical, spectroscopic, and geochemical methods used to identify diagenetic transformation. The new value, of course, must be obtained using the same standard and the same procedure as this paper.

In addition to the mineralogical and structural investigation, we propose a very simple way for the selection of samples with potential diagenetic transformation affecting bone or tooth remains of animals which lived in the past. Assume that for a new sample i we obtained the experimental value ${\mathrm{X}}_{\mathrm{i}}$ = $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#,\mathrm{T}}+1$and ${\mathrm{Y}}_{\mathrm{i}}$ = $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1$ and that, for simplicity, these are not affected by uncertainty. Moreover, ${\hat{\mathrm{Y}}}_{\mathrm{i}}$ is the value estimated from the experimental ${\mathrm{X}}_{\mathrm{i}}$ using the regression line (11) and $\mathrm{s}\left(\mathrm{yx}\right)$ = 0.00064 is the standard error of the regression (11) (Table 2). Consider the value ${\mathrm{t}}_{\left(\mathsf{\alpha }\left(2\right),\mathsf{\nu }=\mathrm{n}-2\right)}$ $\mathrm{s}\left(\mathrm{yx}\right)$, where ${\mathrm{t}}_{\left(\mathsf{\alpha }\left(2\right),\mathsf{\nu }=\mathrm{n}-2\right)}$ = 2.145 is the Student’s t value (two-tailed) for significance level $\mathsf{\alpha }\left(2\right)$= 0.05, $n$ = 16 = numbers of couples of data used for regression (11), and $\nu$ = n − 2 = 14. Moreover, according to Taylor ([55], pp. 188–190), the uncertainty $\mathrm{s}$($\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#,\mathrm{T}}\right)$ = 0.25‰ (Table 2, column “This work”) was added to s(yx). The following values are obtained:

$$\mathrm{s}{\left(\mathrm{yx}\right)}_{\mathrm{tot}}^{}=\sqrt{\mathrm{s}{\left(\mathrm{yx}\right)}^2+{\mathrm{B}}^2{\mathrm{s}}^2(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{C}}^{\#,\mathrm{T}}\right)}=\sqrt{{0.00064}^2+{0.9787}^2\times {0.00025}^2}=0.00069$$

and

$${\mathrm{t}}_{\left(\mathsf{\alpha }\left(2\right),\mathsf{\nu }=\mathrm{n}-2\right)}\mathrm{s}{\left(\mathrm{yx}\right)}_{\mathrm{tot}}=2.145\times 0.00069=1.5‰.$$

Thus:

$${\hat{\mathrm{Y}}}_{\mathrm{i}}\pm t_{\left(0.05,14\right)}\mathrm{s}{\left(\mathrm{yx}\right)}_{\mathrm{tot}}={\hat{\mathrm{Y}}}_{\mathrm{i}}\pm 1.5‰.$$

where ${\hat{\mathrm{Y}}}_{\mathrm{i}}$ is the estimated value. The suspicion of diagenetic transformations could not be rejected for values outside the array defined by ±1.5‰. Figure 2 reports an example referred to Holocene mammal bone remains from Sudan. Based on the selection criteria discussed above, some of the samples could be considered as not reliable for archaeological considerations because they fall outside the array ± 1.5‰ on the y axis around the regression line (11). Obviously, the significance level $\mathsf{\alpha }\left(2\right)$= 0.05 may be changed according to particular needs.

Figure 2. $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ + 1 and $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#}$ + 1 for some Holocen mammal bone remains (Bos and Capra) and from Nile area of Sudan (unpublished data). The two points outside the dotted lines are considered not reliable for archaeological reconstruction. Continuous line represents regression line (11); discontinuous lines define the array ± 1.5‰.

It is noteworthy that if oxygen data are not reliable because they are potentially affected by diagenesis, the values $\mathsf{\delta }\left({}_{}{}^{13}\mathrm{C}/{}_{}{}^{12}\mathrm{C}\right)$ obtained for the carbonate of bioapatite must also be regarded with suspicion and not immediately used to do inference on the diet of the individuals. To summarise, regression line (11) has relevance not only for oxygen, but also for carbon isotopes.

5. Conclusions

(1)

We compared different $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1$ on $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#}+1$ OLS regression lines of data obtained by several authors [20,21,56,57] on bioapatite of teeth (enamel) and bones of modern mammals (Ph = ${\mathrm{PO}}_4^{3-}$, ${\mathrm{HPO}}_4^{3-}$ and Carb =${\mathrm{CO}}_3^{2-}$ of bioapatite). The hypothesis that the slopes of the different regression lines are the same cannot be rejected (p_{same slope} ≅ 0.9); on the contrary, the elevation varies significantly (p_{same elevation} << 0.001). Thus, the data of the different authors considered do not belong to the same statistical population and they cannot be pooled to obtain a total or a common regression line. The new regression line we obtained using the procedure at Section 4.2.3 is the following: $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1$= 0.9787 $(\mathsf{\delta }\left({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O}{)}_{\mathrm{Carb}}^{\#}+1\right)$ + 0.0142, number of data couples = 16, standard error of regression = 0.00064.

(2)

Probably, the systematic difference in the elevation is prevalently due to different methods and standards used in the different laboratories.

(3)

The temperature of H₃PO₄ acid dissolution used for ${\mathrm{CO}}_{2\mathrm{gas}}$ production for spectrometric analyses has some influence on the final isotopic results. Thus, it is better to perform analyses at the same temperature in all laboratories.

(4)

The scattering of the data around the values $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}+1,$ as calculated from the given values $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Carb}}^{\#}+1$ using the regression line reported above, is about 0.0015 (1.5‰) at the significance level of 0.05. In addition to other chemical and physical methods, the scattering of the data around the regression line may be used to select isotopic data which are not appropriate for palaeodiet and palaeclimatic reconstruction: values that fall outside the limiting array defined by the estimated values ${\hat{\mathrm{Y}}}_{\mathrm{i}}$ ± 1.5 ‰—where ${\hat{\mathrm{Y}}}_{\mathrm{i}}$ indicates the estimated value $\mathsf{\delta }{({}_{}{}^{18}\mathrm{O}/{}_{}{}^{16}\mathrm{O})}_{\mathrm{Ph}}$ for a new sample i must be regarded with suspicion. This, of course, is valid only in the case the scientists use the same standard and analytical procedure as this paper.