Influence of Separation Angle on the Dry Pneumatic Magnetic Separation
Abstract
1. Introduction
2. Experimental and Simulation
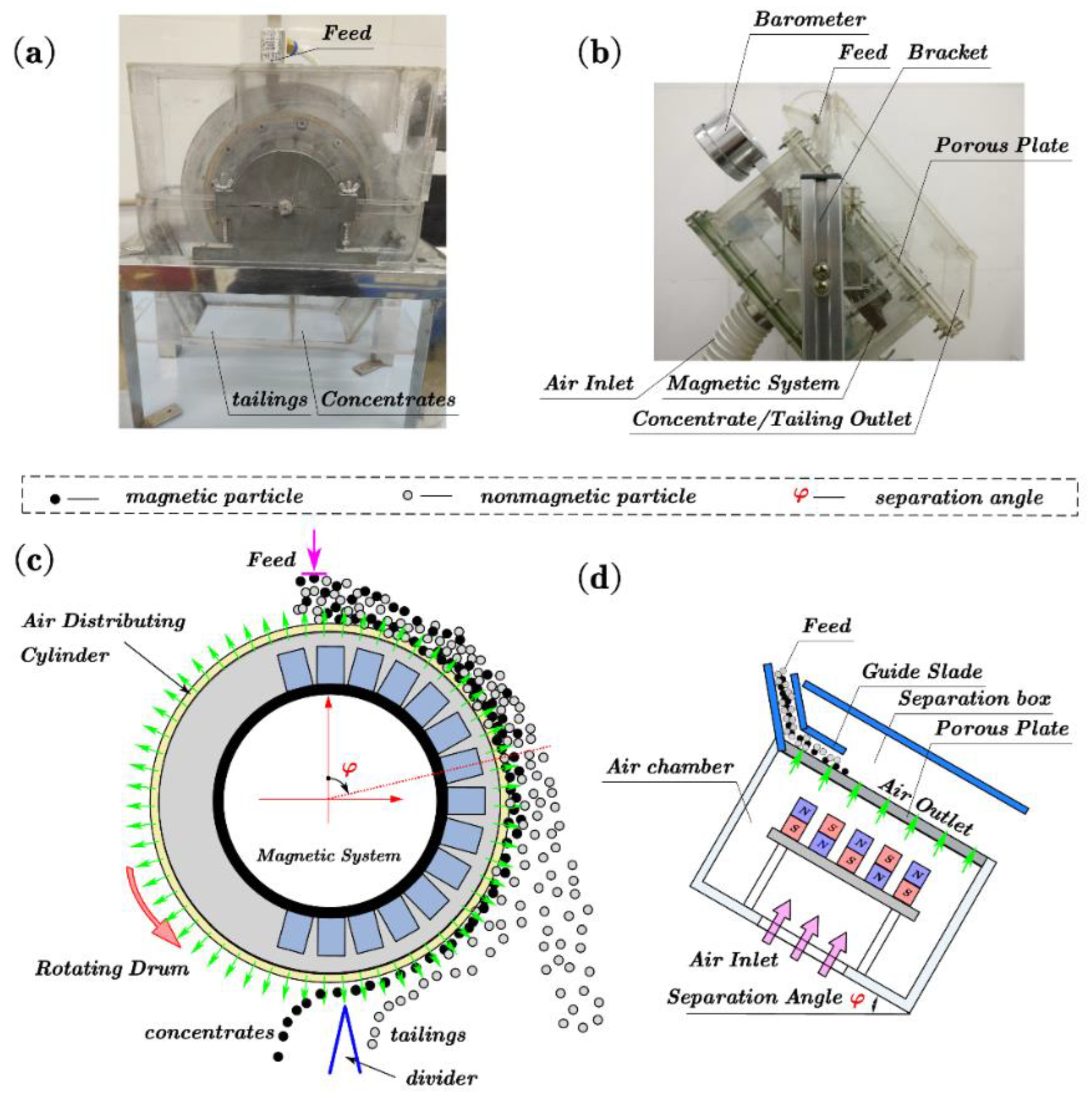
2.1. Separation Apparatus
2.2. Experimental
2.2.1. Method
2.2.2. Samples
2.2.3. Evaluation of Separation Performance
2.3. Simulation
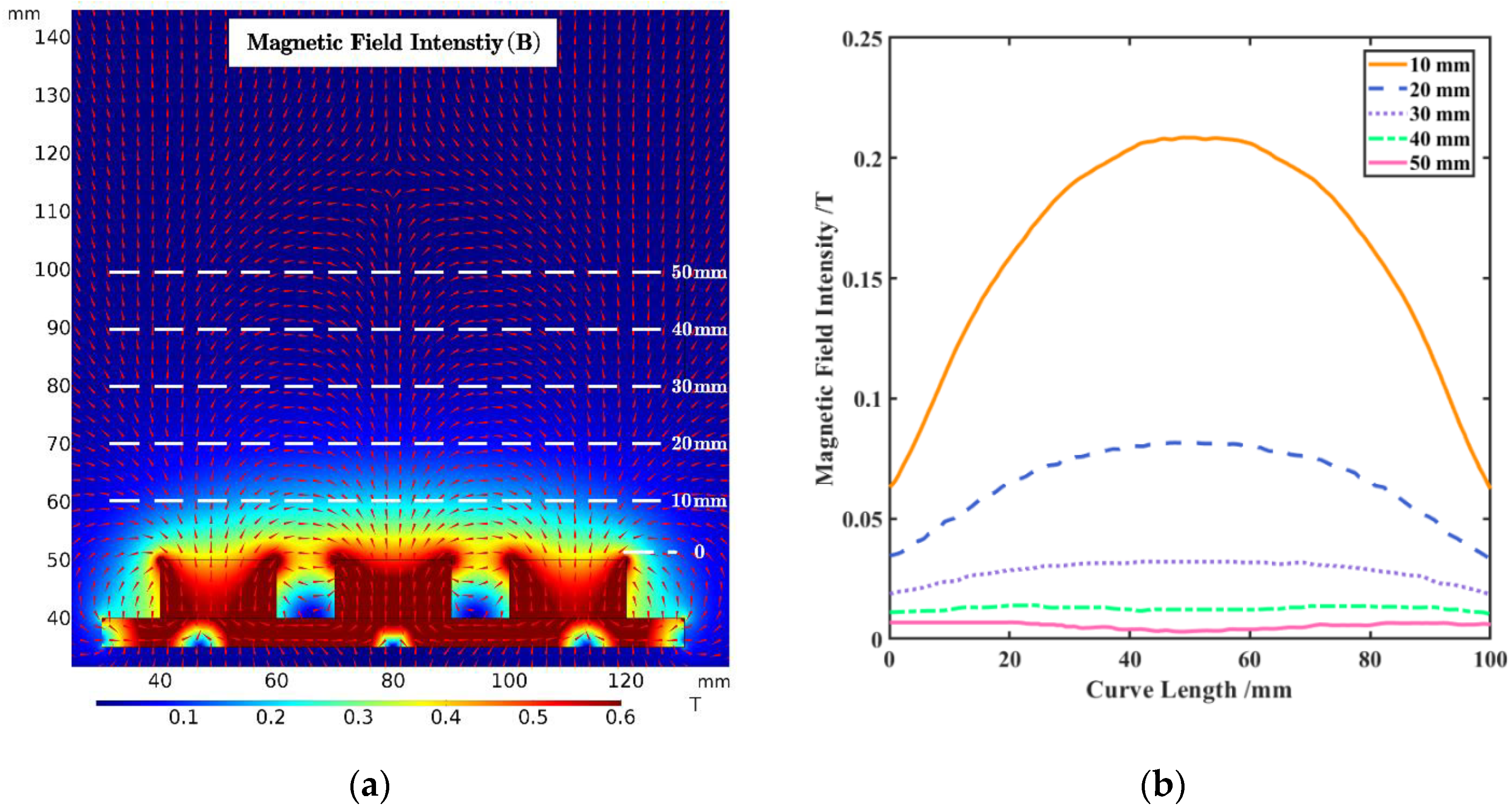
2.3.1. Magnetic Field
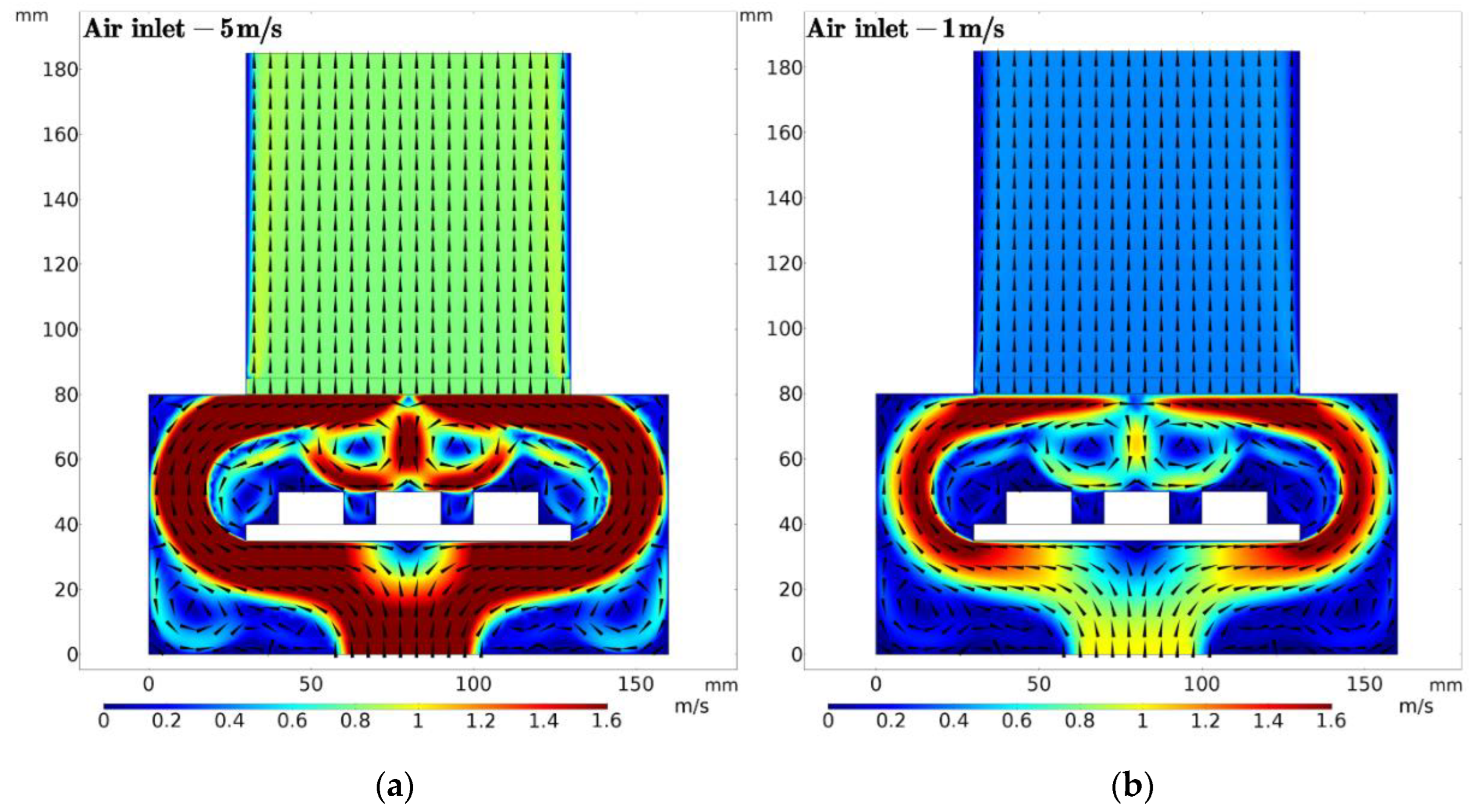
2.3.2. Airflow Field
2.3.3. Particle Tracing
3. Results and Discussions
3.1. Distribution of Magnetic and Airflow Field
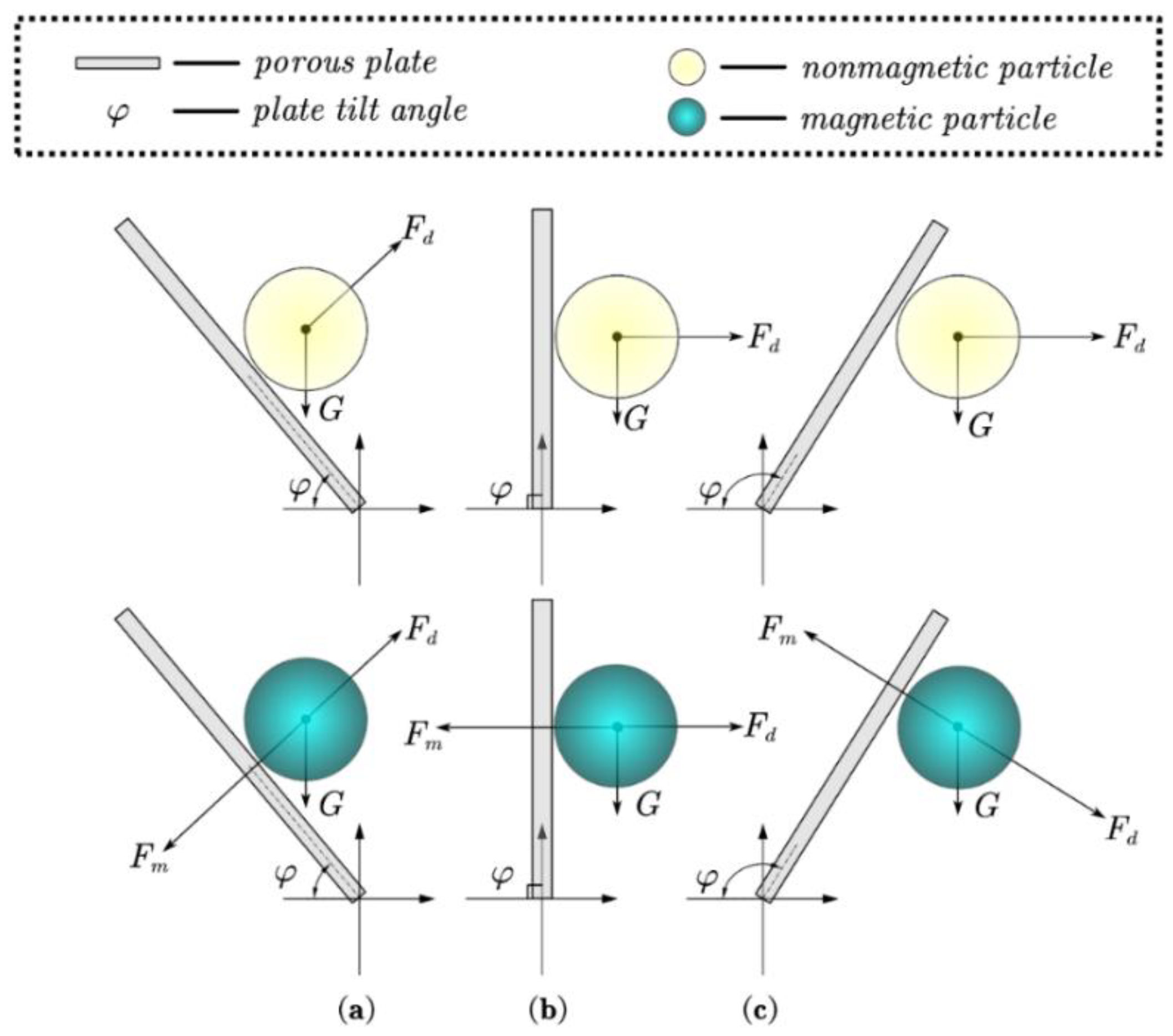
3.2. Matching of Compound Forces
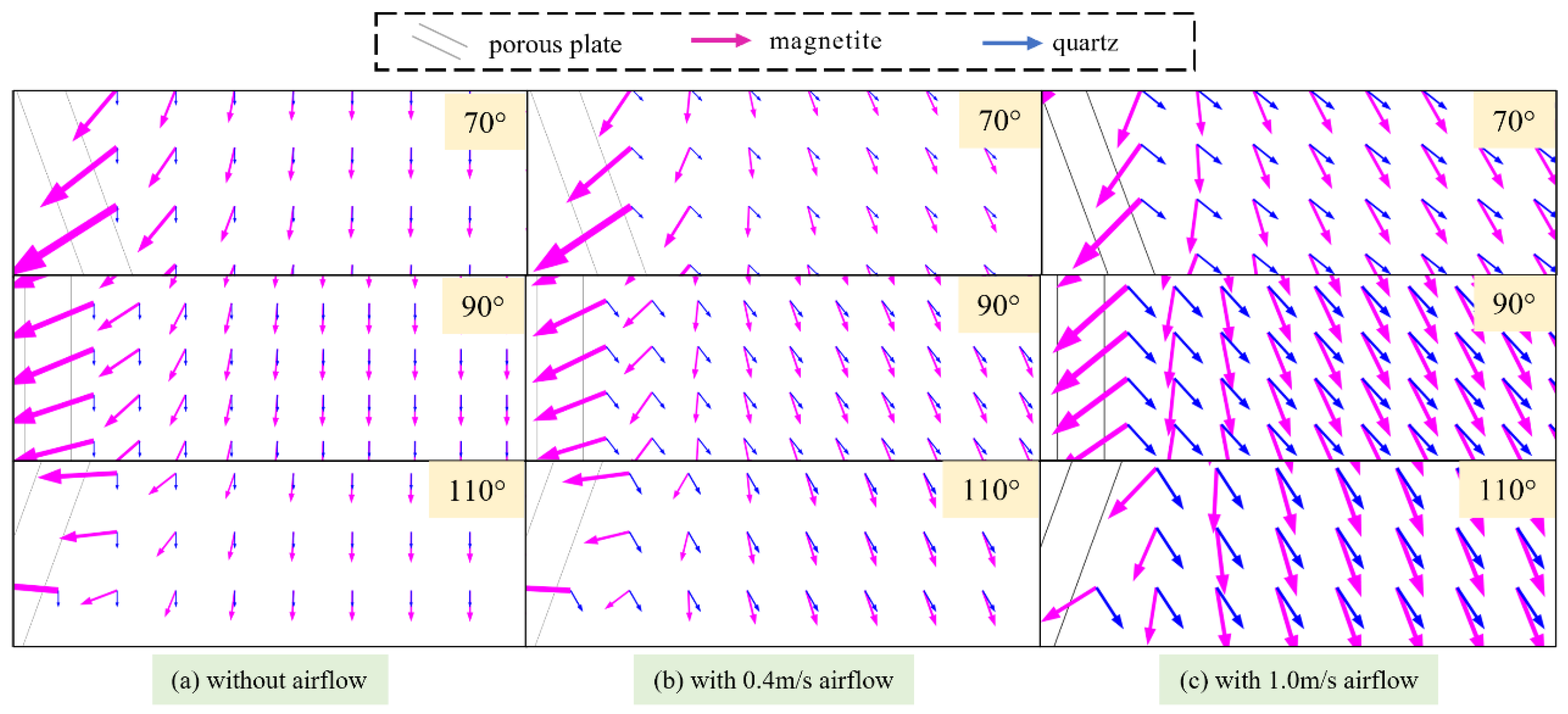
3.3. Particle Trajectory Analysis
3.4. Experimental Verification
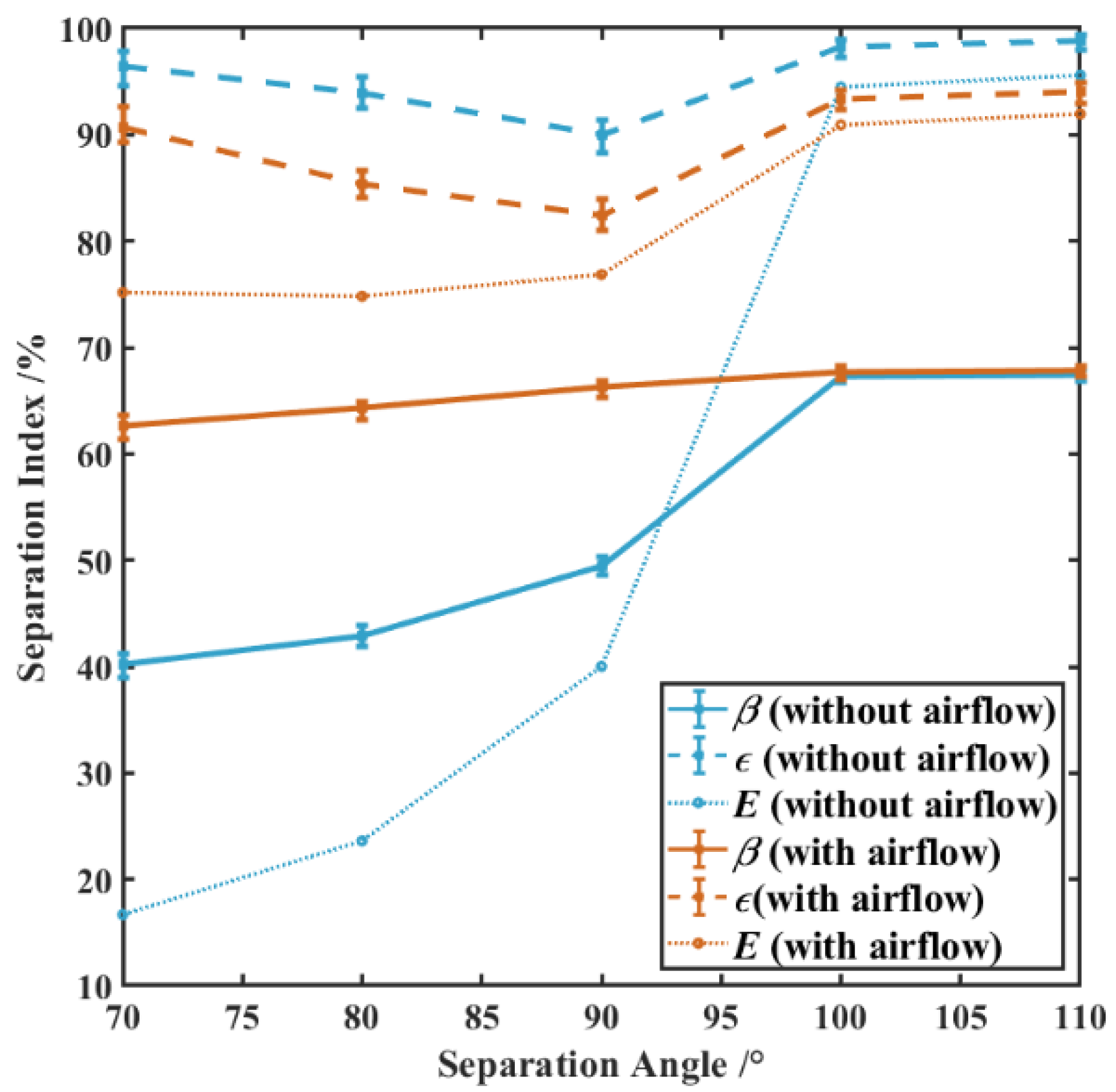
3.4.1. Effects of Separation Angle on Particle Separation
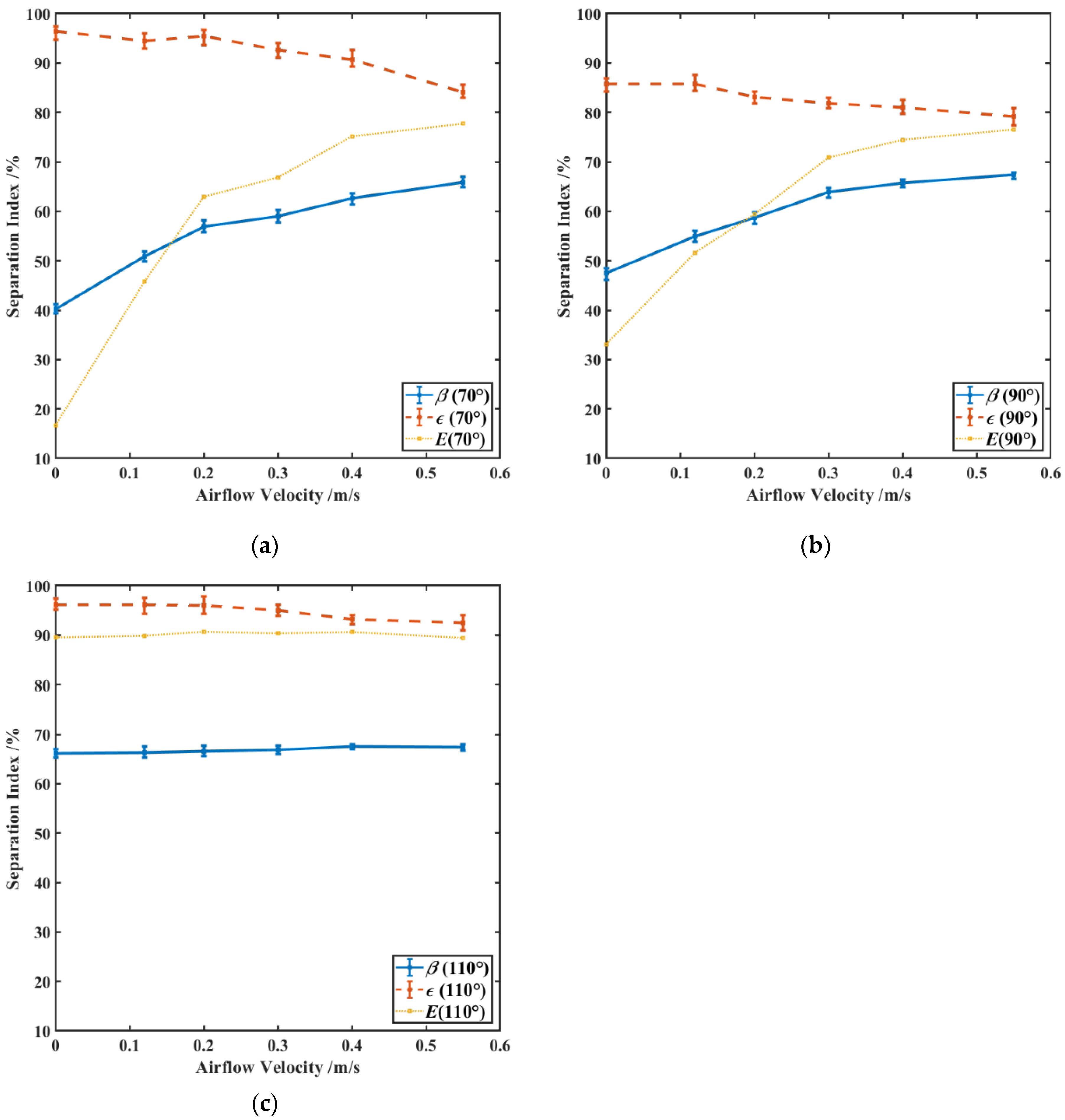
3.4.2. Effects of Airflow Velocity on Particle Separation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chizhevsky, V.B. Study of Fine Material Dry Magnetic Separation Process in Suspension State. Miner. Sep. 2006, 2, 25–28. [Google Scholar]
- Tripathy, S.K.; Banerjee, P.K.; Suresh, N.; Murthy, Y.R.; Singh, V. Dry High-Intensity Magnetic Separation In Mineral Industry—A Review Of Present Status And Future Prospects. Miner. Process. Extr. Metall. Rev. 2017, 38, 339–365. [Google Scholar] [CrossRef]
- Chen, L.; Liao, G.; Qian, Z.; Chen, J. Vibrating High Gradient Magnetic Separation for Purification of Iron Impurities under Dry Condition. Int. J. Mineral Process. 2012, 102–103, 136–140. [Google Scholar] [CrossRef]
- Demidov, I.V.; Vaisberg, L.A.; Blekhman, I.I. Vibrational Dynamics of Paramagnetic Particles and Processes of Separation of Granular Materials. Int. J. Eng. Sci. 2019, 141, 141–156. [Google Scholar] [CrossRef]
- Xu, J.; Chen, J.; Ren, X.; Xiong, T.; Liu, K.; Song, S. A Novel Dry Vibrating HGMS Separator for Purification of Potash Feldspar Ore. Sep. Sci. Technol. 2021, 57, 484–491. [Google Scholar] [CrossRef]
- Augusto, P.A.; Augusto, P.; Castelo-Grande, T. Magnetic Shielding: Application to a New Magnetic Separator and Classifier. J. Magn. Magn. Mater. 2004, 272–276, 2296–2298. [Google Scholar] [CrossRef]
- Lindner, J.; Nirschl, H. A Hybrid Method for Combining High-Gradient Magnetic Separation and Centrifugation for a Continuous Process. Sep. Purif. Technol. 2014, 131, 27–34. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, L.; Yang, R.; Tong, X.; Ren, P.; Zheng, Y. Centrifugal High Gradient Magnetic Separation of Fine Ilmenite. Int. J. Miner. Process. 2017, 168, 48–54. [Google Scholar] [CrossRef]
- Dean, R.S.; Davis, C.W. Method of Separating Magnetic Material. US2132404A, 11 October 1938. [Google Scholar]
- Martinez, E. Gravity-Magnetic Ore Separators and Methods. US4659457A, 21 April 1987. [Google Scholar]
- Yu–Shu, Z.; De–Zhang, L.; Shuyi, L. A Study of Magnetic Aggregation—Gravity Separation for Separation of Coarse Magnetite Ores. Magn. Electr. Sep. 1997, 8, 69–79. [Google Scholar] [CrossRef]
- Ali-Zade, P.; Ustun, O.; Vardarli, F.; Sobolev, K. Development of an Electromagnetic Hydrocyclone Separator for Purification of Wastewater. Water Environ. J. 2008, 22, 11–16. [Google Scholar] [CrossRef]
- Cao, S.; Wei, D.; Li, J. Effect of Magnetic Field in Magnetic Separation Column on Particle Separation Process Based on Numerical Simulation. J. Eng. Sci. Technol. Rev. 2019, 12, 53–58. [Google Scholar] [CrossRef]
- Safikhani, H.; Allahdadi, S. The Effect of Magnetic Field on the Performance of New Design Cyclone Separators. Adv. Powder Technol. 2020, 31, 2541–2554. [Google Scholar] [CrossRef]
- Walker, M.S.; Devernoe, A.L. Mineral Separations Using Rotating Magnetic Fluids. Int. J. Miner. Process. 1991, 31, 195–216. [Google Scholar] [CrossRef]
- Lin, I.J.; Krush-Bram, M.; Rosenhouse, G. The Benefication of Minerals by Magnetic Jigging, Part 3. The Bed Effects and the Multifrequency Magnetic Jig. Int. J. Miner. Process. 1998, 55, 61–72. [Google Scholar] [CrossRef]
- Zhao, T.L.; Dai, S.J. Development of a New Type of Column Magnetic Separator. Adv. Mater. Res. 2013, 826, 25–28. [Google Scholar] [CrossRef]
- Brandner, E.D.; Jamison, R.E. VacuMag Magnetic Separator and Process. US7681736B2, 23 March 2010. [Google Scholar]
- Nakai, Y.; Mishima, F.; Akiyama, Y.; Nishijima, S. Development of High Gradient Magnetic Separation System under Dry Condition. Phys. C Supercond. Appl. 2010, 470, 1812–1817. [Google Scholar] [CrossRef]
- Kozlova, E.V.; Skrypnikov, A.V.; Kozlov, V.G. Air Magnetic Separator for the Preparation of Forestry Seed Material and Its Theoretical Justification. In Proceedings of the Materials Science and Engineering, Novosibirsk, Russian, 12–14 December 2018; IOP Publishing Ltd: Bristol, UK, 2018; Volume 560, pp. 1–6. [Google Scholar]
- Song, S.; Zhang, G.; Luo, Z.; Lv, B. Development of a Fluidized Dry Magnetic Separator and Its Separation Performance Tests. Miner. Process. Extr. Metall. Rev. 2019, 40, 307–313. [Google Scholar] [CrossRef]
- Tang, D.; Wang, F.; Dai, H. Dynamic Behavior of Fine Particles in Dry Medium-Intensity Magnetic Separator Based on k–ε Turbulence Model and Low Reynolds Number k–ε Turbulence Model. Sep. Sci. Technol. 2021, 56, 1383–1396. [Google Scholar] [CrossRef]
- Lu, D.; Liu, J.; Cheng, Z.; Li, X.; Xue, Z.; Li, S.; Zheng, X.; Wang, Y. Development of an Open-Gradient Magnetic Separator in the Aerodynamic Field. Physicochem. Probl. Miner. Process. 2020, 56, 13. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Lu, D.; Zheng, X.; Gao, X. Optimization of Airflow Field for Pneumatic Drum Magnetic Separator to Improve the Separation Efficiency. Minerals 2021, 11, 1228. [Google Scholar] [CrossRef]
- Bars, M.L.; Worster, M.G. Interfacial Conditions between a Pure Fluid and a Porous Medium: Implications for Binary Alloy Solidification. J. Fluid Mech. 2006, 550, 149–173. [Google Scholar] [CrossRef]
- Svoboda, J. Magnetic Techniques for the Treatment of Materials; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; ISBN 978-1-4020-2038-4. [Google Scholar]
- Bagchi, P.; Balachandar, S. Inertial and Viscous Forces on a Rigid Sphere in Straining Flows at Moderate Reynolds Numbers. J. Fluid Mech. 2003, 481, 105–148. [Google Scholar] [CrossRef]
- Guan, X.; Li, X.; Yang, N.; Liu, M. CFD Simulation of Gas-Liquid Flow in Stirred Tanks: Effect of Drag Models. Chem. Eng. J. 2020, 386, 121554. [Google Scholar] [CrossRef]




| Item | Unit | Value |
|---|---|---|
| Magnetic yoke height/width | mm | 5/100 |
| Pole height/width | mm | 10/20 |
| Distance between adjacent poles | mm | 10 |
| Residual magnetism of magnet | T | 1.19 |
| Relative permeability of magnet | 1.05 | |
| Relative permeability of the yoke iron | B-H curve of DT4A |
| Item | Unit | Value |
|---|---|---|
| Porous plate height/width | mm | 5/100 |
| Air chamber height/width | mm | 80/160 |
| Air inlet width | mm | 40 |
| Porosity of porous plate, εp | % | 22.46 |
| Permeability of porous plate, κ | m2 | 1.93 × 10−11 |
| Dynamic viscosity of air (25 °C), η | μPa·s | 18.448 |
| Density of air (25 °C), ρf | kg·m−3 | 1.169 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, Y.; Lu, D.; Zheng, X. Influence of Separation Angle on the Dry Pneumatic Magnetic Separation. Minerals 2022, 12, 1192. https://doi.org/10.3390/min12101192
Li X, Wang Y, Lu D, Zheng X. Influence of Separation Angle on the Dry Pneumatic Magnetic Separation. Minerals. 2022; 12(10):1192. https://doi.org/10.3390/min12101192
Chicago/Turabian StyleLi, Xudong, Yuhua Wang, Dongfang Lu, and Xiayu Zheng. 2022. "Influence of Separation Angle on the Dry Pneumatic Magnetic Separation" Minerals 12, no. 10: 1192. https://doi.org/10.3390/min12101192
APA StyleLi, X., Wang, Y., Lu, D., & Zheng, X. (2022). Influence of Separation Angle on the Dry Pneumatic Magnetic Separation. Minerals, 12(10), 1192. https://doi.org/10.3390/min12101192







