Abstract
Some of the simplifying assumptions frequently used in basin modelling may adversely impact the quality of the constructed models. One such common assumption consists of using a laterally homogeneous crustal basement, despite the fact that lateral variations in its properties may significantly affect the thermal evolution of the model. We propose a new method for the express evaluation of the impact of the basement’s heterogeneity on thermal history reconstruction and on the assessment of maturity of the source rock. The proposed method is based on reduced-rank inversion, aimed at a simultaneous reconstruction of the petrophysical properties of the heterogeneous basement and of its geometry. The method uses structural information taken from geological maps of the basement and gravity anomaly data. We applied our method to a data collection from Western Siberia and carried out a two-dimensional reconstruction of the evolution of the basin and of the lithosphere. We performed a sensitivity analysis of the reconstructed basin model to assess the effect of uncertainties in the basement’s density and its thermal conductivity for the model’s predictions. The proposed method can be used as an express evaluation tool to assess the necessity and relevance of laterally heterogeneous parametrisations prior to a costly three-dimensional full-rank basin modelling. The method is generally applicable to extensional basins except for salt tectonic provinces.
1. Introduction
Temperature is one of the essential parameters for determining the rate and rank of organic matter maturation [1,2]. The reliability of temporal temperature estimations is determined, primarily, by the reliability of the thermal properties used [3], the boundary conditions and the thermal modelling approach [4,5,6]. A reliable thermal model of a basin should consider geological processes of equal importance in both the lithosphere and the sedimentary cover and their effects on each other [1,7].
Basin modellers use a number of simplifying assumptions when reconstructing sedimentary basin evolution through numerical simulation. One common assumption in most basin models is a laterally homogeneous basement. This assumption is usually connected with a scarcity of data or with its poor quality near the bottom of the basin and/or of the crustal basement. This occurs because the resolution of surveys deteriorates with depth due to the natural limitations of geophysical observations, as well as due to economic constraints on costly high-resolution surveys. In some cases this may lead to the introduction of “acoustic” [8] or “economic” [9] basements in the model. Thus, due to a lack of data, basin modellers oftentimes introduce a laterally homogeneous crystalline basement instead of a poorly explored bottom part of the sedimentary lithospheric strata. Such an assumption is actually equivalent to populating the model with incorrect thermophysical properties of the basement, hoping that the effect of this rough approximation on the thermal history could be compensated for by the calibration of the thermal model using wellbore data. However, successful wellbore calibration does not guarantee the exactness of the thermal history reconstruction, especially when it comes to inter-well segments [3].
The heterogeneity of the basement in the basin models is rather scarcely covered in the literature [4,10,11,12,13,14,15,16]. Basement heterogeneity has only been considered in a few works with respect to its effect on the basin’s thermal evolution. Klitzke et al. [10,11], Fjeldskaar et al. [12] and Scheck-Wenderoth et al. [13,14] used seismic imaging to determine the geometry of the basement’s heterogeneous blocks, although the time–depth conversion may involve significant uncertainties at such depths. They subsequently used a gravity data analysis to determine the density of rocks. Fattah et al. [15] varied the crust’s thickness and composition to calibrate the model with regard to gravity data. However, the impact of the basement’s heterogeneity on the heat flow and on the maturity of source rocks was not quantified. In all the above mentioned works [10,11,12,13,14,15], decoupled thermal solutions were used (a comparative analysis of coupled vs. decoupled solutions can be found in [4,5]). To the best of our knowledge, only Hansford [16] and Clark et al. [4] have used a coupled structural and thermal solution to determine the presence of magmatic bodies in the basement and their impact on thermal history. A sensitivity study of the reconstructed thermal properties has not yet been attempted, despite a high variability of the thermal properties and the densities of basement rocks [17,18].
Based on the studied literature, we may conclude that: (1) the heterogeneity of density and of the thermal properties as well as lateral variations of the basement’s geometry are usually ignored in the thermal modelling of basins and of petroleum systems, and (2) the impact of basement’s heterogeneity on the basin thermal history is scarcely covered in the published studies.
One of the major reasons behind both these observations is the complexity of the inversion procedure aimed at the reconstruction of the basement’s properties and of its geometry. The classical inversion procedure is time-consuming and typically requires data from a variety of geophysical studies as well as contributions by experts from a number of fields [19]. At the same time, this classical inversion procedure possesses a certain weakness in terms of basin modelling, whereby it lacks the possibility of a direct reconstruction of the thermal properties, which is crucial for the reconstruction of the thermal history. Thermal properties can only be extracted from subsequent non-unique and highly uncertain interpretations of rock density (see, e.g., in [13,14]). Of course, when wellbore material is available, reliable thermal properties may be obtained through direct measurements on core samples or at least through the interpretation of lithology. A basement is not always drilled, and in the cases in which it is, the wellbore coverage is frequently sparse.
In this study, we propose an express estimation method, which establishes the need for considering the heterogeneous basement for thermal history reconstruction in full-rank three-dimensional (3D) basin models. The express estimation method is based on reduced-rank inversion using the capabilities of two-dimensional (2D) basin modelling simulators. In contrast to the customary inversion, the reduced-rank inversion does not use seismic data as a pre-requisite and allows us to obtain the petrophysical properties of the heterogeneous basement and its geometry. The practical value of the express estimation method is demonstrated in the example of an area in the Western Siberian Basin.
2. Method and Data
The proposed method aims to estimate the impact of basement heterogeneity on thermal models and source-rock maturity models. The method includes a comparative analysis of a set of basin models with a heterogeneous basement with a reference model built with a laterally homogeneous basement. The construction of each 2D basin model follows the workflow presented in Scheme 1. The workflow, overall, repeats the standard procedure (e.g., [20,21]) and is extended by a newly proposed reduced-rank inversion (Scheme 1, step 3; Appendix A) for basement heterogeneity reconstruction. The applicability of the presented method is limited by extensional types of basins without salt tectonics.
The method assumes that the construction of a set of models includes the following: (1) a model with laterally homogeneous properties of the basement as a reference model (Model 1), (2) a model with directly determined basement heterogeneous properties (Model 2) based on the workflow from Scheme 1, (3) two models with minimum (Model 2: ρmin) and maximum (Model 2: ρmax) possible density values to evaluate the uncertainties in the density effect on thermal history reconstruction (following Scheme 1) and (4) a series of models for a sensitivity analysis to assess the impact of uncertainties in thermal conductivity in the heterogeneous basement on the predictions of thermal history and of the petroleum system maturity for all models. Considering the uncertainty evaluations in the heterogeneous basement simultaneously for both density and thermal conductivity allows us to obtain the ultimate possible associated range of the heat flow solutions.
There are four steps that comprise the workflow. In step 1, a classic basin modelling workflow described, e.g., by Hantschel and Kauerauf [21], was used to create a sedimentary cover model. The model was calibrated on measured porosity (φ) and pore pressure (P). Finally, a thermally non-calibrated geological model of a basin was obtained.

Scheme 1.
General workflow of the thermal history reconstruction of a riftogenic basin with a heterogeneous basement, where φ is porosity, P is pressure, T is temperature, Ro is vitrinite reflectance, PWD stands for paleo-water depth, MLC stands for Moho-level calibration, GC stands for gravity calibration and TC stands for thermal calibration. The solid arrows show the path for the coupled solution used in the case study, the dashed arrows show the path for a backstripping-based solution, and the bidirectional arrows indicate additional simulations during model calibration.
In step 2, homogeneous basement layers were introduced into the model. Estimations of the present-day Moho depth were used to determine the crust’s initial (i.e., before the rifting extension) thicknesses. The thermal calibration of the model, performed in step 4, when avoiding step 3, provided a reference model without basement heterogeneity (Model 1); this model should be used in step 3 as a precursor for constructing models with heterogeneous basements (Model 2, Model 2: ρmin, Model 2: ρmax).
After these steps, the modelling workflow bifurcated according to the selected modelling approach, which may involve either coupled or decoupled thermal and structural solutions. We recommend the coupled thermal and structural approach [7] since it considers sediment stretching, coupled temperature and isostasy modelling with subsidence and does not require information on the paleo-water depth, in contrast to the backstripping-based approach with forward temperature modelling [4,5].
In step 3, reconstruction of the heterogeneous basement following the reduced-rank inversion (see a detailed, step-by-step description in Appendix A) started. The inversion aims to reconstruct the heterogeneous basement properties and geometry (width and thickness of each block). The model with the directly determined properties and geometry of the heterogeneous basement was built (Model 2). Here, the following assumptions were made:
- The upper part of the basement is heterogeneous.
- Under the heterogeneous basement is a crystalline basement.
- The densities of the lithospheric layers, upper (ρu_crust) and lower (ρl_crust) crusts and the lithospheric mantle (ρl_mantle) are constant and change with temperature.
- The present-day width of each rectangular block is determined based on the basement maps.
- The first approximation of the thickness of each heterogeneous basement block is set.
- The physical properties of each heterogeneous block are based on the lithological descriptions of maps and their interpretations by standard mixing rules [21].
The physical properties of the rock for lithological mixtures, such as density (ρ), specific heat capacity (Сρ), radiogenic heat production (A) and thermal expansion (α), were calculated using the arithmetic mean rule, while thermal conductivity (λ) was calculated using the geometric mean rule. Measurements on rock samples from outcrops and data from well logs and core samples may significantly narrow the ranges of inferred petrophysical properties. Whenever possible, the techniques for thermal conductivity determination should be used (see, e.g., [22,23]).
The final geometry and density model of the heterogeneous basement was obtained through the iterative simulation technique, e.g., as in Bott [24], matching the observed gravity anomalies to the modelled ones. The densities of the sedimentary basin and the crystalline basement were fixed. The thickness of a heterogeneous block was inversed, while its density was fixed. The latter should be corrected in the rare cases in which the thickness of a block falls out of the range between the minimum determined block thickness and a thickness greater than the crust thickness beneath the block. The modelled anomaly may be recalculated, e.g., as in Heiland [25], only after correcting all block thicknesses and the model simulation.
At the beginning of thermal calibration (Scheme 1, step 4), the value of radiogenic heat production (A) in the crustal layer was fitted to the wellbore values of temperature (T) and vitrinite reflectance (%Ro) at the regional scale [26,27]. If the thermal calibration does not produce a good fit in some wells, which cannot be explained by uncertainty in thermal conductivity, then the basement model needs to be refined within the possible ranges of density and the geometry of the blocks. Thus, the gravity and thermal calibrations complement each other and constrain the diversity of solutions.
Furthermore, following Scheme 1, two additional models with minimum (Model 2: ρmin) and maximum (Model 2: ρmax) heterogeneous basement densities were constructed. In contrast to Model 2, these models had a different last assumption regarding the density of the heterogeneous basement. Here, the minimum and maximum values for the determined rock lithology were based on the database (e.g., [28]).
A sensitivity analysis was performed to estimate the impact of the uncertainties in the thermal conductivity of the heterogeneous basement on thermal history reconstruction with Model 2, Model 2: ρmin and Model 2: ρmax. We considered systematic changes to matrix thermal conductivity (λ) in the ±20% and ±50% range according to [29] and [3], respectively.
When all the models were built and calibrated and once a sensitivity analysis was performed, the significance of the heterogeneous basement’s impact on thermal history reconstruction was determined. Following the analysis, whether the heterogeneous basement is needed in constructing a full-rank 3D basin model can be determined, and, if required, additional geophysical studies (e.g., deep seismic sounding, density and thermal property measurements) should be planned.
3. Central Part of the Western Siberian Basin
The Western Siberian Basin is of great interest for evaluating the presented express estimation methodology’s efficiency from two perspectives. Firstly, this basin is one of the largest petroleum provinces in the world [30]. Secondly, most of the basin modellers prefer to assume the pre-Jurassic strata as a crustal laterally homogeneous layer (e.g., [31,32,33,34,35]), although these strata actually have a complex heterogeneous nature [36]. The reason for such an assumption is twofold. Firstly, the seismic data along the seismic study profile do not provide reliable reflections to reconstruct the Palaeozoic sedimentation. Secondly, according to an appraisal of the existing seismic data of entire Siberia by Cherepanova et al. [37], the rifts in our study area cannot be distinguished in the seismic models.
In this work, we considered these Paleozoic strata and syn-rift regional-scale intrusion in rift-graben zones as a heterogeneous basement formed instantaneously before the modelled Mesozoic–Cenozoic sedimentation. In the literature, the heterogeneous basement is referred to as a pre-Jurassic folded basement [38,39].
3.1. Geological Framework and Data Set
The geological evolution of Western Siberia has been described in detail by several authors [30,39,40,41] and is briefly summarised here. This study used regional sub-meridional seismic profile 6 [39], which crosses the centre of the Western Siberian Basin (Figure 1a).
3.1.1. Heterogeneous Basement
The Western Siberian intra-cratonic basin has experienced three phases of evolution with regard to tectonics [30,41]. The first phase is referred to as the Riphean–Vendian and Paleozoic ages. The corresponding basal structural stage was formed during Hercynian compression and was partly eroded by the end of the Permian period. The basin is composed of a peneplenised folded and metamorphosed orogenic system and platformal blocks [39]. In the second phase, the basin extended during the Permo–Triassic mega-rifting. The voluminous intercontinental flood basalts were extruded in the rift system, covering the basin in the northward direction [42,43]. Both of these stages are reflected in the so-called heterogeneous basement structure.
The lithological description of the heterogeneous basement (Table 1) was transferred from the maps [44,45,46] to bulk material properties for each geological unit following the standard procedure [21]. Density (ρ), thermal conductivity (λ), specific heat capacity (Сρ), radiogenic heat production (A) and the thermal expansion of each block in Model 2 were defined based on the petrophysical database and the application of the mixing rules [21]. The Sekiguchi model [47] is used for the temperature correction of thermal conductivities (λ). Data on the volumetric thermal expansion coefficients (α) are in good agreement with the published values [17,18,48].
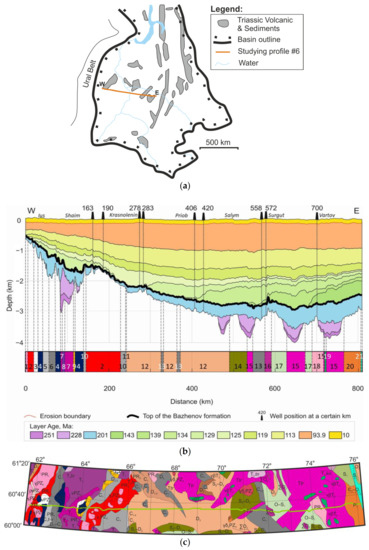
Figure 1.
(a) Schematic map of Western Siberia with the location of the studied profile (modified after [39]); (b) present-day simplified stratigraphy of the regional profile 6 linked with the lateral limits of the heterogeneous basement blocks in Model 2 (modified after [6]). The number of blocks and colours correspond to the material properties presented in Table 1. The names of petroleum regions are presented in italics. (c) The geological map of the heterogeneous basement (modified after [44,45,46]); the geological description used in the study blocks is presented in Table 1. The green curve highlights the profile location.

Table 1.
Material properties of basement units.
Table 1.
Material properties of basement units.
| Unit No. | Colour | Lithology Description of Basement Units (Designation of Rocks by [44,45,46]) ◊ | Physical Properties A | |||||
|---|---|---|---|---|---|---|---|---|
| ρ | α | A | Сρ | λ | ||||
| (kg/m3) | (10−5 K−1) | (µW/m3) | (J/kg/K) | (W/m/K) | ||||
| 1 | Weathered granite; (γ3PZ3) | 2645 | (2500–2800) | 2.4 | 2 | 760 | 2.6 | |
| 2 | Sialitic gneiss, schist; (PR3) | 2600 | (2600 *–2620 *) | 2.4 | 2 | 850 | 3.0 | |
| 3 | Gabbro; (vPZ2) | 2870 | (2800–3100) | 1.6 | 0 | 800 | 2.9 | |
| 4 | Serpentinite, ultrabasit; (∑O2) | 3064 | (3100–3340) | 1.0 | 0 | 830 | 3.0 | |
| 5 | Terrigenous carbonate deposit; (C?) | 2766 | - | 2.6 | 1 | 890 | 2.4 | |
| 6 | Effusive rock; (D3–C1) | 2690 | - | 1.6 | 1 | 820 | 2.3 | |
| 7 | Effusive mixed tuff; (T1) | 2800 | (2780 *–3200) | 1.6 | 1 | 820 | 2.3 | |
| 8 | Basalt; (T1) | 2840 | (2780 *–3200) | 1.6 | 1 | 800 | 1.8 B | |
| 9 | Igneous–sedimentary rock; (T1?) | 2757 | - | 2.2 | 1 | 840 | 2.3 | |
| 10 | Terrigenous–schist rock; (C) | 2740 | - | 2.3 | 1 | 920 | 2.8 | |
| 11 | Organogenic limestone, sandstone, calcareous sandstone and siltstone, basalt, their tuff; (C1–2) | 2733 | - | 2.7 | 1 | 850 | 2.7 | |
| 12 | Clay and organogenic limestone, subordinate tufogenic–sedimentary rock, basalt; (D3) | 2767 | - | 2.7 | 1 | 840 | 2.8 | |
| 13 | Organogenic limestone, clay, carbonaceous schist, siltstone, marl, andesibasalt, rhyolite; (C1) | 2752 | - | 2.4 | 1 | 870 | 2.5 | |
| 14 | Siliceous and silty shale, siltstone, basalt, andesibasalt, their tuff, tufogenic–sedimentary rock, sandstone, gravelite; (S2–D2) | 2749 | - | 2.1 | 1 | 880 | 2.4 | |
| 15 | Basalt, dolerite, their tuff, tufogenic–sedimentary rock, mudstone, siltstone, sandstone, gravelite, andesite, rhyolite; (Ttr) | 2809 | (2750 *–3200) | 1.8 | 1 | 850 | 2.2 | |
| 16 | Serpentinized dunite, harzburgite, lerzolite, pyroxenite, serpentinite; (∑O2) | 2800 | (2750 *–2800 *) | 1.0 | 0 | 780 | 4.1 B | |
| 17 | Shale, siliceous shale, jasper, limestone, basalt, andesibasalt, their tuff; (O–S1) | 2712 | - | 2.5 | 1 | 860 | 2.7 | |
| 18 | Metamorphic schist, sericite–chlorite, sericite and carboneous phyllite, quartzite; (PR2) | 2840 | (2750 *–2900) | 2.7 | 1 | 900 | 2.8 | |
| 19 | Gabbrodolerite, dolerite; (vβT2) | 2909 | (2800–3100) | 1.7 | 0 | 860 | 2.4 | |
| 20 | Siltstone and tuff siltstone basalt, basalt clastolavas, andesite, tuffite, rhyolite; (P?) | 2721 | - | 2.1 | 1 | 860 | 2.0 | |
| 21 | Clay limestone, greenish-grey with lenses of organogenic clastic limestone; (Є3–O1) | 2728 | - | 2.4 | 1 | 850 | 2.3 | |
| Upper crust | 2700 | - | 2.4 | 2 | 1000 | 3.0 | ||
| Lower crust | 2900 | - | 2.4 | 2 | 1000 | 3.0 | ||
| Lithospheric mantle | 3340 | - | 3.2 | 0 | 1000 | 3.5 | ||
◊ The lithology descriptions are based on drilling data [44,45,46]. A Here, ρ is the density; its acceptable range according to [49] is shown in parentheses; α is the volumetric coefficient of thermal expansion; for unit numbers 1–21, A is the radiogenic heat production of the rock matrix; for the crust and lithospheric mantel, A is surface radiogenic heat production (A0) in the equation A(z) = A0 × exp(z/ar), where A(z) is bulk radiogenic heat production, z is the negative value of a depth (km) and ar is the e-fold length parameter (km) [27]. Сρ is the rock matrix specific heat capacity, and λ is the rock matrix thermal conductivity at 20 °C. Values are calculated based on the petrophysical database in [21], with the geometric weighted mean rule for λ and the arithmetic weighted mean rule for ρ, Сρ and A. B Questionable values (see the text for details). * Manually truncated edge of density range by [49] to obtain the gravity anomaly calibration for Model 2: ρmin and Model 2: ρmax.
Thermal conductivity varies in accordance with lithology (at least composition and porosity), alteration state, in situ pressure, temperature, and saturation (see, e.g., [49,50,51]), and published rock thermal conductivity data often fail to provide actual information (see, e.g., [3]). For example, [49] demonstrates the variability in the bulk thermal conductivity values of up to 60% within the volcanic rock sequences with a thickness of less than 1 km in one well. The bulk thermal conductivity decreases as the chemical index of alteration and porosity value increase [50]. For example, the database value of basalt rocks’ matrix thermal conductivity (Table 1, unit 8) was 1.8 W/m/K, while the measured value of basalt rocks’ thermal conductivity was 1.8 to 3.5 W/m/K [3,17,21,51,52,53]. Similarly, basalt rocks’ thermal conductivity from a neighbouring area (Nizhne–Tabachanskaya area of the Western Siberian Palaeozoic basement) varied from 2.46 to 3.33 W/m/K, according to Duchkov et al. [54]. The value of 4.1 W/m/K, connected with lithological unit 16 (Table 1), seemed too high for this rock type since the thermal conductivity of serpentinite equals 2.1 W/m/K according to Kukkonen et al. [52], 2.15 W/m/K as per Seipold and Schilling [55] and 2.77 W/m/K for the serpentinite sample from the Nizhne–Tabachanskaya area of the Western Siberian Palaeozoic basement studied by Duchkov et al. [54]. In the absence of reliable data, we suggested quantifying the impact of uncertainty in the thermal conductivity of the heterogeneous basement on thermal history reconstruction by performing a sensitivity analysis varying λ of the heterogeneous basement blocks by ±20% and ±50% relative to the values determined from the database.
For the same rock type, density values also can exhibit significant variations, see [49] for an example for volcanic rocks and the corresponding ranges for different types of rocks [49]. The variations in density considered in this work were taken from Schön [49] with modifications.
3.1.2. Rift Phases
The Western Siberia Basin is characterised by two rift phases [56]. The first is Permo–Triassic mega-rifting. The second is Neocomian, which is localised in some areas of the basin [56]. According to tectonic analysis in [56], the area of the basin understudy experienced only the Triassic phase. Thus, the rift period was defined from 251 to 228 Ma, with differential thinning of the crust and the mantle [39].
3.1.3. Sedimentary Basin: Stratigraphy, Infill, Erosion
The platformal stage of basin evolution started in the Mesozoic era and was accompanied by uplift and erosion in the Oligocene–Pliocene period. The erosion of sediments with a thickness of 20 to 400 m was set from 23 to 10 Ma [57].
The dataset used in this work was mainly based on the basin model presented in [6]. The section of input stratigraphy is shown in Figure 1b using colour-coded age. Each stratigraphic unit has distinct material properties, as in [6]. The corresponding data are also presented in Table A1.
When modelling the basin evolution, the bulk thermal conductivity of rocks was calculated using the geometric mean rule [58,59]. Athy’s exponential low [60] was used for porosity calculations. The Sekiguchi model [47] was applied to consider the temperature dependence of matrix thermal conductivities. The Waples formula was used for a temperature correction of the specific heat capacity [61].
3.1.4. Petroleum Systems
Oil and gas accumulations have been revealed in eight oil and gas plays (see details in [30,40,62,63,64,65]). The deepest buried play is present at the Paleozoic paleobasin at the top of the heterogeneous basement. The Triassic play is present in the north of the basin and in rift zones. The Togur/Tymen, Vasyugan and Bazhenov–Abalak plays are proven to be in the Lower–Middle Jurassic strata. The Neocomian, Aptian–Albian–Cenomanian and Senonian are plays of the Cretaceous strata. The primary source rock is the Late Jurassic Bazhenov Formation (Fm) (Figure 1b), which plays the most significant role in oil generation [64,65].
3.1.5. Boundary Conditions
At the upper boundary, the temperature decrease was defined in time within the 20–0 °C range, following the method of Isaev [66]. The lower boundary condition for temperature was set at the lithosphere–asthenosphere interface at a constant value of 1300 °C [67].
3.1.6. Gravity Anomaly Data
The reference gravity anomaly values were digitised along the investigated section from a map of the Bouguer anomaly of the Federal Ural district (the map is accessible by a web link in [68]). The map was built with the average topographic density of 2670 kg/m3, with the terrain correction radius r = 200 km, the normal gravity value derived from the Helmert formula (1901–1909) and a datum correction of −14 mGal to the International Gravity Standardisation Net [69]. The gravity survey was performed on a regional scale of 1:7,500,000, with a counter step of εc = 5 mGal. Other details of the gravity anomaly map building are not known. The uncertainty value was not provided; therefore, εt = ±1.5 mGal that corresponds to a typical requirement for the regional-scale Bouguer anomaly map was assumed [70] (see details in Appendix C).
In this work, the desired accuracy (see details in Appendix A) to fit the model and the measured results of the Bouguer anomaly, of σ = 6.5 mGal, was defined as the sum of the counter step (εc) and the uncertainty value of measurements (εt) (see details in Appendix C).
3.2. Construction and Calibration of Basin Models
All of the built basin models had the same configuration: a sedimentary cover, temperature boundary conditions and rifting setting. The models were calibrated by pore and pressure regimes, Moho depth and a wellbore thermal regime. Referring to Scheme 1, Model 1 resulted from the application of steps 1, 2 and 4. Thus, Model 1 was not fitted with the observed gravity anomaly. Model 2 was built with the heterogeneous basement, following all steps in Scheme 1 and the newly proposed inversion procedure (Scheme A1). For our case study, models labelled Model 2: ρmin and Model 2: ρmax were built with the minimum and maximum density values of the basement’s igneous rocks. Based on our modelling results, heterogeneous blocks with a sedimentary genesis had a negligible impact on thermal history reconstruction. Several additional models, which considered the impact of uncertainty in the thermal conductivity (λ) of the heterogeneous basement on thermal history reconstruction, were referred to as Model 2: λ ± 20%; Model 2: λ ± 50%; Model 2: ρmin, λ ± 50% and Model 2: ρmax, λ ± 50%. The matrix thermal conductivity of the crust and the lithospheric mantle remains unchanged.
All basin models were computed by the non-steady-state coupled thermo-tectono-stratigraphic solver [7,71] using TecMod2D software (version 2019.1, GeoModelling Solutions, Zürich, Switzerland).
3.2.1. Construction of a Model with Homogeneous Basement: Model 1
Model 1 was based on the simplifying assumption of a homogeneous lateral properties distribution in the basement, (Figure 2a). The properties used in the model are presented in Table 1, according to [17,18,48,72].
The initial thicknesses at 251 Ma of the upper crust, the lower crust and the lithospheric mantle were set to HUC0 = 30 km, HLC0 = 10 km and HUM0 = 70 km, as in [6] (Figure 2a).

Figure 2.
Initial state of the basin configuration before sedimentation at 251 Ma: (a) Model 1; (b) Model 2 with the preliminary assumption of the heterogeneous basement (Figure 1b) being 1 km thick; (c) Model 2 with the thickness of the heterogeneous basement determined by gravity analysis. Coloured blocks correspond to the heterogeneous basement with assigned petrophysical properties from Table 1. The layer of the lithospheric mantle is not displayed for the convenience of presenting the picture.
3.2.2. Calibration of Model 1
After construction, Model 1 was run to check the calibration of the stratigraphy, porosity and pressure regimes, Moho depth and gravity anomaly:
- A good match between the modelled stratigraphy and the input stratigraphy was obtained with an approximate convergence misfit of 5%. The result was reached after 15 inversion iterations of the forward modelling [7].
- The calculated present-day Moho depth is in good agreement with two published interpretations [37,42] within the interval of 190 km to the eastern end of the profile (Figure 3, red line). The absence of the flexural load by the Ural fold belt on the west in the model explains the discrepancy between the calculated and published data within the left interval of 0 to 190 km.
- The gravity anomaly (Figure 4, red line) was not fitted since the modelled σm = 10.5 mGal was greater than the desired accuracy of σ = 6.5 mGal.
The calibration steps outlined above provided only a robust quality check of the structural and sedimentary evolution models; the thermal solution needed additional calibration using the wellbore data. The dataset considered included present-day temperatures in the boreholes at profile locations of 283, 406, 572 and 700 km (Figure 1b and Figure 5a) and vitrinite reflectance data in the profile points at 163, 190, 278, 283, 420 and 558 km (Figure 1b and Figure 5b) from [6]. Thus, only the borehole at 283 km provided both temperature and vitrinite reflectance simultaneously. The thermal solution was only calibrated on a regional scale, i.e., without local tuning. An exponential reduction of the radiogenic heat production of the crust (A) from a surface value (A0) at a rate given by the e-fold length (Ar) with depth (z) was assumed [27] (see the footnote in Table 1). The e-fold length parameter (Ar) selected for Model 1 was equal to 20.4 km. The well thermal data had a reasonably good match with the modelled thermal regime (Figure 5). Hence, the thermal properties did not require optimisation in this case.
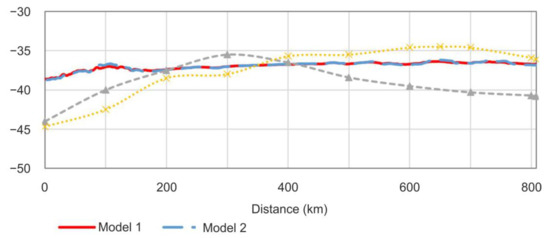
Figure 3.
Present-day Moho depth from the models and open source data: dashed grey [37] and dotted yellow [42] lines.

Figure 4.
Comparison of Bouguer anomaly observed data digitised from the gravity map [68] (grey stripe) and calculated data for Model 1 (solid red line), Model 2 (solid blue line) and two models of the sensitivity study, Model 2: ρmax (dashed black line) and Model 2: ρmin (solid black line). Dotted grey lines show the ±1.5 mGal interval relative to the observed values.
All the modelled temperature values fell within the ±7% interval, relative to the observations (Figure 5a), which is considered acceptable (see details in Appendix C). A simultaneous calibration of temperature and vitrinite reflectance (%Ro) was carried out for three kinetic models, referred to as EasyRo [73], BasinRo [74] and EasyRoDL [75]. Only the first of them provided a successful calibration of the model. Most vitrinite reflectance data fell within ±0.05 %Ro (Figure 5b), which is also acceptable (see details in Appendix C). The only value of vitrinite reflectance measured for the wellbore at 190 km exceeded the model’s permissible confidence interval. Two measured %Ro values for this wellbore (0.45% and 0.66%) were significantly different, although both were obtained from almost the same depth (depth difference ~100 m). This can be explained by either the random error of measurements or the redeposition of organic matter.
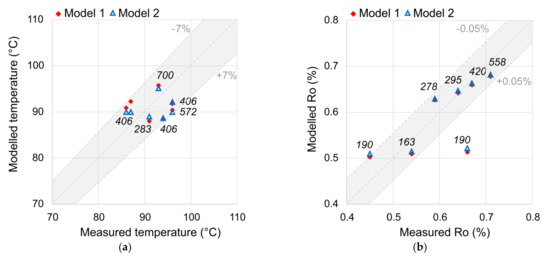
Figure 5.
Calibration results of present-day measured and modelled (a) temperatures and (b) vitrinite reflectance by the EasyRo kinetic model [73]. Italic numbers near the data points correspond to the wellbore location (in km) along the profile. Grey zones show the area of ±7% for temperature and ±0.05% (absolute) for vitrinite reflectance.
The final geological section is presented in Model 1 in in Figure 6a.
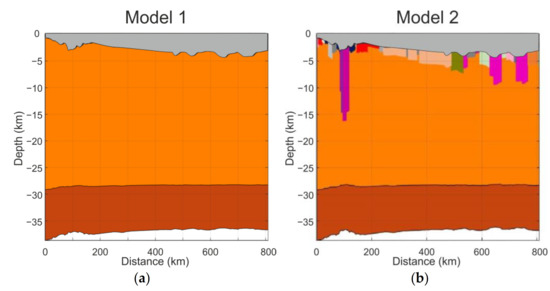
Figure 6.
Reconstructed present-day geological sections for (a) Model 1 and (b) Model 2. The grey area is the basin part. The colour codes beneath the basin part correspond to the basement units presented in Table 1. The corresponding modelled gravity anomalies are presented in Figure 4. The layer of the lithospheric mantle is not displayed for the convenience of presenting the picture.
3.2.3. Construction of Models with the Heterogeneous Basement: Model 2, Model 2: ρmin and Model 2: ρmax
Model 1 was used as a precursor for constructing models with a heterogeneous basement. The upper part of the crust was replaced with the heterogeneous basement (Figure 2b), where each block’s present-day lateral borders were defined using the pre-Jurassic geological map (Figure 1c) and linked to the profile (Figure 1b). The full version of the maps are accessible via the web links in [44,45,46]. The material properties from Table 1 were assigned to each block, and the thicknesses of the heterogeneous basement blocks (Figure 2c) were reconstructed with the help of gravity anomaly fitting (Scheme A1). For Model 2, the density values of units 8 and 18 were manually adjusted from 2870 and 2740 to 2840 and 2840 kg/m3, respectively, (Table 1) according to Schön [49] (p. 116).
The uncertainty of the determined density of the blocks in the basement may affect the thickness of the reconstructed blocks, impacting the entire thermal regime reconstruction. We considered the uncertainty of the density only for igneous rocks since they have a critical impact on thermal history. We built Model 2: ρmin and Model 2: ρmax using the range of acceptable densities for igneous rocks taken from Schön [49] (p. 116) for units 1, 2, 3, 4, 7, 8, 15, 16, 18 and 19. The basement geometry was obtained following the reduced-rank procedure (Scheme A1), varying only the thickness of the heterogeneous blocks when the maximum and minimum acceptable density values were fixed (marked by * in Table 1).
3.2.4. Calibration of Model 2, Model 2: ρmin and Model 2: ρmax
While the calculated gravity anomaly fits the observed patterns for Model 2 with σm = 4.7, for Model 2: ρmin with σm = 5.8 and for Model 2: ρmax with σm = 5.5, slight discrepancies were still visible in some intervals (Figure 4). Hidden bodies beneath the basement surface, the low sensitivity of the large-scale gravity survey to small bodies and/or the effect of density anomalies outside of the studied 2D object could explain such discrepancies.
Once the Bouguer anomaly was fitted, the remaining calibration parameters were rechecked:
- The stratigraphy, porosity and pressure remained unchanged.
- The Moho depth stayed almost unchanged (Figure 3). A negligible difference with respect to Model 1 was observed only in rift-graben zones.
- The thermal regime was refined by the e-fold length parameter (Ar), which was slightly increased to 21 km (to compensate the decreased radiogenic heat production and thermal conductivity in the heterogeneous basement).
The modelled geological section of Model 2 is presented in Figure 6b, and those of Model 2: ρmin and Model 2: ρmax are presented in Figure 7.
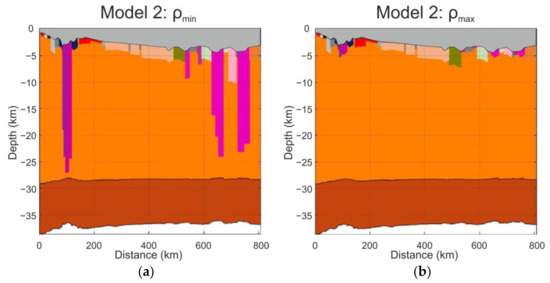
Figure 7.
Reconstructed present-day upper part of the basement design for Model 2: ρmin (a) and Model 2: ρmax (b). The grey area is the basin part. The colour codes beneath the basin part correspond to those of the basement units presented in Table 1. The layer of the lithospheric mantle is not displayed for the convenience of presenting the picture.
4. Results and Discussion
According to the calibration results obtained using the Moho boundary depth (Figure 3), porosity and pressure, present-day temperatures and vitrinite reflectance (Figure 5), we concluded that all the models (Model 1, Model 2, Model 2: ρmin and Model 2: ρmax) were acceptable. However, the additional calibration by gravity data demonstrated an oversimplification of Model 1 that affected the modelling of the thermal regime.
4.1. Results of Accounting for Heterogeneous Basement
4.1.1. Thicknesses of Basement Heterogeneity Blocks
Deep-rooted vertically elongated bodies of magmatic origin mentioned in [42,76,77] are clearly visible at the reconstructed geological section of the basement beneath the rifted zones (coloured violet in Figure 6b). We associated their origin with the latest Palaeozoic to Early Mesozoic times of the global plate boundary and plate kinematics reorganisation [43]. Thus, the magmatic bodies originate from voluminous intracontinental flood basalts.
The basement geometry is in good agreement with studies conducted by Braitenberg and Ebbing [42], who estimated the thickness of intrusive igneous rocks based on gravity and magnetic anomalies of up to 5 km beneath the eastern rift grabens area at around 620–690 km and 720–750 km of the profile intervals. The thickness of the pre-Triassic paleobasin is in good agreement with the interpretation of the seismically derived bottom section of the neighbouring regional seismic profile. The thickness of the paleobasin outside rift-graben zones increases eastward from less than 1 km to ~3.5 km [38]. The modelled heterogeneous blocks’ thicknesses matched the minimal thickness of blocks determined by drilling in adjacent territories [45,46]. On the 256–574 km profile interval, the thickness of units 11, 12 and 13 was more than 66, 250 and 1226 m, respectively [45]. On the profile interval of 574–808 km, the thickness of units 13, 15, 17, 18, 20 and 21 was more than 320, 1500, 500, 200, 380 and 100 m, respectively [46].
4.1.2. Densities of the Basement
A significant underestimation of density heterogeneity within the basement was observed in Model 1 compared with Model 2 (Figure 8), especially beneath the rift graben zones. The granites of the upper crust of Model 1 were less dense than in Model 2 with regard to basalt rocks formed during mega-rifting. The difference in the basement density distribution between Models 1 and 2 resulted in an insignificant change in the Moho boundary position, up to 450 m. The density distribution in the model by Isaev [78] obtained for a sub-parallel 350 km-long seismic profile located about 100 km north from our model demonstrated a similar lateral increase in density up to 150–300 kg/m3 beneath the rift structure in its western part (around 80–120 km of the profile interval).
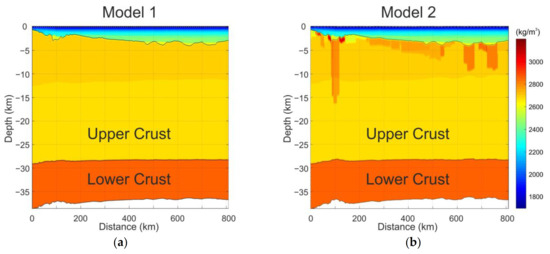
Figure 8.
Present-day distribution of bulk density in the crust and basin domains: (a) Model 1 and (b) Model 2. The density colour code applies to both images. The layer of the lithospheric mantle is not displayed for the convenience of presenting the picture.
4.1.3. Thermal Regime
Generally, the effective thermal conductivity and radiogenic heat production are lower in the heterogeneous basement domain because the substituted upper crust unit has higher thermal conductivity and radiogenic heat production (Table 1) than the heterogeneous basement’s igneous and sedimentary rocks. As a result, in Model 2, the value of radiogenic heat production in the crust increased by the e-fold length parameter (Ar) from 20.4 to 21 km, in order to compensate for the difference in the basal heat flow in the well thermal calibration points. The most significant divergence between the results of Model 2 and Model 1 was observed beneath the rift graben zones in the so-called magmatic roots where thermal wellbore calibration was absent. In this area, in Model 2, the bulk thermal conductivity and radiogenic heat production were 2.0–2.2 W/m/K and 1 μW/m3, respectively, while in Model 1, they were 2.2–2.7 W/m/K and 1–2 μW/m3, respectively. The difference between the magmatic roots’ thermal properties and the crustal layer led to anomalies in temporal variations in the basal heat flow (Figure 9a,b).
In Model 2, the present-day heat flow values in the rift graben zones of the Vartov High (the eastern graben on the profile) are lower by 5 mW/m2 relative to the surrounding areas (Figure 9b), which is entirely consistent with Kurchikov’s [79] geothermal studies. Figure 10a shows the difference in the basal heat flow as a function of time for Models 1 and 2 caused by the basement’s thermal properties. The time-averaged difference in heat flow (Figure 10b) was predominantly positive since heterogeneous basement blocks had lower thermal conductivity and radiogenic heat production values than the corresponding values for the crust (Figure 10). The maximum mean value of the difference corresponded to the rift graben zones and reached 10.2 mW/m2 due to the deepest heterogeneous basement units in this location.
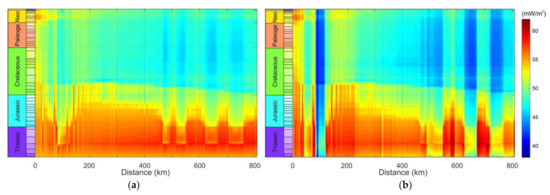
Figure 9.
Heat flow histories of the basement surface: (a) Model 1 and (b) Model 2; the density colour code applies to both images.

Figure 10.
(a) Difference in spatio-temporal variations of calculated basal heat flow between Model 1 and Model 2 (values of plot = values of Model 1 − values of Model 2) as a function of distance from the west end of the profile; (b) mean value of the basal heat flow difference, where ±2σ denotes a two-standard-deviation interval around the mean value.
Unit 16 (578–590 km of the profile) had the lowest negative values (down to −1.5 mW/m2) of the difference as it had a higher thermal conductivity than the crust. All the other negative values occurred due to increased radiogenic heat production impacted by the e-fold length parameter (Ar) for the crust radioactivity in Model 2 during its thermal calibration.
Since the primary source rock in the Western Siberian Basin is the Bazhenov Fm, it is necessary to evaluate the impact of basal heat flow changes on its present-day temperatures and vitrinite reflectance distribution (red and blue lines in Figure 11a,b). Discrepancies were observed between Model 1 and Model 2 estimations of present-day temperature and vitrinite reflectance at the Bazhenov Fm surface in areas with insufficient well coverage. Such discrepancies are associated with the rift graben zones (four segments along the profile with a total length of 210 km), where Model 1 provides higher temperatures and a vitrinite reflectance higher than those of Model 2 by up to ~9 °C and 0.05 %Ro, respectively. The essential feature of this discrepancy is that Model 1 predicts the Main Oil Window along 75 km of the profile, while Model 2 predicts the Early Oil Window (Figure 11b) according to the definition given by Tissot and Welte [80]. Such a difference between the two predictions may lead to a significant divergence in petroleum system evaluation and may result in errors in the estimated mass generation of hydrocarbons, the critical moment, reservoir volumes (for 3D modelling) and other important parameters. The remaining discrepancies in the estimations of temperature and vitrinite reflectance profiles did not exceed 2 °C and 0.02 %Ro, respectively, which is less than the uncertainty of the calibration values (see Appendix C).

Figure 11.
Calculated present-day (a) temperatures and (b) vitrinite reflectance by the EasyRo model [73] of the Ba-zhenov Fm surface and (c) basal heat flow for the investigated models.
4.2. Analysis of Uncertainties in Characteristics of Heterogeneous Basement
4.2.1. Density Uncertainties
The results obtained for Model 2: ρmax were similar to those of Model 1 in terms of the thermal regime (Figure 12). The thin heterogeneous basement (with thickness up to 1.8 km) explains the similarity in temperature (Figure 12a) and maturity (Figure 12b) beneath the rift graben zones. The discrepancy between the models was only observed in the profile zone from 490 to 540 km, which is explained by the presence of the paleobasin thick block, with lower thermal conductivity (2.4 vs. 3.0 W/m/K) and radioactive heat production (1 vs. 2 µW/m3) in Model 2: ρmax heterogeneous basement compared with Model 1 crystalline basement.
Model 2: ρmin demonstrates the lowest limit of the thermal regime governed by the thick heterogeneous basement beneath the rift graben zones (up to 27 km) since its blocks have lower values in terms of thermal properties compared to Model 1.
The difference between Model 2: ρmax and Model 2: ρmin in the temperature and maturity of the Bazhenov Fm surface reached 9 °C and 0.06 %Ro, respectively, and the difference in the basal heat flow was 5 mW/m2 (Figure 12).
The spread between Model 2: ρmin and Model 2: ρmax in terms of temperatures and the vitrinite reflectance on the Bazhenov Fm surface increased with time, while the corresponding residual basal heat flow decreased with time (Figure 13). At the profile location at 645 km, the spread of temperature increased from 0 to 9 °C (Figure 13a) and vitrinite reflectance increased from 0 to 0.06 %Ro (Figure 13b). Residual basal heat flow decreased from 8 to 4.5 mW/m2 (Figure 13c). The latter can be explained by the blanketing effect [81,82,83]. Since Model 2: ρmax has a higher contrast in the total thermal conductivities of the sedimentary cover from the basements, the decrease in the heat flow with the sedimentation rate is more significant.
Due to Model 2: ρmax and Model 2: ρmin, it was possible to determine the range of heterogeneous basement geometry and to quantify its impact on the modelled thermal regime. Such estimates are particularly relevant in the rift graben zones, where the resolution of the available seismic surveys is insufficient for distinguishing certain structural features.

Figure 12.
Calculated present-day (a) temperatures and (b) vitrinite reflectance by the EasyRo model [73] of the Bazhenov Fm surface and (c) basal heat flow for Model 1 and Model 2. The lower edge of the blue infill corresponds to Model 2: ρmin.
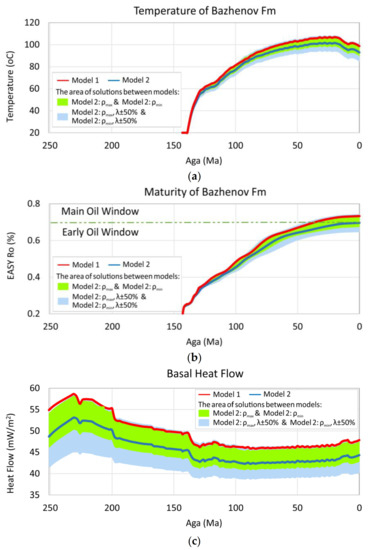
Figure 13.
Extraction of the time-dependent (a) temperatures and (b) vitrinite reflectance by the EasyRo model [73] of the Bazhenov Fm surface and (c) basal heat flow at the 645 km section for all models. The lower boundary of the blue infill corresponds to Model 2: ρmin.
4.2.2. Thermal Conductivity Uncertainties
The results of thermal conductivity uncertainties that impact present-day basal heat flow, surface temperature and vitrinite reflectance of the Bazhenov Fm, are presented in Figure 12 and Figure 13. The difference in thermal conductivity values in Model 2: λ ± 20% relative to Model 2 include minor changes in the basal heat flow of up to ±1.6 mW/m2 (around 4%), corresponding to changes in temperature and vitrinite reflectance values of ±0.9 °C and ±0.01 %Ro, respectively. The difference in thermal conductivity values of Model 2: λ ± 50% relative to Model 2 resulted in a difference in the basal heat flow of up to ±4.8 mW/m2 (around 11%), in temperature of up to ±5 °C and in vitrinite reflectance of up to 0.03 %Ro, which can lead to erroneous estimates of the organic matter’s maturity rank in some intervals of the profile (e.g., 468–485, 577–587 and 644–654 km). These values may increase with the thickness of the igneous rock or when using another temperature dependence for thermal conductivity of basement blocks.
One additional study for Model 2 was conducted in order to estimate the effect of possible errors in the matrix thermal conductivity of units 8 and 16 (Table 1). Taking λ = 3.0 W/m/K instead of 1.8 W/m/K in unit 8 led to an insignificant increase in %Ro of up to 0.01 %Ro and in temperature of up to 3 °C on the Bazhenov Fm surface. Taking λ = 2.1 W/m/K instead of 4.1 W/m/K in unit 16 led to a decrease in %Ro of around 0.01 %Ro and in temperature of around 3 °C in the corresponding area of the Bazhenov Fm surface.
Figure 12 shows the combined present-day sensitivity models’ range of estimations for the surface temperature and vitrinite reflectance of the Bazhenov Fm as well as for basal heat flow. The maximum estimates of the effect of the heterogeneous basement on thermal and source rock maturity models were obtained in the eastern rift graben zones. The upper edge of the thermal solution range generally coincided with the estimates of Model 1, except for extensive intervals of 182–220, 535–592, 630–650, 672–678 and 720–750 km. In these intervals, the maximum overestimations in temperature, vitrinite reflectance and basal heat flow values relative to Model 1 reached 6 °C, 0.28 %Ro and 2.5 mW/m2. However, these differences did not affect the estimations of the organic matter’s maturity rank. Conversely, the lower edge of the thermal solution range provided significantly underestimated values relative to Model 1, particularly in the extended intervals of 88–113 and 490–808 km. In these intervals, the maximum underestimation of temperature, vitrinite reflectance and basal heat flow values relative to Model 1 reached 12 °C, 0.1 %Ro and 6 mW/m2, respectively. Following the lower edge of the thermal solution range, we observed the Early Oil Window maturity rank instead of the Main Oil Window of the Bazhenov Fm surface for the profile intervals of 610–725 and 745–757 km (total 127 km). The spread variation over time between the lower and upper edges of the thermal solutions in terms of temperature and vitrinite reflectance on the Bazhenov Fm surface increased, while the difference in basal heat flow decreased (Figure 13). At the 645th km of the profile, the spread of temperature increased from 0 to 15 °C (Figure 13a) and vitrinite reflectance increased from 0 to 0.09 %Ro (Figure 13b). The difference in basal heat flow decreased from 13 to 8 mW/m2 (Figure 13c). The difference in the basal heat flow decrease is also explained by the blanketing effect as the difference between Model 2: ρmax and Model 2: ρmin.
4.3. Summarising of the Express Estimation
The express estimation of the impact of the heterogeneous basement on thermal and maturity modelling results demonstrated the following. The models with different heterogeneous basement geometries combined with uncertainty studies in thermal conductivities demonstrated the significant impact of the contrasting thermal properties on thermal and maturity models in rift graben zones. The reconstructed Model 2 is in accordance with other available investigations (see Section 4.1). The comparison of Model 2 and the model with a homogeneous basement demonstrates that the latter can overestimate the maturity rank of the Bazhenov Fm surface along 75 km of the profile as the Main Oil Window instead of the Early Oil Window.
Models with estimations of minimum and maximum densities of the heterogeneous basement extended the estimations of the possible impact of a heterogeneous basement on the thermal history of the basin compared with Model 2 estimations. The upper edge of the thermal solution range with the heterogeneous basement almost coincided with the solution without the assumption of a heterogeneous basement (Model 1). However, the lower edge of the thermal solution range exceeded the temperatures and vitrinite reflectance estimates in the Bazhenov Fm within the rift graben zones relative to Model 2 by up to 3 °C and 0.02 %Ro.
Models providing different estimations of thermal conductivity uncertainties in the heterogeneous basement make it possible to determine the ultimate range of modelled thermal histories. As a result, the maturity rank of the main source rock can be underestimated as the Early Oil Window instead of the Main Oil Window along 127 km of the profile, that is, 16% of the total profile length and ~75% of the profile length where the Main Oil Window was forecasted in Model 1.
5. Conclusions
A method was presented for the express estimation of the impact of basement heterogeneity on thermal history and petroleum system modelling.
The method was applied to the case study of the Western Siberian Basin. Reduced-rank inversion was added as an extension to the classic basin modelling workflow, and provided a rough model of deep-rooted bodies and the remnants of the pre-Triassic basin, which is otherwise impossible to create as seismic data, as the basement’s domain cannot be distinguished in seismic models [37]. The introduction of magmatic bodies in the model over rift graben zones significantly changed the basin’s thermal history reconstruction results and forecast kerogen maturity in the rift graben zones. We found that the maturity rank of the Bazhenov Fm can be underestimated as the Early Oil Window instead of the Main Oil Window. The uncertainties in basement characteristics (density, thermal conductivity) result in uncertainties in the temperature and vitrinite reflectance of the Bazhenov Fm in the rift-graben zones, of up to ±5 °C and 0.03 %Ro, relative to the model without the heterogeneous basement.
A full-rank 3D model of the Western Siberian Basin should be constructed accounting for the geometry and properties of the basement in the rift graben zones. Thus, model construction requires additional geophysical studies, such as deep seismic sounding, the building of seismic models, an analysis of gravity and magnetic anomalies, together with the measurement of the density and thermal properties of the rocks. Otherwise, the uncertainty range for the temperature and vitrinite reflectance of the Bazhenov Fm surface may reach 12 °C and 0.1 %Ro.
The presented method can be applied for the extensional basins without salt tectonics. The functionality of the presented method is valid for all similar datasets. The method can be considered most significant for the basin effected by the mega-rifting with deep-rooted mega intrusions.
Author Contributions
Conceptualisation, G.A.P. and E.M.C.; Methodology, G.A.P., E.M.C. and D.V.P.; Software, G.A.P.; Validation, G.A.P.; Formal Analysis, G.A.P., E.M.C. and D.V.P.; Investigation, G.A.P., E.M.C. and D.V.P.; Resources, G.A.P.; Data Curation, G.A.P. and E.M.C.; Writing—Original Draft Preparation, G.A.P., E.M.C.; Writing—Review and Editing, E.M.C. and D.V.P.; Visualisation, G.A.P.; Supervision, D.V.P. and E.M.C.; Project Administration, D.V.P.; Funding Acquisition, D.V.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation under agreement No. 075-10-2020-119 within the framework of the development program for a world-class Research Center.
Data Availability Statement
The data are available upon request with reasonable purpose via an email to the correspondence author.
Acknowledgments
We would like to express our appreciation and thanks to Mikhail Spasennykh for funding acquisition and to Raisa Romushkevich for consultancy on thermal petrophysical properties of rocks at Skoltech. Special thanks are also due to Alexander Minakov, Viktoria Yarushina Vincent Crombez and Elena Vorgacheva for recommendations on improvement. We sincerely thank the anonymous reviewers for their careful reading of our manuscript and for their many corrections, and suggestions that improved the text.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The reconstruction of the basement’s geometry and density presented in Scheme A1 uses an iterative approach similar to Bott’s method [24]. Scheme A1 corresponds to step 3 in Scheme 1.
Firstly, when the above-mentioned assumptions about the basement properties and lateral extension were introduced in the model, the first approximation (z) for each (i = 1, … n) block’s thickness (hi) was made, e.g., z = 1 km. Further, the model was simulated.
The gravity anomaly was calculated according to the formula of vertically sided two-dimensional blocks presented in the work of Heiland [25] (p. 152).
Further, the difference (ΔAi) between the observed (Aobs) and calculated (Acalc) gravity anomalies was estimated for each i block.
The stopping condition of the inverse problem was used as the standard error, as in [84,85],
where σ is the desired accuracy. Some deviations of the modelled gravity anomaly from the measured gravity anomaly may result from compositional differences (e.g., [86]) or 3D density structures that are not considered in the model and may contribute to the uncertainty in the 2D gravity modelling [19]. Otherwise, block thicknesses or, in rare cases, densities need to be refined.

Scheme A1.
Inversion procedure of the geometry and density of a heterogeneous basement.
Next, the residual error of thickness (Δhi) was calculated for each i block by the formula from [24].
where G is the gravity constant.
Δhi = ΔAi/2ΠG,
Next, the new thickness (hinew) of the block could be calculated as
where ε is the regularising multiplier ranging from 0 to 1 defined by the user. If the new block thickness (hinew) is greater than the maximum (hi_max) or less than the minimum (hi_min) determined thicknesses for the i block, correction of the i block density (ρi) is required
where, k is a correction factor ranging from 0 to 1 defined by the user and γ is a multiplier equal to +1 if hinew = hi_min and −1 if hinew = hi_max. In addition, hi_max could be limited, for instance, by hi_crust, and hi_min could be limited by drilling data
hinew =hi − εΔhi∙sign(Δhi),
ρinew= ρi(1 − k) + γkρi,
Further, after the correction of values hi and ρi from 1 to n (as recommended in [24]), the basin model was simulated and the gravity anomaly was calculated. The inversion procedure was rerun while condition (1) was not completed.
There are cases when gravity data fitting for the block is completed along only the part of the block. Therefore, this block needs to be split vertically into several sub-blocks. The Δhi for each sub-block should be calculated separately. This procedure helps to fit the gravity anomaly better [24] and find the ultimate solutions for further estimations in thermal regime changes.
Appendix B

Table A1.
Material properties of modelled stratigraphic units (based on [6]).
Table A1.
Material properties of modelled stratigraphic units (based on [6]).
| Age | Physical Properties * | |||||
|---|---|---|---|---|---|---|
| φ0 | B | ρ | λ | Сρ | A | |
| (Ma) | (1/km) | (kg/m3) | (W/m/K) | (J/kg/K) | (µW/m3) | |
| 0–93.9 | 0.63 | 0.69 | 2705 | 1.9 | 870 | 2 |
| 93.9–113 | 0.59 | 0.59 | 2711 | 2.85 | 880 | 1 |
| 113–119 | 0.49 | 0.41 | 2720 | 3.68 | 890 | 1 |
| 119–125 | 0.63 | 0.67 | 2706 | 2.82 | 870 | 2 |
| 125–129 | 0.52 | 0.48 | 2714 | 2.5 | 880 | 1 |
| 125–129 | 0.52 | 0.48 | 2714 | 3.7 | 870 | 1 |
| 129–134 | 0.52 | 0.48 | 2714 | 2.5 | 880 | 1 |
| 134–139 | 0.52 | 0.48 | 2714 | 2.5 | 880 | 1 |
| 139–143 | 0.52 | 0.48 | 2714 | 2.5 | 880 | 1 |
| 143–201 | 0.58 | 0.58 | 2629 | 2.65 | 860 | 2 |
| 201–251 | 0.15 | 0.23 | 2739 | 2.56 | 870 | 1 |
* Here, φ0 is the surface porosity and B is the scale depth factor in the equation φ(z) = φ0 × exp(B × z), where z is a negative value of the depth (km); ρ is density; λ is thermal conductivity at 20 °C; Сρ is the specific heat capacity; and A is radiogenic heat production of the rock matrix.
Appendix C
Here, we provide information on the uncertainty related to the data on vitrinite reflectance, formation temperature and gravity data. When calibrating the model to the measured data, the value of uncertainty in the calibration data should be considered. This aspect is often omitted in practice; hence a brief analysis (a comprehensive study is a separate study theme) is included here.
For vitrinite reflectance, we deal with the uncertainty in the experimental determination %Ro, considering the kinetics model used for %Ro calculation. Often, if experimental data are absent, specialists use different standard kinetic models (e.g., [73,74,75]). The choice of model must be supported by the best simultaneous fitting of the modelled vitrinite reflectance and temperature with the massive set of measured data. If a large set is absent, models with different kinetics should be considered. An illustrative example of the difference in applying different kinetic models to evaluate maturity is presented in [74]. A comparison of the BasinRo model and the widely used EasyRo model shows that the EasyRo model can overestimate vitrinite reflectance in the interval of 0.5–1.7 %Ro by up to 0.35 %Ro [74].
Within the same field in identical environments, the Ro values often differ by 10–15%. One of the reasons is the insufficient number of measurements at each micro-inclusion of vitrinite (10–15 instead of 100) [87]. Another reason is the value of uncertainty in determining %Ro, depending on the method and equipment used. For measuring the reflectance of macerals, it is crucial to know what parameter of the vitrinite reflectance value is determined—minimal (Rmin), maximal (Rmax) or random (Rr) [88,89,90]. However, this is not often mentioned in publications. With the example of Upper Silesian coal, Komorek and Morga [91] demonstrated that the standard deviations in Rmax and Rr are similar and do not exceed 0.05 %Ro for the range of maturity 0.2–0.9 %Ro. For maturity higher than 0.9 %Ro, the standard deviation increases and Rmax becomes more precise than Rr (up to 0.13 %Ro vs. 0.33 %Ro) and, therefore, acts as a more suitable rank indicator. The standard deviation of vitrinite reflectance measured for dispersed macerals in sedimentary rocks also increases with advancing thermal maturity and increasing anisotropy of the organic matter. In [92], vitrinite reflectance for different types of organic matter (by the method in [93]) is demonstrated, where an increase in standard deviation from 0.04 to 0.19 %Ro in the range of 0.31–1.53 %Ro (without mentioning what method of Ro determination has been used) is observed. Houseknecht and Matthews [94], using the example of Rr measurements of dispersed matter in carboniferous strata, Ouachita Mountains, established that standard deviation σ = 0.083 + 0.145 × Rr (correlation coefficient = 0.808, number of samples = 89). Summarising the review above, for the measured values of vitrinite reflectance 0.45–0.72 %Ro (Figure 5b), the standard deviation in the range 0.01–0.02 %Ro per [91], 0.06–0.09 %Ro per [92] and 0.15–0.19 %Ro per [94] can be estimated.
The uncertainty in the indirect determination of %Ro, e.g., via the recalculation of Tmax from pyrolysis data, includes the uncertainty of the pyrolysis measurement temperature (about ±2 °C with Hawk and Rock-Eval 6 tools according to [95,96]) and the uncertainty caused by the formula used for recalculation. For example, the widely (see, e.g., [97]) used formula %Ro = 0.018 × Tmax − 7.16 by Jarvie et al. [98] implies standard deviation σ = 0.23 %Ro at N = 179 (N is the number of samples), i.e., the uncertainty is much higher than the above-described uncertainty resulting from direct measurements.
Uncertainty related to formation temperature includes the instrumental uncertainty of measurement and the uncertainty of the non-equilibrium formation temperature. The first depends on the equipment used, and according to Blackwell and Spafford [99], it is approximately ±0.5 °C for commercial temperature logs and ±0.05 °C for scientific equipment. The second is caused by uncertainty with undisturbed temperature measurements, as the temperature readings in a well during drilling or completion do not reflect the equilibrium formation temperature [100,101], and the measured temperature values can be underestimated by up to ~22 °C, with standard deviation σ = 10 °C for depths of 500 to 9000 m [102,103]. Various correction schemes have been presented and discussed in the literature (e.g., [104,105] and references therein); however, the uncertainty is rarely estimated. In [102], the application of corrections improved “a prediction of formation temperatures with an error less than ±10 °C at somewhat deeper depths than the log in several boreholes.”
The value of the total error in the Bouguer anomaly [106,107] takes into account several components: an error of reference network observation, εrn; an error of accounting for terrain correction, εr; an error in introducing corrections for free air (depends on the error in the station heights), εF; an error in introducing the Bouguer correction (includes the error in determining the topographic relief and average density of rocks), εB; and an error in calculating the normal gravitational field (associated with the error in calculating the normal value of the acceleration of gravity and determining the coordinates of observation points, εγ (see details in [70,106,108,109] and links therein). The total error of the Bouguer anomaly must have standard limitations for different scales of maps [70]; the total error should not exceed εt = ±0.4 mGal for the 1:5000 scale and εt = ±1.5 mGal for the 1:500,000 scale, which is consistent with [108].
References
- Galushkin, Y.I. Sedimentary Basin Modeling and Estimation of Its Hydrocarbon Potential; Nauchnyi Mir: Moscow, Russia, 2007. [Google Scholar]
- Wangen, M. Physical Principles of Sedimentary Basin Analysis; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Chekhonin, E.; Popov, Y.; Peshkov, G.; Spasennykh, M.; Popov, E.; Romushkevich, R. On the importance of rock thermal conductivity and heat flow density in basin and petroleum system modelling. Basin Res. 2019, 32, 1261–1276. [Google Scholar] [CrossRef]
- Clark, S.A.; Glorstad-Clark, E.; Faleide, J.I.; Schmid, D.; Hartz, E.H.; Fjeldskaar, W. Southwest Barents Sea rift basin evolution: Comparing results from backstripping and timeforward modelling. Basin Res. 2013, 26, 550–566. [Google Scholar] [CrossRef]
- Theissen, S.; Rüpke, L.H. Feedbacks of sedimentation on crustal heat flow: New insights from the Voring Basin, Norwegian Sea. Basin Res. 2010, 22, 976–990. [Google Scholar] [CrossRef]
- Peshkov, G.A.; Chekhonin, E.M.; Rüpke, L.H.; Musikhin, K.A.; Bogdanov, O.A.; Myasnikov, A.V. Impact of differing heat flow solutions on hydrocarbon generation predictions: A case study from West Siberian Basin. Mar. Pet. Geol. 2021, 124, 104807. [Google Scholar] [CrossRef]
- Rüpke, L.H.; Schmalholz, S.M.; Schmid, D.W.; Podladchikov, Y.Y. Automated thermotectonostratigraphic basin reconstruction: Viking Graben case study. AAPG Bull. 2008, 92, 309–326. [Google Scholar] [CrossRef]
- SEG Wiki online Dictionary. Available online: https://wiki.seg.org/wiki/Dictionary:Acoustic_basement (accessed on 10 November 2021).
- Oilfield Glossary, Schlumberger. Available online: https://glossary.oilfield.slb.com/en/terms/b/basement (accessed on 10 November 2021).
- Klitzke, P.; Sippel, J.; Faleide, J.I.; Scheck-Wenderoth, M. A 3D gravity and thermal model for the Barents Sea and Kara Sea. Tectonophysics 2016, 684, 131–147. [Google Scholar] [CrossRef]
- Klitzke, P.; Faleide, J.I.; Scheck-Wenderoth, M.; Sippel, J. A lithosphere-scale structural model of the Barents Sea and Kara Sea region. Solid Earth 2015, 6, 153–172. [Google Scholar] [CrossRef] [Green Version]
- Fjeldskaar, W.; Grunnaleite, I.; Zweigel, J.; Mjelde, R.; Faleide, J.I.; Wilson, J. Modelled palaeo-temperature on Vøring, offshore mid-Norway—The effect of the Lower Crustal Body. Tectonophysics 2009, 474, 544–558. [Google Scholar] [CrossRef]
- Scheck-Wenderoth, M.; Raum, T.; Faleide, J.I.; Mjelde, R.; Horsfield, B. The transition from the continent to the ocean: A deeper view on the Norwegian margin. J. Geol. Soc. 2007, 164, 855–868. [Google Scholar] [CrossRef]
- Scheck-Wenderoth, M.; Maystrenko, Y. How warm are passive continental margins? A 3-D lithosphere-scale study from the Norwegian margin. Geology 2008, 36, 419–422. [Google Scholar] [CrossRef]
- Fattah, R.A.; Meekes, J.A.C.; Colella, S.; Bouman, J.; Schmidt, M.; Ebbing, J. The application of GOCE satellite gravity data for basin and petroleum system modeling: A case-study from the Arabian Peninsula. Search Discov. Artic. 2013, 120130. [Google Scholar]
- Hansford, P.A. Basin Modelling of the South-West Barents Sea. Master’s Thesis, University of Oslo, Oslo, Norway, 2014. [Google Scholar]
- Robertson, E.C. Thermal Properties of Rocks; U.S. Geological Survey, Reston, VA, USA. 1988. [Google Scholar] [CrossRef] [Green Version]
- Haines, H.H. Thermal Expansion and Compressibility of Rocks as a Function of Pressure and Temperature. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1982. [Google Scholar]
- Minakov, A.; Mjelde, R.; Faleide, J.I.; Flueh, E.R.; Dannowski, A.; Keers, H. Mafic intrusions east of Svalbard imaged by active-source seismic tomography. Tectonophysics 2012, 518–521, 106–118. [Google Scholar] [CrossRef]
- Peters, K.E.; Schenk, O.; Scheirer, A.H.; Wygrala, B.; Hantschel, T. Basin and Petroleum System Modeling. In Springer Handbook of Petroleum Technology; Springer: Berlin/Heidelberg, Germany, 2017; pp. 381–417. [Google Scholar]
- Hantschel, T.; Kauerauf, A.I. Fundamentals of Basin and Petroleum Systems Modeling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Popov, E.Y.; Goncharov, A.; Popov, Y.A.; Spasennykh, M.; Chekhonin, E.; Shakirov, A.; Gabova, A. Advanced techniques for determining thermal properties on rock samples and cuttings and indirect estimating for atmospheric and formation conditions. IOP Conf. Ser. Earth Environ. Sci. 2019, 367, 12017. [Google Scholar] [CrossRef]
- Meshalkin, Y.; Shakirov, A.; Popov, E.; Koroteev, D.; Gurbatova, I. Robust well-log based determination of rock thermal conductivity through machine learning. Geophys. J. Int. 2020, 222, 978–988. [Google Scholar] [CrossRef]
- Bott, M.H.P. The use of rapid digital computing methods for direct gravity interpretation of sedimentary basins. Geophys. J. Int. 1960, 3, 63–67. [Google Scholar] [CrossRef] [Green Version]
- Heiland, C.A. Geophysical Exploration; Prentice Hall Inc.: Hoboken, NJ, USA, 1940. [Google Scholar]
- Waples, D.W. A New Model for Heat Flow in Extensional Basins: Radiogenic Heat, Asthenospheric Heat, and the McKenzie Model. Nat. Resour. Res. 2001, 10, 227–238. [Google Scholar] [CrossRef]
- Lachenbruch, A.H. Preliminary geothermal model of the Sierra Nevada. J. Geophys. Res. Space Phys. 1968, 73, 6977–6989. [Google Scholar] [CrossRef]
- Schön, J.H. Physical Properties of Rocks–A Workbook. In Handbook of Petroleum Exploration and Production; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Hicks, P.J.J.; Fraticelli, C.M.; Shosa, J.D.; Hardy, M.J.; Townsley, M.B. Identifying and quantifying significant uncertainties in basin modeling. In Basin Modeling: New Horizons in Research and Applications; Peters, K.E., Curry, D.J., Kacewicz, M., Eds.; AAPG Hedberg Series; AAPG: Tulsa, OK, USA, 2012; Volume 4. [Google Scholar] [CrossRef]
- Ulmishek, G.F. Petroleum Geology and Resources of the West Siberian Basin, Russia; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2003. [Google Scholar]
- Fjellanger, E.; Kontorovich, A.E.; Barboza, S.A.; Burshtein, L.M.; Hardy, M.J.; Livshits, V.R. Charging the giant gas fields of the NW Siberia basin. Geol. Soc. London Pet. Geol. Conf. Ser. 2010, 7, 659–668. [Google Scholar] [CrossRef]
- Kazanenkova, A. Some Aspects of Petroleum System Modeling in the North-Eastern Part of West Siberia Basin. Tyumen 2015-Deep Subsoil and Science Horizons. Eur. Assoc. Geosci. Eng. 2015, 2015, 1–5. [Google Scholar]
- Morozov, N.; Belenkaya, I.; Kasyanenko, A.; Bodryagin, S. Evaluation of the Resource Potential Based on 3D Basin Modeling of Bagenov Fm. Hydrocarbon System. In Proceedings of the SPE Russian Petroleum Technology Conference and Exhibition, Moscow, Russia, 24–26 October 2016; pp. 1–12. [Google Scholar] [CrossRef]
- Romanov, A.G.; Goncharov, I.V.; Gagarin, A.N.; Carruthers, D.J.; Corbett, P.W.M.; Ryazanov, A.V. 3D Modelling of the Hydrocarbon Migration in the Jurassic Petroleum System in Part of the West Siberia Basin. In Proceedings of the Canadian International Petroleum Conference, Calgary, Alberta, 7–9 June 2005; pp. 1–4. [Google Scholar] [CrossRef]
- Safronov, P.I.; Ershov, S.V.; Kim, N.S.; Fomin, A.N. Modeling of processes of generation, migration and accumulation of hydrocarbons in the Jurassic and Cretaceous complexes of the Yenisei-Khatanga Basin. Oil Gas Geol. 2011, 5, 48–55. [Google Scholar]
- Merkulov, V.P.; Volkova, A.A.; Grigoriev, G.S. The Using of 3D Modeling for Processing Gravimetric Data in the Study of Oil and Gas Deposits of the Pre-Jurassic Complex of Western Siberia. Geomodel 2019, 2019, 1–5. [Google Scholar] [CrossRef]
- Cherepanova, Y.; Artemieva, I.M.; Chemia, Z. Crustal structure of the Siberian craton and the West Siberian basin: An appraisal of existing seismic data. Tectonophysics 2013, 609, 154–183. [Google Scholar] [CrossRef] [Green Version]
- Stoupakova, A.; Sokolov, A.; Soboleva, E.; Kiryukhina, T.A.; Kurasov, I.A.; Bordyug, E. Geological survey and petroleum potential of Paleozoic deposits in the Western Siberia. Georesursy 2015, 61, 63–76. [Google Scholar] [CrossRef]
- Vyssotski, A.V.; Vyssotski, V.N.; Nezhdanov, A.A. Evolution of the West Siberian basin. Mar. Pet. Geol. 2006, 23, 93–126. [Google Scholar] [CrossRef]
- Kontorovich, A.E.; Surkov, V.S. Geology and Mineral Resources of Russia; VSEGEI: St. Petersburg, Russia, 2000; Volume 2. [Google Scholar]
- Kontorovich, A.E.; Nesterov, I.I.; Salmanov, F.K.; Surkov, V.S.; Trofimuk, A.A.; Ervye, Y.G. Geology of Oil and Gas of West Siberia; Nedra: Moscow, Russia, 1975. [Google Scholar]
- Braitenberg, C.; Ebbing, J. New insights into the basement structure of the West Siberian Basin from forward and inverse modeling of GRACE satellite gravity data. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Nikishin, A.M.; Ziegler, P.A.; Abbott, D.; Brunet, M.-F.; Cloetingh, S. Permo–Triassic intraplate magmatism and rifting in Eurasia: Implications for mantle plumes and mantle dynamics. Tectonophysics 2002, 351, 3–39. [Google Scholar] [CrossRef]
- Ivanov, K.S.; Koroteev, V.A.; Pecherkin, M.F.; Fedorov, Y.N.; Erokhin, Y.V. The western part of the West Siberian petroleum megabasin: Geologic history and structure of the basement. Russ. Geol. Geophys. 2009, 50, 365–379. [Google Scholar] [CrossRef]
- 45. Map of Jurassic Formations: P-42 (Khanty-Mansiysk). State Geological Map of the Russian Federation Third Generation West Siberian Series Map of Jurassic Formations Lying on the Foundation (Bottom View). Scale: 1: 1000000, Series: West Siberian, Compiled by: Geotex LLC, FSGBI “VSEGEI”, Editor: Kovrigina. 2009. Available online: http://www.geokniga.org/maps/7131 (accessed on 10 November 2021).
- 46. Map of Jurassic Formations: P-43 (Surgut). State Geological Map of the Russian Federation Third Generation Geological Map of Jurassic Formations Lying on the Foundation (Bottom View) West Siberian Series. Scale: 1: 1000000, Series: West Siberian, Compiled by: FSBI “VSEGEI”, FSUE ZapSibNIIIGG. 2010. Available online: http://www.geokniga.org/maps/7936 (accessed on 10 November 2021).
- Sekiguchi, K. A method for determining terrestrial heat flow in oil basinal areas. Tectonophysics 1984, 103, 67–79. [Google Scholar] [CrossRef]
- Allen, P.A.; Allen, J.R. Basin Analysis: Principles and Application to Petroleum Play Assessment, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Schön, J.H. Physical Properties of Rocks: Fundamentals and Principles of Petrophysics; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Lee, E.Y.; Tejada, M.L.G.; Song, I.; Chun, S.S.; Gier, S.; Riquier, L.; White, L.T.; Schnetger, B.; Brumsack, H.; Jones, M.M.; et al. Petrophysical property modifications by alteration in a volcanic sequence at IODP Site U1513, Naturaliste Plateau. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021061. [Google Scholar] [CrossRef]
- Clauser, C.; Huenges, E. Thermal conductivity of rocks and minerals. In Rock Physics and Phase Relations: A Handbook of Physical Constants; AGU: Washington, DC, USA, 1995; Volume 3, pp. 105–126. [Google Scholar]
- Kukkonen, I.T.; Jokinen, J.; Seipold, U. Temperature and pressure dependencies of thermal transport properties of rocks: Implications for uncertainties in thermal lithosphere models and new laboratory measurements of high-grade rocks in the central Fennoscandian shield. Surv. Geophys. 1999, 20, 33–59. [Google Scholar] [CrossRef]
- Norden, B.; Förster, A.; Förster, H.-J.; Fuchs, S. Temperature and pressure corrections applied to rock thermal conductivity: Impact on subsurface temperature prognosis and heat-flow determination in geothermal exploration. Geotherm. Energy 2020, 8, 1–19. [Google Scholar] [CrossRef]
- Duchkov, A.D.; Sokolova, L.S.; Ayunov, D.E. Database of Thermal Properties of Rocks of the Siberian Region of the Russian Federation. Certificate Number RU 2017621489. 25 October 2017. [Google Scholar]
- Seipold, U.; Schilling, F.R. Heat transport in serpentinites. Tectonophysics 2003, 370, 147–162. [Google Scholar] [CrossRef]
- Vibe, Y.; Bunge, H.-P.; Clark, S.R. Anomalous subsidence history of the West Siberian Basin as an indicator for episodes of mantle induced dynamic topography. Gondwana Res. 2018, 53, 99–109. [Google Scholar] [CrossRef]
- Surkov, V.S.; Smirnov, L.V. Tectonic Events of the Cenozoic and Phase Differentiation of Hydrocarbons in Hauterivian-Cenomanian Complex of West Siberian Basin. Geologiya Nefti Gaza. 1995, 11, 3–6. [Google Scholar]
- Deming, D.; Chapman, D.S. Thermal histories and hydrocarbon generation: Example from Utah-Wyoming thrust belt. AAPG Bull. 1989, 73, 1455–1471. [Google Scholar] [CrossRef]
- Woodside, W.; Messmer, J.H. Thermal conductivity of porous media. I. Unconsolidated sands. J. Appl. Phys. 1961, 32, 1688–1699. [Google Scholar] [CrossRef]
- Athy, L.F. Density, porosity, and compaction of sedimentary rocks. AAPG Bull. 1930, 14, 1–24. [Google Scholar] [CrossRef]
- Waples, D.W.; Waples, J.S. A review and evaluation of specific heat capacities of rocks, minerals, and subsurface fluids. Part 1: Minerals and nonporous rocks. Nat. Resour. Res. 2004, 13, 97–122. [Google Scholar] [CrossRef]
- Rudkevich, M.Y.; Ozeranskaya, L.S.; Chistyakova, N.F. Petroleum Complexes of Western Siberia Basin; Nedra: Moscow, Russia, 1988. [Google Scholar]
- Brekhuntsov, A.M.; Monastyrev, B.V.; Nesterov, I.I. Distribution patterns of oil and gas accumulations in West Siberia. Russ. Geol. Geophys. 2011, 52, 781–791. [Google Scholar] [CrossRef]
- Peters, K.E.; Kontorovich, A.E.; Huizinga, B.J.; Moldowan, J.M.; Lee, C.Y. Multiple Oil Families in the West Siberian Basin. AAPG Bull. 1994, 78, 893–909. [Google Scholar] [CrossRef]
- Ablya, E.; Nadezhkin, D.; Bordyug, E.; Korneva, T.; Kodlaeva, E.; Mukhutdinov, R.; Sugden, M.; Van Bergen, P. Paleozoic-sourced petroleum systems of the Western Siberian Basin–What is the evidence? Org. Geochem. 2008, 39, 1176–1184. [Google Scholar] [CrossRef]
- Isaev, V.I.; Rylova, T.B.; Gumerova, A.A. Paleoclimate of Western Siberia and Realization of the Generation Potential of Oil Source Deposits. Bull. Tomsk Polytech. Univ. 2014, 324, 93–101. [Google Scholar]
- Fischer, K.M.; Ford, H.A.; Abt, D.L.; Rychert, C.A. The lithosphere-asthenosphere boundary. Annu. Rev. Earth Planet. Sci. 2010, 38, 551–575. [Google Scholar] [CrossRef] [Green Version]
- Gravimetric Map of the Ural Federal District. Package of Operational Geological Information (GIS Atlas). VSEGEI. 2019. Available online: https://vsegei.ru/ru/info/gisatlas/ufo/okrug/f_22_gravika.jpg (accessed on 10 November 2021).
- Morelli, C.; Gantar, C.; McConnell, R.K.; Szabo, B.; Uotila, U. The International Gravity Standardization Net 1971 (IGSN 71); Osservatorio Geofisico Sperimentale: Trieste, Italy, 1972. [Google Scholar]
- Khmelevskoy, V.K.; Gorbachev, Y.I.; Kalinin, A.V.; Popov, M.G.; Seliverstov, N.I.; Shevnin, V.A. Geophysical research methods. In Textbook for Geological Specialties of Universities; KGPU: Petropavlovsk-Kamchatsky, Russia, 2004. [Google Scholar]
- Poplavskii, K.N.; Podladchikov, Y.Y.; Stephenson, R.A. Two-dimensional inverse modeling of sedimentary basin subsidence. J. Geophys. Res. Solid Earth 2001, 106, 6657–6671. [Google Scholar] [CrossRef] [Green Version]
- Čermák, V.; Rybach, L. Thermal conductivity and specific heat of minerals and rocks. In Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology, New Series, Group V (Geophysics and Space Research), Volume Ia, (Physical Properties of Rocks); Angenheister, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 305–343. [Google Scholar]
- Sweeney, J.J.; Burnham, A.K. Evaluation of a simple model of vitrinite reflectance based on chemical kinetics. AAPG Bull. 1990, 74, 1559–1570. [Google Scholar] [CrossRef]
- Nielsen, S.B.; Clausen, O.R.; McGregor, E. Basin%Ro: A vitrinite reflectance model derived from basin and laboratory data. Basin Res. 2017, 29, 515–536. [Google Scholar] [CrossRef]
- Schenk, O.; Peters, K.; Burnham, A. Evaluation of alternatives to Easy% Ro for calibration of basin and petroleum system models. In Proceedings of the 79th EAGE Conference and Exhibition, Paris, France, 12–15 June 2017; Volume 2017, pp. 1–5. [Google Scholar] [CrossRef]
- Nezhdanov, A.A.; Ogibenin, V.V.; Melnikova, M.V.; Smirnov, A.S. Structures and stratification of the Triassic-Jurassic formations in the northern part of Western Siberia. ROGTEC 2012, 31, 62–69. [Google Scholar]
- Blackbourn, G. The Palaeozoic of Western Siberia. ROGTEC 2014, 21, 12–23. [Google Scholar]
- Isaev, V.I.; Gulenok, R.Y.; Isaeva, O.S.; Lobova, G.A. Density modeling of the basement of sedimentary sequences and prediction of oil-gas accumulations: Evidence from South Sakhalin and West Siberia. Russ. J. Pac. Geol. 2008, 2, 191–204. [Google Scholar] [CrossRef]
- Kurchikov, A.R. Тhe geothermal regime of hydrocarbon pools in West Siberia. Geol. Geophys. 2001, 42, 1846–1853. [Google Scholar]
- Tissot, B.P.; Welte, D.H. Petroleum Formation and Occurrence, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Wangen, M. The blanketing effect in sedimentary basins. Basin Res. 1995, 7, 283–298. [Google Scholar] [CrossRef]
- Lucazeau, F.; Le Douaran, S. The blanketing effect of sediments in basins formed by extension: A numerical model. Application to the Gulf of Lion and Viking graben. Earth Planet. Sci. Lett. 1985, 74, 92–102. [Google Scholar] [CrossRef]
- Kim, Y.; Huh, M.; Lee, E.Y. Numerical Modelling to Evaluate Sedimentation Effects on Heat Flow and Subsidence during Continental Rifting. Geosciences 2020, 10, 451. [Google Scholar] [CrossRef]
- Essa, K.S. A fast interpretation method for inverse modeling of residual gravity anomalies caused by simple geometry. J. Geol. Res. 2012, 2012, 327037. [Google Scholar] [CrossRef] [Green Version]
- Martyshko, P.S.; Ladovskii, I.V.; Byzov, D.D.; Tsidaev, A.G. Gravity data inversion with method of local corrections for finite elements models. Geosciences 2018, 8, 373. [Google Scholar] [CrossRef] [Green Version]
- Christensen, N.I.; Mooney, W.D. Seismic velocity structure and composition of the continental crust: A global view. J. Geophys. Res. Solid Earth 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
- Kurchikov, A.R.; Stavitsky, B. Geothermy of Oil and Gas Bearing Areas of Western Siberia; Nedra: Moscow, Russia, 1987. [Google Scholar]
- National Standard of the Russian Federation Р 55659-2013. (ISO 7404-5:2009); Methods for the Petrographic Analysis of Coals. Part 5: Method of Determining the Reflectance of Vitrinite 2015; Standartinform: Moscow, Russia, 2015.
- ASTM D2798-20; Standard Test Method for Microscopical Determination of the Vitrinite Reflectance of Coal. ASTM International: West Conshohocken, PA, USA, 2020. [CrossRef]
- International Committee for Coal Petrology (ICCP). International Handbook of Coal Petrography (Supplement to 2nd ed.); CNRS, Academy of Sciences of the USSR: Paris, France, 1971. [Google Scholar]
- Komorek, J.; Morga, R. Relationship between the maximum and the random reflectance of vitrinite for coal from the Upper Silesian Coal Basin (Poland). Fuel 2002, 81, 969–971. [Google Scholar] [CrossRef]
- Hackley, P.; Araujo, C.V.; Borrego, A.; Bouzinos, A.; Cardott, B.J.; Cook, A.C.; Eble, C.; Flores, D.; Gentzis, T.; Gonçalves, P.A.; et al. Standardization of reflectance measurements in dispersed organic matter: Results of an exercise to improve interlaboratory agreement. Mar. Pet. Geol. 2015, 59, 22–34. [Google Scholar] [CrossRef]
- ASTM D7708-14; Standard Test Method for Microscopical Determination of the Reflectance of Vitrinite Dispersed in Sedimentary Rocks; ASTM International: West Conshohocken, PA, USA, 2014.
- Houseknecht, D.; Matthews, S. Thermal maturity of Carboniferous strata, Ouachita Mountains. AAPG Bull. 1985, 69, 335–345. [Google Scholar] [CrossRef]
- Vtorushina, E.A.; Bulatov, T.D.; Kozlov, I.V.; Vtorushin, M.N. The advanced technique for determination of pyrolysis parameters of rocks. Oil Gas Geol. 2018, 2, 71–77. [Google Scholar] [CrossRef]
- Yang, S.; Horsfield, B. Critical review of the uncertainty of Tmax in revealing the thermal maturity of organic matter in sedimentary rocks. Int. J. Coal Geol. 2020, 225, 103500. [Google Scholar] [CrossRef]
- Wust, R.A.J.; Nassichuk, B.R.; Brezovski, R.; Hackley, P.C.; Willment, N. Vitrinite reflectance versus pyrolysis Tmax data: Assessing thermal maturity in shale plays with special reference to the Duvernay shale play of the Western Canadian Sedimentary Basin, Alberta, Canada. In Proceedings of the SPE Unconventional Resources Conference and Exhibition-Asia Pacific, Society of Petroleum Engineers, Brisbane, Australia, 11–13 November 2013. [Google Scholar] [CrossRef] [Green Version]
- Jarvie, D.M.; Claxton, B.L.; Henk, F.; Breyer, J.T. Oil and shale gas from the Barnett Shale, Ft. Worth Basin, Texas. AAPG Annu. Meet. Program 2001, 10, A100. [Google Scholar]
- Blackwell, D.D.; Spafford, R.E. 14. Experimental Methods in Continental Heat Flow. Methods Exp. Phys. 1987, 24, 189–226. [Google Scholar]
- Hermanrud, C.; Cao, S.; Lerche, I. Estimates of virgin rock temperature derived from BHT measurements: Bias and error. Geophysics 1990, 55, 924–931. [Google Scholar] [CrossRef]
- Waples, D.W.; Ramly, M. A statistical method for correcting log-derived temperatures. Pet. Geosci. 2001, 7, 231–240. [Google Scholar] [CrossRef]
- Förster, A. Analysis of borehole temperature data in the Northeast German Basin: Continuous logs versus bottom-hole temperatures. Pet. Geosci. 2001, 7, 241–254. [Google Scholar] [CrossRef] [Green Version]
- Gallardo, J.; Blackwell, D.D. Thermal structure of the Anadarko Basin. AAPG Bull. 1999, 83, 333–361. [Google Scholar] [CrossRef]
- Schumacher, S.; Moeck, I. A new method for correcting temperature log profiles in low-enthalpy plays. Geotherm. Energy 2020, 8, 27. [Google Scholar] [CrossRef]
- Peters, K.E.; Nelson, P.H. Criteria to determine borehole formation temperatures for calibration of basin and petroleum system models. SEPM Spec. Publ. 2012, 103, 5–15. [Google Scholar]
- LaFehr, T.R. Standardization in gravity reduction. Geophysics 1991, 56, 1170–1178. [Google Scholar] [CrossRef]
- Chapin, D.A. The theory of the Bouguer gravity anomaly: A tutorial. Lead. Edge 1996, 15, 361–363. [Google Scholar] [CrossRef]
- Jacoby, W.; Smilde, P.L. Gravity Interpretation: Fundamentals and Application of Gravity Inversion and Geological Interpretation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Talwani, M. Errors in the total Bouguer reduction. Geophysics 1998, 63, 1125–1130. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).