An Application of Simultaneous Stochastic Optimization at a Large Open-Pit Gold Mining Complex under Supply Uncertainty
Abstract
1. Introduction
2. Method
2.1. Definitions and Notation
2.2. Decision Variables
2.3. Objective Function
2.4. Constraints
2.5. Solution Approach
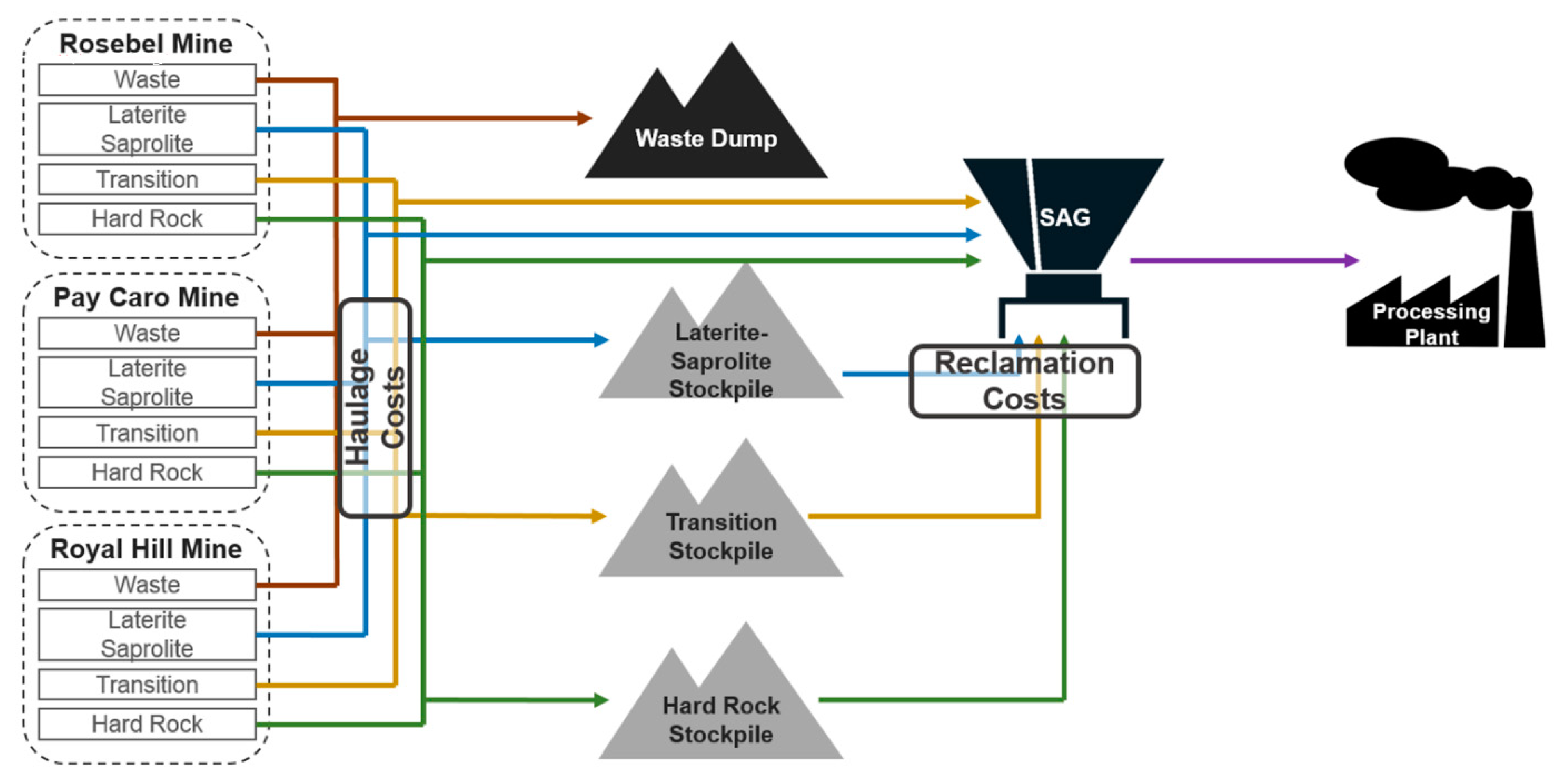
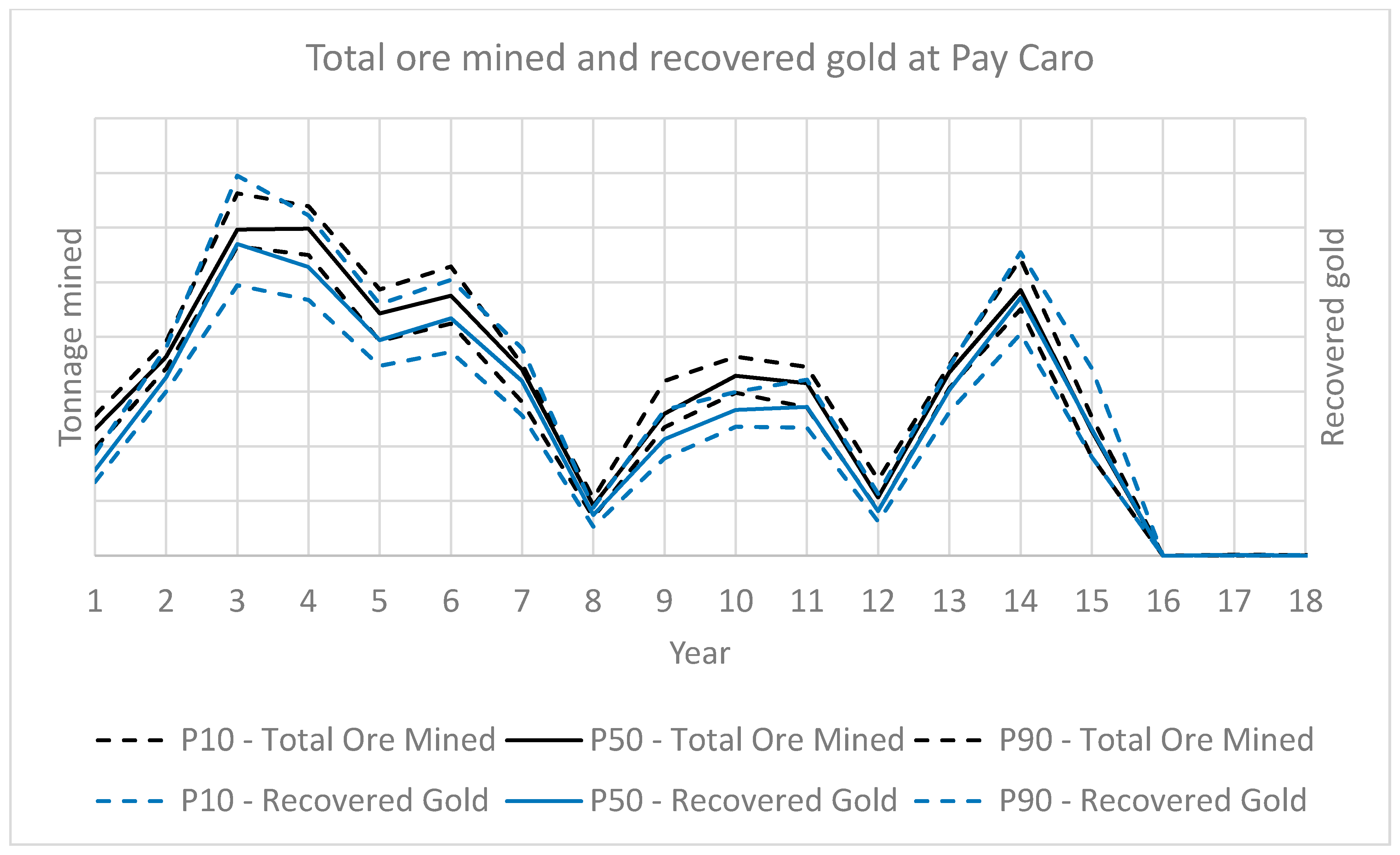
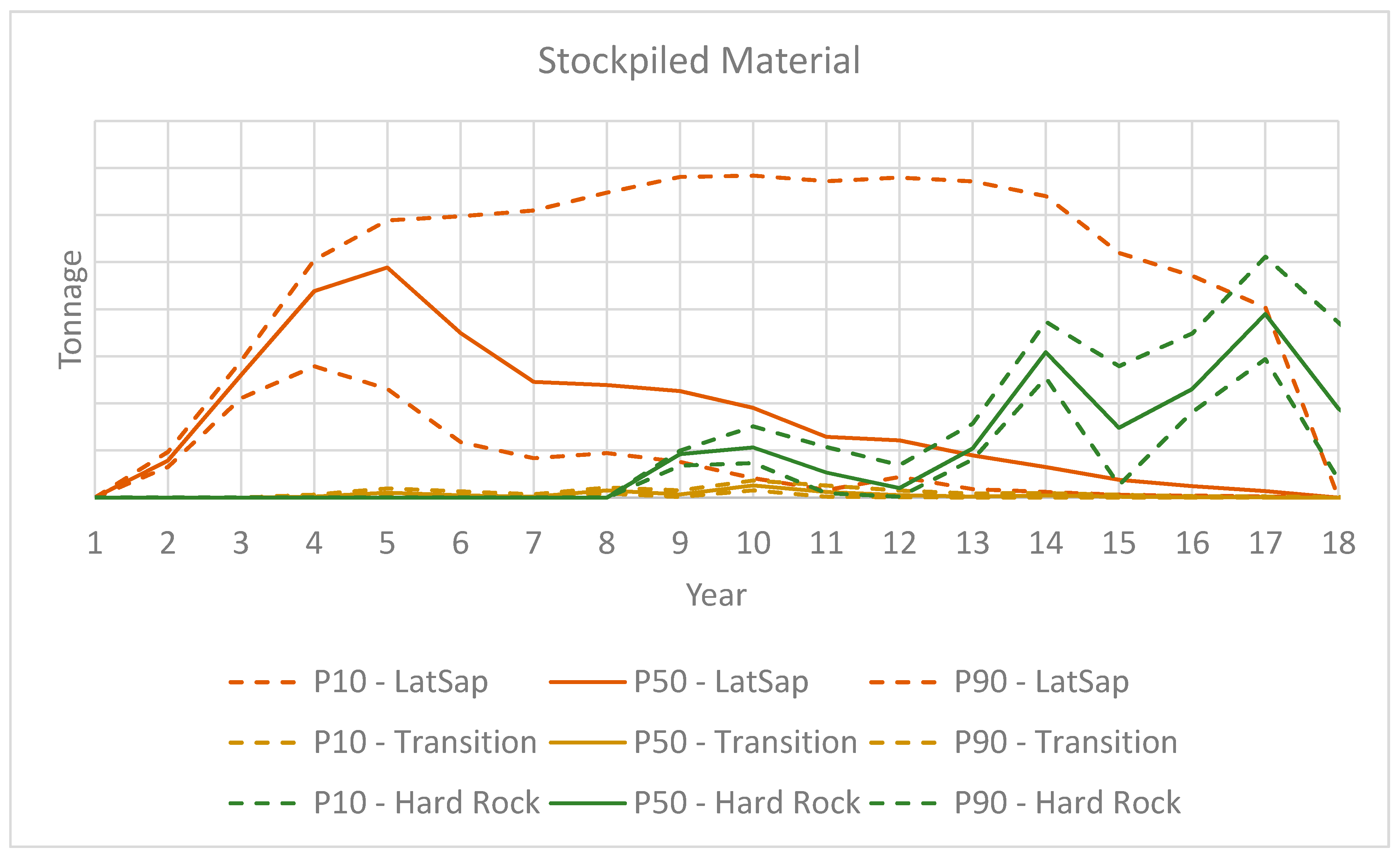
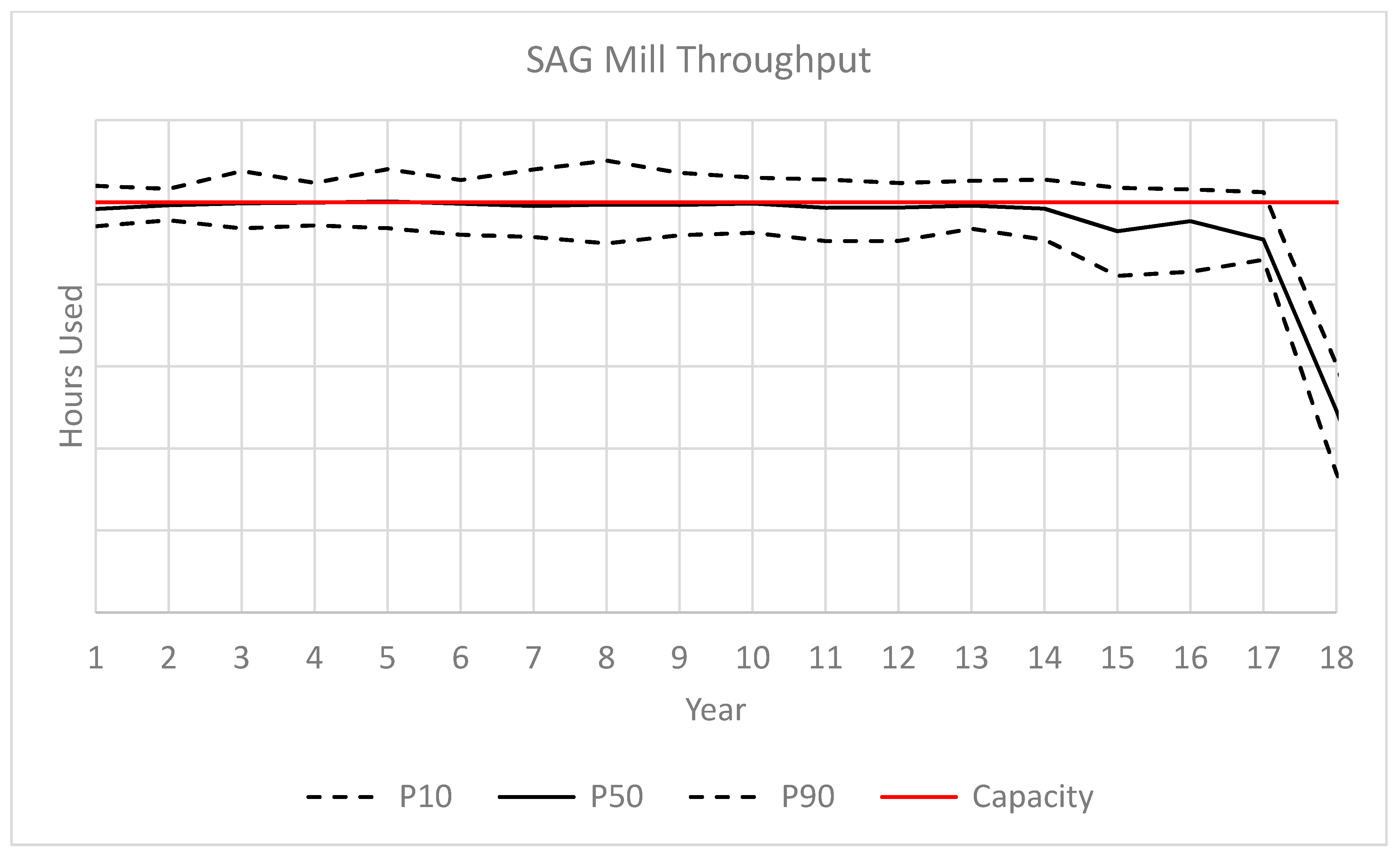
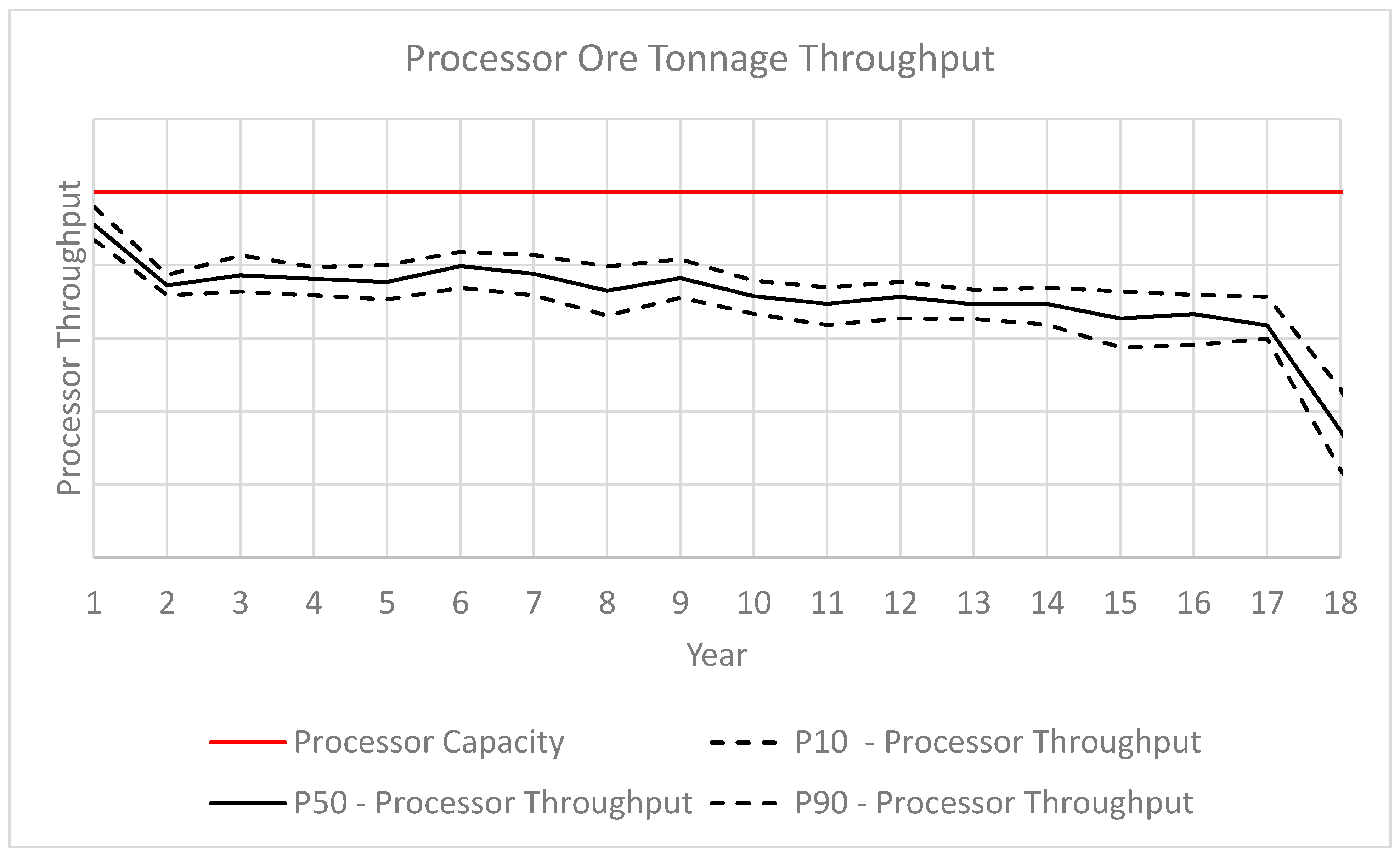
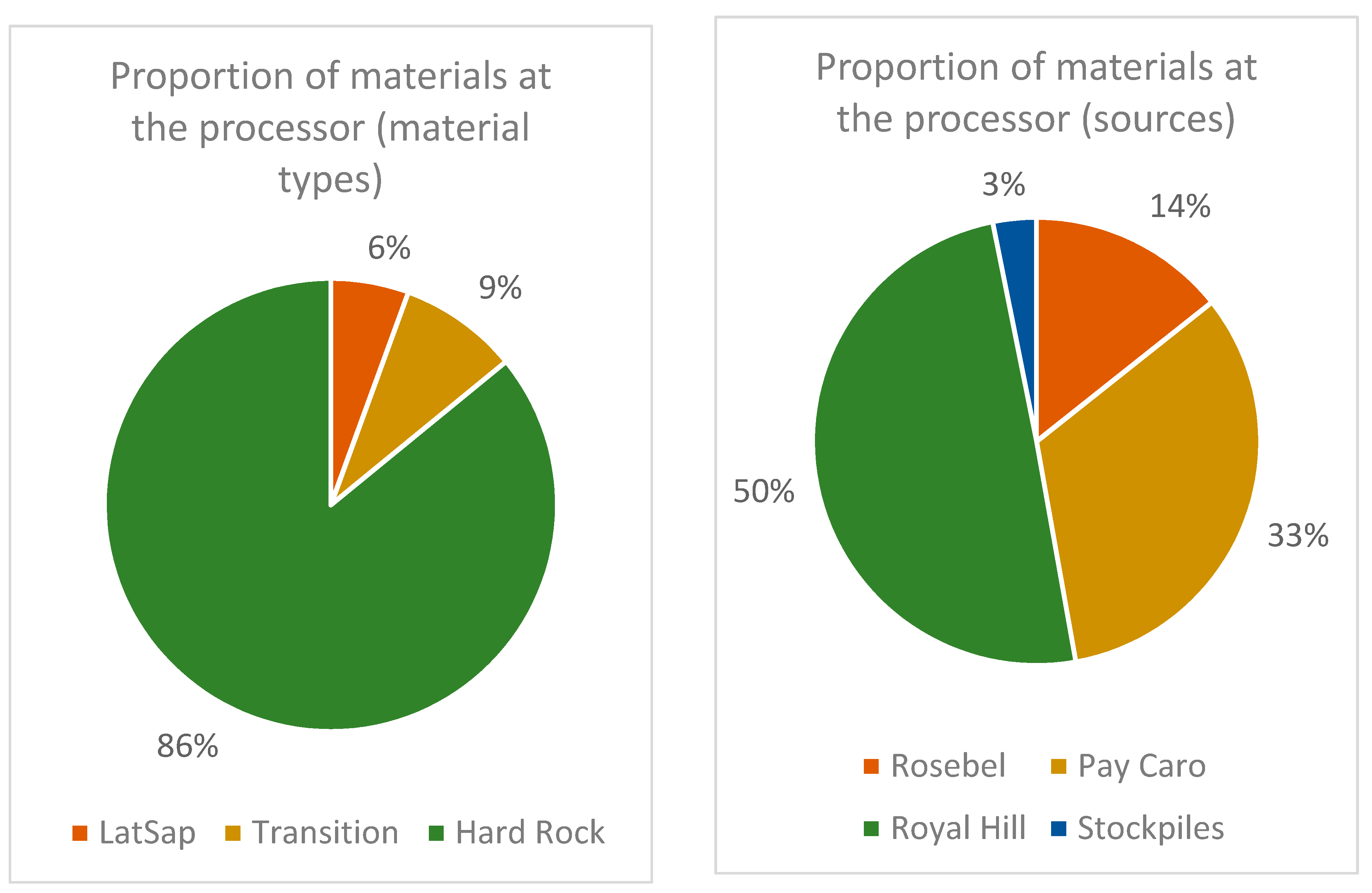
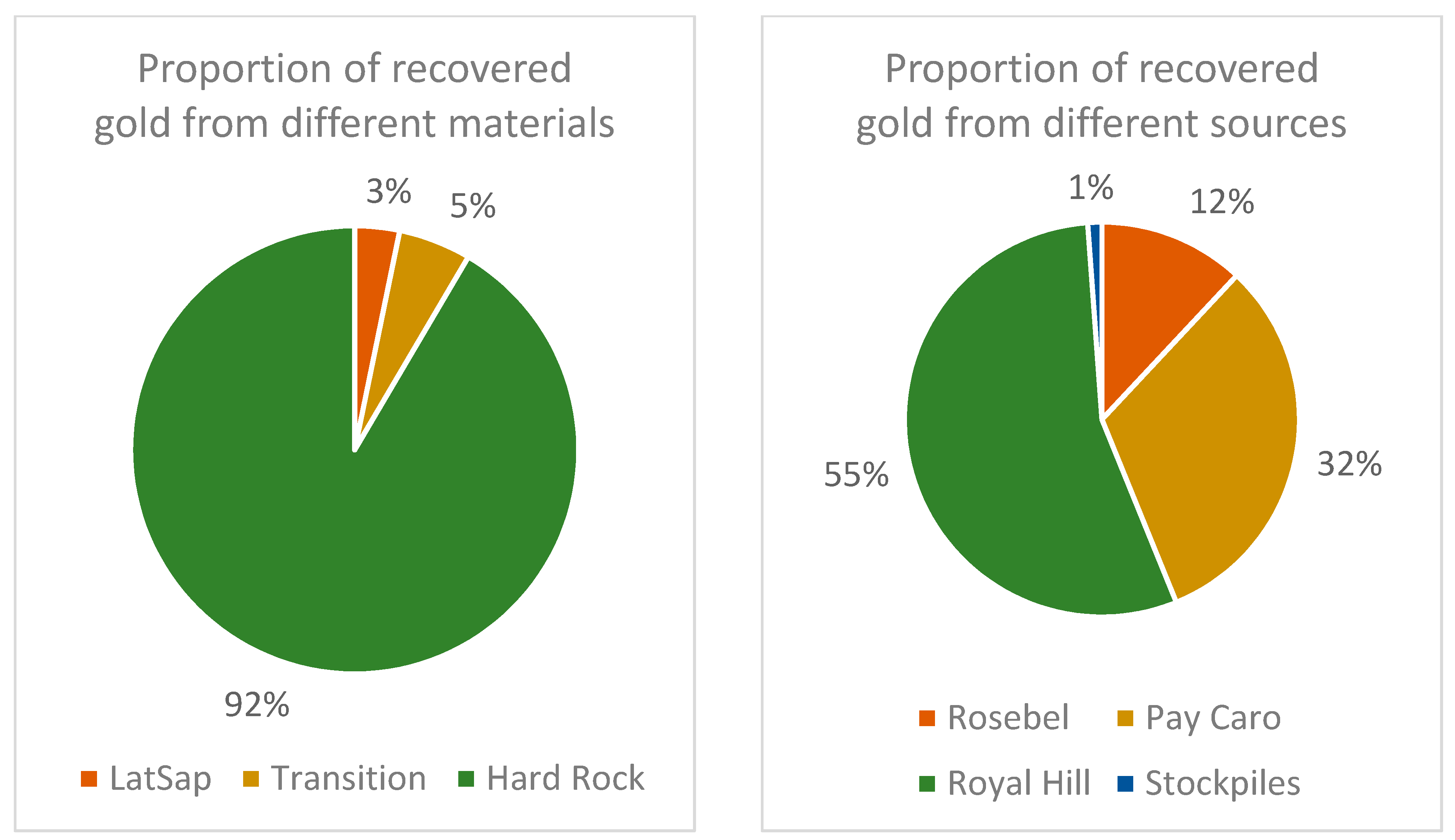
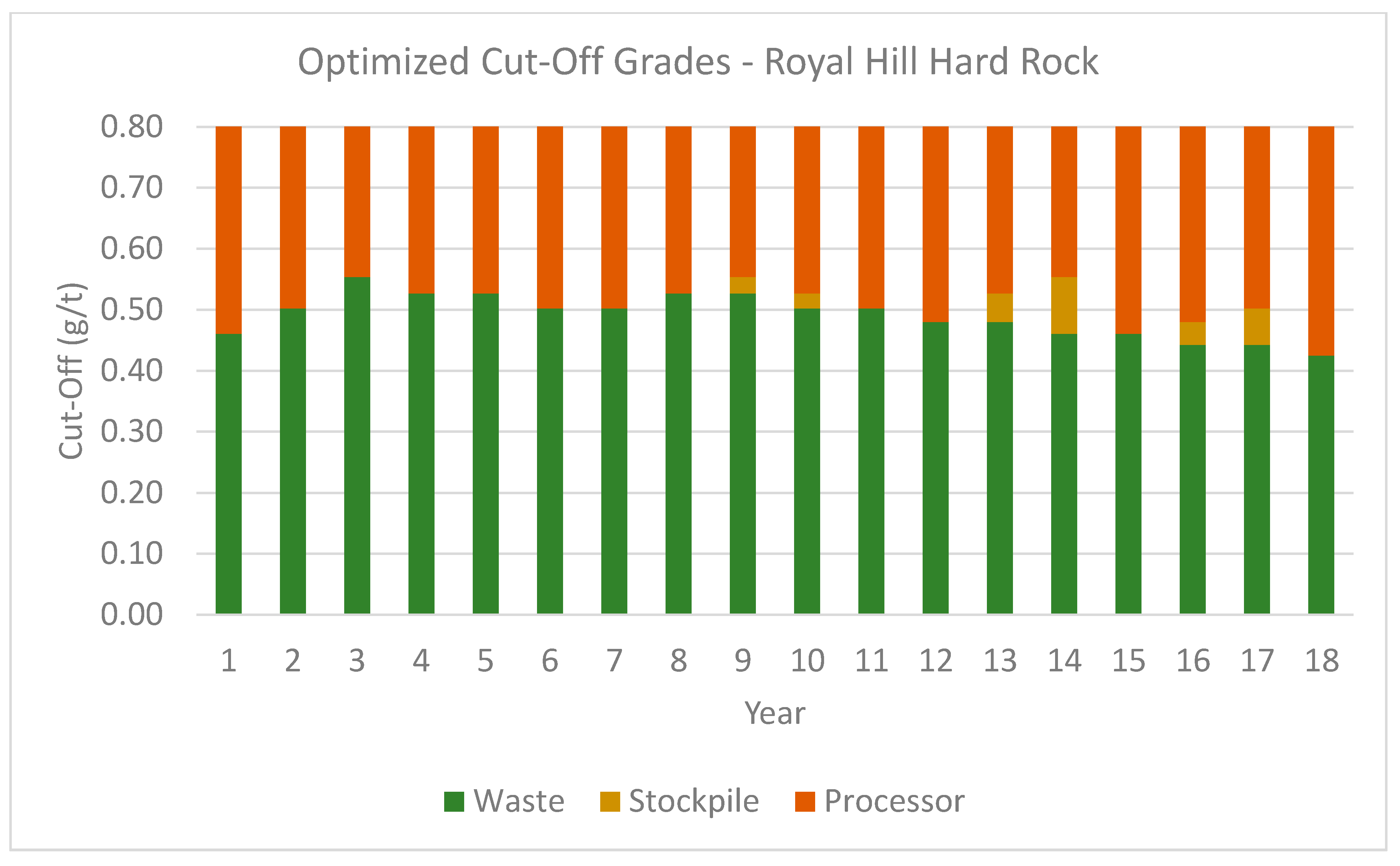
3. Case Study at a Gold Mining Complex
3.1. Overview
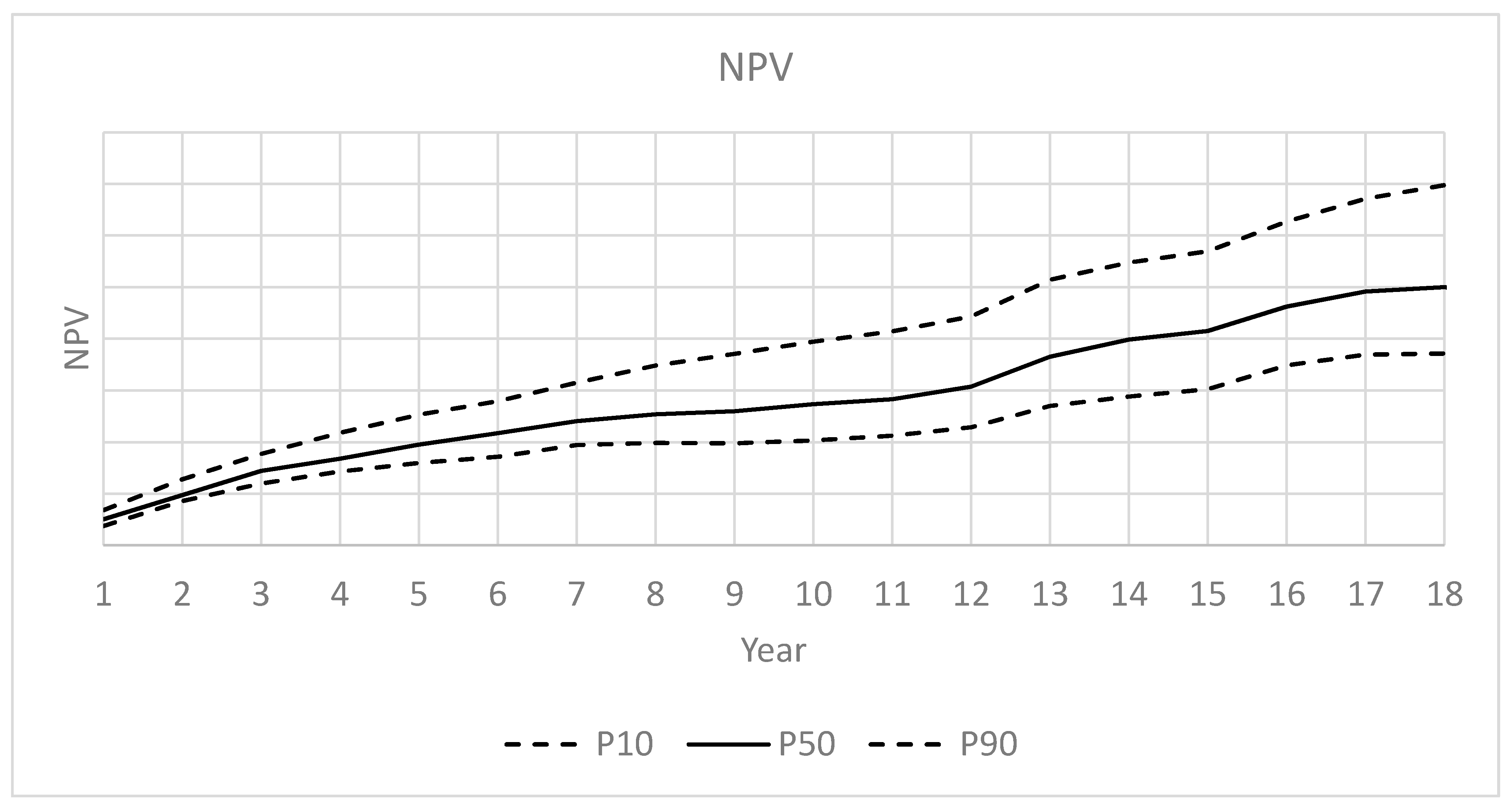
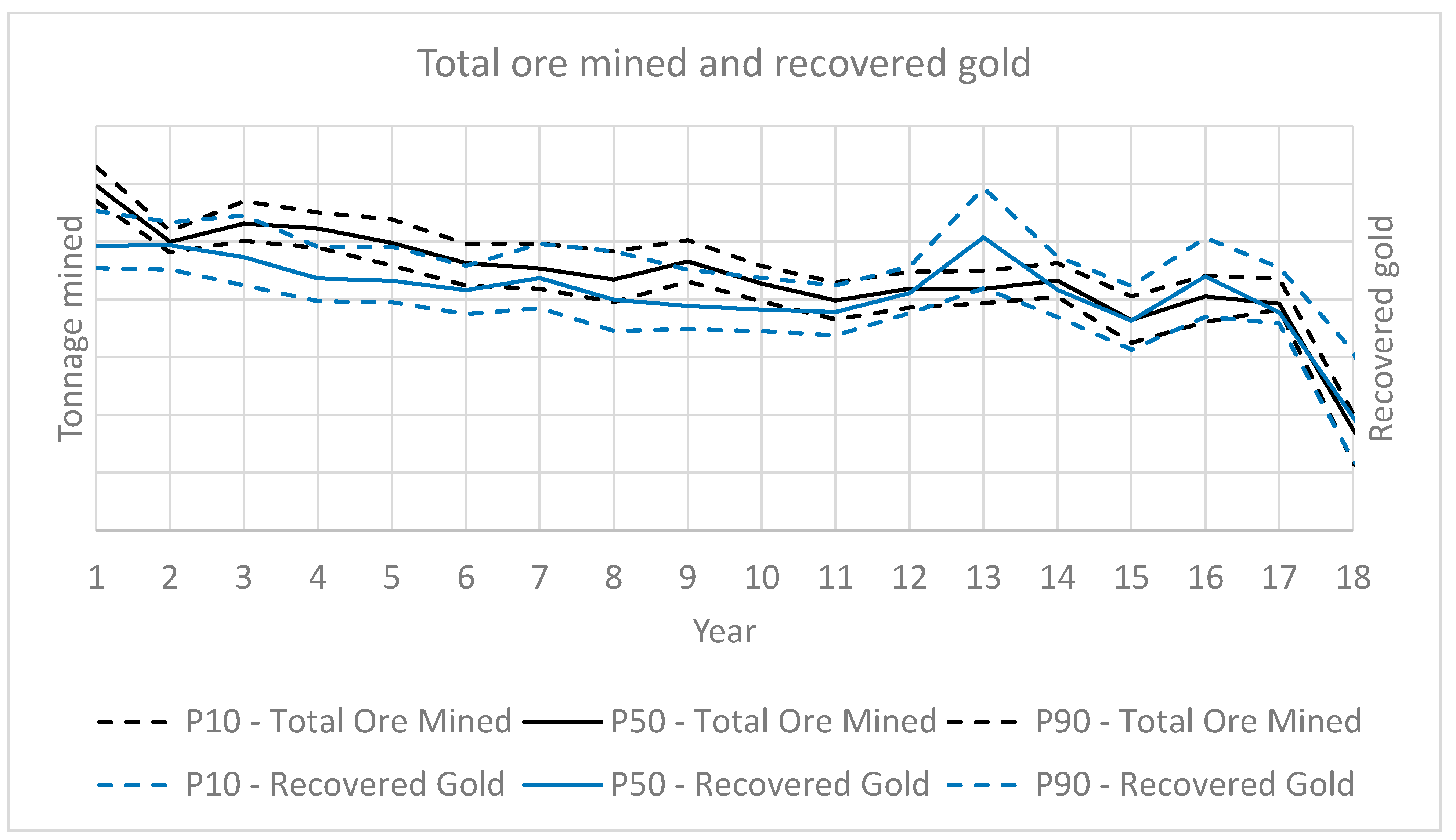
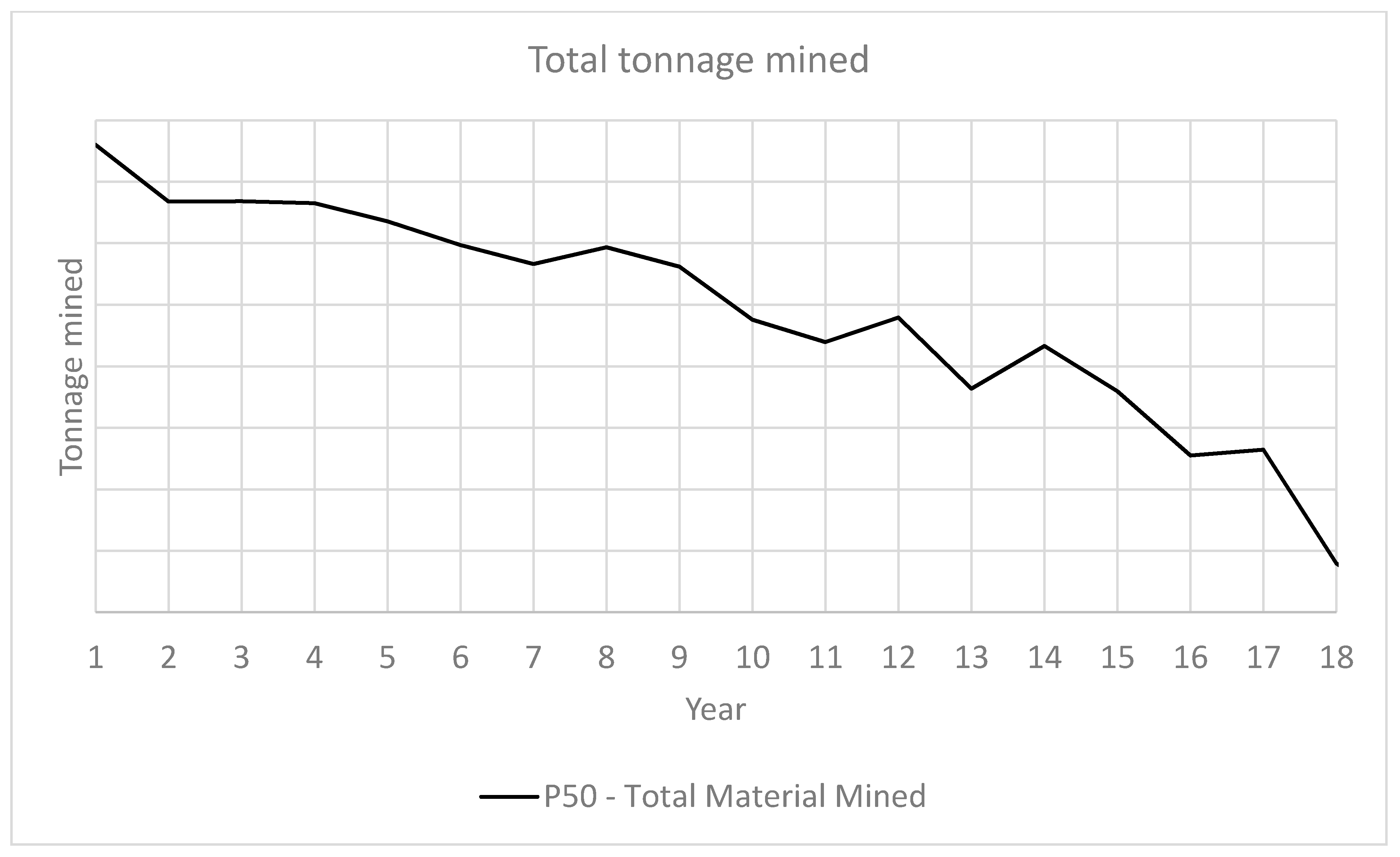
3.2. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Montiel, L.; Dimitrakopoulos, R. Optimizing mining complexes with multiple processing and transportation alternatives: An uncertainty-based approach. Eur. J. Oper. Res. 2015, 247, 166–178. [Google Scholar] [CrossRef]
- Montiel, L.; Dimitrakopoulos, R. A heuristic approach for the stochastic optimization of mine production schedules. J. Heuristics 2017, 23, 397–415. [Google Scholar] [CrossRef]
- Montiel, L.; Dimitrakopoulos, R. Simultaneous stochastic optimization of production scheduling at Twin Creeks Mining Complex, Nevada. Min. Eng. 2018, 70, 48–56. [Google Scholar] [CrossRef]
- Goodfellow, R.C.; Dimitrakopoulos, R. Global optimization of open pit mining complexes with uncertainty. Appl. Soft Comput. 2016, 40, 292–304. [Google Scholar] [CrossRef]
- Goodfellow, R.C.; Dimitrakopoulos, R. Simultaneous stochastic optimization of mining complexes and mineral value chains. Math. Geosci. 2017, 49, 341–360. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Gomez Gómez-Hernández, J.J.; Srivastava, R.M. One step at a time: The origins of sequential simulation and beyond. Math. Geosci. 2021. [Google Scholar] [CrossRef]
- Hoerger, S.; Hoffman, L.; Seymour, F. Mine planning at Newmont’s Nevada operations. Min. Eng. 1999, 51, 26–30. [Google Scholar]
- Stone, P.; Froyland, G.; Menabde, M.; Law, B.; Pasyar, R.; Monkhouse, P.H.L. Blasor—Blended iron ore mine planning optimisation at Yandi, Western Australia. In Orebody Modelling and Strategic Mine Planning; Spectrum Series 14; Dimitrakopoulos, R., Ed.; AusIMM: Carlton, Australia, 2007; Volume 14, pp. 133–136. [Google Scholar]
- Whittle, G. Global asset optimisation. In Orebody Modelling and Strategic Mine Planning; Spectrum Series 14; Dimitrakopoulos, R., Ed.; AusIMM: Carlton, Australia, 2007; Volume 14, pp. 361–366. [Google Scholar]
- Whittle, J. The global optimiser works-What next? In Advances in Applied Strategic Mine Planning; Dimitrakopoulos, R., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 31–37. [Google Scholar] [CrossRef]
- Whittle, J. Not for the faint-hearted. In Proceedings of the Orebody Modelling and Strategic Mine Planning Symposium, Perth, Australia, 22–24 November 2010; AusIMM: Carlton, Australia, 2010; pp. 3–6. [Google Scholar]
- Pimentel, B.S.; Mateus, G.R.; Almeida, F.A. Mathematical models for optimizing the global mining supply chain. In Intelligent Systems in Operations: Methods, Models and Applications in the Supply Chain; IGI Global: Hershey, PA, USA, 2010; pp. 133–163. [Google Scholar]
- Ramazan, S.; Dimitrakopoulos, R. Stochastic optimisation of long-term production scheduling for open pit mines with a new integer programming formulation. In Orebody Modelling and Strategic Mine Planning; Spectrum Series 14; Dimitrakopoulos, R., Ed.; AusIMM: Carlton, Australia, 2007; Volume 14, pp. 385–394. [Google Scholar]
- Ramazan, S.; Dimitrakopoulos, R. Production scheduling with uncertain supply: A new solution to the open pit mining problem. Optim. Eng. 2013, 14, 361–380. [Google Scholar] [CrossRef]
- Paithankar, A.; Chatterjee, S. Open pit mine production schedule optimization using a hybrid of maximum-flow and genetic algorithms. Appl. Soft Comput. 2019, 81, 105507. [Google Scholar] [CrossRef]
- Menabde, M.; Froyland, G.; Stone, P.; Yeates, G.A. Mining schedule optimisation for conditionally simulated orebodies. In Orebody Modelling and Strategic Mine Planning; Spectrum Series 14; Dimitrakopoulos, R., Ed.; AusIMM: Carlton, Australia, 2007; Volume 14, pp. 379–384. [Google Scholar]
- Githiria, J.; Musingwini, C. A stochastic cut-off grade optimization model to incorporate uncertainty for improved project value. J. S. Afr. Inst. Min. Met. 2019, 119, 217–228. [Google Scholar] [CrossRef]
- Khan, A.; Asad, M.W.A. A method for optimal cut-off grade policy in open pit mining operations under uncertain supply. Resour. Policy 2019, 60, 178–184. [Google Scholar] [CrossRef]
- Mai, N.L.; Topal, E.; Erten, O.; Sommerville, B. A new risk-based optimisation method for the iron ore production scheduling using stochastic integer programming. Resour. Policy 2019, 62, 571–579. [Google Scholar] [CrossRef]
- Morales, N.; Seguel, S.; Cáceres, A.; Jélvez, E.; Alarcón, M. Incorporation of Geometallurgical Attributes and Geological Uncertainty into Long-Term Open-Pit Mine Planning. Minerals 2019, 9, 108. [Google Scholar] [CrossRef]
- Montiel, L.; Dimitrakopoulos, R.; Kawahata, K. Globally optimising open-pit and underground mining operations under geological uncertainty. Min. Technol. 2016, 125, 2–14. [Google Scholar] [CrossRef]
- Saliba, Z.; Dimitrakopoulos, R. Simultaneous stochastic optimization of an open pit gold mining complex with supply and market uncertainty. Min. Technol. 2019, 128, 216–229. [Google Scholar] [CrossRef]
- Levinson, Z.; Dimitrakopoulos, R. Simultaneous stochastic optimisation of an open-pit gold mining complex with waste management. Int. J. Min. Reclam. Environ. 2019, 34, 415–429. [Google Scholar] [CrossRef]
- Saliba, Z.; Dimitrakopoulos, R. An application of simultaneous stochastic optimisation of an open-pit mining complex with tailings management. Int. J. Min. Reclam. Environ. 2020, 34, 592–607. [Google Scholar] [CrossRef]
- Kumar, A.; Dimitrakopoulos, R. Application of simultaneous stochastic optimization with geometallurgical decisions at a copper–gold mining complex. Min. Technol. 2019, 128, 88–105. [Google Scholar] [CrossRef]
- Del Castillo, M.F.; Dimitrakopoulos, R. Dynamically optimizing the strategic plan of mining complexes under supply uncertainty. Resour. Policy 2019, 60, 83–93. [Google Scholar] [CrossRef]
- Levinson, Z.; Dimitrakopoulos, R. Adaptive simultaneous stochastic optimization of a gold mining complex: A case study. J. S. Afr. Inst. Min. Met. 2020, 120, 221–232. [Google Scholar] [CrossRef] [PubMed]
- Paithankar, A.; Chatterjee, S.; Goodfellow, R.; Asad, M.W.A. Simultaneous stochastic optimization of production sequence and dynamic cut-off grades in an open pit mining operation. Resour. Policy 2020, 66, 101634. [Google Scholar] [CrossRef]
- Godoy, M. The Effective Management of Geological Risk in Long-Term Production Scheduling of Open Pit Mines. Ph.D. Thesis, University of Queensland, Brisbane, QLD, Australia, 2003. [Google Scholar]
- Boucher, A.; Dimitrakopoulos, R. Block simulation of multiple correlated variables. Math. Geosci. 2009, 41, 215–237. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Ramazan, S. Uncertainty-based production scheduling in open pit mining. SME Trans. 2004, 316, 106–112. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- NI43-101 Technical Report. Rosebel Gold Mine, Suriname; IAMGOLD Corporation: Toronto, ON, Canada, 2018.
- Albor, F.; Dimitrakopoulos, R. Stochastic mine design optimisation based on simulated annealing: Pit limits, production schedules, multiple orebody scenarios and sensitivity analysis. Min. Technol. 2009, 118, 79–90. [Google Scholar] [CrossRef]



| General | Material-Dependent | Mine-Dependent |
|---|---|---|
| Economic Discount Rate | Gold Recovery Rate | Reclamation Cost |
| Geological Risk Discount Rate | Drill and Blast Cost | Haulage Costs |
| Gold Price | Processing Cost | Incremental Mining Cost |
| Selling Cost | Administration Cost | |
| Royalties | Sustaining Capital Cost | |
| Loading Cost | ||
| Dump Maintenance Cost | ||
| Closure Cost |
| Constraints | Capacity |
|---|---|
| Mining Capacity (years 1–5) | 67.3 Mt/y |
| Mining Capacity (years 6–18) | 74.0 Mt/y |
| SAG Mill Capacity | 876 h/y |
| Processing Capacity | 8.83 Mt/y |
| Constraint | Distance |
|---|---|
| Smoothness | 48 m |
| Max sink rate | 63 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
LaRoche-Boisvert, M.; Dimitrakopoulos, R. An Application of Simultaneous Stochastic Optimization at a Large Open-Pit Gold Mining Complex under Supply Uncertainty. Minerals 2021, 11, 172. https://doi.org/10.3390/min11020172
LaRoche-Boisvert M, Dimitrakopoulos R. An Application of Simultaneous Stochastic Optimization at a Large Open-Pit Gold Mining Complex under Supply Uncertainty. Minerals. 2021; 11(2):172. https://doi.org/10.3390/min11020172
Chicago/Turabian StyleLaRoche-Boisvert, Mélanie, and Roussos Dimitrakopoulos. 2021. "An Application of Simultaneous Stochastic Optimization at a Large Open-Pit Gold Mining Complex under Supply Uncertainty" Minerals 11, no. 2: 172. https://doi.org/10.3390/min11020172
APA StyleLaRoche-Boisvert, M., & Dimitrakopoulos, R. (2021). An Application of Simultaneous Stochastic Optimization at a Large Open-Pit Gold Mining Complex under Supply Uncertainty. Minerals, 11(2), 172. https://doi.org/10.3390/min11020172





