Quantification of Soil Losses along the Coastal Protected Areas in Kenya
Abstract
1. Introduction
2. Materials and Methods
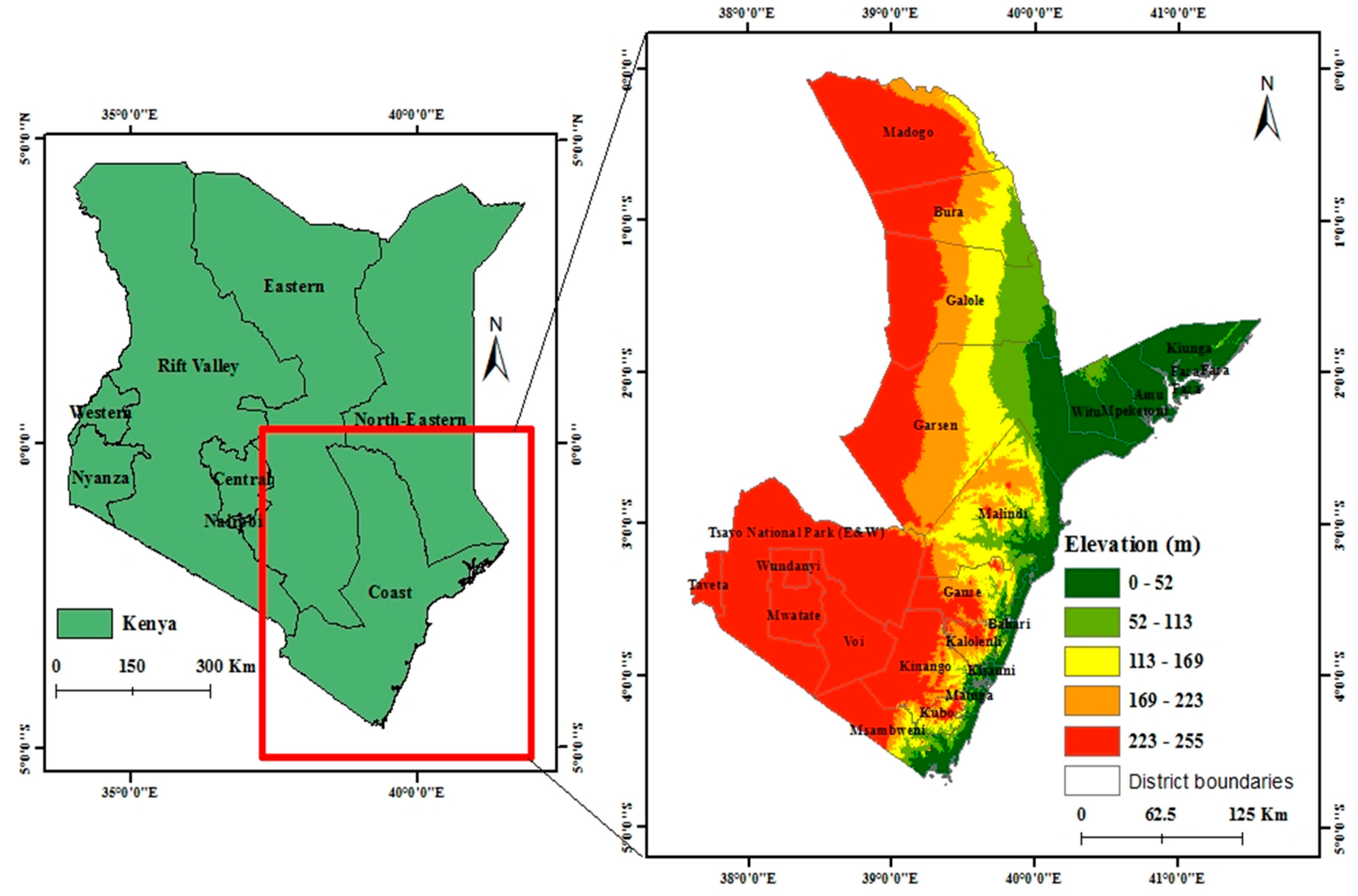
2.1. Study Area Description
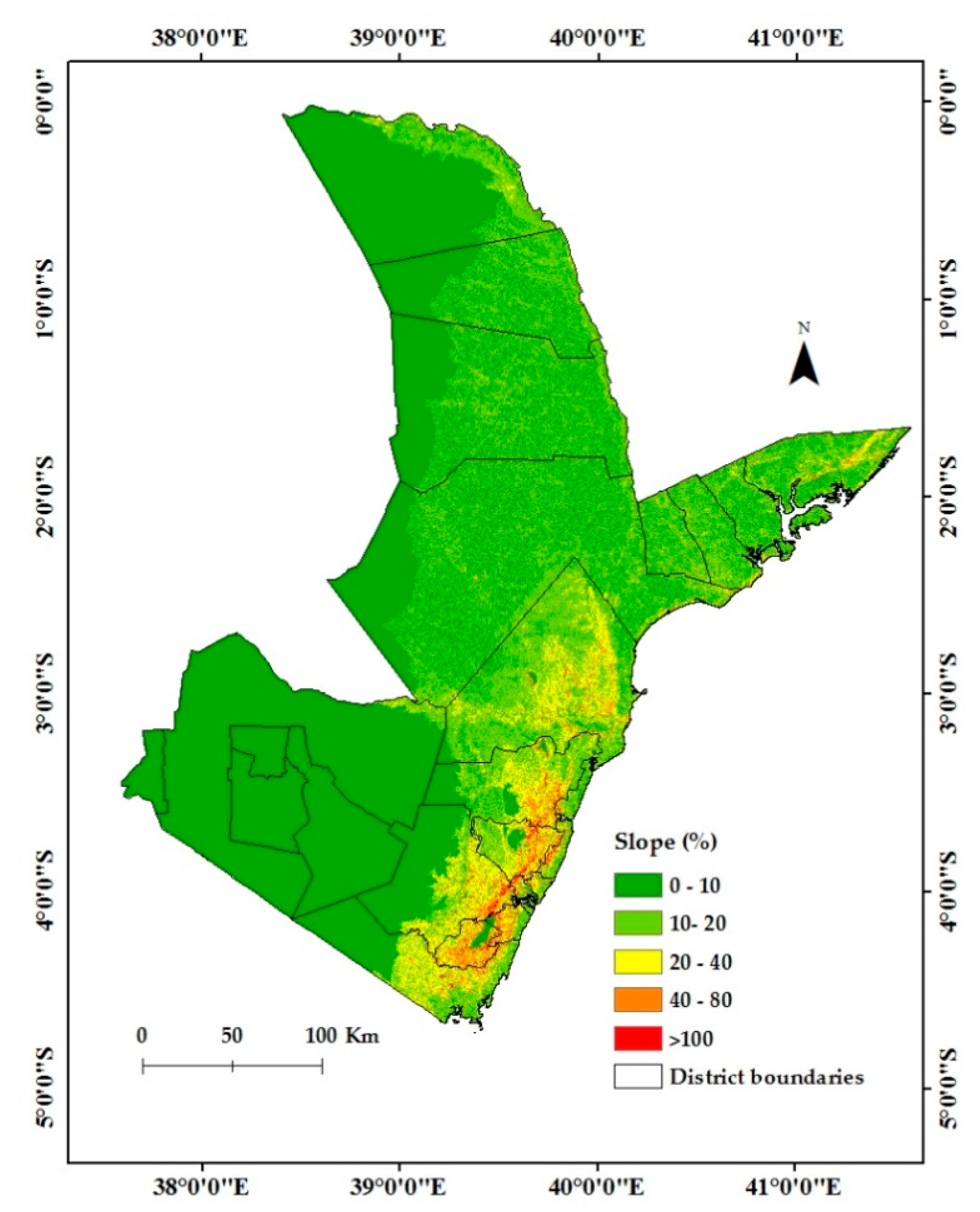
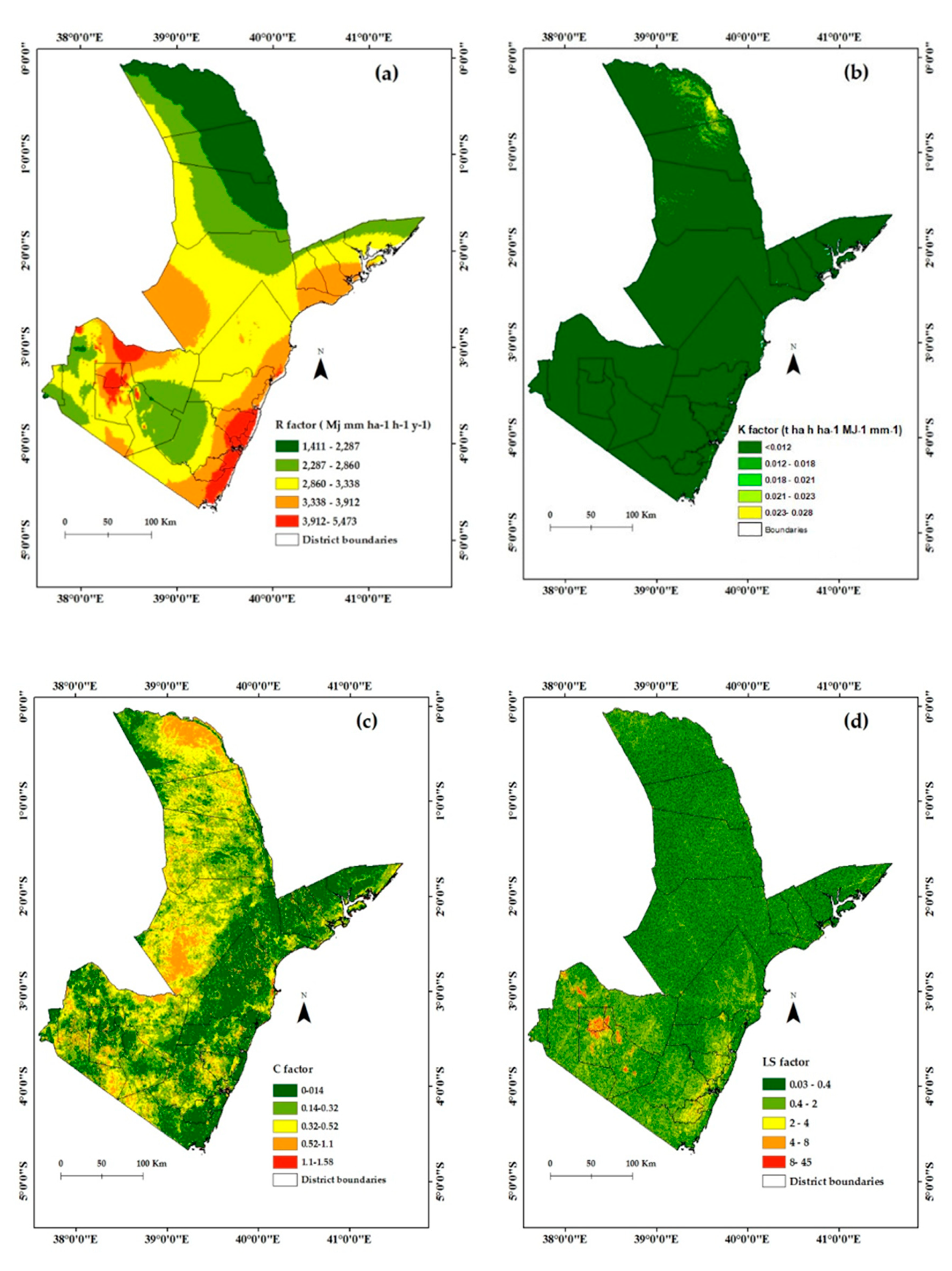
2.2. Methodological Framework
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ojwang, R.O.; Dietrich, J.; Anebagilu, P.K.; Beyer, M.; Rottensteiner, F. Rooftop rainwater harvesting for Mombasa: Scenario development with image classification and water resources simulation. Water (Switzerland) 2017, 9, 359. [Google Scholar] [CrossRef]
- Awuor, C.B.; Orindi, V.A.Y.O.; Adwera, A.O. Climate change and coastal cities: The case of Mombasa, Kenya. Environ. Urban. 2008, 20, 231–242. [Google Scholar] [CrossRef]
- Sudha Rani, N.N.V.; Satyanarayana, A.N.V.; Bhaskaran, P.K. Coastal vulnerability assessment studies over India: A review. Nat. Hazards 2015, 77, 405–428. [Google Scholar] [CrossRef]
- Beach, W.P.; Kebede, A.S.; Nicholls, R.J.; Hanson, S.; Mokrech, M. Impacts of Climate Change and Sea-Level Rise: A Preliminary Case Study of Mombasa, Kenya. J. Coast. Res. 2012, 28, 8–19. [Google Scholar]
- Musingi, J.K.; Kithha, S.M.; Wambua, B.N. The urban growth of Mombasa coastal town and its implication for surface and groundwater resources. In Proceedings of the International Symposium Held During IUGG 99, the XXII General Assembly of the International Union of Geodesy and Geophysics, Birmingham, UK, 18–30 July 1999; pp. 419–422. [Google Scholar]
- Koirala, P.; Thakuri, S.; Joshi, S.; Chauhan, R. Estimation of Soil Erosion in Nepal using a RUSLE modeling and geospatial tool. Geoscience 2019, 9, 147. [Google Scholar] [CrossRef]
- Claessens, L.; Van Breuge, P.; Notenbaert, A.; Herrero, M.; De Steeg, J. Van Mapping potential soil erosion in East Africa using the Universal Soil Loss Equation and secondary data. IAHS-AISH Publ. 2008, 398–407. [Google Scholar]
- Chittenden, D.B. Prevention and Control of Soil Erosion: The State of the Art; Special Report- Higway Research; Pennsylvania Department of Transportation: Harrisburg, PA, USA, 1973; pp. 123–150.
- Ganasri, B.P.; Ramesh, H. Assessment of soil erosion by RUSLE model using remote sensing and GIS—A case study of Nethravathi Basin. Geosci. Front. 2016, 7, 953–961. [Google Scholar] [CrossRef]
- Sujatha, E.; Sridhar, V. Spatial Prediction of Erosion Risk of a Small Mountainous Watershed Using RUSLE: A Case-Study of the Palar Sub-Watershed in Kodaikanal, South India. Water 2018, 10, 1608. [Google Scholar] [CrossRef]
- Reichmann, O.; Chen, Y.; Iggy, L.M. Spatial model assessment of P transport from soils to waterways in an Eastern Mediterranean Watershed. Water (Switzerland) 2013, 5, 262–279. [Google Scholar] [CrossRef]
- Barungi, M.; Edriss, A.; Mugisha, J.; Waithaka, M.; Tukahirwa, J. Factors Influencing the Adoption of Soil Erosion Control Technologies by Farmers Along the Slopes of Mt. Elgon in Eastern Uganda. J. Sustain. Dev. 2013, 6, 9. [Google Scholar] [CrossRef]
- Ozsahin, E.; Duru, U.; Eroglu, I. Land use and land cover changes (LULCC), a key to understand soil erosion intensities in the Maritsa Basin. Water (Switzerland) 2018, 10, 335. [Google Scholar] [CrossRef]
- Woldemariam, G.; Iguala, A.; Tekalign, S.; Reddy, R. Spatial Modeling of Soil Erosion Risk and Its Implication for Conservation Planning: The Case of the Gobele Watershed, East Hararghe Zone, Ethiopia. Land 2018, 7, 25. [Google Scholar] [CrossRef]
- Ayele, T.; Ahmed, N.; Ribbe, L.; Heinrich, J. Science of the Total Environment Hydrological responses to land use/cover changes in the source region of the Upper Blue Nile Basin, Ethiopia. Sci. Total Environ. 2017, 575, 724–741. [Google Scholar]
- Chandra, S.; Manisa, P. Application of RUSLE model for soil loss estimation of Jaipanda watershed, West Bengal. Spat. Inf. Res. 2017, 25, 399–409. [Google Scholar]
- Reitsma, K.D.; Dunn, B.H.; Mishra, U.; Clay, S.A.; DeSutter, T.; Clay, D.E. Land-use change impact on soil sustainability in a climate and vegetation transition zone. Agron. J. 2015, 107, 2363–2372. [Google Scholar] [CrossRef]
- Pérez-Molina, E.; Sliuzas, R.; Flacke, J.; Jetten, V. Developing a cellular automata model of urban growth to inform spatial policy for flood mitigation: A case study in Kampala, Uganda. Comput. Environ. Urban Syst. 2017, 65, 53–65. [Google Scholar] [CrossRef]
- Pelacani, S.; Märker, M.; Rodolfi, G. Simulation of soil erosion and deposition in a changing land use: A modelling approach to implement the support practice factor. Geomorphology 2008, 99, 329–340. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, Y.D.; Xu, C.Y.; Chen, X.; Chen, X.; Singh, V.P. Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. J. Hydrol. 2007, 336, 316–333. [Google Scholar] [CrossRef]
- Smith, H.J. Application of empirical soil loss models in southern Africa: A review. S. Afr. J. Plant Soil 1999, 16, 158–163. [Google Scholar] [CrossRef]
- Nam, P.; YANG, D.; KANAE, S.; OKI, T.; MUSIAKE, K. Global Soil Loss Estimate Using RUSLE Model: The Use of Global Spatial Datasets on Estimating Erosive Parameters. Geoinformatics 2003, 14, 49–53. [Google Scholar] [CrossRef]
- Alexandridis, T.K.; Sotiropoulou, A.M.; Bilas, G.; Karapetsas, N.; Silleos, N.G. The Effects of Seasonality in Estimating the C-Factor of Soil Erosion Studies. L. Degrad. Dev. 2015, 26, 596–603. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Panagos, P.; Borrelli, P.; Meusburger, K. A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences 2015, 5, 117–126. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Lim, K.J.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Alewell, C.; Lugato, E.; Montanarella, L. Estimating the soil erosion cover-management factor at the European scale. Land use policy 2015, 48, 38–50. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; USDA, Science and Education Administration: Washington, DC, USA, 1978; ISBN 19786726437.
- Mendoza-ponce, A.; Corona-núñez, R.; Kraxner, F.; Leduc, S.; Patrizio, P. Identifying e ff ects of land use cover changes and climate change on terrestrial ecosystems and carbon stocks in Mexico. Glob. Environ. Chang. 2018, 53, 12–23. [Google Scholar] [CrossRef]
- Alphan, H.; Derse, M.A. Change detection in Southern Turkey using normalized difference vegetation index (NDVI). J. Environ. Eng. Landsc. Manag. 2013, 21, 12–18. [Google Scholar] [CrossRef]
- Hunink, J.E.; Niadas, I.A.; Antonaropoulos, P.; Droogers, P.; de Vente, J. Targeting of intervention areas to reduce reservoir sedimentation in the Tana catchment (Kenya) using SWAT. Hydrol. Sci. J. 2013, 58, 600–614. [Google Scholar] [CrossRef]
- Willy, D.K.; Holm-Müller, K. Social influence and collective action effects on farm level soil conservation effort in rural Kenya. Ecol. Econ. 2013, 90, 94–103. [Google Scholar] [CrossRef]
- Saiz, G.; Wandera, F.M.; Pelster, D.E.; Ngetich, W.; Okalebo, J.R.; Rufino, M.C.; Butterbach-Bahl, K. Long-term assessment of soil and water conservation measures (Fanya-juu terraces) on soil organic matter in South Eastern Kenya. Geoderma 2016, 274, 1–9. [Google Scholar] [CrossRef]
- Were, K.O.; Dick, T.B.; Singh, B.R. Remotely sensing the spatial and temporal land cover changes in Eastern Mau forest reserve and Lake Nakuru drainage basin, Kenya. Appl. Geogr. 2013, 41, 75–86. [Google Scholar] [CrossRef]
- Elhag, M.; Kojchevska, T.; Boteva, S. EPM for Soil Loss Estimation in Different Geomorphologic Conditions and Data Conversion by Using GIS. IOP Conf. Ser. Earth Environ. Sci. 2019, 221. [Google Scholar] [CrossRef]
- Bahrawi, J.A.; Elhag, M.; Aldhebiani, A.Y.; Galal, H.K.; Hegazy, A.K.; Alghailani, E. Soil Erosion Estimation Using Remote Sensing Techniques in Wadi Yalamlam Basin, Saudi Arabia. Adv. Mater. Sci. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, S.; Bai, X.; Li, Y.; Tian, Y.; Li, Y.; Wu, L.; Luo, G. Soil erosion evolution and spatial correlation analysis in a typical karst geomorphology using RUSLE with GIS. Solid Earth 2017, 8, 721–736. [Google Scholar] [CrossRef]
- Taye, G.; Vanmaercke, M.; Poesen, J.; Van Wesemael, B.; Tesfaye, S.; Teka, D.; Nyssen, J.; Deckers, J.; Haregeweyn, N. Determining RUSLE P- and C-factors for stone bunds and trenches in rangeland and cropland, North Ethiopia. L. Degrad. Dev. 2018, 29, 812–824. [Google Scholar] [CrossRef]
- Morán-tejeda, E.; Zabalza, J.; Rahman, K.; Gago-silva, A.; López-moreno, J.I.; Vicente-serrano, S.; Lehmann, A.; Tague, C.L.; Beniston, M. Hydrological impacts of climate and land-use changes in a mountain watershed: Uncertainty estimation based on model comparison. ECOHydrology 2014. [Google Scholar] [CrossRef]
- Wang, L. An Assessment of the Impact of Urbanization on Soil Erosion in Inner Mongolia. Int. J. Environ. Res. Public Health 2018, 15, 550. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, J.; Yang, Q.; Baartman, J.E.; Gai, L.; Yang, X.; Li, S.; Yu, J.; Ritsema, C.J.; Geissen, V. An Improved Method for Calculating Slope Length (Λ) and the Ls Parameters of the Revised Universal Soil Loss Equation for Large Watersheds. Geoderma 2017, 308, 36–45. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Karamage, F.; Zhang, C.; Liu, T.; Maganda, A.; Isabwe, A. Soil erosion risk assessment in Uganda. Forests 2017, 8, 52. [Google Scholar] [CrossRef]
- Benchettouh, A.; Kouri, L.; Jebari, S. Spatial estimation of soil erosion risk using RUSLE/GIS techniques and practices conservation suggested for reducing soil erosion in Wadi Mina watershed (northwest, Algeria). Arab. J. Geosci. 2017, 10. [Google Scholar] [CrossRef]
- Fantappiè, M.; Priori, S.; Costantini, E.A.C. Soil erosion risk, Sicilian Region (1:250,000 scale). J. Maps 2015, 2, 323–341. [Google Scholar] [CrossRef]
- Karamage, F.; Shao, H.; Chen, X.; Ndayisaba, F.; Nahayo, L.; Kayiranga, A.; Omifolaji, J.K.; Liu, T.; Zhang, C. Deforestation effects on soil erosion in the Lake Kivu Basin, D.R. Congo-Rwanda. Forests 2016, 7, 281. [Google Scholar] [CrossRef]
- Aiello, A.; Adamo, M.; Canora, F. Remote sensing and GIS to assess soil erosion with RUSLE3D and USPED at river basin scale in southern Italy. Catena 2015, 131, 174–185. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation; USDA-ARS, Southwest Watershed Research Center: Tucson, Arizona, 1996; p. 703.
- Ongoma, V.; Chen, H.; Gao, C.; Nyongesa, A.M.; Polong, F. Future changes in climate extremes over Equatorial East Africa based on CMIP5 multimodel ensemble. Nat. Hazards 2018, 90, 901–920. [Google Scholar] [CrossRef]
- Boillat, S.; Gerber, J.; Oberlack, C.; Zaehringer, J.G.; Speranza, C.I.; Rist, S. Distant Interactions, Power, and Environmental Justice in Protected Area Governance: A Telecoupling Perspective. Sustainability 2018, 10, 3954. [Google Scholar] [CrossRef]
- Coad, L.; Leverington, F.; Knights, K.; Geldmann, J.; Eassom, A.; Kapos, V.; Kingston, N.; De Lima, M.; Zamora, C.; Cuardros, I.; et al. Measuring impact of protected area management interventions: Current and future use of the Global Database of Protected Area Management Effectiveness. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370. [Google Scholar] [CrossRef]
- Recanatesi, F.; Giuliani, C.; Ripa, M.N. Monitoring Mediterranean Oak Decline in a Peri-Urban Protected Area Using the NDVI and Sentinel-2 Images: The Case Study of Castelporziano State Natural Reserve. Sustainability 2018, 10, 3308. [Google Scholar] [CrossRef]
- Rodríguez-rodríguez, D.; Martínez-vega, J.; Echavarría, P. Int J Appl Earth Obs Geoinformation A twenty year GIS-based assessment of environmental sustainability of land use changes in and around protected areas of a fast developing country: Spain. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 169–179. [Google Scholar] [CrossRef]
- Rodrigues, A.S.; Andelman, S.J.; Bakarr, M.I.; Boitani, L.; Brooks, T.M.; Cowling, R.M.; Fishpool, L.D.; Da Fonseca, G.A.; Gaston, K.J.; Hoffmann, M. Effectiveness of the Global Protected Area Network in Representing Species Diversity. Nature 2004, 428, 640–643. [Google Scholar] [CrossRef] [PubMed]
- Meigh, J.R.; McKenzie, A.A.; Sene, K.J. A grid-based approach to water scarcity estimates for Eastern and Southern Africa. Water Resources Manag. 1999, 13, 85–115. [Google Scholar] [CrossRef]
- Moges, D.M.; Bhat, H.G. Integration of geospatial technologies with RUSLE for analysis of land use/cover change impact on soil erosion: Case study in Rib watershed, north-western highland Ethiopia. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- Gelagay, H.S.; Minale, A.S. Soil loss estimation using GIS and Remote sensing techniques: A case of Koga watershed, Northwestern Ethiopia. Int. Soil Water Conserv. Res. 2016, 4, 126–136. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; van der Zanden, E.H.; Poesen, J.; Alewell, C. Modelling the effect of support practices (P-factor) on the reduction of soil erosion by water at European scale. Environ. Sci. Policy 2015, 51, 23–34. [Google Scholar] [CrossRef]
- Ojwang, L.; Rosendo, S.; Mwangi, M.; Celliers, L.; Obura, D.; Muiti, A. Earth ’ s Future Special Section: Assessment of Coastal Governance for Climate Change Adaptation in Kenya Earth ’ s Future. Assess. Coast. Gov. Clim. Chang. Adapt. Kenya Earth’s Futur. 2017, 5, 1119–1132. [Google Scholar]
- Teng, H.; Viscarra Rossel, R.A.; Shi, Z.; Behrens, T.; Chappell, A.; Bui, E. Assimilating satellite imagery and visible-near infrared spectroscopy to model and map soil loss by water erosion in Australia. Environ. Model. Softw. 2016, 77, 156–167. [Google Scholar] [CrossRef]
- Thomas, J.; Joseph, S.; Thrivikramji, K.P. Assessment of soil erosion in a tropical mountain river basin of the southern Western Ghats, India using RUSLE and GIS. Geosci. Front. 2018, 9, 893–906. [Google Scholar] [CrossRef]
- Onyando, J.; Kisoyan, P.; Chemelil, M. Estimation of Potential Soil Erosion for River Perkerra Catchment in Kenya. Water Resources Manag. 2005, 19, 133–143. [Google Scholar] [CrossRef]
- Gaubi, I.; Chaabani, A.; Ben Mammou, A.; Hamza, M.H. A GIS-based soil erosion prediction using the Revised Universal Soil Loss Equation (RUSLE) (Lebna watershed, Cap Bon, Tunisia). Nat. Hazards 2017, 86, 219–239. [Google Scholar] [CrossRef]
- da Cunha, E.R.; Bacani, V.M.; Panachuki, E. Modeling soil erosion using RUSLE and GIS in a watershed occupied by rural settlement in the Brazilian Cerrado. Nat. Hazards 2017, 85, 851–868. [Google Scholar] [CrossRef]
- Van der Knijff, J.M.; Jones, R.J.; Montanarella, L. Soil erosion risk assessment in Italy. Eur. Soil Bur. 2000, EUR 19044, 34. [Google Scholar]
- Naqvi, H.R.; Mallick, J.; Devi, L.M.; Siddiqui, M.A. Multi-temporal annual soil loss risk mapping employing Revised Universal Soil Loss Equation (RUSLE) model in Nun Nadi Watershed, Uttrakhand (India). Arab. J. Geosci. 2013, 6, 4045–4056. [Google Scholar] [CrossRef]
- Soil Property Maps of Africa at 250 m Resolution | ISRIC. Available online: https://www.isric.org/projects/soil-property-maps-africa-250-m-resolution (accessed on 16 April 2020).
- Lal, R. Soil degradation by erosion. L. Degrad. Dev. 2001, 12, 519–539. [Google Scholar] [CrossRef]
- Fenta, A.A.; Tsunekawa, A.; Haregeweyn, N.; Poesen, J.; Tsubo, M.; Borrelli, P.; Panagos, P.; Vanmaercke, M.; Broeckx, J.; Yasuda, H.; et al. Land susceptibility to water and wind erosion risks in the East Africa region. Sci. Total Environ. 2020, 703, 135016. [Google Scholar] [CrossRef] [PubMed]
- Africa Soil Information Service (AfSIS) | ISRIC. Available online: https://www.isric.org/projects/africa-soil-information-service-afsis (accessed on 16 April 2020).
- Schürz, C.; Mehdi, B.; Kiesel, J.; Schulz, K.; Herrnegger, M. A systematic assessment of uncertainties in large scale soil loss estimation from different representations of USLE input factors – A case study for Kenya and Uganda. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–35. [Google Scholar] [CrossRef]
- Garcin, Y.; Schildgen, T.F.; Torres Acosta, V.; Melnick, D.; Guillemoteau, J.; Willenbring, J.; Strecker, M.R. Short-lived increase in erosion during the African Humid Period: Evidence from the northern Kenya Rift. Earth Planet. Sci. Lett. 2017, 459, 58–69. [Google Scholar] [CrossRef]
- Ongwenyi, G.S.; Kithiia, S.M.; Denga, F.O. An overview of soil erosion and sedimentation problems in Kenya. Sediment Probl. Strateg. Monit. Predict. Control 1993, 216–221. [Google Scholar]
- Arsiso, B.K.; Mengistu Tsidu, G.; Stoffberg, G.H.; Tadesse, T. Influence of urbanization-driven land use/cover change on climate: The case of Addis Ababa, Ethiopia. Phys. Chem. Earth 2018, 105, 212–223. [Google Scholar] [CrossRef]
- Hategekimana, Y.; Yu, L.; Nie, Y.; Zhu, J.; Liu, F.; Guo, F. Integration of multi-parametric fuzzy analytic hierarchy process and GIS along the UNESCO World Heritage: A flood hazard index, Mombasa County, Kenya. Nat. Hazards 2018. [Google Scholar] [CrossRef]
- FAO and ITPS Status of the World’s Soil Resources (SWSR)—Main Report, Food and Agriculture organization of the United Nations; FAO and ITPS Status of the World’s Soil Resources (SWSR): Rome, Italy, 2015; ISBN 978-92-5-109004-6.
- Mullan, D.; Favis-mortlock, D.; Fealy, R. Agricultural and Forest Meteorology Addressing key limitations associated with modelling soil erosion under the impacts of future climate change. Agric. For. Meteorol. 2012, 156, 18–30. [Google Scholar] [CrossRef]
- Millward, A.A.; Mersey, J.E. Adapting the RUSLE to model soil erosion potential in a mountainous tropical watershed. Catena 1999, 38, 109–129. [Google Scholar] [CrossRef]
- Tadesse, L.; Suryabhagavan, K.V.; Sridhar, G.; Legesse, G. International Soil and Water Conservation Research Landuse and landcover changes and Soil erosion in Yezat Watershed, North Western Ethiopia. Int. Soil Water Conserv. Res. 2017, 5, 85–94. [Google Scholar] [CrossRef]

| Factor. | Environmental Variables | Resolution | Sources |
|---|---|---|---|
| Terrain | DEM | 30 m | Shuttle Radar Topography Mission (SRTM) |
| Slope | 30 m | Shuttle Radar Topography Mission (SRTM) | |
| Flow accumulation | 30 m | Shuttle Radar Topography Mission (SRTM) | |
| Aspect | 30 m | Shuttle Radar Topography Mission (SRTM) | |
| Topographic | 30 m | Shuttle Radar Topography Mission (SRTM) | |
| Climate | Mean annual rainfall | https://earthengine.google.com/ | |
| Vegetation | NDVI | 30 m | (https://earthexplorer.usgs.gov/) |
| Land | Land use land cover | 20 m | RCMD GeoPortal ( http://geoportal.rcmrd.org/ ) |
| Soil | Soil type | http://www.isric.org/data/afsoilgrids250m) | |
| Sand | http://www.isric.org/data/afsoilgrids250m) | ||
| Silt | http://www.isric.org/data/afsoilgrids250m) | ||
| Clay | http://www.isric.org/data/afsoilgrids250m) | ||
| Organic carbon | http://www.isric.org/data/afsoilgrids250m) |
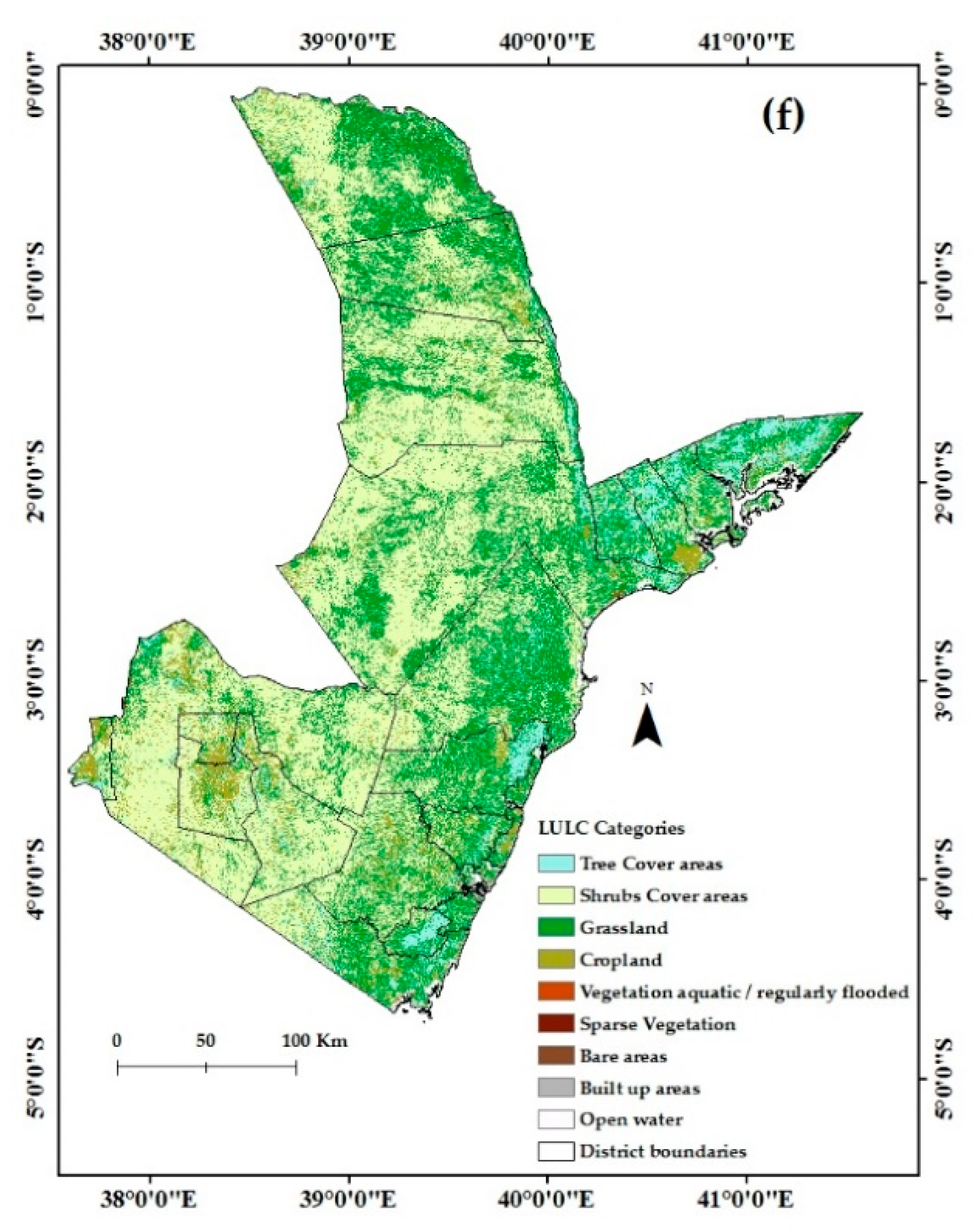
| Land Use Land Cover | Area in Sq. mi | Area (%) | Average Soil Loss (t·ha−1·y−1) |
|---|---|---|---|
| Tree Cover areas | 7.0974 | 5.39 | 6.21 |
| Shrubs Cover areas | 69.27576 | 52.6 | 6.23 |
| Grassland | 46.01648 | 34 | 6.43 |
| Cropland | 8.36488 | 6.35 | 9.14 |
| Aquatic Vegetation | 0.074074 | 0.06 | 5.345 |
| Sparse vegetation | 0.159122 | 0.12 | 6.92 |
| Bare areas | 0.449932 | 0.34 | 7.66 |
| Built up areas | 0.165981 | 0.13 | 17.52 |
| Open Water | 0.097394 | 0.07 | 0 |
| Total | 131.701 | 100 % |
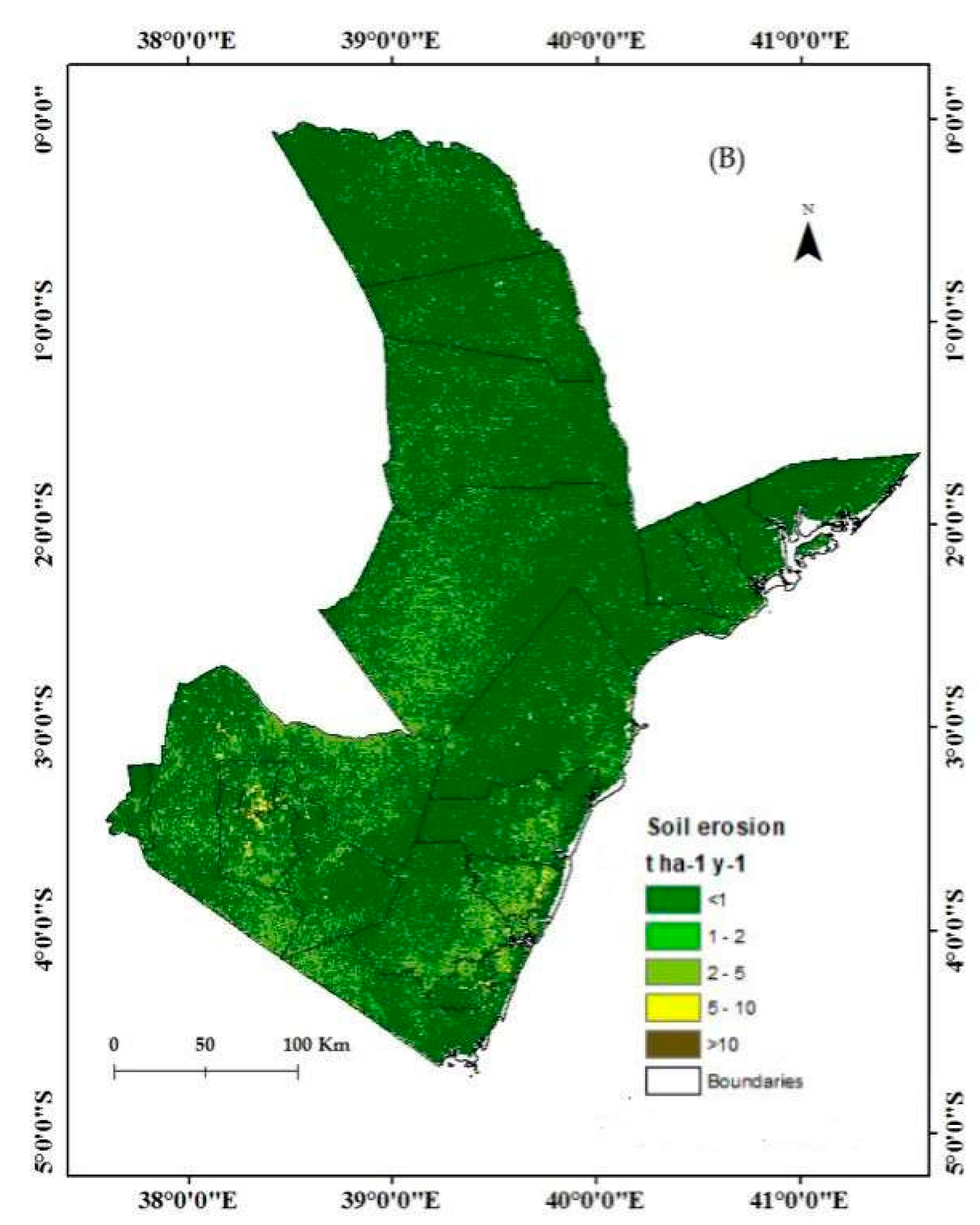
| District Name | Mean Soil Loss (t·ha−1·y−1) |
|---|---|
| Amu | 2.61 |
| Witu | 2.71 |
| Kiunga | 2.75 |
| Madogo | 3.89 |
| Bura | 4.42 |
| Galole | 4.52 |
| Mpeketoni | 4.54 |
| Malindi | 4.87 |
| Taveta | 4.9 |
| Faza | 6.1 |
| Garsen | 6.19 |
| Bahari | 6.54 |
| Ganze | 6.66 |
| Voi | 7.1 |
| Msambweni | 7.62 |
| Kinango | 9.07 |
| Tsavo National Park (E&W) | 9.12 |
| Island | 9.9 |
| Kubo | 14.36 |
| Mwatate | 15.9 |
| Kisauni | 16.23 |
| Matuga | 19.32 |
| Kalolenli | 19.709 |
| Wundanyi | 26.51 |
| Changamwe | 26.7 |
| Likoni | 27.9 |
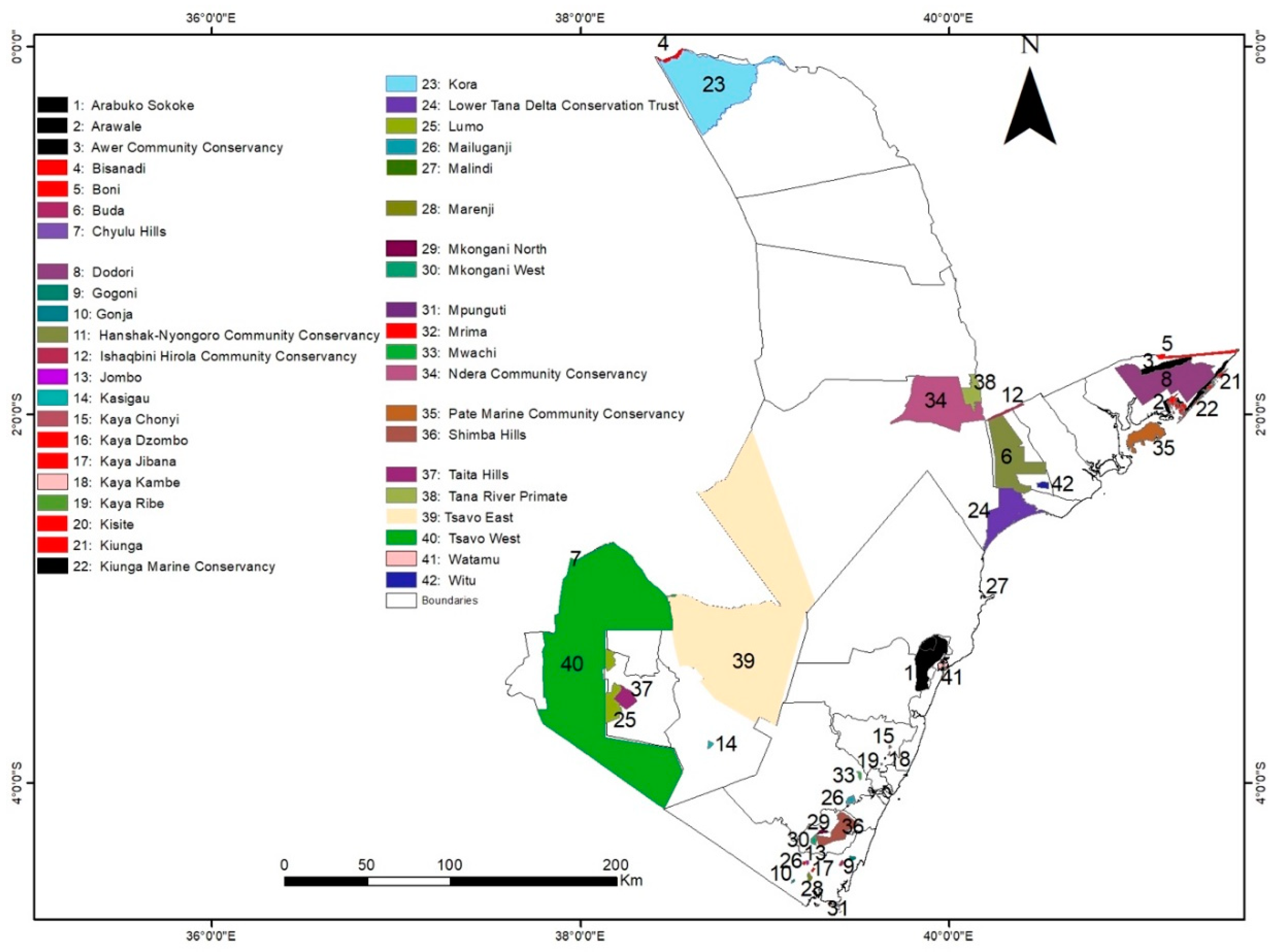
| Name of Protected Area at the Coast | Mean Soil Loss (t·ha−1·y−1) |
|---|---|
| Kaya Dzombo | 0.13 |
| Witu | 0.31 |
| Kaya Ribe | 0.42 |
| Kaya Jibana | 0.49 |
| Mkongani West | 0.53 |
| Buda | 0.8 |
| Kaya Chonyi | 0.94 |
| Kasigau | 1.12 |
| Awer Community Conservancy | 1.32 |
| Marenji | 1.39 |
| Kaya Kambe | 1.67 |
| Kora | 2.47 |
| Hanshak-Nyongoro Community Conservancy | 2.58 |
| Tana River Primate | 2.59 |
| Dodori | 3.24 |
| Arabuko Sokoke | 3.47 |
| Ndera Community Conservancy | 3.54 |
| Mrima | 3.69 |
| Lower Tana Delta Conservation Trust | 4.56 |
| Watamu | 5.05 |
| Jombo | 5.94 |
| Pate Marine Community Conservancy | 6.19 |
| Kiunga Marine Conservancy | 6.48 |
| Gogoni | 7.41 |
| Kiunga | 8.5 |
| Mkongani North | 8.63 |
| Lumo | 8.67 |
| Mwachi | 8.72 |
| Tsavo East | 8.86 |
| Tsavo West | 9.33 |
| Taita Hills | 11.12 |
| Mailuganji | 13.75 |
| Shimba Hills | 15.06 |
| Gonja | 18.52 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hategekimana, Y.; Allam, M.; Meng, Q.; Nie, Y.; Mohamed, E. Quantification of Soil Losses along the Coastal Protected Areas in Kenya. Land 2020, 9, 137. https://doi.org/10.3390/land9050137
Hategekimana Y, Allam M, Meng Q, Nie Y, Mohamed E. Quantification of Soil Losses along the Coastal Protected Areas in Kenya. Land. 2020; 9(5):137. https://doi.org/10.3390/land9050137
Chicago/Turabian StyleHategekimana, Yves, Mona Allam, Qingyan Meng, Yueping Nie, and Elhag Mohamed. 2020. "Quantification of Soil Losses along the Coastal Protected Areas in Kenya" Land 9, no. 5: 137. https://doi.org/10.3390/land9050137
APA StyleHategekimana, Y., Allam, M., Meng, Q., Nie, Y., & Mohamed, E. (2020). Quantification of Soil Losses along the Coastal Protected Areas in Kenya. Land, 9(5), 137. https://doi.org/10.3390/land9050137






