Investigation of the Dominant Factors Influencing the ERA15 Temperature Increments at the Subtropical and Temperate Belts with a Focus over the Eastern Mediterranean Region

Abstract

A stepwise multi regression-based statistics was employed for prioritizing the influence of several factors, anthropogenic and/or natural, on the ERA15 temperature increments. The 5 factors that are defined as predictors are: topography, aerosol index (TOMS-AI), tropospheric vertical velocity along with two anthropogenic factors, population density and land use changes (Land Use Change Index (LUCI) and Normalized Difference Vegetation Index (NDVI) trends). The seismic hazard assessment factor was also chosen as the “dummy variable” for validity. Special focus was given to the land use change factor, which was based on two different data sets; Human Impacts on Terrestrial Ecosystems (HITE) data of historical land use/land cover data and of NDVI trends during 1982 and 1991. The increment analysis updates of temperature, increments analysis update (IAU) (T), the predicted variable, was obtained from the ERA15 (1979–1993) reanalysis. The research consists of both spatial and vertical analyses, as well as the potential synergies of selected variables. The spatial geographic analysis is divided into three categories; (1) coarse region; (2) subregion analysis; and (c) a “small cell” of 4° × 4° analysis covering the global domain. It is shown that the following three factors, topography, TOMS-AI and NDVI, are statistically significant (at the p < 0.05 level) in the relationship with the IAU (T), which means that they are the most effective predictors of IAU (T), especially at the 700-hPa level during March–June. The 850-hPa level presents the weakest contribution to IAU (T), probably due to the contradicting influences of the various variables at this level. It was found that the land use effect, as expressed by the NDVI trends factor, shows a strong decrease with height and is one of the most influential near-surface factors over the East Mediterranean (EM), which explains up to 20% of the temperature increments in January at 700 hPa. Moreover, its influence is significant (p < 0.05) through all of the different stages of the multiple regression runs, a major finding not quantified earlier. The choice of monthly means was found to be not optimal, particularly for the tropospheric vertical velocity, due to the averaging of the synoptic systems within a month.

1. Introduction

The investigation and analyses of the sources for NWP (numerical weather prediction) errors constitute a major component in accurately simulating and predicting the weather and climate conditions.

In recent years, analyses of different factors that are being considered as responsible for NWP errors were comprehensively employed on each specific factor, such as topography [1], aerosols [2,3], land use changes [4] and others. However, there is not any comprehensive investigation of the importance of a set of factors that are known to contribute much to the model errors. It is the primary goal of the present study to perform such a first multi-factor investigation. Moreover, the research combines both physical and natural factors, among them topography, atmospheric aerosols through TOMS-AI, tropospheric vertical velocity, along with two more dominantly anthropogenic factors: the population density and land use (LU) changes. The LU changes here consist of two datasets, the Land Use Change Index (LUCI) [5] and the Normalized Difference Vegetation Index (NDVI) trends [6]. The mid-tropospheric vertical velocity was chosen in order to estimate the potential contribution of the synoptic systems intensity to the NWP errors. Another chosen factor is the seismic hazard assessment factor, which served as a “dummy variable” in this study for validation. It is important to note that in order to partially avoid the complex non-linear interaction in each model, which quickly transports the model errors through the whole model domain within a relatively short time of a few hours, the current research analyzes the reanalysis increments. These increments are based on the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis (ERA15), which is a validated data set assimilated for 15 years, 1979–1993. The ERA15 employs the “first guess” determined by a short-term forecast, together with the observation as the input data for the analysis. The increments analysis update (IAU) is defined as the 6-h “first guess” forecast values subtracted from the analysis values [7]. The 15-year monthly means of temperature increments IAU (T) are employed in the current study. Our focus on the temperature increments at the first stage is due to the fact that temperature is considered as a relatively “stable” and more predictable variable in NWP models and, therefore, reduces the numerical “noise”, which may obstruct the relationships that are being sought [2]. The main goal is to quantify the influence of various factors, physical and anthropogenic, on the NWP errors. Moreover, the calculated ranking of these factors in the context of temperature increments will serve as representative of the NWP errors. It should be noticed that since the present analysis is based on monthly means data rather than daily predictions, the reference to NWP everywhere here is with an emphasis on climate model predictions and less on shorter range weather predictions.

2. Research Area and Data

2.1. Research Area

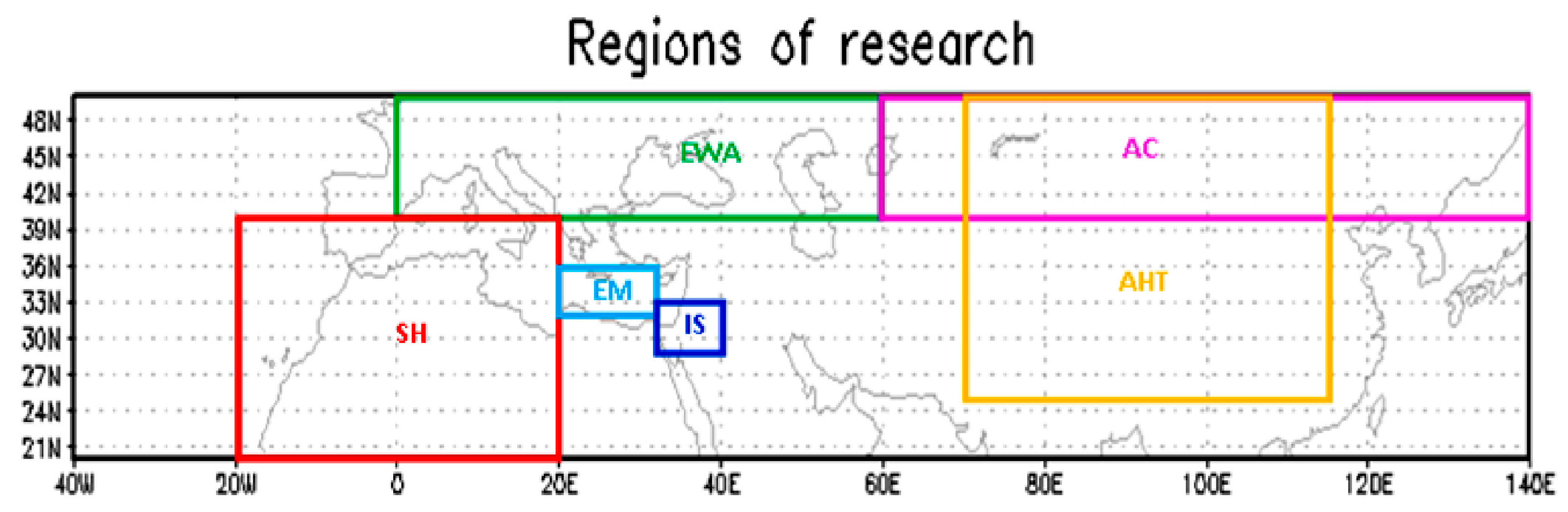
First, a “large-scale” analysis is preformed and then focused over the Eastern Mediterranean (EM) region, with a more detailed study of the land use change variable, which was analyzed as an index (LUCI) and as a trend (NDVI) (Section 2.2). The research consists of both spatial and vertical analyses, as well as the synergy of selected variables in order to investigate the potential contributions of the interactions among these factors. The spatial analysis consists of three categories; (1) full region (in brevity, GLOBal region, GLOB)—an analysis of the full research domain, which encompasses the range of 40°W–140°E longitude and 20°N–50°N latitude. This area consists of Asia, Europe, North Africa, the Mediterranean and the eastern part of the Atlantic Ocean (Figure 1). This GLOB region was chosen, because it contains all of the specific subregions we were interested in, as well as those investigated earlier for specific factors ([2], Eastern Atlantic; [3], Sahara). (2) The subregion analysis (Figure 1)—the division of the full domain into six subregions based on the factor that was estimated to be dominant at the specific subregion. At this stage, the EM region was explored in detail. (3) The “small cell” analysis—a division of the GLOB domain into relatively small cells of 4° × 4°. The vertical analysis investigates the following pressure levels; 1000, 850, 700 and 500 hPa. Further vertical investigation was achieved by employing vertical cross-section analysis with zooming on selected points for the vertical profiles. The third part of the research analyzes the synergies among the factors, which enable one to study potential interactions among the different factors on the temperature increments. The selected factors’ combination effect includes: the (population density/NDVI) trends for enhancing the anthropogenic effect and the (topography/seismic) hazard synergy for enhancing the terrain effect.

2.2. Land Use Change Data

The land use change was estimated by the data of NDVI trends, the ranges being 1982–1991 MAM (March, April and May) and JJA (June, July and August), with 1° × 1° spatial resolution. Angert et al. [6], found that for 1982–1991, the summer (JJA) NDVI trend is significant (r > 0.8) over the large land areas that showed pronounced greening and was associated with warming. The extra tropical spring (MAM) NDVI shows an increasing trend (r = 0.79) in the 1982–1991 time period, in parallel with the spring temperature trend (r = 0.80).The spatial analysis shows spring greening over broad areas in the period 1982–1991. This greening is probably at least partly related to the broad-scale warming that took place for this period over most of the Northern Hemisphere. Similar to the summer trends, the statistical analysis of the spring trends found significant trends (r > 0.8) in the areas that showed pronounced greening or browning. Although the period that was chosen is short for climatic analysis, the main scope is to demonstrate the unique and pioneering research method.

Figure 1. The research area (GLOB, 180° × 30°) and subregions. AC, Asian continental (80° × 10°), AHT; Asian high terrain (45° × 25°); EM, Eastern Mediterranean (12° × 4°); EWA, Europe and West Asia (60° × 10°); IS, Israel (8° × 4°) and the vicinity; SH, Sahara Desert (40° × 20°)*.

Figure 1. The research area (GLOB, 180° × 30°) and subregions. AC, Asian continental (80° × 10°), AHT; Asian high terrain (45° × 25°); EM, Eastern Mediterranean (12° × 4°); EWA, Europe and West Asia (60° × 10°); IS, Israel (8° × 4°) and the vicinity; SH, Sahara Desert (40° × 20°)*.

* The sensitivity to the exact definition of the boundaries of each subdomain was not tested, because most of the subdomains include a very large number of points, and it was assumed to be insensitive to their exact boundary locations.

2.3. ERA15 and the Temperature Increments

In 1994, The European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis (ERA) project had produced 15 years of validated data sets of assimilated data for the period 1979–1993. The data assimilation (DA) scheme of ERA15 makes use of a numerical forecast model to propagate the atmospheric information from data-rich to data-sparse areas [8]. Results from the analysis, following initialization, are consequently used as initial conditions for the next forecast and are repeated in a cyclic fashion every 6 h. Therefore, ERA15 is basically relying on a continuous DA over a long period, which is equivalent to running a Global Circulation Model (GCM) forecast model and relaxing towards the observations and forcing the atmospheric fields at six hourly intervals.

For each variable of the observed data, which is processed by the ECMWF analysis, a comprehensive set of difference information is computed. These include the differences between the initialized analysis based on all observations available and the model’s first guess values. This information, together with all observations, is employed as input for the analysis and is called “analysis feedback” [8]. This process result is the source data for the present study. A further statistic extensively used for monitoring purposes is the set of increments added to the first guess in order to produce the final reanalysis. The analysis increments (INC) are defined as,

INC = AN − FG

(1)

where AN stands for the analysis values and FG are the first-guess forecast values. The FG values are being determined by the GCM, which basically has ignored the land use changes/trends by using a constant value for each grid-point through the years. This update process is on the basis of a 6-h cyclic routine and is called the “incremental analysis update” (IAU) [8].

The current research employs these ERA15 temperature increments. The basic idea of this research is that the temperature increments, IAU (T), may be considered as “model errors”, since they would become zero if the model first-guess was completely correct. The 18 UTC temperature increments were averaged monthly at four pressure levels, 1000, 850, 700 and 500 hPa. Previous studies [2,3,9,10,11], have demonstrated a strong connection between dust and temperature increments at 12 UTC. Therefore, the 18 UTC values were chosen in order to somewhat decrease the well-studied and dominant dust effect on the increments at noon time and, thus, emphasize the effects of the other variables.

2.4. Other Independent Factors

The TOMS Aerosol Index represents a vertically-integrated measure of the aerosols or the dust load [12]. The data of TOMS AI, which is employed in the current study, are monthly means for the period of 1979–1992. The TOMS-AI data were obtained on-line [13]. It should be pointed out that TOMS-AI is only sensitive to absorbing aerosols, such as smoke and dust, not to non-absorbing aerosols, such as industrial pollution.

The gridded population density data was obtained from the Center for International Earth Science Information Network (CIESIN), Columbia University [14], in order to estimate the potential local anthropogenic impacts on atmospheric temperatures. The anthropogenic effect could be of different sources (land use change, urban heat, emissions, etc.), but their incorporation in prediction models is still lacking. The CIESIN gridded population density data was also mentioned in a previous study by Mitchell et al. [15] as a good comparable source for research examining the vulnerability of human and natural systems to present climate variability and future climate change. Population density was also found as a good proxy to urban effects on solar insolation dimming [16,17,18].

Omega is the vertical velocity in pressure coordinates (ω = dp/dt) and can be estimated according to the omega equation. The omega data employed here are monthly means obtained from the atmospheric reanalysis project of NCEP [19].

The omega was chosen as a representative variable for the intensity of the synoptic system. Therefore, it will help in estimating the importance of the synoptic state on the temperature increments. The assumption is that deep synoptic systems, which are being characterized by steeper gradients, may yield larger temperature increments due to the inaccurate forecast of the synoptic state.

The terrain data employed here is the Terrain Base global digital terrain model, which contains a complete matrix of land elevation and ocean depth values for the entire world gridded at 5-minute intervals [20].

The seismic hazard assessment data of The Global Seismic Hazard Assessment Program [21] was chosen to serve as a dummy variable, assumed to have no connection to tropospheric temperature increments, in order to examine the goodness of the multi-regression equation and its ability to simulate and to quantify the real factors contributing to the model errors. In fact, the seismic hazard data was eventually found to be highly correlated with topography and, thus, cannot really serve as a good “dummy variable”. The full factor list is shown in Table 1.

Table 1. The different factors employed in the different regression models. Factors 1–7 serve as predictors (independent), while 8, the IAU (T), serves as the predicted variable (dependent). MAM, March, April and May; JJA, June, July and August.

No.	Factor	Description (units)
1	LUCI	Land Use Change Index (index)
2	NDVI x	Where x is a seasonal average of MAM and JJA (NDVI/day)
3	TOMS	TOMS-AI (index)
4	OMEGA	Vertical-p velocity omega (OMEGA) at 500 hPa (hPa∙d−1)
5	TOPO	Topography (m)
6	POPU	Population density with natural log transformation (person/km2)
7	SEIS	The seismic hazard assessment (%)
8	IAU(T)	Increment analysis update of temperature (K/day)

Table 1. The different factors employed in the different regression models. Factors 1–7 serve as predictors (independent), while 8, the IAU (T), serves as the predicted variable (dependent). MAM, March, April and May; JJA, June, July and August.

No.	Factor	Description (units)
1	LUCI	Land Use Change Index (index)
2	NDVI x	Where x is a seasonal average of MAM and JJA (NDVI/day)
3	TOMS	TOMS-AI (index)
4	OMEGA	Vertical-p velocity omega (OMEGA) at 500 hPa (hPa∙d−1)
5	TOPO	Topography (m)
6	POPU	Population density with natural log transformation (person/km2)
7	SEIS	The seismic hazard assessment (%)
8	IAU(T)	Increment analysis update of temperature (K/day)

3. Main Research Goals

The main goal of the current study is to examine and quantify several potential contributors to the temperature forecast errors in numerical weather prediction (NWP) models. It should be noted that the choice of monthly means, may not be so representative, because of the averaging of several synoptic systems within a month. This point will be later discussed; Also, our goal is to demonstrate a statistical technique of partitioning and quantifying the numerical models temperature potential sources of error into model deficiency components and to estimate the contributions to the model temperature error from each of the factors. In particular, the IAU (T) is employed in order to estimate the potential contribution of land use changes (LUC) to the climatic trends in the past decades.

4. Methodology

A stepwise multi regression-based statistics was employed for prioritizing the influence of the aforementioned selected factors, i.e., anthropogenic and physical, on the ERA15 temperature increments (e.g., Draper and Smith, 1998 [22]). This statistical procedure consists of different stepwise multiple regression runs with varying ensembles of factors, which enables the prioritizing and the evaluation of the contribution of each factor to the temperature increments or “errors” of the model. A weakness of this procedure is the assumption of linear relationships. However, no linearity was assumed when employing the factor separation approach in which synergies among factors were also analyzed (e.g., Section 8 for the EM subregion).

Different Multi-Regression Runs

For creating the ultimate combination of factors, which enters the regression process, and, thus, to enable the optimal model error explanation, different sensitivity runs were done as follows:

(1)

Dummy variable run (the basic run, as shown at Table 2 for the seismic hazard factor)

This run employs the seismic hazard assessment, a parameter that has no apparent relationship with temperature increments. This step will test the goodness of the regression results in the case of negligible or lack of effect of the dummy variable in the regression equation, as expected. Moreover, it can pinpoint a weakness of the regression if this parameter has a major influence on the regression equation by frequently entering the equation. This regression run serves as the basic run of this research, which encompasses all of the factors that are considered important.

Table 2. Summary of multiple regression results of the dummy variable run, the “basic run” for the different research regions (full and subdomains) predicting Incremental Analysis Updates for the month of May (MAY-IAU) (T) (y). +: positive association; –: negative association. The variable abbreviations are described in Table 1. Predictors are given as a regression model equation in order of importance. All coefficients are significant at p < 0.05. All abbreviations are defined in Table 1.

Model + Variables Entered (x1, x2, x3, x4, …, xn)	R2	N	Regression Run	Pressure Level
y = 0.55TOPO + 0.21POPU + 0.08SEIS + 0.02TOMS + 0.01NDVI∙MAM	0.4	22,021	Basic-GLOB	500
y = 0.68TOPO + 0.05SEIS − 0.06NDVI∙MAM + 0.03POPU − 0.02TOMS	0.53	22,021	Basic-GLOB	700
y = 0.37TOPO + 0.29TOMS + 0.11SEIS + 0.04NDVI∙MAM − 0.04OMEGA + 0.03POPU	0.28	22,021	Basic-GLOB	850
y = 0.66TOMS + 0.18NDVI∙MAM +0.09POPU − 0.03OMEGA + 0.02TOPO − 0.02SEIS	0.43	22,021	Basic-GLOB	1000
y = 0.305SEIS − 0.156OMEGA + 0.112POPU + 0.038TOMS + 0.026NDVI∙MAM		22,021	Omitting Topo	500
y = 0.340SEIS − 0.183OMEGA − 0.101POPU − 0.044NDVI∙MAM		22,021	Omitting Topo	700
y = 0.259SEIS + 0.303TOMS − 0.141OMEGA + 0.045NDVI∙MAM − 0.034POPU		22,021	Omitting Topo	850
y = 0.664TOMS + 0.178NDVI∙MAM + 0.087POPU − 0.029OMEGA		22,021	Omitting Topo	1000
y = 0.18TOPO + 0.19TOMS + 0.13OMEGA + 0.07SEIS + 0.06NDVI∙MAM − 0.05POPU	0.19	3381	Basic-AC	500
y = 0.71TOPO − 0.13NDVI∙MAM + 0.19TOMS − 0.12POPU + 0.06 SEIS + 0.07OMEGA	0.51	3381	Basic-AC	700
y = 0.74TOPO + 0.71TOMS + 0.43OMEGA − 0.31POPU + 0.06NDVI∙MAM	0.47	3381	Basic-AC	850
y = −0.39POPU + 0.72TOMS + 0.51OMEGA + 0.08TOPO + 0.03SEIS	0.43	3381	Basic-AC	1000
y = 0.61TOPO + 0.32TOMS + 0.13POPU − 0.06OMEGA + 0.03SEIS	0.33	6681	Basic-AHT	500
y = 0.65TOPO − 0.29POPU + 0.22TOMS − 0.08OMEGA	0.49	6681	Basic-AHT	700
y = −0.50POPU − 0.17TOPO + 0.18OMEGA − 0.14NDVI∙MAM + 0.14TOMS + 0.07SEIS	0.29	6681	Basic-AHT	850
y = 0.37TOMS − 0.28TOPO − 0.19POPU + 0.13OMEGA − 0.10NDVI∙MAM − 0.03SEIS	0.67	6681	Basic-AHT	1000
y = −0.20OMEGA − 0.13 SEIS + 0.11TOPO + 0.01NDVI∙MAM	0.23	2541	Basic-EWA	500
y = −0.16TOPO − 0.02NDVI∙MAM − 0.10OMEGA + 0.09TOMS − 0.02POPU	0.15	2541	Basic-EWA	700
y = 0.73TOPO − 0.26OMEGA + 0.22TOMS − 0.04POPU	0.48	2541	Basic-EWA	850
y = 0.19NDVI∙MAM + 0.76TOMS − 0.13SEIS + 0.20TOPO + 0.07POPU + 0.09OMEGA	0.27	2541	Basic-EWA	1000
y = 0.14POPU − 0.06NDVI∙MAM + 0.06TOMS − 0.08TOPO + 0.14SEIS + 0.04OMEGA	0.12	3321	Basic-SH	500
y = −0.21NDVI∙MAM − 0.06TOMS − 0.06OMEGA + 0.14SEIS	0.14	3321	Basic-SH	700
y = 2.54TOPO + 0.29NDVI∙MAM − 0.32SEIS − 0.08OMEGA	0.7	3321	Basic-SH	850
y = 0.76TOPO + 0.54TOMS + 0.34NDVI∙MAM − 0.29OMEGA + 0.19POPU	0.63	3321	Basic-SH	1000
y = −0.32TOMS − 0.17OMEGA + 0.16NDVI∙MAM	0.52	225	Basic-EM	500
y = −0.63TOMS + 0.05 SEIS	0.51	225	Basic-EM	700
y = −0.33TOMS + 0.12OMEGA + 0.16NDVI∙MAM	0.4	225	Basic-EM	850
y = 1.14TOMS + 0.20SEIS − 0.39OMEGA + 0.33NDVI∙MAM	0.7	225	Basic-EM	1000
y = 0.11SEIS − 0.18TOMS + 0.10OMEGA + 0.22TOPO + 0.06POPU − 0.08NDVI∙MAM	0.53	153	Basic-IS	500
y = 0.16NDVI∙MAM − 0.27TOMS − 0.45TOPO − 0.07OMEGA + 0.10POPU − 0.11SEIS	0.6	153	Basic-IS	700
y = −0.33OMEGA + 0.98TOPO − 0.31TOMS − 0.11SEIS	0.75	153	Basic-IS	850
y = 1.73TOPO + 0.83TOMS − 0.24OMEGA + 0.33SEIS	0.8	153	Basic-IS	1000

Table 2. Summary of multiple regression results of the dummy variable run, the “basic run” for the different research regions (full and subdomains) predicting Incremental Analysis Updates for the month of May (MAY-IAU) (T) (y). +: positive association; –: negative association. The variable abbreviations are described in Table 1. Predictors are given as a regression model equation in order of importance. All coefficients are significant at p < 0.05. All abbreviations are defined in Table 1.

Model + Variables Entered (x1, x2, x3, x4, …, xn)	R2	N	Regression Run	Pressure Level
y = 0.55TOPO + 0.21POPU + 0.08SEIS + 0.02TOMS + 0.01NDVI∙MAM	0.4	22,021	Basic-GLOB	500
y = 0.68TOPO + 0.05SEIS − 0.06NDVI∙MAM + 0.03POPU − 0.02TOMS	0.53	22,021	Basic-GLOB	700
y = 0.37TOPO + 0.29TOMS + 0.11SEIS + 0.04NDVI∙MAM − 0.04OMEGA + 0.03POPU	0.28	22,021	Basic-GLOB	850
y = 0.66TOMS + 0.18NDVI∙MAM +0.09POPU − 0.03OMEGA + 0.02TOPO − 0.02SEIS	0.43	22,021	Basic-GLOB	1000
y = 0.305SEIS − 0.156OMEGA + 0.112POPU + 0.038TOMS + 0.026NDVI∙MAM		22,021	Omitting Topo	500
y = 0.340SEIS − 0.183OMEGA − 0.101POPU − 0.044NDVI∙MAM		22,021	Omitting Topo	700
y = 0.259SEIS + 0.303TOMS − 0.141OMEGA + 0.045NDVI∙MAM − 0.034POPU		22,021	Omitting Topo	850
y = 0.664TOMS + 0.178NDVI∙MAM + 0.087POPU − 0.029OMEGA		22,021	Omitting Topo	1000
y = 0.18TOPO + 0.19TOMS + 0.13OMEGA + 0.07SEIS + 0.06NDVI∙MAM − 0.05POPU	0.19	3381	Basic-AC	500
y = 0.71TOPO − 0.13NDVI∙MAM + 0.19TOMS − 0.12POPU + 0.06 SEIS + 0.07OMEGA	0.51	3381	Basic-AC	700
y = 0.74TOPO + 0.71TOMS + 0.43OMEGA − 0.31POPU + 0.06NDVI∙MAM	0.47	3381	Basic-AC	850
y = −0.39POPU + 0.72TOMS + 0.51OMEGA + 0.08TOPO + 0.03SEIS	0.43	3381	Basic-AC	1000
y = 0.61TOPO + 0.32TOMS + 0.13POPU − 0.06OMEGA + 0.03SEIS	0.33	6681	Basic-AHT	500
y = 0.65TOPO − 0.29POPU + 0.22TOMS − 0.08OMEGA	0.49	6681	Basic-AHT	700
y = −0.50POPU − 0.17TOPO + 0.18OMEGA − 0.14NDVI∙MAM + 0.14TOMS + 0.07SEIS	0.29	6681	Basic-AHT	850
y = 0.37TOMS − 0.28TOPO − 0.19POPU + 0.13OMEGA − 0.10NDVI∙MAM − 0.03SEIS	0.67	6681	Basic-AHT	1000
y = −0.20OMEGA − 0.13 SEIS + 0.11TOPO + 0.01NDVI∙MAM	0.23	2541	Basic-EWA	500
y = −0.16TOPO − 0.02NDVI∙MAM − 0.10OMEGA + 0.09TOMS − 0.02POPU	0.15	2541	Basic-EWA	700
y = 0.73TOPO − 0.26OMEGA + 0.22TOMS − 0.04POPU	0.48	2541	Basic-EWA	850
y = 0.19NDVI∙MAM + 0.76TOMS − 0.13SEIS + 0.20TOPO + 0.07POPU + 0.09OMEGA	0.27	2541	Basic-EWA	1000
y = 0.14POPU − 0.06NDVI∙MAM + 0.06TOMS − 0.08TOPO + 0.14SEIS + 0.04OMEGA	0.12	3321	Basic-SH	500
y = −0.21NDVI∙MAM − 0.06TOMS − 0.06OMEGA + 0.14SEIS	0.14	3321	Basic-SH	700
y = 2.54TOPO + 0.29NDVI∙MAM − 0.32SEIS − 0.08OMEGA	0.7	3321	Basic-SH	850
y = 0.76TOPO + 0.54TOMS + 0.34NDVI∙MAM − 0.29OMEGA + 0.19POPU	0.63	3321	Basic-SH	1000
y = −0.32TOMS − 0.17OMEGA + 0.16NDVI∙MAM	0.52	225	Basic-EM	500
y = −0.63TOMS + 0.05 SEIS	0.51	225	Basic-EM	700
y = −0.33TOMS + 0.12OMEGA + 0.16NDVI∙MAM	0.4	225	Basic-EM	850
y = 1.14TOMS + 0.20SEIS − 0.39OMEGA + 0.33NDVI∙MAM	0.7	225	Basic-EM	1000
y = 0.11SEIS − 0.18TOMS + 0.10OMEGA + 0.22TOPO + 0.06POPU − 0.08NDVI∙MAM	0.53	153	Basic-IS	500
y = 0.16NDVI∙MAM − 0.27TOMS − 0.45TOPO − 0.07OMEGA + 0.10POPU − 0.11SEIS	0.6	153	Basic-IS	700
y = −0.33OMEGA + 0.98TOPO − 0.31TOMS − 0.11SEIS	0.75	153	Basic-IS	850
y = 1.73TOPO + 0.83TOMS − 0.24OMEGA + 0.33SEIS	0.8	153	Basic-IS	1000

(2)

The “Longitude and Latitude run”

Longitude and latitude were also introduced to the current regression run in order to examine the potential effect of the geographic position. The main finding was that moving eastward with longitude in the research area is strongly influenced by the sea-land transition, which has a significant effect on the IAU (T).

(3)

The ”No-Topography run”

The no-topography run removes the influence of one of the most influential factors. This yields the artificial strengthening of the secondary or even less influential factors in the regression, which are highly correlated with the topography, such as the seismic hazard dummy variable. In the no-topography run, the statistical F ratio threshold to enter the regression equation was set to p < 0.05 and the F to remove it set as p > 0.1. The last step allows the entrance of more factors, although less significant, but to enable a better control run. This run has particularly emphasized the high correlation between the topography and the seismic hazard assessment and, hence, demonstrated the important fact that elimination of a strong factor results in the reflection of its influence through a less influential factor, even with weak influence, like the current research’s dummy variable, which has a relation with the strong factor. Similar results were found by Alpert et al. [23] and Alpert and Sholokhman [24] in the analysis of synergic terms when an important factor is omitted.

All of the different regression runs will be employed at the first step only to the coarse region (GLOB) and to the 850 hPa level. This level was chosen as being an intermediate level, which absorbs and is being strongly influenced by both ground and high altitude processes (largely anthropogenic and synoptic). Furthermore, the 850-hPa level can “host” several model errors. In the next step, the optimal run was employed on all levels and subregions. Then, the multi-regression was expanded to the rest of the levels. 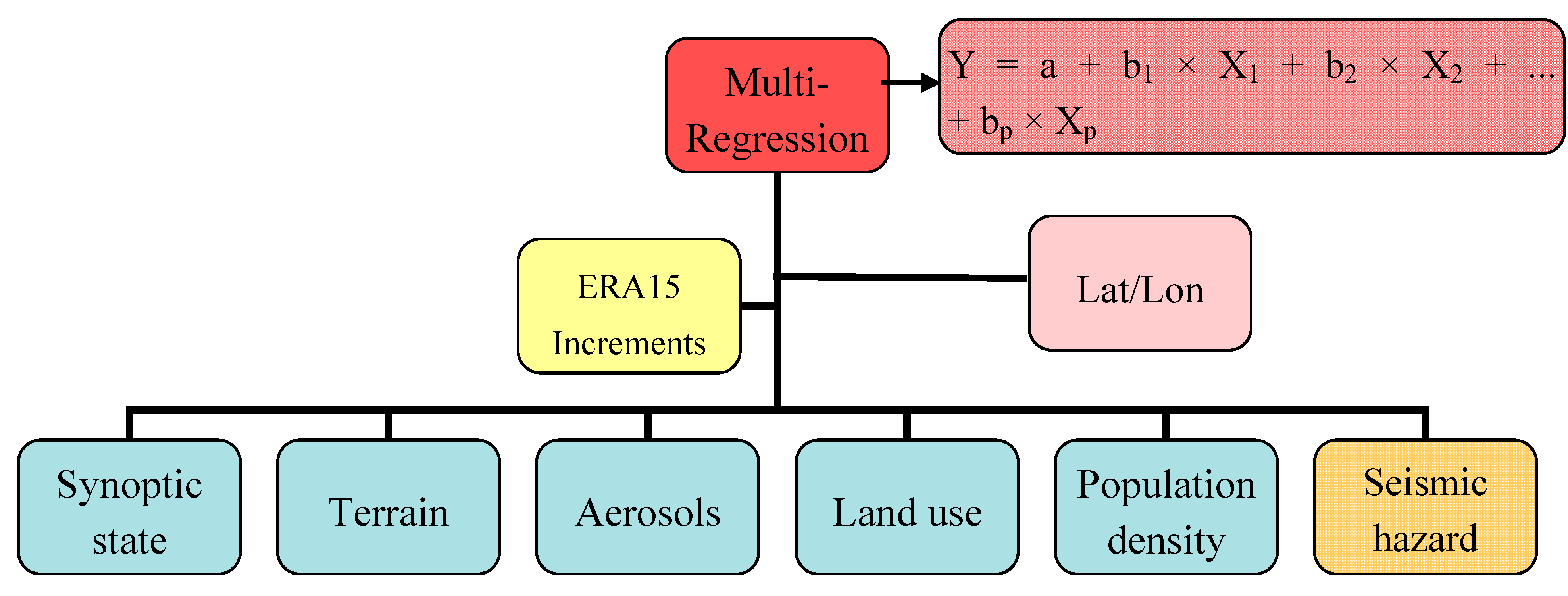Figure 2 presents a flow chart of the multi-regression procedure.

Figure 2. Flow chart of the multi-regression procedure; Y is the dependent variable (ERA15 increments), which can be expressed in terms of a constant (a) and slopes (b) times each of the independent X variables (TOMS, omega, topography, seismic hazard (marked with orange for being the dummy variable), population density and land use data). The constant is also referred to as the intercept, and the slope as the regression coefficient or b coefficient.

Figure 2. Flow chart of the multi-regression procedure; Y is the dependent variable (ERA15 increments), which can be expressed in terms of a constant (a) and slopes (b) times each of the independent X variables (TOMS, omega, topography, seismic hazard (marked with orange for being the dummy variable), population density and land use data). The constant is also referred to as the intercept, and the slope as the regression coefficient or b coefficient.

5. Analysis of the Regression Model Results: Preliminary Results

The results of the spatial analysis of the subregions (as summarized in Table 3) have justified the division of the full domain (GLOB) into subregions according to the analyzed factors and highlight the influence of each factor in each subregion, as well as at each vertical level. The leading factors for each region in the determination of the model errors are as follow (in parenthesis is the number of pixels at each domain);

• GLOB full domain: topography at 700 hPa and TOMS-AI at 1000 hPa (22,021).
• Eastern Mediterranean:

  • East Mediterranean (EM): TOMS-AI and weak effect of NDVI JJA at 1000 hPa (225).
  • Israel (IS): TOMS-AI at 700 hPa and NDVI JJA at 1000 hPa (153).
• Asia Continental (AC): topography at 700 hPa and TOMS-AI at 1000 hPa (3381).
• Asia High Terrain (AHT): topography and TOMS-AI at 700 hPa (6681).
• Europe West Asia (EWA): TOMS-AI at 1000 and 850 hPa, topography at 850 hPa and NDVI in the JJA months at 1000 hPa (2541).
• Sahara (SH): topography at 850 and 1000 hPa (3321).

Following these analyses, the AHT subregion may be considered as an optimal region to explain the IAU (T), due to its demonstration of the highest multiple regression coefficients of determination and also the variable regression coefficients for the participating factors. Similar results were obtained at the subregion “characteristic” analysis and at the “small cell” analysis, which will be explained next.

Figure 3 shows the annual course of the multi-regression values of R² at 500 and 850 hPa for the GLOB (A) and for all the sub-regions; EM (B), IS (C), SH (D), AC (E), AHT (F) and EWA (G).

Table 3. Qualitative summary of the multi-regression results for the different research regions. Bold: absolute dominant variable in the annual course. The yellow marking indicates a negative coefficient value.

Level (hPa)	Annual Range of R2							Factors in Priority (Top 3)
Region	GLOB	AC	AHT	EWA	SH	EM	IS	GLOB	AC	AHT	EWA	SH	EM	IS
1000	0.24 0.42	0.02 0.24	0.08 0.3	0.11 0. 38	0.01 0.21	0.02 0.37	0.01 0.12	TOMS	TOMS	TOMS	TOMS	Topo	TOMS	Topo
								Topo	Omega	Topo	Topo	TOMS	NDVI	TOMS
								Popu	Topo/Popu	Popu	NDVI/Omega	NDVI/Popu	Seis	Omega/NDVI
850	0.19 0.39	0.09 0.24	0.01 0.31	0.12 0.34	0.08 0.38	0.01 0.05	0.01 0.32	Topo	Topo	Topo	Topo	Topo	NDVI	Topo
								TOMS	TOMS	Popu	TOMS	NDVI	TOMS	NDVI
								Omega	Omega	Omega	Omega	Seis		Omega
700	0.27 0.55	0.01 0.45	0.20 0.51	0.01 0.32	0.02 0.42	0.00 0.06	0.01 0.33	Topo	Topo	Topo	Omega	Topo	TOMS	Topo
								TOMS	TOMS	TOMS	Topo	NDVI	NDVI	TOMS
								Seismic	Omega	Omega	TOMS
500	0.29 0.40	0.04 0.26	0.18 0.34	0.01 0.11	0.01 0.11	0.01 0.16	0.01 0.24	Topo	TOMS	Topo	Omega	Omega	TOMS	TOMS
								TOMS/Popu	Omega	Omega	TOMS	TOMS	Omega	Seis
								Omega	Topo/Popu	TOMS	NDVI		NDVI

Table 3. Qualitative summary of the multi-regression results for the different research regions. Bold: absolute dominant variable in the annual course. The yellow marking indicates a negative coefficient value.

Level (hPa)	Annual Range of R2							Factors in Priority (Top 3)
Region	GLOB	AC	AHT	EWA	SH	EM	IS	GLOB	AC	AHT	EWA	SH	EM	IS
1000	0.24 0.42	0.02 0.24	0.08 0.3	0.11 0. 38	0.01 0.21	0.02 0.37	0.01 0.12	TOMS	TOMS	TOMS	TOMS	Topo	TOMS	Topo
								Topo	Omega	Topo	Topo	TOMS	NDVI	TOMS
								Popu	Topo/Popu	Popu	NDVI/Omega	NDVI/Popu	Seis	Omega/NDVI
850	0.19 0.39	0.09 0.24	0.01 0.31	0.12 0.34	0.08 0.38	0.01 0.05	0.01 0.32	Topo	Topo	Topo	Topo	Topo	NDVI	Topo
								TOMS	TOMS	Popu	TOMS	NDVI	TOMS	NDVI
								Omega	Omega	Omega	Omega	Seis		Omega
700	0.27 0.55	0.01 0.45	0.20 0.51	0.01 0.32	0.02 0.42	0.00 0.06	0.01 0.33	Topo	Topo	Topo	Omega	Topo	TOMS	Topo
								TOMS	TOMS	TOMS	Topo	NDVI	NDVI	TOMS
								Seismic	Omega	Omega	TOMS
500	0.29 0.40	0.04 0.26	0.18 0.34	0.01 0.11	0.01 0.11	0.01 0.16	0.01 0.24	Topo	TOMS	Topo	Omega	Omega	TOMS	TOMS
								TOMS/Popu	Omega	Omega	TOMS	TOMS	Omega	Seis
								Omega	Topo/Popu	TOMS	NDVI		NDVI

Figure 3. The annual course of the multi-regression R² values at the different pressure levels at the full research region (A, GLOB) and at each subregion (B–G).

Figure 3. The annual course of the multi-regression R² values at the different pressure levels at the full research region (A, GLOB) and at each subregion (B–G).

6. “Small Cell” Analysis

This stage consists of 898,032 regression runs (18,709 × 12 month × 4 pressure levels), in which each regression has a population of 81 grid points (the result of the division of the research area into 4° × 4° cells, yielding 9 × 9 grid points due to the resolution of 0.5 degrees). Each grid point serves as the middle point of each cell and gets a regression equation. Due to the latter fact, the 3312 GLOB region threshold points were cut off to enable the representation of each grid point as the cell’s center. It was found that 20,543 regression equations are undefined, 36,087 are insignificant and 841,402 equations out of the total 898,032 runs (equivalent to 95.9%) are significant at the p < 0.05 level (R² > 0.000175).

Due to the large amount of regressions runs, the analysis of the current research step consists of the temporal distribution of the coefficient of determination (R²). As previously noted, R² is one of the major statistical parameters to test the quality and success of the multiple regression predictors to predict the dependent variable. Table 4 summarizes the R² monthly variation of the current regression runs at the different pressure levels.

Table 4. Annual categorization of R² values for the 4° by 4°-cell regression run, at the different pressure levels. Each cell consists of 81 grid points (N = 81), and values are significant at the p < 0.05 level.

Pressure Level (hPa)	Jane	February	March	April	May	June	July	August	Septemper	October	November	December
500	L	L	L	L	L	L	L	L	L	L	L	L
700	L	L	VH	VH	VH	VH	H	H	H	H	M	L
850	L	L	M	L	L	VL	VL	VL	VL	L	L	L
1000	L	L	L	L	M	M	L	L	L	L	L	L

Values categorization as follows: very high ( , R²_{4 × 4} value > 0.45; high ( ), R²_{4 × 4} value 0.4–0.45; moderate ( ), R²_{4 × 4} value 0.35–0.4; low ( ), R²_{4 × 4} value 0.15–0.3; very low ( )—R²_{4 × 4} value < 0.15.

Table 4. Annual categorization of R² values for the 4° by 4°-cell regression run, at the different pressure levels. Each cell consists of 81 grid points (N = 81), and values are significant at the p < 0.05 level.

Pressure Level (hPa)	Jane	February	March	April	May	June	July	August	Septemper	October	November	December
500	L	L	L	L	L	L	L	L	L	L	L	L
700	L	L	VH	VH	VH	VH	H	H	H	H	M	L
850	L	L	M	L	L	VL	VL	VL	VL	L	L	L
1000	L	L	L	L	M	M	L	L	L	L	L	L

Values categorization as follows: very high ( , R²_{4 × 4} value > 0.45; high ( ), R²_{4 × 4} value 0.4–0.45; moderate ( ), R²_{4 × 4} value 0.35–0.4; low ( ), R²_{4 × 4} value 0.15–0.3; very low ( )—R²_{4 × 4} value < 0.15.

The main conclusions from our findings follow:

The regression fits best at 700 hPa in March through October, with an average of R²_{4 × 4} > 0.4. High values of R²_{4 × 4} > 0.45 were obtained for spring months (March–June).

The 850-hPa level exhibits the worst regression fit with R²_{4 × 4} < 0.15, which represent very low values in the summer months (June–September). The rest of the months represent low values, except March, with moderate values (0.35 < R²_{4 × 4} < 0.4).

These results are supported by our earlier studies, which emphasized the important role of the 700-hPa level in explaining temperature increments, on the one hand, and the 850 hPa as the less important level. In general, the 850-hPa level is considered as a “noisy” level. The reason for that could be the effects that are both from above (upper-troposphere) and from below, i.e., the turbulent planetary boundary layer, since the 850-hPa level is often inside or near the top of the planetary boundary layer.

7. Analyzing the Spatial Distribution of the Multi-Regression Coefficients of the Different Variables

7.1. Spatial “Small Cell” Analysis

• The combination of the R²_{4 × 4} and regression coefficients of the different factors at 700 hPa during March–June demonstrates the importance of the NDVI trends and the seismic hazard assessment factor. The latter variable shows up in spite of being chosen as the “dummy variable”, probably due to its close relation with topography.
• The following regions have demonstrated the best multiple regression correlations to explain the IAU (T); the Atlas Mountains (especially the eastern slope), the Sahara Desert (Ahaggar Mountains), the Nile Valley and Delta, the Euphrates Valley, the Persian Gulf coast of Saudi Arabia, the Aral Sea and its vicinity and the BoHai Bay vicinity (West of Beijing). This fact is especially true at 700 hPa for the period of March–June, as noted earlier (Figure 4).

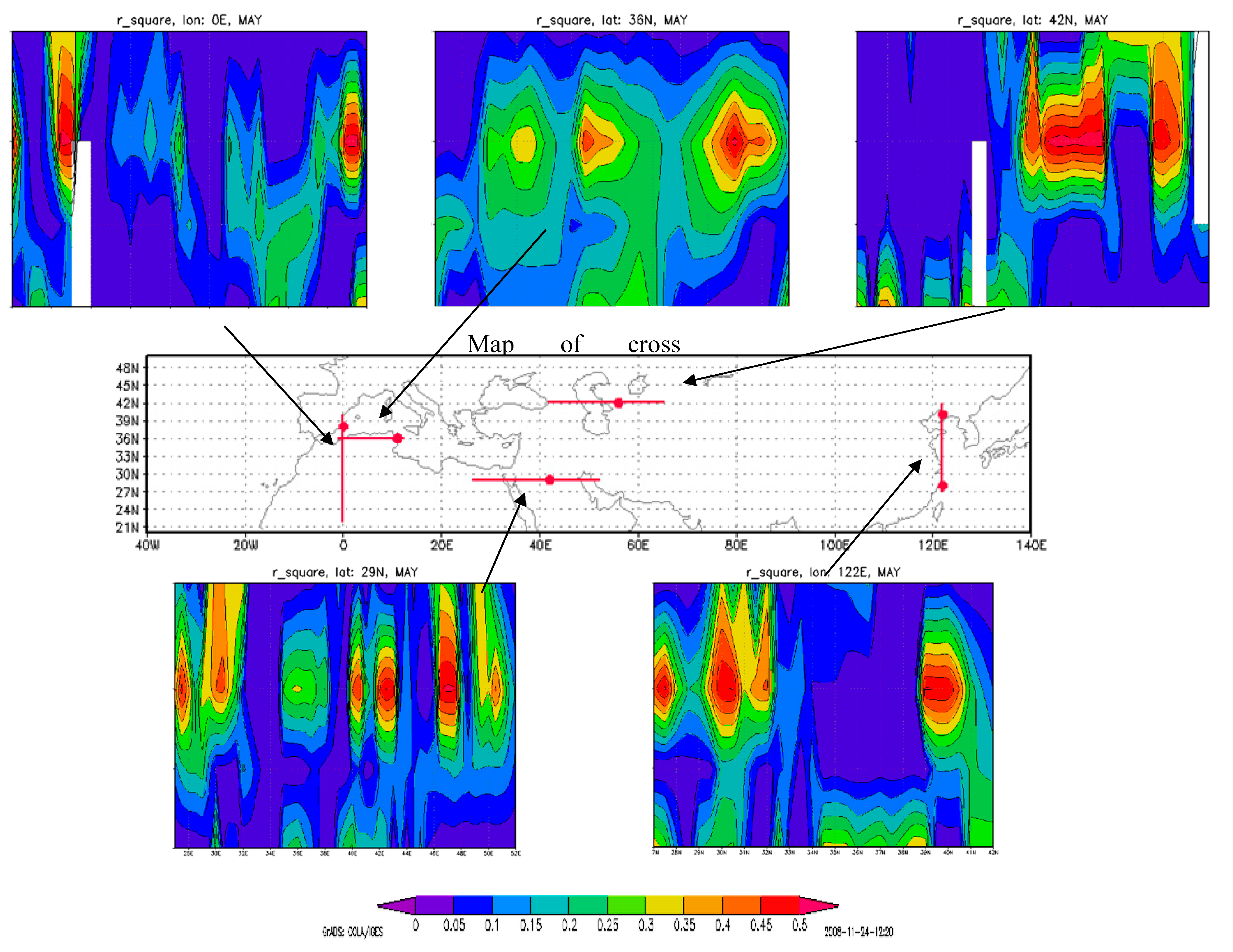
Figure 4. Map of zonal and meridional vertical cross-sections of R²_{4 × 4} values with zooming on May. All values are significant at the p < 0.05 level. Missing values (white spots) represent R²_{4 × 4} values that are insignificant.

Figure 4. Map of zonal and meridional vertical cross-sections of R²_{4 × 4} values with zooming on May. All values are significant at the p < 0.05 level. Missing values (white spots) represent R²_{4 × 4} values that are insignificant.

7.2. Vertical Analysis of Layers and Factors

The vertical analysis consists of subregions and “small cell” analyses, as well as cross-sections and some specific points. The main findings are;

• The dominant level in explaining the IAU (T) at each step of the analyses is 700 hPa. The “small cell” analysis strengthens this finding by identifying the period of months with the highest explanation of IAU (T), which is March to June. The important role of the 700-hPa level in explaining the IAU (T) is probably due to the fact that this level represents both upper atmospheric processes and is still being affected by land-atmospheric interaction processes, avoiding the larger “noise” of these influences typical for the 850 hPa. Hence, the 700-hPa level seems to “filter” the noise from the boundary-layer, as compared to 850 hPa.
• The 1000-hPa level is second in contributing to the IAU (T) (Table 5) The 850-hPa level demonstrated the weakest relation and contribution to the temperature increments.
• The 700-hPa level demonstrates the best explanation for the ERA15 temperature increments in the “small cell” analysis. The vertical cross-section (Figure 4) also supports this result.
• The topography coefficients are highest at 850 hPa and 700 hPa, which fit the high terrain of the region. These levels are the most favorable in representing the topography factor in the regression equations due to the averaged terrain height, which often reaches their altitudes.
• As expected, the TOMS-AI coefficients tend to show a decrease with height, although the starting point in the vertical varies; at most points, it starts at the lowest level of 1000 hPa. The coefficients occupy all pressure levels that were studied, mainly 1000 and 850 hPa, but also can reach up the 500 hPa. It also depends on the distance from the aerosols’ sources.
• The vertical profiles for the population density multiple regression coefficients show no specific trend with height. Although it was expected to have its maximum near the ground level, the stronger factors, such as TOMS-AI and “NDVI trends”, which have also a close relation to the ground level, become dominant in the model errors. It is noticeable, however, that the highest pressure level being reached by the population density coefficients is strongly related to the respective population density in the region. In other words, the highest population density regions do show the strongest vertical influence on temperature increments.
• The “NDVI trends” factor is present at each of the profile points and demonstrates, as expected, a clear dependency with height, i.e., the coefficients’ values decrease with height. The NDVI factor is best represented at 1000 and 850 hPa, but can be found also at the higher levels of 700 and 500 hPa.
• The omega 500 factor vertical analysis has no clear trend in the vertical direction. There are vertical changes at different geographic locations. For instance, the marine vicinity is characterized by significant coefficients of omega 500 at the lower levels of the atmosphere, while at continental locations, this factor enters at higher levels. The latter finding can be attributed to the interaction of the synoptic state with sea-land breeze, which is dominant in coastal regions and, due to its “small scale” or local effect, is not being represented well by the model resolution. Moreover, due to a lack of a clear trend in its influence on the IAU (T), it seems that the omega 500 factor fails to represent the synoptic state well. Perhaps this is due to the fact that monthly averages are smoothing the daily time scale, which is important for synoptic systems.
• The seismic hazard assessment regression coefficients decrease with height at points where the coefficients show a clear vertical structure. Their entrance into the regression equations is quite compatible with the spatial distribution of the factor itself.

Table 5. The parameter (or factor) prioritization for the GLOB and for each subdomain. The colors represent the three dominant parameters: gold, the most influential parameter; silver, the second; bronze, the third. The months in which these effects are taking place are in brackets.

	Area	GLOB	AC	AHT	EWA	SH	EM	IS
Level (hPa)
500
700		TOPO	TOPO (4–9)	TOPO (11–5),		TOPO		TOMS-AI (4)
				* TOMS-AI (11–3)
850					* TOMS-AI (12–3)	TOPO		NDVI MAM
					TOPO (4–9)	NDVI MAM (4)
1000		TOMS-AI (5–10)	TOMS-AI (5–9)		TOMS-AI (3–6)		TOMS-AI (4–5,11)
					NDVI JJA (5–9)		* NDVI JJA (4–5,11)

Variables denoted with a star (*) demonstrate an inverse proportion with the increments (i.e., the negative sign of the coefficient).

Table 5. The parameter (or factor) prioritization for the GLOB and for each subdomain. The colors represent the three dominant parameters: gold, the most influential parameter; silver, the second; bronze, the third. The months in which these effects are taking place are in brackets.

	Area	GLOB	AC	AHT	EWA	SH	EM	IS
Level (hPa)
500
700		TOPO	TOPO (4–9)	TOPO (11–5),		TOPO		TOMS-AI (4)
				* TOMS-AI (11–3)
850					* TOMS-AI (12–3)	TOPO		NDVI MAM
					TOPO (4–9)	NDVI MAM (4)
1000		TOMS-AI (5–10)	TOMS-AI (5–9)		TOMS-AI (3–6)		TOMS-AI (4–5,11)
					NDVI JJA (5–9)		* NDVI JJA (4–5,11)

Variables denoted with a star (*) demonstrate an inverse proportion with the increments (i.e., the negative sign of the coefficient).

8. Factors Analysis: Focusing on the Eastern Mediterranean Region

A major goal of the present research is to perform the quantification and prioritization of factors, especially that of the land use effect on the EM region, as they influence “model errors”. The full region of research (GLOB) approximately centers the EM region, while in the progress of the research of the main area was divided into six subregions that represent different climatic areas and potentially different dominant climatic factors. Two sub-regions out of the six are representing and characterizing the EM region. The two subregions that are being identified with the EM region are: the EM subregion (20° E–32° E; 32° N–36° N), which encompasses the middle part of the EM Sea (Figure 1), mainly a maritime region with only the island of Crete; and the Israel and vicinity (IS) subregion. The IS subregion (32° E–40° E; 29° N–33° N) encompasses Israel, Northern Sinai and Jordan. The IS region represents a complex area of different climatic definitions, from sea-land interactions, through complex topography and an inland desert.

This study discovered that the NDVI trends, as a representative factor of land use change, has a significant (p < 0.05) and large impact on temperature increments, generally and especially over the EM region (Figure 3B). While the EM demonstrates a bias and, therefore, not a clear effect of the NDVI trends on IAU (T), the IS (Figure 3C) exhibits a high fraction of explanation up to 20% of the IAU (T) originating from the NDVI trends. This finding is in line with the hypotheses of earlier studies, such as Otterman et al. [25], Ben-Gai et al. [26], De Ridder and Gallee [27] and Perlin and Alpert [4], who have suggested a strong link between land use changes in the EM region and rainfall regime through the enhancement of thermal convection and induced rainfall.

The EM subregion demonstrates no preference to the synergy effect in the multiple regression process.

9. Conclusions

The main results of this study is that the following three factors, topography, TOMS-AI and NDVI, are statistically significant (at the p < 0.05 level) in their relationship with the IAU (T). That means that these three factors are the most effective IAU (T) predictors, especially at the 700-hPa altitude during March–June. In contrast, the 850-hPa level presents the weakest contribution to IAU (T), due to the contradicting influences of the various variables at this level, which may have been canceling each other out. However, this should prompt future research.

Validation determined that the various multiple regression runs at the spatial subregion analysis had succeeded to prioritize and predict the key factors that determined the division of the full domain (GLOB) into subregions. The land use as expressed by the NDVI trends shows, as expected, a very clear decrease with height and is one of the most influential factors over the EM region. NDVI trends explain up to 20% of the IAU (T) in the IS subregion in January at 700 hPa. Moreover, the effect of land use change influence is significant through all stages and all combinations of the different multiple regression runs at the level of p < 0.05. This is a major finding that was conjectured, but not quantified, earlier.

In contrast to the NDVI trend factor, the calculated LUCI data, which consists of historical land use and land cover change data (HITE CD-ROM [5]), had failed to suggest a sufficient explanation of the IAU (T). One reason could be that the LUCI categorization does not enter well into the regression approach.

Apparently, averaged monthly mean values of omega 500 data fail to represent well the synoptic state; therefore, no clear trend of influence on IAU (T) was indicated. It seems that standardization of this dataset would yield a better representation of the synoptic influence on IAU (T).

The analysis presented here is the first to quantify some of the potential sources for “model errors”. Thus, it helps in prioritizing the most important factors that contribute to climate model “errors”. In addition, this study suggests to the NWP community of researchers the areas and topics of major interest in order to improve our current weather and climate models. For instance, considering the conclusions above, a better parameterization of the land use change factor in the models has a high potential to improve the NWP models in general and particularly over the EM region.

This research does not suggest any particular parameterization for the incorporation of any specific factor into the model. However, it serves as basic research for the modelers’ community by pointing to the “right” factor candidates to be inserted or improved in the models’ equations. Additional studies should deal with the optimal parameterization of these factors with respect to the research findings.