A Multidimensional Framework for Quantitative Analysis and Evaluation of Landscape Spatial Structure in Urban Parks: Integrating 3D Point Cloud and Network Analysis
Abstract
1. Introduction
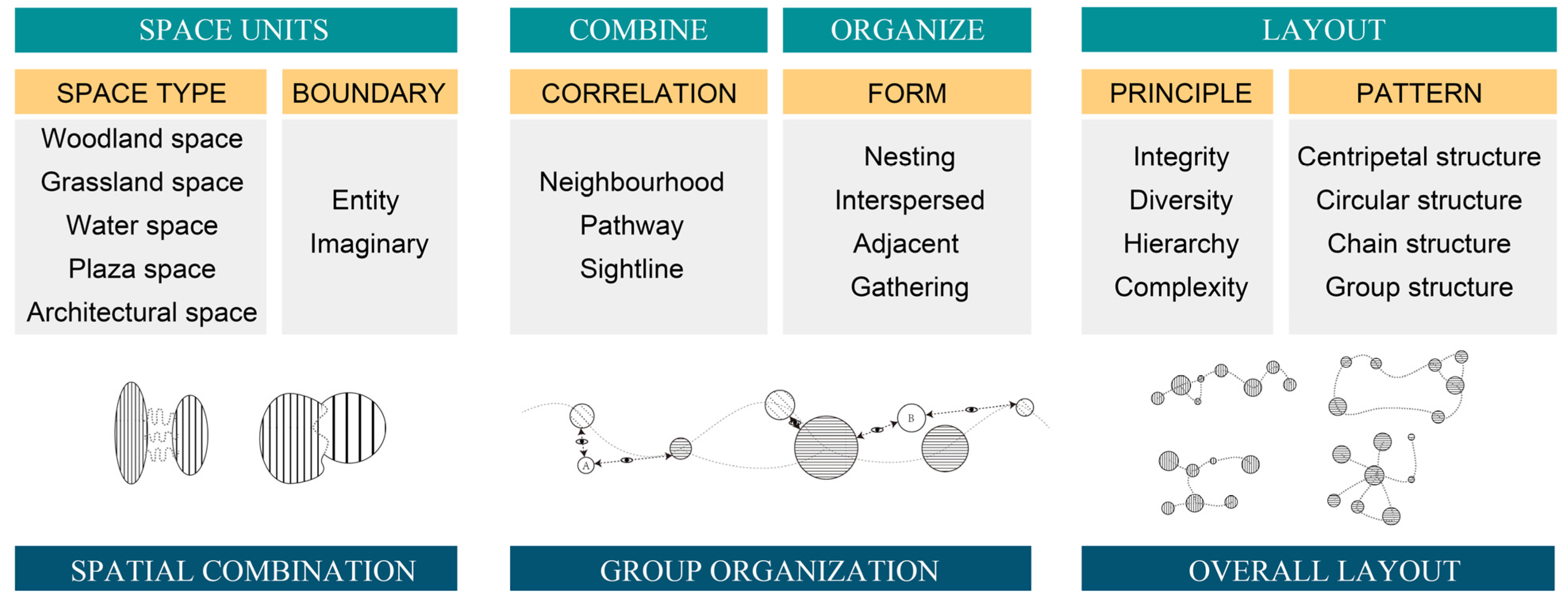
2. Theoretical Framework
- Spatial combination
- 2.
- Group organization
- 3.
- Overall layout
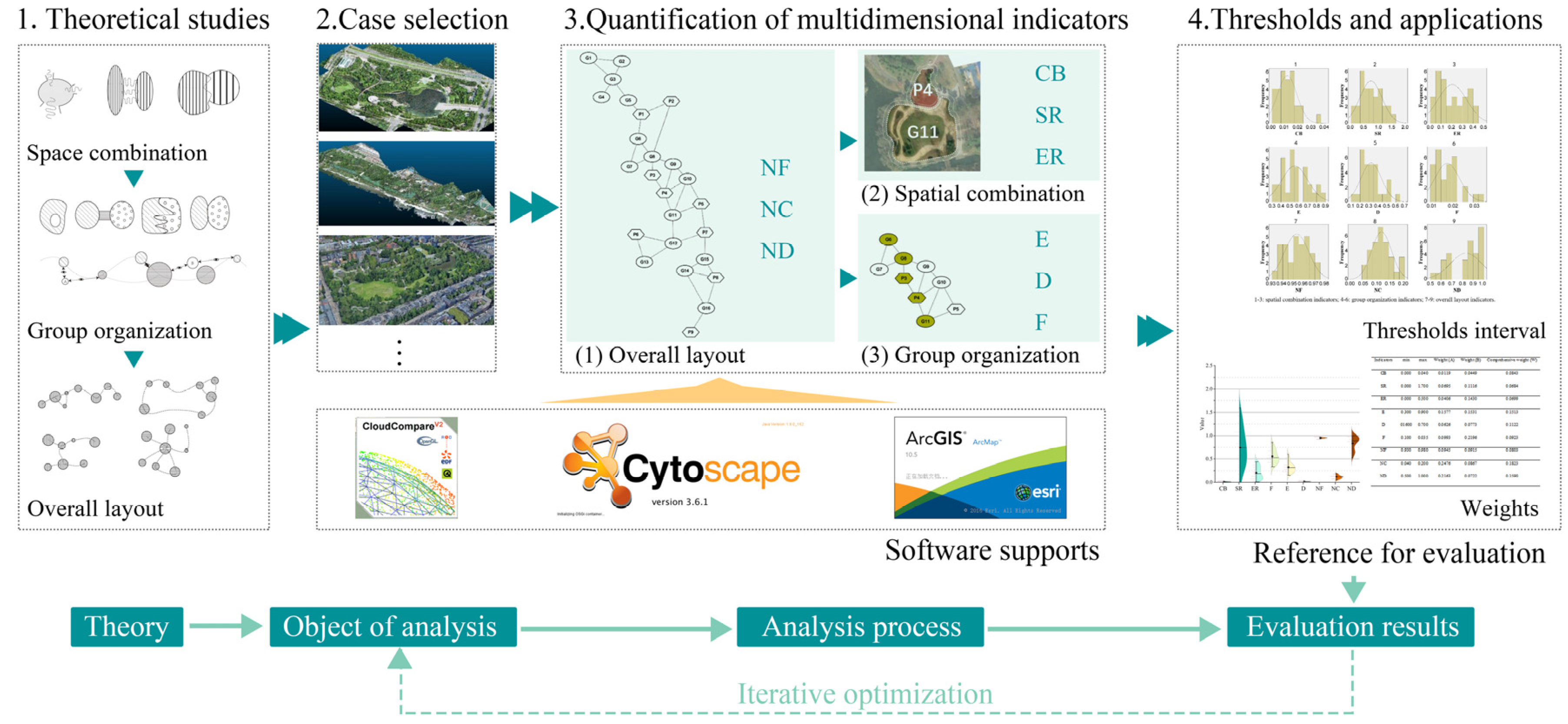
3. Materials and Methods
3.1. Study Area and Data Processing
3.2. Spatial Structure Modelling Process
3.2.1. Extraction of Space Units
3.2.2. Construction of Spatial Unit Connections
3.3. Evaluation Indicators and Weights
3.3.1. Evaluation Indicator System and Quantitative Method
3.3.2. Calculating the Weight of Evaluation Indicators
4. Results
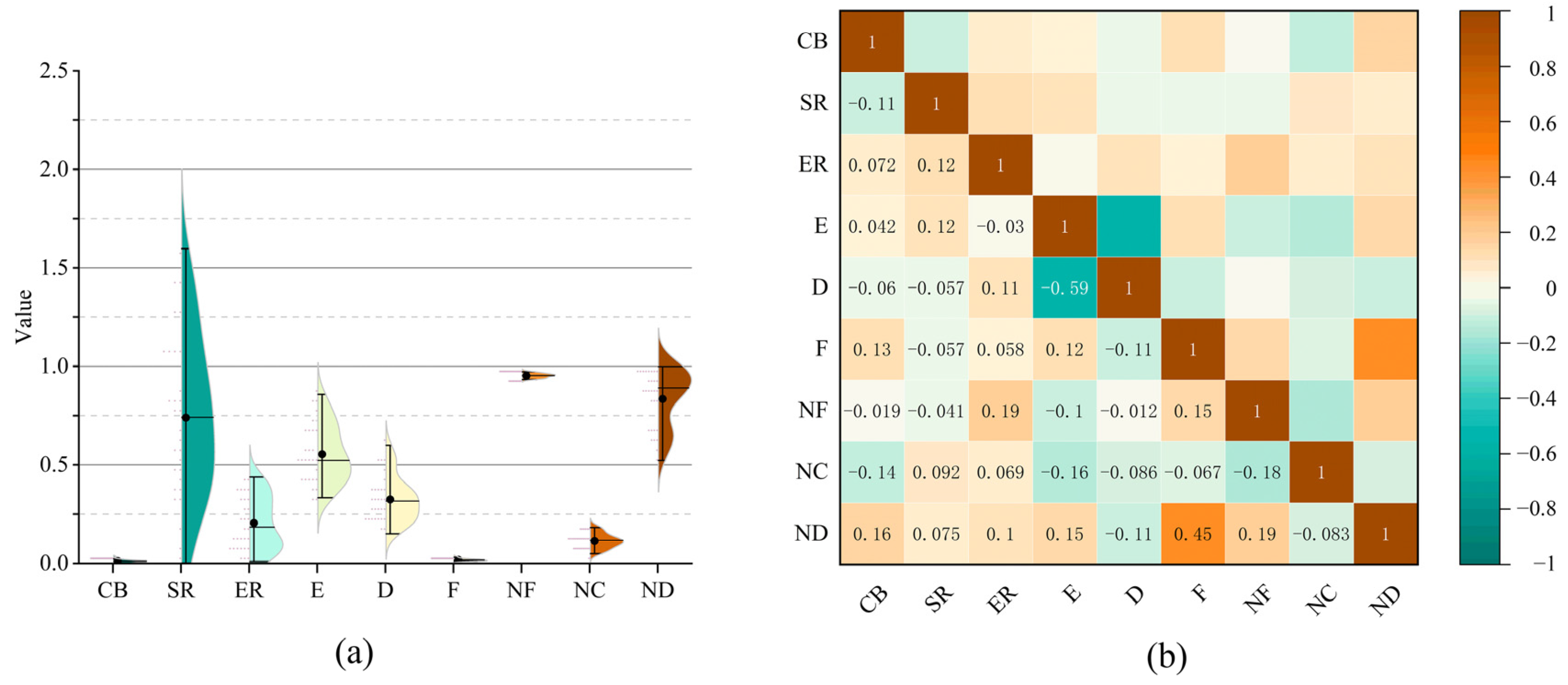
4.1. Indicator Results of Spatial Structure Cases
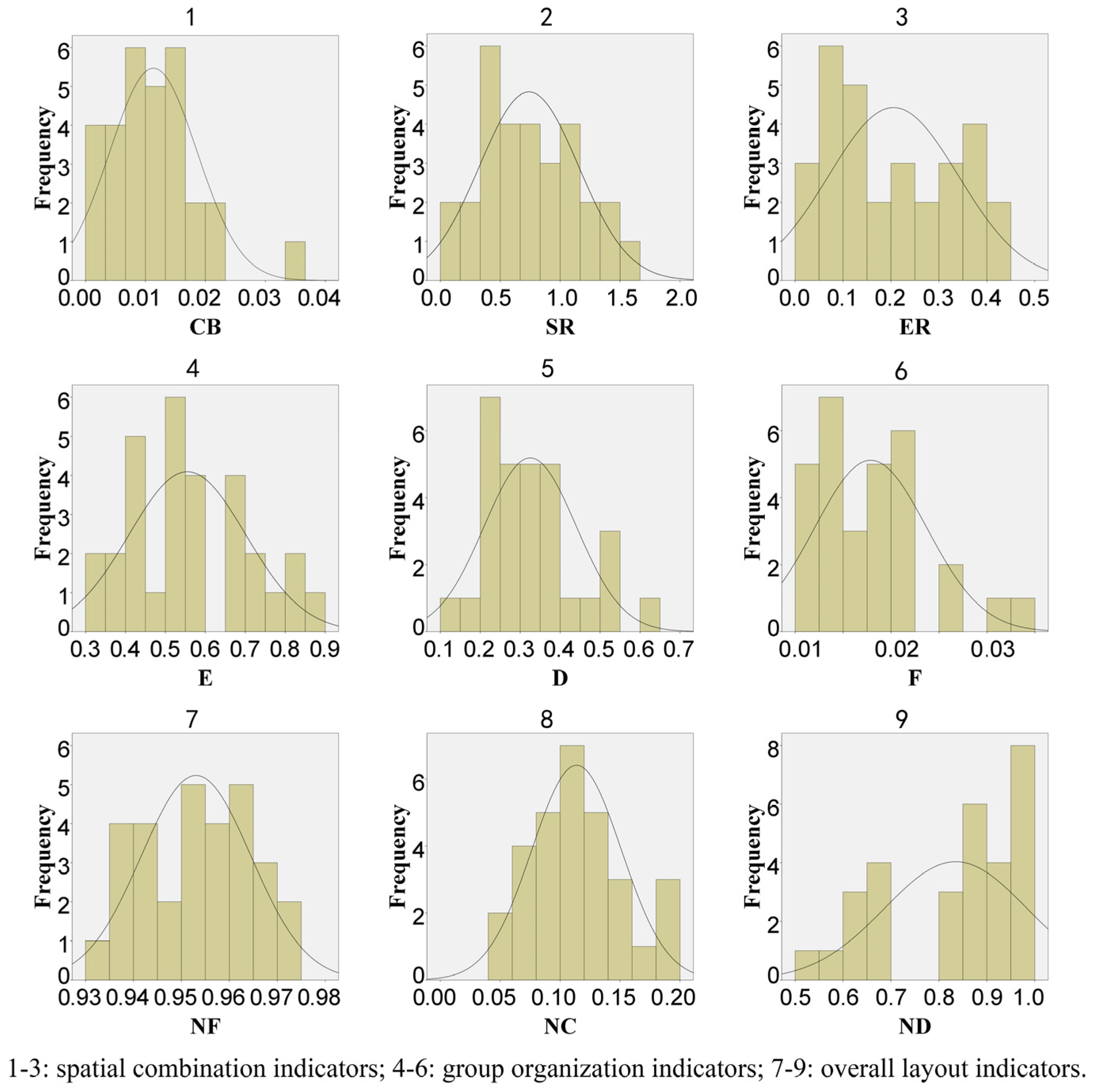
4.2. Analysis and Value Range of Spatial Structure Indicators
4.3. Indicator Weights
4.4. Evaluation Results and Comparison
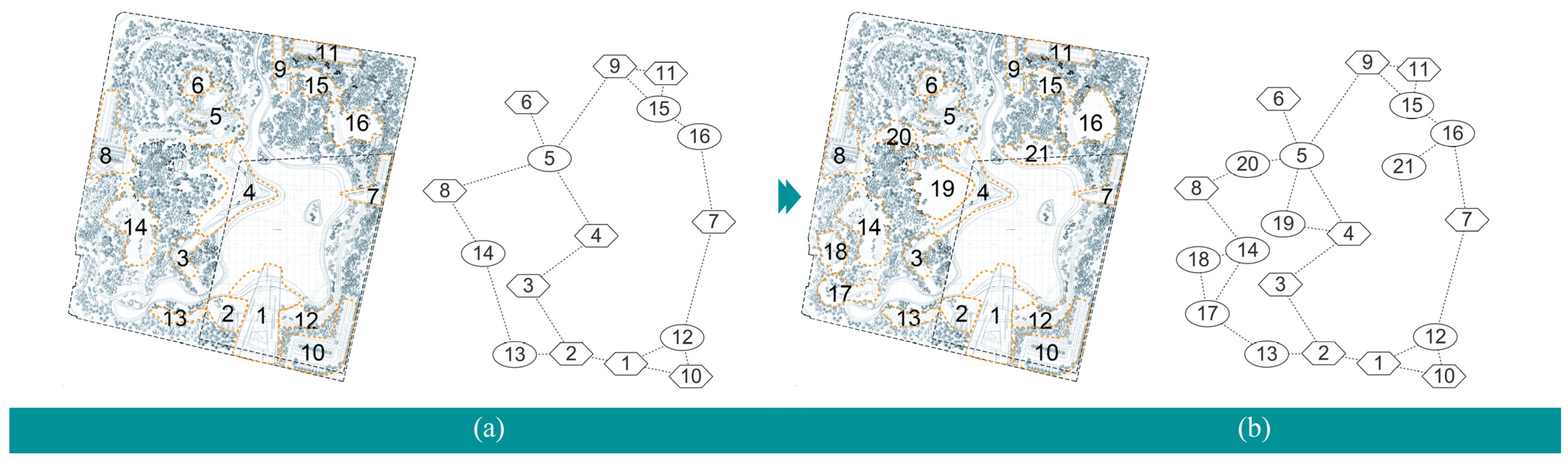
4.5. Design Applications
5. Discussion
5.1. Quantitative Characteristics of Landscape Spatial Structures
5.2. Comparison with Existing Methods
- Quantitative analysis based on three-dimensional data
- Systematicity of the Indicator System
- Evaluation system and reference standards
5.3. Applications
- Green space diagnosis: The research methodology and conclusions support the spatial structure diagnosis of existing green spaces, especially the lack of attractiveness and poor service spaces, by comprehensively evaluating and ranking them, analyzing which are the lower scoring green spaces, and which specific features represented by indicators are problematic, and serve as a focus of optimization in the process of urban regeneration.
- Design guidance: By focusing on spatial structure principles and bubble diagrams, the method assists designers in understanding landscape spatial organization and design. On one hand, the findings help to understand the role relationships between the characteristics of spatial structure; on the other hand, the generalized thresholds can guide designers to a proper design. This ensures alignment with the intended design vision during the creation of spatial layouts and path planning.
- Design evaluation and optimization: The method supports the multidimensional analysis and evaluation of design solutions, enabling comparative assessments and design optimization. Pre-assessment and validation of schemes before construction can help identify whether the design of spatial organization and structure is appropriate, and make timely adjustments to minimize post-construction modifications and improve resource efficiency and achievability.
- Operational management: The method assists park managers in evaluating the functionality and aesthetics of spatial organization. Over time, as factors such as vegetation growth and facility updates alter spatial structures, the method allows for quantitative assessments of the built environment. This enables managers to identify weak points, adjust spatial units and their connections as needed through operations such as vegetation construction and transplanting, and improve the overall functionality and user experience.
5.4. Limitations
6. Conclusions
- Three-dimensional spatial analysis based on point cloud modeling: Based on point cloud modeling, the complex 3D spatial characteristics of the landscape can be accurately restored. The study proposes the method of spatial unit extraction and structural model construction for complex communities and landscapes from a 3D perspective, which makes up for the lack of and insufficiency of spatial analysis through 2D planes, such as 2D planes that may lead to ignoring the bottom space shaded by plants, especially the activity sites and paths in the understory space. This approach promotes 3D spatial morphology analysis and visualization.
- Multidimensional research and analysis: Based on the logic of spatial organization, this study deepens the understanding of landscape spatial structure from the multidimensional perspective of spatial combination, organization, and layout, and establishes a systematic assessment framework for the comprehensive evaluation of landscape design.
- Standard reference and objective weights: Based on the case study, this study summarizes the law of spatial structure organization and establishes a standard reference for spatial structure evaluation. By combining the Entropy Weight Method (EWM) and the Analytic Hierarchy Process (AHP), the objectivity of indicator weights is enhanced, ensuring more reliable evaluation results. The findings show that extensibility (E), spatial diversity (ND) and network centralization (NC) are the key features of landscape spatial structure. The indicators have appropriate numerical intervals, and the intervals of each indicator are summarized separately in this study. Appropriate spatial differences and sprawling rhythmic sequences, as well as centralized overall structure, can promote comfortable user participation and experience.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
| No. | Name | Area/hm2 | City/Country | Reasons for Selection |
|---|---|---|---|---|
| 1 | Lovers Park | 31.9 | Nanjing, China | First Prize of Landscape Design of the Ministry of Construction of the People’s Republic of China; National Science and Technology Progress Award |
| 2 | Hexi Ecological Park | 24.4 | Asia Pacific Excellence Awards 2019; designed by AECOM | |
| 3 | Green Expo Garden | 49.95 | popularity and public recognition | |
| 4 | Xuqiu Park | 9.56 | long history; popularity and public recognition | |
| 5 | Xuanwu Lake Park-Ying part | 7.3 | long history; popularity and public recognition; one of the three famous lakes in Jiangnan | |
| 6 | Xuanwu Lake Park-Liang part | 8.81 | ||
| 7 | Xuanwu Lake Park-Cui part | 6.59 | ||
| 8 | Punggol Park | 19.6 | Singapore | popularity and public recognition |
| 9 | Bishan-Ang Mo Kio Park (A) | 39.3 | 2016 ASLA Honourable Mention in the Universal Design category; designed by Ramboll Studio Dreiseitl | |
| 10 | Bishan-Ang Mo Kio Park (B) | 30 | ||
| 11 | Oosterpark | 15.1 | Amsterdam, The Netherlands | designer’s masterpieces; designed by American landscape architect Max Oostram |
| 12 | Beatrixpark | 34.7 | designer’s masterpieces; designed by Jakoba (Ko) Mulder | |
| 13 | Vondelpark | 44.9 | honoring playwright and poet Vondel; long history; popularity and public recognition | |
| 14 | Sarphati park | 5.02 | popularity and public recognition | |
| 15 | Rembrandt park | 48.27 | long history; popularity and public recognition | |
| 16 | Noorderpark | 22.9 | Utrecht, The Netherlands | designer’s masterpieces; designed by cc-studio |
| 17 | Het Park | 26.5 | Rotterdam, The Netherlands | designer’s masterpieces; designed by Zocher; long history; popularity and public recognition |
| 18 | Stadt Park | 16.9 | Vienna, Austria | designer’s masterpieces; long history; popularity and public recognition |
| 19 | Parc des Buttes-Chaumont | 28.1 | Paris, France | long history; popularity and public recognition; built according to plans by Jean-Charles Adolphe Alphand |
| 20 | Parc Montsouris | 17.9 | one of the four large urban public parks; designed by Jean-Charles Adolphe Alphand; long history; popularity and public recognition | |
| 21 | Parque Tezozómoc | 32.7 | Mexico | designer’s masterpieces; designed by Mario Schjetnan |
| 22 | Constitution Park | 18.6 | Washington, USA | architecture firm Skidmore, Owings, and Merrill (SOM) and Modern landscape architect Dan Kiley completed Constitution Gardens in 1976; long history; popularity and public recognition |
| 23 | Morningside Park | 16.7 | New York, USA | designer’s masterpieces; designed by Frederick Law Olmsted and Calvert Vaux; long history; popularity and public recognition |
| 24 | Fort Greene Park | 13.7 | famed landscape architects Olmsted and Vaux began designing its new layout. | |
| 25 | Claremont Park | 19.2 | long history; popularity and public recognition | |
| 26 | Crocheron Park | 25.3 | popularity and public recognition | |
| 27 | Public Garden | 10.9 | Boston, USA | National Historic Landmark |
| 28 | Gold Star Family Park | 5.15 | Chicago, USA | popularity and public recognition |
| 29 | Miller River Park | 7.76 | Stanford, USA | plan by Sasaki Associates; popularity and public recognition |
| 30 | Buffalo Bayou Park (eastern part) | 44.3 | Houston, USA | popularity and public recognition |
Appendix A.2
| No. | Name | CB | SR | ER | E | D | F | NF | NC | ND |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Lovers Park | 0.0170 | 0.8438 | 0.0819 | 0.4286 | 0.3810 | 0.0157 | 0.960 | 0.100 | 0.943 |
| 2 | Hexi Ecological Park | 0.0129 | 1.2826 | 0.0584 | 0.5714 | 0.3330 | 0.0157 | 0.947 | 0.072 | 0.900 |
| 3 | Green Expo Garden | 0.0118 | 0.4691 | 0.2445 | 0.8000 | 0.3000 | 0.0138 | 0.936 | 0.057 | 0.893 |
| 4 | Xuqiu Park | 0.0182 | 0.8410 | 0.4381 | 0.6667 | 0.2000 | 0.0184 | 0.938 | 0.118 | 0.918 |
| 5 | Xuanwu Lake Park-Ying part | 0.0103 | 0.5666 | 0.1272 | 0.7143 | 0.1905 | 0.0215 | 0.964 | 0.151 | 0.998 |
| 6 | Xuanwu Lake Park-Liang part | 0.0145 | 0.6074 | 0.2315 | 0.6667 | 0.2333 | 0.0211 | 0.958 | 0.092 | 0.991 |
| 7 | Xuanwu Lake Park-Cui part | 0.0134 | 1.0727 | 0.1732 | 0.6667 | 0.2333 | 0.0348 | 0.948 | 0.083 | 0.971 |
| 8 | Punggol Park | 0.0064 | 1.2776 | 0.0826 | 0.3750 | 0.3570 | 0.0254 | 0.938 | 0.181 | 0.896 |
| 9 | Bishan-Ang Mo Kio Park (A) | 0.0125 | 0.3408 | 0.3913 | 0.3750 | 0.3570 | 0.0161 | 0.970 | 0.116 | 0.684 |
| 10 | Bishan-Ang Mo Kio Park (B) | 0.0145 | 0.8268 | 0.3237 | 0.4286 | 0.3810 | 0.0223 | 0.973 | 0.061 | 0.639 |
| 11 | Oosterpark | 0.0039 | 0.6967 | 0.0667 | 0.5714 | 0.2860 | 0.0303 | 0.955 | 0.124 | 0.994 |
| 12 | Beatrixpark | 0.0203 | 0.8618 | 0.2602 | 0.5000 | 0.4000 | 0.0123 | 0.944 | 0.103 | 0.918 |
| 13 | Vondelpark | 0.0088 | 1.4019 | 0.2867 | 0.7143 | 0.2860 | 0.0138 | 0.969 | 0.118 | 0.974 |
| 14 | Sarphati park | 0.0096 | 0.3582 | 0.3943 | 0.5000 | 0.2000 | 0.0195 | 0.961 | 0.159 | 0.991 |
| 15 | Rembrandt park | 0.0085 | 1.0606 | 0.0445 | 0.5714 | 0.2143 | 0.0139 | 0.965 | 0.095 | 0.696 |
| 16 | Noorderpark | 0.0115 | 0.4276 | 0.0570 | 0.4286 | 0.5240 | 0.0128 | 0.933 | 0.181 | 0.567 |
| 17 | Het Park | 0.0337 | 0.1993 | 0.0258 | 0.4545 | 0.2180 | 0.0121 | 0.944 | 0.162 | 0.650 |
| 18 | Stadt Park | 0.0222 | 0.0710 | 0.3629 | 0.3333 | 0.6000 | 0.0262 | 0.960 | 0.092 | 0.999 |
| 19 | Parc des Buttes-Chaumont | 0.0010 | 0.3148 | 0.0093 | 0.4286 | 0.3330 | 0.0111 | 0.963 | 0.049 | 0.826 |
| 20 | Parc Montsouris | 0.0047 | 1.0839 | 0.1340 | 0.5000 | 0.2860 | 0.0132 | 0.957 | 0.123 | 0.887 |
| 21 | Parque Tezozómoc | 0.0138 | 0.7856 | 0.2483 | 0.4286 | 0.5240 | 0.0109 | 0.957 | 0.139 | 0.887 |
| 22 | Constitution Gardens | 0.0031 | 0.5937 | 0.3098 | 0.5455 | 0.2000 | 0.0109 | 0.941 | 0.117 | 0.523 |
| 23 | Morningside Park | 0.0159 | 0.7907 | 0.1121 | 0.8571 | 0.1500 | 0.0177 | 0.950 | 0.099 | 0.934 |
| 24 | Fort Greene Park | 0.0051 | 0.3673 | 0.1312 | 0.5714 | 0.3810 | 0.0202 | 0.952 | 0.103 | 0.959 |
| 25 | Claremont Park | 0.0027 | 0.0021 | 0.1943 | 0.5000 | 0.5330 | 0.0190 | 0.952 | 0.074 | 0.863 |
| 26 | Crocheron Park | 0.0025 | 1.5973 | 0.3886 | 0.5000 | 0.4670 | 0.0128 | 0.938 | 0.124 | 0.811 |
| 27 | Public Garden | 0.0085 | 1.4097 | 0.3457 | 0.3333 | 0.3330 | 0.0179 | 0.957 | 0.128 | 0.828 |
| 28 | Gold Star Family Park | 0.0097 | 0.4637 | 0.1039 | 0.6667 | 0.2667 | 0.0212 | 0.940 | 0.182 | 0.619 |
| 29 | Miller River Park | 0.0092 | 1.0563 | 0.4325 | 0.7500 | 0.3333 | 0.0148 | 0.972 | 0.144 | 0.684 |
| 30 | Buffalo Bayou Park (eastern part) | 0.0140 | 0.5337 | 0.0993 | 0.8000 | 0.2500 | 0.0209 | 0.951 | 0.064 | 0.610 |
Appendix A.3
| No. | Name | CB | SR | ER | F | E | D | NF | NC | ND | SC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Lovers Park | 0.918 | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.993 |
| 2 | Hexi Ecological Park | 1.000 | 0.656 | 0.862 | 1.000 | 1.000 | 1.000 | 1.000 | 0.700 | 1.000 | 0.912 |
| 3 | Green Expo Garden | 1.000 | 1.000 | 1.000 | 0.429 | 1.000 | 1.000 | 0.556 | 0.450 | 1.000 | 0.778 |
| 4 | Xuqiu Park | 0.871 | 1.000 | 0.362 | 1.000 | 0.909 | 1.000 | 0.667 | 1.000 | 1.000 | 0.908 |
| 5 | Xuanwu Lake Park-Ying part | 1.000 | 1.000 | 1.000 | 0.797 | 0.879 | 0.967 | 0.889 | 0.817 | 0.807 | 0.880 |
| 6 | Xuanwu Lake Park-Liang part | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.996 | 1.000 | 1.000 | 0.842 | 0.975 |
| 7 | Xuanwu Lake Park-Cui part | 1.000 | 0.986 | 1.000 | 1.000 | 1.000 | 0.016 | 1.000 | 0.883 | 0.951 | 0.879 |
| 8 | Punggol Park | 1.000 | 0.664 | 1.000 | 0.768 | 1.000 | 0.687 | 0.639 | 0.317 | 1.000 | 0.760 |
| 9 | Bishan-Ang Mo Kio Park (A) | 1.000 | 0.887 | 0.635 | 0.768 | 1.000 | 1.000 | 0.572 | 1.000 | 1.000 | 0.897 |
| 10 | Bishan-Ang Mo Kio Park (B) | 1.000 | 1.000 | 1.000 | 0.998 | 1.000 | 0.906 | 0.390 | 0.517 | 0.758 | 0.815 |
| 11 | Oosterpark | 0.914 | 1.000 | 0.911 | 1.000 | 1.000 | 0.335 | 1.000 | 1.000 | 0.826 | 0.897 |
| 12 | Beatrixpark | 0.787 | 1.000 | 1.000 | 1.000 | 0.940 | 0.949 | 1.000 | 1.000 | 1.000 | 0.971 |
| 13 | Vondelpark | 1.000 | 0.469 | 1.000 | 0.797 | 1.000 | 1.000 | 0.625 | 1.000 | 0.932 | 0.892 |
| 14 | Sarphati park | 1.000 | 0.914 | 0.618 | 1.000 | 0.909 | 1.000 | 1.000 | 0.683 | 0.842 | 0.874 |
| 15 | Rembrandt park | 1.000 | 1.000 | 0.781 | 1.000 | 0.954 | 1.000 | 0.833 | 1.000 | 1.000 | 0.966 |
| 16 | Noorderpark | 1.000 | 1.000 | 0.854 | 0.998 | 0.552 | 0.983 | 0.407 | 0.317 | 0.361 | 0.664 |
| 17 | Het Park | 0.253 | 0.664 | 0.671 | 1.000 | 0.966 | 0.938 | 1.000 | 0.633 | 0.815 | 0.785 |
| 18 | Stadt Park | 0.712 | 0.462 | 0.802 | 0.589 | 0.313 | 0.629 | 1.000 | 1.000 | 0.800 | 0.720 |
| 19 | Parc des Buttes-Chaumont | 0.801 | 0.846 | 0.575 | 0.998 | 1.000 | 0.868 | 0.947 | 0.317 | 1.000 | 0.802 |
| 20 | Parc Montsouris | 0.948 | 0.969 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.993 |
| 21 | Parque Tezozómoc | 1.000 | 1.000 | 1.000 | 0.998 | 0.552 | 0.851 | 1.000 | 1.000 | 1.000 | 0.936 |
| 22 | Constitution Gardens | 0.885 | 1.000 | 1.000 | 1.000 | 0.909 | 0.850 | 0.843 | 1.000 | 0.123 | 0.814 |
| 23 | Morningside Park | 0.964 | 1.000 | 1.000 | 0.184 | 0.752 | 1.000 | 1.000 | 1.000 | 1.000 | 0.846 |
| 24 | Fort Greene Park | 0.956 | 0.928 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.991 |
| 25 | Claremont Park | 0.868 | 0.354 | 1.000 | 1.000 | 0.524 | 1.000 | 1.000 | 0.733 | 1.000 | 0.843 |
| 26 | Crocheron Park | 0.860 | 0.161 | 0.652 | 1.000 | 0.730 | 0.987 | 0.639 | 1.000 | 1.000 | 0.846 |
| 27 | Public Garden | 1.000 | 0.456 | 0.903 | 0.589 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.894 |
| 28 | Gold Star Family Park | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.987 | 0.778 | 0.300 | 0.649 | 0.797 |
| 29 | Miller River Park | 1.000 | 1.000 | 0.395 | 0.644 | 1.000 | 1.000 | 0.444 | 0.933 | 1.000 | 0.847 |
| 30 | Buffalo Bayou Park (eastern part) | 1.000 | 1.000 | 1.000 | 0.429 | 1.000 | 1.000 | 1.000 | 0.567 | 0.597 | 0.771 |
References
- Bertram, C.; Rehdanz, K. Preferences for Cultural Urban Ecosystem Services: Comparing Attitudes, Perception, and Use. Ecosyst. Serv. 2015, 12, 187–199. [Google Scholar] [CrossRef]
- Mostafazadeh, R.; Alaei, N.; Mirchooli, F.; Hussain, S. Changes in Urban Green Space Configuration and Connectivity Using Spatial Graph-Based Metrics in Ardabil Developing City, Iran. Environ. Monit. Assess. 2024, 196, 778. [Google Scholar] [CrossRef]
- Ulrich, R.S. View Through a Window May Influence Recovery from Surgery. Science 1984, 224, 420–421. [Google Scholar] [CrossRef] [PubMed]
- Maas, J.; Verheij, R.A.; Groenewegen, P.P.; De Vries, S.; Spreeuwenberg, P. Green Space, Urbanity, and Health: How Strong Is the Relation? J. Epidemiol. Community Health 2006, 60, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Lin, G. The Relationship between Urban Green Space and Social Health of Individuals: A Scoping Review. Urban For. Urban Green. 2023, 85, 127969. [Google Scholar] [CrossRef]
- Li, Y.; Lin, G. Demand-Side Effects of Urban Green Spaces: How Attractiveness Helps Overcome Subjective Barriers to Health Behaviours. Urban For. Urban Green. 2024, 94, 128277. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Moscardó, V.; Vallina Rodríguez, A.; Lázaro, E. Spatial Statistical Analysis of the Relationship between Self-Reported Mental Health during the COVID-19 Lockdown and Closeness to Green Infrastructure. Urban For. Urban Green. 2022, 68, 127457. [Google Scholar] [CrossRef]
- Europe, C.O. European Landscape Convention. In Proceedings of the Report and Convention, Florence, Italy, 20 October 2000. [Google Scholar]
- Madureira, H.; Nunes, F.; Oliveira, J.V.; Cormier, L.; Madureira, T. Urban Residents’ Beliefs Concerning Green Space Benefits in Four Cities in France and Portugal. Urban For. Urban Green. 2015, 14, 56–64. [Google Scholar] [CrossRef]
- Zhang, L.; Hao, P.; Dong, L.; Wang, Y. Optimization Strategy for Maintenance Management of Herbaceous Layer in Urban Parks Based on Spontaneous Plants: A Case Study of Xicheng District, Beijing. Landsc. Archit. 2024, 31, 46–54. [Google Scholar] [CrossRef]
- Chen, Y.; La Rosa, D.; Yue, W.; Xu, Z.; Zhuo, Y. Do Larger Cities Enjoy Better Green Space Accessibility? Evidence from China. Environ. Impact Assess. Rev. 2024, 107, 107544. [Google Scholar] [CrossRef]
- Zhang, L. An Improved Indicator Standardization Method for Multi-Indicator Composite Evaluation: A Case Study in the Evaluation of Ecological Civilization Construction in China. Environ. Impact Assess. Rev. 2024, 108, 107600. [Google Scholar] [CrossRef]
- Jim, C.Y. Green-Space Preservation and Allocation for Sustainable Greening of Compact Cities. Cities 2004, 21, 311–320. [Google Scholar] [CrossRef]
- Gehl, J. Life Between Buildings: Using Public Space, 6th ed.; Island Press: Washington, DC, USA, 2011; ISBN 978-1-59726-827-1. [Google Scholar]
- Byrne, J.; Sipe, N. Green and Open Space Planning for Urban Consolidation—A Review of the Literature and Best Practice; Urban Res. Program, Issues Paper 11; Griffith University: Brisbane, Australia, 2010. [Google Scholar]
- Alaei, N.; Mohammadzadeh, F.; Mostafazadeh, R.; Talebi Khiavi, H. Assessing Spatiotemporal Urban Green Space per Capita and Its Connectivity in a Small Size City in Northwest Iran. GeoJournal 2024, 89, 148. [Google Scholar] [CrossRef]
- Chiesura, A. The Role of Urban Parks for the Sustainable City. Landsc. Urban Plan. 2004, 68, 129–138. [Google Scholar] [CrossRef]
- Antrop, M. Why Landscapes of the Past Are Important for the Future. Landsc. Urban Plan. 2005, 70, 21–34. [Google Scholar] [CrossRef]
- Dee, C. Form and Fabric in Landscape Architecture: A Visual Introduction; Taylor & Francis: Oxfordshire, UK, 2004; ISBN 0-203-63907-3. [Google Scholar]
- Moraitis, K. Composing the Landscape: Analyzing Landscape Architecture as Design Formation. Land 2024, 13, 827. [Google Scholar] [CrossRef]
- Li, X. Study on the Structures and Images of Landscape Planting. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2006. [Google Scholar]
- Cheng, Z.; Cheng, Y. Research on the Spatial Structure of Landscape Architecture from Design Intention to Function Use; Wichmann Verlag: Berlin, Germany, 2024. [Google Scholar]
- Liu, M. Mapping Landscape Spaces: Understanding, Interpretation, and the Use of Spatial-Visual Landscape Characteristics in Landscape Design. A+BE|Archit. Built Environ. 2020, 20, 1–248. [Google Scholar] [CrossRef]
- Zlatanova, S.; Yan, J.; Wang, Y.; Diakité, A.; Isikdag, U.; Sithole, G.; Barton, J. Spaces in Spatial Science and Urban Applications—State of the Art Review. ISPRS Int. J. Geo-Inf. 2020, 9, 58. [Google Scholar] [CrossRef]
- Yoon, C. Characterization of Bubble Diagram in the Process of Architectural Form Generation. Archit. Res. 2000, 2, 7–15. [Google Scholar]
- Chen, R.; Zhao, J.; Yao, X.; Jiang, S.; He, Y.; Bao, B.; Luo, X.; Xu, S.; Wang, C. Generative Design of Outdoor Green Spaces Based on Generative Adversarial Networks. Buildings 2023, 13, 1083. [Google Scholar] [CrossRef]
- Caneparo, L. Semantic Knowledge in Generation of 3D Layouts for Decision-Making. Autom. Constr. 2022, 134, 104012. [Google Scholar] [CrossRef]
- Pérez-Martínez, I.; Martínez-Rojas, M.; Soto-Hidalgo, J.M. A Methodology for Urban Planning Generation: A Novel Approach Based on Generative Design. Eng. Appl. Artif. Intell. 2023, 124, 106609. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z.; Deng, Q. Exploration on Diversity Generation of Campus Layout Based on GAN. Computational Design and Robotic Fabrication. In Hybrid Intelligence; Philip, F., Chai, Y., Chao, Y., Li, K., Sun, T., Eds.; Springer Nature: Singapore, 2023; pp. 233–243. ISBN 978-981-19863-6-9. [Google Scholar]
- Fan, B.; Gu, J.; Ai, S.; Chen, X.; Du, S.; Cheng, Y. Digital Characteristics of Spatial Layout in Urban Park Scene Space: Spatial Classification, Quantitative Indicators, and Design Applications Based on Completed Park Cases. Land 2024, 13, 2251. [Google Scholar] [CrossRef]
- Slager, C.T.J.; de Vries, B. Landscape Generator: Method to Generate Landscape Configurations for Spatial Plan-Making. Comput. Environ. Urban Syst. 2013, 39, 1–11. [Google Scholar] [CrossRef]
- Garau, C.; Annunziata, A.; Yamu, C. A Walkability Assessment Tool Coupling Multi-Criteria Analysis and Space Syntax: The Case Study of Iglesias, Italy. Eur. Plan. Stud. 2024, 32, 211–233. [Google Scholar] [CrossRef]
- Qi, K.; Fan, Z.Q. Evaluation Method for Landscape Connectivity Based on Graph Theory: A Case Study of Natural Forests in Minqing County, Fujian Province. Acta Ecol. Sin 2016, 36, 7580–7593. [Google Scholar]
- Modica, G.; Praticò, S.; Laudari, L.; Ledda, A.; Di Fazio, S.; De Montis, A. Implementation of Multispecies Ecological Networks at the Regional Scale: Analysis and Multi-Temporal Assessment. J. Environ. Manag. 2021, 289, 112494. [Google Scholar] [CrossRef]
- Wang, L.; Han, X.; He, J.; Jung, T. Measuring Residents’ Perceptions of City Streets to Inform Better Street Planning through Deep Learning and Space Syntax. ISPRS J. Photogramm. Remote Sens. 2022, 190, 215–230. [Google Scholar] [CrossRef]
- Zhou, J.; Hou, Q. Resilience Assessment and Planning of Suburban Rural Settlements Based on Complex Network. Sustain. Prod. Consum. 2021, 28, 1645–1662. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, Y. Prediction of Pedestrian Distribution and Matching Analysis Based on Landscape Structure System. Landsc. Archit. 2020, 27, 104–109. [Google Scholar]
- Weng, X.; Shao, D.; Du, J.; Wang, X. On the Application of Spatial Sequence in the Theme Expression of Urban Exhibition Garden:A Case Study of Xingtai Exhibition Garden in Hebei Province. Archit. Cult. 2023, 3, 250–252. [Google Scholar]
- Qi, J.; Lin, E.S.; Yok Tan, P.; Chun Man Ho, R.; Sia, A.; Olszewska-Guizzo, A.; Zhang, X.; Waykool, R. Development and Application of 3D Spatial Metrics Using Point Clouds for Landscape Visual Quality Assessment. Landsc. Urban Plan. 2022, 228, 104585. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Y.; Zlatanova, S.; Cheng, S. Quantitative Analysis Method of the Organizational Characteristics and Typical Types of Landscape Spatial Sequences Applied with a 3D Point Cloud Model. Land 2024, 13, 770. [Google Scholar] [CrossRef]
- Yamu, C.; van Nes, A.; Garau, C. Bill Hillier’s Legacy: Space Syntax—A Synopsis of Basic Concepts, Measures, and Empirical Application. Sustainability 2021, 13, 3394. [Google Scholar] [CrossRef]
- Niu, H.; Xiu, Z.; Xiao, D. Impact of Land-Use Change on Ecological Vulnerability in the Yellow River Basin Based on a Complex Network Model. Ecol. Indic. 2024, 166, 112212. [Google Scholar] [CrossRef]
- Shi, Y.L.; Huang, Y.; Xiao, L. Spatial structure and layout optimization of mountain park based on social network analysis. Chin. Landsc. Archit. 2020, 36, 91–96. [Google Scholar] [CrossRef]
- Wang, Y.J.; Cheng, S.; Cheng, Z.; Cheng, Y. Exploring the Construction and Analysis Method of Landscape Spatial Structure Based on Complex Networks. Environ. Plan. B Urban Anal. City Sci. 2023, 23, 745–762. [Google Scholar] [CrossRef]
- Lu, S.M. Network characteristics in the spatial structure of Qushui Garden, a classical garden in Shanghai. Chin. Landsc. Archit. 2011, 27, 60–64. [Google Scholar]
- Wang, Y.C. Schema Language: A New Paradigm of Landscape Local Expression and Spatial Logic; China Building Industry Press: Beijing, China, 2018. [Google Scholar]
- Yang, X.J.; Liu, X.Y.; Ye, J. Landscape Architecture Research and Practice from the Perspective of Topology. Urban Archit. 2021, 18, 157–160. [Google Scholar]
- Freytag, A. Topology and Phenomenology in Landscape Architecture. In Landschaftsarchitekturtheorie: Aktuelle Zugänge, Perspektiven und Positionen; Berr, K., Ed.; Springer Fachmedien: Wiesbaden, Germany, 2018; pp. 195–225. ISBN 978-3-658-18838-2. [Google Scholar]
- Do, E.Y.-L.; Gross, M.D. Thinking with Diagrams in Architectural Design. Artif. Intell. Rev. 2001, 15, 135–149. [Google Scholar] [CrossRef]
- Lian, J.; Nijhuis, S.; Bracken, G.; Wu, X.; Wu, X.; Chen, D. Conservation and Development of the Historic Garden in a Landscape Context: A Systematic Literature Review. Landsc. Urban Plan. 2024, 246, 105027. [Google Scholar] [CrossRef]
- Qin, X.; Yang, D.; Wangari, V.W. Quantitative Characterization and Evaluation of Highway Greening Landscape Spatial Quality Based on Deep Learning. Environ. Impact Assess. Rev. 2024, 107, 107559. [Google Scholar] [CrossRef]
- Wen, H.; Lin, H.; Liu, X.; Guo, W.; Yao, J.; He, B.-J. An Assessment of the Psychologically Restorative Effects of the Environmental Characteristics of University Common Spaces. Environ. Impact Assess. Rev. 2025, 110, 107645. [Google Scholar] [CrossRef]
- Urech, P.R.; Dissegna, M.A.; Girot, C.; Grêt-Regamey, A. Point Cloud Modeling as a Bridge between Landscape Design and Planning. Landsc. Urban Plan. 2020, 203, 103903. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Y.; Zlatanova, S.; Palazzo, E. Identification of Physical and Visual Enclosure of Landscape Space Units with the Help of Point Clouds. Spat. Cogn. Comput. 2020, 20, 257–279. [Google Scholar] [CrossRef]
- Brown, G.; Weber, D. Public Participation GIS: A New Method for National Park Planning. Landsc. Urban Plan. 2011, 102, 1–15. [Google Scholar] [CrossRef]
- Tachikawa, R.; Kunii, Y. Comprehensive Quantitative Understanding of the Landscape Using Tls Point Cloud Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLIII-B2-2022, 297–302. [Google Scholar] [CrossRef]
- Long, C.; Sun, Z.; Wang, Y. Study on the Walking Behavior of the Elderly and the Spatial Organization Characters of Urban Parks—Based on Space Syntax Theory. Archit. Cult. 2018, 9, 148–149. [Google Scholar]
- Chen, Y. Application of Depthmap Software in Spatial Structure Analysis of Garden. Exp. Technol. Manag. 2009, 26, 87–89. [Google Scholar]
- Cheng, Y.N. The Theory and Method of Modern Landscape Design; Southeast University Press: Nanjing, China, 2014. [Google Scholar]
- Pattanayak, H.S.; Verma, H.K.; Sangal, A.L. Lengthening of Average Path Length in Social Networks Due to the Effect of Community Structure. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 8401–8421. [Google Scholar] [CrossRef]
- Hou, Y.; Zhao, X.; Zhang, B. Significance Analysis between Morning Exercise and Spatial Organization Characteristics of Urban Park—Taking 4 Urban Parks in Harbin for Example. Landsc. Archit. 2017, 24, 109–116. [Google Scholar]
- Deng, P.; Huang, Q.; Liu, F.; Wang, Z.; Liu, M. The Research on Identification and Spatial Pattern of Urban Mixed Land-Use: A Case Study of Chengdu. Ecol. Indic. 2023, 154, 110891. [Google Scholar] [CrossRef]
- Wang, Y. The Logical Thinking and Framework of Landscape Space Pattern Language. Landsc. Archit. 2017, 4, 89–98. [Google Scholar]
- Liu, B.; Zhang, T. Landscape Space Sequence Organization Based on Visual Sense. Chin. Landsc. Archit. 2010, 26, 31–35. [Google Scholar]
- Casey, E.S. The Edge (s) of Landscape: A Study in Liminology. In The Place of Landscape: Concepts, Contexts, Studies; The MIT Press: Cambridge, MA, USA, 2011; pp. 91–109. [Google Scholar]
- Wang, Z. Research on the Design Method of “Space with Path” in Architecture. Ph.D. Thesis, Tianjin University, Tianjin, China, 2019. [Google Scholar]
- Feng, J.Z. Over Landscaping Organizing. Chin. Landsc. Archit. 2010, 10, 20–22. [Google Scholar]
- Liu, M.; Nijhuis, S. Mapping Landscape Spaces: Methods for Understanding Spatial-Visual Characteristics in Landscape Design. Environ. Impact Assess. Rev. 2020, 82, 106376. [Google Scholar] [CrossRef]
- Jessel, B. Elements, Characteristics and Character–Information Functions of Landscapes in Terms of Indicators. Ecol. Indic. 2006, 6, 153–167. [Google Scholar]
- Yue, W.; Xu, J.; Tan, W.; Zhao, J.; Su, F. Spatial Scale Analysis of the Diversities of Urban Landscape: A Case Study within the External Circle Highway of Shanghai City. Acta Ecol. Sin. 2005, 1, 122–128. [Google Scholar]
- Yoshinobu, A. Exterior Space Design; China Building Industry Press: Beijing, China, 1985. [Google Scholar]
- Yang, W.; Kedron, P.; Frazier, A.E. Percentage of Area Protected Can Substitute for More Complicated Structural Metrics When Monitoring Protected Area Connectivity. Ecol. Indic. 2024, 158, 111387. [Google Scholar] [CrossRef]
- Liu, J. Introduction to Social Network Analysis; Social Sciences Academic Press: Beijing, China, 2004. [Google Scholar]
- Wang, Y.J. Research on the Composition of Landscape Space Assisted by Digital Technology. Ph.D. Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Bartesaghi, P.; Clemente, G.P.; Grassi, R. Clustering Coefficients as Measures of the Complex Interactions in a Directed Weighted Multilayer Network. Phys. A Stat. Mech. Its Appl. 2023, 610, 128413. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A Review of Fuzzy AHP Methods for Decision-Making with Subjective Judgements. Expert Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Yu, D.; Kou, G.; Xu, Z.; Shi, S. Analysis of Collaboration Evolution in AHP Research: 1982–2018. Int. J. Info. Tech. Dec. Mak. 2021, 20, 7–36. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 1–5. [Google Scholar] [CrossRef]
- Sun, N.; Li, C.; Guo, B.; Sun, X.; Yao, Y.; Wang, Y. Urban Flooding Risk Assessment Based on FAHP–EWM Combination Weighting: A Case Study of Beijing. Geomat. Nat. Hazards Risk 2023, 14, 2240943. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, J.; Hao, H.; Wang, K. A Large-Scale Measurement Method of Esthetical Appreciation Laws Based on the Multimodal Machine Learning. Zhuangshi 2021, 7, 106–111. [Google Scholar]
- Buchholz, T.; Rametsteiner, E.; Volk, T.A.; Luzadis, V.A. Multi Criteria Analysis for Bioenergy Systems Assessments. Energy Policy 2009, 37, 484–495. [Google Scholar] [CrossRef]
- Mendoza, G.A.; Martins, H. Multi-Criteria Decision Analysis in Natural Resource Management: A Critical Review of Methods and New Modelling Paradigms. For. Ecol. Manag. 2006, 230, 1–22. [Google Scholar] [CrossRef]
- Bock, H.-H.; Diday, E. Analysis of Symbolic Data: Exploratory Methods for Extracting Statistical Information from Complex Data; Springer Science & Business Media: Heidelberg, Germany, 2012. [Google Scholar]
- Saaty, T.L. Decision Making with the Analytic Hierarchy Process. Int. J. Softw. Sci. Comput. 2008, 1, 83. [Google Scholar] [CrossRef]
- Grove, M.; Zhang, T. Forged by Floods: Wuhan Yangtze Riverfront Park. Landsc. Archit. Front. 2020, 8, 130–145. [Google Scholar] [CrossRef]
- Qi, J.; Lin, E.S.; Tan, P.Y.; Zhang, X.; Ho, R.; Sia, A.; Olszewska-Guizzo, A.; Waykool, R. Applying 3D Spatial Metrics for Landscape Planning: Creating and Measuring Landscape Scenarios by a Point Cloud-Based Approach. Ecol. Inform. 2024, 79, 102436. [Google Scholar] [CrossRef]
- Wang, S.; Li, A. Identify the Significant Landscape Characteristics for the Perceived Restorativeness of 8 Perceived Sensory Dimensions in Urban Green Space. Heliyon 2024, 10, e27925. [Google Scholar] [CrossRef] [PubMed]
- Baljon, J.L. Designing Parks: An Examination of Contemporary Approaches to Design in Landscape Architecture Based on a Comparative Design Analysis of Entries for the Concours International; Wageningen University and Research: Wageningen, The Netherlands, 1992. [Google Scholar]
- Zhang, Q.H.; Zhang, Y.X. Research on the Spatial Sequence of Memorial Landscape Based on Visual Sense—A Case Study of Nanjing Yuhuatai Martyrs’ Cemetery. Chin. Landsc. Arch. 2019, 35, 55–60. [Google Scholar]
- Zhai, Y.J. Application of spatial organization analysis and design management of urban parks based on space syntax theory: A preliminary study on the method of convex map analysis. Chin. Landsc. Archit. 2016, 32, 80–84. [Google Scholar]
- Akcelik, G.N.; Choe, K.W.; Rosenberg, M.D.; Schertz, K.E.; Meidenbauer, K.L.; Zhang, T.; Rim, N.; Tucker, R.; Talen, E.; Berman, M.G. Quantifying Urban Environments: Aesthetic Preference through the Lens of Prospect-Refuge Theory. J. Environ. Psychol. 2024, 97, 102344. [Google Scholar] [CrossRef]
- Guangkun, Z.; Yingsheng, H.; Shengdong, L. Study on the Accessibility of Public Space on Huangpu River Waterfront—Public Transportation Evaluation and Optimization Strategy Based on Social Network Analysis. Chin. Landsc. Archit. 2020, 36, 64–69. [Google Scholar] [CrossRef]
- Tveit, M.; Ode, Å.; Fry, G. Key Concepts in a Framework for Analysing Visual Landscape Character. Landsc. Res. 2006, 31, 229–255. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, E.S.; Tan, P.Y.; Qi, J.; Waykool, R. Assessment of Visual Landscape Quality of Urban Green Spaces Using Image-Based Metrics Derived from Perceived Sensory Dimensions. Environ. Impact Assess. Rev. 2023, 102, 107200. [Google Scholar] [CrossRef]
- Jose, V.R.R.; Nau, R.F.; Winkler, R.L. Sensitivity to Distance and Baseline Distributions in Forecast Evaluation. Manage. Sci. 2009, 55, 582–590. [Google Scholar] [CrossRef][Green Version]
- Kitchenham, B.A.; Pickard, L.; Linkman, S.; Jones, P. A Framework for Evaluating a Software Bidding Model. Inf. Softw. Technol. 2005, 47, 747–760. [Google Scholar] [CrossRef]
- Cai, K.; Huang, W.; Lin, G. Bridging Landscape Preference and Landscape Design: A Study on the Preference and Optimal Combination of Landscape Elements Based on Conjoint Analysis. Urban For. Urban Green. 2022, 73, 127615. [Google Scholar] [CrossRef]
- Dane, G.; Evers, S.; van den Berg, P.; Klippel, A.; Verduijn, T.; Wallgrün, J.O.; Arentze, T. Experiencing the Future: Evaluating a New Framework for the Participatory Co-Design of Healthy Public Spaces Using Immersive Virtual Reality. Comput. Environ. Urban Syst. 2024, 114, 102194. [Google Scholar] [CrossRef]
- Huang, P.; Yao, P.; Hao, Z.; Peng, H.; Guo, L. Improved Constrained k-Means Algorithm for Clustering with Domain Knowledge. Mathematics 2021, 9, 2390. [Google Scholar] [CrossRef]
- Basu, S.; Banerjee, A.; Mooney, R.J. Active Semi-Supervision for Pairwise Constrained Clustering. In Proceedings of the Fourth SIAM International Conference on Data Mining; Berry, M.W., Dayal, U., Kamath, C., Skillicorn, D., Eds.; Siam: Philadelphia, PA, USA, 2004; pp. 333–344. [Google Scholar]


| Aspects | Characteristics | Indicators | Explanation | Calculation Formula |
|---|---|---|---|---|
| Spatial combination | Degree of spatial connectivity | Interface cross-boundary ratio (CB) | Describes the degree of association between two spaces by calculating the ratio of the length of the boundary intersection to the average area of the neighboring units [74]. | Lb = length of boundary intersection between space units i and j Si, Sj = bottom areas of space units i and j CB = ratio of boundary intersection of space units |
| Open and shadowy contrast | Size change rate (SR) | Describes the degree of change in size between two spatial units, with the value taken as an absolute value, independent of the order of the tour [74]. | = bottom surface area of space units i and j SR = rate of change of space unit size | |
| Enclosure changes rate (ER) | Describes the change in the degree of permeability between two spatial units. Values are taken as absolute values; thus, facilitating the comparison of the rate of change in the enclosure of different spatial units. | = interfacial enclosure of spatial units i and j = rate of change of spatial unit enclosure | ||
| Group organization | Degree of compactness | Structural extensibility (E) * | Describes the degree of extension of the spatial group structure to reflect the spread of the group [60]. | = structural diameter of space group c N = number of space units in group c E = structural extension of group c |
| Connection density (D) * | Describes the degree of connectivity between spatial units in structure [44,75]. The spatial structure is saturated when all spatial units within a group are interconnected, and this spatial structure is the tightest. | = number of associations between spatial units in the group structure N = number of spatial units in the group D = density of spatial connections in the group | ||
| Degree of spatial transition | Frequency of spatial change (F) | Describes the number of transition changes of spatial units within a sequence of a certain length to reflect the frequency of spatial change rhythms [60]. | = number of spatial units on the sequence r = length of the serial path of the serial sequence r F = frequency of spatial change in sequence r | |
| Overall layout | Level of spatial density | Spatial fragmentation (NF) | Describes the degree of spatial fragmentation. The fragmentation index is inversely proportional to the degree of fragmentation of the spatial pattern, with a higher index meaning a lower degree of spatial fragmentation [42]. | MPS = average size of spatial units n = total number of spatial units A = total area of spatial units FN = spatial fragmentation |
| Layout aggregation | Network centralization (NC) * | Describes the tendency of a structure network to concentrate towards a particular node and is used to measure the degree of overall structural equilibrium [44,72]. The greater the network centrality, the stronger the tendency of the overall structure of the space to concentrate towards a certain point. | and, The = absolute centrality of each space unit n = number of units in the space structure CRD = relative centrality of each space unit | |
| Degree of spatial heterogeneity | Spatial diversity (ND) | Describe the number of spatial landscape types and the proportion of each landscape type, reflecting the degree of spatial diversity [72]. | total number of space units pi = number of certain spatial units as a proportion of the total number ND = overall spatial diversity |
| Indicators | Min | Max | Median | AVG | SD | IQR | CV | Skewness | Kurtosis | p |
|---|---|---|---|---|---|---|---|---|---|---|
| CB | 0.001 | 0.034 | 0.011 | 0.011 | 0.007 | 0.008 | 60.565% | 1.113 | 2.583 | 0.046 * |
| SR | 0.002 | 1.597 | 0.741 | 0.74 | 0.413 | 0.651 | 55.847% | 0.252 | −0.641 | 0.703 |
| ER | 0.009 | 0.438 | 0.184 | 0.205 | 0.135 | 0.247 | 65.876% | 0.29 | −1.316 | 0.038 * |
| E | 0.333 | 0.857 | 0.523 | 0.555 | 0.146 | 0.238 | 26.336% | 0.388 | −0.803 | 0.172 |
| D | 0.15 | 0.6 | 0.317 | 0.325 | 0.115 | 0.152 | 35.490% | 0.741 | −0.065 | 0.068 |
| F | 0.011 | 0.035 | 0.017 | 0.018 | 0.006 | 0.008 | 32.713% | 1.116 | 1.248 | 0.014 * |
| NF | 0.933 | 0.973 | 0.953 | 0.953 | 0.011 | 0.018 | 1.199% | −0.015 | −0.985 | 0.43 |
| NC | 0.049 | 0.182 | 0.117 | 0.114 | 0.037 | 0.051 | 32.845% | 0.223 | −0.623 | 0.449 |
| ND | 0.523 | 0.999 | 0.89 | 0.835 | 0.148 | 0.278 | 17.763% | −0.713 | −0.875 | 0.003 ** |
| Indicators | Interval [a, b] | Weight (A) | Weight (B) | Comprehensive Weight (W) |
|---|---|---|---|---|
| CB | [0.003, 0.020] | 0.0119 | 0.0449 | 0.0843 |
| SR | [0.211, 1.390] | 0.0695 | 0.1116 | 0.0684 |
| ER | [0.046, 0.394] | 0.0406 | 0.1430 | 0.0699 |
| E | [0.375, 0.795] | 0.1577 | 0.1531 | 0.1513 |
| D | [0.200, 0.524] | 0.0626 | 0.0773 | 0.1122 |
| F | [0.0111, 0.026] | 0.0993 | 0.2196 | 0.0923 |
| NF | [0.938, 0.970] | 0.0945 | 0.0915 | 0.0803 |
| NC | [0.061, 0.179] | 0.2476 | 0.0867 | 0.1823 |
| ND | [0.611, 0.994] | 0.2163 | 0.0722 | 0.1590 |
| Spatial Combination | Indicators Value | Comprehensive Score (SC) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CB | SR | ER | F | E | D | NF | NC | ND | ||||
| Before optimization | 16 | 15 | 0.0091 | 0.9006 | 0.0941 | 0.857 | 0.150 | 0.015 | 0.969 | 0.124 | 0.954 | 0.692 |
| 6 | 5 | 0.0151 | 1.1380 | 0.1287 | ||||||||
| 3 | 4 | 0.0069 | 0.9585 | 1.1821 | ||||||||
| 4 | 5 | 0.0057 | 0.0859 | 1.0891 | ||||||||
| 2 | 1 | 0.0124 | 0.9785 | 0.1086 | ||||||||
| After optimization | 16 | 15 | 0.0120 | 0.9090 | 0.1160 | 0.714 | 0.333 | 0.015 | 0.976 | 0.139 | 0.985 | 0.826 |
| 6 | 5 | 0.0150 | 1.1220 | 0.1590 | ||||||||
| 3 | 4 | 0.0080 | 0.9580 | 0.3850 | ||||||||
| 4 | 5 | 0.0080 | 0.0880 | 0.3560 | ||||||||
| 2 | 1 | 0.0120 | 0.9810 | 0.1440 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Cheng, Y. A Multidimensional Framework for Quantitative Analysis and Evaluation of Landscape Spatial Structure in Urban Parks: Integrating 3D Point Cloud and Network Analysis. Land 2025, 14, 826. https://doi.org/10.3390/land14040826
Cheng Z, Cheng Y. A Multidimensional Framework for Quantitative Analysis and Evaluation of Landscape Spatial Structure in Urban Parks: Integrating 3D Point Cloud and Network Analysis. Land. 2025; 14(4):826. https://doi.org/10.3390/land14040826
Chicago/Turabian StyleCheng, Ziqian, and Yuning Cheng. 2025. "A Multidimensional Framework for Quantitative Analysis and Evaluation of Landscape Spatial Structure in Urban Parks: Integrating 3D Point Cloud and Network Analysis" Land 14, no. 4: 826. https://doi.org/10.3390/land14040826
APA StyleCheng, Z., & Cheng, Y. (2025). A Multidimensional Framework for Quantitative Analysis and Evaluation of Landscape Spatial Structure in Urban Parks: Integrating 3D Point Cloud and Network Analysis. Land, 14(4), 826. https://doi.org/10.3390/land14040826






