Abstract
Landscape spatial structure serves as the foundational framework for vegetation arrangement and spatial organization, playing a crucial role in assessing landscape morphology. Traditional 2D graph theory methods have provided insights into planar structural characteristics but fail to capture the complexity of three-dimensional spatial attributes and organizational processes inherent in landscape systems. To address these limitations, this study proposes a novel multidimensional framework for the quantitative analysis and evaluation of landscape spatial structure by integrating 3D point cloud technology with spatial network analysis. The methodology consists of three key components: (1) the formulation of multidimensional spatial organization theory, (2) spatial unit extraction and structure analysis through ArcGIS 10.5 and Cytoscape v3.6.1, and (3) the development of an indicator system for evaluating spatial structure organization. The framework was validated through the analysis of 30 urban parks, where the regularity and range of indicators are generalized to establish evaluation criteria and determine weights. The findings indicate that spatial structure indicators are moderation indicators with optimal value ranges. The evaluation system was subsequently applied across the 30 parks for comprehensive evaluation. A total of 6 of 30 parks have comprehensive scores over 0.95. In practical application, the design score of Shuyang Park improved from 0.692 to 0.826 after evaluation and optimization, demonstrating the method’s effectiveness. This study underscores the potential of digital methodologies in advancing landscape spatial structure modeling, enhancing the understanding of spatial organization, and transitioning subjective assessments toward evidence-based objective evaluations. The proposed methodology and findings offer valuable insights for diagnosing, assessing, optimizing, and managing urban green spaces.
1. Introduction
Urban green spaces, such as parks, gardens, and green corridors, have been widely recognized for providing benefits to urban residents, including ecological services (e.g., air purification, climate regulation, and biodiversity conservation) [1,2], physical benefits (e.g., opportunities for exercise and movement), psychological restoration (e.g., stress reduction and mood enhancement) [3,4], and social functions (e.g., fostering community interaction and cohesion) [5,6,7]. Landscape is a broader term that encompasses the spatial, perceptual, and cultural dimensions of land, whether natural, designed, or built [8]. As one type of green space and designed landscape, urban parks emphasize their spatial organization, service efficiency, and experiential qualities. Due to vegetation growth and a lack of management mechanisms, many parks struggle to sustain their environmental quality and service level, with gradual changes in park space, the weakening of structural functions, and a decline in spatial functionality [9,10]. The maintenance and enhancement of urban parks are crucial aspects of urban development and renewal [11,12]. Planners and designers should not only focus on the area of green space, but also consider the quality of the green space [13]. Spatial quality emphasizes the perceptual and functional attributes of space that influence user experience and behavior patterns. Utilization efficiency is reflected as the degree to how effectively visitors utilize different spatial areas in the park, and is related to its intended function and design effects [14,15]. Based on a certain amount of existing green space, to improve quality and efficiency, optimal design, including adjustments to spatial configuration, functional zoning and vegetation structure, along with scientific management including data-driven monitoring and maintenance strategies, enables park design to be aligned with actual use patterns and better meet ecological and social needs, which have become significant issues in the process of contemporary urban regeneration [11,16,17].
The term landscape originates from the Dutch word. In planning and design fields, landscape encompasses the spatial arrangement of natural and built elements perceived and interpreted by humans [8,18]. In this study, landscape is studied from a spatial structural- and design-based perspective, where the landscape spatial structure refers to the configuration of spatial units and their relationships within green spaces. Spatial structure is the basic framework of vegetation and spatial organization, as well as the artistic law of forming integrity and systematicity [19,20,21]. From a design perspective, it is the physical organization of spatial units and their relationship patterns, and the basic framework that influences and constrains the group of landscape system elements [22]. Park layout design is the result of interactions between multiple interrelated spaces aimed at function, system, and aesthetics [23]. A well-designed spatial structure allows for a logical arrangement of functions and guides visitors through a more enjoyable and rich experience [24]. With the development of artificial intelligence and machine learning, bubble diagrams and structural schematics can show spatial structure [19,25] and be used as design base inputs to derive multiple designs of the same origin [26,27]. Structural layout also plays a key role of design guidance and control in intelligent design and optimization [28,29,30,31].
Current research on landscape spatial structure mostly relies on graph-theoretic models, which simplify the complex 3D topography and vegetation layer relationship into a planar network topology, resulting in the weakening of the line-of-sight relationship and spatial permeability between vegetation [32,33]. Past studies have explored the planar connectivity, spatial layout, and network structure of green spaces from a planning perspective, but lack consideration of spatial elevation and the surrounding environment [34,35,36]. In design-scale spatial structure studies, 2D spatial analysis improves computational efficiency, but have difficulty revealing spatial organization characteristics from the overall topography and vegetation [37,38]. Some studies have tried to introduce 3D models into spatial analysis, and currently, most of them focus on local spatial analysis, ignoring the organizational study of the overall spatial network [39,40]. The study of spatial structure layout and organization, considering landscape 3D characteristics, remains to be explored.
Research on landscape spatial structure primarily employs space syntax and complex network analysis as the main analytical methods. Space syntax takes road axes as the fundamental units, simplifying space into a homogeneous linear structure [41]. It analyzes structure through metrics of connectivity and integration, which fail to capture the expansion and contraction characteristics of landscape spaces, particularly non-linear spaces. Complex networks were initially applied to large-scale urban spatial structure studies [42] and were later introduced into small-scale park space research [43,44], which can simultaneously express spatial organization and path connectivity relationships. SNA generalizes spatial structures into three core elements—unit spaces (nodes), boundaries, and connections (links)—and utilizes this framework to examine spatial organization strategies [44,45]. Spatial articulation transition and spatial sequence organization relate to the details of spatial structural organization and are influenced by 3D spatial morphology, but have received less attention in research.
Previous studies [22,25,46,47,48] on spatial organization have typically focused on qualitative analysis methods, with less emphasis on quantitative or scientific analysis. Traditional bubble diagrams and structural schematics aid in landscape design [25,49] or use descriptive or illustrative language to analyze spatial arrangement, composition, and sight lines [20,23,50], which can be used to qualitatively explain spatial relationships in the landscape. In recent years, urban space optimization and quality enhancement based on quantitative analysis and evaluation have gained increased attention [51,52]. The integration of digital technology, such as point cloud data and 3D modeling techniques, has significantly advanced the precision of landscape spatial analysis [53,54]. Quantitative analysis methods including spatial syntax, ArcGIS, and spatial network analysis (SNA) have been applied in spatial structure analysis. Digitization and 3D spatial analysis have become research trends [39]. However, most of the current analysis methods are based on mapping diagrams to comparatively assess the relative differences between parts of the same green space, which is suitable for problem checking and local optimization within the design [37,55]. Due to the lack of laws and standards for guidance, there is no objective basis for green space design analysis, problem diagnosis, and quality assessment as a reference. In the process of multi-program design comparison and urban green space assessment, it still relies on subjective comparison [56].
The current research on landscape spatial structure presents several challenges. Firstly, spatial structure analysis based on traditional graph theory simplifies space in 2D, and some studies analyze the spatial structure with the help of two-dimensional planes [37,57] or sections in the height of sight [58], ignoring the diverse connectivity and complexity from 3D characteristics of landscape space [44,59]. Secondly, the analysis tools, mainly based on spatial syntax and complex network abstract paths and spaces into lines and points [60,61], and the research on spatial organization, often emphasize the overall structure and ignore the details of spatial combinations and sequential organization in the process of constructing landscape spatial structure, which lacks the comprehensive and systematic framework for spatial structure analysis. Thirdly, the existing studies present results in the form of mapping [35,62], and the analysis and comparison still rely on subjectivity, lacking quantitative guidance and evaluation standard references. In addition, due to the lack of a multidimensional and standardized evaluation system, the comparison between different plans still requires subjective comparison.
This study aims to explore the following questions with the help of point cloud data and quantitative analysis methods: (a) how can landscape spatial structures of urban parks be characterized, (b) what spatial numerical regularities contribute to functional and perceptually effective spatial structures, and (c) how to quantitatively evaluate, analyze, and optimize landscape spatial structures with a data-driven approach. To address the above issues, this study proposes a multidimensional quantitative evaluation method for spatial structure based on the framework of “spatial combination–group organization–overall layout”. Firstly, based on previous research, a multidimensional landscape spatial organization theory system of “spatial combination, group and sequence, and overall pattern” is proposed. Secondly, we establish a multidimensional quantitative indicator system of landscape spatial structure, and put forward the extraction and construction method of a spatial structure based on 3D point clouds to calculate the indicators. And thirdly, the quantitative method is applied to 30 typical cases to quantitatively summarize the spatial structure characteristics and construct an evaluation system. In the application part, the study conducts a horizontal comparison of 30 case parks to assess the method’s usability. In addition, the study conducted a comprehensive evaluation and optimization of the spatial structure with an urban park practice project located in Shuyang as an applied case study. The design project meets the selection criteria of the 30 case parks (including park area, functional type, no special topography, etc.) and falls into the same category of parks. The spatial configurations before and after optimization are compared to verify the effectiveness of the proposed evaluation method.
2. Theoretical Framework
Landscape design is rooted in the concept of space, aiming to achieve a cohesive organization of spatial sequences. The landscape spatial graphic language is developed through the structuring and deconstruction of landscape space to modularize the overall landscape [63]. The systemic and composite characteristics of a landscape determine that local adjustments in the design process will affect the whole, and taking into account the characteristic relationships of multiple levels is necessary for planning and design and comprehensive adjustment. The modeling framework from unit to whole helps designers to sort out and recognize the complex spatial organization of a landscape, and the multidimensional spatial structure characteristic system can assist with systematic cognition and control the design from part to whole, which makes up for the insufficiency of landscape 3D spatial analysis perspectives limited to a certain scale or feature. As illustrated in Figure 1, the landscape space is conceptualized as a series of nested units surrounded by vegetation and other elements.
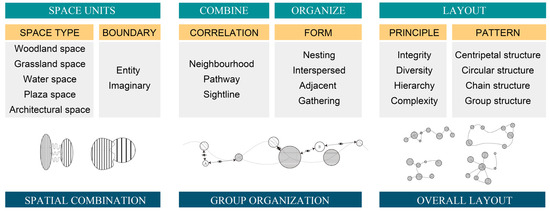
Figure 1.
Multidimensional landscape space structure organization.
- Spatial combination
A landscape can be subdivided into multiple spatial units, each characterized by distinct forms, scales, and 3D attributes. Three-dimensional space better demonstrates that the combination of two spatial units with different characteristics creates a dynamic spatial experience, as one transitions from one landscape to another [64]. Spatial units can be arranged in various ways, such as nested, interspersed, adjacent, or connected by pathways. The interactions between spatial units—whether through penetration, interweaving, or variation—are used to describe their organizational patterns [65]. The combination and contrast of spatial units provides visitors with a sense of boundless meaning within the confines of a limited space [66].
- 2.
- Group organization
A landscape group consists of multiple spatial units organized according to specific principles and patterns, following a logical sequence that collectively presents a distinct spatial rhythm and order [38,64]. Feng emphasizes that group landscape design integrates local and individual spatial experiences throughout the entire space. It directs attention where emphasis is needed and conceals where discretion is preferred, resulting in a harmonious composition with rhythmic pauses. This design approach, inspired from nature, carefully selects, shapes, processes, and enhances landscape elements [67]. Structural pattern, scale, and organizational rhythm of the group are essential characteristics that define its spatial qualities [68].
- 3.
- Overall layout
The overall atmosphere of a landscape is shaped by the various internal spatial nodes and their layout relationships. Visitors perceive the space not as fragmented or isolated elements, but as a cohesive and integrated experience [59]. From the planning perspective, the density and distribution characteristics of spatial units [69] describe the overall spatial layout, while the diversity of spatial types reflects the richness and variety within the landscape [70]. Together, these characteristics contribute to the landscape’s overall expression within a specific area.
Based on this logic, the research proposes the construction framework of a “multidimensional landscape spatial structure”. This framework develops spatial organization by analyzing the characteristics and influencing factors at three levels: the combination of spatial units, the organization of group structures, and the overall spatial layout. In a standard-sized park, it is possible to achieve a simultaneous examination of spatial organization from three perspectives. At the overall level, the spatial structure encompasses the organizational framework of all spaces and partitioning schemes. The group organization level focuses on the local network within different zones, while the spatial combination level details how individual spaces are interconnected. This framework provides a comprehensive, three-dimensional view of spatial organization, and allows for the flexibility to target analysis at specific levels according to research objectives.
3. Materials and Methods
This study aims to establish a multidimensional spatial structure quantitative analysis and evaluation system, summarize indicator patterns and value ranges through case studies, establish evaluation references, and apply to the design evaluation and optimization of practical cases. As outlined in the technical route shown in Figure 2, the spatial structure is extracted and constructed using ArcGIS 10.5 and Cytoscape v3.6.1. Secondly, combining the theory of spatial organization and previous research, the study selects 9 key quantitative indicators and develops an indicator system that evaluates the “Spatial combination–group organization–overall layout” of urban park spatial structures. Thirdly, taking 30 typical parks as research cases, the study quantifies key spatial structure indicators, analyzes and summarizes indicator value ranges, and establishes the evaluation weights and baselines. This approach provides a methodology for guiding the spatial design, management, and renewal of urban parks, offering a structured path for optimizing park layouts and improving their functionality and aesthetic quality.
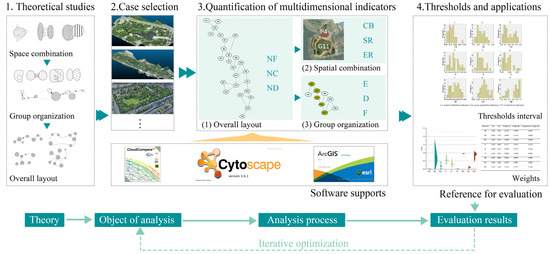
Figure 2.
The workflow for the quantification and evaluation of spatial structure.
3.1. Study Area and Data Processing
This study selects small- and medium-scale urban comprehensive parks as case studies, conducting a quantitative analysis of spatial structure to identify and summarize patterns that can serve as a reference for evaluating and optimizing spatial designs. The selected case studies adhere to specific criteria: modern urban comprehensive parks under 50 hectares in the built environment; natural parks without significant topographical features such as large mountains or terraces; parks with good overall evaluation and a certain degree of representativeness; and parks with available spatial data.
Based on the above criteria, 30 urban parks from 14 cities were selected as research cases, as detailed in Appendix A.1. The selected city parks exhibit diverse spatial patterns, and have been well recognized and evaluated by industry experts or tourists for their quality.
For precise and scientific spatial structure construction and analysis, 3D point cloud data of international parks were sourced from Open Topography (https://opentopography.org/). For parks located in Nanjing, China, the 3D point cloud data collected from oblique photography and field research were combined to complete the spatial extraction and construction.
3.2. Spatial Structure Modelling Process
3.2.1. Extraction of Space Units
As illustrated in Figure 3a, the study constructs the raster model of a park based on 3D point cloud data using ArcGIS and conducts slope analysis. Slope changes in the raster (representing the edges of plant communities and buildings) were extracted as boundaries. Discontinuous spatial interfaces are completed manually by filling in boundary gaps smaller than 5 m, gaps significantly smaller than the scale of spatial units, or boundaries between areas with different functions [54]. The spatial unit in this study focuses on the space available for visitors’ activities. According to the theory of minimum external modulus [71], units with an area less than 400 m2 (20 × 20 m) are either excluded or merged with adjacent units.
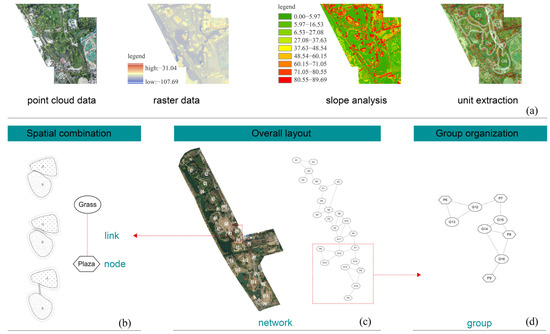
Figure 3.
Spatial structure modelling process. (a) Process of spatial unit extraction. (b) Linkage of spatial combinations. (c) Construction of overall spatial networks. (d) Organization of the group.
3.2.2. Construction of Spatial Unit Connections
The construction of spatial structures involves two key components: network nodes (spatial units) and network links (spatial associations), as shown in Figure 3b. In the spatial structure model, connections between spatial units can take various forms, including overlapping interfaces and short paths that serve as transitional links [44]. Structural models are constructed using Cytoscape software, a powerful tool for building and analyzing spatial networks through automated drawing. The study constructs spatial structure networks based on the relationships between spatial units in the park, forming overall networks (Figure 3c). The group organizations of representative zoning districts are selected for the study based on design features (Figure 3d).
For the 30 selected cases, the study employed raster modelling and spatial unit delineation based on 3D point cloud data, resulting in 653 spatial units as research objects. According to the partitioning and usage patterns, 30 core unit combinations and 30 core spatial groups were selected as representative samples for multidimensional quantitative analysis.
3.3. Evaluation Indicators and Weights
3.3.1. Evaluation Indicator System and Quantitative Method
The study collects indicators for describing the spatial combination, group organization, and overall layout in landscape architecture based on prior research. While the indicators of overall layout have been widely applied in previous studies [42,44,45,72], less attention has been given to spatial combination and group organization. This study introduces spatial enclosure and area variability as new indicators to characterize spatial combination. For group organization, the indicators are derived from local network analysis [73]. By integrating the characteristics of urban parks and the relevance of each indicator, the study identifies three groups of nine quantitative indicators for analysis. These indicators form a multidimensional framework for landscape space analysis, case study evaluation, and pattern identification, as summarized in Table 1.

Table 1.
Spatial structure indicator framework and calculation methods.
3.3.2. Calculating the Weight of Evaluation Indicators
The evaluation of spatial organization is jointly influenced by various indicators in different dimensions, and determining the weights of evaluation indicators is crucial for achieving a comprehensive assessment. Currently, the methods for calculating indicator weights can be categorized into two groups: subjective weighting methods and objective weighting methods. The Analytic Hierarchy Process (AHP) primarily relies on human decision-making and experience, which introduces a high level of subjectivity [76,77]. In contrast, the Entropy Weight Method (EWM) uses objective data to reveal the characteristics of sample data, offering a more objective assessment [78]. This study combines AHP and EWM to assign weights for weight assignment, which enables AHP to effectively represent designers’ intentions and evaluation objectives, while EWM enhances the objectivity of the weight assignment process [79].
Comprehensive weight determination is carried out through a matrix approach. The coefficients and are assigned to subjective and objective weights, respectively, where i = 1, 2, …, n, and the formula used is as follows:
where represents the subjective weight obtained through AHP, and represents the objective weight obtained through EWM. The formula for calculating the combined weights of the indicators is as follows:
The comprehensive weights of landscape spatial structure evaluation indicators () were calculated.
Landscape design and cognition have regularity, and the designer’s empirical judgment and machine learning are essentially based on the learning of the law [80]. This paper takes the value range summarized in the case study as the evaluation reference. An indicator is considered ideal when its value lies within the interval; conversely, values outside the interval, whether excessive or deficient, signify a suboptimal spatial structure. The greater the deviation, the more poorly the spatial structure is characterized.
Based on the above rationale, the method for normalizing data for interval-type indicators is as follows:
where and are estimated using the fitting function derived from the existing sample values and data distribution patterns, ensuring that the predicted range covers all possible indicator values. Quantitative values are scored as 1 when they fall within the specified interval, with the score gradually decreasing to 0 as the values move outside the interval.
4. Results
4.1. Indicator Results of Spatial Structure Cases
The detailed results of quantitative spatial data are shown in Appendix A.2. The distribution of the nine indicators was analyzed and visualized with the help of SPSS 22 and Origin 2024, as shown in Figure 4a and Table 2. The analysis reveals that the values of each indicator fall within specific intervals, but there are notable variations in the range and span of these intervals.
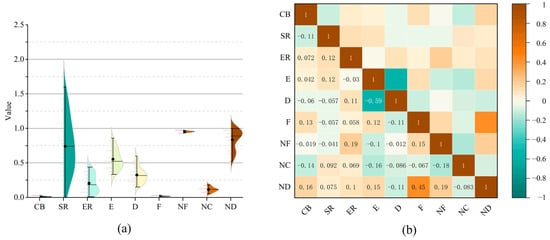
Figure 4.
Distribution analysis and correlation analysis of data on spatial structure indicators. (a) Violin plot of spatial structure indicators. (b) Correlation analysis of data on spatial structure indicators.

Table 2.
Analysis of the quantitative data on the spatial structure.
In terms of distribution intervals, indicators such as CB, D, NF, and NC show relatively narrow fluctuation ranges, with SD values below 0.05 and IQR values below 0.1. In contrast, the SR indicator exhibits the largest fluctuation range, with an SD value of 0.431 and an IQR value of 0.651. This suggests that for space combination, the intersection between two spaces has limited variability (as seen with the CB indicator), while the SR indicator allows for a wider degree of variability, as the areas of the two spaces can be contrasted significantly. Regarding local and overall structures, indicators related to spatial connectivity density, spatial aggregation, and overall fragmentation show smaller variation ranges, which are due to the need for coordinated adjustments across multiple spaces. The CV values for group organization and overall layout indicators range from 1.19% to 35.49%, indicating a more concentrated distribution. In contrast, the CV values for spatial combination indicators are all above 50%, typically around 55–65%. In particular, the CB indicator displays a more scattered distribution despite having a smaller value range. This analysis suggests that during spatial optimization, the spatial combination allows for more flexibility in adjustment, whereas the group organization and overall structure require more strict requirements to maintain functional cohesion and provide an enhanced visitor experience.
In general, the differentiation of the distribution intervals is closely related to the magnitude of the numerical values, making numerical normalization essential for comprehensive evaluation. This step is necessary to eliminate the influence of varying dimensions and to enhance the comparability between different cross-section comparisons. The analysis of data distribution indicates that all the indicators exhibit a continued and concentrated distribution pattern. This feature helps to determine the reference ranges for evaluation and to identify the presence of extreme values, allowing for more precise analysis and adjustments during evaluation.
4.2. Analysis and Value Range of Spatial Structure Indicators
Thresholds can serve as reference intervals and criteria for evaluation and decision-making, as well as reflecting the tendencies and preferences of their representations by the data [81,82]. The threshold generalization based on the distribution pattern of indicators in this study contributes to summarizing the common structural characteristics among case studies and provides reference standards for landscape spatial structure design.
As shown in Table 2, the sample size in this study was below 50; thus, the S-W test was used to assess the normality of the data. The indicators A1, A3, B3, and C3 demonstrated significance (p < 0.05), indicating that these data sets do not follow a normal distribution. However, the absolute values of kurtosis (less than 10) and skewness (less than 3) suggest that these data can still be treated as normal distribution. In addition, the indicators A2, B1, B2, C1, and C2 did not present significance (p > 0.05), indicating that these data sets have the trait of normality.
As depicted in Figure 5, the distribution of values for each indicator is generally continuous, with only a few discrete or extreme values. In Constitution Park, two small spatial units encased in woodland exhibit the highest value for the CB indicator at 0.0337, indicating a strong interconnection between them due to their close proximity and enclosure. In the Vienna Stadt Park, the central sports and recreation cluster has nearly all neighboring spaces connected, yielding the highest spatial connectivity density at 0.60, reflecting a high degree of spatial compactness. The entrance axis sequence in the Oosterpark demonstrates a nested relationship between spatial units, shortening the sequence length and leading to the highest frequency of spatial variation (F = 0.303) over a relatively short distance. In terms of spatial diversity, this paper focuses on the balance between hard space (e.g., paved areas) and soft space (e.g., green spaces). The ND indicator measures this balance. A value close to one signifies a balanced proportion of the two types of space, as seen in Vienna Stadt Park, where 13 hard spaces and 12 soft spaces offer a rich variety in the visitor experience. Conversely, the ND of Constitution Park is 0.523, as hard spaces are limited to the entrance and a waterfront platform. These variations across different parks highlight how the quantitative indicators can reflect distinct spatial organizational characteristics, providing insights into design diversity and spatial relationships.
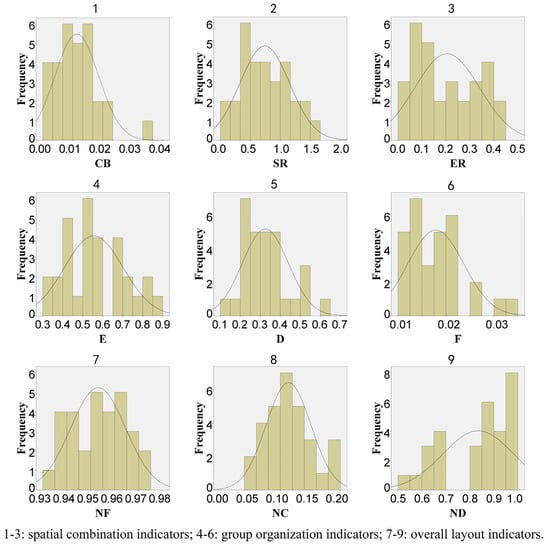
Figure 5.
Distribution analysis of data on spatial structure indicators.
To reduce the impact of extreme values on the reference intervals, the study applied the 10–90th percentile range as the interval value as shown in Table 3. From the perspective of spatial combination, the ratio of the boundary intersection of two spaces is appropriate at [0.003, 0.020], and the two spaces are connected by a narrower area, which can realize the conversion of sight and space. SR and ER can achieve better spatial contrast and difference of perceptual experience at [0.211, 1.390] and [0.046, 0.394], respectively. In the combination of spatial units, it is necessary to consider the two major factors of area and enclosure in an integrated way. Changes in the same direction will enhance the degree of spatial contrast, while a reverse change will weaken it. From the perspective of group organization, the value interval of E and D of the spatial group is usually [0.375, 0.795], and the value interval of D is usually [0.200, 0.524], in which the space can be regarded as coherent, which can give people an impression of the group as a whole. In addition, this indicator is related to the mode of the spatial grouping, such as radioactive, parallel type, etc., which are not discussed further here. When F is at [0.0111, 0.026], the spatial connection frequency is more suitable, and if the spatial connection is sparse during the tour, it will be boring. From the perspective of the overall layout, the spatial density (NF) is suitable at [0.938, 0.970], which reflects the overall number and size of spaces. And NC is at [0.061, 0.179], with appropriate connectivity and flow between spaces, which can functionally support each other and provide flexible and diverse tour experiences. The spatial diversity (ND) is at [0.611, 0.994], when the proportion of soft and hard spaces is more appropriate, without being too artificial or too natural, and meeting the needs of functional services and recreational perception.

Table 3.
The interval and weights of landscape spatial structure evaluation indicators.
4.3. Indicator Weights
It was found that indicator correlations were low (Figure 4b), which implies indicator independence, reducing the redundancy of information, as well as enriching the evaluation system and providing deeper insights [83,84]. Table 3 presents the objective weights of the indicators, calculated with the help of the Entropy Weight Method (EWM) to obtain Weight (A). EWM is based on the concept of entropy in information theory, which relates the degree of data discrete of the indicator to the amount of information [78]. The results show that indicators related to the overall layout have the highest weights (0.0945–0.2476), while spatial combination indicators hold lower weights (0.0119–0.0695). This highlights the critical role of the overall layout in spatial structure analysis, while the combination of spatial units has less impact. Notably, the extension of the core group (E) plays a significant role, with a weight of 0.1577.
Weight B is derived using the Analytic Hierarchy Process (AHP). In landscape design, spatial combination is pivotal to spatial experience. During landscape tours, visitors more readily perceive spatial changes and sequences, making them important structural elements that influence the overall tour experience. Consequently, spatial combination and group organization receive higher importance in the assignment of subjective weights, with weights of SR, ER, E, and F all above 0.1. Notably, the frequency of spatial change has the most significant impact on structural relationships (F = 0.2196).
The objective weights (Weight A) and subjective weights (Weight B) are combined through the matrix approach to determine the overall weights (W), as shown in Table 3. The highest weighted indicators are E, NC, and ND, with values of 0.15, 0.18, and 0.16. This indicates that the degree of structural aggregation and the extension of groups significantly influence the overall and local structure.
4.4. Evaluation Results and Comparison
The nine indicator values of the 30 parks were normalized, as detailed in Appendix A.3. Based on the comprehensive weights established in the previous analysis, a weighted comprehensive index was calculated for the nine indicators to determine the overall spatial structure score (SC) for each park.
As illustrated in Figure 6, the spatial structure comprehensive scores of these parks are generally high, indicating well-organized spatial structures. Research conducted both online and offline reveals that these parks are frequently designed by prominent designers, have received awards, or enjoy significant local popularity, reflecting a degree of public recognition that corresponds with the comprehensive evaluation results of this study. Notably, parks 1, 6, 12, 15, 20, and 24 achieved the highest comprehensive scores among the 30 parks, each exceeding 0.95. These parks exhibit well-organized spatial structures in terms of spatial combination, group organization, and overall layout, with indicator scores predominantly ranging between 0.8 and 1, suggesting that few values fell outside the ranges. In contrast, parks 3, 8, 16, 17, 18, and 30 received lower comprehensive scores (0.8 or below), with several indicators falling outside the ranges. Combined with remote sensing images, it can be found that parks with lower scores often exhibit spatial priorities and structures that are less perceptible. For instance, parks identified in cases 8, 18, and 30 face constraints imposed by site conditions, such as municipal rivers or large water bodies, which affect their spatial structure organization [85].
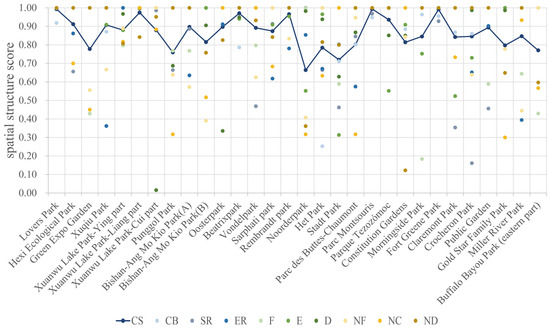
Figure 6.
Analysis of evaluation scores of spatial structure indicators for 30 parks.
4.5. Design Applications
In this study, the Shuyang City Park design project is selected as a practical case study. The comprehensive park covers an area of about 17.96 hectares and is located in a flat urban environment with no special topography. Based on site analysis and conceptual intention, the designer developed preliminary spatial units and structural planning and design for the park. Combined with the CAD plan and 3D model of the preliminary scheme, spatial model construction and analysis were carried out with the help of Cytoscape v3.6.1 and ArcGIS 10.5 to compare indicator results with the reference ranges and find indicators that need to be upgraded. In the process of design optimization, the indicators with higher weights were prioritized to be adjusted to fit within the ranges by increasing the number and types of spaces, adjusting the vegetation enclosure and planting density of key spaces, optimizing spatial connections, and so on.
The visualization and indicator values of the spatial structure before and after optimization are shown in Table 4 and Figure 7, which shows that the comprehensive score of the spatial structure has been effectively improved. This example proves the feasibility and versatility of the method, and provides a basis for quantitative design and generative design.

Table 4.
Quantitative analysis and comprehensive score of the spatial structure before and after optimization in design.
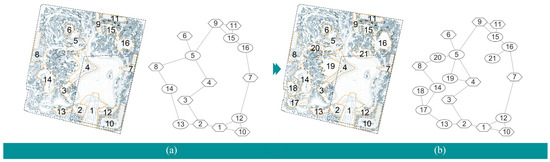
Figure 7.
Design schemes before and after optimization (1–20 represent space unit numbers). (a) Design scheme and spatial structure before optimization. (b) Design scheme and spatial structure after optimization.
5. Discussion
5.1. Quantitative Characteristics of Landscape Spatial Structures
In general, the indicators proposed by the study have been effectively quantified, and the correlation analysis of the quantification results shows that the numerical correlation between the indicators is weak (Figure 4b), which proves the independence of the indicators, and indicates that the indicator system quantitatively characterizes the spatial organization, grouping, and layout from multiple aspects, with rich information and low overlap. When the design is adjusted, the spatial structure characteristics of different dimensions will still be affected through linkage, which is consistent with the findings of previous studies [30,44], and the paper provides additional quantification on specific spatial and connectivity characteristics. Compared with previous studies on constructing indicator systems [40,86], this study further explores the linkage mechanism between indicators. Within a certain level, there are correlations between indicators, for example, D and E are negatively correlated. When the extension of the cluster is larger, the spatial connection within the cluster tends to be mainly string-connected, so the density of cluster connection is naturally lower. There is also a certain correlation between different levels. For example, F and ND are positively correlated, and when the group, as a representative of the overall layout, has a variety of internal spatial variations, the spatial diversity in the overall layout is also relatively good.
Combined with the results of weight analysis, it can be found that the weights obtained by EWM indicate that the three indicators, E, NC, and ND, are the most important indicators for characterizing the spatial structure, which reflect the spatial type composition, the number of connections in the overall layout, and the pattern of spatial organization of core groups, which proves the importance of the key features in the previous research [43,87]. The weights obtained by AHP indicate that the spatial structure characteristics felt by people during the visit are more focused on the micro aspect, focusing on the organization of space to space and the pattern of important groups or axes. In addition, the generalization of the indicator intervals in this study proves again that the spatial characteristics of the landscape are regular [40], and are innovatively applied to the designation of objective evaluation criteria, which confirms the value of the indicator intervals on the basis of previous studies.
The organization of landscape spatial structure is multilayered. The overall level is concerned with the relationship between all spaces, such as the proportion of spatial types and the density of spatial distribution. It can be seen from the ND value range that the types in the spatial structure are usually diverse, but the natural soft space types usually account for more than 50%, which is consistent with the results of previous studies [44,88]. NF and NC reflect the distribution of spatial units and the network relationship, and the space for activities is usually not fully covered, and the remaining space is filled by plants and structures, etc., which act as spatial enclosures and ornamental objects. Therefore, these two indicators control the spaces at appropriate scales to provide a sense of comfort and security, while the moderate connections established between spaces can help functional scenes build service relationships [30].
Spatial groups reveal the organization of park partitions or typical sequences from a mesoscopic perspective, guiding designers to optimize local spatial structures. The multi-space transformation is closely related to the subjective feeling of people. F and D indicators affect the spatial change and time change in the visiting process, and it is necessary to macroscopically control the whole visiting route and organize the spatial nodes [64]. According to the value of E, to summarize the regularity of group extension, it can be found that the number of units in the group is usually more than the number of units on the diameter of the structure; even if it is the core sequence, it will be associated with branch units. During tours, people can choose by themselves to travel along the sequences or take other paths [89].
Spatial combination indicators show the connectivity of two spaces and analyze the detailed characteristics of spatial structures or the rhythm and fluctuation of sequences. Spatial combination indicators show the connectivity of two spaces and can be used to analyze the detailed characteristics of spatial structures or the rhythm and fluctuation of sequences. Two neighboring spaces usually differ in terms of spatial area, enclosure, etc., and continuous spatial variations bring about different spatial sequence perceptions, such as fluctuating, reversal, and moderate sequences [40].
5.2. Comparison with Existing Methods
The analysis and assessment method proposed in this study advances digitization and improves science in three key aspects: three-dimensional spatial analysis, an indicator system, and a comprehensive assessment baseline, which fills the gaps in the systematic analysis and evaluation of spatial structures of park scales, and improves scientific validity. The innovations of the method are reflected in the following aspects:
- Quantitative analysis based on three-dimensional data
Traditional methods of spatial structural analysis often rely on graphical methods that simplify the space to a two-dimensional image, which limit the accuracy of comparisons and optimizations [90], especially when dealing with subtle variations between objects under evaluation. The use of 3D point cloud data provides a detailed replication of the landscape environment, overcoming the operational inaccuracies associated with field surveys. Several scholars have explored the quantification of 3D spatial and visual morphology [86,91]. Additionally, the extraction of spatial units and the construction of structural models using ArcGIS 10.5 and Cytoscape v3.6.1 significantly reduces the errors previously introduced by manual analysis. These advancements enable a more scientific and quantitative evaluation of landscape spatial structures, enhancing the accuracy and objectivity of comparison and optimization.
- Systematicity of the Indicator System
Different from previous studies that focus solely on either the overall structure [20,45,92] or individual spaces [93,94], this study begins with the principles and processes of spatial organization, taking into account the overall pattern, group organization, and detailed features of spatial combination. This approach aligns with visitors’ multidimensional perception of landscape space. The multidimensional assessment and optimization approach allows for interactive adjustments across different dimensions of spatial organization. Modifications at spatial combinations can impact both group organization and the overall layout, while comprehensive analysis and evaluation contribute to effective structural optimization of the entire system [30].
- Evaluation system and reference standards
Previous studies often relied on subjective scoring methods or comparative analyses within research objects, limiting the potential for standardization and broader application [38,58]. In contrast, this paper establishes an evaluation system for landscape spatial patterns grounded in design theory. Effective model evaluation requires a clear standard and baseline for comparison, especially when dealing with ordered event spaces [95,96]. By quantifying a series of typical cases, the study summarizes the preferred indicator ranges and evaluation baselines, and assigns indicator weights based on sample data and their numerical characteristics. This method is grounded in a comprehensive analysis of existing exemplary cases, generalizing the universal principles of structural features to establish an evaluation standard, which provides the analysis and evaluation of spatial organization with an objective and uniform reference framework.
5.3. Applications
The landscape spatial structure analysis method, grounded in quantitative multidimensional spatial analysis, facilitates the rapid calculation of spatial structure and visualization of spatial relationships using ArcGIS 10.5 and Cytoscape v3.6.1. This approach enhances the dynamic correlation between design and metrics, enabling designers to make informed, quantitative adjustments to landscape spatial design and organization [97,98]. It can be applied to guide landscape design, assessment, and management, including the following aspects:
- Green space diagnosis: The research methodology and conclusions support the spatial structure diagnosis of existing green spaces, especially the lack of attractiveness and poor service spaces, by comprehensively evaluating and ranking them, analyzing which are the lower scoring green spaces, and which specific features represented by indicators are problematic, and serve as a focus of optimization in the process of urban regeneration.
- Design guidance: By focusing on spatial structure principles and bubble diagrams, the method assists designers in understanding landscape spatial organization and design. On one hand, the findings help to understand the role relationships between the characteristics of spatial structure; on the other hand, the generalized thresholds can guide designers to a proper design. This ensures alignment with the intended design vision during the creation of spatial layouts and path planning.
- Design evaluation and optimization: The method supports the multidimensional analysis and evaluation of design solutions, enabling comparative assessments and design optimization. Pre-assessment and validation of schemes before construction can help identify whether the design of spatial organization and structure is appropriate, and make timely adjustments to minimize post-construction modifications and improve resource efficiency and achievability.
- Operational management: The method assists park managers in evaluating the functionality and aesthetics of spatial organization. Over time, as factors such as vegetation growth and facility updates alter spatial structures, the method allows for quantitative assessments of the built environment. This enables managers to identify weak points, adjust spatial units and their connections as needed through operations such as vegetation construction and transplanting, and improve the overall functionality and user experience.
5.4. Limitations
In this study, the types of landscape spatial objects and case selection are deliberately limited, using the same type of case Shuyang Park as a representative example to test the method’s feasibility. The constraints on conditions and types were necessary to form clusters and identify common patterns within a smaller dataset [99,100]. However, the applicability of the proposed method to other landscape types, such as mountain parks and wetlands, requires further validation through a larger and more diverse set of case studies. Second, the limited number of cases used in this study may affect the precision of the evaluation baselines and the weightings calculated by the Entropy Weight Method (EWM). Future research will aim to expand the sample size to improve the reliability of these baselines and weightings, and apply the method to a broader range of landscape space types. Third, a 5 m range was applied as the boundary completion rule to address the discontinuities encountered during the extraction and construction of spatial structure. However, in practical applications, spatial units and their boundaries differ significantly based on the scale of the park. It is essential for researchers to adapt the constraints of spatial extraction and structural construction according to the specific features of their study objects to achieve accurate and reliable structural network models and evaluation outcomes.
In addition, a landscape is considered to be a complex dynamic system, including natural elements such as vegetation, soil, water bodies, and artificial elements such as structures, while ecological processes, visual forms, social use functions, etc. are also important components. They are interdependent and interact to influence each other. The spatial structure will be intrinsically linked to a variety of elements. This paper focuses on the study of landscape spatial structure from a morphological perspective, which is currently targeted and limited. Further research could incorporate other landscape dimensions, such as ecological efficiency and elemental organization, sensory experience, and functional requirements to develop a more comprehensive indicator system, ultimately improving the overall benefits in design and maintenance.
6. Conclusions
This paper explores landscape spatial morphology by focusing on spatial structure, employing 3D point cloud technology and spatial network analysis to propose an innovative multidimensional framework and methodology for analyzing and evaluating the spatial structure of urban parks. The study summarizes the systematic characteristics of landscape spatial structure as well as confirms the reliability and validity of the evaluation system with relevant cases. These findings provide practical guidelines for optimizing the structure of urban parks to improve usability. The main contributions of the findings to the field of landscape design are summarized as follows:
- Three-dimensional spatial analysis based on point cloud modeling: Based on point cloud modeling, the complex 3D spatial characteristics of the landscape can be accurately restored. The study proposes the method of spatial unit extraction and structural model construction for complex communities and landscapes from a 3D perspective, which makes up for the lack of and insufficiency of spatial analysis through 2D planes, such as 2D planes that may lead to ignoring the bottom space shaded by plants, especially the activity sites and paths in the understory space. This approach promotes 3D spatial morphology analysis and visualization.
- Multidimensional research and analysis: Based on the logic of spatial organization, this study deepens the understanding of landscape spatial structure from the multidimensional perspective of spatial combination, organization, and layout, and establishes a systematic assessment framework for the comprehensive evaluation of landscape design.
- Standard reference and objective weights: Based on the case study, this study summarizes the law of spatial structure organization and establishes a standard reference for spatial structure evaluation. By combining the Entropy Weight Method (EWM) and the Analytic Hierarchy Process (AHP), the objectivity of indicator weights is enhanced, ensuring more reliable evaluation results. The findings show that extensibility (E), spatial diversity (ND) and network centralization (NC) are the key features of landscape spatial structure. The indicators have appropriate numerical intervals, and the intervals of each indicator are summarized separately in this study. Appropriate spatial differences and sprawling rhythmic sequences, as well as centralized overall structure, can promote comfortable user participation and experience.
The proposed evaluation method improves the comprehensiveness, scientific, and objectivity of landscape spatial analysis, while facilitating the visualization and 3D analysis of spatial structure. As urbanization accelerates, cities face challenges such as green space fragmentation, inefficient spatial design, and climate resilience. This evaluation method can guide landscape designers in executing scientific and accurate spatial structure organization, as well as comprehensive comparison and optimization of landscape design schemes. This research contributes to addressing these issues by: (a) providing quantitative guidelines for optimizing park structures, promoting sustainable urban renewal, (b) offering digital assessment tools to diagnose and improve existing urban green spaces, ensuring functional adaptability in response to environmental and demographic changes, and (c) supporting evidence-based decision-making in landscape planning, reducing reliance on subjective assessment. Additionally, the 3D spatial analysis approach can be integrated into design curricula, equipping students with quantitative evaluation methods for future practice. On a broader level, the generalization of characteristic regularity through excellent case studies as a factor in determining evaluation criteria and weights provides a viable method for reducing subjectivity in design evaluation. This method also has the potential to be extended and applied to other types of spatial pattern evaluation, providing a valuable reference for future research and practice.
This study provides a systematic approach to quantifying landscape spatial structure, but it still needs to be extended and thoroughly researched. Future research will consider combining spatial structure with human behavioral data and real experiences to further cognize the interaction between spatial structure and people. Meanwhile, the changes in spatial structure brought about by seasonal changes and vegetation growth can also be considered, or ecological benefits and functional factors can be added to construct a more comprehensive spatial evaluation system.
Author Contributions
Conceptualization, Z.C. and Y.C.; methodology, Z.C. and Y.C.; software, Z.C.; validation, Z.C.; formal analysis, Z.C.; investigation, Z.C.; resources, Z.C.; data curation, Z.C.; writing—original draft preparation, Z.C.; writing—review and editing, Z.C. and Y.C.; visualization, Z.C.; supervision, Y.C.; project administration, Y.C.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets included in this article are not immediately available as they are part of an ongoing study. Requests for access to the datasets should be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1

Table A1.
30 park cases and related information.
Table A1.
30 park cases and related information.
| No. | Name | Area/hm2 | City/Country | Reasons for Selection |
|---|---|---|---|---|
| 1 | Lovers Park | 31.9 | Nanjing, China | First Prize of Landscape Design of the Ministry of Construction of the People’s Republic of China; National Science and Technology Progress Award |
| 2 | Hexi Ecological Park | 24.4 | Asia Pacific Excellence Awards 2019; designed by AECOM | |
| 3 | Green Expo Garden | 49.95 | popularity and public recognition | |
| 4 | Xuqiu Park | 9.56 | long history; popularity and public recognition | |
| 5 | Xuanwu Lake Park-Ying part | 7.3 | long history; popularity and public recognition; one of the three famous lakes in Jiangnan | |
| 6 | Xuanwu Lake Park-Liang part | 8.81 | ||
| 7 | Xuanwu Lake Park-Cui part | 6.59 | ||
| 8 | Punggol Park | 19.6 | Singapore | popularity and public recognition |
| 9 | Bishan-Ang Mo Kio Park (A) | 39.3 | 2016 ASLA Honourable Mention in the Universal Design category; designed by Ramboll Studio Dreiseitl | |
| 10 | Bishan-Ang Mo Kio Park (B) | 30 | ||
| 11 | Oosterpark | 15.1 | Amsterdam, The Netherlands | designer’s masterpieces; designed by American landscape architect Max Oostram |
| 12 | Beatrixpark | 34.7 | designer’s masterpieces; designed by Jakoba (Ko) Mulder | |
| 13 | Vondelpark | 44.9 | honoring playwright and poet Vondel; long history; popularity and public recognition | |
| 14 | Sarphati park | 5.02 | popularity and public recognition | |
| 15 | Rembrandt park | 48.27 | long history; popularity and public recognition | |
| 16 | Noorderpark | 22.9 | Utrecht, The Netherlands | designer’s masterpieces; designed by cc-studio |
| 17 | Het Park | 26.5 | Rotterdam, The Netherlands | designer’s masterpieces; designed by Zocher; long history; popularity and public recognition |
| 18 | Stadt Park | 16.9 | Vienna, Austria | designer’s masterpieces; long history; popularity and public recognition |
| 19 | Parc des Buttes-Chaumont | 28.1 | Paris, France | long history; popularity and public recognition; built according to plans by Jean-Charles Adolphe Alphand |
| 20 | Parc Montsouris | 17.9 | one of the four large urban public parks; designed by Jean-Charles Adolphe Alphand; long history; popularity and public recognition | |
| 21 | Parque Tezozómoc | 32.7 | Mexico | designer’s masterpieces; designed by Mario Schjetnan |
| 22 | Constitution Park | 18.6 | Washington, USA | architecture firm Skidmore, Owings, and Merrill (SOM) and Modern landscape architect Dan Kiley completed Constitution Gardens in 1976; long history; popularity and public recognition |
| 23 | Morningside Park | 16.7 | New York, USA | designer’s masterpieces; designed by Frederick Law Olmsted and Calvert Vaux; long history; popularity and public recognition |
| 24 | Fort Greene Park | 13.7 | famed landscape architects Olmsted and Vaux began designing its new layout. | |
| 25 | Claremont Park | 19.2 | long history; popularity and public recognition | |
| 26 | Crocheron Park | 25.3 | popularity and public recognition | |
| 27 | Public Garden | 10.9 | Boston, USA | National Historic Landmark |
| 28 | Gold Star Family Park | 5.15 | Chicago, USA | popularity and public recognition |
| 29 | Miller River Park | 7.76 | Stanford, USA | plan by Sasaki Associates; popularity and public recognition |
| 30 | Buffalo Bayou Park (eastern part) | 44.3 | Houston, USA | popularity and public recognition |
Appendix A.2

Table A2.
Quantitative results of landscape spatial structure indicators for 30 parks.
Table A2.
Quantitative results of landscape spatial structure indicators for 30 parks.
| No. | Name | CB | SR | ER | E | D | F | NF | NC | ND |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Lovers Park | 0.0170 | 0.8438 | 0.0819 | 0.4286 | 0.3810 | 0.0157 | 0.960 | 0.100 | 0.943 |
| 2 | Hexi Ecological Park | 0.0129 | 1.2826 | 0.0584 | 0.5714 | 0.3330 | 0.0157 | 0.947 | 0.072 | 0.900 |
| 3 | Green Expo Garden | 0.0118 | 0.4691 | 0.2445 | 0.8000 | 0.3000 | 0.0138 | 0.936 | 0.057 | 0.893 |
| 4 | Xuqiu Park | 0.0182 | 0.8410 | 0.4381 | 0.6667 | 0.2000 | 0.0184 | 0.938 | 0.118 | 0.918 |
| 5 | Xuanwu Lake Park-Ying part | 0.0103 | 0.5666 | 0.1272 | 0.7143 | 0.1905 | 0.0215 | 0.964 | 0.151 | 0.998 |
| 6 | Xuanwu Lake Park-Liang part | 0.0145 | 0.6074 | 0.2315 | 0.6667 | 0.2333 | 0.0211 | 0.958 | 0.092 | 0.991 |
| 7 | Xuanwu Lake Park-Cui part | 0.0134 | 1.0727 | 0.1732 | 0.6667 | 0.2333 | 0.0348 | 0.948 | 0.083 | 0.971 |
| 8 | Punggol Park | 0.0064 | 1.2776 | 0.0826 | 0.3750 | 0.3570 | 0.0254 | 0.938 | 0.181 | 0.896 |
| 9 | Bishan-Ang Mo Kio Park (A) | 0.0125 | 0.3408 | 0.3913 | 0.3750 | 0.3570 | 0.0161 | 0.970 | 0.116 | 0.684 |
| 10 | Bishan-Ang Mo Kio Park (B) | 0.0145 | 0.8268 | 0.3237 | 0.4286 | 0.3810 | 0.0223 | 0.973 | 0.061 | 0.639 |
| 11 | Oosterpark | 0.0039 | 0.6967 | 0.0667 | 0.5714 | 0.2860 | 0.0303 | 0.955 | 0.124 | 0.994 |
| 12 | Beatrixpark | 0.0203 | 0.8618 | 0.2602 | 0.5000 | 0.4000 | 0.0123 | 0.944 | 0.103 | 0.918 |
| 13 | Vondelpark | 0.0088 | 1.4019 | 0.2867 | 0.7143 | 0.2860 | 0.0138 | 0.969 | 0.118 | 0.974 |
| 14 | Sarphati park | 0.0096 | 0.3582 | 0.3943 | 0.5000 | 0.2000 | 0.0195 | 0.961 | 0.159 | 0.991 |
| 15 | Rembrandt park | 0.0085 | 1.0606 | 0.0445 | 0.5714 | 0.2143 | 0.0139 | 0.965 | 0.095 | 0.696 |
| 16 | Noorderpark | 0.0115 | 0.4276 | 0.0570 | 0.4286 | 0.5240 | 0.0128 | 0.933 | 0.181 | 0.567 |
| 17 | Het Park | 0.0337 | 0.1993 | 0.0258 | 0.4545 | 0.2180 | 0.0121 | 0.944 | 0.162 | 0.650 |
| 18 | Stadt Park | 0.0222 | 0.0710 | 0.3629 | 0.3333 | 0.6000 | 0.0262 | 0.960 | 0.092 | 0.999 |
| 19 | Parc des Buttes-Chaumont | 0.0010 | 0.3148 | 0.0093 | 0.4286 | 0.3330 | 0.0111 | 0.963 | 0.049 | 0.826 |
| 20 | Parc Montsouris | 0.0047 | 1.0839 | 0.1340 | 0.5000 | 0.2860 | 0.0132 | 0.957 | 0.123 | 0.887 |
| 21 | Parque Tezozómoc | 0.0138 | 0.7856 | 0.2483 | 0.4286 | 0.5240 | 0.0109 | 0.957 | 0.139 | 0.887 |
| 22 | Constitution Gardens | 0.0031 | 0.5937 | 0.3098 | 0.5455 | 0.2000 | 0.0109 | 0.941 | 0.117 | 0.523 |
| 23 | Morningside Park | 0.0159 | 0.7907 | 0.1121 | 0.8571 | 0.1500 | 0.0177 | 0.950 | 0.099 | 0.934 |
| 24 | Fort Greene Park | 0.0051 | 0.3673 | 0.1312 | 0.5714 | 0.3810 | 0.0202 | 0.952 | 0.103 | 0.959 |
| 25 | Claremont Park | 0.0027 | 0.0021 | 0.1943 | 0.5000 | 0.5330 | 0.0190 | 0.952 | 0.074 | 0.863 |
| 26 | Crocheron Park | 0.0025 | 1.5973 | 0.3886 | 0.5000 | 0.4670 | 0.0128 | 0.938 | 0.124 | 0.811 |
| 27 | Public Garden | 0.0085 | 1.4097 | 0.3457 | 0.3333 | 0.3330 | 0.0179 | 0.957 | 0.128 | 0.828 |
| 28 | Gold Star Family Park | 0.0097 | 0.4637 | 0.1039 | 0.6667 | 0.2667 | 0.0212 | 0.940 | 0.182 | 0.619 |
| 29 | Miller River Park | 0.0092 | 1.0563 | 0.4325 | 0.7500 | 0.3333 | 0.0148 | 0.972 | 0.144 | 0.684 |
| 30 | Buffalo Bayou Park (eastern part) | 0.0140 | 0.5337 | 0.0993 | 0.8000 | 0.2500 | 0.0209 | 0.951 | 0.064 | 0.610 |
Appendix A.3

Table A3.
Evaluation score for spatial structure indicators.
Table A3.
Evaluation score for spatial structure indicators.
| No. | Name | CB | SR | ER | F | E | D | NF | NC | ND | SC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Lovers Park | 0.918 | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.993 |
| 2 | Hexi Ecological Park | 1.000 | 0.656 | 0.862 | 1.000 | 1.000 | 1.000 | 1.000 | 0.700 | 1.000 | 0.912 |
| 3 | Green Expo Garden | 1.000 | 1.000 | 1.000 | 0.429 | 1.000 | 1.000 | 0.556 | 0.450 | 1.000 | 0.778 |
| 4 | Xuqiu Park | 0.871 | 1.000 | 0.362 | 1.000 | 0.909 | 1.000 | 0.667 | 1.000 | 1.000 | 0.908 |
| 5 | Xuanwu Lake Park-Ying part | 1.000 | 1.000 | 1.000 | 0.797 | 0.879 | 0.967 | 0.889 | 0.817 | 0.807 | 0.880 |
| 6 | Xuanwu Lake Park-Liang part | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.996 | 1.000 | 1.000 | 0.842 | 0.975 |
| 7 | Xuanwu Lake Park-Cui part | 1.000 | 0.986 | 1.000 | 1.000 | 1.000 | 0.016 | 1.000 | 0.883 | 0.951 | 0.879 |
| 8 | Punggol Park | 1.000 | 0.664 | 1.000 | 0.768 | 1.000 | 0.687 | 0.639 | 0.317 | 1.000 | 0.760 |
| 9 | Bishan-Ang Mo Kio Park (A) | 1.000 | 0.887 | 0.635 | 0.768 | 1.000 | 1.000 | 0.572 | 1.000 | 1.000 | 0.897 |
| 10 | Bishan-Ang Mo Kio Park (B) | 1.000 | 1.000 | 1.000 | 0.998 | 1.000 | 0.906 | 0.390 | 0.517 | 0.758 | 0.815 |
| 11 | Oosterpark | 0.914 | 1.000 | 0.911 | 1.000 | 1.000 | 0.335 | 1.000 | 1.000 | 0.826 | 0.897 |
| 12 | Beatrixpark | 0.787 | 1.000 | 1.000 | 1.000 | 0.940 | 0.949 | 1.000 | 1.000 | 1.000 | 0.971 |
| 13 | Vondelpark | 1.000 | 0.469 | 1.000 | 0.797 | 1.000 | 1.000 | 0.625 | 1.000 | 0.932 | 0.892 |
| 14 | Sarphati park | 1.000 | 0.914 | 0.618 | 1.000 | 0.909 | 1.000 | 1.000 | 0.683 | 0.842 | 0.874 |
| 15 | Rembrandt park | 1.000 | 1.000 | 0.781 | 1.000 | 0.954 | 1.000 | 0.833 | 1.000 | 1.000 | 0.966 |
| 16 | Noorderpark | 1.000 | 1.000 | 0.854 | 0.998 | 0.552 | 0.983 | 0.407 | 0.317 | 0.361 | 0.664 |
| 17 | Het Park | 0.253 | 0.664 | 0.671 | 1.000 | 0.966 | 0.938 | 1.000 | 0.633 | 0.815 | 0.785 |
| 18 | Stadt Park | 0.712 | 0.462 | 0.802 | 0.589 | 0.313 | 0.629 | 1.000 | 1.000 | 0.800 | 0.720 |
| 19 | Parc des Buttes-Chaumont | 0.801 | 0.846 | 0.575 | 0.998 | 1.000 | 0.868 | 0.947 | 0.317 | 1.000 | 0.802 |
| 20 | Parc Montsouris | 0.948 | 0.969 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.993 |
| 21 | Parque Tezozómoc | 1.000 | 1.000 | 1.000 | 0.998 | 0.552 | 0.851 | 1.000 | 1.000 | 1.000 | 0.936 |
| 22 | Constitution Gardens | 0.885 | 1.000 | 1.000 | 1.000 | 0.909 | 0.850 | 0.843 | 1.000 | 0.123 | 0.814 |
| 23 | Morningside Park | 0.964 | 1.000 | 1.000 | 0.184 | 0.752 | 1.000 | 1.000 | 1.000 | 1.000 | 0.846 |
| 24 | Fort Greene Park | 0.956 | 0.928 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.991 |
| 25 | Claremont Park | 0.868 | 0.354 | 1.000 | 1.000 | 0.524 | 1.000 | 1.000 | 0.733 | 1.000 | 0.843 |
| 26 | Crocheron Park | 0.860 | 0.161 | 0.652 | 1.000 | 0.730 | 0.987 | 0.639 | 1.000 | 1.000 | 0.846 |
| 27 | Public Garden | 1.000 | 0.456 | 0.903 | 0.589 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.894 |
| 28 | Gold Star Family Park | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.987 | 0.778 | 0.300 | 0.649 | 0.797 |
| 29 | Miller River Park | 1.000 | 1.000 | 0.395 | 0.644 | 1.000 | 1.000 | 0.444 | 0.933 | 1.000 | 0.847 |
| 30 | Buffalo Bayou Park (eastern part) | 1.000 | 1.000 | 1.000 | 0.429 | 1.000 | 1.000 | 1.000 | 0.567 | 0.597 | 0.771 |
References
- Bertram, C.; Rehdanz, K. Preferences for Cultural Urban Ecosystem Services: Comparing Attitudes, Perception, and Use. Ecosyst. Serv. 2015, 12, 187–199. [Google Scholar] [CrossRef]
- Mostafazadeh, R.; Alaei, N.; Mirchooli, F.; Hussain, S. Changes in Urban Green Space Configuration and Connectivity Using Spatial Graph-Based Metrics in Ardabil Developing City, Iran. Environ. Monit. Assess. 2024, 196, 778. [Google Scholar] [CrossRef]
- Ulrich, R.S. View Through a Window May Influence Recovery from Surgery. Science 1984, 224, 420–421. [Google Scholar] [CrossRef] [PubMed]
- Maas, J.; Verheij, R.A.; Groenewegen, P.P.; De Vries, S.; Spreeuwenberg, P. Green Space, Urbanity, and Health: How Strong Is the Relation? J. Epidemiol. Community Health 2006, 60, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Lin, G. The Relationship between Urban Green Space and Social Health of Individuals: A Scoping Review. Urban For. Urban Green. 2023, 85, 127969. [Google Scholar] [CrossRef]
- Li, Y.; Lin, G. Demand-Side Effects of Urban Green Spaces: How Attractiveness Helps Overcome Subjective Barriers to Health Behaviours. Urban For. Urban Green. 2024, 94, 128277. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Moscardó, V.; Vallina Rodríguez, A.; Lázaro, E. Spatial Statistical Analysis of the Relationship between Self-Reported Mental Health during the COVID-19 Lockdown and Closeness to Green Infrastructure. Urban For. Urban Green. 2022, 68, 127457. [Google Scholar] [CrossRef]
- Europe, C.O. European Landscape Convention. In Proceedings of the Report and Convention, Florence, Italy, 20 October 2000. [Google Scholar]
- Madureira, H.; Nunes, F.; Oliveira, J.V.; Cormier, L.; Madureira, T. Urban Residents’ Beliefs Concerning Green Space Benefits in Four Cities in France and Portugal. Urban For. Urban Green. 2015, 14, 56–64. [Google Scholar] [CrossRef]
- Zhang, L.; Hao, P.; Dong, L.; Wang, Y. Optimization Strategy for Maintenance Management of Herbaceous Layer in Urban Parks Based on Spontaneous Plants: A Case Study of Xicheng District, Beijing. Landsc. Archit. 2024, 31, 46–54. [Google Scholar] [CrossRef]
- Chen, Y.; La Rosa, D.; Yue, W.; Xu, Z.; Zhuo, Y. Do Larger Cities Enjoy Better Green Space Accessibility? Evidence from China. Environ. Impact Assess. Rev. 2024, 107, 107544. [Google Scholar] [CrossRef]
- Zhang, L. An Improved Indicator Standardization Method for Multi-Indicator Composite Evaluation: A Case Study in the Evaluation of Ecological Civilization Construction in China. Environ. Impact Assess. Rev. 2024, 108, 107600. [Google Scholar] [CrossRef]
- Jim, C.Y. Green-Space Preservation and Allocation for Sustainable Greening of Compact Cities. Cities 2004, 21, 311–320. [Google Scholar] [CrossRef]
- Gehl, J. Life Between Buildings: Using Public Space, 6th ed.; Island Press: Washington, DC, USA, 2011; ISBN 978-1-59726-827-1. [Google Scholar]
- Byrne, J.; Sipe, N. Green and Open Space Planning for Urban Consolidation—A Review of the Literature and Best Practice; Urban Res. Program, Issues Paper 11; Griffith University: Brisbane, Australia, 2010. [Google Scholar]
- Alaei, N.; Mohammadzadeh, F.; Mostafazadeh, R.; Talebi Khiavi, H. Assessing Spatiotemporal Urban Green Space per Capita and Its Connectivity in a Small Size City in Northwest Iran. GeoJournal 2024, 89, 148. [Google Scholar] [CrossRef]
- Chiesura, A. The Role of Urban Parks for the Sustainable City. Landsc. Urban Plan. 2004, 68, 129–138. [Google Scholar] [CrossRef]
- Antrop, M. Why Landscapes of the Past Are Important for the Future. Landsc. Urban Plan. 2005, 70, 21–34. [Google Scholar] [CrossRef]
- Dee, C. Form and Fabric in Landscape Architecture: A Visual Introduction; Taylor & Francis: Oxfordshire, UK, 2004; ISBN 0-203-63907-3. [Google Scholar]
- Moraitis, K. Composing the Landscape: Analyzing Landscape Architecture as Design Formation. Land 2024, 13, 827. [Google Scholar] [CrossRef]
- Li, X. Study on the Structures and Images of Landscape Planting. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2006. [Google Scholar]
- Cheng, Z.; Cheng, Y. Research on the Spatial Structure of Landscape Architecture from Design Intention to Function Use; Wichmann Verlag: Berlin, Germany, 2024. [Google Scholar]
- Liu, M. Mapping Landscape Spaces: Understanding, Interpretation, and the Use of Spatial-Visual Landscape Characteristics in Landscape Design. A+BE|Archit. Built Environ. 2020, 20, 1–248. [Google Scholar] [CrossRef]
- Zlatanova, S.; Yan, J.; Wang, Y.; Diakité, A.; Isikdag, U.; Sithole, G.; Barton, J. Spaces in Spatial Science and Urban Applications—State of the Art Review. ISPRS Int. J. Geo-Inf. 2020, 9, 58. [Google Scholar] [CrossRef]
- Yoon, C. Characterization of Bubble Diagram in the Process of Architectural Form Generation. Archit. Res. 2000, 2, 7–15. [Google Scholar]
- Chen, R.; Zhao, J.; Yao, X.; Jiang, S.; He, Y.; Bao, B.; Luo, X.; Xu, S.; Wang, C. Generative Design of Outdoor Green Spaces Based on Generative Adversarial Networks. Buildings 2023, 13, 1083. [Google Scholar] [CrossRef]
- Caneparo, L. Semantic Knowledge in Generation of 3D Layouts for Decision-Making. Autom. Constr. 2022, 134, 104012. [Google Scholar] [CrossRef]
- Pérez-Martínez, I.; Martínez-Rojas, M.; Soto-Hidalgo, J.M. A Methodology for Urban Planning Generation: A Novel Approach Based on Generative Design. Eng. Appl. Artif. Intell. 2023, 124, 106609. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z.; Deng, Q. Exploration on Diversity Generation of Campus Layout Based on GAN. Computational Design and Robotic Fabrication. In Hybrid Intelligence; Philip, F., Chai, Y., Chao, Y., Li, K., Sun, T., Eds.; Springer Nature: Singapore, 2023; pp. 233–243. ISBN 978-981-19863-6-9. [Google Scholar]
- Fan, B.; Gu, J.; Ai, S.; Chen, X.; Du, S.; Cheng, Y. Digital Characteristics of Spatial Layout in Urban Park Scene Space: Spatial Classification, Quantitative Indicators, and Design Applications Based on Completed Park Cases. Land 2024, 13, 2251. [Google Scholar] [CrossRef]
- Slager, C.T.J.; de Vries, B. Landscape Generator: Method to Generate Landscape Configurations for Spatial Plan-Making. Comput. Environ. Urban Syst. 2013, 39, 1–11. [Google Scholar] [CrossRef]
- Garau, C.; Annunziata, A.; Yamu, C. A Walkability Assessment Tool Coupling Multi-Criteria Analysis and Space Syntax: The Case Study of Iglesias, Italy. Eur. Plan. Stud. 2024, 32, 211–233. [Google Scholar] [CrossRef]
- Qi, K.; Fan, Z.Q. Evaluation Method for Landscape Connectivity Based on Graph Theory: A Case Study of Natural Forests in Minqing County, Fujian Province. Acta Ecol. Sin 2016, 36, 7580–7593. [Google Scholar]
- Modica, G.; Praticò, S.; Laudari, L.; Ledda, A.; Di Fazio, S.; De Montis, A. Implementation of Multispecies Ecological Networks at the Regional Scale: Analysis and Multi-Temporal Assessment. J. Environ. Manag. 2021, 289, 112494. [Google Scholar] [CrossRef]
- Wang, L.; Han, X.; He, J.; Jung, T. Measuring Residents’ Perceptions of City Streets to Inform Better Street Planning through Deep Learning and Space Syntax. ISPRS J. Photogramm. Remote Sens. 2022, 190, 215–230. [Google Scholar] [CrossRef]
- Zhou, J.; Hou, Q. Resilience Assessment and Planning of Suburban Rural Settlements Based on Complex Network. Sustain. Prod. Consum. 2021, 28, 1645–1662. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, Y. Prediction of Pedestrian Distribution and Matching Analysis Based on Landscape Structure System. Landsc. Archit. 2020, 27, 104–109. [Google Scholar]
- Weng, X.; Shao, D.; Du, J.; Wang, X. On the Application of Spatial Sequence in the Theme Expression of Urban Exhibition Garden:A Case Study of Xingtai Exhibition Garden in Hebei Province. Archit. Cult. 2023, 3, 250–252. [Google Scholar]
- Qi, J.; Lin, E.S.; Yok Tan, P.; Chun Man Ho, R.; Sia, A.; Olszewska-Guizzo, A.; Zhang, X.; Waykool, R. Development and Application of 3D Spatial Metrics Using Point Clouds for Landscape Visual Quality Assessment. Landsc. Urban Plan. 2022, 228, 104585. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Y.; Zlatanova, S.; Cheng, S. Quantitative Analysis Method of the Organizational Characteristics and Typical Types of Landscape Spatial Sequences Applied with a 3D Point Cloud Model. Land 2024, 13, 770. [Google Scholar] [CrossRef]
- Yamu, C.; van Nes, A.; Garau, C. Bill Hillier’s Legacy: Space Syntax—A Synopsis of Basic Concepts, Measures, and Empirical Application. Sustainability 2021, 13, 3394. [Google Scholar] [CrossRef]
- Niu, H.; Xiu, Z.; Xiao, D. Impact of Land-Use Change on Ecological Vulnerability in the Yellow River Basin Based on a Complex Network Model. Ecol. Indic. 2024, 166, 112212. [Google Scholar] [CrossRef]
- Shi, Y.L.; Huang, Y.; Xiao, L. Spatial structure and layout optimization of mountain park based on social network analysis. Chin. Landsc. Archit. 2020, 36, 91–96. [Google Scholar] [CrossRef]
- Wang, Y.J.; Cheng, S.; Cheng, Z.; Cheng, Y. Exploring the Construction and Analysis Method of Landscape Spatial Structure Based on Complex Networks. Environ. Plan. B Urban Anal. City Sci. 2023, 23, 745–762. [Google Scholar] [CrossRef]
- Lu, S.M. Network characteristics in the spatial structure of Qushui Garden, a classical garden in Shanghai. Chin. Landsc. Archit. 2011, 27, 60–64. [Google Scholar]
- Wang, Y.C. Schema Language: A New Paradigm of Landscape Local Expression and Spatial Logic; China Building Industry Press: Beijing, China, 2018. [Google Scholar]
- Yang, X.J.; Liu, X.Y.; Ye, J. Landscape Architecture Research and Practice from the Perspective of Topology. Urban Archit. 2021, 18, 157–160. [Google Scholar]
- Freytag, A. Topology and Phenomenology in Landscape Architecture. In Landschaftsarchitekturtheorie: Aktuelle Zugänge, Perspektiven und Positionen; Berr, K., Ed.; Springer Fachmedien: Wiesbaden, Germany, 2018; pp. 195–225. ISBN 978-3-658-18838-2. [Google Scholar]
- Do, E.Y.-L.; Gross, M.D. Thinking with Diagrams in Architectural Design. Artif. Intell. Rev. 2001, 15, 135–149. [Google Scholar] [CrossRef]
- Lian, J.; Nijhuis, S.; Bracken, G.; Wu, X.; Wu, X.; Chen, D. Conservation and Development of the Historic Garden in a Landscape Context: A Systematic Literature Review. Landsc. Urban Plan. 2024, 246, 105027. [Google Scholar] [CrossRef]
- Qin, X.; Yang, D.; Wangari, V.W. Quantitative Characterization and Evaluation of Highway Greening Landscape Spatial Quality Based on Deep Learning. Environ. Impact Assess. Rev. 2024, 107, 107559. [Google Scholar] [CrossRef]
- Wen, H.; Lin, H.; Liu, X.; Guo, W.; Yao, J.; He, B.-J. An Assessment of the Psychologically Restorative Effects of the Environmental Characteristics of University Common Spaces. Environ. Impact Assess. Rev. 2025, 110, 107645. [Google Scholar] [CrossRef]
- Urech, P.R.; Dissegna, M.A.; Girot, C.; Grêt-Regamey, A. Point Cloud Modeling as a Bridge between Landscape Design and Planning. Landsc. Urban Plan. 2020, 203, 103903. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Y.; Zlatanova, S.; Palazzo, E. Identification of Physical and Visual Enclosure of Landscape Space Units with the Help of Point Clouds. Spat. Cogn. Comput. 2020, 20, 257–279. [Google Scholar] [CrossRef]
- Brown, G.; Weber, D. Public Participation GIS: A New Method for National Park Planning. Landsc. Urban Plan. 2011, 102, 1–15. [Google Scholar] [CrossRef]
- Tachikawa, R.; Kunii, Y. Comprehensive Quantitative Understanding of the Landscape Using Tls Point Cloud Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLIII-B2-2022, 297–302. [Google Scholar] [CrossRef]
- Long, C.; Sun, Z.; Wang, Y. Study on the Walking Behavior of the Elderly and the Spatial Organization Characters of Urban Parks—Based on Space Syntax Theory. Archit. Cult. 2018, 9, 148–149. [Google Scholar]
- Chen, Y. Application of Depthmap Software in Spatial Structure Analysis of Garden. Exp. Technol. Manag. 2009, 26, 87–89. [Google Scholar]
- Cheng, Y.N. The Theory and Method of Modern Landscape Design; Southeast University Press: Nanjing, China, 2014. [Google Scholar]
- Pattanayak, H.S.; Verma, H.K.; Sangal, A.L. Lengthening of Average Path Length in Social Networks Due to the Effect of Community Structure. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 8401–8421. [Google Scholar] [CrossRef]
- Hou, Y.; Zhao, X.; Zhang, B. Significance Analysis between Morning Exercise and Spatial Organization Characteristics of Urban Park—Taking 4 Urban Parks in Harbin for Example. Landsc. Archit. 2017, 24, 109–116. [Google Scholar]
- Deng, P.; Huang, Q.; Liu, F.; Wang, Z.; Liu, M. The Research on Identification and Spatial Pattern of Urban Mixed Land-Use: A Case Study of Chengdu. Ecol. Indic. 2023, 154, 110891. [Google Scholar] [CrossRef]
- Wang, Y. The Logical Thinking and Framework of Landscape Space Pattern Language. Landsc. Archit. 2017, 4, 89–98. [Google Scholar]
- Liu, B.; Zhang, T. Landscape Space Sequence Organization Based on Visual Sense. Chin. Landsc. Archit. 2010, 26, 31–35. [Google Scholar]
- Casey, E.S. The Edge (s) of Landscape: A Study in Liminology. In The Place of Landscape: Concepts, Contexts, Studies; The MIT Press: Cambridge, MA, USA, 2011; pp. 91–109. [Google Scholar]
- Wang, Z. Research on the Design Method of “Space with Path” in Architecture. Ph.D. Thesis, Tianjin University, Tianjin, China, 2019. [Google Scholar]
- Feng, J.Z. Over Landscaping Organizing. Chin. Landsc. Archit. 2010, 10, 20–22. [Google Scholar]
- Liu, M.; Nijhuis, S. Mapping Landscape Spaces: Methods for Understanding Spatial-Visual Characteristics in Landscape Design. Environ. Impact Assess. Rev. 2020, 82, 106376. [Google Scholar] [CrossRef]
- Jessel, B. Elements, Characteristics and Character–Information Functions of Landscapes in Terms of Indicators. Ecol. Indic. 2006, 6, 153–167. [Google Scholar]
- Yue, W.; Xu, J.; Tan, W.; Zhao, J.; Su, F. Spatial Scale Analysis of the Diversities of Urban Landscape: A Case Study within the External Circle Highway of Shanghai City. Acta Ecol. Sin. 2005, 1, 122–128. [Google Scholar]
- Yoshinobu, A. Exterior Space Design; China Building Industry Press: Beijing, China, 1985. [Google Scholar]
- Yang, W.; Kedron, P.; Frazier, A.E. Percentage of Area Protected Can Substitute for More Complicated Structural Metrics When Monitoring Protected Area Connectivity. Ecol. Indic. 2024, 158, 111387. [Google Scholar] [CrossRef]
- Liu, J. Introduction to Social Network Analysis; Social Sciences Academic Press: Beijing, China, 2004. [Google Scholar]
- Wang, Y.J. Research on the Composition of Landscape Space Assisted by Digital Technology. Ph.D. Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Bartesaghi, P.; Clemente, G.P.; Grassi, R. Clustering Coefficients as Measures of the Complex Interactions in a Directed Weighted Multilayer Network. Phys. A Stat. Mech. Its Appl. 2023, 610, 128413. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A Review of Fuzzy AHP Methods for Decision-Making with Subjective Judgements. Expert Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Yu, D.; Kou, G.; Xu, Z.; Shi, S. Analysis of Collaboration Evolution in AHP Research: 1982–2018. Int. J. Info. Tech. Dec. Mak. 2021, 20, 7–36. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 1–5. [Google Scholar] [CrossRef]
- Sun, N.; Li, C.; Guo, B.; Sun, X.; Yao, Y.; Wang, Y. Urban Flooding Risk Assessment Based on FAHP–EWM Combination Weighting: A Case Study of Beijing. Geomat. Nat. Hazards Risk 2023, 14, 2240943. [Google Scholar] [CrossRef]
- Chen, R.; Zhao, J.; Hao, H.; Wang, K. A Large-Scale Measurement Method of Esthetical Appreciation Laws Based on the Multimodal Machine Learning. Zhuangshi 2021, 7, 106–111. [Google Scholar]
- Buchholz, T.; Rametsteiner, E.; Volk, T.A.; Luzadis, V.A. Multi Criteria Analysis for Bioenergy Systems Assessments. Energy Policy 2009, 37, 484–495. [Google Scholar] [CrossRef]
- Mendoza, G.A.; Martins, H. Multi-Criteria Decision Analysis in Natural Resource Management: A Critical Review of Methods and New Modelling Paradigms. For. Ecol. Manag. 2006, 230, 1–22. [Google Scholar] [CrossRef]
- Bock, H.-H.; Diday, E. Analysis of Symbolic Data: Exploratory Methods for Extracting Statistical Information from Complex Data; Springer Science & Business Media: Heidelberg, Germany, 2012. [Google Scholar]
- Saaty, T.L. Decision Making with the Analytic Hierarchy Process. Int. J. Softw. Sci. Comput. 2008, 1, 83. [Google Scholar] [CrossRef]
- Grove, M.; Zhang, T. Forged by Floods: Wuhan Yangtze Riverfront Park. Landsc. Archit. Front. 2020, 8, 130–145. [Google Scholar] [CrossRef]
- Qi, J.; Lin, E.S.; Tan, P.Y.; Zhang, X.; Ho, R.; Sia, A.; Olszewska-Guizzo, A.; Waykool, R. Applying 3D Spatial Metrics for Landscape Planning: Creating and Measuring Landscape Scenarios by a Point Cloud-Based Approach. Ecol. Inform. 2024, 79, 102436. [Google Scholar] [CrossRef]
- Wang, S.; Li, A. Identify the Significant Landscape Characteristics for the Perceived Restorativeness of 8 Perceived Sensory Dimensions in Urban Green Space. Heliyon 2024, 10, e27925. [Google Scholar] [CrossRef] [PubMed]
- Baljon, J.L. Designing Parks: An Examination of Contemporary Approaches to Design in Landscape Architecture Based on a Comparative Design Analysis of Entries for the Concours International; Wageningen University and Research: Wageningen, The Netherlands, 1992. [Google Scholar]
- Zhang, Q.H.; Zhang, Y.X. Research on the Spatial Sequence of Memorial Landscape Based on Visual Sense—A Case Study of Nanjing Yuhuatai Martyrs’ Cemetery. Chin. Landsc. Arch. 2019, 35, 55–60. [Google Scholar]
- Zhai, Y.J. Application of spatial organization analysis and design management of urban parks based on space syntax theory: A preliminary study on the method of convex map analysis. Chin. Landsc. Archit. 2016, 32, 80–84. [Google Scholar]
- Akcelik, G.N.; Choe, K.W.; Rosenberg, M.D.; Schertz, K.E.; Meidenbauer, K.L.; Zhang, T.; Rim, N.; Tucker, R.; Talen, E.; Berman, M.G. Quantifying Urban Environments: Aesthetic Preference through the Lens of Prospect-Refuge Theory. J. Environ. Psychol. 2024, 97, 102344. [Google Scholar] [CrossRef]
- Guangkun, Z.; Yingsheng, H.; Shengdong, L. Study on the Accessibility of Public Space on Huangpu River Waterfront—Public Transportation Evaluation and Optimization Strategy Based on Social Network Analysis. Chin. Landsc. Archit. 2020, 36, 64–69. [Google Scholar] [CrossRef]
- Tveit, M.; Ode, Å.; Fry, G. Key Concepts in a Framework for Analysing Visual Landscape Character. Landsc. Res. 2006, 31, 229–255. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, E.S.; Tan, P.Y.; Qi, J.; Waykool, R. Assessment of Visual Landscape Quality of Urban Green Spaces Using Image-Based Metrics Derived from Perceived Sensory Dimensions. Environ. Impact Assess. Rev. 2023, 102, 107200. [Google Scholar] [CrossRef]
- Jose, V.R.R.; Nau, R.F.; Winkler, R.L. Sensitivity to Distance and Baseline Distributions in Forecast Evaluation. Manage. Sci. 2009, 55, 582–590. [Google Scholar] [CrossRef][Green Version]
- Kitchenham, B.A.; Pickard, L.; Linkman, S.; Jones, P. A Framework for Evaluating a Software Bidding Model. Inf. Softw. Technol. 2005, 47, 747–760. [Google Scholar] [CrossRef]
- Cai, K.; Huang, W.; Lin, G. Bridging Landscape Preference and Landscape Design: A Study on the Preference and Optimal Combination of Landscape Elements Based on Conjoint Analysis. Urban For. Urban Green. 2022, 73, 127615. [Google Scholar] [CrossRef]
- Dane, G.; Evers, S.; van den Berg, P.; Klippel, A.; Verduijn, T.; Wallgrün, J.O.; Arentze, T. Experiencing the Future: Evaluating a New Framework for the Participatory Co-Design of Healthy Public Spaces Using Immersive Virtual Reality. Comput. Environ. Urban Syst. 2024, 114, 102194. [Google Scholar] [CrossRef]
- Huang, P.; Yao, P.; Hao, Z.; Peng, H.; Guo, L. Improved Constrained k-Means Algorithm for Clustering with Domain Knowledge. Mathematics 2021, 9, 2390. [Google Scholar] [CrossRef]
- Basu, S.; Banerjee, A.; Mooney, R.J. Active Semi-Supervision for Pairwise Constrained Clustering. In Proceedings of the Fourth SIAM International Conference on Data Mining; Berry, M.W., Dayal, U., Kamath, C., Skillicorn, D., Eds.; Siam: Philadelphia, PA, USA, 2004; pp. 333–344. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).