Study on Intelligent Classing of Public Welfare Forestland in Kunyu City
Abstract
1. Introduction
2. Materials and Methods
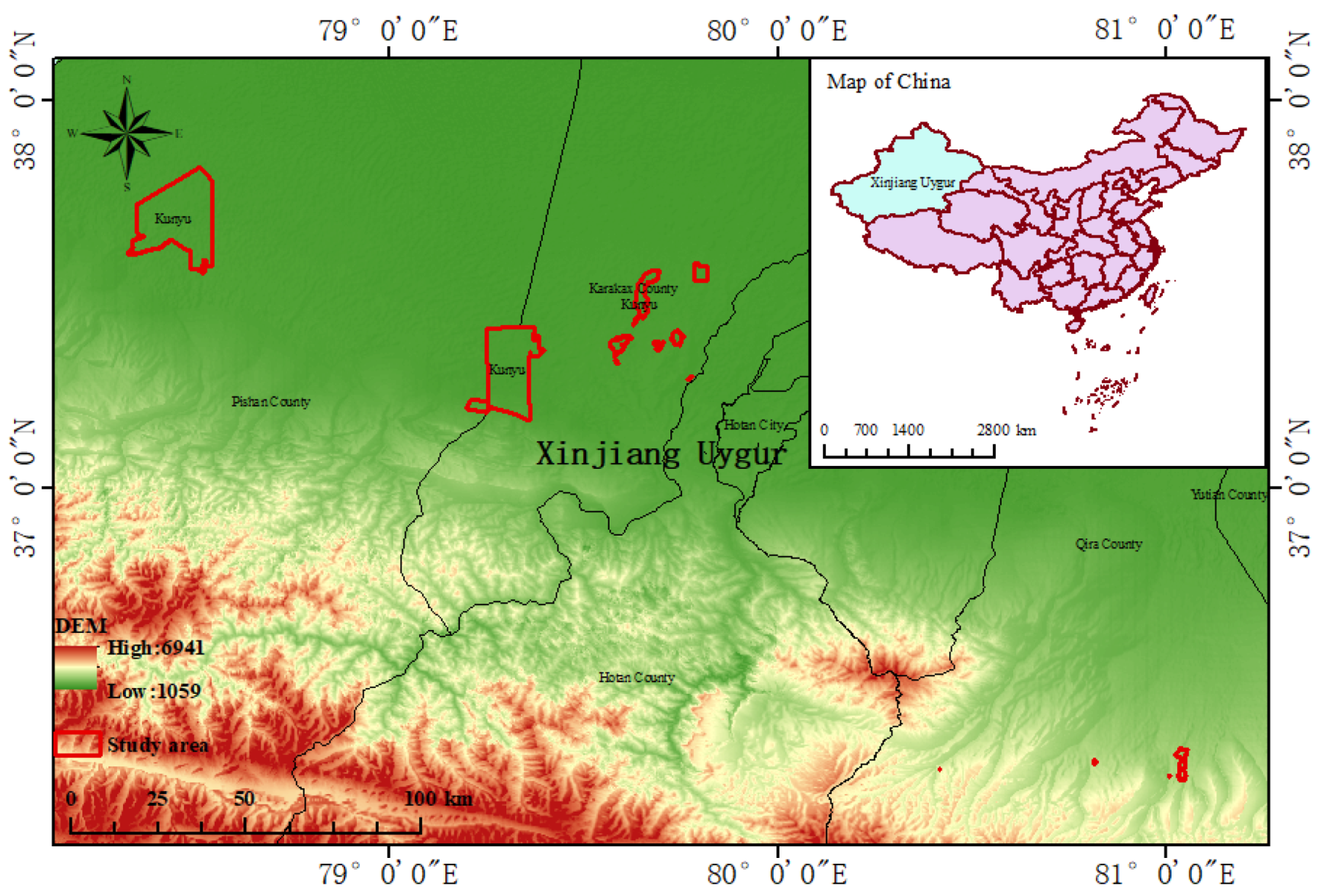
2.1. Research Area
2.2. Data Sources and Preprocessing
2.3. Model Establishment
2.3.1. Sample Training Set
2.3.2. Support Vector Machine Model
2.3.3. Parameter Optimization
2.3.4. K-Fold Cross-Validation
2.3.5. Model Evaluation Metrics
2.4. Software Tools
3. Results and Analysis
3.1. SVM Parameter Optimization
3.1.1. Grid Search
3.1.2. Genetic Algorithm
3.1.3. Particle Swarm Optimization
3.2. Validation and Comparison of Model Generalization Ability
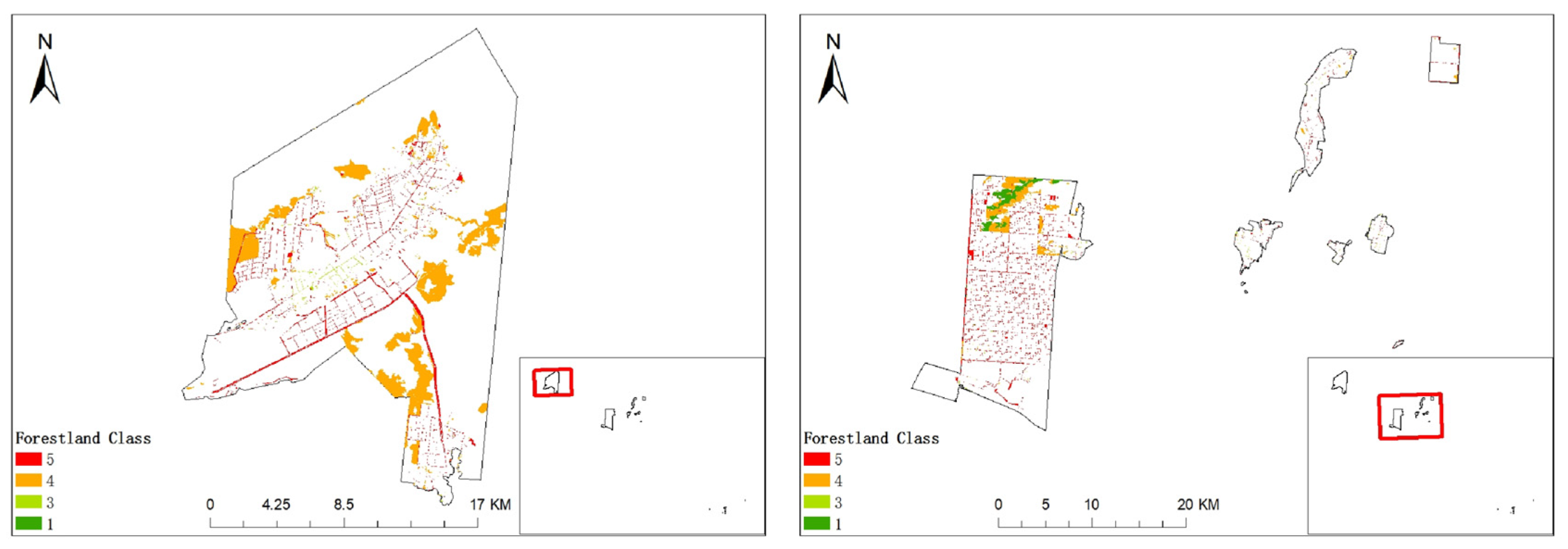
3.3. SVM Model for Classification of Public Welfare Forestland in Kunyu City
4. Discussion
4.1. Model Parameter Optimization
4.2. Evaluation Metrics for Imbalanced Datasets
4.3. Performance of Different Classifications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Li, W. Land Price Model Based on Forest Land Classification. Mod. Inf. Technol. 2019, 3, 18–19. [Google Scholar] [CrossRef]
- Wu, Y.; Xue, H.; Wu, K. Construction of technical specification for forest land grading. China Land 2022, 20–21. [Google Scholar] [CrossRef]
- Yang, H.; Feng, X.; Cui, W.; Zhang, X. Discussion on the construction and management of protected natural areas in Xinjiang Production and Construction Corps. For. Constr. 2023, 9–12. [Google Scholar]
- Qiu, Y.; Zheng, Y. A Background Analysis and Technical Framework on Forest Land Classification and Evaluation. For. Resour. Manag. Ment. 2006, 1–5. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Wang, B.; Li, X. A novel ensemble method for k-nearest neighbor. Pattern Recognit. J. Pattern Recognit. Soc. 2019, 85, 13–25. [Google Scholar] [CrossRef]
- Trabelsi, A.; Elouedi, Z.; Lefevre, E. Decision tree classifiers for evidential attribute values and class labels. Fuzzy Set. Syst. 2019, 366, 46–62. [Google Scholar] [CrossRef]
- Zhang, M.; Qu, H.; Xie, X.; Kurths, J. Supervised learning in spiking neural networks with noise-threshold. Neurocomputing 2017, 219, 333–349. [Google Scholar] [CrossRef]
- Fernandez-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we Need Hundreds of Classifiers to Solve Real World Classification Problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Burbidge, R.; Trotter, M.; Buxton, B.; Holden, S. Drug design by machine learning: Support vector machines for pharmaceutical data analysis. Comput. Chem. 2001, 26, 5–14. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Wang, L.; Tian, J.; Liu, J. Farmland classification based on data mining classification method. Trans. CSAE 2009, 25, 262–267. [Google Scholar]
- Zhang, Z.H.; Nie, Y.; Ma, Z.Y. Evaluation of cultivated land quality based on BP neural network method: A case study at Xiangyang urban area. China Agric. Inform. 2019, 31, 72–83. [Google Scholar]
- Fan, S.; Qiu, L.; Ru, K.; Chen, Q.; Hu, Y. Classification method of agricultural land quality based on back propagation neural network and support vector machine. J. China Agric. Univ. 2018, 23, 138–148. [Google Scholar]
- Zhu, X.; Zhang, L.T.; Jin, H.H. Cultivated Land Quality Assessment Methodology Based on Factor Method and SVM Model. Chin. J. Soil. Sci. 2020, 51, 561–567. [Google Scholar] [CrossRef]
- Ren, B.; Zhang, Q.; Zhou, X. Research on Cultivated Land Quality Evaluation Based on Data Mining Model. Jiangxi Sci. 2022, 40, 1091–1095. [Google Scholar] [CrossRef]
- Ali, A.H.; Abdullah, M.Z. An Efficient Model for Data Classification Based on SVM Grid Parameter Optimization and PSO Feature Weight Selection. Int. J. Integr. Eng. 2020, 12, 1–12. [Google Scholar]
- Wumaier, T.; Xu, C.; Guo, H.Y.; Jin, Z.J.; Zhou, H.J. Fault Diagnosis of Wind Turbines Based on a Support Vector Machine Optimized by the Sparrow Search Algorithm. IEEE Access 2021, 9, 69307–69315. [Google Scholar] [CrossRef]
- Huang, W.; Liu, H.; Zhang, Y.; Mi, R.; Tong, C.; Xiao, W.; Shuai, B. Railway dangerous goods transportation system risk identification: Comparisons among SVM, PSO-SVM, GA-SVM and GS-SVM. Appl. Soft Comput. 2021, 109, 16. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Xu, P.Y.; Liu, J.; He, J.X.; Yang, H.T.; Zeng, Y.; He, Y.Y.; Yang, C.F. Comparison of LR, 5-CV SVM, GA SVM, and PSO SVM for landslide susceptibility assessment in Tibetan Plateau area, China. J. Mt. Sci.-Engl. 2023, 20, 979–995. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, P.X.; Peng, P.A.; Khandelwal, M.; Qiu, Y.G. Performance Evaluation of Rockburst Prediction Based on PSO-SVM, HHO-SVM, and MFO-SVM Hybrid Models. Min. Met. Explor. 2023, 40, 617–635. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, S.L.; Qiu, Y.G.; Armaghani, D.; Zhou, A.N.; Yong, W.X. Predicting tunnel squeezing using support vector machine optimized by whale optimization algorithm. Acta. Geotech. 2022, 17, 1343–1366. [Google Scholar] [CrossRef]
- Gao, X.; Hou, J. An improved SVM integrated GS-PCA fault diagnosis approach of Tennessee Eastman process. Neurocomputing 2016, 174, 906–911. [Google Scholar] [CrossRef]
- Wu, C.H.; Tzeng, G.H.; Goo, Y.J.; Fang, W.C. A real-valued genetic algorithm to optimize the parameters of support vector machine for predicting bankruptcy. Expert. Syst. Appl. 2007, 32, 397–408. [Google Scholar] [CrossRef]
- Huang, C.; Dun, J.F. A distributed PSO-SVM hybrid system with feature selection and parameter optimization. Appl. Soft Comput. 2008, 8, 1381–1391. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Song, S.; Zhan, Z.; Long, Z.; Zhang, J.; Yao, L. Comparative study of SVM methods combined with voxel selection for object category classification on fMRI data. PLoS ONE 2011, 6, e17191. [Google Scholar] [CrossRef]
- Wang, J.; Ran, R.; Song, Z.; Sun, J. Short-Term Photovoltaic Power Generation Forecasting Based on Environmental Factors and GA-SVM. J. Electr. Eng. Technol. 2017, 12, 64–71. [Google Scholar] [CrossRef]
- Phan, A.V.; Le Nguyen, M.; Bui, L.T. Feature weighting and SVM parameters optimization based on genetic algorithms for classification problems. Appl. Intell. 2017, 46, 455–469. [Google Scholar] [CrossRef]
- Li, X.Z.N. A Method of Depression Recognition Based on Visual Information. J. Med. Imaging Health Inform. 2017, 7, 1572–1579. [Google Scholar] [CrossRef]
- Sukawattanavijit, C.; Chen, J.; Zhang, H.S. GA-SVM Algorithm for Improving Land-Cover Classification Using SAR and Optical Remote Sensing Data. IEEE Geosci. Remote Sens. 2017, 14, 284–288. [Google Scholar] [CrossRef]
- Sajan, K.S.; Kumar, V.; Tyagi, B. Genetic algorithm based support vector machine for on-line voltage stability monitoring. Int. J. Elec. Power 2015, 73, 200–208. [Google Scholar] [CrossRef]
- Xue, X.H.; Xiao, M. Application of genetic algorithm-based support vector machines for prediction of soil liquefaction. Env. Earth Sci. 2016, 75, 874. [Google Scholar] [CrossRef]
- Richardson, E.; Trevizani, R.; Greenbaum, J.A.; Carter, H.; Nielsen, M.; Peters, B. The receiver operating characteristic curve accurately assesses imbalanced datasets. Patterns 2024, 5, 100994. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, Y.Z.; Xie, D.J. Implications of imbalanced datasets for empirical ROC-AUC estimation in binary classification tasks. J. Stat. Comput. Sim. 2024, 94, 183–203. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef]
- Sharma, N.; Saharia, M.; Ramana, G.V. High resolution landslide susceptibility mapping using ensemble machine learning and geospatial big data. Catena 2024, 235, 107653. [Google Scholar] [CrossRef]
- Lanjewar, M.G.; Morajkar, P.; Payaswini, P. Modified transfer learning frameworks to identify potato leaf diseases. Multimed. Tools Appl. 2023, 83, 50401–50423. [Google Scholar] [CrossRef]
- Sun, K.; Li, G.; Chen, H.; Liu, J.; Li, J.; Hu, W. A novel efficient SVM-based fault diagnosis method for multi-split air conditioning system’s refrigerant charge fault amount. Appl. Therm. Eng. 2016, 108, 989–998. [Google Scholar] [CrossRef]
- Biswas, P.; Samanta, T. A Method for Fault Detection in Wireless Sensor Network Based on Pearson’s Correlation Coefficient and Support Vector Machine Classification. Wirel. Pers. Commun. 2022, 123, 2649–2664. [Google Scholar] [CrossRef]
- Koziarski, M.; Wozniak, M.; Krawczyk, B. Combined Cleaning and Resampling algorithm for multi-class imbalanced data with label noise. Knowl.-Based Syst. 2020, 204, 106223. [Google Scholar] [CrossRef]
- Wah, Y.B.; Ismail, A.; Azid, N.; Jaafar, J.; Aziz, I.A.; Hasan, M.H.; Zain, J.M. Machine Learning and Synthetic Minority Oversampling Techniques for Imbalanced Data: Improving Machine Failure Prediction. CMC-Comput. Mater. Con. 2023, 75, 4821–4841. [Google Scholar] [CrossRef]
- Peng, L.Z.; Zhang, H.L.; Yang, B.; Chen, Y.H. A new approach for imbalanced data classification based on data gravitation. Inf. Sci. 2014, 288, 347–373. [Google Scholar] [CrossRef]
- Chao, X.R.; Kou, G.; Peng, Y.; Fernández, A. An efficiency curve for evaluating imbalanced classifiers considering intrinsic data characteristics: Experimental analysis. Inf. Sci. 2022, 608, 1131–1156. [Google Scholar] [CrossRef]
- Guo, J.; Wang, M.; Sun, L.; Xu, D. New method of fault diagnosis for rolling bearing imbalance data set based ongenerative adversarial network. Comput. Integr. Manuf. Syst. 2022, 28, 2825–2835. [Google Scholar] [CrossRef]
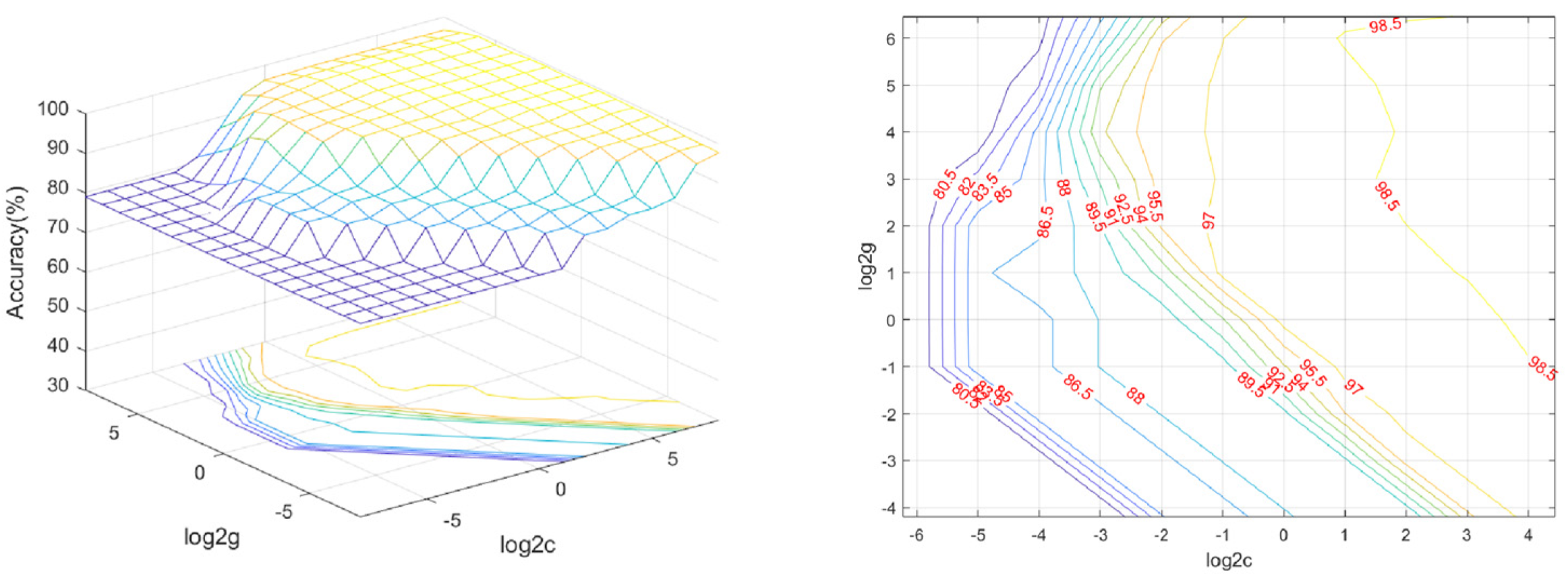
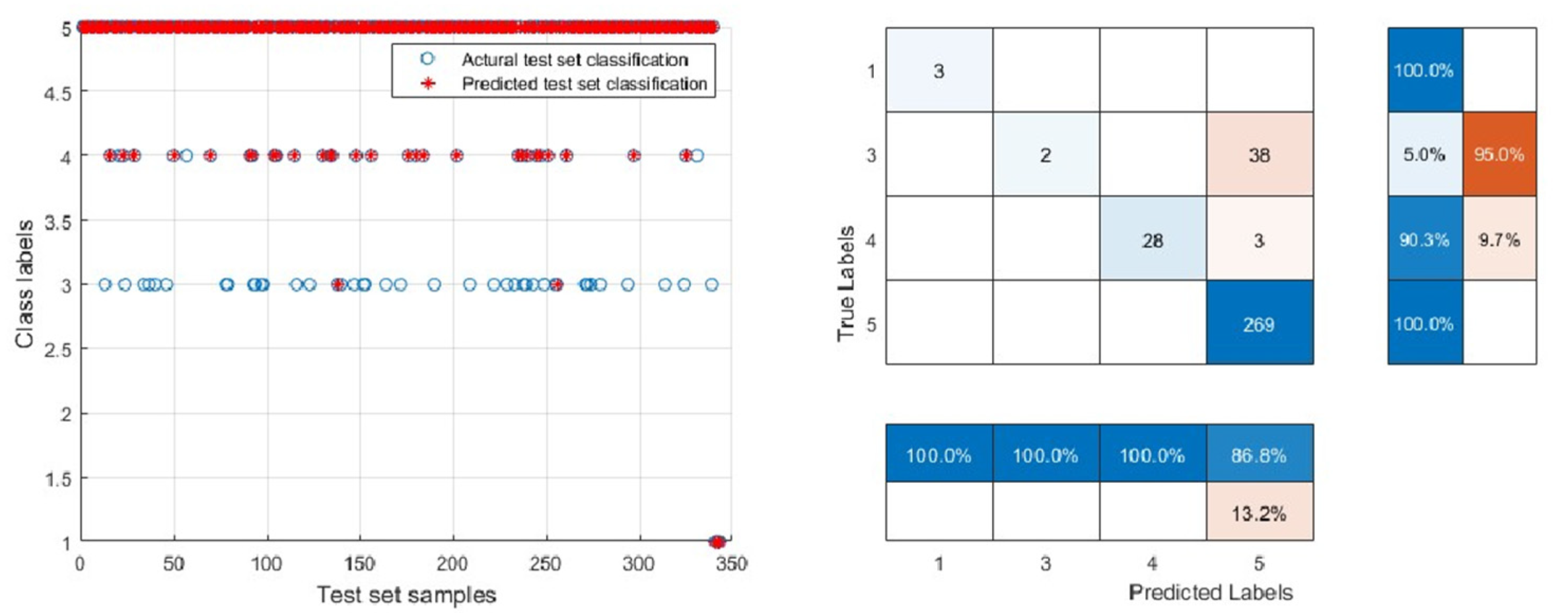
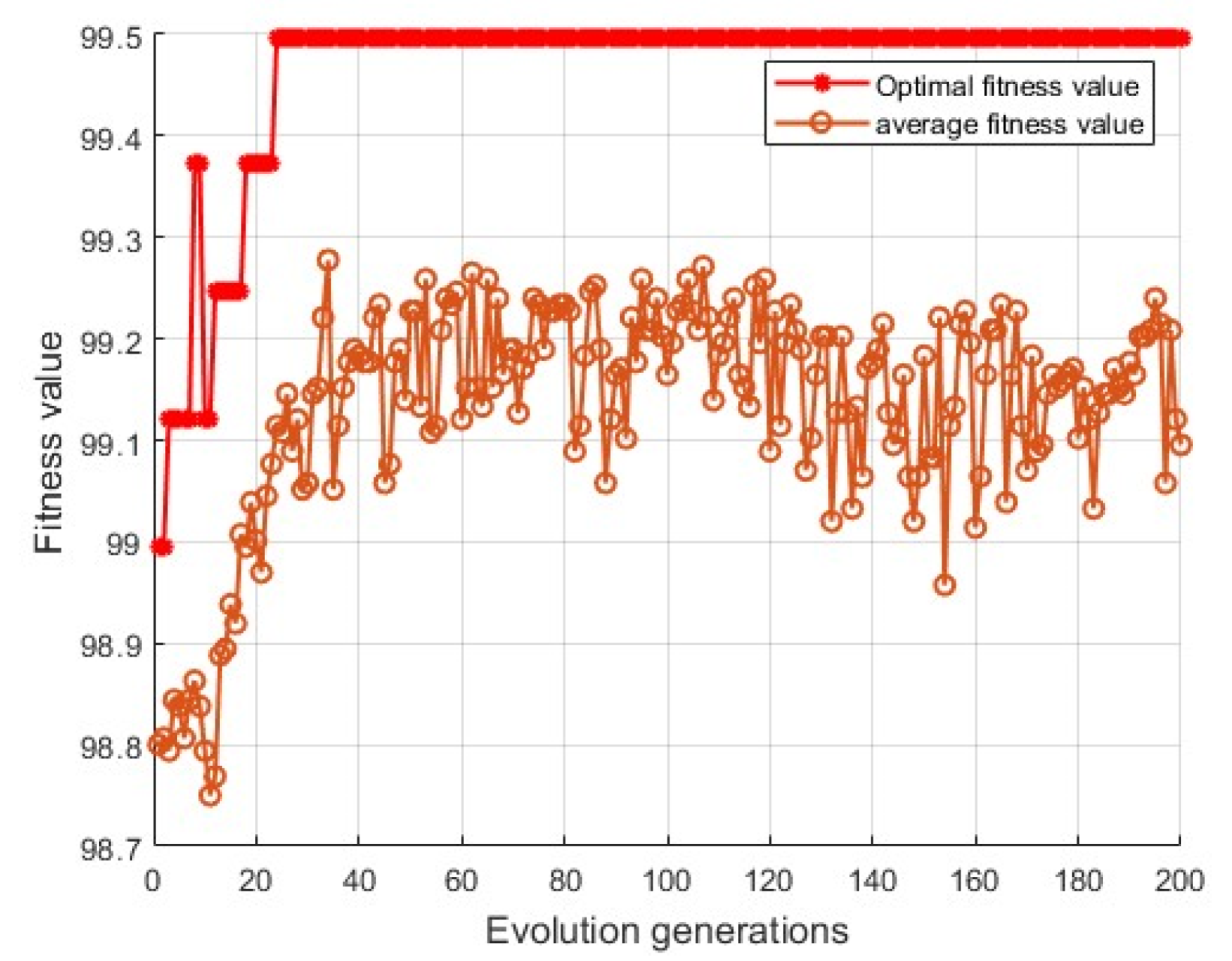
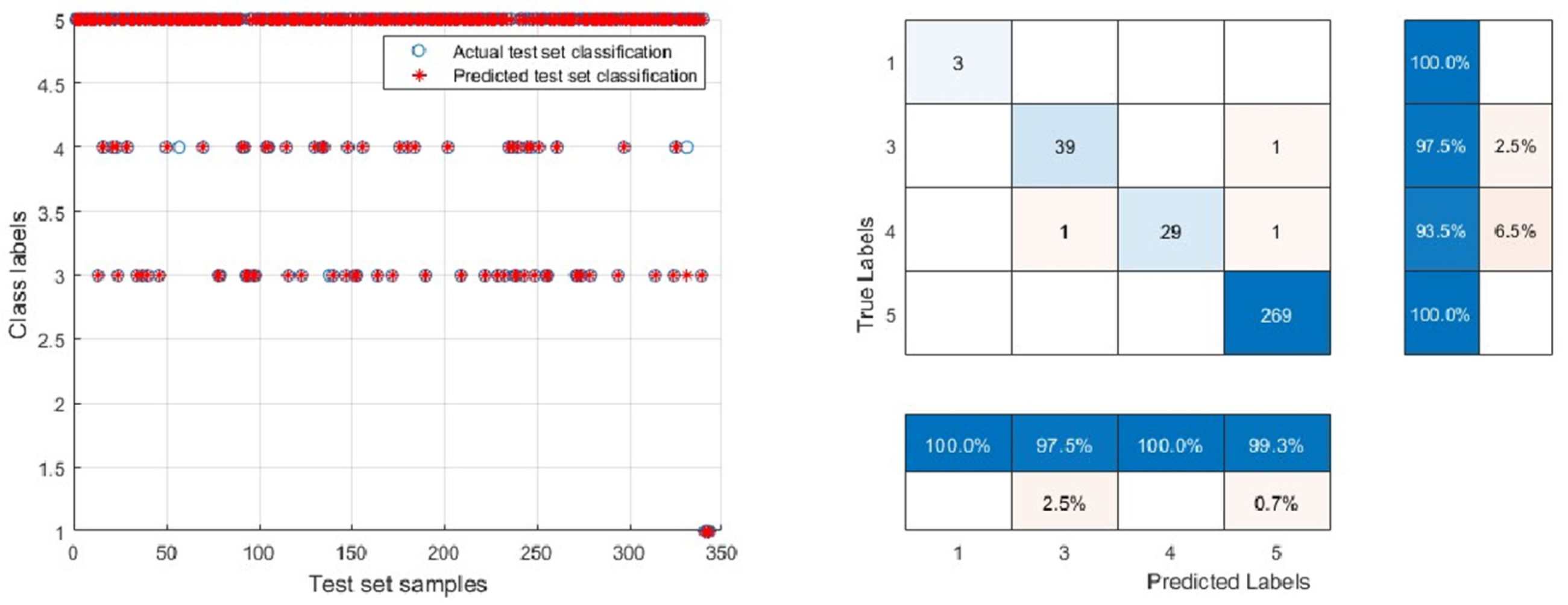
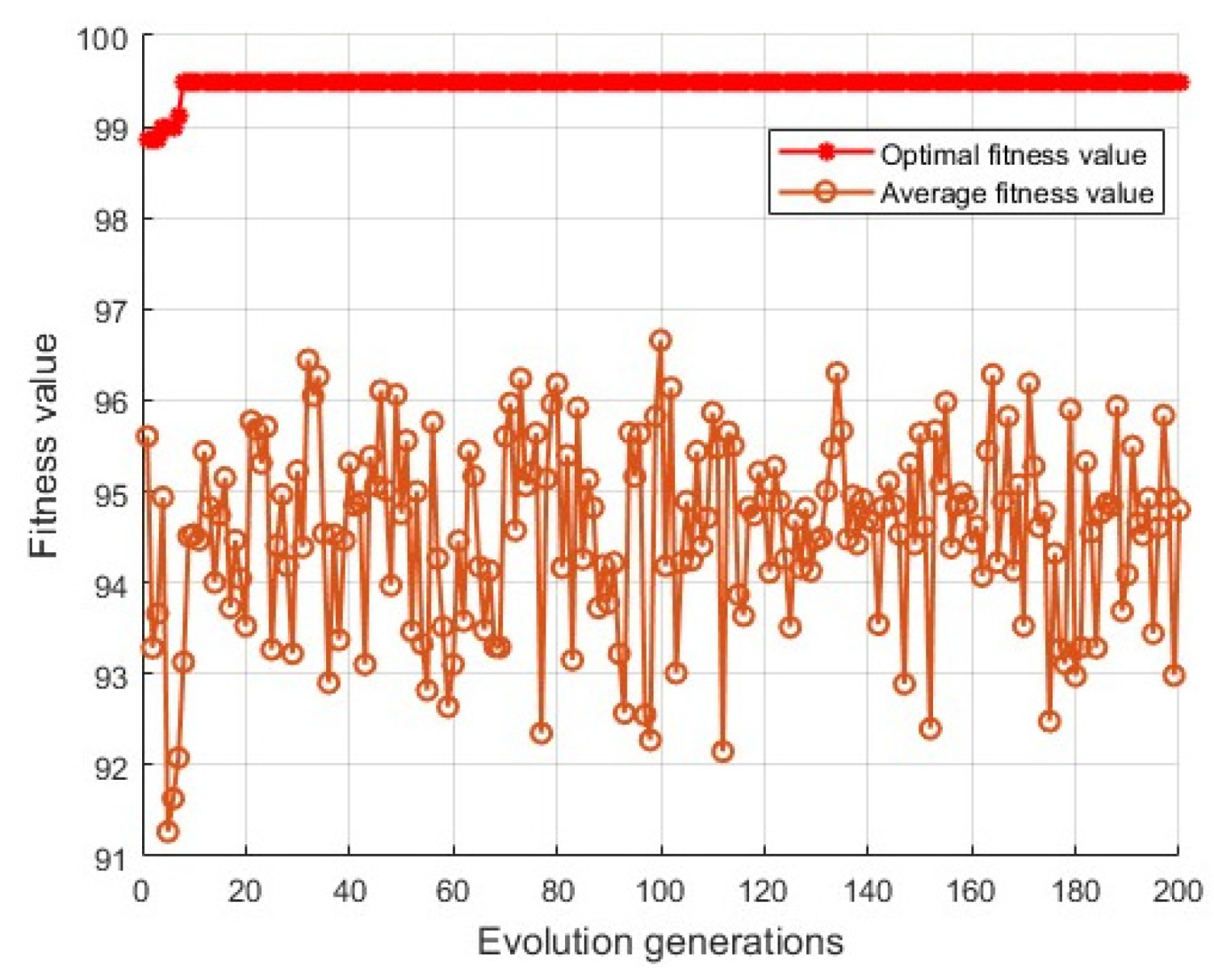
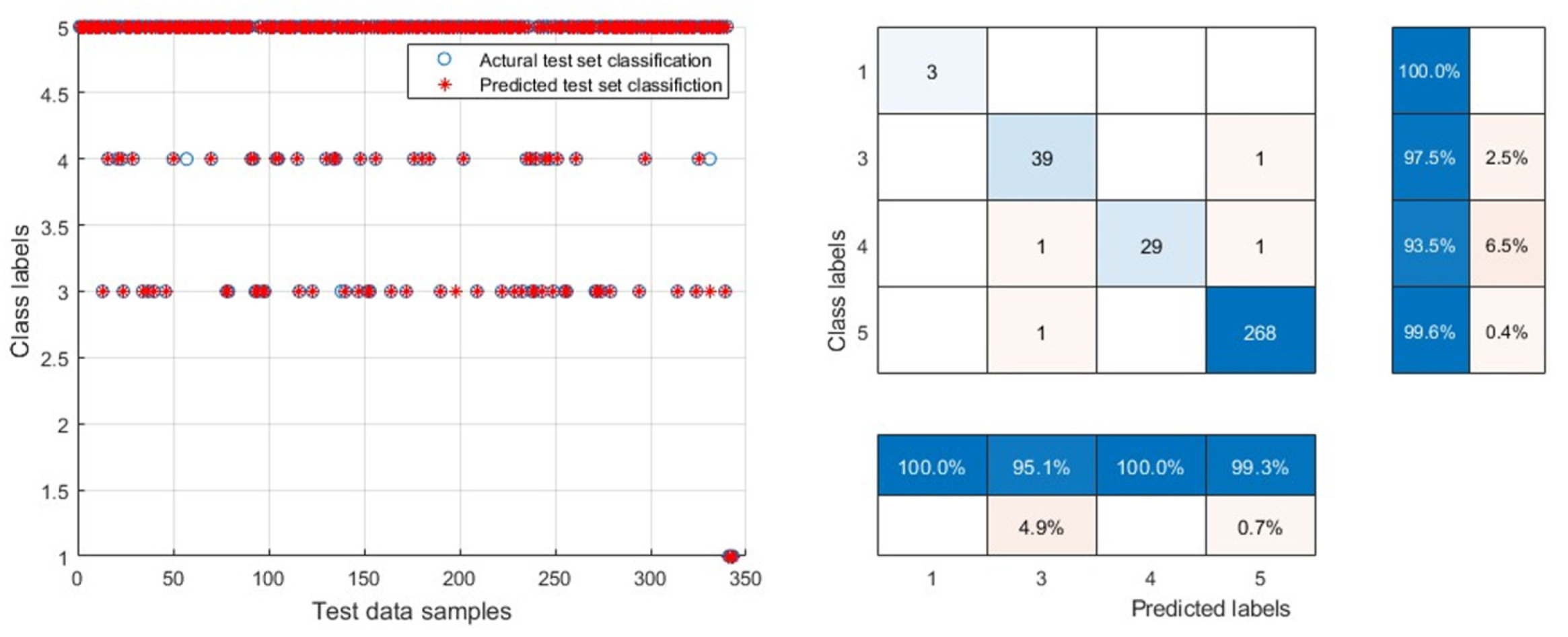
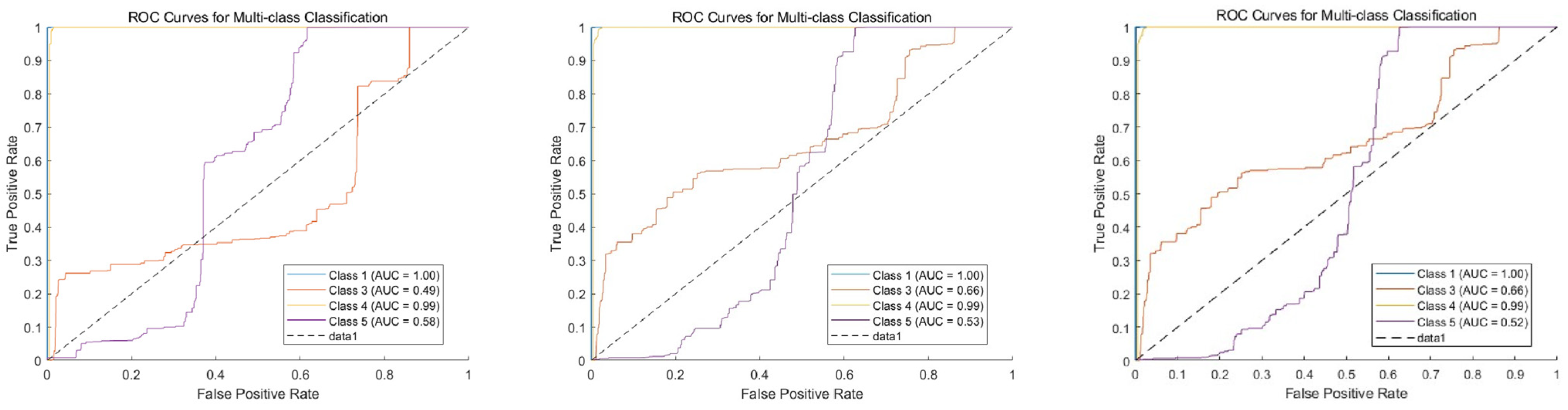
| SVM Type | Best C | Best g | Test Set Classification Accuracy/% [Number of Errors/Total Number of Samples] | MCC | Run Time t/s |
|---|---|---|---|---|---|
| GS-SVM | 128 | 4 | 88.0466 [302/343] | 0.6747 | 6.9008 |
| GA-SVM | 75.5214 | 4.7097 | 99.1254 [340/343] | 0.9796 | 53.1456 |
| PSO-SVM | 100 | 5.0707 | 98.8338 [339/343] | 0.9697 | 125.5197 |
| Classifier Type | Forestland Classification | ||||
|---|---|---|---|---|---|
| Class 1 | Class 3 | Class 4 | Class 5 | ||
| GS-SVM | Class 1 | 26 | / | / | / |
| Class 3 | / | 13 | / | 10 | |
| Class 4 | / | / | 359 | 3 | |
| Class 5 | / | 586 | 19 | 4670 | |
| GA-SVM | Class 1 | 26 | / | / | / |
| Class3 | / | 595 | 1 | 3 | |
| Class 4 | / | / | 370 | 5 | |
| Class 5 | / | 4 | 7 | 4765 | |
| PSO-SVM | Class 1 | 26 | / | / | / |
| Class 3 | / | 595 | 1 | 5 | |
| Class 4 | / | / | 370 | 5 | |
| Class 5 | / | 4 | 7 | 4673 | |
| Forestland Classification | Class 1 | Class 3 | Class 4 | Class 5 | Overall | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | MCC | Accuracy | MCC | Accuracy | MCC | Accuracy | MCC | Accuracy | MCC | |
| GS-SVM | 100% | 1 | 2.20% | 0.096 | 95% | 0.969 | 99.70% | 0.580 | 89.13% | 0.661 |
| GA-SVM | 100% | 1 | 99.30% | 0.991 | 97.90% | 0.982 | 99.80% | 0.987 | 99.65% | 0.990 |
| PSO-SVM | 100% | 1 | 98.80% | 0.960 | 98.70% | 0.970 | 99.80% | 0.962 | 99.61% | 0.973 |
| Class | Shrub Forestland | Other Forestland | Arbor Forestland | Total | ||||
|---|---|---|---|---|---|---|---|---|
| Patch Count | Area (ha) | Patch Count | Area (ha) | Patch Count | Area (ha) | Patch Count | Area (ha) | |
| 1 | 25 | 586.78 | 1 | 9.97 | - | - | 26 | 596.75 |
| 3 | 23 | 9.46 | 110 | 42.95 | 466 | 183.04 | 599 | 235.45 |
| 4 | 290 | 4016.59 | 47 | 90.15 | 38 | 28.83 | 375 | 4135.57 |
| 5 | 197 | 153.31 | 1518 | 1231.80 | 2971 | 1496.70 | 4686 | 2881.81 |
| Total | 535 | 4766.14 | 1676 | 1374.87 | 3475 | 1708.57 | 5686 | 7849.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, M.; Yang, H.; Wu, J.; Qi, J. Study on Intelligent Classing of Public Welfare Forestland in Kunyu City. Land 2025, 14, 89. https://doi.org/10.3390/land14010089
Sha M, Yang H, Wu J, Qi J. Study on Intelligent Classing of Public Welfare Forestland in Kunyu City. Land. 2025; 14(1):89. https://doi.org/10.3390/land14010089
Chicago/Turabian StyleSha, Meng, Hua Yang, Jianwei Wu, and Jianning Qi. 2025. "Study on Intelligent Classing of Public Welfare Forestland in Kunyu City" Land 14, no. 1: 89. https://doi.org/10.3390/land14010089
APA StyleSha, M., Yang, H., Wu, J., & Qi, J. (2025). Study on Intelligent Classing of Public Welfare Forestland in Kunyu City. Land, 14(1), 89. https://doi.org/10.3390/land14010089






