Uncertainty Modelling of Groundwater-Dependent Vegetation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. GDV Species
2.3. Study Site and Field Data
2.4. Datasets
2.5. Phenometric Modelling
2.5.1. Moisture-Adjusted Vegetation Index
2.5.2. Description of Phenometrics
2.5.3. Choosing Between Phenometrics
2.6. Ecological Niche Modelling
2.7. Uncertainty Modelling
Image Thresholding
3. Results
3.1. Phenometric Modelling
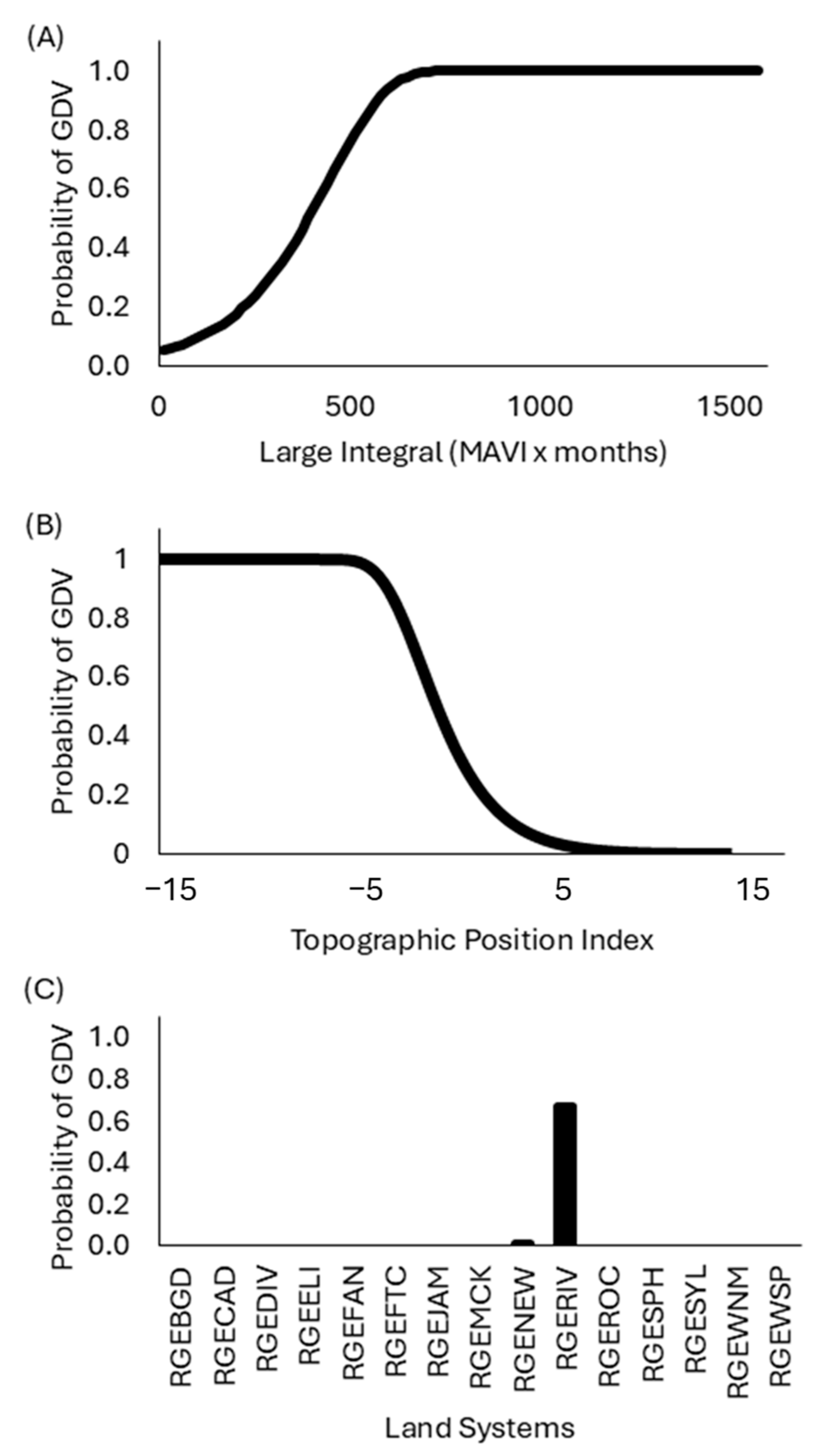
3.2. Ecological Niche Modelling
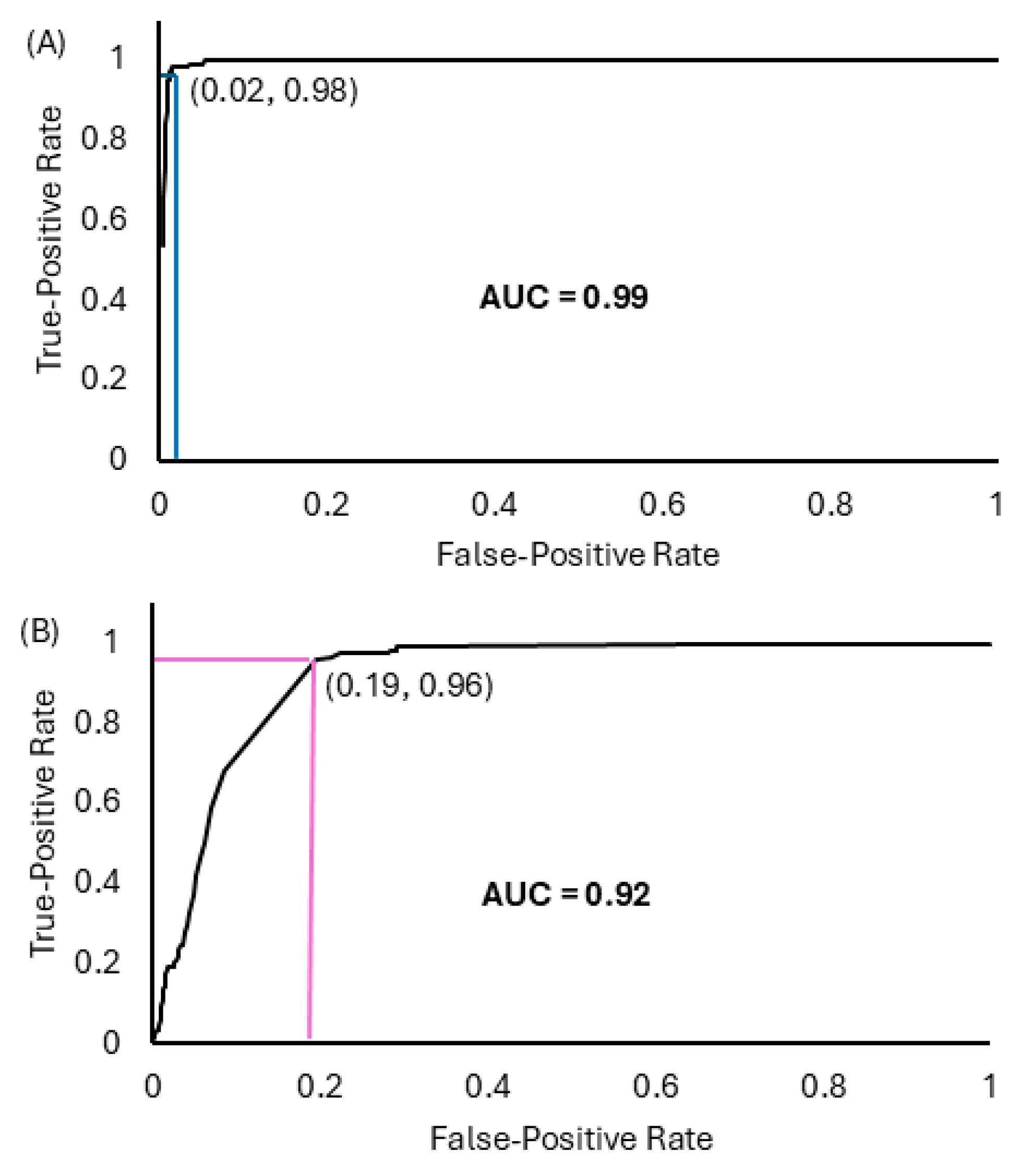
3.3. Uncertainty Modelling
Image Thresholding
4. Discussion
4.1. Phenometric Modelling
4.2. Ecological Niche Modelling
4.3. Uncertainty Modelling and Image Thresholding
4.4. Recommendations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Collection | Acquisition Date | Platform | Instrument | Product | Orbit Number | Processing Level |
|---|---|---|---|---|---|---|
| S2 | 9 January 2019 | S2B | MSI | S2MSIL2A | 17 | L2A |
| S2 | 3 February 2019 | S2A | MSI | S2MSIL2A | 17 | L2A |
| S2 | 5 March 2019 | S2A | MSI | S2MSIL2A | 17 | L2A |
| - | Interpolated | - | - | - | - | - |
| S2 | 4 May 2019 | S2A | MSI | S2MSIL2A | 17 | L2A |
| S2 | 3 June 2019 | S2A | MSI | S2MSIL2A | 17 | L2A |
| S2 | 3 July 2019 | S2A | MSI | S2MSIL2A | 17 | L2A |
| S2 | 7 August 2019 | S2B | MSI | S2MSIL2A | 17 | L2A |
| S2 | 5 September 2019 | S2B | MSI | S2MSIL2A | 17 | L2A |
| S2 | 5 October 2019 | S2B | MSI | S2MSIL2A | 17 | L2A |
| S2 | 5 November2019 | S2B | MSI | S2MSIL2A | 17 | L2A |
| S2 | 5 December 2019 | S2B | MSI | S2MSIL2A | 17 | L2A |
| Code | Name | Description |
|---|---|---|
| RGEBGD | Boolgeeda | Stony lower slopes and plains below hill systems supporting hard and soft spinifex grasslands or mulga shrublands. |
| RGECAD | Cadgie | Hardpan plains with thin sand cover and sandy banks supporting mulga shrublands with soft and hard spinifex. |
| RGEDIV | Divide | Gently undulating sandplains with minor dunes, supporting hard spinifex hummock grasslands with numerous shrubs. |
| RGEELI | Elimunna | Stony plains on basalt supporting sparse acacia and cassia shrublands and patchy tussock grasslands. |
| RGEFAN | Fan | Washplains and Gilgai plains supporting groved mulga tall shrublands and minor tussock grasslands. |
| RGEFTC | Fortescue | Alluvial plains and flood plains supporting patchy grassy eucalypt and acacia woodlands and shrublands and tussock grasslands. |
| RGEJAM | Jamindie | Stony hardpan plains and rises supporting groved mulga shrublands, occasionally with spinifex understorey. |
| RGEMCK | McKay | Hills, ridges, plateaux remnants and breakaways of meta sedimentary and sedimentary rocks supporting hard spinifex grasslands with acacias and occasional eucalypts. |
| RGENEW | Newman | Rugged jaspilite plateaux, ridges and mountains supporting hard spinifex grasslands. |
| RGERIV | River | Narrow, seasonally active flood plains and major river channels supporting moderately close, tall shrublands or woodlands of acacias and fringing communities of eucalypts, sometimes with tussock grasses or spinifex. |
| RGEROC | Rocklea | Basalt hills, plateaux, lower slopes and minor stony plains supporting hard spinifex and occasionally soft spinifex grasslands with scattered shrubs. |
| RGESPH | Spearhole | Gently undulating gravelly hardpan plains and dissected slopes supporting groved mulga shrublands and hard spinifex. |
| RGESYL | Sylvania | Gritty surfaced plains and low rises on granite supporting acacia–eremophila–cassia shrublands. |
| RGEWNM | Wannamunna | Hardpan plains and internal drainage tracts supporting mulga shrublands and woodlands and occasionally eucalypt woodlands. |
| RGEWSP | Washplain | Hardpan plains supporting groved mulga shrublands. |
References
- Eamus, D.; Froend, R. Groundwater-dependent ecosystems: The where, what and why of GDEs. Aust. J. Bot. 2006, 54, 91–96. [Google Scholar] [CrossRef]
- Brown, J.; Bach, L.; Aldous, A.; Wyers, A.; DeGagné, J. Groundwater-dependent ecosystems in Oregon: An assessment of their distribution and associated threats. Front. Ecol. Environ. 2010, 9, 97–102. [Google Scholar] [CrossRef]
- El-Hokayem, L.; De Vita, P.; Conrad, C. Local identification of groundwater dependent vegetation using high-resolution sentinel-2 data—A Mediterranean case study. Ecol. Indic. 2023, 146, 109784. [Google Scholar] [CrossRef]
- Doody, T.; Hancock, P.; Pritchard, J. Assessing groundwater-dependent ecosystems: IESC information guidelines explanatory note. In Report Prepared for the Independent Expert Scientific Committee on Coal Seam Gas and Large Coal Mining Development Through the Department of the Environment and Energy, Commonwealth of Australia; IESC: Canberra, Australia, 2019. [Google Scholar]
- Eamus, D.; Froend, R.H.; Loomes, R.C.; Hose, G.; Murray, B. A functional methodology for determining the groundwater regime needed to maintain the health of groundwater-dependent vegetation. Aust. J. Bot. 2006, 54, 97–114. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, J.; Wang, P.; Zhang, Y.; Yu, Q. Interpreting the groundwater attributes influencing the distribution patterns of groundwater-dependent vegetation in northwestern China. Ecohydrology 2011, 5, 628–636. [Google Scholar] [CrossRef]
- Barbeta, A.; Peñuelas, J. Relative contribution of groundwater to plant transpiration estimated with stable isotopes. Sci. Rep. 2017, 7, 10580. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.; van Kempen, C.M.; Reckman, J.W.; Vasak, S.; Bierkens, M.F. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef]
- Antunes, C.; Díaz Barradas, M.C.; Zunzunegui, M.; Vieira, S.; Pereira, Â.; Anjos, A.; Correia, O.; Pereira, M.; Máguas, C. Contrasting plant water-use responses to groundwater depth in coastal dune ecosystems. Funct. Ecol. 2018, 32, 1931–1943. [Google Scholar] [CrossRef]
- Jin, X.; Liu, J.; Wang, S.; Xia, W. Vegetation Dynamics and their response to groundwater and climate variables in Qaidam Basin, China. Int. J. Remote Sens. 2016, 37, 710–728. [Google Scholar] [CrossRef]
- Fildes, S.G.; Doody, T.M.; Bruce, D.; Clark, I.F.; Batelaan, O. Mapping groundwater dependent ecosystem potential in a semi-arid environment using a remote sensing-based multiple-lines-of-evidence approach. Int. J. Digit. Earth 2023, 16, 375–406. [Google Scholar] [CrossRef]
- Rohde, M.M.; Froend, R.; Howard, J. A global synthesis of managing groundwater dependent ecosystems under sustainable groundwater policy. Groundwater 2017, 55, 293–301. [Google Scholar] [CrossRef] [PubMed]
- Pérez Hoyos, I.; Krakauer, N.; Khanbilvardi, R.; Armstrong, R. A review of advances in the identification and characterization of groundwater dependent ecosystems using geospatial technologies. Geosciences 2016, 6, 17. [Google Scholar] [CrossRef]
- Everitt, J.H.; Deloach, C.J. Remote Sensing of Chinese Tamarisk (Tamarix chinensis) and associated vegetation. Weed Sci. 1990, 38, 273–278. [Google Scholar] [CrossRef]
- Liu, C.; Liu, H.; Yu, Y.; Zhao, W.; Zhang, Z.; Guo, L.; Yetemen, O. Mapping groundwater-dependent ecosystems in arid Central Asia: Implications for controlling regional land degradation. Sci. Total Environ. 2021, 797, 149027. [Google Scholar] [CrossRef] [PubMed]
- Barron, O.V.; Emelyanova, I.; Van Niel, T.G.; Pollock, D.; Hodgson, G. Mapping groundwater-dependent ecosystems using remote sensing measures of vegetation and moisture dynamics. Hydrol. Process. 2012, 28, 372–385. [Google Scholar] [CrossRef]
- Kriegler, F.J.; Malila, W.A.; Nalepka, R.F.; Richardson, W. Preprocessing transformations and their effect on multispectral recognition. Remote Sens. Environ. 1969, VI, 97–132. [Google Scholar]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Tweed, S.O.; Leblanc, M.; Webb, J.A.; Lubczynski, M.W. Remote Sensing and GIS for mapping groundwater recharge and discharge areas in salinity prone catchments, southeastern Australia. Hydrogeol. J. 2006, 15, 75–96. [Google Scholar] [CrossRef]
- Mackey, B.; Berry, S.; Hugh, S.; Ferrier, S.; Harwood, T.D.; Williams, K.J. Ecosystem greenspots: Identifying potential drought, fire, and climate-change micro-refuges. Ecol. Appl. 2012, 22, 1852–1864. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Davison, J.E.; Casady, G.M.; Marsh, S.E. Phenological characterization of Desert Sky Island vegetation communities with remotely sensed and climate time series data. Remote Sens. 2010, 2, 388–415. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Rowlands, D.D.; Sabaka, T.J.; Loomis, B.D.; Horwath, M.; Arendt, A.A. Chapter 10: Gravimetry measurements from space. In Remote Sensing of the Cryosphere; Tedesco, M., Ed.; Wiley Blackwell: Oxford, UK, 2015; pp. 231–247. ISBN 9781118368855. [Google Scholar]
- Qiu, Y.; Wang, D.; Yu, X.; Jia, G.; Li, H. Effects of groundwater table decline on vegetation in groundwater-dependent ecosystems. Forests 2023, 14, 2326. [Google Scholar] [CrossRef]
- Gow, L.J.; Barrett, D.J.; Renzullo, L.J.; Phinn, S.R.; O’Grady, A.P. Characterising groundwater use by vegetation using a surface energy balance model and satellite observations of land surface temperature. Environ. Model. Softw. 2016, 80, 66–82. [Google Scholar] [CrossRef]
- Sarkar, S.K.; Rudra, R.R.; Talukdar, S.; Das, P.C.; Nur, S.; Alam, E.; Islam, K.; Islam, A.R. Future groundwater potential mapping using machine learning algorithms and climate change scenarios in Bangladesh. Sci. Rep. 2024, 14, 10328. [Google Scholar] [CrossRef] [PubMed]
- Robinson, T.; Di Virgilio, G.; Temple-Smith, D.; Hesford, J.; Wardell-Johnson, G. Characterisation of range restriction amongst the rare flora of Banded Ironstone Formation ranges in semiarid south-western Australia. Aust. J. Bot. 2019, 67, 234–247. [Google Scholar] [CrossRef]
- Keppel, G.; Robinson, T.P.; Wardell-Johnson, G.W.; Yates, C.J.; Van Niel, K.P.; Byrne, M.; Schut, A.G.T. A low-altitude mountain range as an important refugium for two narrow endemics in the southwest Australian Floristic Region Biodiversity Hotspot. Ann. Bot. 2016, 119, 289–300. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yates, C.J.; Robinson, T.P.; Wardell-Johnson, G.W.; Keppel, G.; Hopper, S.D.; Schut, A.G.T.; Byrne, M. High species diversity and turnover in granite inselberg floras highlight the need for a conservation strategy protecting many outcrops. Ecol. Evol. 2019, 9, 7660–7675. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Alcaide, S.; Martínez-Santos, P. Review: Advances in groundwater potential mapping. Hydrogeol. J. 2019, 27, 2307–2324. [Google Scholar] [CrossRef]
- Al Saud, M. Mapping potential areas for groundwater storage in Wadi Aurnah Basin, western Arabian Peninsula, using remote sensing and geographic information system techniques. Hydrogeol. J. 2010, 18, 1481–1495. [Google Scholar] [CrossRef]
- Agarwal, E.; Agarwal, R.; Garg, R.D.; Garg, P.K. Delineation of Groundwater Potential Zone: An AHP/ANP approach. J. Earth Syst. Sci. 2013, 122, 887–898. [Google Scholar] [CrossRef]
- Abrams, W.; Ghoneim, E.; Shew, R.; LaMaskin, T.; Al-Bloushi, K.; Hussein, S.; AbuBakr, M.; Al-Mulla, E.; Al-Awar, M.; El-Baz, F. Delineation of groundwater potential (GWP) in the Northern United Arab Emirates and Oman using geospatial technologies in conjunction with simple additive weight (SAW), Analytical Hierarchy Process (AHP), and probabilistic frequency ratio (PFR) techniques. J. Arid. Environ. 2018, 157, 77–96. [Google Scholar] [CrossRef]
- Duran-Llacer, I.; Arumí, J.L.; Arriagada, L.; Aguayo, M.; Rojas, O.; González-Rodríguez, L.; Martínez-Retureta, R.; Oyarzún, R.; Singh, S.K. A new method to map groundwater-dependent ecosystem zones in semi-arid environments: A case study in Chile. Sci. Total Environ. 2022, 816, 151528. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Niyazi, B. Groundwater Potential Mapping Using Remote Sensing Techniques and Weights of Evidence GIS Model: A Case Study from Wadi Yalamlam Basin, Makkah Province, Western Saudi Arabia. Environ. Earth Sci. 2015, 74, 5129–5142. [Google Scholar] [CrossRef]
- Jari, A.; Bachaoui, E.M.; Hajaj, S.; Khaddari, A.; Khandouch, Y.; El Harti, A.; Jellouli, A.; Namous, M. Investigating machine learning and ensemble learning models in groundwater potential mapping in arid region: Case study from Tan-tan water-scarce region, Morocco. Front. Water 2023, 5, 1305998. [Google Scholar] [CrossRef]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Ghorbani Nejad, S.; Falah, F.; Daneshfar, M.; Haghizadeh, A.; Rahmati, O. Delineation of groundwater potential zones using remote sensing and GIS-based data-driven models. Geocarto Int. 2016, 32, 167–187. [Google Scholar] [CrossRef]
- Booth, C.; Adams, V.; Kruse, B.; Douglass, L. The Enduring Pilbara: A conservation vision for a land rich in nature, culture and resources. In The Enduring Pilbara; Centre for Conservation Geography and University of Tasmania: Hobart, Australia, 2021. [Google Scholar]
- Evans, L.R.; Youngs, J. Conservation of trial dewatering discharge through re-injection in the Pilbara region, Western Australia. In Groundwater and Ecosystems; CRC Press: Boca Raton, FL, USA, 2013; pp. 131–142. [Google Scholar]
- IBRA. Interim Biogeographic Regionalisation for Australia (IBRA), Version 7 (Regions). 2012. Available online: https://fed.dcceew.gov.au/ (accessed on 22 November 2024).
- Zomer, R.J.; Xu, J.; Trabuco, A. Version 3 of the Global Aridity Index and Potential Evapotranspiration Database. Sci. Data 2022, 9, 409. [Google Scholar] [CrossRef]
- Sudmeyer, R. Climate in the Pilbara; Bulletin 4873; Department of Agriculture and Food: Perth, Australia, 2016. [Google Scholar]
- Van Vreeswyk, A.M.E.; Payne, A.L.; Leighton, K.A.; Hennig, P. Technical Bulletin No. 92: An Inventory and Condition Survey of the Pilbara Region, Western Australia; Department of Agriculture: Perth, Australia, 2004; p. 424. [Google Scholar]
- Payne, A.L.; Mitchell, A.A. An Assessment of the Impact of Ophthalmia Dam on the Floodplains of the Fortescue River on Ethel Creek and Roy Hill Stations; Department of Primary Industries and Regional Development: Perth, Australia, 1999. [Google Scholar]
- Fox, J.E.D.; Burrows, C.L.; Hopkins, M.K. Monitoring revegetation of a severely degraded rangeland, Western Australia. In Proceedings of the 3rd Queensland Environmental Conference, Brisbane, Australia, 15–16 May 2000. [Google Scholar]
- ESRI. ArcGIS Collector Software, Version 10.4.0.0; Environmental Systems Research Institute: Redlands, CA, USA, 2019. [Google Scholar]
- McLean, E.H. Patterns of Water Use by the Riparian Tree Melaleuca argentea in Semi-Arid Northwest Australia. Ph.D. Thesis, The University of Western Australia, Crawley, Australia, 2014. [Google Scholar]
- O’Grady, A.P.; Carter, J.L.; Bruce, J. Can we predict groundwater discharge from terrestrial ecosystems using existing eco-hydrological concepts? Hydrol. Earth Syst. Sci. 2011, 15, 3731–3739. [Google Scholar] [CrossRef]
- Pfautsch, S.; Dodson, W.; Madden, S.; Adams, M.A. Assessing the impact of large-scale water table modifications on riparian trees: A case study from Australia. Ecohydrology 2014, 8, 642–651. [Google Scholar] [CrossRef]
- Eamus, D.; Zolfaghar, S.; Villalobos-Vega, R.; Cleverly, J.; Huete, A. Groundwater-dependent ecosystems: Recent insights from satellite and field-based studies. Hydrol. Earth Syst. Sci. 2015, 19, 4229–4256. [Google Scholar] [CrossRef]
- Onshore Environmental Consultants. Orebody (OB) 29, 30, 35—Groundwater Dependent Vegetation Impact Assessment; Onshore Environmental Consultants: Yallingup, Australia, 2013; p. 17. [Google Scholar]
- Zhu, G.; Ju, W.; Chen, J.M.; Liu, Y. A Novel Moisture Adjusted Vegetation Index (MAVI) to Reduce Background Reflectance and Topographical Effects on LAI Retrieval. PLoS ONE 2014, 9, e102560. [Google Scholar] [CrossRef]
- Eklundh, L.; Jönsson, P. TIMESAT 3.3 with Seasonal Trend Decomposition and Parallel Processing—Software Manual; Lund University: Lund, Sweden, 2017; p. 92. [Google Scholar]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; Wiley & Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Vining, D.J.; Gladish, G.W. Receiver operating characteristic curves: A basic understanding. RadioGraphics 1992, 12, 1147–1154. [Google Scholar] [CrossRef] [PubMed]
- Pontius, R.G.; Schneider, L.C. Land-cover change model validation by an ROC method for the Ipswich Watershed, Massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar] [CrossRef]
- Fielding, A.H.; Bell, J.F. A Review of Methods for the Assessment of Prediction Errors in Conservation Presence/Absence Models. Environ. Conserv. 1997, 24, 38–49. [Google Scholar] [CrossRef]
- ESRI. ArcGIS PRO, Version 3.1.0; Environmental Systems Research Institute: Redlands, CA, USA, 2023. [Google Scholar]
- Sørensen, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Boehner, J. System for Automated Geoscientific Analyses (SAGA), Version 7.8.2; Copernicus Publications: Göttingen, Germany, 2020. [Google Scholar]
- Iwahashi, J.; Pike, R.J. Automated classifications of topography from DEMs by an unsupervised nested-means algorithm and a three-part geometric signature. Geomorphology 2007, 86, 409–440. [Google Scholar] [CrossRef]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Boehner, J.; Koethe, R.; Conrad, O.; Gross, J.; Ringeler, A.; Selige, T. Soil Regionalisation by Means of Terrain Analysis and Process Parameterisation. In Soil Classification 2001; Micheli, E., Nachtergaele, F., Montanarella, L., Eds.; European Soil Bureau: Ispra, Italy, 2002; pp. 213–222. Available online: https://edepot.wur.nl/486064 (accessed on 13 December 2024).
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Dempster, A.P. A generalization of Bayesian inference. J. R. Stat. Soc. Ser. B Stat. Methodol. 1968, 30, 205–232. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Barnett, J.A. Computational methods for a mathematical theory of evidence. Classic Works of the Dempster-Shafer Theory of Belief Functions. In Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI), Vancouver, WA, Canada, 24–28 August 1981; Volume II, pp. 868–875. [Google Scholar]
- Beynon, M.; Curry, B.; Morgan, P. The Dempster–Shafer Theory of Evidence: An alternative approach to multicriteria decision modelling. Omega 2000, 28, 37–50. [Google Scholar] [CrossRef]
- Gordon, J.; Shortliffe, E.H. A method for managing evidential reasoning in a hierarchical hypothesis space. Artif. Intell. 1985, 26, 323–357. [Google Scholar] [CrossRef]
- Carranza, E.J.; Hale, M. Evidential belief functions for data-driven geologically constrained mapping of gold potential, Baguio District, Philippines. Ore Geol. Rev. 2003, 22, 117–132. [Google Scholar] [CrossRef]
- Eastman, R.J. Fuzzy Sets and Dempster Shaffer Theory of Evidence. In IDRISI Kilimanjaro Manual; Clark University: Worcester, MA, USA, 2003. [Google Scholar]
- Robinson, T.P.; van Klinken, R.D.; Metternicht, G. Comparison of alternative strategies for Invasive Species Distribution Modeling. Ecol. Model. 2010, 221, 2261–2269. [Google Scholar] [CrossRef]
- Jiménez-Valverde, A.; Lobo, L.M. Threshold criteria for conversion of probability of species presence to either–or presence–absence. Acta Oecol. 2007, 31, 361–369. [Google Scholar] [CrossRef]
- Lippitt, C.D.; Rogan, J.; Toledano, J.; Sangermano, F.; Eastman, R.J.; Mastro, V.; Sawyer, A. Incorporating anthropogenic variables into a species distribution model to map gypsy moth risk. Ecol. Model. 2008, 210, 339–350. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Score to ROC, Informedness, Markedness & Correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Terrett, M.; Fryer, D.; Doody, T.; Nguyen, H.; Castellazzi, P. SARGDV: Efficient identification of groundwater-dependent vegetation using synthetic aperture radar. arXiv 2020, arXiv:2009.03129. [Google Scholar]
- Pasquarella, V.J.; Holden, C.E.; Kaufman, L.; Woodcock, C.E. From imagery to ecology: Leveraging time series of all available Landsat observations to map and monitor ecosystem state and dynamics. Remote Sens. Ecol. Conserv. 2016, 2, 152–170. [Google Scholar] [CrossRef]
- Brim Box, J.; Leiper, I.; Nano, C.; Stokeld, D.; Jobson, P.; Tomlinson, A.; Cobban, D.; Bond, T.; Randall, D.; Box, P. Mapping terrestrial groundwater-dependent ecosystems in arid Australia using Landsat-8 time-series data and singular value decomposition. Remote Sens. Ecol. Conserv. 2022, 8, 464–476. [Google Scholar] [CrossRef]
- Sun, X.; Yuan, L.; Liu, M.; Liang, S.; Li, D.; Liu, L. Quantitative Estimation for the Impact of Mining Activities on Vegetation Phenology and Identifying Its Controlling Factors from Sentinel-2 Time Series. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102814. [Google Scholar] [CrossRef]
- Wang, B.; Li, P.; Zhu, X. Quantification of Vegetation Phenological Disturbance Characteristics in Open-Pit Coal Mines of Arid and Semi-Arid Regions Using Harmonized Landsat 8 and Sentinel-2. Remote Sens. 2023, 15, 5257. [Google Scholar] [CrossRef]
- Miller, G.R.; Chen, X.; Rubin, Y.; Ma, S.; Baldocchi, D.D. Groundwater uptake by woody vegetation in a semiarid oak savanna. Water Resour. Res. 2010, 46, W10503. [Google Scholar] [CrossRef]
- Williamson, S.D.; van Dongen, R.; Trotter, L.; Palmer, R.; Robinson, T.P. Fishing for Feral Cats in a Naturally Fragmented Rocky Landscape Using Movement Data. Remote Sens. 2021, 13, 4925. [Google Scholar] [CrossRef]
- Robinson, T.P.; van Klinken, R.D.; Metternicht, G. Spatial and temporal rates and patterns of mesquite (Prosopis species) invasion in Western Australia. J. Arid Environ. 2008, 72, 175–188. [Google Scholar] [CrossRef]
- Nano, C.; Jobson, P.; Randall, D.; Box, J.B. Ecological Characteristics of Potential Groundwater Dependent Vegetation in the Western Davenport Water Control District; Technical Report 19/2021; Department of Environment and Natural Resources, Northern Territory Government: Alice Springs, NT, Australia, 2021; ISBN 978-1-74350-310-2. [Google Scholar]


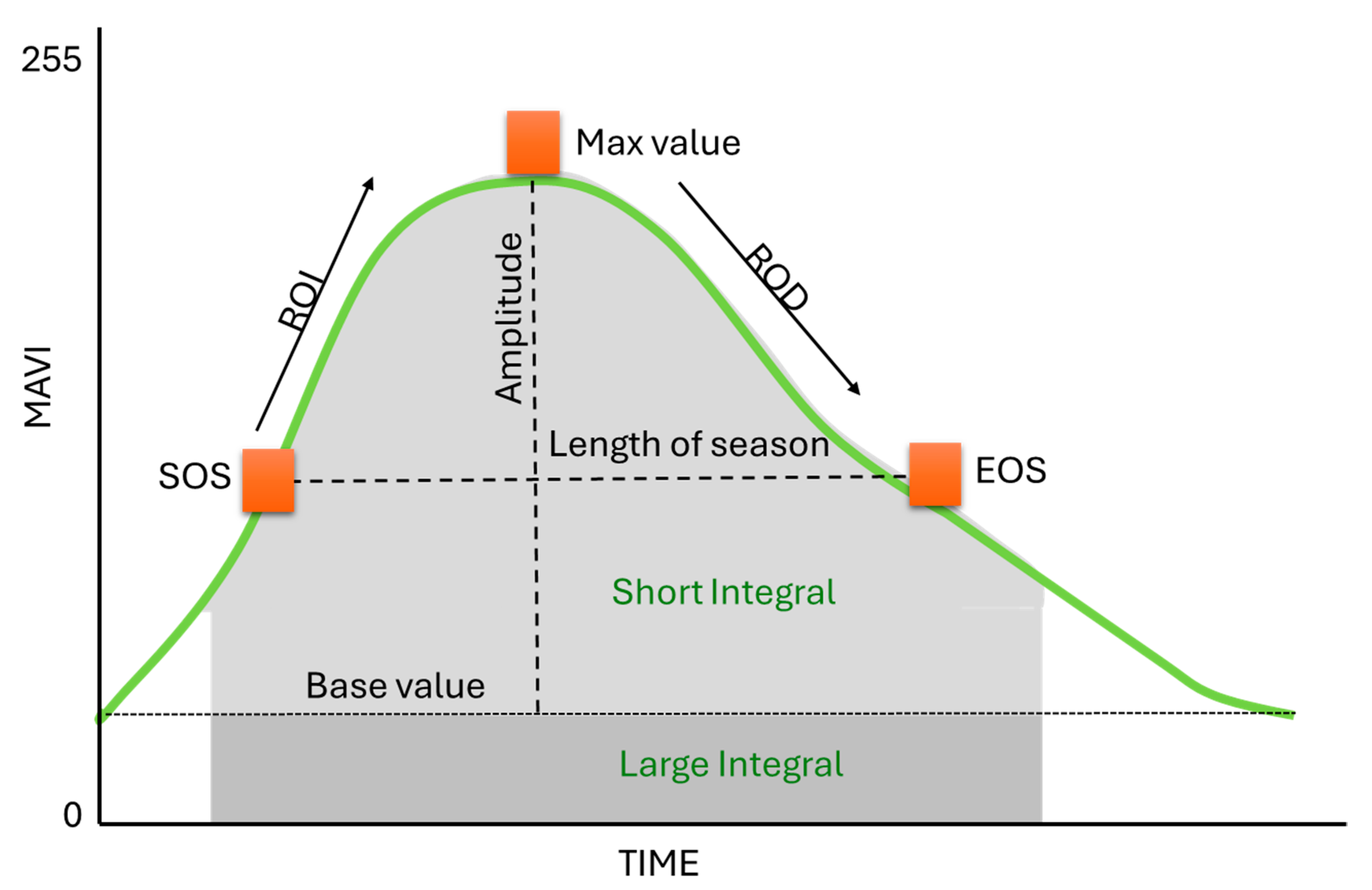

| Name | Abbrev. | Definition | Units |
|---|---|---|---|
| Length of Season | LOS | The number of months between the SOS and EOS | Months |
| Base Value | BV | The average of the smallest left and right values | MAVI |
| Max Value | MV | The maximum MAVI value in the time series | MAVI |
| Amplitude | AMP | The difference between the MV and the base value BV | MAVI |
| Start of Season | SOS | Where the left part of the function reaches 50% of the AMP | MAVI |
| End of Season | EOS | Where the right part of the function reaches 50% of the AMP | MAVI |
| Rate of Increase | ROI | The rate of vegetation “green-up” at the beginning of the season | MAVI/months |
| Rate of Decrease | ROD | The rate of vegetation “green-down” at the end of the season | MAVI/months |
| Large Integral | LI | Area under the curve between SOS and EOS | MAVI × months |
| Small Integral | SI | Area under the curve, above the BV, between SOS and EOS | MAVI × months |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robinson, T.P.; Trotter, L.; Wardell-Johnson, G.W. Uncertainty Modelling of Groundwater-Dependent Vegetation. Land 2024, 13, 2208. https://doi.org/10.3390/land13122208
Robinson TP, Trotter L, Wardell-Johnson GW. Uncertainty Modelling of Groundwater-Dependent Vegetation. Land. 2024; 13(12):2208. https://doi.org/10.3390/land13122208
Chicago/Turabian StyleRobinson, Todd P., Lewis Trotter, and Grant W. Wardell-Johnson. 2024. "Uncertainty Modelling of Groundwater-Dependent Vegetation" Land 13, no. 12: 2208. https://doi.org/10.3390/land13122208
APA StyleRobinson, T. P., Trotter, L., & Wardell-Johnson, G. W. (2024). Uncertainty Modelling of Groundwater-Dependent Vegetation. Land, 13(12), 2208. https://doi.org/10.3390/land13122208






