Impact of Refined Boundary Conditions of Land Objects on Urban Hydrological Process Simulation
Abstract
1. Introduction
2. Study Area and Data
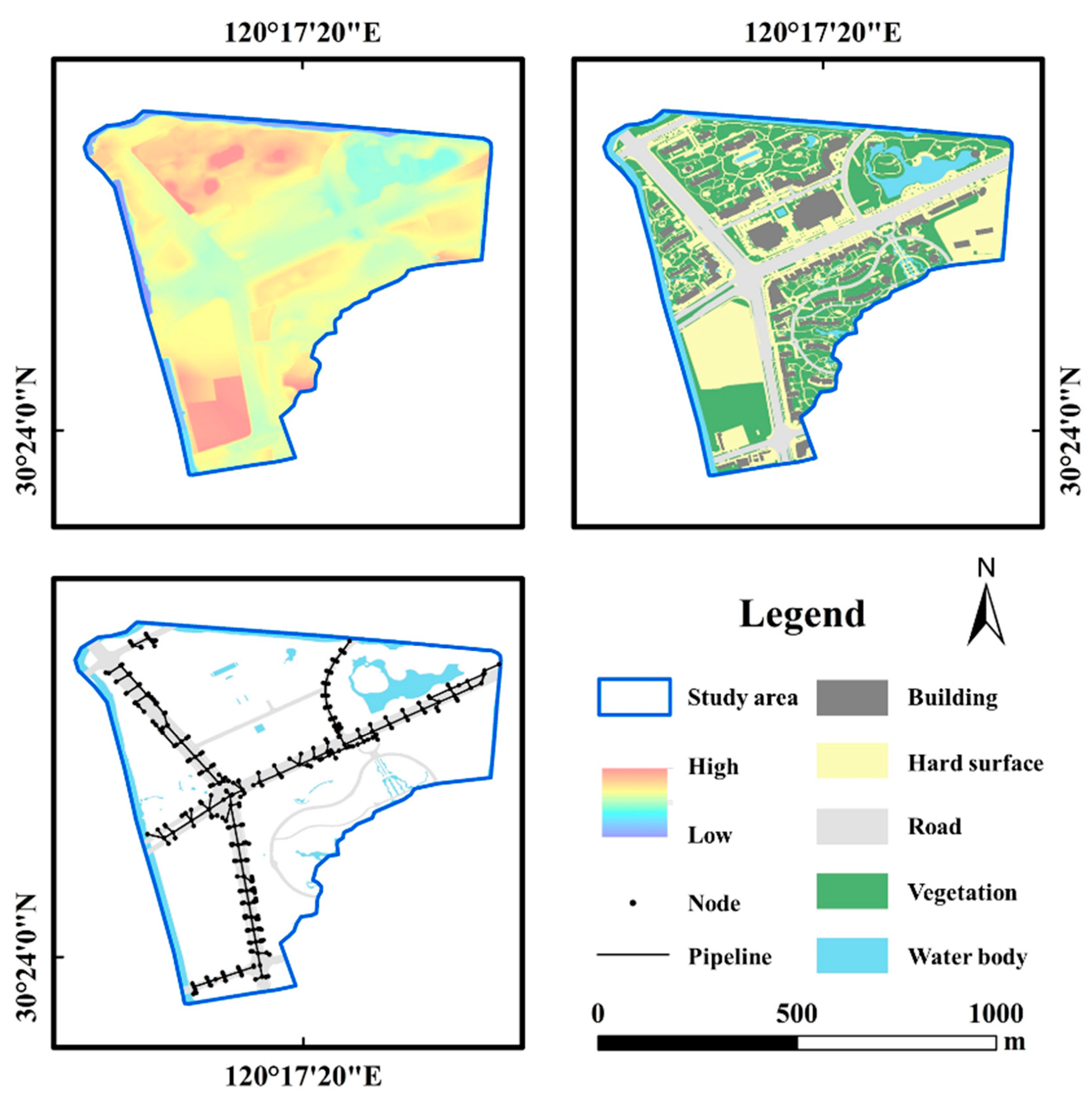
2.1. Overview of the Study Area
2.2. Data Sources and Processing
2.2.1. Basic Geographic Data
- Digital elevation data
- b.
- Land use data
- c.
- Drainage network data
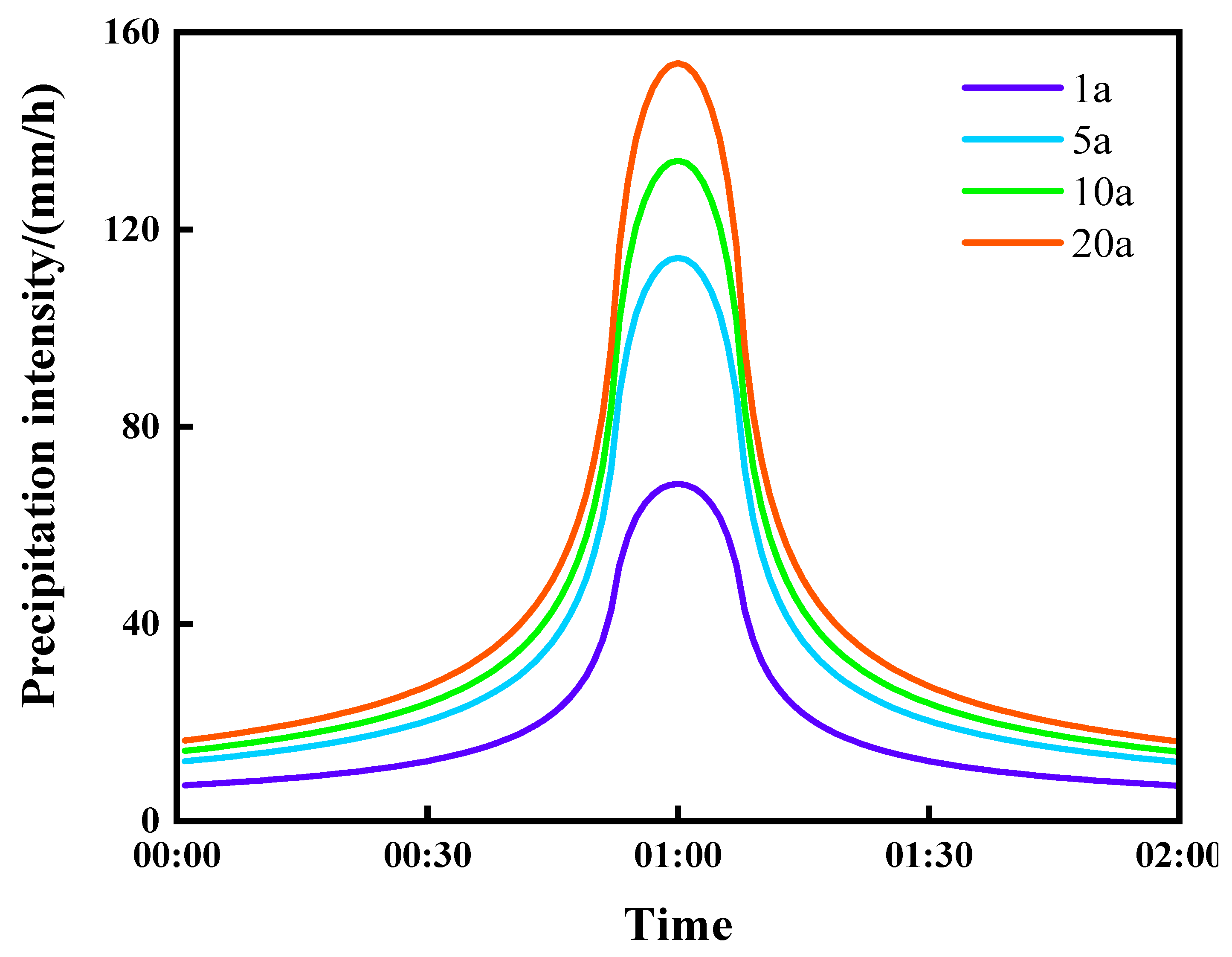
2.2.2. Precipitation Data
- Measured rainfall data
- b.
- Designing storm events
2.3. Principles of Coupled Urban Hydrological Modeling
2.3.1. One-Dimensional Hydrological–Hydrodynamic Model
- The continuity equation is used to describe the conservation of mass in the water flow:
- 2.
- The momentum equation is used to describe the conservation of momentum in the water flow:
2.3.2. Two-Dimensional Hydrodynamic Model
- Continuity equations for flow balancing:
- 2.
- Uniform flow equation for neighboring image element flow:
3. Materials and Methods
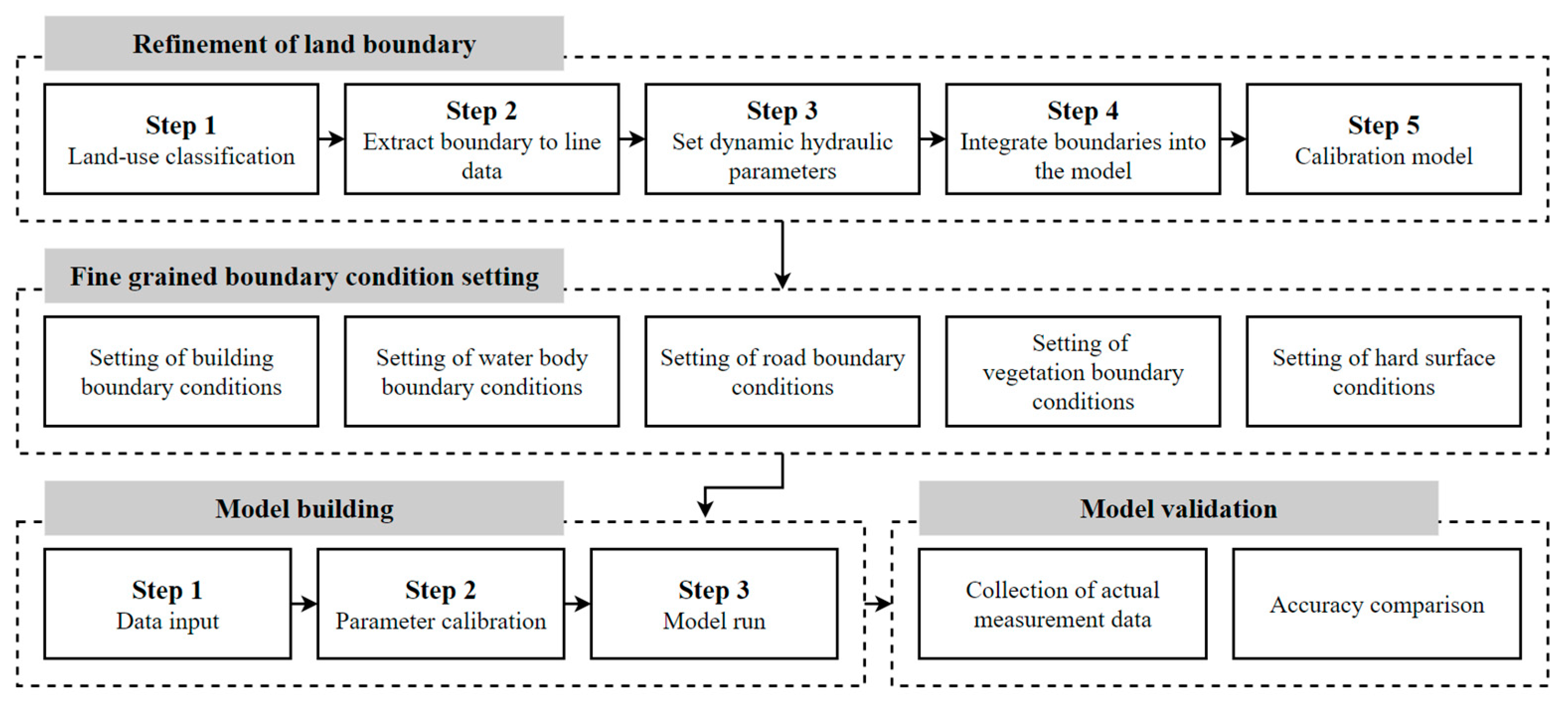
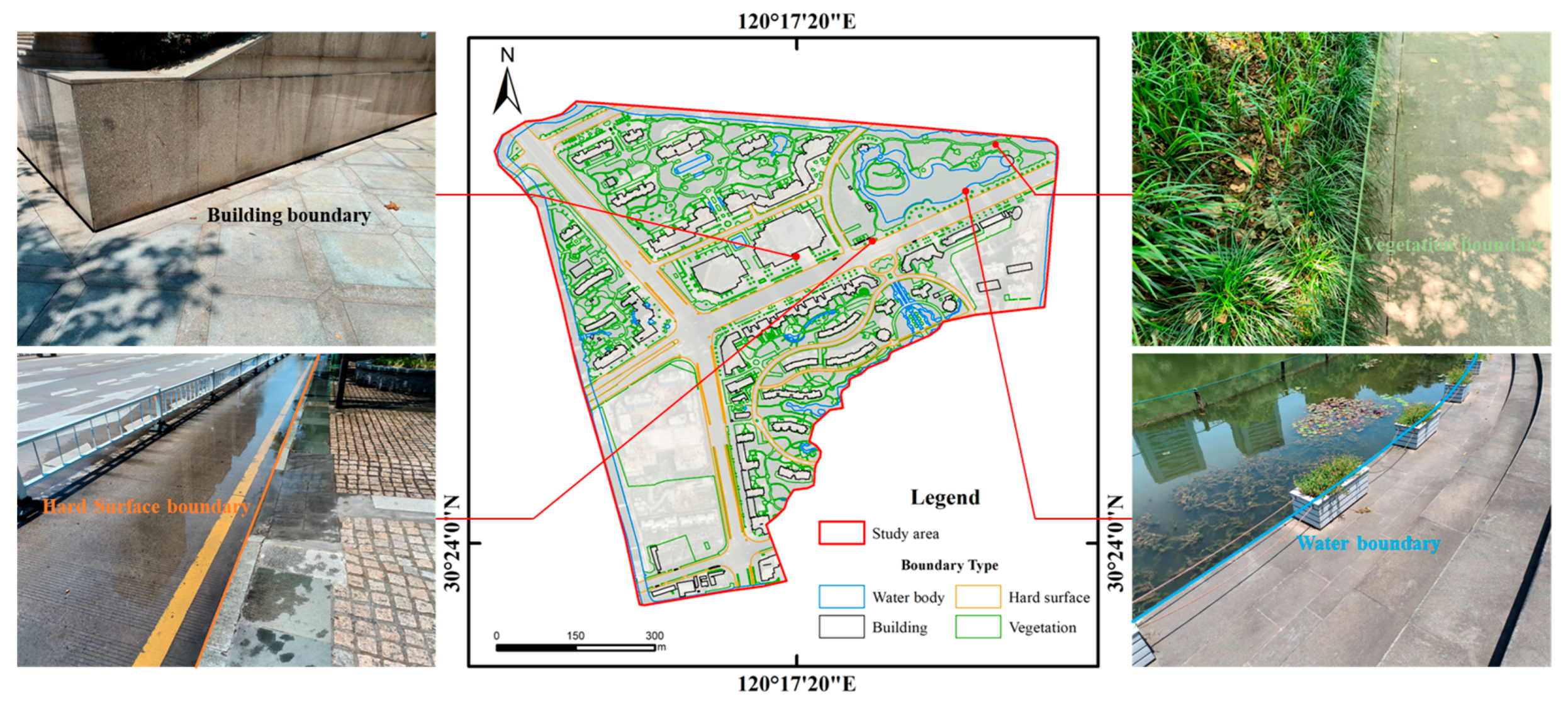
3.1. Land Feature Boundary Refinement
3.2. Refined Boundary Condition Setting
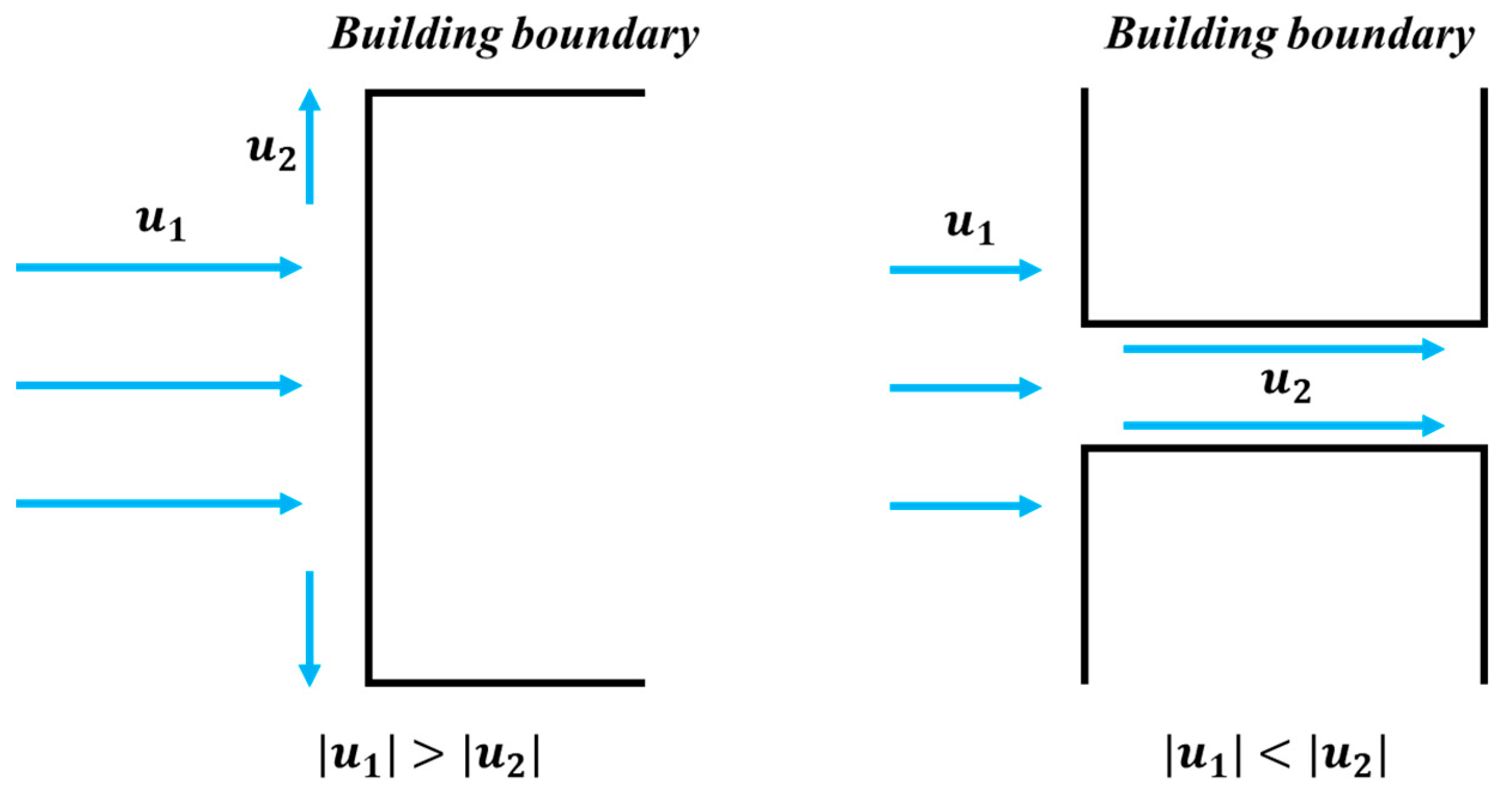
3.2.1. Setting of Building Boundary Conditions
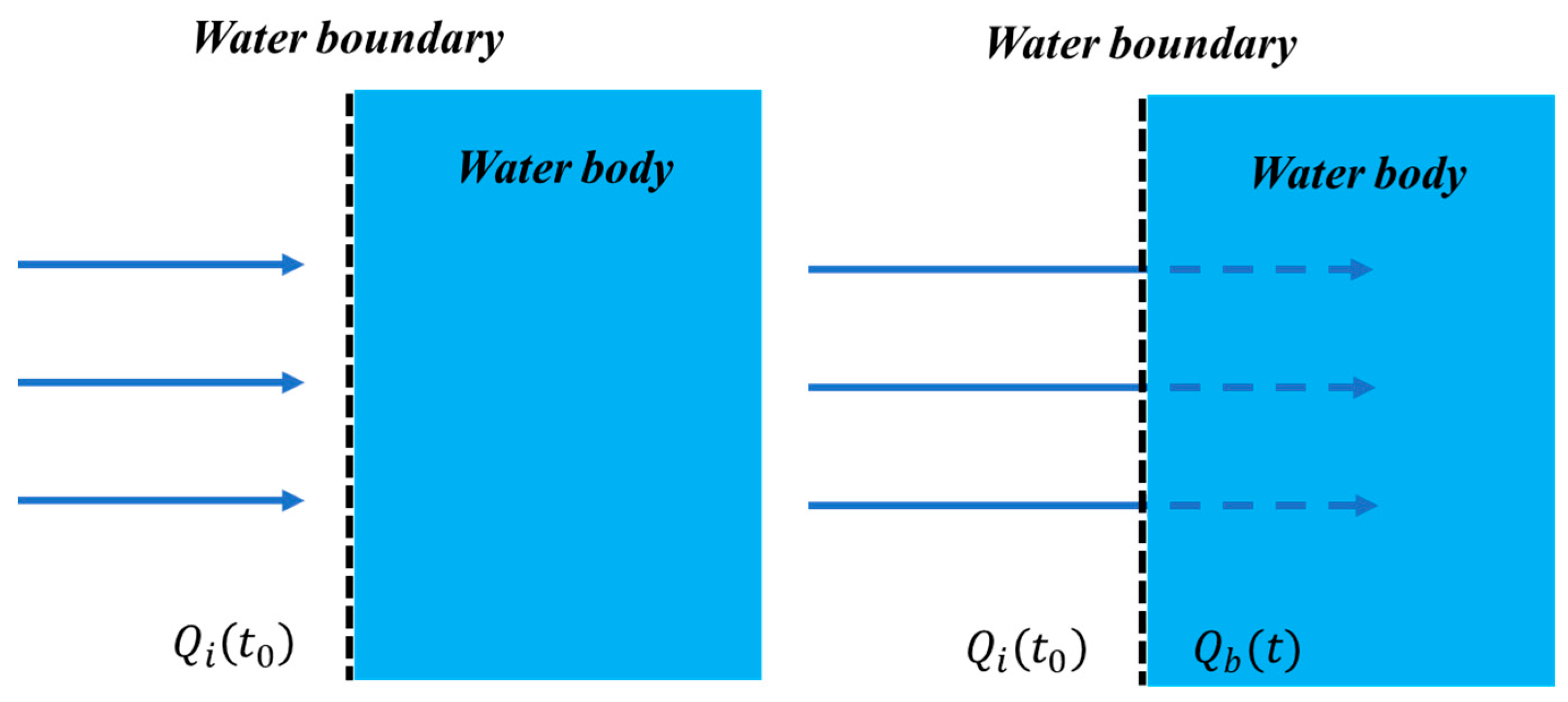
3.2.2. Setting of Water Body Boundary Conditions
3.2.3. Setting of Road Boundary Conditions
3.2.4. Setting of Vegetation Boundary Conditions
3.2.5. Setting of Hard Surface Boundary Conditions
3.3. Model Building
3.4. Model Validation
4. Results
4.1. Analysis of Model Simulation Results
4.2. Comparative Analysis of Model Performance Before and After Boundary Condition Refinement
4.3. Study of Accumulated Water Dynamics After Refinement of Boundary Conditions
5. Discussion
5.1. Influence of Boundary Conditions on the Accuracy and Extent of Simulation of Accumulated Water
5.2. Influence of Boundary Conditions on the Dynamic Behavior of Accumulated Water
6. Conclusions
- (1)
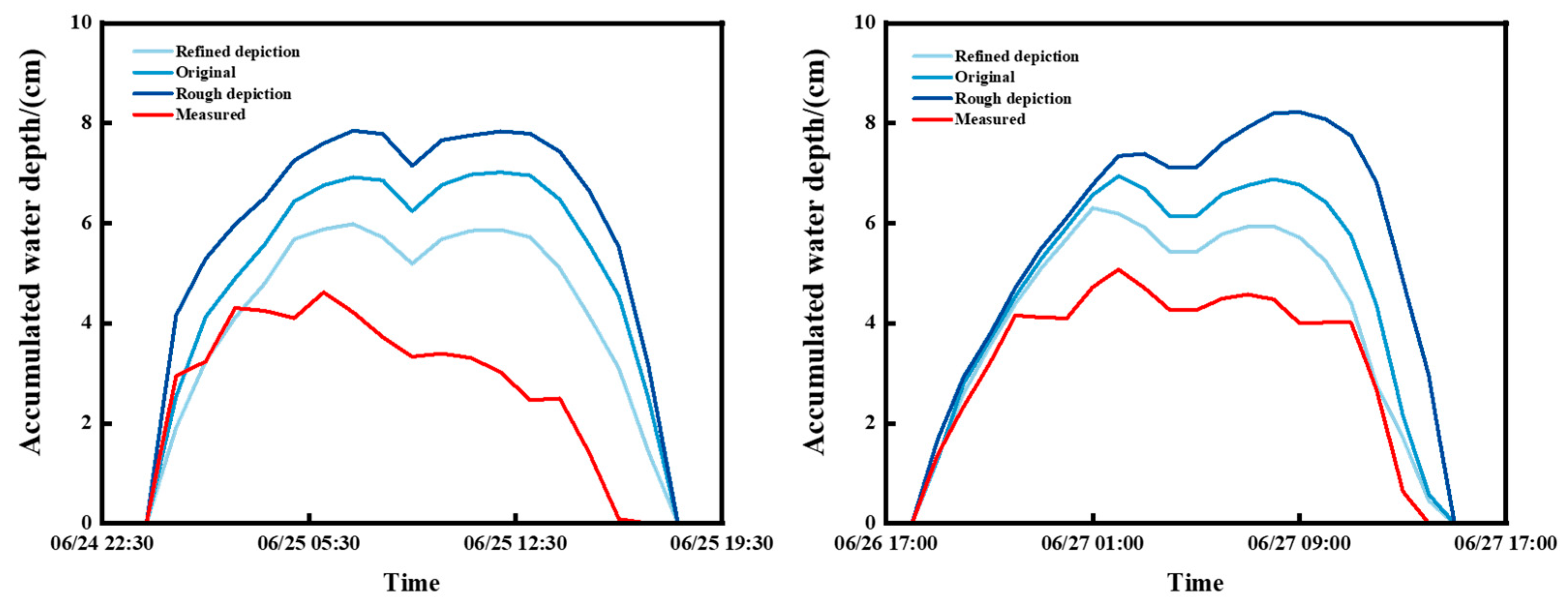
- The accumulated water depth change curves for three boundary condition scenarios of the refined depiction, original simulation, and rough depiction were compared using the measured precipitation as the validation data. The results show that the accumulated water curves of the refined depiction scenarios for the 20240625 and 20240627 precipitation events were the closest to the measured curves, with mean absolute errors of 0.60 cm and 0.49 cm, respectively, and the smallest overall errors. The rough depiction scenarios had the largest errors of 1.35 cm and 1.33 cm, respectively. From the results, it can be seen that compared with the original and rough depiction, the results of the refined depiction have higher accuracy, which is improved by 28.1% and 16.5%, respectively. Therefore, it is proved that the model after the refined boundary can simulate the real hydrological situation of the city under heavy rainfall conditions.
- (2)
- Three boundary condition scenarios, the refined depiction, original simulation, and rough depiction, were simulated over four precipitation return periods, 1a, 5a, 10a, and 20a. The results show that the simulated accumulated water area in the rough depiction scenario was significantly larger than that of the other two scenarios as the return period increased. The refined depiction scenario had the smallest extent of accumulated water and was more realistic because it took into account factors such as vegetation infiltration and changes in the water velocity to avoid the excessive spreading of accumulated water to features where it should not be. The difference in the average accumulated water area between the refined and original scenarios amounted to 21.45%, while the difference in the average accumulated water area in the rough depiction scenario amounted to 32.18%. Overall, the refined depiction scenario provided the most accurate simulation results for the extent of the accumulated water during each return period.
- (3)
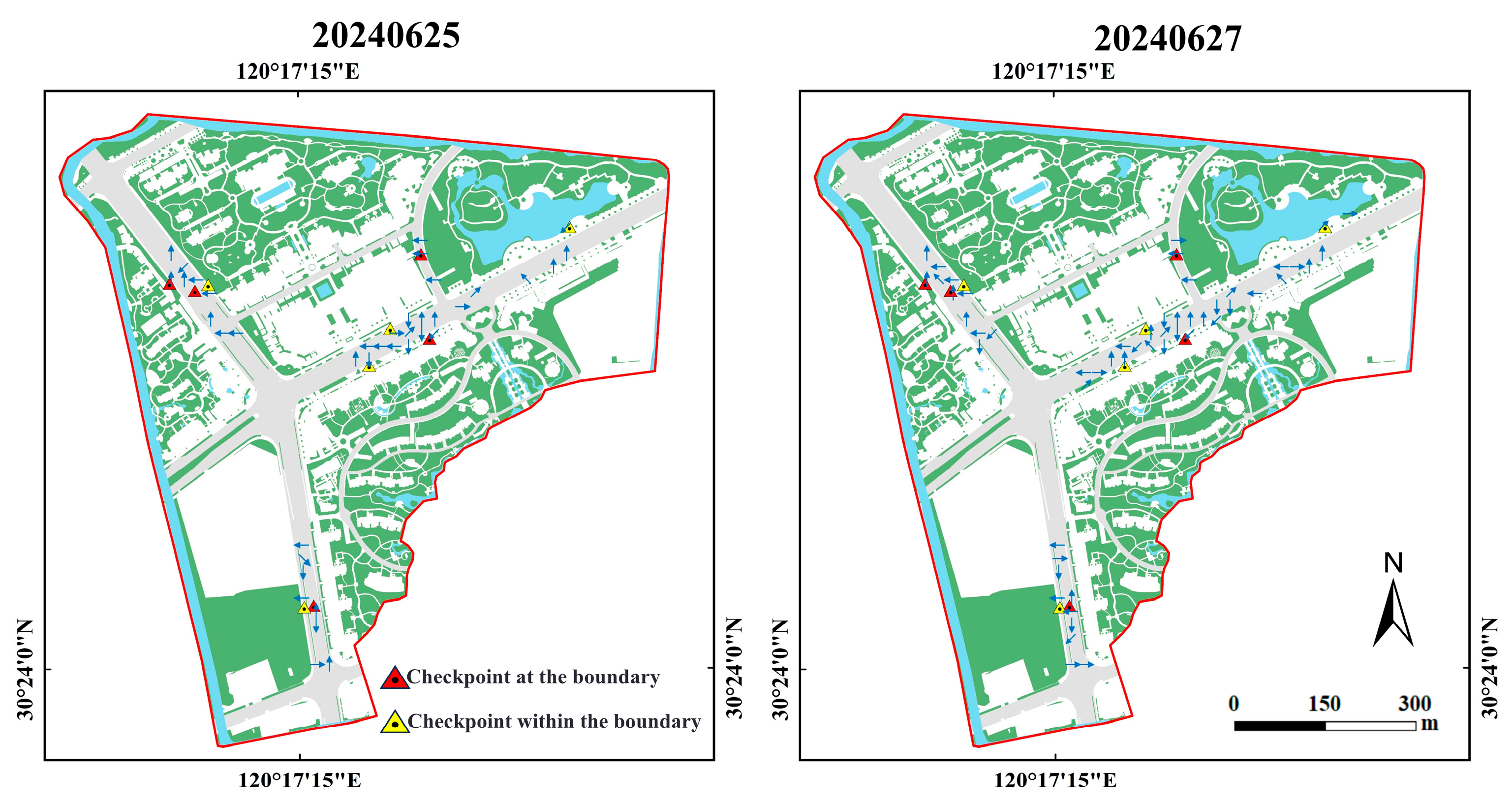
- According to the analysis of the dynamic process of the accumulated water, it was mainly distributed along the road, and the flow direction of the accumulated water inside the boundary was influenced by the topography, flowing from high to low; however, the accumulated water around the boundary was influenced by the boundary conditions, and the flow direction was changed. In particular, during the heavy precipitation event of 20240627, the accumulated water spread within the boundaries of the other land features, and the direction of the accumulated water after interacting with different boundaries showed diverse changes. It was also found that the flow rate of the accumulated water inside the boundary was higher than that on the boundary, and that the fastest diffusion of the accumulated water was on the hard surface, while the slowest diffusion of the accumulated water was on the vegetation. These results show that refined boundary conditions not only affect the static distribution of accumulated water, but also significantly influence the dynamic behavior of accumulated water.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cristiano, E.; ten Veldhuis, M.-C.; Van De Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar]
- Rezaei, A.R.; Ismail, Z.B.; Niksokhan, M.H.; Ramli, A.H.; Sidek, L.M.; Dayarian, M.A. Investigating the effective factors influencing surface runoff generation in urban catchments—A review. Desalin. Water Treat. 2019, 164, 276–292. [Google Scholar]
- Williams, E.S.; Wise, W.R. Hhydrologic impacts of alternative approaches to storm water management and land development 1. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 443–455. [Google Scholar]
- Wang, Y.; Zhang, X.; Xu, J.; Pan, G.; Zhao, Y.; Liu, Y.; Liu, H.; Liu, J. Accumulated impacts of imperviousness on surface and subsurface hydrology—Continuous modelling at urban street block scale. J. Hydrol. 2022, 608, 127621. [Google Scholar] [CrossRef]
- Shen, Y.; Morsy, M.M.; Huxley, C.; Tahvildari, N.; Goodall, J.L. Flood risk assessment and increased resilience for coastal urban watersheds under the combined impact of storm tide and heavy rainfall. J. Hydrol. 2019, 579, 124159. [Google Scholar]
- Xu, H.; Gao, J.; Yu, X.; Qin, Q.; Du, S.; Wen, J. Assessment of Rainstorm Waterlogging Disaster Risk in Rapidly Urbanizing Areas Based on Land Use Scenario Simulation: A Case Study of Jiangqiao Town in Shanghai, China. Land 2024, 13, 1088. [Google Scholar] [CrossRef]
- Wu, X.; Yu, D.; Chen, Z.; Wilby, R.L. An evaluation of the impacts of land surface modification, storm sewer development, and rainfall variation on waterlogging risk in Shanghai. Nat. Hazards 2012, 63, 305–323. [Google Scholar]
- Zhao, Y.; Rong, Y.; Liu, Y.; Lin, T.; Kong, L.; Dai, Q.; Wang, R. Investigating Urban Flooding and Nutrient Export under Different Urban Development Scenarios in the Rouge River Watershed in Michigan, USA. Land 2023, 12, 2163. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Y.; Zhou, J. Assessing the long-term impact of urbanization on run-off using a remote-sensing-supported hydrological model. Int. J. Remote Sens. 2015, 36, 5336–5352. [Google Scholar]
- Bian, G.; Wang, G.; Chen, J.; Zhang, J.; Song, M. Spatial and seasonal variations of hydrological responses to climate and land-use changes in a highly urbanized basin of Southeastern China. Hydrol. Res. 2021, 52, 506–522. [Google Scholar]
- Jahan, K.; Pradhanang, S.M.; Bhuiyan, M.A.E. Surface runoff responses to suburban growth: An integration of remote sensing, GIS, and curve number. Land 2021, 10, 452. [Google Scholar] [CrossRef]
- Zhai, H.; Lv, C.; Liu, W.; Yang, C.; Fan, D.; Wang, Z.; Guan, Q. Understanding spatio-temporal patterns of land use/land cover change under urbanization in Wuhan, China, 2000–2019. Remote Sens. 2021, 13, 3331. [Google Scholar] [CrossRef]
- Hassan, M.M. Monitoring land use/land cover change, urban growth dynamics and landscape pattern analysis in five fastest urbanized cities in Bangladesh. Remote Sens. Appl. Soc. Environ. 2017, 7, 69–83. [Google Scholar] [CrossRef]
- Hu, P.; Li, F.; Sun, X.; Liu, Y.; Chen, X.; Hu, D. Assessment of land-use/cover changes and its ecological effect in rapidly urbanized areas—Taking Pearl River Delta urban agglomeration as a case. Sustainability 2021, 13, 5075. [Google Scholar] [CrossRef]
- Hu, S.; Fan, Y.; Zhang, T. Assessing the effect of land use change on surface runoff in a rapidly urbanized city: A case study of the central area of Beijing. Land 2020, 9, 17. [Google Scholar] [CrossRef]
- Zimmermann, E.; Bracalenti, L.; Piacentini, R.; Inostroza, L. Urban flood risk reduction by increasing green areas for adaptation to climate change. Procedia Eng. 2016, 161, 2241–2246. [Google Scholar]
- Chithra, S.; Nair, M.H.; Amarnath, A.; Anjana, N. Impacts of impervious surfaces on the environment. Int. J. Eng. Sci. Invent. 2015, 4, 27–31. [Google Scholar]
- Yao, L.; Wei, W.; Chen, L. How does imperviousness impact the urban rainfall-runoff process under various storm cases? Ecol. Indic. 2016, 60, 893–905. [Google Scholar]
- Archer, N.; Bonell, M.; Coles, N.; MacDonald, A.; Auton, C.; Stevenson, R. Soil characteristics and landcover relationships on soil hydraulic conductivity at a hillslope scale: A view towards local flood management. J. Hydrol. 2013, 497, 208–222. [Google Scholar] [CrossRef]
- Balugani, E.; Lubczynski, M.; Reyes-Acosta, L.; Van Der Tol, C.; Francés, A.; Metselaar, K. Groundwater and unsaturated zone evaporation and transpiration in a semi-arid open woodland. J. Hydrol. 2017, 547, 54–66. [Google Scholar] [CrossRef]
- Suprayogo, D.; van Noordwijk, M.; Hairiah, K.; Meilasari, N.; Rabbani, A.L.; Ishaq, R.M.; Widianto, W. Infiltration-friendly agroforestry land uses on volcanic slopes in the Rejoso Watershed, East Java, Indonesia. Land 2020, 9, 240. [Google Scholar] [CrossRef]
- Bai, T.; Mayer, A.L.; Shuster, W.D.; Tian, G. The hydrologic role of urban green space in mitigating flooding (Luohe, China). Sustainability 2018, 10, 3584. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.-L.; Zhang, G.-L. Water infiltration in urban soils and its effects on the quantity and quality of runoff. J. Soils Sediments 2011, 11, 751–761. [Google Scholar] [CrossRef]
- Zhang, B.; Xie, G.; Zhang, C.; Zhang, J. The economic benefits of rainwater-runoff reduction by urban green spaces: A case study in Beijing, China. J. Environ. Manag. 2012, 100, 65–71. [Google Scholar] [CrossRef]
- Sitharam, T. Efficacy of coastal reservoirs to address India’s water shortage by impounding excess river flood waters near the coast. J. Sustain. Urban. Plan. Prog. 2017, 2, 49–54. [Google Scholar] [CrossRef]
- Lee, E.; Lee, D.; Kim, S.; Lee, K. Design strategies to reduce surface water flooding in a historical district. J. Flood Risk Manag. 2018, 11, S838–S854. [Google Scholar] [CrossRef]
- Munir, B.A.; Iqbal, J. Flash flood water management practices in Dera Ghazi Khan City (Pakistan): A remote sensing and GIS prospective. Nat. Hazards 2016, 81, 1303–1321. [Google Scholar] [CrossRef]
- Rodriguez, F.; Andrieu, H.; Morena, F. A distributed hydrological model for urbanized areas–Model development and application to case studies. J. Hydrol. 2008, 351, 268–287. [Google Scholar] [CrossRef]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Jantz, C.; Drzyzga, S.; Maret, M. Calibrating and validating a simulation model to identify drivers of urban land cover change in the Baltimore, MD metropolitan region. Land 2014, 3, 1158–1179. [Google Scholar] [CrossRef]
- Ma, Z.; Yao, R.; Sun, P.; Zhuang, Z.; Ge, C.; Zou, Y.; Lv, Y. Quantitative evaluation of runoff simulation and its driving forces based on hydrological model and multisource precipitation fusion. Land 2023, 12, 636. [Google Scholar] [CrossRef]
- Patel, R. Mathematical Model of the Kaipara Catchment. Doctoral Dissertation, The University of Auckland, Auckland, New Zealand, 1981. [Google Scholar]
- Granata, F.; Gargano, R.; De Marinis, G. Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA’s storm water management model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Flint, L.E.; Flint, A.L.; Thorne, J.H.; Boynton, R. Fine-scale hydrologic modeling for regional landscape applications: The California Basin Characterization Model development and performance. Ecol. Process. 2013, 2, 25. [Google Scholar] [CrossRef]
- Raza, A.; Ahrends, H.; Habib-Ur-Rahman, M.; Gaiser, T. Modeling approaches to assess soil erosion by water at the field scale with special emphasis on heterogeneity of soils and crops. Land 2021, 10, 422. [Google Scholar] [CrossRef]
- Feng, B.; Zhang, Y.; Bourke, R. Urbanization impacts on flood risks based on urban growth data and coupled flood models. Nat. Hazards 2021, 106, 613–627. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, X.; Feng, Q.; Yu, T.; Engel, B.A. Analyzing the impacts of topographic factors and land cover characteristics on waterlogging events in urban functional zones. Sci. Total Environ. 2023, 904, 166669. [Google Scholar]
- Yang, K.; Hou, H.; Li, Y.; Chen, Y.; Wang, L.; Wang, P.; Hu, T. Future urban waterlogging simulation based on LULC forecast model: A case study in Haining City, China. Sustain. Cities Soc. 2022, 87, 104167. [Google Scholar] [CrossRef]
- Lancia, M.; Zheng, C.; He, X.; Lerner, D.N.; Andrews, C.; Tian, Y. Hydrogeological constraints and opportunities for “Sponge City” development: Shenzhen, southern China. J. Hydrol. Reg. Stud. 2020, 28, 100679. [Google Scholar] [CrossRef]
- Li, Y.; Hu, T.; Zheng, G.; Shen, L.; Fan, J.; Zhang, D. An improved simplified urban storm inundation model based on urban terrain and catchment modification. Water 2019, 11, 2335. [Google Scholar] [CrossRef]
- Chen, G.; Hou, J.; Wang, T.; Lv, J.; Jing, J.; Ma, X.; Yang, S.; Deng, C.; Ma, Y.; Ji, G. The effect of spatial–temporal characteristics of rainfall on urban inundation processes. Hydrol. Process. 2022, 36, e14655. [Google Scholar] [CrossRef]
- Ma, B.; Wu, Z.; Wang, H.; Guo, Y.J.W. Study on the classification of urban waterlogging rainstorms and rainfall thresholds in cities lacking actual data. Water 2020, 12, 3328. [Google Scholar] [CrossRef]
- Piyumi, M.; Abenayake, C.; Jayasinghe, A.; Wijegunarathna, E. Urban flood modeling application: Assess the effectiveness of building regulation in coping with urban flooding under precipitation uncertainty. Sustain. Cities Soc. 2021, 75, 103294. [Google Scholar] [CrossRef]
- Tian, X.; Schleiss, M.; Bouwens, C.; van de Giesen, N. Critical rainfall thresholds for urban pluvial flooding inferred from citizen observations. Sci. Total Environ. 2019, 689, 258–268. [Google Scholar] [CrossRef]
- Towsif Khan, S.; Chapa, F.; Hack, J. Highly resolved rainfall-runoff simulation of retrofitted green stormwater infrastructure at the micro-watershed scale. Land 2020, 9, 339. [Google Scholar] [CrossRef]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model(SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Jang, S.; Cho, M.; Yoon, J.; Yoon, Y.; Kim, S.; Kim, G.; Kim, L.; Aksoy, H. Using SWMM as a tool for hydrologic impact assessment. Desalination 2007, 212, 344–356. [Google Scholar] [CrossRef]
- Freire Diogo, A.; Antunes do Carmo, J. Peak flows and stormwater networks design—Current and future management of urban surface watersheds. Water 2019, 11, 759. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, K.V.; Caloiero, T.; Mehta, D.J.; Singh, K. Comprehensive overview of flood modeling approaches: A review of recent advances. Hydrology 2023, 10, 141. [Google Scholar] [CrossRef]
- Karim, F.; Armin, M.A.; Ahmedt-Aristizabal, D.; Tychsen-Smith, L.; Petersson, L. A review of hydrodynamic and machine learning approaches for flood inundation modeling. Water 2023, 15, 566. [Google Scholar] [CrossRef]
- Wijaya, O.T.; Yang, T.-H. A novel hybrid approach based on cellular automata and a digital elevation model for rapid flood assessment. Water 2021, 13, 1311. [Google Scholar] [CrossRef]
- Ni, Y.; Cao, Z.; Liu, Q.; Liu, Q. A 2D hydrodynamic model for shallow water flows with significant infiltration losses. Hydrol. Process. 2020, 34, 2263–2280. [Google Scholar] [CrossRef]
- Arnold Jr, C.L.; Gibbons, C.J. Impervious surface coverage: The emergence of a key environmental indicator. J. Am. Plan. Assoc. 1996, 62, 243–258. [Google Scholar] [CrossRef]
- Findlay, S.; Quinn, J.M.; Hickey, C.W.; Burrell, G.; Downes, M. Effects of land use and riparian flowpath on delivery of dissolved organic carbon to streams. Limnol. Oceanogr. 2001, 46, 345–355. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Zhuang, D.; Fu, Z.; Wang, K.; Chen, H. Evaluating the hydrological function of vegetation restoration in fragile karst area: Insights from the continuous surface and subsurface runoff monitoring. Soil Tillage Res. 2023, 234, 105847. [Google Scholar] [CrossRef]
- Rowe, P.G.; Kan, H.Y. Urban Intensities: Contemporary Housing Types and Territories; Birkhäuser: Basel, Switzerland, 2014. [Google Scholar]
- Sanz-Ramos, M.; Bladé, E.; González-Escalona, F.; Olivares, G.; Aragón-Hernández, J.L. Interpreting the manning roughness coefficient in overland flow simulations with coupled hydrological-hydraulic distributed models. Water 2021, 13, 3433. [Google Scholar] [CrossRef]
- Jato Espino, D. Hydrological Modelling of Urban Catchments Under Climate Change for the Design of a Spatial Decision Support System to Mitigate Flooding Using Pervious Pavements Meeting the Principles of Sustainability. Ph.D. Thesis, University of Cantabria, Santander, Spain, 2016. [Google Scholar]
- Rueda, F.; Moreno-Ostos, E.; Armengol, J. The residence time of river water in reservoirs. Ecol. Model. 2006, 191, 260–274. [Google Scholar] [CrossRef]
- Hahn, C.; Prasuhn, V.; Stamm, C.; Milledge, D.G.; Schulin, R. A comparison of three simple approaches to identify critical areas for runoff and dissolved reactive phosphorus losses. Hydrol. Earth Syst. Sci. 2014, 18, 2975–2991. [Google Scholar] [CrossRef]
- Lefebvre, A.; Thompson, C.; Amos, C. Influence of Zostera marina canopies on unidirectional flow, hydraulic roughness and sediment movement. Cont. Shelf Res. 2010, 30, 1783–1794. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Muthusamy, M.; Casado, M.R.; Butler, D.; Leinster, P. Understanding the effects of Digital Elevation Model resolution in urban fluvial flood modelling. J. Hydrol. 2021, 596, 126088. [Google Scholar] [CrossRef]
- Jiang, W.; Yu, J.; Wang, Q.; Yue, Q. Understanding the effects of digital elevation model resolution and building treatment for urban flood modelling. J. Hydrol. Reg. Stud. 2022, 42, 101122. [Google Scholar] [CrossRef]
- Mason, D.C.; Bevington, J.; Dance, S.L.; Revilla-Romero, B.; Smith, R.; Vetra-Carvalho, S.; Cloke, H.L. Improving urban flood mapping by merging synthetic aperture radar-derived flood footprints with flood hazard maps. Water 2021, 13, 1577. [Google Scholar] [CrossRef]
- Hou, J.; Wang, N.; Guo, K.; Li, D.; Jing, H.; Wang, T.; Hinkelmann, R. Effects of the temporal resolution of storm data on numerical simulations of urban flood inundation. J. Hydrol. 2020, 589, 125100. [Google Scholar] [CrossRef]
- Yang, W.; Zheng, C.; Jiang, X.; Wang, H.; Lian, J.; Hu, D.; Zheng, A. Study on urban flood simulation based on a novel model of SWTM coupling D8 flow direction and backflow effect. J. Hydrol. 2023, 621, 129608. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Zheng, S.; Chen, G.; Zhao, P.; Wang, C. High efficiency integrated urban flood inundation simulation based on the urban hydrologic unit. J. Hydrol. 2024, 630, 130724. [Google Scholar] [CrossRef]




| Parameter | Roughness Coefficient | Permeability Retention | Capacity | Surface Slope | Coverage |
|---|---|---|---|---|---|
| Value | 0.03 | 0 mm/h | 0 mm | 1–2% | 100% |
| Parameter | Roughness Coefficient | Permeability Retention | Capacity | Surface Slope | Coverage |
|---|---|---|---|---|---|
| Value | 0.08 | 1 mm/h | 5 mm | 10% | 80% |
| Parameter | Roughness Coefficient | Permeability Retention | Capacity | Surface Slope | Coverage |
|---|---|---|---|---|---|
| Value | 0.010 | 0 mm/h | 0 mm | 0% | 90% |
| Events | 20240511 | 20240530 | 20240609 | Total |
|---|---|---|---|---|
| Value | 93.8% | 91.3% | 91.7% | 92.0% |
| Refined Depiction | Original | Rough Depiction | |
|---|---|---|---|
| 20240625 | 0.60 cm | 0.82 cm | 1.35 cm |
| 20240627 | 0.49 cm | 0.72 cm | 1.33 cm |
| Total | 0.54 cm | 0.77 cm | 1.34 cm |
| Checkpoint Type | 20240625 (m/s) | 20240627 (m/s) | Average Value (m/s) | |
|---|---|---|---|---|
| Within the boundary | Road | 0.068 | 0.063 | 0.057 |
| Road | 0.053 | 0.056 | ||
| Road | 0.053 | 0.063 | ||
| Hard surface | 0.08 | 0.077 | ||
| Vegetation | 0.012 | 0.051 | ||
| At the boundary | 0.048 | 0.038 | 0.037 | |
| 0.049 | 0.042 | |||
| 0.03 | 0.048 | |||
| 0.011 | 0.03 | |||
| 0.043 | 0.032 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Zhang, Y.; Lou, Y.; Tang, Z.; Wang, P.; Hu, T. Impact of Refined Boundary Conditions of Land Objects on Urban Hydrological Process Simulation. Land 2024, 13, 1808. https://doi.org/10.3390/land13111808
Chen C, Zhang Y, Lou Y, Tang Z, Wang P, Hu T. Impact of Refined Boundary Conditions of Land Objects on Urban Hydrological Process Simulation. Land. 2024; 13(11):1808. https://doi.org/10.3390/land13111808
Chicago/Turabian StyleChen, Chaohui, Yindong Zhang, Yihan Lou, Ziyi Tang, Pin Wang, and Tangao Hu. 2024. "Impact of Refined Boundary Conditions of Land Objects on Urban Hydrological Process Simulation" Land 13, no. 11: 1808. https://doi.org/10.3390/land13111808
APA StyleChen, C., Zhang, Y., Lou, Y., Tang, Z., Wang, P., & Hu, T. (2024). Impact of Refined Boundary Conditions of Land Objects on Urban Hydrological Process Simulation. Land, 13(11), 1808. https://doi.org/10.3390/land13111808







