Abstract
One argument for containing urban densities is that cities need a critical population density to sustain sufficiently available public transportation. However, the question of whether denser cities foster shorter public transport networks empirically is problematic because real-world transport nets are a product of many additional factors presumably not related to urban form. This paper adopts a network expansion simulation approach to generate and analyze counterfactual data on network lengths for 36 world cities, in which all networks are generated with similar expansion restrictions and objectives. Denser cities are found to have shorter simulated public transport networks, regardless of the tested model parameters. This provides additional proof that densities are needed to facilitate the provision of proximate public transport infrastructure, with potentially self-reinforcing effects.
1. Introduction
By limiting distances between inhabitants, urban density is suggested to be a major determinant of urban transport efficiency, as manifested in energy consumption and greenhouse gas emissions for transport [,], private vehicle use and fuel consumption [], modal split [], trip frequency, and share of active transport []. Containing urban expansion is, therefore, one stated goal of the UN Sustainable Development Goals []. However, urban density is clearly not a panacea for all of society’s problems. The beneficial effects of density on transport in support of ‘town-cramming’ are confounded because people with different traveling preferences are likely sorted spatially []; the effect of densification on congestion is not accounted for []; and the benefits of densification on transport energy consumption would be very limited []. Others argue that, through economies of scale, urban efficiency primarily increases with population size [], and in fact, only residual deviations from general scaling laws are attributable to population densities []. Higher-density residential developments are often considered less desirable, and realizing high densities in urban expansion projects may be relatively costly because of institutional barriers [] and the common necessity of public intervention []. Densification of the existing urban fabric is plausibly even more expensive. Urban density loss and urban expansion thus persist even in regions facing population decline []. Clearly, sound arguments in favor of dense urban development are called for.
Many studies focus on the effect that urban densities and public transport availability have on modal shifts. Bento et al. [] study vehicle ownership and private vehicle usage in cities in the United States in relation to, amongst others, urban densities, public transport network length, and distance to public transport stops. They find that shorter distances to the central business district and shorter distances to public transport stops reduce private vehicle usage, while more compact city forms and lower distances to public transport also reduce vehicle ownership. Levinson and Kumar [] similarly find higher transit mode shares in higher-density cities. Rickwood et al. [] propose the existence of positive feedback between densities, public transport availability, and transit ridership shares. Proximate public transport supply would be necessary to facilitate ridership, and high densities would be necessary to facilitate proximate public transport stops.
Whether denser land use can indeed foster proximate public transport availability is the topic of this paper. We expect that lower-density cities would require a much more sizeable network (and hitherto investment) to supply proximate public transport to a sizeable part of the population. Other explanations may be that cities need sufficient population mass to allow proximate public transport supply or the effect of regional urban form, as the existence of a commuting zone or satellite suburbs may considerably affect the difficulty of providing proximate public transport.
One way to analyze public transport availability is through the analysis of available data on public transport supply []. Unfortunately, for a comparison of public transport networks, real-world public transport networks are not very useful, as political preferences, budgetary considerations, and physical geography play an important role in network expansion considerations and, thus, in network outcomes []. In fact, it is plausible that, through path dependency, urban forms and public transport availability coincide [,]. For a fair comparison, network expansion considerations need to be held equal among all observations. In order to obtain the wanted ceteris paribus data, counterfactual data have been produced for this study by adopting a simulation approach. The sole aim of that approach is to simulate network expansion until a fixed percentage of a city’s population is connected by the network in order to verify whether higher-density cities can achieve high public transport availability at a comparatively limited cost. We assume here that longer transport networks are more costly to construct and operate. The next section will describe the simulation method; subsequent sections will present results and reflect on the method. Some final remarks will conclude the method and suggest venues for improvement.
Besides providing a counterfactual, comparable dataset of public transport networks in cities around the world, this paper also contributes to the developing field of network expansion studies. Novel elements in this paper are the adaptation of a simulation approach to provide data for multiple world cities, the analysis of aggregate outcomes of the simulations, and a sensitivity test that verifies the robustness of the found results when key parameters are changed. Contributions to network expansion have, inter alia, been made by physicists, economists, and quantitative geographers.
Transport network development can be described as an innovation diffusion process []. It is described as a sequential game [], with many agents and intermediate additions that shape the future market. The sequential nature of the process causes that, even with considerable coordination, the outcome of the process is a Nash equilibrium rather than an aggregate optimum [,]. Tied to this are economic considerations. Through network externalities [], the value of a transport network increases more than proportionally with the number of people it connects. Network externalities can thus lock-in, in which an entire market adapts to the available network, thus contributing to the positive feedback described by Rickwood et al. [].
In geographic terms, it can roughly be described in three stages, in which new links have different roles []. Transport networks prefer routes with presumably high demand []. Levinson [] found that the sequence of metro station openings in London more or less followed the population density ranks of boroughs. Yamins et al. [] proposed a two-step procedure to simulate road network diffusion within a city to explore whether road structures can realistically be simulated. Other contributions used network models to investigate the closure of road links [] and first-mover advantages []. Raimbault [] modeled the co-evolution of railway networks and urban populations, although the geographic paths of the expanding network could be omitted there. Raimbault and Le Néchet [] have setup a model that simulates interactions between land use and transport, by which transport network upgrades aim at maximizing aggregate or local accessibility gains.
2. Simulation Method
For this paper, network expansion simulations have been executed using the so-called Public Transport Allocator (PTA) heuristics []. These heuristics have been set up for this exercise to simulate an ad hoc style of network expansion, iteratively building one link with a high estimated return on investment until the expansion process is deemed complete. Those routines have been applied to model networks in 36 world cities. Subsequently, the lengths of those networks were compared, and general linkages between density and network length were identified. All simulation results are available through []. A key aspect of the method is that it iteratively forms a network by finding presumably profitable paths between termini, described as nodes. Those nodes are considered representative of the location of population masses in this application, observed in a 1 km2 regular lattice of grid cells.
The methodological description further follows the vocabulary proposed by Rodrigue et al. [], discerning connections, which are target attachments that reduce travel costs between two selected termini but have no geographical form; paths, which are a spatially explicit collection of lines that form the connection between two selected termini and potentially pass intermediate nodes; and links, which are the individual line attachments between all observed nodes that can jointly form a path (see Figure 1).
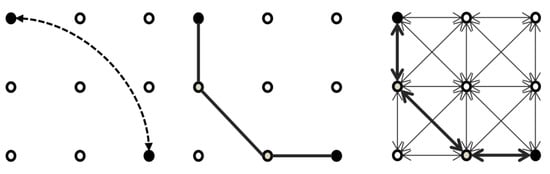
Figure 1.
Graphical representation of key methodological terms that are used in this paper. Nodes are given as circles. Selected termini are filled with black circles. Intermediate nodes are circles filled with gray. A single connection (left, dashed arrow) is repeatedly selected from an OD matrix for a travel time improvement. This connection does not have a spatial form. A single path (middle, thick line) is sought between the connection points through an optimization routine. Such a path can comprise multiple links (right, arrows) between intermediate and termini nodes. The links that comprise the selected path are indicated by thicker arrows; they receive a travel cost improvement vis-à-vis links that have not been selected.
The modeling procedure is shown schematically in Figure 2 and will be described in detail in the following sections, which deal with preparation, matrix-based connection selection, path designation, and end-state evaluation. A glossary of variables and parameters is given in Table A1 in Appendix A. The simulation approach draws roughly from the Transport Link Scanner model []. It thus treats network development as a sequential game [], in which market conditions are affected by every addition to the network.
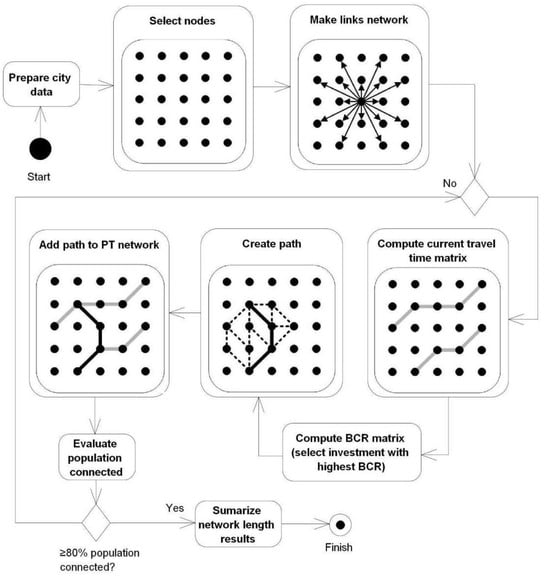
Figure 2.
Schematic representation of modeling approach to obtain network lengths for a city.
At the 1 km2 resolution adopted in this study, the number of nodes is much larger in some world cities than the roughly 1000 considered in the Transport Link Scanner application. In addition, to connect 80% of the population of a city, many more model iterations are needed. Thus, the computational burden is much larger compared to []. To be practically able to simulate urban transport network growth, the adopted approach has been simplified considerably. Only the first two steps are included. Those steps are the repeated selection of one connection, based on the estimated costs and benefits of upgrading connections between pairs of termini, and the generation of the most profitable path for the selected connection. The process is broadly similar to Yamins et al. [] in that iteratively, only one pair is selected for an upgrade, and subsequently, an optimal route is searched between the selected termini. Salient differences with Yamins et al. are that in this paper, (1) pairs are selected assuming that the investing agent aims at maximizing passenger kilometers traveled on the new link; (2) routes are sought that balance the additional returns from a detour versus the additional costs; and (3) the simulations are run using granular, observed population distributions in multiple world cities.
The population distribution is exogenous and held fixed throughout the simulations. Only one agent is expected to be active at any investment, and only the return on investment on the new link is expected to be relevant to select investments. In addition, network effects that can come into play, for example, when the hinterland of a terminus uses a new link as part of multimodal travel, are discarded in the computation of return on investment. When estimating the return on investment, only returns from direct trips between termini are taken into account. Despite the simplifications, the routine still takes multiple days to simulate expansion in extended cities. The computational complexity is described in Appendix B.
2.1. Preparation
The modeling sequence starts by isolating all inhabited grid cells g ∈ G, with G consisting of all grid cells that have their center within the geography expected to be part of a city. Functional Urban Areas (FUA) [] have been used to delineate separate urban systems. Gridded populations in 2015 and the FUA boundaries derived from those grids were obtained from the 2019 release of the GHSL global grids []. It must be emphasized that the used population grids were created by disaggregating population census results over remotely sensed built-up fractions so that population totals and the boundaries of urban systems may deviate from official statistics. The geographic centers of grid cells g are used here to represent the terminus of spatial interaction with the population in those grid cells, despite the fact that population-weighted centers are a more accurate representation of population location in spatial interaction applications []. Given the fairly abstract modeling approach taken here, the additional inaccuracies caused by spatial aggregation are considered hardly relevant.
Links are added from all inhabited grid cells g to all other inhabited grid cells g that are maximally two steps away from the grid cell of interest, so that all grid cells have direct links with a maximum of 16 grid cells in their neighborhood (see Figure 3 for a schematic representation). It is important to note that links to direct neighbors (for example, 0°, 45°, and 90° from an origin node) only connect first-tier neighbors directly. Second-tier neighbors are not connected directly because those connections can be made by passing over the direct neighbor. We do not expect that omitting these links would affect the results negatively, as there are no inherent penalties imposed on passing through intermediate nodes. Grid cells that do not have any neighbors within two steps are given single links to the closest neighbor(s) that are within the closest distance.
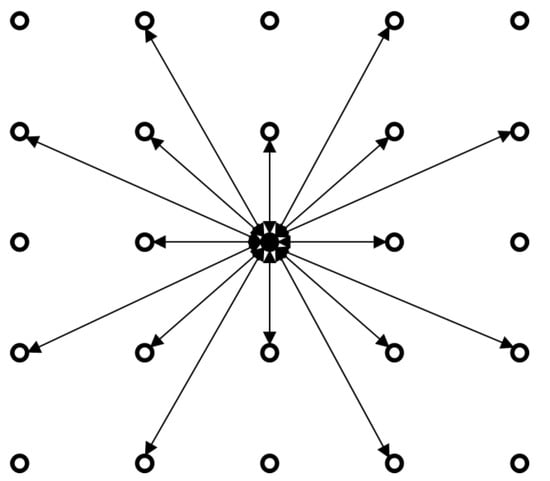
Figure 3.
Schematic representation of links generated for one node in the network. The central node (represented by a black circle) obtains direct links (represented by arrows) to the 16 closest nodes (represented by circles).
At the start, all links are attributed a relatively low effective speed for transversal of that link on foot. In the reported application, effective walking speed V0 is set to 4 km/h, which is considered a realistic walking speed when assuming walking at 4.5 km/h and presumable detours that are not taken into account in the drawn straight lines. Other parameters that are set a-priori are (with the main settings between parentheses) the assumed effective speed V1 of the introduced public transport mode (30 km/h); the fixed monetary costs X of a link (the equivalent of 10 km of line); the fixed waiting time W for accessing upgraded links from an entry node (10 min); and the maximum circuity γ with which a path may deviate from the straight line (1.5). The chosen parameter values represent admittedly ad hoc values that are not necessarily representative of the travel characteristics or the public transport systems in the studied cities. A limited sensitivity analysis has, therefore, been executed to explore the effects of the adopted settings. In a later section, we will discuss this sensitivity analysis in more detail.
2.2. Matrix-Based Connection Selection
As in Yamins et al. [] and Levinson and Xie [], this approach comprises an iterative procedure that repeatedly searches for candidate connections to upgrade, selects one connection, and adds that connection as a plausible path to the modeled network so that the links that form that path obtain a lower transversal time. In every model iteration, the approach starts by computing a travel time matrix between all inhabited grid cells using a shortest path algorithm based on the network of links, including prior upgrades. All links are expected to be able to exchange passengers at joint nodes without incurring additional travel costs, regardless of the direction of those links or whether any links are upgraded or not.
Subsequently, for each origin–destination pair, the return on investment of a public transport network connection between that particular pair is estimated. The return on investment of upgrading the connection between i and j is estimated as (1):
where B0 and B1 are expected passenger mileage with (B1) or without (B0), an upgrade between termini i and j; C consists of construction costs; and X is an additional fixed cost. The cost is estimated to be the length of the shortest possible path between termini. We acknowledge that in the real world, physical geography can pose considerable challenges for network construction, which may limit network construction paths and cause substantial variation in cost density. As in other contributions [,], this will be ignored for the sake of simplicity, along with other practically relevant factors such as institutional and private organizations. B0 and B1 are computed using an origin-constrained gravity model, where B0 is computed as (2):
in which P is the population at the origin or destination. The potential accessibility of the node is used to constrain trip production, as in a singly constrained interaction model []. It is computed as . Given that social interaction grows superlinearly with city size [], some elasticity of consumption on potential accessibility may be supposed, as can be specified in Alonso’s General Theory of Movements model []. In the absence of fitting general parameters, a fully origin-constrained specification is considered the most conservative and has, therefore, been maintained here. Both and depend on the function , which is a distance decay function of travel times obtained from the concurrent network. In the application, this function is defined as . Finally, L is the Euclidean distance between i and j. That variable proxies for the length of trips between the termini, so the benefits depend on the estimated trip length. Without a doubt, the choice of revenue model is relevant for the outcomes; it may be expected that simulating transport systems with other revenue models (for example, fixed fees to enter the system) may yield very different outcomes.
In the same vein as (2), the expected passenger mileage with an upgrade is (3):
where is a distance decay function of travel times that are obtained in case a network upgrade is constructed for the od-pair at hand. Upgraded travel times are computed as , so that travel time savings depend on the Euclidean distance between termini and the upgrade speed and are limited due to the fixed waiting time penalty in W. That penalty is expected to simulate unavoidable delays due to scheduling, which presumably are most felt in the travel time savings of short trips. The computationally simplest way to solve this equation would be by computing A1 as the accessibility if all links were upgraded. However, with many destinations, assuming general travel time improvements will substantially overestimate the change between A0 and A1, thus leading to the underestimation of the benefits of a single investment between two termini. We therefore introduce a modest adaptation of A1, which we compute with a value specific to each pair of termini rather than generally per origin, so that (4):
where A1 includes the additional interactions between i and j obtained when upgrading only the connection between the termini at hand. The returns on investments from (1) are estimated for all potential origin–destination pairs. The od-pair with the highest return on investment is selected, after which an optimal path is searched for that pair.
2.3. Path Designation
The shortest path between two termini is not necessarily the most attractive path for an upgrade. In the modeling routines, a path can detour from the straight line if a detour makes line operation more profitable while still providing a substantial travel time improvement between the selected termini. A corridor allocation problem-solving approach [,] is used to find the most attractive path between termini. Using such a corridor allocation approach, the routine derives a number of potential paths and estimates their return on investment. Subsequently, only one path is selected that, within a specific maximum distance, meets the highest proxied return on investment. Thus, only the links comprising one path are selected for a speed upgrade in every model iteration.
The maximum distance is computed as the minimum value from two separate criteria, namely the maximum circuity parameter , and the maximum distance at which the potential travel time gains between the selected termini are maximally halved to ensure that the link will remain reasonably profitable for the selected pair of termini. Thus, maximum detour distance is computed as (5):
in which is the Euclidean distance between i and j, is the maximum distance based on circuity, and indicates the maximum detour that is possible if at least half the potential travel time gains are obtained, so that (6):
Subsequently, for each link on the network, the following impedance is computed:
in which the impedance of every link depends on the population connected to the nodes that each link connects, the construction costs of each link, and the length of the link. This impedance is used in the shortest path searching method to find the most profitable path. For the sake of simplicity, construction costs are held linear with link length; more intricate specifications may be imputed [,] but were neglected to avoid incomparability of network outcomes between cities. The return on investment of a path is computed separately for two cases. In cases where the length of the path is lower than , the return on investment is computed as the sum of the population connected by the path, divided by the sum of construction costs; or, in cases where the length of the path exceeds , the return on investment is computed as the inverse of the length of the path.
The k parameter affects the balance between the left (return on investment) component and the total length of the link. With k = 0, the balance leans towards return on investment; with k = 1, only length considerations are taken into account, and the method should yield the shortest path. The routines implemented here start from k = 0 and gradually increase the value of k, with the aim of finding the link with the best-proxied return on investment. We consider the outcome close to an optimal path, given the limited information in the procedure, and therefore, a reasonable proxy for a plausible path.
2.4. End State Evaluation
The selected links are flagged in the network as being upgraded and obtain the public transport travel speed instead of the walking travel speed. A grid cell is flagged as connected if an upgraded link terminates in its node, so that (8):
Subsequently, the percentage computed population is computed as (9):
Finally, the decision is made to end the simulation or end it based on the criterion . If the connected population is at least the target connected percentage, the final result network of public transport network links is stored as a shapefile. If not, the procedure continues by repeating step 1 on the network, including the public transport link added in this modeling iteration.
3. Results
The outlined simulation method is applied to obtain results for cities across the globe. To do so, gridded populations from the Global Human Settlement Layer [] have been selected within the bounds of the Functional Urban Areas [] of cities that are deemed either well-known or representative of a specific style of urbanization; all continents have more or less equal numbers of cities. The full list of cities and their results is in Table A2 in Appendix C. The approach is programmed to be executed by the open-source GeoDMS software (version 8.043), using the efficient routines of that software for the generation of travel time matrices. The programmed routines are available upon request. Execution times varied substantially for the selected cities, depending on the number of model iterations needed to connect 80% of a city’s population. Cities with modestly populated areas, such as Hong Kong, took a couple of hours; extensive cities, such as Tokyo and Houston, took multiple days. Examples of the iterative network simulation process are shown in Figure 4.
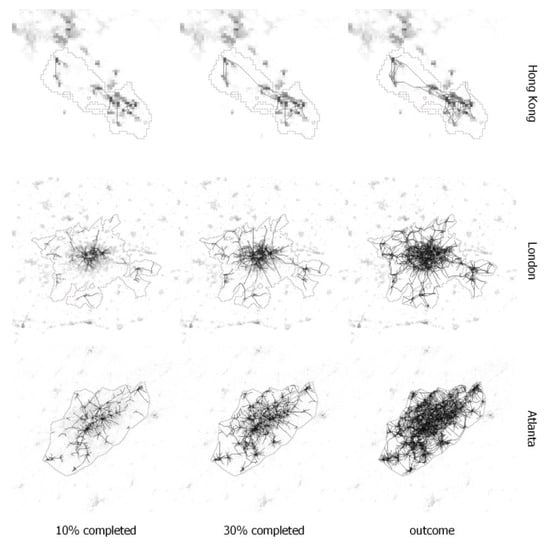
Figure 4.
Network allocation results at different stages of the iterative procedure in three selected cities. Black lines indicate simulation results. Dotted lines represent FUA boundaries. Population distribution is given on a grayscale, with darker tones indicating higher population numbers.
Simulated network lengths were aggregated into a single statistic for each FUA, along with a number of other variables. It is well known that aggregate urban statistics depend on the delineation of analyzed areal units [,], so any comparison between cities is easily invalidated. FUA areas are used here as units of analysis because they provide an objective delineation of wider urban areas based on geographic characteristics rather than chance, physical geography, or political considerations; we expect that they, therefore, provide a fairer basis for comparing the performance of the selected cities than administrative boundaries.
To measure urban efficiency, network lengths are measured per capita. Shorter networks per capita are deemed more efficient. We find that population-weighted densities are the key determinant for outcome per capita network lengths. Those population-weighted densities are a particularly useful measure here, as, compared to regular density measures, they are relatively insensitive to delineation issues []. Figure 5 shows a plot of the resulting network length per capita over a city’s population-weighted densities. The same loglinear improvement of efficiency with density, as previously shown in, for example, Newman and Kenworthy [], is clearly visible here. One immediately obvious result is that denser cities are more efficient in providing transport, with lengths per capita increasing drastically when population-weighted densities fall below 5000 per square kilometer.
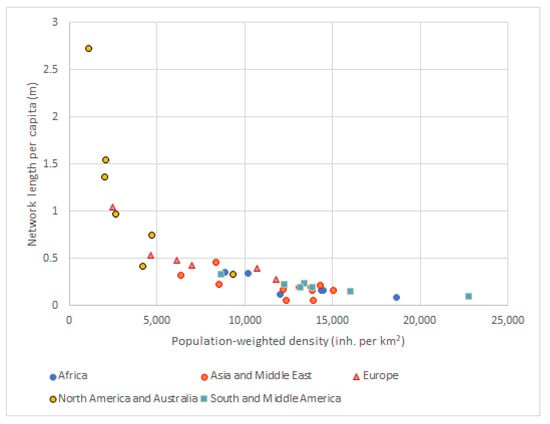
Figure 5.
Modeled network length per capita and population-weighted density for cities in world regions.
Clearly, there is still variance in modeled network lengths between cities with similar densities, indicating that not only urban densities are relevant for model outcomes. Multivariate OLS regression analyses were executed to measure the relevance of potentially relevant factors to the modeled network length. Variables that were tested are population-weighted density, total population, absolute population, the share of population living in an FUA’s center, the number of necessary modeling iterations, and dummy variables indicating the world region. With regard to the percentage of a population living in an FUA’s center, those are measured as the percentage of a population living in so-called high-density clusters within an FUA. The remainder of an FUA’s population is expected to live in commuting zones. Many model specifications were fitted, the results of which all pointed towards the same conclusions. The results from only three fitted specifications are reported here, and other results are available upon request. The most straightforward regression (i) explained variance in network lengths per capita (, using population-weighted densities D, population P, and %PC, the share of the population living in the area identified as an FUA’s center. Thus (10):
A second regression (ii) additionally controlled whether differences in city characteristics between world regions have an impact on model outcomes. This was accomplished by replacing the constant with separate constants for the world regions R in (11):
The identified world regions are Africa, Asia, the Middle East, Europe, North America, Australia, and South and Middle America. Australia was combined with North America here because of the similarities in urbanization styles that those regions have.
Last, to control whether the effect of population-weighted density holds in a regular scaling regression [], a third regression fits an equation similar to (iii), however, on total network length, so that (12):
Other tested specifications did not yield very promising results. Most importantly, including the number of model iterations, total population, or absolute center population did not yield significant estimators in any specification1. Given the sizeable explained variance in all three regressions, we expect that the major explanatory factors are captured in these regressions. From pairwise correlations, the variable has limited correlation (with a Pearson r-score below 0.41), except for and , which do exhibit considerable correlation (0.76). Given that these variables do not seem to cause mutually inflated significance levels, we exclude problematic multicollinearity in our results.
The results of the regressions (10, 11, 12) are given in Table 1. In all cases, population-weighted densities have, with considerable significance, a negative effect on modeled network length. This confirms that, per capita, modeled transport networks are substantially shorter with higher population densities.

Table 1.
Regression results.
From the results of (12), it follows that total network length responds slightly sublinearly to city size, indicating the existence of economies of scale [] in the modeled infrastructure provision. However, while population-weighted densities have significantly negative effects in all tested models, no significant city size effects remain when explaining the variance in per capita network size in (10) and (11). The implication is that cities can obtain shorter transport infrastructure by increasing density, regardless of their scale. Population-weighted density and total population have a limited correlation (D and P have an r of ~0.25, ln D and ln P have an r of ~0.35), so size benefits are not implicitly captured in the density variable. Thus, the length of the simulated network is subject to economies of density, not scale. This is contradictory to findings from scaling law studies [,]. One explanation may be that scale-specific aspects that play out, e.g., capacity requirements and traffic coordination costs, are not included in the simulation approach.
The share of the population in city centers has a monotonously negative effect on modeled network length as well, but only significantly so in models in which absolute (not loglinear) population-weighted density was used, confirming that population densities are the dominant explanatory variable here. The fact that the share of the population living in an FUA’s center does not significantly affect network outcomes is surprising. A possible explanation for the lack of significance could be the bias of the model for central areas. If the selected cities all have a substantial part of the population in central areas, the simulated networks are almost exclusively allocated in the center, and the commuting zones remain unconnected. Figure 6 shows a linear relationship between the share of the population living in a commuting zone and the percentage of the network allocated in that commuting zone. Clearly, the simulation method is not necessarily biased toward central areas. A possible explanation is that due to the optimization of passenger kilometers in the simulation approach, the revenue benefits from higher population densities in central areas are offset by the fact that commuting zones typically require longer travel distances, so connecting people in commuting zones yields a higher per-capita number of kilometers traveled.
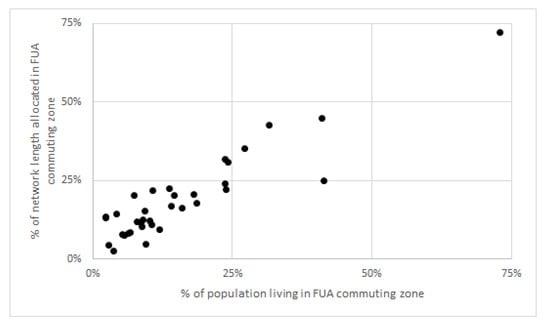
Figure 6.
Percentage of simulated networks allocated in commuting zones as a function of the population living in commuting zones.
Despite the lack of significance, models, including the share of the population living in the center, are nonetheless presented, as that variable does seem to quite robustly contribute to explaining variance in modeled network length, even with the relatively low number of observations used in this study. The negative effect of the share of the center population indicates that, to a limited degree, the concentration of population in a single city center is more efficient than, for instance, distributing population over several satellite settlements, even if those satellites are populated at a high density.
Regression (11) introduces region-specific fixed effects to control for regional variances in infrastructure efficiency. The effect that those region-specific estimators have on the coefficients for population density and share of the center population suggests that regions have structurally different values of the explanatory variables. This is corroborated by the fact shown in Figure 2 that, for example, the selected cities in North America and Australia have relatively low population-weighted densities, while the selected Asian cities have relatively high population-weighted densities. The effect of regional fixed effects is such that, in general, the modeled Asian and African cities have lower per capita network lengths than their European, North American, and Australian counterparts.
4. Robustness of Results
The method introduced here is based on a number of assumptions that, given current data availability, are impossible to verify. In this section, the sensitivity of the found results is therefore verified by testing outcomes when the values of key parameters are changed.
4.1. Target Value
For every city, the simulation approach continued allocating connections until the target value of 80% of city residents had access to a transit connection. From Figure 7, it follows that the findings are robust despite the chosen target values; after more than 10% of the population is connected, results per FUA follow reasonably stable upward network length trajectories. It seems safe to conclude that any network that connects more than 10% of an FUA’s population can be constructed more efficiently if population densities are higher.
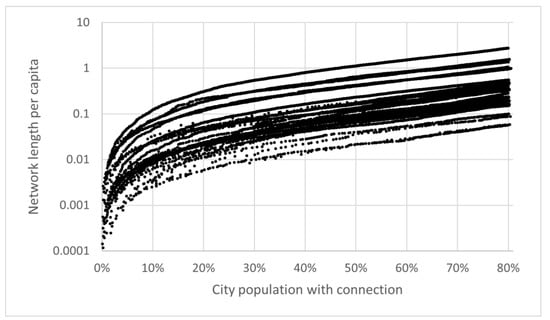
Figure 7.
Population connected versus cumulative modeled network length per capita (log scales).
4.2. Other Relevant Model Parameters
In order to test the robustness of the conclusions, the network allocation approach has been repeated 42 times with randomly defined numerical assumptions2. To reduce the computational burden, the simulations have only been repeated for six selected cities that vary substantially in structure and density and need a limited number of model iterations to obtain a final modeling result. Those cities are Accra (Ghana), Berlin (Germany), Brasilia (Brazil), Doha (Qatar), Hong Kong (China), and Portland (USA). Given the computational complexity of the model, the limited availability of computing power, and the large number of parameters that may be relevant, sensitivity tests were not executed by changing one parameter at a time but rather by devising separate runs with randomized parameter settings in each run. For a comparable exercise, see []. In each run, all six selected cities are run with the same randomly selected parameter values. The values used for this article’s main results and the bounds of the ranges from which random values were drawn are given in Table 2.

Table 2.
Parameter settings were used to obtain the main results and the ranges of values from which values were drawn randomly in the sensitivity tests.
In total, the results for 6 cities F were run 42 times with parameters from the set of runs S, so that N = 252. To verify whether the previously established linkages between per capita network length, density, city size, and population in the city center hold, an extended version of Equation (10) has been fitted so that (13):
in which is a matrix of dichotomous values indicating membership to a particular run so that functions as a run-specific fixed effect, capturing variance across results due to the parameter settings of that run. Thus, the other estimators pick up cross-sectional variance within each run linked to the explanatory variable distribution.
The results of this exercise are given in Table 3. Clearly, higher population-weighted densities robustly reduce the overall necessary network lengths. As in the previous findings, the percentage of the population living in a city center does not significantly affect network lengths. Surprisingly, city size does stand out as a significant factor here, so the bigger selected cities have, per capita, shorter networks, regardless of density. Clearly, economies of scale do exist in the subset of selected cities; this effect may be somewhat inflated due to selection bias, as limited allocation iterations were a criterion in the selection of the cities analyzed here. Nevertheless, as in the main results, the correlation between city size and population-weighted densities is very limited in the selected cities.

Table 3.
Results of regressing Equation (13).
In order to develop intuition on the results of parameter choices in the simulation approach, a second regression specification has been used to uncover the single effects of parameter settings on model outcomes. To do so, a city-specific fixed effect model is introduced, in which
in which is a city-specific fixed effect that picks up effects pertaining to urban structure, and is a vector of parameter values for one specific variable. This regression has been repeated for all six parameters that were varied in the executed runs, as indicated in Table 2.
The results of repeatedly fitting regression (14) are given in Table 4. From the high degree of explained variance and considerable significance of all fixed effect estimators, it follows that the selected cities have fairly stable results despite imputed parameter settings—although, surprisingly, the city of Portland has insignificant estimators in the models explaining variance in V0 and . This is presumably related to the insignificant estimation results for those variables.

Table 4.
Effects of parameter variation in the sensitivity tests from regressing Equation (14).
Two parameters have no significant effect on outcome network length, namely initial speed (V0) and degree of circuity (). By diminishing the relative profitability of network additions, it is likely that higher initial speeds in V0 would have a profound impact on network lengths if they were cut off with a minimum profitability criterion. However, this is not taken into account in the analysis at hand. Circuity () likely has an ambiguous impact on network lengths. On the one hand, longer detours cause longer additions; on the other hand, if slight detours connect a larger share of the population, fewer additions are needed to reach the target population share.
The other parameters verified in this sensitivity test have structurally positive effects on per-capita network length. With higher public transport speeds in V1, travel times over long distances are further reduced. Network upgrades lead to larger increases in relatively long-distance interactions, so that longer-distance investments become more attractive. Thus, higher values in V1 lead to longer networks. Both fixed costs in X and fixed time penalties in W increase network lengths. As both elements penalize short-distance investments, the established effects seem plausible. The effect of the distance decay parameter in is a bit counterintuitive but may be considered plausible as well when taking into account that all values in are negative. Thus, a distance decay factor of −2 causes a shorter final network outcome than a distance decay factor of −1 due to the greater relevance of long-distance destinations in the case that .
5. Discussion
This paper introduces a network expansion simulation method to establish whether density fosters shorter public transport networks and subsequently discusses the results of simulating such networks in cities throughout the world. This approach is useful as it allows us to assess the impact of population densities given the counterfactual situation that all analyzed cities have public transport networks, with stops proximate to a larger share of the population, that are based on the same shaping principles. The results confirm that population-weighted density is a crucial factor in explaining simulated network outcomes; denser cities can have shorter and, thus, presumably more efficient networks while having infrastructure that is proximate to citizens. On the other hand, neither population size nor urban structure have significant effects on network length. Overall, the results presented here complement earlier contributions that favor high densities, as those foster, amongst others, public transport availability, ridership, and mode share [,,,]. A sensitivity analysis corroborates that the results are robust for a wider range of simulation parameters.
It must be stressed that the results are based on a hypothetical approach with unrealistic assumptions. Commonly, history matters for network outcomes [], for example, through first-mover advantages []. The adopted simulation approach does model network expansion as a sequential process in which prior investments shape future investments. However, it treats all the analyzed cities as tabula rasa, not taking into account the existing infrastructure. Furthermore, the costs of overcoming distance were held equal across all cities analyzed. The analysis thus does not take into account the many factors that may affect the supply of public transport locally, for instance, restrictive physical geography, legal conditions, ownership issues, or environmental considerations, even if those matter empirically [].
Another assumption that could not be tested regards the relation between network length and network efficiency, which in this paper is considered linear. On the one hand, hauling more passengers over shorter networks likely enables economies of density []. On the other hand, higher transport densities presumably come with an increased demand for infrastructure capacity and higher coordination costs []. In addition, the assumption that additional link upgrades always decrease overall transport costs does not hold when congestion is taken into account (and reduces travel flow) []. All in all, more research is needed to establish the bounds of density and efficient public transport provision.
Public transport networks are subject to network externalities [] and presumably through positive feedback loops of urban density, public transport availability, and public transport ridership []. A city that wants to achieve a modal shift towards sustainable transportation may improve the proximate availability of public transport stops at a lower cost if its citizens live at a higher density. This also emphasizes the problem that cities with low densities are locked into passenger car mobility lock-in [], as it may be prohibitively costly to roll out a public transport network that provides sufficient proximate connectivity to public transport infrastructure across a low-density urban system.
Author Contributions
Conceptualization, C.J.-C. and L.D.; software, C.J.-C. and A.K.; visualization, C.J.-C. and A.K.; writing—original draft preparation, C.J.-C.; writing—review and editing, C.J.-C. and L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
Author Chris Jacobs-Crisioni was employed by the company Bureau Jacobs-Crisioni. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The views expressed are purely those of the authors and may not in any circumstances be regarded as stating an official position of the European Commission.
Appendix A

Table A1.
Equations Nomenclature.
Table A1.
Equations Nomenclature.
| Balancing factors based on population at the destination (), initial travel times () | |
| Balancing factors based on population at the destination (), upgraded travel times () | |
| Expected passenger mileage between nodes, given initial travel times () | |
| Expected passenger mileage between nodes, given upgraded travel times () | |
| , | Proxy of construction costs between nodes on the link |
| Path distance between selected origin and destination nodes | |
| Maximum circuity parameter used in path designation grid search | |
| Impedance variable of a link, as used in path designation grid search | |
| Grid cell subscript (separate 1 km grids form origin and destination nodes) | |
| Origin node subscript | |
| Destination node subscript | |
| Iteration of the path designation grid search | |
| Euclidean distance between origin and destination nodes pair | |
| Maximum desirable path distance imposed in path designation grid search | |
| ,, | Grid cell, origin node, destination node population |
| Initial travel times (i.e., at the start of an investment round) | |
| Upgraded travel times (i.e., if an upgrade was constructed between i and j | |
| Flag indicating whether a node is connected to an upgraded network link or not | |
| Initial travel speeds (before upgrade) | |
| Upgrade travel speeds (after upgrade) | |
| Imposed fixed waiting time penalty for accessing upgraded links | |
| Imposed fixed cost for constructing a network upgrade |
Appendix B. Computational Complexity
For any selected city, the model:
First, it selects a set of nodes and creates a reference network from a full network of links between all nodes (complexity: , with n between 591 in Kinshasa and 15,114 in Houston). Given that the created network connects, by means of bidirectional links, every node to 16 neighboring nodes, the reference number of links in a network, NL, would approach with very large cities. However, due to irregular city forms and border effects, in practice.
Then, it starts an iterative sequence of investment allocations. The number of steps s in that sequence depends on the target percentage of the population that needs to be connected, city size, and density (complexity: s, ranging from 65 for Hong Kong to 2900 for Atlanta).
In each iteration, an OD matrix is filled in, containing the concurrent travel times between all nodes. These matrices are filled using GeoDMS dijkstra_m routines, which grow single trees from every origin node to all destination nodes (complexity: , the latter factor NL indicates the effect of the searched network size on Dijkstra’s shortest path finding routines).
Candidate benefit–cost rates are evaluated, and the best candidate connection for additional network investment is subsequently selected from all potential connections (complexity: )
Subsequently, in every iteration, a grid search is performed to find the optimal path for the selected connection. To do so, a single shortest path tree is grown 11 times from the same origin point with varying impedance definitions (complexity: ).
Lastly, link attributes in the network are updated to reflect network upgrades (complexity: ).
In summary, the adopted routines roughly have a computational complexity of .
Appendix C

Table A2.
Main Results.
Table A2.
Main Results.
| City | Population (M) | Simulated Network Length per Capita (km) | Population-Weighted Density (km2) |
| Tokyo | 36.5 | 0.22 | 8549 |
| Jakarta | 29.7 | 0.17 | 12,195 |
| Cairo | 23.5 | 0.12 | 12,038 |
| Mumbai | 22.3 | 0.06 | 13,908 |
| Sao Paolo | 21.7 | 0.19 | 13,179 |
| Mexico City | 21.4 | 0.19 | 13,840 |
| New York | 19.5 | 0.34 | 9316 |
| Moscow | 16.4 | 0.28 | 11,805 |
| Los Angeles | 15.6 | 0.55 | 4174 |
| Tehran | 13.4 | 0.16 | 13,866 |
| Ho Chi Minh City | 12.8 | 0.22 | 14,312 |
| London | 12.6 | 0.42 | 6985 |
| Lagos | 12.3 | 0.16 | 14,463 |
| Paris | 11.2 | 0.39 | 10,716 |
| Rio de Janeiro | 10.8 | 0.23 | 12,266 |
| Lima | 9.7 | 0.15 | 16,009 |
| Bogota | 9.1 | 0.10 | 22,787 |
| Shenzhen | 8.7 | 0.20 | 13,123 |
| Santiago | 7.1 | 0.23 | 13,368 |
| Houston | 6.4 | 1.55 | 2061 |
| Riyadh | 6.3 | 0.33 | 6373 |
| Dortmund | 5.8 | 1.05 | 2450 |
| Hong Kong | 5.8 | 0.06 | 12,354 |
| Kinshasa | 5.8 | 0.09 | 18,657 |
| Atlanta | 5.6 | 2.73 | 1110 |
| Accra | 4.8 | 0.35 | 8890 |
| Melbourne | 4.4 | 0.98 | 2663 |
| Casablanca | 4.4 | 0.16 | 14,355 |
| Berlin | 4.3 | 0.54 | 4625 |
| Montreal | 4.1 | 0.75 | 4676 |
| Cape Town | 3.8 | 0.34 | 10,169 |
| Pyongyang | 3.0 | 0.19 | 13,767 |
| Portland | 2.3 | 1.36 | 2014 |
| Brasilia | 2.0 | 0.33 | 8647 |
| Doha | 1.8 | 0.46 | 8381 |
| Sevilla | 1.3 | 0.49 | 6153 |
Notes
| 1 | Results are available upon request. |
| 2 | In total, 42 repetitions could be finished in the limited amount of time that the computing power available to the authors could be dedicated to this exercise. |
References
- Newman, P.W.G.; Kenworthy, J. The Transport Energy Trade-Off: Fuel-Efficient Traffic versus Fuel-Efficient Cities? Transp. Res. A 1988, 22A, 163–174. [Google Scholar] [CrossRef]
- Kenworthy, J. Transport Energy Use and Greenhouse Gases in Urban Passenger Transport Systems: A Study of 84 Global Cities. In Proceedings of the International Sustainability Conference, Fremantle, Australia, 17–19 September 2003. [Google Scholar]
- Brownstone, D.; Golob, T.F. The Impact of Residential Density on Vehicle Usage and Energy Consumption. J. Urban Econ. 2009, 65, 91–98. [Google Scholar] [CrossRef]
- Rode, P.; Floater, G.; Thomopoulos, N.; Docherty, J.; Schwinger, P.; Mahendra, A.; Fang, W. Accessibility in Cities: Transport and Urban Form. In Disrupting Mobility. Lecture Notes in Mobility; Meyer, G., Shaheen, S., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Cervero, R.; Kockelman, K. Travel Demand and the 3Ds: Density, Diversity, and Design. Transp. Res. Part D Transp. Environ. 1997, 2, 199–219. [Google Scholar] [CrossRef]
- UN Goal 11: Make Cities and Human Settlements Inclusive, Safe, Resilient and Sustainable. Available online: https://unstats.un.org/sdgs/report/2017/goal-11/ (accessed on 15 December 2023).
- Hall, P. Sustainable Cities or Town Cramming. In Planning for a Sustainable Future; Layard, A., Davoudi, S., Eds.; E&FN Spon: London, UK, 2001; pp. 101–114. [Google Scholar]
- Ferreira, A.; Batey, P. On Why Planning Should Not Reinforce Self-Reinforcing Trends: A Cautionary Analysis of the Compact-City Proposal Applied to Large Cities. Environ. Plan. B Plan. Des. 2011, 38, 231–247. [Google Scholar] [CrossRef]
- Breheny, M. The Compact City and Transport Energy Consumption. Trans. Inst. Br. Geogr. 1995, 20, 81–101. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, Innovation, Scaling, and the Pace of Life in Cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Lobo, J.; Strumsky, D.; West, G.B. Urban Scaling and Its Deviations: Revealing the Structure of Wealth, Innovation and Crime across Cities. PLoS ONE 2010, 5, e13541. [Google Scholar] [CrossRef]
- Zhao, P. The Implications of and Institutional Barriers to Compact Land Development for Transportation: Evidence from Bejing. J. Transp. Land Use 2013, 6, 29–42. [Google Scholar] [CrossRef][Green Version]
- Broitman, D.; Koomen, E. Residential Density Change: Densification and Urban Expansion. Comput. Environ. Urban Syst. 2015, 54, 32–46. [Google Scholar] [CrossRef]
- Ustaoglu, E.; Jacobs-Crisioni, C. What Drives Residential Land Expansion and Densification? An Analysis of Growing and Shrinking Regions. Land 2022, 11, 1679. [Google Scholar] [CrossRef]
- Bento, A.M.; Cropper, M.L.; Mobarak, A.M.; Vinha, K. The Effects of Urban Spatial Structure on Travel Demand in the United States. Rev. Econ. Stat. 2005, 87, 466–478. [Google Scholar] [CrossRef]
- Levinson, D.M.; Kumar, A. Density and the Journey to Work. Growth Chang. 1997, 28, 147–172. [Google Scholar] [CrossRef]
- Rickwood, P.; Glazebrook, G.; Searle, G. Urban Structure and Energy—A Review. Urban Policy Res. 2008, 26, 57–81. [Google Scholar] [CrossRef]
- Kujala, R.; Weckström, C.; Darst, R.K.; Mladenović, M.N.; Saramäki, J. A Collection of Public Transport Network Data Sets for 25 Cities. Sci. Data 2018, 5, 180089. [Google Scholar] [CrossRef]
- Jacobs-Crisioni, C. Spatial Data Analyses of Urban Land Use and Accessibility. Ph.D. Thesis, VU University Amsterdam, Amsterdam, The Netherlands, 2016. [Google Scholar]
- Low, N.; Astle, R. Path Dependence in Urban Transport: An Institutional Analysis of Urban Passenger Transport in Melbourne, Australia, 1956–2006. Transp. Policy 2009, 16, 47–58. [Google Scholar] [CrossRef]
- Driscoll, P.A. Breaking Carbon Lock-In: Path Dependencies in Large-Scale Transportation Infrastructure Projects. Plan. Pract. Res. 2014, 29, 317–330. [Google Scholar] [CrossRef]
- Nakicenovic, N. Overland Transportation Networks: History of Development and Future Prospects. In Networks in Action; Batten, D., Casti, J., Thord, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 195–228. [Google Scholar]
- Economides, E. The Economics of Networks. Int. J. Ind. Organ. 1996, 14, 673–699. [Google Scholar] [CrossRef]
- Youn, H.; Gastner, M.T.; Jeong, H. The Price of Anarchy in Transportation Networks: Efficiency and Optimality Control. Phys. Rev. Lett. 2008, 101, 128701. [Google Scholar] [CrossRef]
- Anshelevich, E.; Dasgupta, A.; Tardos, E.; Wexler, T. Near-Optimal Network Design with Selfish Agents. In Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 9–11 June 2003; ACM: New York, NY, USA, 2003; Volume 4, pp. 511–520. [Google Scholar]
- Taaffe, E.J.; Morrill, R.L.; Gould, P.R. Transport Expansion in Underdeveloped Countries: A Comparative Analysis. Geogr. Rev. 1963, 53, 503–529. [Google Scholar] [CrossRef]
- Kolars, J.; Malin, H.J. Population and Accessibility: An Analysis of Turkish Railroads. Geogr. Rev. 1970, 60, 229–246. [Google Scholar] [CrossRef]
- Levinson, D. Density and Dispersion: The Co-Development of Land Use and Rail in London. J. Econ. Geogr. 2008, 8, 55–77. [Google Scholar] [CrossRef]
- Yamins, D.; Rasmussen, S.; Fogel, D. Growing Urban Roads. Netw. Spat. Econ. 2003, 3, 69–85. [Google Scholar] [CrossRef]
- Xie, F.; Levinson, D. The Weakest Link: The Decline of the Surface Transportation Network. Transp. Res. E 2008, 44, 100–113. [Google Scholar] [CrossRef]
- Levinson, D.; Xie, F. Does First Last? The Existence and Extent of First Mover Advantages on Spatial Networks. J. Transp. Land Use 2011, 4, 47–69. [Google Scholar] [CrossRef][Green Version]
- Raimbault, J. Modeling the Co-Evolution of Cities and Networks. arXiv 2018, arXiv:1804.09430. [Google Scholar]
- Raimbault, J.; Le Néchet, F. Introducing Endogenous Transport Provision in a LUTI Model to Explore Polycentric Governance Systems. J. Transp. Geogr. 2021, 94, 103115. [Google Scholar] [CrossRef]
- Jacobs-Crisioni, C. Public Transport Allocator. Available online: https://github.com/cjacobscrisioni/PublicTransportAllocator.git (accessed on 15 December 2023).
- Andrius Kucas; Jacobs Crisioni, C.; Dijkstra, L. Simulated World-City Public Transport Networks. European Commission, Joint Research Centre (JRC) [Dataset] PID. 2022. Available online: http://data.europa.eu/89h/eb8e348f-dc93-415a-9998-fb10f1787ba2 (accessed on 23 November 2023).
- Rodrigue, J.-P.; Comtois, C.; Slack, B. The Geography of Transport Systems, 2nd ed.; Routledge: London, UK; New York, NY, USA, 2006. [Google Scholar]
- Jacobs-Crisioni, C.; Koopmans, C.C. Transport Link Scanner: Simulating Geographic Transport Network Expansion through Individual Investments. J. Geogr. Syst. 2016, 18, 265–301. [Google Scholar] [CrossRef]
- Brezzi, M.; Veneri, P. Assessing Polycentric Urban Systems in the OECD: Country, Regional and Metropolitan Perspectives. Eur. Plan. Stud. 2015, 23, 1128–1145. [Google Scholar] [CrossRef]
- Schiavina, M.; Freire, S.; MacManus, K. GHS-POP R2019A-GHS Population Grid Multitemporal (1975-1990-2000-2015); European Commission, Joint Research Centre: Ispra, Italy, 2019. [Google Scholar]
- Stępniak, M.; Jacobs-Crisioni, C. Reducing the Uncertainty Induced by Spatial Aggregation in Accessibility and Spatial Interaction Applications. J. Transp. Geogr. 2017, 61, 17–29. [Google Scholar] [CrossRef]
- Wilson, A. A Statistical Theory of Spatial Distribution Models. Transp. Res. 1967, 1, 253–269. [Google Scholar] [CrossRef]
- Schläpfer, M.; Bettencourt, L.M.A.; Grauwin, S.; Raschke, M.; Claxton, R.; Smoreda, Z.; West, G.B.; Ratti, C. The Scaling of Human Interactions with City Size. J. R. Soc. Interface 2014, 11, 20130789. [Google Scholar] [CrossRef] [PubMed]
- Alonso, W. Alonso, W. A Theory of Movements. In Human Settlement Systems: International Perspectives on Structure, Change and Public Policy; Hansen, N.M., Ed.; Ballinger: Cambridge, MA, USA, 1978; pp. 197–211. [Google Scholar]
- Goodchild, M.F. An Evaluation of Lattice Solutions to the Corridor Location Problem. Environ. Plan. A 1977, 9, 727–738. [Google Scholar] [CrossRef]
- Freire, S.; MacManus, K.; Pesaresi, M.; Doxsey-Whitfield, E.; Mills, J. Development of New Open and Free Multi-Temporal Global Population Grids at 250 m Resolution. In Proceedings of the 19th AGILE Conference on Geographic Information Science, Helsinki, Finland, 14–17 June 2016. [Google Scholar]
- Jacobs-Crisioni, C.; Rietveld, P.; Koomen, E. The Impact of Spatial Aggregation on Urban Development Analyses. Appl. Geogr. 2014, 47, 46–56. [Google Scholar] [CrossRef]
- Cottineau, C.; Hatna, E.; Arcaute, E.; Batty, M. Diverse Cities or the Systematic Paradox of Urban Scaling Laws. Comput. Environ. Urban Syst. 2017, 63, 80–94. [Google Scholar] [CrossRef]
- Morton, A.B. Population-Weighted Density, Density-Weighted Population, Granularity, Paradoxes: A Recapitulation. arXiv 2014, arXiv:1412.4332. [Google Scholar]
- Jafino, B.A.; Kwakkel, J.; Van Delden, H. Identifying Distinctive Future Land-Use Patterns That Matter: An Inductive Model-Driven Scenario Development Approach. In Proceedings of the ECTQG 21st European Colloquium on Theoretical and Quantitative Geography, Luxembourg, 5–9 September 2019; pp. 154–155. [Google Scholar]
- Hendricks, K.; Piccione, M.; Tan, G. Equilibria in Networks. Econometrica 1999, 67, 1407–1434. [Google Scholar] [CrossRef]
- Braess, D. Über Ein Paradoxon Aus Der Verkehrsplanung. Unternehmensforschung 1968, 12, 258–268. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).