Urbanization Heat Flux Modeling Confirms It Is a Likely Cause of Significant Global Warming: Urbanization Mitigation Requirements
Abstract
1. Introduction
Document Smart Diagram
2. Key Data and Methods
2.1. The Global Background, Microclimate, and the Global Warming Flux
2.1.1. Global Background Amplification
2.1.2. Estimating Microclimate UHI Amplification
2.2. UHI Amplification in Humid Environments
2.3. Urban Pollution of Aerosol, Haze, and other Similar Effects
2.4. AHR Data and Method
2.5. AHR Baseline Estimates and Global Background Amplification
3. Results
3.1. Part 1: AHR Estimates
3.1.1. AHR Global Secondary Effects
3.1.2. UHI Microclimate Amplification Models
3.1.3. UHI GHG Amplification Estimate in Dry Climates: Model 1
3.1.4. UHI Amplification Estimate in Humid Climates: Model 2
3.1.5. Dry and Humid UHI Mixed Climate Amplification Estimate: Model 3
3.1.6. UHI Footprint Amplification Estimate: Model 4
3.1.7. Dry and Humid Rural Mixed Climate Amplification Estimate: Model 5
3.1.8. Estimating AHR Influence on Global Warming Using Microclimate Amplification Models
3.1.9. Area and AHR Local Baseline Heat Flux Estimates
3.1.10. Supporting Amplification Models 1–4 in Dry and Wet Environments with UHI ΔTs Estimates
| ISA %Areas * | Climate | Baseline PAHR-UHI Wm−2 Equation (15) | Baseline °C Equation (17) | Dry Amp. Equation (8) | Wet Amp. Equation (9) | AU Wet & Dry Combined E × F | AHR PAHR-LS Wm−2 D × G | Estimate AHR °C Equation (16) | GHG-WVF Amp. Au ΔT Percent Effect |
|---|---|---|---|---|---|---|---|---|---|
| A | B | D | E | F | G | H | J | K | |
| Model 1 (Dry) | |||||||||
| 0.22 | Dry | 7.53 | 1.26 | 1.2 | 1 | 1.2 | 9.03 | 1.5 | 17% |
| 0.255 | Dry | 6.5 | 1.085 | 1.2 | 1 | 1.2 | 7.79 | 1.3 | 17% |
| 0.33 | Dry | 5.02 | 0.84 | 1.2 | 1 | 1.2 | 6.02 | 1.01 | 17% |
| Model 2 (Wet) | |||||||||
| 0.22 | Humid | 7.53 | 1.26 | 1.2 | 2.125 | 2.55 | 19.2 | 3.17 | 60% |
| 0.255 | Humid | 6.5 | 1.09 | 1.2 | 2.125 | 2.55 | 16.6 | 2.74 | 60% |
| 0.33 | Humid | 5.02 | 0.84 | 1.2 | 2.125 | 2.55 | 12.8 | 2.13 | 61% |
3.1.10.1. Further Supporting Models 1–4 in Dry and Wet Environments
| ISA% Areas | Climate | Baseline PAHR-UHI Wm−2 Equation (19) | Baseline °C Equation (17) | Dry Amp. Equation (8) | Wet Amp. Equations (9) and (12) xAFI = 1.45 | AU Wet & Dry Combined E × F | PAHR-LS Wm−2 D × G | °C Equation (16) | GHG-WVF Amp. Au ΔT Percent Effect |
|---|---|---|---|---|---|---|---|---|---|
| A | B | D | E | F | G | H | J | K | |
| Model 1 (Dry) | |||||||||
| 0.22 | Dry | 11.53 | 1.92 | 1.2 | 1 × 1.45 | 1.74 | 20.1 | 3.31 | 42% |
| 0.255 | Dry | 10.5 | 1.75 | 1.2 | 1 × 1.45 | 1.74 | 18.3 | 3.02 | 42% |
| 0.33 | Dry | 9.02 | 1.50 | 1.2 | 1 × 1.45 | 1.74 | 15.7 | 2.61 | 42% |
| Model 2 (Wet) | |||||||||
| 0.22 | Humid | 11.53 | 1.92 | 1.2 | 2.125 × 1.45 | 3.7 | 42.6 | 6.92 | 72% |
| 0.255 | Humid | 10.5 | 1.75 | 1.2 | 2.125 × 1.45 | 3.7 | 38.8 | 6.32 | 72% |
| 0.33 | Humid | 9.02 | 1.50 | 1.2 | 2.125 × 1.45 | 5.7 | 33.4 | 5.45 | 72% |
3.2. Part II: Impermeable Surfaces Albedo Land Cover Change Effects
3.2.1. GW Effect due to Solar Heating of ISAs with Secondary Effects
3.2.1.1. Irradiance and ISA Percentages Adjustment Modeling Factors
3.2.1.2. Global Warming Estimates due to Solar Heating of ISAs
| LSCT CΔT Average above Ambient 14.5 °C | Albedo Average Estimate At LSCT * Equation (A7) | Solar Heating ISA Forcing Wm−2 Equation (A1) | Total Solar Heating ISD Watts (Using ISA 1.3E6 km2) | Col. D Div by Area of Earth Wm−2 | Col. E Div by 5.1 Wm−2 %GW As in Equation (5) | Global Amp Factor 1.62 × 2.15 Table 3 | F-Solar UHI | F-Solar Rural | Local Amp. Factor Equations (11) and (12) | Local Rural Amp ARural Equation (13) | UHI Global % F × G × H × J | Rural %GW F × G × I × K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | L | M |
| GHG-WVF Amplification (Col. J) | ||||||||||||
| 0 | 0.300 | 0.000 | 0.000 | 0.000 | 0.00% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 0.0% | 0.0% |
| 1 | 0.284 | 5.43 | 7.05 × 1012 | 0.014 | 0.27% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 0.3% | 0.2% |
| 5 | 0.219 | 27.70 | 3.60 × 1013 | 0.071 | 1.38% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 2.3% | 1.1% |
| 8 | 0.168 | 45.02 | 5.85 × 1013 | 0.115 | 2.25% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 2.2% | 1.8% |
| 9 | 0.150 | 50.91 | 6.62 × 1013 | 0.130 | 2.54% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 2.4% | 2.0% |
| 10 | 0.133 | 56.87 | 7.39 × 1013 | 0.145 | 2.84% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 2.7% | 2.3% |
| 11 | 0.115 | 62.88 | 8.17 × 1013 | 0.160 | 3.14% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 3.0% | 2.50% |
| 12 | 0.097 | 68.95 | 8.96 × 1013 | 0.176 | 3.45% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 3.3% | 2.74% |
| 13 | 0.079 | 75.08 | 9.76 × 1013 | 0.191 | 3.75% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 3.5% | 2.90% |
| 14 | 0.061 | 81.28 | 1.06 × 1014 | 0.207 | 4.06% | 3.48 | 0.1253 | 0.208 | 2.2 | 1.1 | 3.9% | 3.2% |
| Footprint Amplification (Col. J) | ||||||||||||
| 0 | 0.300 | 0.000 | 0.000 | 0.000 | 0.00% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 0.0% | 0.0% |
| 1 | 0.284 | 5.43 | 7.05 × 1012 | 0.014 | 0.27% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 0.4% | 0.2% |
| 5 | 0.219 | 27.70 | 3.60 × 1013 | 0.071 | 1.38% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 1.9% | 1.1% |
| 8 | 0.168 | 45.02 | 5.85 × 1013 | 0.115 | 2.25% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 3.1% | 1.8% |
| 9 | 0.150 | 50.91 | 6.62 × 1013 | 0.130 | 2.54% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 3.5% | 2.0% |
| 10 | 0.133 | 56.87 | 7.39 × 1013 | 0.145 | 2.84% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 4.0% | 2.3% |
| 11 | 0.115 | 62.88 | 8.17 × 1013 | 0.160 | 3.14% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 4.4% | 2.50% |
| 12 | 0.097 | 68.95 | 8.96 × 1013 | 0.176 | 3.45% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 4.8% | 2.74% |
| 13 | 0.079 | 75.08 | 9.76 × 1013 | 0.191 | 3.75% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 5.1% | 2.90% |
| 14 | 0.061 | 81.28 | 1.06 × 1014 | 0.207 | 4.06% | 3.48 | 0.1253 | 0.208 | 3.2 | 1.1 | 5.7% | 3.2% |
3.2.1.3. Example Calculation
3.2.2. Combined Results
| UHI LSCT CΔT (°C) above Ambient (%ISA) | UHI ISA Albedo Value | Rural LSCT CΔT (°C) above Ambient (%ISA) | ISA Albedo Rural Values | Local Amp UHI | Rural Local Amp | GW% from AHR | GW% from All ISA | GW% from ISA of Roads | Urban ISA GW% (Rural ISA GW%) | Total ISA & AHR GW% |
|---|---|---|---|---|---|---|---|---|---|---|
| GHG-WVF Amplification | ||||||||||
| 10 (50%) | 0.133 | 11 (50%) | 0.115 | 2.2 | 1.1 | 4.74 | 5.4 | 0.76 | 3.3 (2.1) | 10.1 |
| 10 (41%) | 0.133 | 11 (59%) | 0.115 | 2.2 | 1.1 | 4.74 | 5.2 | 0.73 | 2.7 (2.5) | 9.95 |
| 10 (33%) | 0.133 | 11 (67%) | 0.115 | 2.2 | 1.1 | 4.74 | 5.0 | 0.7 | 2.2 (2.84) | 9.8 |
| Footprint Amplification | ||||||||||
| 9 (50%) | 0.15 | 10 (50%) | 0.133 | 3.2 | 1.1 | 6.5 | 6.2 | 0.87 | 4.3 (1.9) | 12.7 |
| 9 (41%) | 0.15 | 10 (59%) | 0.133 | 3.2 | 1.1 | 6.5 | 5.8 | 0.81 | 3.5 (2.3) | 12.3 |
| 9 (33%) | 0.15 | 10 (67%) | 0.133 | 3.2 | 1.1 | 6.5 | 5.5 | 0.77 | 2.9 (2.6) | 12.0 |
| 10 (50%) | 0.133 | 11 (50%) | 0.115 | 3.2 | 1.1 | 6.5 | 7.1 | 1.0 | 5.0 (2.1) | 13.6 |
| 10 (41%) | 0.133 | 11 (59%) | 0.115 | 3.2 | 1.1 | 6.5 | 6.5 | 0.91 | 4.0 (2.5) | 13.0 |
| 10 (33%) | 0.133 | 11 (67%) | 0.115 | 3.2 | 1.1 | 6.5 | 6.14 | 0.86 | 3.3 (2.84) | 12.6 |
| 11 (50%) | 0.115 | 12 (50%) | 0.097 | 3.2 | 1.1 | 6.5 | 7.6 | 1.1 | 5.3 (2.3) | 14.1 |
| 11 (41%) | 0.115 | 12 (59%) | 0.097 | 3.2 | 1.1 | 6.5 | 7.1 | 1.0 | 4.4 (2.7) | 13.6 |
| 11 (33%) | 0.115 | 12 (67%) | 0.097 | 3.2 | 1.1 | 6.5 | 6.6 | 0.92 | 3.5 (3.1) | 13.1 |
| Road Estimate | ||||||||||
| 12 (41%) | 0.097 | 12 (59%) | 0.097 | 3.2 | 1.1 | NA | 7.6 | 1.1 * | 4.8 (2.7) | NA |
| Footprint Average Results | ||||||||||
| 10 (41%) | 0.133 | 11 (59%) | 0.115 | 3.2 | 1.1 | 6.5 | 6.5 | 1.1 * | 4.0 (2.5) | 13.0 |
3.3. Mitigating Urbanization Heat Fluxes
3.3.1. Natural Reflectivity of Land as UHI Comparison
3.3.2. Estimating the UHI Solar Geoengineering Requirements
4. Discussion
4.1. Mciroclimate Amplification Control for City Cooling Requirments
4.2. Satellite Assessments
5. Conclusions
- AHR from 1950–2021 due to energy consumption is estimated to have a maximum GW influence of 6.5% (Equation (14)). This is mainly related to population growth. Here, we see that the energy consumption increase in 2021 was 1.2% and this is highly correlated to a population growth rate [3] that decreased to 0.89% (Section 3.1.8).
- Unshaded ISAs from 1950 to 2019 are estimated to have an average GW influence of 6.5% (Table 7). This is broken down with average contributions of 4.0% from urban ISAs and 2.5% from rural ISAs.
- Heat fluxes from unshaded ISAs and AHR combined are estimated to have an average GW influence of 13% (Table 7) over the approximate time period of about 70 years from 1950.
- The main microclimate amplification factor justified with data was 3.2 (Table 7) in Model 4 (Section 3.1.10). It is assumed that UHIs dominate urban effects.
- Unshaded ISAs that helped match ground-based observations indicated that urban ISA temperatures would likely average 10 °C above a global ambient temperature with an average albedo of 0.133, while rural ISAs were estimated at 11 °C above ambient with an average albedo of 0.115. (Rural ISAs are anticipated to have a higher temperature due to increases in the percentage of asphalt roads and roofs, Table 7).
- The ISA average breakdown was 59% rural and 41% urban (Table 7).
- GHGs with water vapor feedback were found in modeling to be a major amplifier of AHR microclimate heat fluxes increasing UHI ΔTs by about 48% (Equation (19)).
- Roads are estimated to contribute 1.1% to GW but may be higher due to a lack of data and satellite resolution (see Section 3.2.2). New roads were observed to be darker and smoother and will likely clean better in the rain, therefore, unfortunately, will likely be much hotter over their lifetime maintaining low albedos compared to old roads. The overuse of black asphalt on roads and roofs are highly dangerous to our environment, contributing significantly to urban heat wave intensity, city temperatures, and global warming, suggesting that such practices should be banned.
- Changing roads from asphalt to concrete or similar type surface reflectance can increase their reflectivity by about a factor of 5 and reduce global warming by at least 5.5%.
- Without considering any secondary amplification effects, results indicated that AHR and solar heating of ISAs heat fluxes would equate to about 0.7% and 1% GW influence, respectively.
- A heat flux likely scenario found AHR and unshaded ISAs in cities may average 6.5 Wm−2 and 4.0 Wm−2 (Equation (20)) respectively totaling a 10.5 Wm−2 baseline value and this was estimated to increase UHI ΔT to about 1.75 °C which could be further amplified in dry and wet microclimates to about 3 °C to 6.3 °C (Table 5), respectively.
- Given average climate conditions, it is possible to mitigate much of the UHI effect with an albedo increase of 0.1 which is anticipated to lower the average impermeable surface temperatures by about 9 °C (Equation (29)) that studies show can be accomplished with cost-effective cool roads and roofs.
- Not accounting for UHFs and their microclimate and global amplification effects may result in climate model attribution errors of 2XUHF influence (1 × UHF due to not including the urbanization influence, and 1 × UHF in overestimating the current GHG influence, as illustrated in Section 3.3). The suggested correction in Appendix F is an urbanization forcing of 0.31 Wm−2 and with feedback influence (×2.15) yields a value of 0.66 Wm−2. This results in a possible 13% urbanization warming effect that occurred between 1950–2019.
- The forcing estimate for UHF 0.31 Wm−2 (Section 3.3) led to an extra increase in atmospheric water vapor averaging 204 ppm (Appendix F, Equation (13))
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
Appendix A
Appendix B. Albedo UHI Mitigation Assessment
Appendix C. Local vs. Global Water Vapor Feedback Amplification Estimate Comparisons
Appendix C.1. Global Water Vapor Feedback Amplification
Appendix C.2. Local Water Vapor Feedback Amplification
Appendix D. UHI CO2 Surface & Dome Re-Radiation
Appendix E. Model 3 Humidity Correction for Dry Areas
Appendix F. Water Vapor Feedback and Radiation Energy Flux Breakdown with UHF
Appendix G. Satellite Issues in Urbanization Assessments
References
- Zhang, P.; Ren, G.; Qin, Y.; Zhai, Y.; Zhai, T.; Tysa, S.K.; Xue, X.; Yang, G.; Sun, X. Urbanization effects on estimates of global trends in mean and extreme air temperature. J. Clim. 2021, 34, 1923–1945. [Google Scholar] [CrossRef]
- IPCC AR6. Regional Fact Sheet—Urban Areas. 2021. Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/factsheets/IPCC_AR6_WGI_Regional_Fact_Sheet_Urban_areas.pdf (accessed on 11 January 2023).
- Feinberg, A. Climate change trends due to population growth: Feedback and CO2 doubling temperature opposing rates. Preprint 2023. submitted. [Google Scholar]
- Worldbank. Urban Development. 2020. Available online: https://www.worldbank.org/en/topic/urbandevelopment/overview#1 (accessed on 4 December 2021).
- IEA (International Energy Agency). World Energy Outlook. 2018. Available online: https://iea.blob.core.windows.net/assets/77ecf96c-5f4b-4d0d-9d93-d81b938217cb/World_Energy_Outlook_2018.pdf (accessed on 23 December 2022).
- Yang, Q.; Huang, X.; Tang, Q. The footprint of urban heat island effect in 302 Chinese cities: Temporal trends and associated factors. Sci. Total Environ. 2019, 665, 652–662. [Google Scholar] [CrossRef] [PubMed]
- Koerner, B.; Klopatek, J. Anthropogenic and natural CO2 emission sources in an arid urban environment. Environ. Pollut. 2002, 116, S45–S51. [Google Scholar] [CrossRef]
- Bohnenstengel, S.; Davis, M.; Belcher, S. Impact of anthropogenic emissions on London’s temperatures. Q. J. R. Meteorol. Soc. 2014, 140, 687–698. [Google Scholar] [CrossRef]
- Feinberg, A. A Re-Radiation Model for the Earth’s Energy Budget and the Albedo Advantage in Global Warming Mitigation. Dyn. Atmos. Ocean. 2022, 97, 101267. [Google Scholar] [CrossRef]
- Block, A. Impacts of anthropogenic heat on regional climate patterns. Geophys. Res. Lett. 2004, 31, L12211. [Google Scholar] [CrossRef]
- Makar, P.A.; Gravel, S.; Chirkov, V.; Strawbridge, K.B.; Froude, F.; Arnold, J.; Brook, J. Heat flux, urban properties, and regional weather. Atmos. Environ. 2006, 40, 2750–2766. [Google Scholar] [CrossRef]
- Narumi, D.; Kondo, A.; Shimod, Y. Effects of anthropogenic heat release upon the urban climate in a Japanese megacity. Environ. Res. 2009, 109, 421–431. [Google Scholar] [CrossRef]
- Feng, J.-M.; Wang, Y.-L.; Ma, Z.-G.; Liu, Y.-H. Simulating the Regional Impacts of Urbanization and Anthropogenic Heat Release on Climate across China. J. Clim. 2012, 25, 7187–7203. [Google Scholar] [CrossRef]
- Yang, W.; Luan, Y.; Liu, X.; Yu, X.; Miao, L.; Cui, X. A new global anthropogenic heat estimation based on high-resolution nighttime light data. Sci. Data 2017, 4, 170116. [Google Scholar] [CrossRef] [PubMed]
- Flanner, M.G. Integrating anthropogenic heat flux with global climate models. Geophys. Res. Lett. 2009, 36, L02801. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.; Oleson, K. Strong, contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Feinberg, A. Urban Heat Island High Water-Vapor Feedback Estimates and Heatwave Issues: A Temperature Difference Approach to Feedback Assessments. Science 2022, 4, 44. [Google Scholar] [CrossRef]
- Kiersten, L.; Möller, G. Urban Heat Island Effect: Measuring the Urban Heat Island Effect. In Principles of Sustainability; University of Idaho: Moscow, ID, USA, 2022; Chapter 4; Available online: https://www.webpages.uidaho.edu/sustainability/ch04-p05d.html (accessed on 22 November 2022).
- Guo, T.; He, T.; Liang, S.; Roujean, J.; Zhou, Y.; Huang, X. Multi-decadal analysis of high-resolution albedo changes induced by urbanization over contrasted Chinese cities based on Landsat data. Remote Sens. Environ. 2022, 269, 112832. Available online: http://www.sciencedirect.com/science/article/pii/S0034425721005526 (accessed on 22 November 2022). [CrossRef]
- He, T.; Liang, S.; Song, D.X. Analysis of global land surface albedo climatology and spatial-temporal variation during 1981–2010 from multiple satellite products. J. Geophys. Res. Atmos. 2014, 119, 10281–10298. [Google Scholar] [CrossRef]
- Ouyang, Z.; Sciusco, P.; Jiao, T.; Feron, S.; Lei, C.; Li, F.; John, R.; Fan, P.; Li, X.; William, C.; et al. Albedo changes caused by future urbanization contribute to global warming. Nat. Commun. 2022, 13, 3800. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. Energy Production and Consumption, Our World in Data. 2022. Available online: https://ourworldindata.org/energy-production-consumption (accessed on 29 December 2022).
- Liu, R.; Su, H.; Liou, K.; Jiang, J.; Gu, Y.; Liu, S.; Shiu, C. An Assessment of Tropospheric Water Vapor Feedback Using Radiative Kernels. JGR Atmos. 2018, 123, 1499–1509. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Klein Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and surface. In Climate change (2013) the Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Feinberg, A. Urban heat island amplification estimates on global warming using an albedo model. SN Appl. Sci. 2020, 2, 2178. [Google Scholar] [CrossRef]
- Cherlet, M.; Hutchinson, C.; Reynolds, J.; Hill, J.; Sommer, S.; von Maltitz, G. (Eds.) Distribution of the world’s Big Cities, World Atlas of Desertification; Publication Office of the European Union: Luxembourg, 2018; Available online: https://wad.jrc.ec.europa.eu/aridityurban (accessed on 20 November 2022).
- Sun, Z.; Du, W.; Jiang, H.; Weng, Q.; Guo, H.; Han, Y.; Xing, Q.; Ma, Y. Global 10-m impervious surface area mapping: A big earth data based extraction and updating approach. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102800. [Google Scholar] [CrossRef]
- Huang, X.; Yang, J.; Wang, W.; Liu, Z. Mapping 10 m global impervious surface area (GISA-10m) using multi-source geospatial data. Earth Syst. Sci. Data 2022, 14, 3649–3672. [Google Scholar] [CrossRef]
- Dessler, A.; Zhang, Z.; Yang, P. Water-vapor climate feedback inferred from climate fluctuations, 2003–2008. Geophys. Res. Lett. 2008, 35, 20. [Google Scholar] [CrossRef]
- Gordon, N.; Jonko, A.; Forster, P.; Shell, K. An observationally based constraint on the water-vapor feedback. J. Geophys. Res. 2013, 118, 12435–12443. [Google Scholar] [CrossRef]
- Pigeon, G.; Legain, D.; Durand, P.; Masson, V. Anthropogenic heat release in an old European agglomeration (Toulouse, France). Int. J. Climatol. 2007, 27, 1969–1981. [Google Scholar] [CrossRef]
- Chen, B.; Dong, L.; Shi, G.; LIi, L.; Chen, L. Anthropogenic Heat Release: Estimation of Global Distribution and Possible Climate Effect. J. Meteorol. Soc. Japan. Ser. II 2014, 92, 157–165. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Zhang, L.; Sun, G.; Liu, Y. The footprint of urban heat island effect in China. Sci. Rep. 2015, 5, 11160. [Google Scholar] [CrossRef]
- Fan, Y.; Li, Y.; Bejan, A.; Wang, Y.; Yang, X. Horizontal extent of the urban heat dome flow. Sci. Rep. 2017, 7, 11681. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Tang, J.; Leung, L.; Liao, H. Intensified Humid Heat Events Under Global Warming. Geophys. Res. Lett. 2021, 48, e2020GL091462. [Google Scholar] [CrossRef]
- Schär, C.; Vidale, P.L.; Lüthi, D.; Frei, C.; Häberli, C.; Liniger, M.A.; Appenzeller, C. The role of increasing temperature variability in European summer heatwaves. Nature 2004, 427, 332–336. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E. Synergistic interactions between urban Heat Islands and heat waves: The impact in cities is larger than the sum of its parts. J. Appl. Meteorol. Climatol. 2013, 52, 2051–2064. [Google Scholar] [CrossRef]
- Russo, S.; Sillmann, J.; Sterl, A. Humid heat waves at different warming levels. Sci. Rep. 2017, 7, 7477. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Ruby Leung, L.; Zhao, N.; Zhao, C.; Qian, Y.; Hu, K.; Liu, X.; Chen, B. Contribution of urbanization to the increase of extreme heat events in an urban agglomeration in east China. Geophys. Res. Lett. 2017, 44, 6940–6950. [Google Scholar] [CrossRef]
- Liao, W.; Liu, X.; Li, D.; Luo, M.; Wang, D.; Wang, S.; Baldwin, J.; Lin, L.; Li, X.; Feng, K.; et al. Stronger Contributions of Urbanization to Heat Wave Trends in Wet Climates. Geophys. Res. Lett. Am. Geophys. Union (AGU) 2018, 45, 11310–11317. [Google Scholar] [CrossRef]
- Li, C.; Sun, Y.; Zwiers, F.; Wang, D.; Zhang, X.; Chen, G.; Wu, H. Rapid Warming in Summer Wet Bulb Globe Temperature in China with Human-Induced Climate Change. J. Clim. 2020, 33, 5697–5711. [Google Scholar] [CrossRef]
- Kong, D.; Gu, X.; Li, J.; Ren, G.; Liu, J. Contributions of Global Warming and Urbanization to the Intensification of Human-Perceived Heatwaves Over China. JPG Atmos. 2020, 125, e2019JD032175. [Google Scholar] [CrossRef]
- Zou, Z.; Yan, C.; Yu, L.; Jiang, X.; Ding, J.; Qin, L.; Wang, B.; Qiu, G. Impacts of land use/land cover types on interactions between urban heat island effects and heat waves. Build. Environ. 2021, 204, 108138. [Google Scholar] [CrossRef]
- Dewan, A.; Kiselev, G.; Botje, D.; Mahmud, G.; Bhuian, H.; Hassan, Q. Surface urban heat island intensity in five major cities of Bangladesh: Patterns, drivers and trends. Sustain. Cities Soc. 2021, 71, 102926. [Google Scholar] [CrossRef]
- Zhang, S.; Ren, G.; Ren, Y.; Tysa, S. Linkage of extreme temperature change with atmospheric and locally anthropogenic factors in China mainland. Atmos. Res. 2022, 277, 106307. [Google Scholar] [CrossRef]
- Yu, H.; Liu, S.; Dickinson, R. Radiative effects of aerosols on the evolution of the atmospheric boundary layer. J. Geophys. Res.-Atmos. 2002, 107, AAC 3–1–AAC 3–14. [Google Scholar] [CrossRef]
- Lai, L. The influence of urban heat island phenomenon on PM concentration: An observation study during the summer half-year in metropolitan Taipei, Taiwan. Theor. Appl. Climatol. 2018, 131, 227–243. [Google Scholar] [CrossRef]
- Potter, C.; Alexander, O. Impacts of the San Francisco Bay Area shelter-in-place during the COVID-19 pandemic on urban heat fluxes. Urban Clim. 2021, 37, 100828. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Lee, X.; Liu, S.; Schultz, N.; Xiao, W.; Zhang, M.; Zhao, L. Urban heat islands in China enhanced by haze pollution. Nat. Commun. 2016, 7, 12509. [Google Scholar] [CrossRef] [PubMed]
- Feinberg, A. A Molecular Level Study Indicates the Capability of CO2 Warming Amplification in UHIs Can Significantly Impact Microclimate Warming to the Global Level. Preprint. 2021. Available online: https://www.researchgate.net/publication/352466630_A_Molecular_Level_Study_Indicates_the_Capability_of_CO2_Warming_Amplification_in_UHIs_can_Significantly_Impact_Microclimate_Warming_to_the_Global_Level (accessed on 29 November 2021).
- NASA Global Climate Change. 2022. Available online: https://climate.nasa.gov/vital-signs/global-temperature/ (accessed on 25 November 2022).
- Chaisson, E.J. Long-term global heating from energy use. Eos Trans. AGU 2008, 89, 253. [Google Scholar] [CrossRef]
- Feinberg, A. Solar Geoengineering Modeling and Applications for Mitigating Global Warming: Assessing Key Parameters and the Urban Heat Island Influence. Front. Clim. 2022, 4, 870071. [Google Scholar] [CrossRef]
- Liu, Z.; He, C.; Zhou, Y.; Wu, J. How much of the world’s land has been urbanized, really? A hierarchical framework for avoiding confusion. Landsc. Ecol. 2014, 29, 763–771. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, C.; Zhou, Y.; Li, X.; Shen, S.; Song, C. A global dataset of annual urban extents (1992–2020) from harmonized nighttime lights. Earth Syst. Sci. Data 2022, 14, 517–534. [Google Scholar] [CrossRef]
- Theobald, D.; Kennedy, C.; Chen, B.; Oakleaf, J.; Baruch-Mordo, S.; Kiesecker, J. Earth transformed: Detailed mapping of global human modification from 1990 to 2017. Earth Syst. Sci. Data 2020, 12, 1953–1972. [Google Scholar] [CrossRef]
- Liu, Z.; Lai, J.; Zhan, W.; Bechtel, B.; Voogt, J.; Quan, J.; Hu, L.; Fu, P.; Huang, F.; Li, L.; et al. Urban Heat Islands Significantly Reduced by COVID-19 Lockdown. Geophys. Res. Lett. 2022, 49, e2021GL096842. [Google Scholar] [CrossRef]
- Climate Central. Hot Zones: Urban Heat Islands, Research brief by Climate Central. 2021. Available online: https://assets.ctfassets.net/cxgxgstp8r5d/1XZZjkLYwtcmKL5k3wEinl/5f8c9b5b2d8dd56e1bda7f51278fc3d2/2021_UHI_Report.pdf (accessed on 20 November 2022).
- Rasmussen, C.; Lee, J.; Wang, A. NASA’s ECOSTRESS Sees Las Vegas Streets Turn Up the Heat, Jet Propulsion Lab. 2022. Available online: https://www.nasa.gov/feature/jpl/nasa-s-ecostress-sees-las-vegas-streets-turn-up-the-heat (accessed on 25 November 2022).
- Kowal-Vern, A.; Matthews, M.; Richey, K.; Ruiz, K.; Peck, M.; Jain, A.; Foster, K. “Streets of Fire” revisited: Contact burns. Burn. Trauma 2019, 7, s41038-019-0169-9. [Google Scholar] [CrossRef]
- Gewirtz, E. How Hot Is Too Hot for a Dog’s Paws?, American Kennel Club. 2021. Available online: https://www.akc.org/expert-advice/health/heatstroke-in-dogs/ (accessed on 29 November 2021).
- Morabito, M.; Crisci, A.; Georgiadis, T.; Orlandini, S.; Munafò, M.; Congedo, L.; Rota, P.; Zazzi, M. Urban Imperviousness Effects on Summer Surface Temperatures Nearby Residential Buildings in Different Urban Zones of Parma. Remote Sens. 2018, 10, 26. [Google Scholar] [CrossRef]
- Mentaschi, L.; Duveiller, G.; Zulian, G.; Corbane, C.; Pesaresi, M.; Maes, J.; Stocchino, A.; Feyen, L. Global long-term mapping of surface temperature shows intensified intra-city urban heat island extremes. Glob. Environ. Chang. 2022, 72, 102441. [Google Scholar] [CrossRef]
- Knox, P. How Hot Does Pavement Get in Summer? Climate and Agriculture in the Southeast. 2022. Available online: https://site.extension.uga.edu/climate/2022/05/how-hot-does-pavement-get/ (accessed on 25 November 2022).
- Feinberg, A. Department of Transportation Asphalt Roads Causing Heat & Heatwaves in Cities, YouTube presentation. 2022. Available online: https://www.youtube.com/watch?v=SXEm3XN8cr8 (accessed on 25 November 2022).
- Sugawara, H.; Takamura, T. Surface albedo in cities (0.12): Case study in Sapporo and Tokyo, Japan. Bound Layer Meteorol. 2014, 153, 539–553. [Google Scholar] [CrossRef]
- Trlica, A.; Hutyra, L.; Schaaf, C.; Erb, A.; Wang, J. Albedo, Land Cover, and Daytime Surface Temperature Variation Across an Urbanized Landscape. Earth’s Future 2017, 5, 1084–1101. [Google Scholar] [CrossRef]
- MIT Study on Roads; AzariJafari, H.; Kirchain, R.; Gregory, J. Mitigating Climate Change with Reflective Pavements. CSHub Top. Summ. 2020, 2020. Available online: https://cshub.mit.edu/sites/default/files/images/Albedo%201113_0.pdf (accessed on 25 November 2022).
- Akbari, H.; Matthews, D.; Seto, D. The long-term effect of increasing the albedo of urban areas. Environ. Res. Lett. 2012, 7, 024004. [Google Scholar] [CrossRef]
- EPA. Reducing Urban Heat Islands: Compendium of Strategies. 2014. Available online: https://www.epa.gov/sites/default/files/2014-08/documents/coolpavescompendium_ch5.pdf (accessed on 12 March 2023).
- EPA. Study Cambridge Systematics. Cool Pavement Report, Heat Island Reduction Initiative. 2005. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.648.3147&rep=rep1&type=pd (accessed on 12 March 2023).
- Octopus Energy. 2023. Available online: https://octopus.energy/blog/when-will-fossil-fuels-run-out/#:~:text=If%20we%20keep%20burning%20fossil,will%20be%20depleted%20by%202060 (accessed on 12 March 2023).
- Widory, D.; Javoy, M. The carbon isotope composition of atmospheric CO2 in Paris. Earth Planet. Sci. Lett. 2003, 215, 289–298. [Google Scholar] [CrossRef]
- Gratani, L.; Varone, L. Daily and seasonal variation of CO2 in the city of Rome in relationship with the traffic volume. Atmos. Environ. 2005, 39, 2619–2624. [Google Scholar] [CrossRef]
- George, K.; Ziska, L.H.; Bunce, J.A.; Quebedeaux, B. Elevated atmospheric CO2 concentration and temperature across an urban–rural transect. Atmos. Environ. 2007, 41, 7654–7665. [Google Scholar] [CrossRef]
- Velasco, E.; Pressley, S.; Allwine, E.; Westberg, H.; Lamb, B. Measurements of CO2 fluxes from the Mexico City urban landscape. Atmos. Environ. 2005, 39, 7433–7446. [Google Scholar] [CrossRef]
- NOAA Climat Ratios. 2021. Available online: https://gml.noaa.gov/outreach/lesson_plans/Climate%20Ratios.pdf (accessed on 16 December 2022).
- Ossfoundation. 2023. Available online: https://ossfoundation.us/projects/environment/global-warming/atmospheric-composition (accessed on 23 March 2023).
- Butler, J.; Montzka, S. The NOAA Annual Greenhouse Gas Index, Earth System Researh Lab. Global Monitoring Laboratory. 2020. Available online: https://www.esrl.noaa.gov/gmd/aggi/aggi.html (accessed on 23 March 2023).
- Myhre, G.; Highwood, E.J.; Shine, K.P.; Stordal, F. New estimates of radiative forcing due to well mixed greenhouse gases. Geophys. Res. Lett. 1998, 25, 2715–2718. [Google Scholar] [CrossRef]
- ASC. 2023. Available online: https://www.acs.org/climatescience/atmosphericwarming/climatsensitivity.html (accessed on 23 March 2023).
- Kiehl, J.T.; Trenberth, K.E. Earth’s Annual Global Mean Energy Budget. Bull. Amer. Meteor. Soc. 1997, 78, 197–208. [Google Scholar] [CrossRef]
- Natural Resources Canada, Fundamental of Remote Sensing. Available online: https://natural-resources.canada.ca/sites/www.nrcan.gc.ca/files/earthsciences/pdf/resource/tutor/fundam/pdf/fundamentals_e.pdf (accessed on 23 March 2023).
- Cordero, R.R.; Feron, S.; Sepúlveda, E.; Damiani, A.; Carrera, J.M.; Jorquera, J.; Alfonso, J.A.; Fuenzalida, R.; Rivas, M.; MacDonell, S.; et al. Evaluation of MODIS-derived estimates of the albedo over the Atacama Desert using ground-based spectral measurements. Sci. Rep. 2021, 11, 19822. [Google Scholar] [CrossRef] [PubMed]
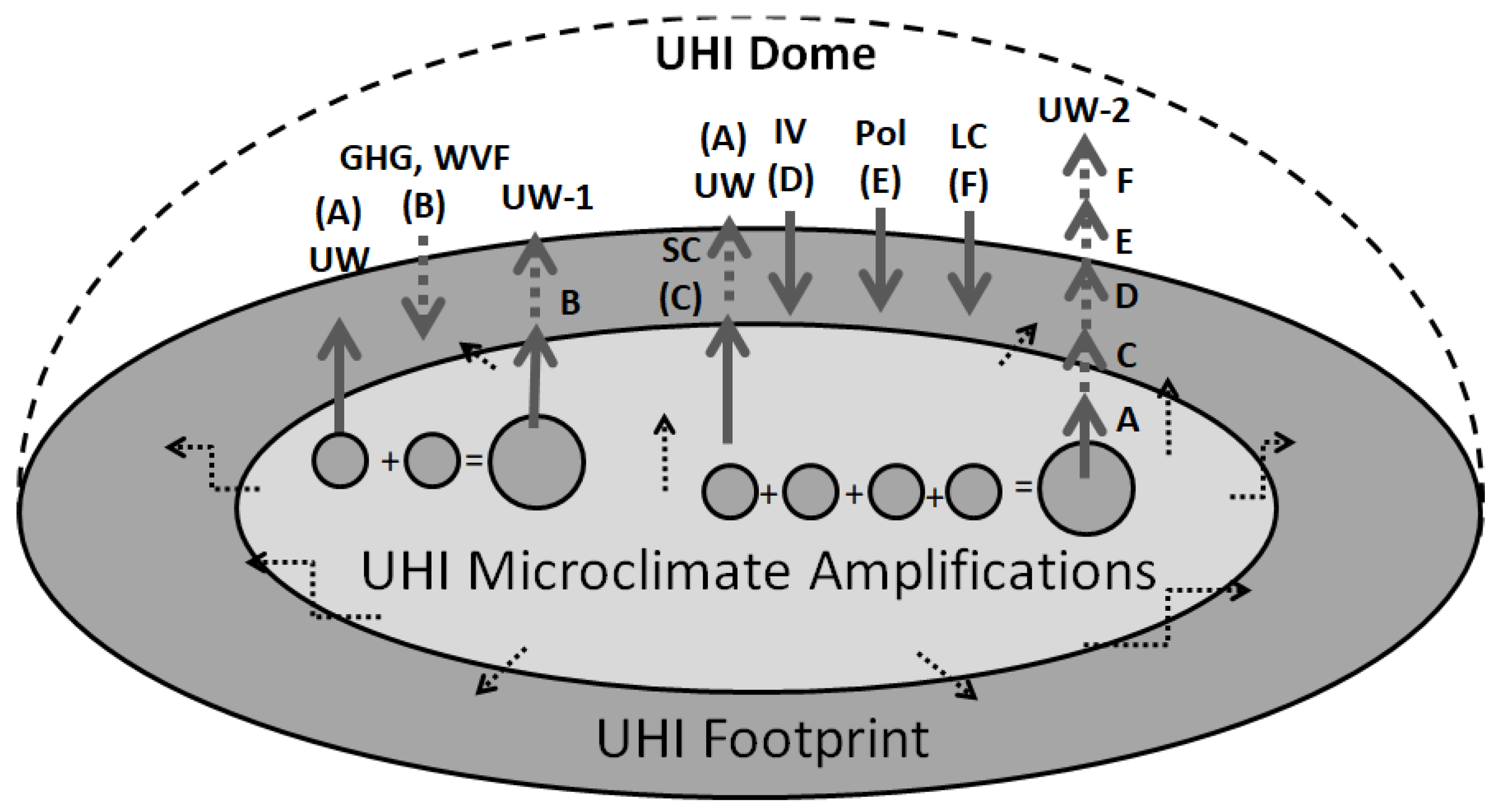
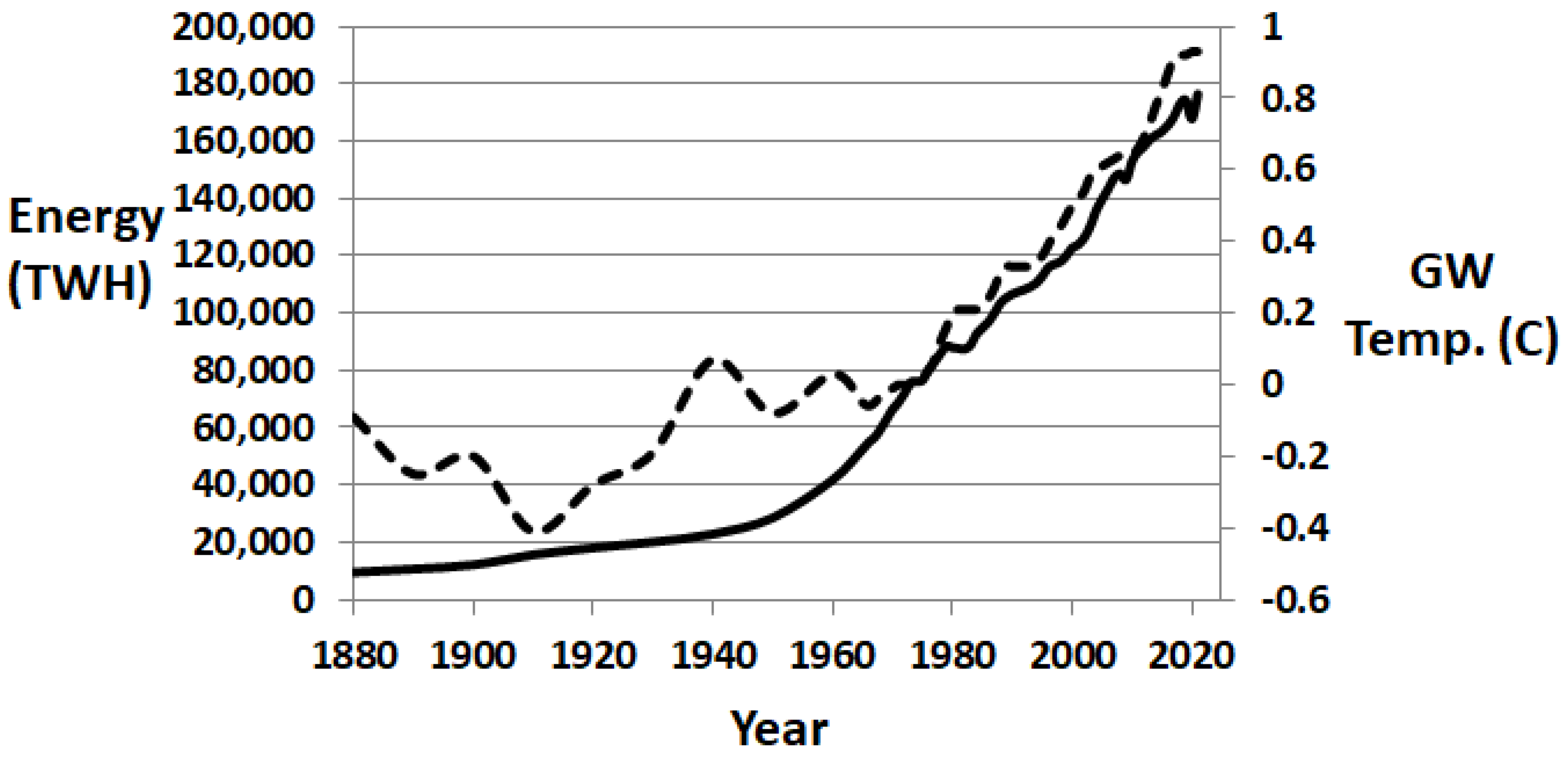
| Urbanization Heat Flux Assessment | |||||
|---|---|---|---|---|---|
| Urban Flux Type | Amplification Models | Model Verifications | Flux Type Results | Results | |
| Part 1: 3.1 AHR GW Baseline Data Section 2.4, Section 2.5 and Section 3.1.9 → Part II: 3.2 ISA GW Baseline Est. Section 3.2.1 → | Tables 2 and 3, Figure 1 Aerosol Etc. Section 2.3 Global background Section 3.1.1 UHI GHG: Section 3.1.3, Appendix D Model 1 UHI WVF Section 2.2 and Section 3.1.4 Model 2 Dry & Wet Mixed Section 3.1.5 Model 3 Footprint Section 2.1.1 and Section 3.1.6 Model 4 Rural Section 3.1.7 Model 5 → Table 3, Figure 1 | Wet & Dry Model 3 Footprint Model 4 Section 3.1.10 Tables 3–5 → | AHR 6.5% GW: Section 3.1.8, Equation (14) → ISA 6.5% GW: Section 3.2.1 Table 6 → | AHR+ISA GW 13% GW Section 3.2.2 Table 7 | |
| Mitigation & Helpful Information | |||||
| Mitigation of UHF Section 3.3 and Section 4.1 | GW Breakdown of Energy Flux, Appendix F | UHI WVF, Appendix E and Appendix F | |||
| Urban SG requirements, Section 3.3.2 | Global background feedback, Tables 2–4 Section 2, Section 2.5, Section 3.1.1, and Section 3.2.1.3, Appendix C and Appendix F | Irradiance, Section 3.2.1.1 | |||
| Helpful Equations: Appendix A and Appendix B | Satellite Issues, Section 4.2, Appendix G | ||||
| Data Type | Values | Description | Reference(s) | Applicable Sections |
|---|---|---|---|---|
| Fossil Fuel | 176,431 TWh | Consumption in 2021 | [22] | Section 2.4 |
| UHI WVF | 3.4 Wm−2 K−1 | UHI WVF in humid climates | [17] | Section 2.2, Section 3.1.4 |
| Global WVF | 1.6 Wm−2 K−1 | Global WVF | [23] | Section 3.1.4 |
| Global Warming | 5.1 Wm−2, 0.95 °C | From 1950–2019 | [9] | Section 2.5, Section 2.1.1, Section 3.2.1.2 |
| Forcing | 2.38 Wm−2 | From 1950–2019 | [9] | Section 2.3, Section 3.1.8, Section 3.2.1.2, Appendix F |
| UHI ΔT Increase | 3.3 K | UHIs ΔT increase in wet cities | [16] | Section 2.2, Section 3.1.4 |
| Cloud Percent | 47% | Irradiance through clouds | [24] | Section 3.2.1.1 |
| Unshaded% ISAs | 65%, 75% | Urban & rural unshaded %ISAs | Estimated, solar canyon | Section 3.2.1.1 |
| Global Feedback | 2.15 | WVF Amplification Factor | [9] | Section 2.2, Section 2.3, Section 3.1.8, Section 3.2.1.2 |
| Global GHG Factor | 1.62 | GHG Amplification with 62% re-radiation | [9,24] | Section 3.1.1, Section 3.1.8, Section 3.2.1.2 |
| UHI Footprint | 3.2 | UHI Amplification model | [25], Section 3.1.10.1 | Section 3.1.1, Section 3.1.6, Section 3.1.10.1, Section 3.2.1.2 |
| % Urban Climate | 67% vs. 33% | Cities in wet versus dry climates | [26] | Section 3.1.5 |
| ISA | 1.29 M km2 | 0.255% of the earth | [27] | Section 3.1.9 |
| ISA Roads | 14% of ISA | Road % of ISA | [28] | Section 3.2.2 |
| ISA% Urban | 33%, 40%, 50% | Urban vs. Rural %ISA | [28] | Section 3.1.9, Section 3.2.1.1, Section 3.2.1.2, Section 3.2.2 |
| Secondary Effect | Amplification Factor | Reference |
|---|---|---|
| Global Amplification Estimates | ||
| Global re-radiation GHGs | 1.62 | [9,24] |
| Global feedback (water-vapor and other effects) | (>2) 2.15 | [9,23,29,30] |
| Global combined amplification effects | 3.48 = 1.62 × 2.15 | |
| Microclimate Amplification Estimates (humid vs. dry climates) | ||
| Physics-based Modeling | 1.2 | Model 1: Section 3.1.3 dry climates |
| Physics-based Modeling | 2.55 | Model 2: Section 3.1.4 humid climates |
| Physics-based Modeling | 2.2 | Model 3: Section 3.1.5, mixed climates |
| UHI Estimate | 3.2 | Model 4 (footprint): Section 3.1.6 |
| Rural Area Estimate | 1.1 | Model 5: Section 3.1.7 |
| Global × Microclimate (Local) Amplification Estimates | ||
| Global & UHI local combined amplification effects | 1.62 × 2.15 × ALocal | Section 3.2.1 and Section 3.2.2, (Example in Equation (6)) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feinberg, A. Urbanization Heat Flux Modeling Confirms It Is a Likely Cause of Significant Global Warming: Urbanization Mitigation Requirements. Land 2023, 12, 1222. https://doi.org/10.3390/land12061222
Feinberg A. Urbanization Heat Flux Modeling Confirms It Is a Likely Cause of Significant Global Warming: Urbanization Mitigation Requirements. Land. 2023; 12(6):1222. https://doi.org/10.3390/land12061222
Chicago/Turabian StyleFeinberg, Alec. 2023. "Urbanization Heat Flux Modeling Confirms It Is a Likely Cause of Significant Global Warming: Urbanization Mitigation Requirements" Land 12, no. 6: 1222. https://doi.org/10.3390/land12061222
APA StyleFeinberg, A. (2023). Urbanization Heat Flux Modeling Confirms It Is a Likely Cause of Significant Global Warming: Urbanization Mitigation Requirements. Land, 12(6), 1222. https://doi.org/10.3390/land12061222







