Evaluation for Water and Land Resources System Efficiency and Influencing Factors in China: A Two-Stage Network DEA Model
Abstract
:1. Introduction
2. Data and Methodology
2.1. Study Area
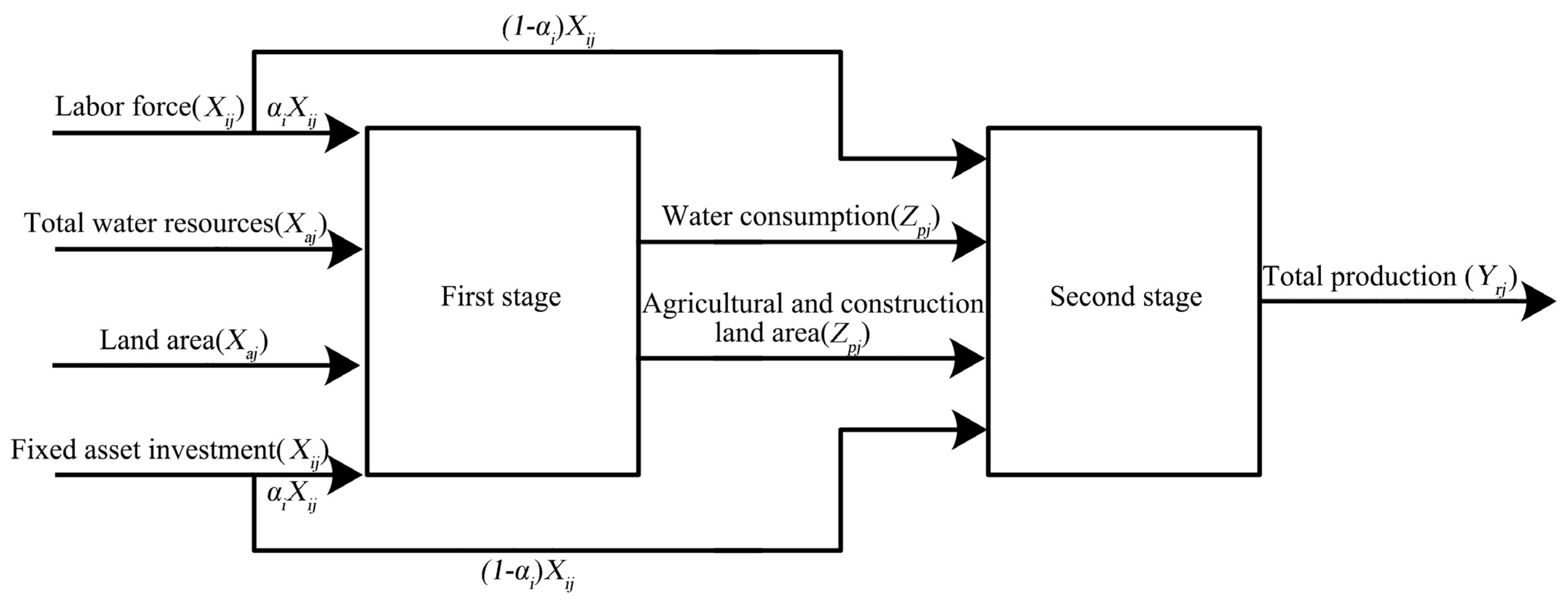
2.2. Two-Stage Network DEA Model with Shared Input Correlations
2.3. Spatial Autocorrelation Analysis
2.4. Geographically Weighted Regression (GWR) Analysis
2.5. Data Sources
3. Results and Analysis
3.1. Measurement of Water and Land Resources System Efficiency
3.2. Characteristics of Water and Land Resources System Efficiency in Different Regions
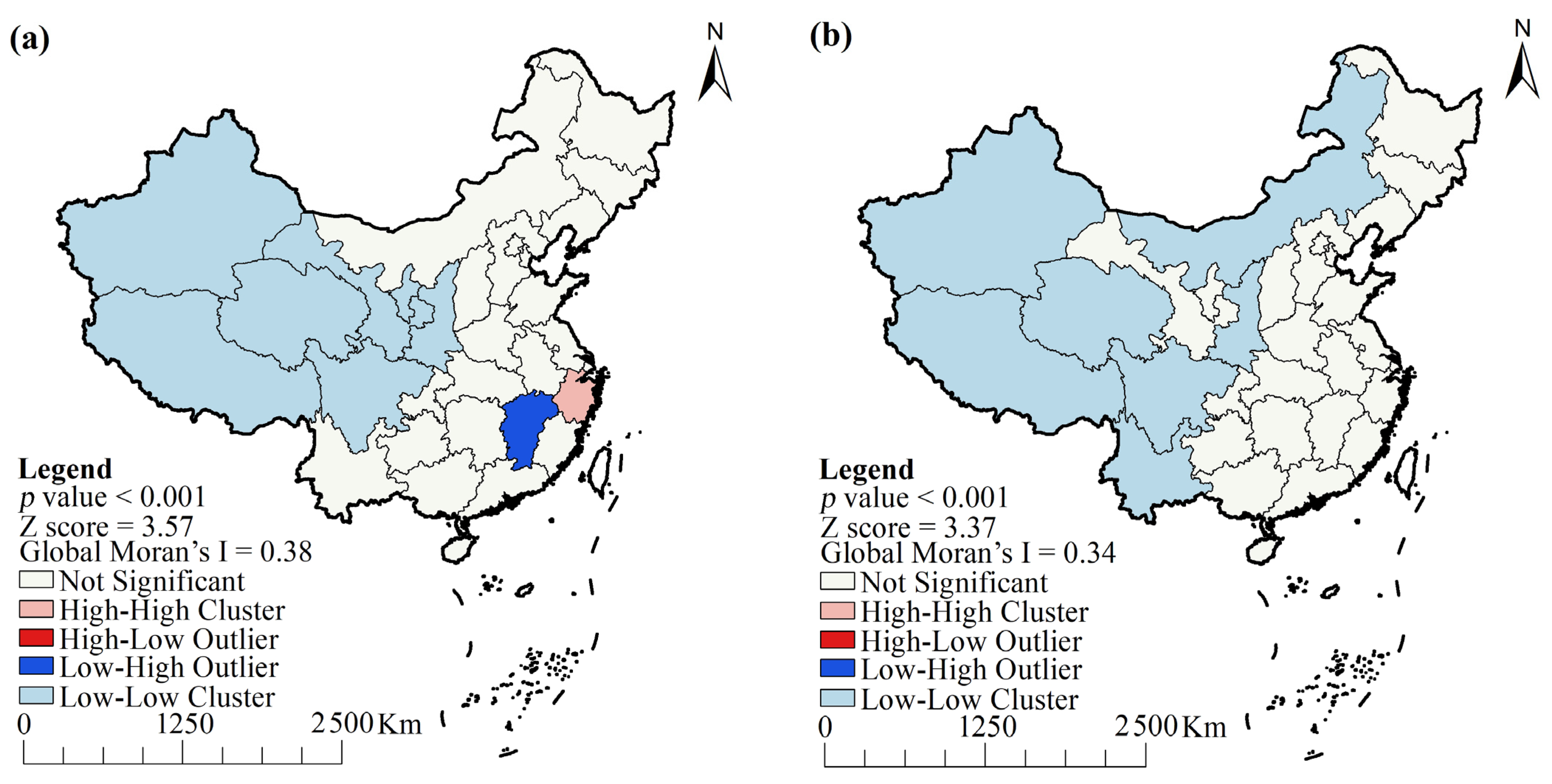
3.3. Spatial Correlations of Water and Land Resources System Efficiency in China
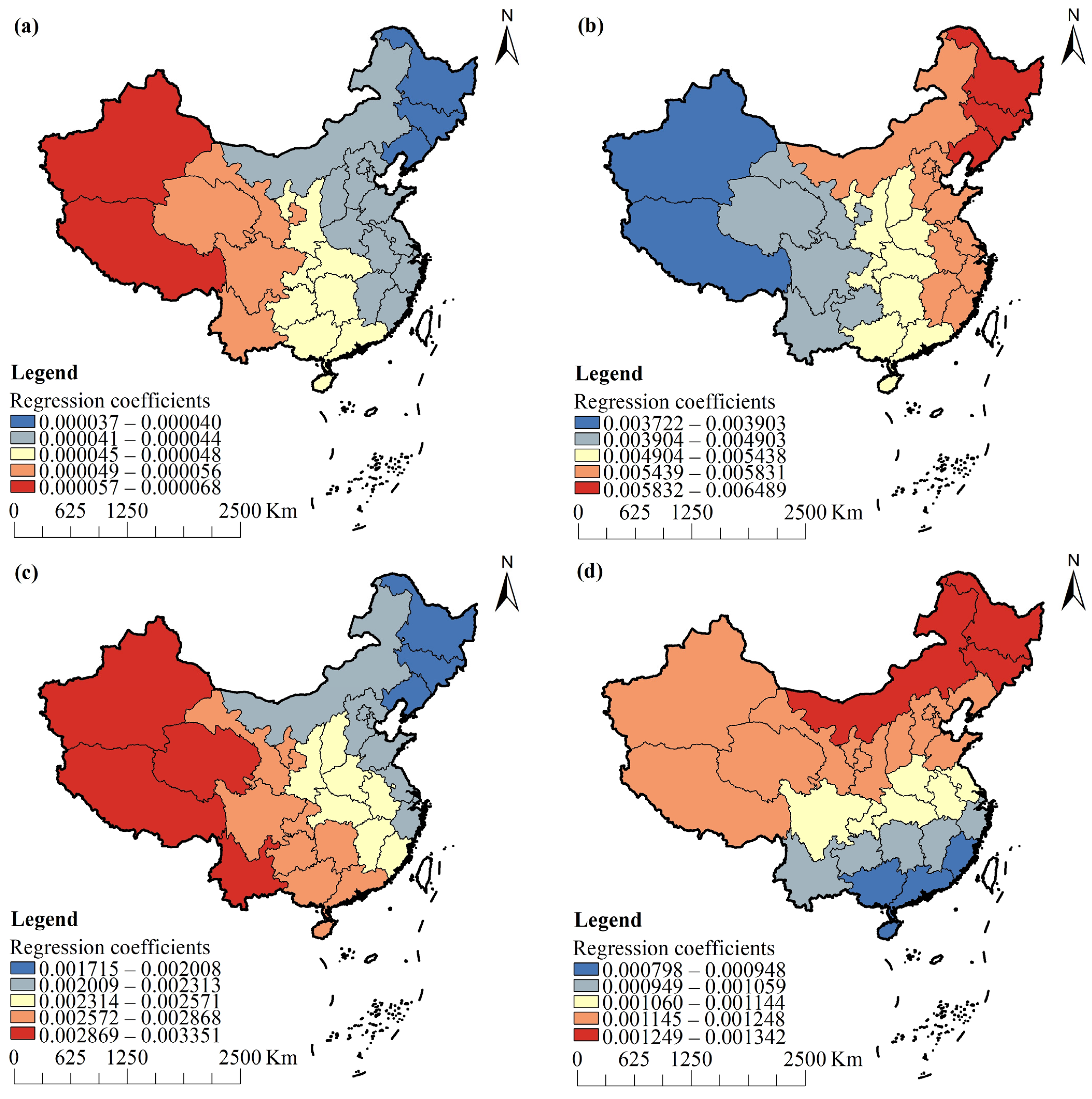
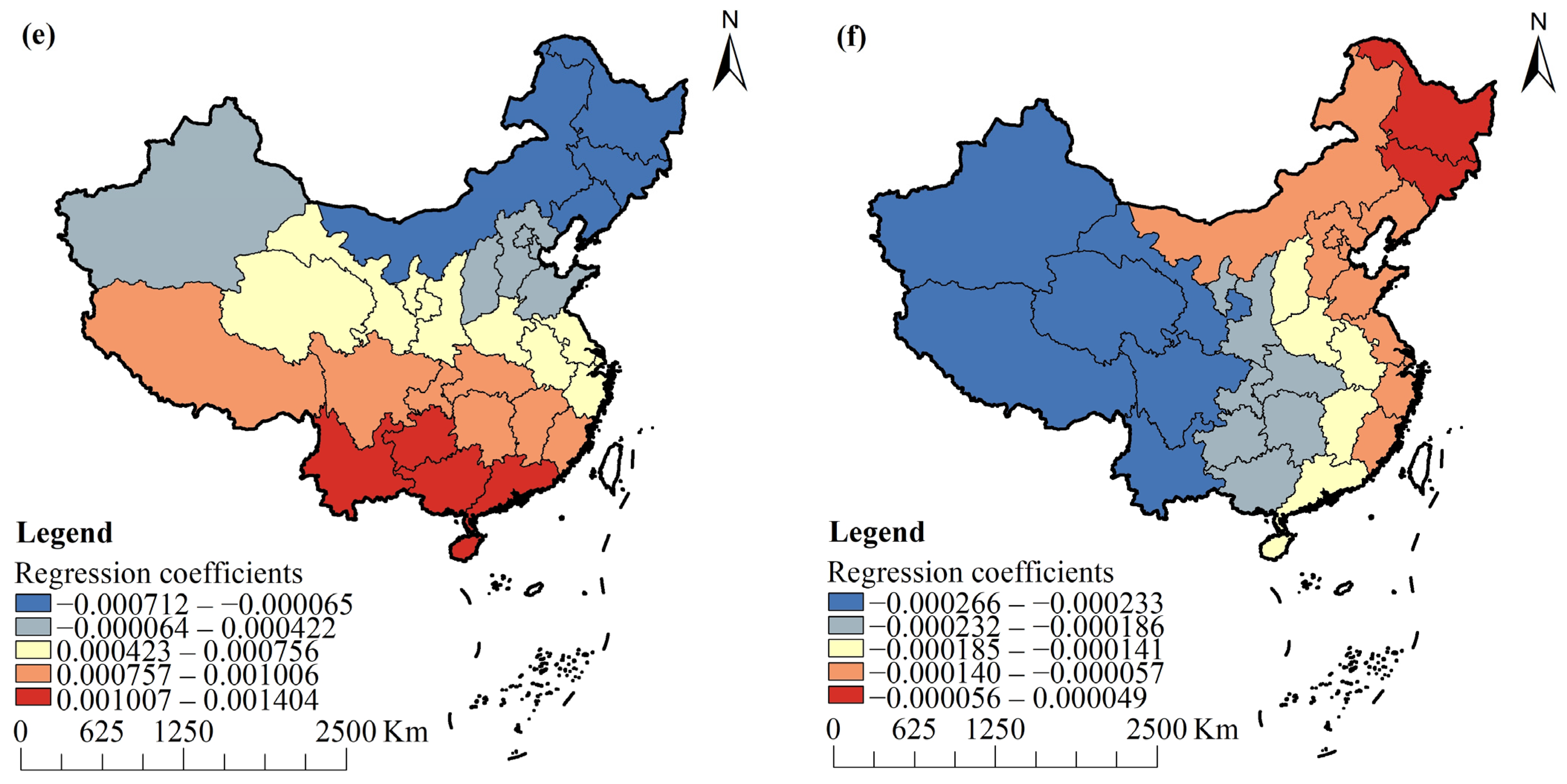
3.4. Influencing Factors of Water and Land Resources System Efficiency
4. Conclusions and Discussion
4.1. Conclusions
- (1)
- The overall efficiency of water and land resource system fluctuates widely in different regions, with a rate of change between −0.0315/a–0.01448/a. The average efficiency values of most provinces in the first stage are higher than the average efficiency values in the second stage, indicating that economic benefit transformation is the weak link of the water and land resources system. The overall average efficiency, the first-stage average efficiency and the second-stage average efficiency of the water and land resource system, shows obvious regional differences, all showing them to be high in the eastern coastal areas, and low in the western inland areas.
- (2)
- The low development-low economic benefit transformation type of water and land resources system is mainly distributed in northern China, the low development-high economic benefit transformation type is mainly distributed in the Huang-Huai-Hai Plain and the Middle-Lower Yangtze Plain China, the high development-low economic benefit transformation type is mainly distributed in southwestern and northwestern China, and the high development-high economic benefit transformation type is mainly distributed in eastern China.
- (3)
- The overall efficiency of the water and land resource system has significant spatial positive correlation, and this spatial positive correlation has an increasing trend. High-High Clusters are mainly concentrated in the North China Plain and Southeast Coast. Low-Low Clusters occupy more provinces, mainly in western and northern China.
- (4)
- The influence of each driving factor on the overall efficiency of water and land resources system has spatial heterogeneity. The urbanization level has the most significant positive impact, with spatial pattern decreasing from northeast to southwest. Population density, the proportion of output value of secondary and tertiary industries, and the effective irrigation all have a positive impact. The impact of the proportion of construction land is bidirectional, showing a negative correlation in northeastern China and a positive correlation in other provinces. The per land pesticide application is negatively correlated with the overall efficiency of water and land resources system in general.
4.2. Policy Suggestions
4.3. Limitations and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, B.; Han, M.Y.; Peng, K.; Zhou, S.L.; Shao, L.; Wu, X.F.; Wei, W.D.; Liu, S.Y.; Li, Z.; Li, J.S.; et al. Global land-water nexus: Agricultural land and freshwater use embodied in worldwide supply chains. Sci. Total Environ. 2018, 613–614, 931–943. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wang, Z. Water-land resource carrying capacity in China: Changing trends, main driving forces, and implications. J. Clean. Prod. 2022, 331, 130003. [Google Scholar] [CrossRef]
- Wang, S.; Yang, F.L.; Xu, L.; Du, J. Multi-scale analysis of the water resources carrying capacity of the Liaohe Basin based on ecological footprints. J. Clean. Prod. 2013, 53, 158–166. [Google Scholar] [CrossRef]
- Yang, J.; Lei, K.; Khu, S.; Meng, W. Assessment of Water Resources Carrying Capacity for Sustainable Development Based on a System Dynamics Model: A Case Study of Tieling City, China. Water Resour. Manag. 2015, 29, 885–899. [Google Scholar] [CrossRef]
- Sun, Z.; Jia, S.F.; Yan, J.B.; Zhu, W.B.; Liang, Y. Study on the Matching Pattern of Water and Potential Arable Land Resources in China. J. Nat. Resour. 2018, 33, 2057–2066. [Google Scholar]
- Li, T.T.; Long, H.L.; Zhang, Y.N.; Tu, S.S.; Ge, D.Z.; Li, Y.R.; Hu, B.Q. Analysis of the spatial mismatch of grain production and farmland resources in China based on the potential crop rotation system. Land Use Policy 2017, 60, 26–36. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W.; Li, H.; Wang, Z.; Zhang, B.; Zhong, K. Impact of Water and Land Resources Matching on Agricultural Sustainable Economic Growth: Empirical Analysis with Spatial Spillover Effects from Yellow River Basin, China. Sustainability 2022, 14, 2742. [Google Scholar] [CrossRef]
- Wang, J.H.; He, G.H.; He, F.; Zhao, Y.; Wang, H.Y.; Li, H.H.; Zhu, Y.N.; Liu, H.Q. Utilization and matching patterns of water and land resources in China. South-North Water Transf. Water Sci. Technol. 2019, 17, 1–8. [Google Scholar]
- Song, M.; Wang, R.; Zeng, X. Water resources utilization efficiency and influence factors under environmental restrictions. J. Clean. Prod. 2018, 184, 611–621. [Google Scholar] [CrossRef]
- Geng, Q.L.; Ren, Q.F.; Nolan, R.H.; Wu, P.T.; Yu, Q. Assessing China’s agricultural water use efficiency in a green-blue water perspective: A study based on data envelopment analysis. Ecol. Indic. 2019, 96, 329–335. [Google Scholar] [CrossRef]
- Luan, F.; Zhang, Y.; Liu, Y. Research on land and water resources matching efficiency based on water footprint in Sanjiang plain. Chin. J. Agric. Resour. Reg. Plan. 2018, 39, 30–35+82. [Google Scholar]
- Xu, N.; Zhang, J.; Zhang, R.; Tian, F. Study on matching characteristics of agriculture water and soil resources based on DEA —Take Gansu province 5 watershed as an example. Chin. J. Agric. Resour. Reg. Plan. 2020, 41, 277–285. [Google Scholar]
- Huang, K.W.; Yuan, P.; Liu, G. Research on water and soil resources matching in Sichuan province based on DEA. China Rural. Water Hydropower 2015, 396, 58–61+65. [Google Scholar]
- Tone, K.; Tsutsui, M. Network DEA: A slacks-based measure approach. Eur. J. Oper. Res. 2009, 197, 243–252. [Google Scholar] [CrossRef]
- Wu, H.Q.; Yang, J.Y.; Wu, W.S.; Chen, Y. Interest rate liberalization and bank efficiency: A DEA analysis of Chinese commercial banks. Cent. Eur. J. Oper. Res. 2022, 29, 1–32. [Google Scholar] [CrossRef]
- Wang, M.; Feng, C. Regional total-factor productivity and environmental governance efficiency of China’s industrial sectors: A two-stage network-based super DEA approach. J. Clean. Prod. 2020, 273, 123110. [Google Scholar] [CrossRef]
- Liang, X.; Li, J.; Guo, G.; Li, S.; Gong, Q. Evaluation for water resource system efficiency and influencing factors in western China: A two-stage network DEA-Tobit model. J. Clean. Prod. 2021, 328, 129674. [Google Scholar] [CrossRef]
- Castelli, L.; Pesenti, R.; Ukovich, W. A classication of DEA models when the internal structure of the decision making units is considered. Ann. Oper. Res. 2010, 173, 207–235. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, L.; Yang, F.; Zhu, J. Evaluation of information technology investment: A data envelopment analysis approach. Comput. Oper. Res. 2006, 33, 1368–1379. [Google Scholar] [CrossRef]
- Bi, G.; Liang, L.; Yang, F. A DEA-based eciency-measuring model for two-stage production systems with constrained resources. Chin. J. Manag. Sci. 2009, 17, 71–75. [Google Scholar]
- Zha, Y.; Liang, L. Two-stage cooperation model with input freely distributed among the stages. Eur. J. Oper. Res. 2010, 205, 332–338. [Google Scholar] [CrossRef]
- Tan, C.; Peng, Q.; Ding, T.; Zhou, Z. Regional Assessment of Land and Water Carrying Capacity and Utilization Efficiency in China. Sustainability 2021, 13, 9183. [Google Scholar] [CrossRef]
- Yu, H.; Shao, C.; Wang, X.; Hao, C. Transformation Path of Ecological Product Value and Efficiency Evaluation: The Case of the Qilihai Wetland in Tianjin. Int. J. Environ. Res. Public Health 2022, 19, 14575. [Google Scholar] [CrossRef]
- Kao, C.; Hwang, S. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan. Eur. J. Oper. Res. 2008, 185, 418–429. [Google Scholar] [CrossRef]
- Jiang, B.; Chen, H.; Li, J.; Lio, W. The uncertain two-stage network DEA models. Soft Comput. 2021, 25, 421–429. [Google Scholar] [CrossRef]
- Chen, K.; Guan, J. Network DEA-based efficiency measurement and decomposition for a relational two-stage production system with shared inputs. Syst. Eng.-Theory Pract. 2011, 31, 1211–1221. [Google Scholar]
- Wang, Y.; Pan, J.; Pei, R.; Yi, B.; Yang, G. Assessing the technological innovation efficiency of China’s high-tech industries with a two-stage network DEA approach. Socio-Econ. Plan. Sci. 2020, 71, 100810. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Programming with linear fractional functional. Nav. Res. Log. 1962, 9, 181–185. [Google Scholar] [CrossRef]
- Moran, P.A.P. The interpretation of statistical maps. J. Roy. Stat. Soc. B 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Chen, Y.; Yin, G.; Liu, K. Regional differences in the industrial water use efficiency of China: The spatial spillover effect and relevant factors. Resour. Conserv. Recycl. 2021, 167, 105239. [Google Scholar] [CrossRef]
- Xie, H.; Chen, Q.; Lu, F.; Wu, Q.; Wang, W. Spatial-temporal disparities, saving potential and influential factors of industrial land use efficiency: A case study in urban agglomeration in the middle reaches of the Yangtze River. Land Use Policy 2018, 75, 518–529. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Y.; Zhang, X.; Liu, Q. Industrial and Agricultural Water Use Efficiency and Influencing Factors in the Process of Urbanization in the Middle and Lower Reaches of the Yellow River Basin, China. Land 2022, 11, 1248. [Google Scholar] [CrossRef]
- Wolde, Z.; Wei, W.; Ketema, H.; Yirsaw, E.; Temesegn, H. Indicators of Land, Water, Energy and Food (LWEF) Nexus Resource Drivers: A Perspective on Environmental Degradation in the Gidabo Watershed, Southern Ethiopia. Int. J. Environ. Res. Public Health 2021, 18, 5181. [Google Scholar] [CrossRef] [PubMed]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D Stat. 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Some notes on parametric significance tests for geographically weighted regression. J. Regional. Sci. 1999, 39, 497–524. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Z. Natural and human impacts on ecosystem services in Guanzhong—Tianshui economic region of China. Environ. Sci. Pollut. Res. 2016, 23, 6803–6815. [Google Scholar] [CrossRef]
- Ouyang, W.; Gao, X.; Hao, Z.; Liu, H.; Shi, Y.; Hao, F. Farmland shift due to climate warming and impacts on temporal-spatial distributions of water resources in a middle-high latitude agricultural watershed. J. Hydrol. 2017, 547, 156–167. [Google Scholar] [CrossRef]
- Li, X.; Jiang, W.; Duan, D. Spatio-temporal analysis of irrigation water use coefficients in China. J. Environ. Manag. 2020, 262, 110242. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, X.; Zhong, T.; Chen, Y.; Yang, H.; Chen, Z.; Xu, G.; Niu, L.; Li, H. Can annual land use plan control and regulate construction land growth in China? Land Use Policy 2020, 99, 105026. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, H.; Ji, Z. The Evaluation and Analysis of Benefit of Land Resource Use in Economic Perspective. In Applied Mechanics and Materials; Vehicle, Mechatronics and Information Technologies II; Trans Tech Publications Ltd.: Zürich, Switzerland, 2014; Volume 543–547, pp. 4273–4277. [Google Scholar]
- Cheng, K.; Pan, G.; Smith, P.; Luo, T.; Li, L.; Zheng, J.; Zhang, X.; Han, X.; Yan, M. Carbon footprint of China’s crop production—An estimation using agro-statistics data over 1993–2007. Agric. Ecosyst. Environ. 2011, 142, 231–237. [Google Scholar] [CrossRef]
- Zhao, Y.; Pei, Y. Risk evaluation of groundwater pollution by pesticides in China: A short review. Procedia Environ. Sci. 2012, 13, 1739–1747. [Google Scholar] [CrossRef]
- Khoveyni, M.; Eslami, R. Two-stage network DEA with shared resources: Illustrating the drawbacks and measuring the overall efficiency. Knowl-Based. Syst. 2022, 250, 108725. [Google Scholar] [CrossRef]
- Boda, M.; Dlouhý, M.; Zimková, E. Modeling a shared hierarchical structure in data envelopment analysis: An application to bank branches. Expert. Syst. Appl. 2020, 162, 113700. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, M. Spatial-temporal change in urban agricultural land use efficiency from the perspective of agricultural multi-functionality: A case study of the Xi’an metropolitan zone. J. Geogr. Sci. 2017, 27, 1499–1520. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, H.; Yan, P.; Yang, Y.; Li, J.; Xia, J. Analysis of water–carbon–ecological footprints and resource–environment pressure in the Triangle of Central China. Ecol. Indic. 2021, 125, 107448. [Google Scholar] [CrossRef]
- Li, M.; Li, J.; Singh, V.; Fu, Q.; Liu, D.; Yang, G. Efficient allocation of agricultural land and water resources for soil environment protection using a mixed optimization-simulation approach under uncertainty. Geoderma 2019, 353, 55–69. [Google Scholar] [CrossRef]




| Region | 2005 | 2010 | 2015 | 2020 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall | First Stage | Second Stage | Overall | First Stage | Second Stage | Overall | First Stage | Second Stage | Overall | First Stage | Second Stage | |
| Beijing | 0.876 | 0.531 | 1.000 | 0.868 | 0.713 | 1.000 | 0.985 | 0.969 | 1.000 | 1.000 | 1.000 | 1.000 |
| Tianjin | 0.865 | 0.574 | 0.977 | 0.920 | 0.852 | 1.000 | 0.995 | 0.990 | 1.000 | 0.808 | 0.993 | 0.622 |
| Hebei | 0.747 | 0.668 | 0.780 | 0.525 | 0.833 | 0.163 | 0.560 | 0.994 | 0.127 | 0.541 | 0.986 | 0.095 |
| Shanxi | 0.637 | 0.302 | 0.728 | 0.487 | 0.744 | 0.223 | 0.504 | 0.884 | 0.076 | 0.506 | 0.878 | 0.128 |
| Inner Monglia | 0.543 | 1.000 | 0.320 | 0.565 | 1.000 | 0.382 | 0.616 | 1.000 | 0.519 | 0.517 | 1.000 | 0.085 |
| NR | 0.734 | 0.615 | 0.761 | 0.673 | 0.828 | 0.554 | 0.732 | 0.968 | 0.544 | 0.674 | 0.972 | 0.386 |
| Liaoning | 0.627 | 0.583 | 0.644 | 0.538 | 0.644 | 0.499 | 0.579 | 0.983 | 0.247 | 0.682 | 0.774 | 0.659 |
| Jilin | 0.606 | 0.692 | 0.576 | 0.518 | 0.971 | 0.064 | 0.526 | 0.993 | 0.100 | 0.508 | 0.978 | 0.033 |
| Heilongjiang | 0.852 | 0.747 | 0.879 | 0.546 | 1.000 | 0.295 | 0.533 | 1.000 | 0.111 | 0.510 | 1.000 | 0.042 |
| NER | 0.695 | 0.674 | 0.700 | 0.534 | 0.872 | 0.286 | 0.546 | 0.992 | 0.152 | 0.567 | 0.917 | 0.245 |
| Shanghai | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Jiangsu | 0.791 | 1.000 | 0.738 | 0.638 | 0.878 | 0.400 | 0.713 | 1.000 | 0.588 | 0.700 | 1.000 | 0.578 |
| Zhejiang | 0.709 | 0.578 | 0.750 | 0.695 | 0.573 | 0.742 | 0.614 | 0.885 | 0.459 | 0.584 | 0.864 | 0.415 |
| Anhui | 0.675 | 0.851 | 0.600 | 0.523 | 0.920 | 0.117 | 0.506 | 0.871 | 0.111 | 0.529 | 0.887 | 0.153 |
| Fujian | 0.829 | 0.799 | 0.839 | 0.601 | 0.788 | 0.525 | 0.580 | 1.000 | 0.338 | 0.627 | 0.725 | 0.599 |
| Jiangxi | 0.599 | 0.842 | 0.480 | 0.520 | 0.963 | 0.081 | 0.524 | 0.971 | 0.088 | 0.526 | 0.969 | 0.088 |
| Shandong | 0.679 | 0.447 | 0.754 | 0.551 | 0.709 | 0.351 | 0.647 | 0.997 | 0.310 | 0.559 | 0.821 | 0.260 |
| ER | 0.755 | 0.788 | 0.737 | 0.647 | 0.833 | 0.459 | 0.655 | 0.961 | 0.414 | 0.646 | 0.895 | 0.442 |
| Henan | 0.757 | 0.649 | 0.801 | 0.509 | 0.758 | 0.207 | 0.550 | 0.911 | 0.163 | 0.538 | 0.859 | 0.183 |
| Hubei | 0.722 | 0.810 | 0.688 | 0.552 | 0.831 | 0.435 | 0.535 | 0.935 | 0.136 | 0.534 | 0.929 | 0.129 |
| Hunan | 0.731 | 0.980 | 0.635 | 0.583 | 0.945 | 0.433 | 0.532 | 0.956 | 0.117 | 0.535 | 0.959 | 0.113 |
| Guangdong | 0.976 | 0.903 | 1.000 | 0.867 | 0.980 | 0.840 | 0.674 | 0.793 | 0.628 | 0.594 | 0.879 | 0.296 |
| Guangxi | 0.717 | 1.000 | 0.654 | 0.537 | 1.000 | 0.127 | 0.509 | 0.937 | 0.075 | 0.500 | 0.931 | 0.047 |
| Hainan | 0.702 | 0.861 | 0.635 | 0.557 | 0.896 | 0.407 | 0.529 | 0.975 | 0.095 | 0.530 | 0.975 | 0.091 |
| CSR | 0.768 | 0.867 | 0.735 | 0.601 | 0.902 | 0.408 | 0.555 | 0.918 | 0.203 | 0.538 | 0.922 | 0.143 |
| Chongqing | 0.545 | 0.633 | 0.505 | 0.517 | 0.941 | 0.077 | 0.533 | 0.905 | 0.136 | 0.530 | 0.871 | 0.157 |
| Sichuan | 0.590 | 0.594 | 0.589 | 0.509 | 0.976 | 0.039 | 0.504 | 0.973 | 0.025 | 0.502 | 0.972 | 0.022 |
| Guizhou | 0.584 | 0.737 | 0.542 | 0.509 | 0.909 | 0.181 | 0.490 | 0.924 | 0.025 | 0.488 | 0.919 | 0.022 |
| Yunnan | 0.572 | 0.747 | 0.517 | 0.499 | 0.982 | 0.011 | 0.496 | 0.968 | 0.011 | 0.495 | 0.961 | 0.012 |
| Tibet | 0.519 | 1.000 | 0.174 | 0.501 | 1.000 | 0.007 | 0.500 | 1.000 | 0.002 | 0.501 | 1.000 | 0.016 |
| SWR | 0.562 | 0.742 | 0.465 | 0.507 | 0.961 | 0.063 | 0.505 | 0.954 | 0.040 | 0.503 | 0.944 | 0.046 |
| Shaanxi | 0.583 | 0.828 | 0.443 | 0.517 | 1.000 | 0.039 | 0.530 | 1.000 | 0.065 | 0.534 | 1.000 | 0.079 |
| Gansu | 0.615 | 0.822 | 0.539 | 0.479 | 0.841 | 0.185 | 0.423 | 0.707 | 0.089 | 0.413 | 0.665 | 0.093 |
| Qinghai | 0.525 | 1.000 | 0.143 | 0.507 | 1.000 | 0.084 | 0.503 | 1.000 | 0.036 | 0.501 | 1.000 | 0.038 |
| Ningxia | 0.532 | 1.000 | 0.285 | 0.529 | 1.000 | 0.060 | 0.533 | 1.000 | 0.071 | 0.531 | 1.000 | 0.063 |
| Xinjiang | 0.610 | 1.000 | 0.532 | 0.527 | 1.000 | 0.181 | 0.507 | 1.000 | 0.056 | 0.506 | 1.000 | 0.056 |
| NWR | 0.573 | 0.930 | 0.388 | 0.512 | 0.968 | 0.110 | 0.499 | 0.941 | 0.064 | 0.497 | 0.933 | 0.066 |
| Model | R2 | Adjusted R2 | AICc |
|---|---|---|---|
| GWR | 0.978 | 0.969 | −110.937 |
| OLS | 0.866 | 0.856 | −104.036 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Jiang, W.; Liu, Y.; Liu, Y. Evaluation for Water and Land Resources System Efficiency and Influencing Factors in China: A Two-Stage Network DEA Model. Land 2023, 12, 396. https://doi.org/10.3390/land12020396
Liu C, Jiang W, Liu Y, Liu Y. Evaluation for Water and Land Resources System Efficiency and Influencing Factors in China: A Two-Stage Network DEA Model. Land. 2023; 12(2):396. https://doi.org/10.3390/land12020396
Chicago/Turabian StyleLiu, Cong, Wenlai Jiang, Yang Liu, and Yunfei Liu. 2023. "Evaluation for Water and Land Resources System Efficiency and Influencing Factors in China: A Two-Stage Network DEA Model" Land 12, no. 2: 396. https://doi.org/10.3390/land12020396
APA StyleLiu, C., Jiang, W., Liu, Y., & Liu, Y. (2023). Evaluation for Water and Land Resources System Efficiency and Influencing Factors in China: A Two-Stage Network DEA Model. Land, 12(2), 396. https://doi.org/10.3390/land12020396





