Abstract
Climate change impacts the electric power system by affecting both the load and generation. It is paramount to understand this impact in the context of renewable energy as their market share has increased and will continue to grow. This study investigates the impact of climate change on the supply of renewable energy through applying novel metrics of intermittency, power production and storage required by the renewable energy plants as a function of historical climate data variability. Here we focus on and compare two disparate locations, Palma de Mallorca in the Balearic Islands and Cordova, Alaska. The main results of this analysis of wind, solar radiation and precipitation over the 1950–2020 period show that climate change impacts both the total supply available and its variability. Importantly, this impact is found to vary significantly with location. This analysis demonstrates the feasibility of a process to evaluate the local optimal mix of renewables, the changing needs for energy storage as well as the ability to evaluate the impact on grid reliability regarding both penetration of the increasing renewable resources and changes in the variability of the resource. This framework can be used to quantify the impact on both transmission grids and microgrids and can guide possible mitigation paths.
1. Introduction
The role of climate change has long been recognized for disrupting the energy sector via impacts on energy generation and demand through episodic disturbances from extreme weather events, increases in peak demand for cooling, and impacts due to variable water availability [1]. Renewable energy systems that rely on the sun and water are particularly sensitive to the vagaries of climate variability and change [2]. Vagaries such as increased cloud cover [3] could decrease the availability of solar power, decreased precipitation could reduce the availability of hydropower [4], increased winds (if utilizable) could increase the availability of wind power [5]. Opposite climate variations may occur in different regions of the world, highlighting the need for regional analyses in any framework. In addition to secular changes in the climate, there is growing evidence that increased variability accompanies climate change [6,7]; there are more extreme events in wind, precipitation, storms and other variables [8,9,10]. Extreme events can have as large an impact on the usability of the renewable energy [11,12] resources as the secular change in the resource and must be considered in determining energy storage needs.
Extreme events can impact the electric power system in several ways. On the load side, demand can change. For example, heat waves can increase demand and load variability. On the generation (supply) side, as discussed above, changes in weather and climate can impact the availability of solar, wind and hydropower (both positively and negatively). Finally, and very importantly, the increased variability in these can greatly increase the stress on the system [13,14] and the need for increased energy storage capabilities [15,16,17] in order to ensure that the supply can meet the demand when the resource is at its minimum and the load is at its maximum. It should be noted that some renewable energy resources can be more broadly distributed (i.e., not concentrated in a very large generation facility) which can to some degree ameliorate the increased stress from the high variability [13,14]. As penetration of these renewable resources increases these effects become only more important. Global warming affects all possible renewable energy sources.
One of the motivations for this study comes from recent reviews that highlight several gaps. A review and synthesis of studies on the impacts of climate change on renewable energy shows that most research has focused on hydropower and solar and highlights the need for regional analysis [18]. The uncertainty of climate impacts on energy at regional and global scales from a review of the literature motivates the need for a coordinated effort to develop a consistent framework for such assessments [19], which drives this attempt to contribute to the development of such a framework.
Here we will examine the possible impact on three of these energy sources: solar, hydro and wind. To do this in the preliminary analysis we look at two locations that are far apart both in distance and climate region. One is Palma de Mallorca in the Balearic Islands, a subtropical location, while the other is Cordova in Alaska, a subarctic location. At each of these two locations we have approximately 60 years of meteorological data, which should be sufficient to detect any impact of global warming [20]. During this period the average 2 m air temperature of the Earth [21] increased about 1 °C (Figure 1). The 2 m air temperature increase is 0.16, 0.20, and 0.30 °C per decade for the globe, Palma de Mallorca, and Cordova, respectively. Cordova displays the largest interannual variability of the three series due to its high latitude location, where climatologically high latitude variability is larger than that in the subtropics (Palma de Mallorca). These climatological contrasts at Palma de Mallorca and Cordova highlight the regional variations in climate relevant for renewable energy.
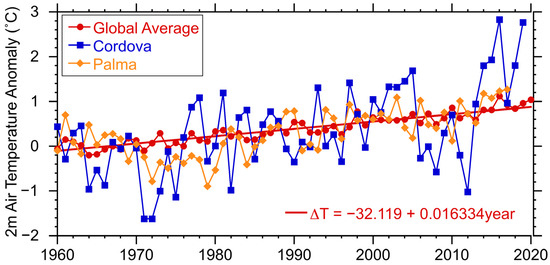
Figure 1.
Annual average 2 m air temperature anomaly (°C) for the globe (red), Cordova Alaska (blue) and Palma de Mallorca Spain (orange) over the 1960–2020 period. The global temperature anomaly trend (red line) is 0.16 °C per decade. The global data are provided by NOAA [21] and the Cordova and Palma de Mallorca data are from the nearest grid point from the ERA5 reanalysis [22].
The “amount” of a resource available is of key importance to power production. To investigate the potential impact of climate change on power production we first examine any secular change in the resource. However, because renewable energy sources are already characterized by great variability, one of the concerns is the possible increase in this variability from climate. To measure the variability, we use multifractal analysis of the data, calculating the intermittency coefficient C(1) (as described in the next section) together with the impact that this variability has on the storage needed. The fundamental goal of this work is to allow exploration of the storage needs for various renewable electric power sources and how they might change under climate change. Additionally, the analysis seeks to understand the change in stress on the power transmission system and the change in risk and reliability [23,24,25] inherent to that system. This paper demonstrates the preliminary steps towards this goal.
2. Materials and Methods
2.1. Methods
In order to measure the impact of the climate change on the energy production of the renewable energies and to examine trends in the resource, we will measure the variability of the meteorological data to quantify how that impacts the needed energy storage. Here we describe the analysis tools that are used in this study.
2.1.1. Intermittency
To evaluate the variability of the meteorological data, we use multi-fractal analysis and calculate the intermittency of temporal signals. The method is described in [26,27]. Given a meteorological time series X = {xi, i = 1,…, N} that has been sampled at a constant sampling rate, we calculate:
where
This measure can be averaged over sub-blocks of data of length n < N, as follows:
We then calculate the q-moments, . In a given range of n-values, these moments are expected to scale like [26]:
where K(1) ≡ 0. If the time series X is mono-fractal, the function K(q) is asymptotically linear in q, otherwise the series is multi-fractal. We can now introduce the parameter C(q) which is defined as [28]:
The parameter C(1) is the intermittency parameter. Due to the singularity at q = 1, the intermittency parameter must be calculated as:
The value of C(1) goes from 0, for a mono-fractal (low intermittency) time series, to 1 (high intermittency) as the multi-fractal character increases. The reason one uses this parameter is to quantify the level of multi-fractality (or intermittency) of the measured signals. For most of the data analyzed here the sampling rate is one day.
For precipitation data we included the intermittency sampled on both an hourly and daily basis. For example, other time scales would be of interest for wind data but that will be presented elsewhere. We discuss the average rate of annual change obtained from the linear fit and the corresponding uncertainty determination. This linear fit should not be thought of as an actual functional description of the data (i.e., it need not be linear), but simply as a measure of the average rate of change over the time period considered.
2.1.2. Calculating the Storage Needed
An important component of the reliability of the power production which is impacted by the variability of the renewable energy is the energy storage. In this work we do not include the details of the energy storage devices as that is beyond the scope of this work and would detract from the main results. Here we calculate the energy storage needed in order to be able to guarantee an average power supply in the presence of the highly variable power production as described in reference [29]. First, we need to evaluate the daily power flow that can be delivered to the customers in order to maximize efficiency and minimize the cost of storage. We use P(t) as the daily averaged power produced. For example, if P(t) is the averaged solar power (or wind power) for every day and PF(t) is the actual power flow out of the plant, we can estimate the energy storage needed to ensure this power flow by calculating:
The power flow out PF(t) is the one that minimizes the maximum of R with the condition R > 0 for all times. Then, maximum value of R(t) along the time interval of interest, MaxR, gives us the storage needed.
The result of this storage calculation is strongly affected by large events. Therefore, it conveys different information than the intermittency.
In this work we are trying to evaluate the effect of climate change, so we consider isolated electric power production facilities assuming they have the same characteristics in each location. If we were taking this one step further, we would include the power production plants in the corresponding grid and then the storage needs would change as would the optimal size of the plant. However, here we are not yet discussing the effects off and on the grid. We are also assuming a constant power production during each month. In a more realistic case, we would optimize the production to the conditions of the grid and local climate. With these assumptions the needed storage is a good measure of the impact of climate, although it must be viewed as a relative measure in time and location.
2.2. Meteorological Data
The basic historical reanalysis data that we have used is ERA5 and is obtained from the European Centre for Medium Range Weather Forecasting (ECMWF) Copernicus Climate Change Service [22]. Reanalysis combines observational data and gap-fills using a weather forecast model to construct a gridded data set of the atmosphere. From this source we have obtained hourly data from 1960 to 2020 for temperature, total surface solar radiation, precipitation amount and wind speed. We have combined the hourly data to construct daily data. It is on this daily time scale that we analyzed the data to model the generation power of the renewable energy [29].
The first characteristic that the data allow us to evaluate is the local impact of climate change on the two locations that we are considering. These results are shown in Figure 1.
At both locations, we can see a consistent increase in the yearly averaged temperature. Moreover, in both cases the increase is similar to or slightly larger than the increase in the averaged global temperature. The slope of the global temperature data is ~0.016 °C/year while the Palma de Mallorca data show ~0.020 °C/year and Cordova with ~0.029 °C/year. This suggests that it should be possible to detect the impact of this warming on the local renewable sources. It is also worth noting that the rate of change is larger in Cordova than it is in Palma de Mallorca, consistent with the notion of polar amplification [30].
In Palma de Mallorca we complement the ERA5 data with meteorological station data from AEMET [31] to evaluate the consistency of the input data.
3. Results
3.1. Impact on Solar Plants
The first data set we analyze is the one relevant to solar power. The ERA5 reanalysis has hourly data for total surface solar radiation that can be directly related to the solar power production. This includes both the direct and indirect solar radiation received and therefore available at the surface. Importantly, in this work we do not scale this to account for the efficiency of the conversion, i.e., we are not including any particular model for the solar power “plant” including the actual efficiency of the solar cells. First, we measure the intermittency, C(1), of this data on a daily scale. We do not look at the hourly data for the solar due to the dominance of the diurnal cycle in that time series. In Figure 2 we plot the result for the two locations.
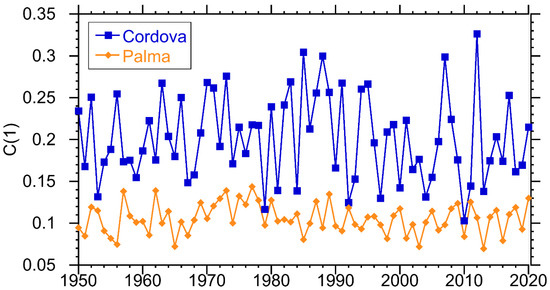
Figure 2.
Intermittency parameter for the solar radiation at Cordova and Palma de Mallorca. The intermittency parameter is unitless.
Clearly the level of intermittency is much larger in Cordova (averaging ~0.2) than in Palma de Mallorca (averaging ~0.1). Additionally, the variance in the intermittency parameter is much larger in Cordova. The large fluctuations in the intermittency parameter make it very difficult to assess the existence of a secular trend, which is perhaps a slow increase in time. If a trend does exist, it is very small and requires longer data sets measure reliably.
We can look in both cases at the storage needs for a plant. To do that, we group the data in increments of five years and based on the performance needs for the plant we calculate the storage required in each period. The results are shown in Figure 3. We see that the storage needed for a power plant is larger in Cordova than in Palma de Mallorca; this is consistent with the high intermittency of the Cordova data. Additionally, we can see that both locations exhibit an increase in the storage need that is consistent with the secular trend likely due to global warming. Although there was no clear increase in the case of the intermittency parameter, there is some correlation between the storage needs and the intermittency parameter.
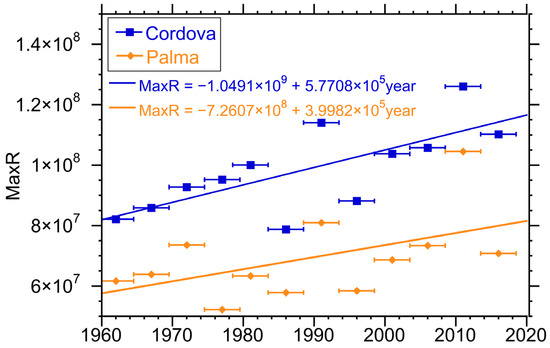
Figure 3.
Storage needed for solar plants at Cordova and Palma de Mallorca. Units for storage are kilowatt hours. Horizontal bars indicate interval over which the parameter was calculated.
Because of the secular changes due to climate change, another relevant issue to be analyzed is the power production at the plant. These secular changes are changes in the actual average incident surface radiation due to changes in cloud cover, number of sunny days and cloud opacity. In Figure 4 we show the averaged production, again over periods of five years at the two locations as a function of time. Pout is the surrogate for the amount of resource (Solar, Wind and Hydro) available. Trends in these resources are similar to the temperature trends in Figure 1 in this case simply normalized to an imaginary “standard” power plant to give a power output which is then needed for the storage calculation. The actual values can be scaled based on the “real” conversion efficiency of the plant and the “real” size of the plant, neither of which would change the trend. Therefore, the values for the <Pout> are not meaningful by themselves.
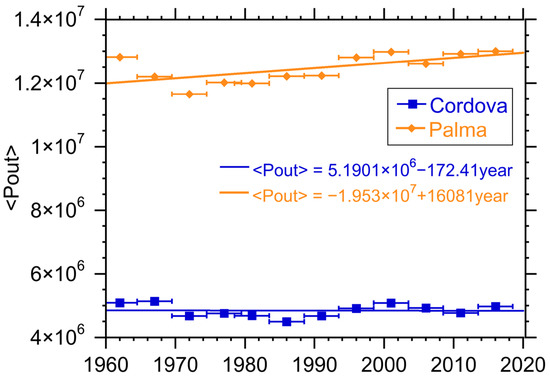
Figure 4.
Averaged power production at solar plants at Cordova and Palma de Mallorca. Units for averaged power production are kilowatts. Horizontal bars indicate interval over which the parameter was calculated.
We can first see that in Palma de Mallorca the production of solar power is higher than in Cordova. This is, of course, consistent with Cordova being a much cloudier location than Palma de Mallorca as well as the much larger intermittency in Cordova. Furthermore, the production in Palma de Mallorca clearly increases over time while for Cordova it remains practically flat. Looking in detail one finds in Cordova a small increase from 1970 to 2019, but the optimal production in the 1950s and 1960s was high and that distorts the overall growth.
One possible measure of the efficiency of highly variable renewable energy power plants is the ratio of the energy storage needed, MaxR, to the averaged energy production in one day, <E>, that is MaxR/<E>. The lower this quantity is, the more “efficient” the system is in the sense that less energy storage is needed per power production unit. It is important to note that this is very different than the “efficiency” of conversion (i.e., the efficiency of a solar cell being the fraction of the incoming radiation that is converted to electricity), which is often used in power conversion. In Figure 5, we have plotted this quantity for both locations. It is clear from the figure that in Palma de Mallorca that solar energy can be a much more efficient system, as one could also conclude from the previous results. The very low efficiency of solar for Cordova is due to the large intermittency and high variability, which makes it very costly from a storage perspective to get high reliability power from solar.
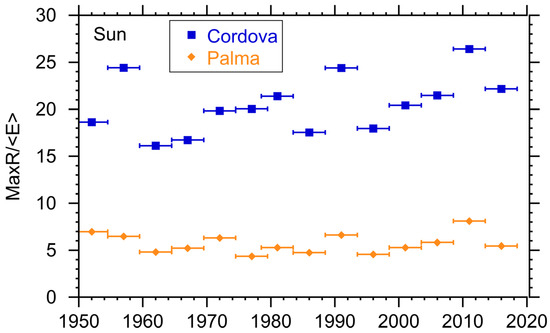
Figure 5.
Ratio of the energy storage needed to the average daily energy produced by solar plants in Cordova and Palma de Mallorca. MaxR/<E> is unitless. Horizontal bars indicate interval over which the parameter was calculated.
3.2. Impact on Hydro Plants
Globally there is clear evidence of the impact of the climate change on precipitation, and in some regions there is a significant increase in the intensity and intermittency of precipitation events [6,7]. There have already been evaluations of the impact of climate change on hydro production in some locations, like New Zealand [32], but in this work we will concentrate on the same two regions we have analyzed in the previous section.
We consider the precipitation data, which is the data relevant to hydro plants. Once again, the ERA5 dataset has hourly data for precipitation for both locations that can be used to evaluate the power production. Again, we are not using a specific generation model used for the hydropower plants. Rather, we are using the available water from precipitation as a surrogate for the available power. First, we measure the intermittency of this data on both hourly and daily time scales. In Figure 6 and Figure 7 we show the results for the two locations.
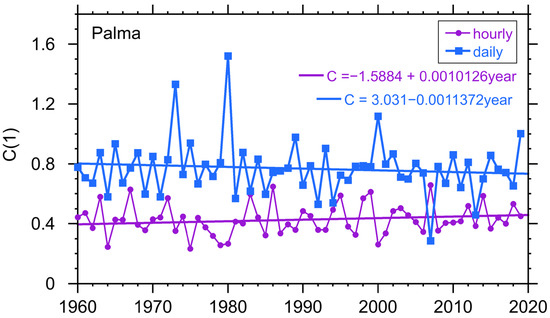
Figure 6.
Intermittency parameter for the precipitation in Palma de Mallorca for hourly and daily data. The intermittency parameter is unitless.
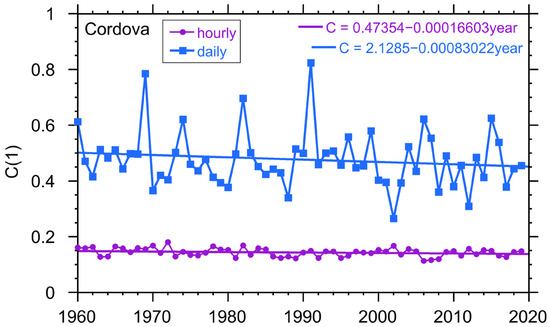
Figure 7.
Intermittency parameter for the precipitation in Cordova for hourly and daily data. The intermittency parameter is unitless.
We can see once again that the fluctuations in the intermittency parameter can be large. This time the intermittency and variance in the Palma de Mallorca data is much larger, on the order of a factor of two for both the hourly and daily data. This is the opposite of the intermittency result for solar radiation, which makes sense because Cordova is a consistently rainy location with an average annual precipitation of 3769 mm and with 125 rainy days/year, while Palma de Mallorca averages only 402 mm of precipitation per year. These results however do have some secular behavior with Palma de Mallorca showing an increase in the intermittency in the hourly data while Cordova has a small decrease in the hourly data.
To confirm these analyses in a location where climate change effects on precipitation are already being documented [33] we have done an analysis of the intermittency in a location in northern California, Lake Oroville, where we know the impact has been clear. In Figure 8, we show the intermittency parameter as a function of time calculated using ERA5 data for Lake Oroville.
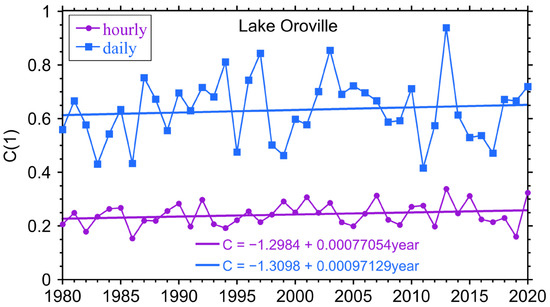
Figure 8.
Intermittency parameter for the precipitation in Lake Orville for hourly and daily data. The intermittency parameter is unitless.
We see a consistent increase with time of the averaged intermittency, but more importantly the peaks of the intermittency increase at an even faster rate. These results for the Lake Oroville data are consistent with the increased drought periods and more extreme rainfall events. We therefore have clear evidence of different impacts on the intermittency as well as on secular trends in different regions. This validates the value of this type of analysis for power production.
It is worth repeating that when looking at the intermittency data we discuss the average rate of annual change obtained from the linear fit and the corresponding uncertainty determination. The data clearly have a great deal of variability, and this linear fit should not be thought of as an actual functional description of the data (i.e., it need not be linear), but simply as a measure of the average rate of change over the time period considered. The slopes and uncertainties are shown in Table 1. The main points to be gleaned from this table are: (1) the hourly data have less uncertainty in the slope calculation; (2) the Cordova intermittency is decreasing with time (i.e., has a negative slope) with the sign of the slope outside the error bars, particularly for the hourly data; (3) the Palma de Mallorca data show an increasing intermittency in the hourly data (outside the error bars), but for the daily data both signs of the slope are inside the error bars; and (4) the Oroville data have an increasing intermittency with once again the hourly data slope sign outside the error bars.

Table 1.
The fitted linear slopes and the uncertainty in those slopes for the precipitation intermittency data.
Returning to the study locations of Cordoba and Palma de Mallorca, we examine the storage needs for hydro plants. Again, we bin the data in five-year periods and based on the optimal performance needs for the plant we calculate the storage required in each period. The results are shown in Figure 9, where we can see that neither Palma de Mallorca nor Cordova show any significant change in their storage needs over the time period. Particularly, we can see that in both places there is no significant increase in the storage needs in time, in the case of Palma de Mallorca, there a slight decrease.
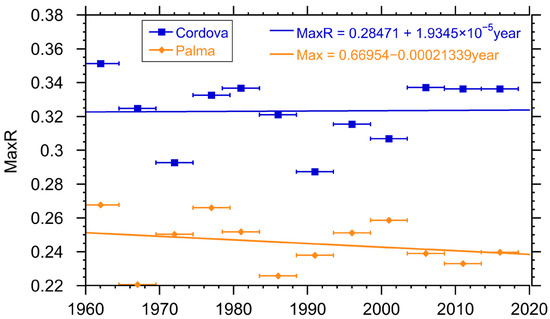
Figure 9.
Storage needed for hydro plants in Cordova and Palma de Mallorca. Storage has units of kilowatt hours. Horizontal bars indicate interval over which the parameter was calculated.
This different impact in the two locations is also reflected in the averaged power production. The power production is shown in Figure 10. As expected, due to the differences in total precipitations the optimal power production in Palma de Mallorca is much lower than in Cordova. In Palma de Mallorca that power shows a slight decrease over time while Cordova shows a small increase. Again, Pout is the surrogate for the amount of resource, hydro in this case, available.
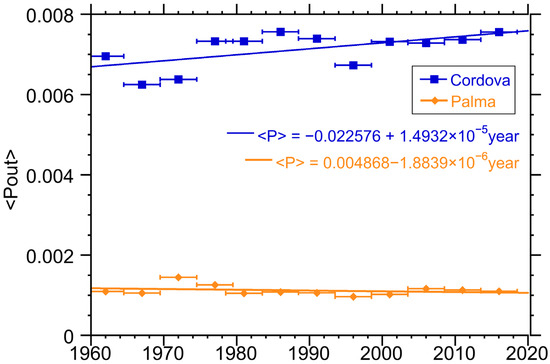
Figure 10.
Power production at hydro plants in Cordova and Palma de Mallorca. Power has units of kilowatts. Horizontal bars indicate interval over which the parameter was calculated.
It is these slight trends in the overall optimal production combined with the opposite trends in the intermittency, which keep the storage needs fairly constant.
Finally, we compare the efficiency in both locations as we did in the previous section. The results are in Figure 11. Clearly the efficiency is considerably better in Cordova, a smaller number in our metric. As with the solar power, this is due to a combination of the increased amount of hydro available (more precipitation) and the decreased intermittency in Cordova when compared to Palma de Mallorca.
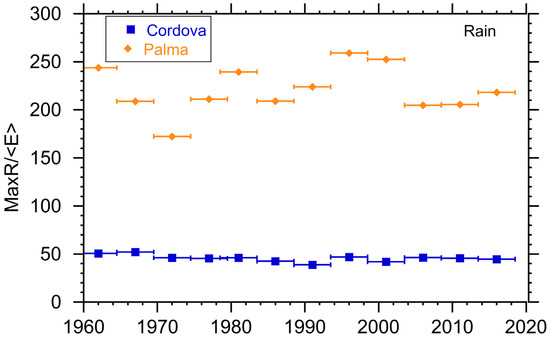
Figure 11.
Ratio of the energy storage needed to the average daily energy produced by hydro plants in Cordova and Palma de Mallorca. MaxR/E is unitless. Horizontal bars indicate interval over which the parameter was calculated.
3.3. Impact on Wind Plants
The final renewable resource investigated here is wind power, and wind power generation is rapidly increasing its penetration into the sustainable generation mix. Some countries have already exceeded 40% penetration (Denmark for example), with a number of others over 20% penetration and many aiming for at least 20% by the end of the decade. This is a remarkable increase over the last two decades. It is also notable that wind is one of the most highly variable sources on multiple time scales from the minutes time scale to annual time scales. In this work we look at how the availability of the resource (how much wind power is available) and the variability of the wind energy is changing as the climate is changing. We use the ERA5 wind speed data, which constructed by combining the U and V speeds in quadrature. Once again, the ERA5 dataset has hourly data for the winds for both locations that can be used to evaluate the power production. As before, we are not using a specific generation model for the wind plants. Rather, we are simply using the available wind speed cubed for the available power. First, we measure the intermittency of these data on both hourly and daily time scales. In Figure 12 (hourly) and Figure 13 (daily) we show the intermittency in the wind power for the two locations. At both the hourly and daily time scales the intermittency is much larger for Palma de Mallorca than it is for Cordova. On the hourly time scale, Palma de Mallorca had an average value for C(1) of ~0.08 while Cordova’s was a factor of ~1.5 smaller with an average value of ~0.055 for the intermittency. The daily intermittency data show an even larger difference, with a factor >2 separating Palma de Mallorca, with an average of ~0.6, from Cordova with an average value of ~0.25. The variance in the intermittency data is large, so without a longer time series it is difficult to make definitive statements about the secular trends; however, there seems to be a consistent positive trend in all the data showing an increase in intermittency over the time period studied.
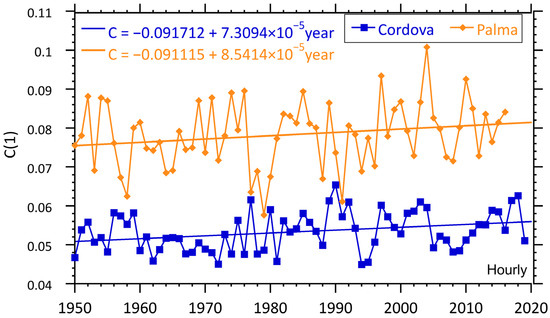
Figure 12.
Intermittency parameter for the wind in Palma de Mallorca and Cordova for hourly data. The intermittency parameter is unitless.
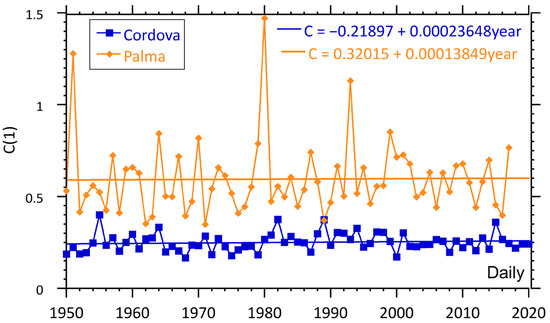
Figure 13.
Intermittency parameter for the wind in Palma de Mallorca and Cordova for daily data. The intermittency parameter is unitless.
As before we now look at the storage needed for a plant for both locations, MaxR. To do that we again group the data in increments of five years; based on the optimal performance needs for the plant described earlier we calculate the storage required in each period. The results are shown in Figure 14. We see that the storage needed for a power plant is much larger in Cordova than in Palma de Mallorca (more than two orders of magnitude larger!) and there is a large amount of scatter in the storage data. The much larger storage needs for Cordova seem inconsistent with the smaller values for the intermittency shown before. The data also show that both locations exhibit a weak increase in the storage needed that is consistent with the secular trend in the intermittency but with much more scatter. Both the much larger storage needs for Cordova and the weaker trends in both can be understood by looking next at the available power.
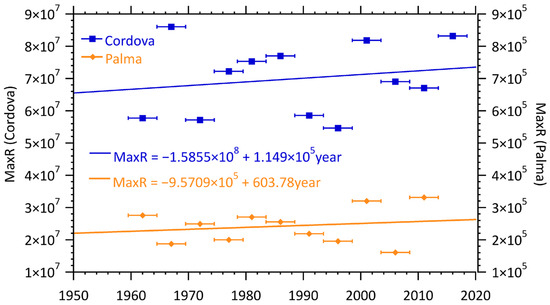
Figure 14.
Storage needed for wind plants in Cordova and Palma de Mallorca. Storage has units of kilo-watt hours. Horizontal bars indicate interval over which the parameter was calculated.
The secular changes in wind due to climate change leads to a similar change in available power production at the plant. In Figure 15 we show the averaged production, again calculated over periods of five years at the two locations as a function of time. Once again, Pout is the surrogate for the amount of resource, wind in this case, available.
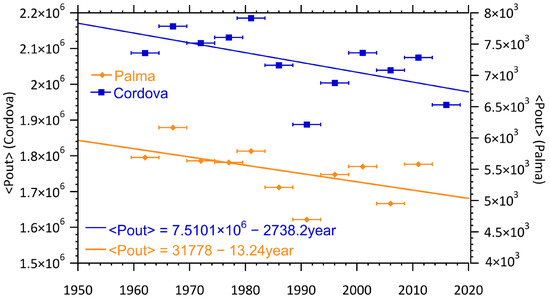
Figure 15.
Averaged power production at wind plants at Cordova and Palma de Mallorca. Units for averaged power production are kilowatts. Horizontal bars indicate interval over which the parameter was calculated.
Two very notable characteristics are seen: first, Cordova has more than two orders of magnitude more available wind power than Palma de Mallorca (in contrast to the available solar power); and second, there is a marked decreasing secular trend in available wind power at both locations. These two characteristics can explain the larger storage needs for Cordova and the weak trends in the storage. With greatly increased (orders of magnitude) power capacity, comes increased storage needs even with moderately smaller (factor of two) intermittency. Likewise, the trend of increasing variability (the intermittency) is masked by the trend in decreasing available power in the storage needs leading to the weak and highly variable increase in storage needs.
Finally, using our measure of the efficiency for renewable energy power plants MaxR/<E> we evaluate the “efficiency” of wind power at the two locations. Keep in mind that the lower this quantity is, the more “efficient” the system is in the sense that less energy storage is needed per power production unit. In Figure 16, we have plotted this quantity for both locations. It is clear from the figure that wind power in Cordova is a much more efficient power system with an average value of ~32 than wind in Palma de Mallorca with an average value of ~50. The very low efficiency of wind for Palma de Mallorca is due to both the larger intermittency and high variability, which makes it very costly from a storage perspective to get high reliability power from wind and the much lower available power.
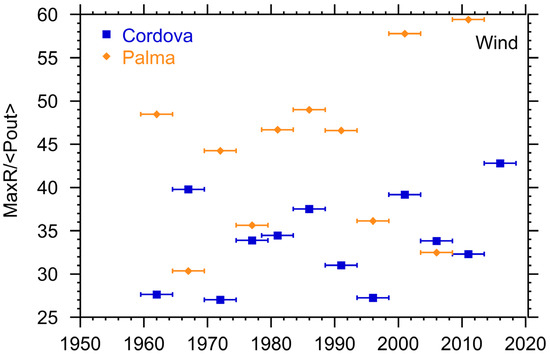
Figure 16.
Ratio of the energy storage needed to the average daily energy produced by wind plants in Cordova and Palma de Mallorca. MaxR/E is unitless. Horizontal bars indicate interval over which the parameter was calculated.
4. Discussion
Resilience and reliability [23,24,25] of the power systems are critical to the operation of modern society. As renewable energy sources increase their penetration in the power system the impact of their variability grows. As the magnitude and effects of climate change increase, many of the renewable resources (such as solar, hydro, and wind generation) will also be impacted both through the availability of the resources and the variability of those resources. In this paper we have done a preliminary analysis of the effects from climate change observed over the last 60 years for two locations. As mentioned in previous sections, this work is not meant to be a detailed analysis of the actual power conversion or storage which we do not include. Rather, it is an analysis of the available power and needed storage and the impact of climate change on those. We show the impact on precipitation (hydropower), surface solar radiation (solar power) and wind (wind power). The two locations we investigated, Cordova and Palma de Mallorca, were chosen because they are well separated in both distance and climate regions (polar versus subtropical). It was found that even over this limited time the effects of climate change can be seen in some of the characteristics we measured (but not in others) and there were fundamental differences in the impacts at the two locations. At both locations the storage needs increased with time for solar and weakly for wind but changed little for hydro. The efficiency (using storage needed per production unit as our measure of efficiency) of the hydropower and wind was much higher in Cordova than Palma de Mallorca but was reversed for solar power with Palma de Mallorca much higher efficiency than Cordova. The solar and hydro results are to be expected due to the nature of the weather at the two locations; however, the wind results were not as obvious a priori. This shows that this measure (or one like it) can be used to investigate the appropriate mix of renewable generation that makes the most sense at various locations. It is worth pointing out that currently there are no hydro plants on the Balearic Island though there was one that operated from 1908 until 1962.
In each of these measures the variability of the resource is an important component of the measure. However, the variability, which we characterized with the intermittency parameter, also has a large impact directly on grid reliability [13,14] as does the degree of distribution of the renewable resource. The intermittency parameter for the precipitation showed a small increase for Palma de Mallorca, a larger increase for Lake Oroville, and little change for Cordova. It showed little change for the solar radiation data but more of a secular increase for the wind data. Both the change over time of the intermittency parameter and the differences with location are very important for understanding risk (failure risk) for both transmission grids and microgrids, as the penetration of the high variability renewable electric power generation sources increases. The novel part of this work is threefold: first, it is the development of new metrics for impact based on both the intermittency of the variable of interest and following from that the storage needs; next is the application of these to two locations (plus partly to a third) as proof of the idea; then finally the results showing that climate change impacts on renewable resources vary significantly with location. This perhaps should be obvious but is often lost in the global impact discussion. These metrics form the structure for a framework that can quantify the impacts of climate and climate change on both transmission systems and microgrids. It importantly also points toward how one can mitigate the impacts with energy storage.
5. Conclusions
The work presented here is aimed at understanding the interaction between climate change and sustainable electrical energy production and transmission. This work describes a framework for understanding the local impacts of climate change on the different sources of renewable energy such as solar, wind and hydro. Three locations, spanning very different regions both spatially and climatologically, are used as examples of applying this framework. The locations studied here are: Cordova (Alaska), a northern coastal town; Oroville (California), an inland midlatitude town/reservoir impacted by its relative proximity to the Pacific coast; and finally, Palma de Mallorca, a community on an island in the Mediterranean with a hot Mediterranean climate. The most important two take-away messages from this work are as follows. First, climate change can have a significant impact on both the availability of different renewables and the variability of the resource. This can have a major influence on the needed local energy storage as well as the reliability of the transmission grid that utilizes the resource. Second, the world of climate impact is complicated. That trite statement is very important to keep in mind when trying to generalize from a particular case because the climate impacts are very location dependent. In some locations the resource can become both more available and less variable, for example hydro in Cordova and solar in Palma de Mallorca. In other locations it can be more available but more variable such as hydro in Lake Oroville. In yet other cases there can be less of the resource available and more variable for example perhaps solar in Cordova and wind in both locations. The availability of a given resource and the variability of that resource determine the storage needs, and the utility of a particular energy resource. Additionally, and importantly, the variability and amount of renewable penetration in the generation mix helps determine the transmission grid reliability. This new framework will allow for optimization of the renewable resource used and the storage supplied to the specific location including the impact of climate change in the planning. The next step in this work is to apply these methods to longer time series, more locations and future climate scenarios to quantify the impacts and risk in various locations as we move into the new climate conditions.
Author Contributions
The contributions to the manuscript were as follows: Conceptualization, B.A.C. and D.E.N.; methodology, U.S.B., B.A.C., J.M.R.B., D.E.N., P.C. and D.G.; software and validation, U.S.B., B.A.C., J.M.R.B., D.E.N., P.C. and D.G.; formal analysis and investigation, U.S.B., B.A.C., J.M.R.B., D.E.N., P.C. and D.G.; writing—original draft preparation, U.S.B., B.A.C. and D.E.N.; visualization U.S.B. and B.A.C.; and writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
P.C. and D.G. acknowledge financial support from Ministerio de Ciencia e Innovación (Spain), the Agencia Estatal de Investigación (AEI, Spain), and the Fondo Europeo de Desarrollo Regional (FEDER, EU) under grant PACSS (RTI2018-093732-B-C22) and the Maria de Maeztu program for Units of Excellence in R&D (MDM-2017-0711). D.N. gratefully acknowledges support from DOE Project GMLC 1.5.02—Resilient Alaskan Distribution system Improvements using Automation, Network analysis, Control, and Energy storage (RADIANCE). U.S.B. acknowledges support from the National Science Foundation under award #OIA-1753748 and by the State of Alaska for material which this work is based upon.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The raw data presented in this study are openly available in their respective repositories. NOAA Climate at a Glance data are available at: https://www.ncdc.noaa.gov/cag/ (accessed on 30 June 2022). The European Center Reanalysis version 5 is available at: https://cds.climate.copernicus.eu/ (accessed on 30 June 2022). Meteorological station data for Palma de Mallorca are available from the Agencia Estal de Meteorologia of Spain at: http://www.aemet.es/en/portada/ (accessed on 31 August 2021).
Acknowledgments
The results contain modified Copernicus Climate Change Service information 2021. Neither the European Commission nor ECMWF is responsible for any use that may be made of the Copernicus information or data it contains. Uranus, a supercomputer cluster located at Universidad Carlos III de Madrid (Spain) funded jointly by EU FEDER funds and by the Spanish Government via the National Research Project Nos. UNC313-4E-2361, ENE2009-12213-C03-03, ENE2012-33219, and ENE2012-31753 was used for this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wilbanks, T.; Bilello, D.; Schmalzer, D.; Scott, M. Climate Change and Energy Supply and Use: Technical Report for the U.S. Department of Energy in Support of the National Climate Assessment; Island Press: Washington, DC, USA, 2013. [Google Scholar]
- Gernaat, D.E.H.J.; de Boer, H.S.; Daioglou, V.; Yalew, S.G.; Müller, C.; van Vuuren, D.P. Climate change impacts on renewable energy supply. Nat. Clim. Chang. 2021, 11, 119–125. [Google Scholar] [CrossRef]
- Vavrus, S.J.; Bhatt, U.S.; Alexeev, V.A. Factors Influencing Simulated Changes in Future Arctic Cloudiness. J. Clim. 2011, 24, 4817–4830. [Google Scholar] [CrossRef]
- Lader, R.T.; Bhatt, U.S.; Walsh, J.E.; Bieniek, P.A. Downscaled projections of hydroclimatic extremes in Southeast Alaska. Earth Interact. 2022, 1–32. [Google Scholar] [CrossRef]
- Pryor, S.; Barthelmie, R. Climate change impacts on wind energy: A review. Renew. Sustain. Energy Rev. 2010, 14, 430–437. [Google Scholar] [CrossRef]
- Bathiany, S.; Dakos, V.; Scheffer, M.; Lenton, T.M. Climate models predict increasing temperature variability in poor countries. Sci. Adv. 2018, 4, eaar5809. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Knutti, R.; Lehner, F.; Deser, C.; Sanderson, B. Precipitation variability increases in a warmer climate. Sci. Rep. 2017, 7, 17966. [Google Scholar] [CrossRef]
- Vogel, M.M.; Hauser, M.; Seneviratne, S.I. Projected changes in hot, dry and wet extreme events clusters in CMIP6 multi-model ensemble. Environ. Res. Lett. 2020, 15, 094021. [Google Scholar] [CrossRef]
- Pes, M.P.; Pereira, E.B.; Marengo, J.A.; Martins, F.R.; Heinemann, D.; Schmidt, M. Climate trends on the extreme winds in Brazil. Renew. Energy 2017, 109, 110–120. [Google Scholar] [CrossRef]
- Day, J.J.; Hodges, K.I. Growing Land-Sea Temperature Contrast and the Intensification of Arctic Cyclones. Geophys. Res. Lett. 2018, 45, 3673–3681. [Google Scholar] [CrossRef]
- Feron, S.; Cordero, R.R.; Damiani, A.; Jackson, R.B. Climate change extremes and photovoltaic power output. Nat. Sustain. 2020, 4, 270–276. [Google Scholar] [CrossRef]
- Jing, R.; Wang, X.; Zhao, Y.; Zhou, Y.; Wu, J.; Lin, J. Planning urban energy systems adapting to extreme weather. Adv. Appl. Energy 2021, 3, 100053. [Google Scholar] [CrossRef]
- Newman, D.E.; Carreras, B.A.; Kirchner, M.; Dobson, I. The Impact of Distributed Generation on Power Transmission Grid Dynamics. In Proceedings of the 2011 44th Hawaii International Conference on System Sciences, Kauai, HI, USA, 4–7 January 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Carreras, B.A.; Colet, P.; Reynolds-Barredo, J.M.; Gomila, D. Resilience and performance of the power grid with high penetration of renewable energy sources. IEEE Access 2021, 9, 132663–132674. [Google Scholar] [CrossRef]
- Carreras, B.; Reynolds-Barredo, J.-M.; Newman, D.; Dobson, I. The Impact of Incorporating Wind Energy in the Electric Grid. In Proceedings of the 53rd Hawaii International Conference on System Sciences, Maui, HI, USA, 7–10 January 2020. [Google Scholar]
- Carreras, B.; Barredo, J.M.R.; Newman, D.E. Optimizing the Impact of Incorporating Wind Energy on the Electric Grid. J. Strat. Innov. Sustain. 2020, 15, 27–42. [Google Scholar] [CrossRef]
- Dalala, Z.; Al-Omari, M.; Al-Addous, M.; Bdour, M.; Al-Khasawneh, Y.; Alkasrawi, M. Increased renewable energy penetration in national electrical grids constraints and solutions. Energy 2022, 246, 123361. [Google Scholar] [CrossRef]
- Solaun, K.; Cerdá, E. Climate change impacts on renewable energy generation. A review of quantitative projections. Renew. Sustain. Energy Rev. 2019, 116, 109415. [Google Scholar] [CrossRef]
- Yalew, S.G.; van Vliet, M.T.; Gernaat, D.E.H.J.; Ludwig, F.; Miara, A.; Park, C.; Byers, E.; De Cian, E.; Piontek, F.; Iyer, G.; et al. Impacts of climate change on energy systems in global and regional scenarios. Nat. Energy 2020, 5, 794–802. [Google Scholar] [CrossRef]
- Stott, P.A.; Gillett, N.P.; Hegerl, G.C.; Karoly, D.J.; Stone, D.A.; Zhang, X.; Zwiers, F. Detection and attribution of climate change: A regional perspective. WIREs Clim. Chang. 2010, 1, 192–211. [Google Scholar] [CrossRef]
- NOAA National Centers for Environmental Information, Climate at a Glance: Global Mapping. Available online: :https://www.ncdc.noaa.gov/cag/ (accessed on 3 June 2021).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Carreras, B.A.; Newman, D.E.; Dobson, I. North American Blackout Time Series Statistics and Implications for Blackout Risk. IEEE Trans. Power Syst. 2016, 31, 4406–4414. [Google Scholar] [CrossRef]
- Carreras, B.A.; Newman, D.E.; Dobson, I. Does size matter? Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 023104. [Google Scholar] [CrossRef]
- Newman, D.; Carreras, B.; Degala, N.; Dobson, I. Risk Metrics for Dynamic Complex Infrastructure Systems Such as the Power Transmission Grid. In Proceedings of the 2012 45th Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2012; pp. 2082–2090. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 1987, 59, 1424–1427. [Google Scholar] [CrossRef] [PubMed]
- Meneveau, C.; Sreenivasan, K.R. The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 1991, 224, 429–484. [Google Scholar] [CrossRef]
- Carreras, B.A.; Lynch, V.; Newman, D.E.; Balbin, R.; Bleuel, J.; Pedrosa, M.A.; Endler, M.; van Milligen, B.; Sánchez, E.; Hidalgo, C. Intermittency of plasma edge fluctuation data: Multifractal analysis. Phys. Plasmas 2000, 7, 3278–3287. [Google Scholar] [CrossRef]
- Hentschel, H.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Phys. D Nonlinear Phenom. 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Bekryaev, R.V.; Polyakov, I.V.; Alexeev, V. Role of Polar Amplification in Long-Term Surface Air Temperature Variations and Modern Arctic Warming. J. Clim. 2010, 23, 3888–3906. [Google Scholar] [CrossRef]
- Agencia Estal de Meteorologia: AEMET. Available online: http://www.aemet.es/en/portada (accessed on 20 August 2021).
- Zakeri, G. Potential Impact of Climate Change on the New Zealand Electricity Market. In Proceedings of the 53rd Hawaii International Conference on System Sciences, Maui, HI, USA, 7–10 January 2020. [Google Scholar]
- Swain, D.L.; Langenbrunner, B.; Neelin, J.D.; Hall, A. Increasing precipitation volatility in twenty-first-century California. Nat. Clim. Chang. 2018, 8, 427–433. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).