Determination of Soil Hydraulic Properties from Infiltration Data Using Various Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Porous Media
2.2. Approaches to Estimate S and Ks from One-Dimensional (1D) Infiltration Experiments
2.2.1. Nonlinear Optimization Method Using the Solver Application in Excel
- (1)
- Green and Ampt [3]:
- (2)
- Talsma and Parlange [5]:
- (3)
- Haverkamp et al. [8] presented a quasi-exact analytical solution of the Richards [1] equation for 1D cumulative infiltration, i, which was firstly proposed by Parlange et al. [6] and redefined later by Haverkamp et al. [7]:where Κi and Κs are the hydraulic conductivities corresponding to the initial water content θi and water content at saturation θs, respectively, and β is an integral shape parameter that ranges between 0.3 and 2 for sand to clay soils [11,19].
- (4)
- For short and intermediate infiltration times and Ki = 0, Equation (3) can be simplified as the following two-term approximate expansion [8]:
- (5)
- (6)
- Valiantzas [9]:
2.2.2. Linearization Approach
2.2.3. Latorre et al. Approach (NSH Method)
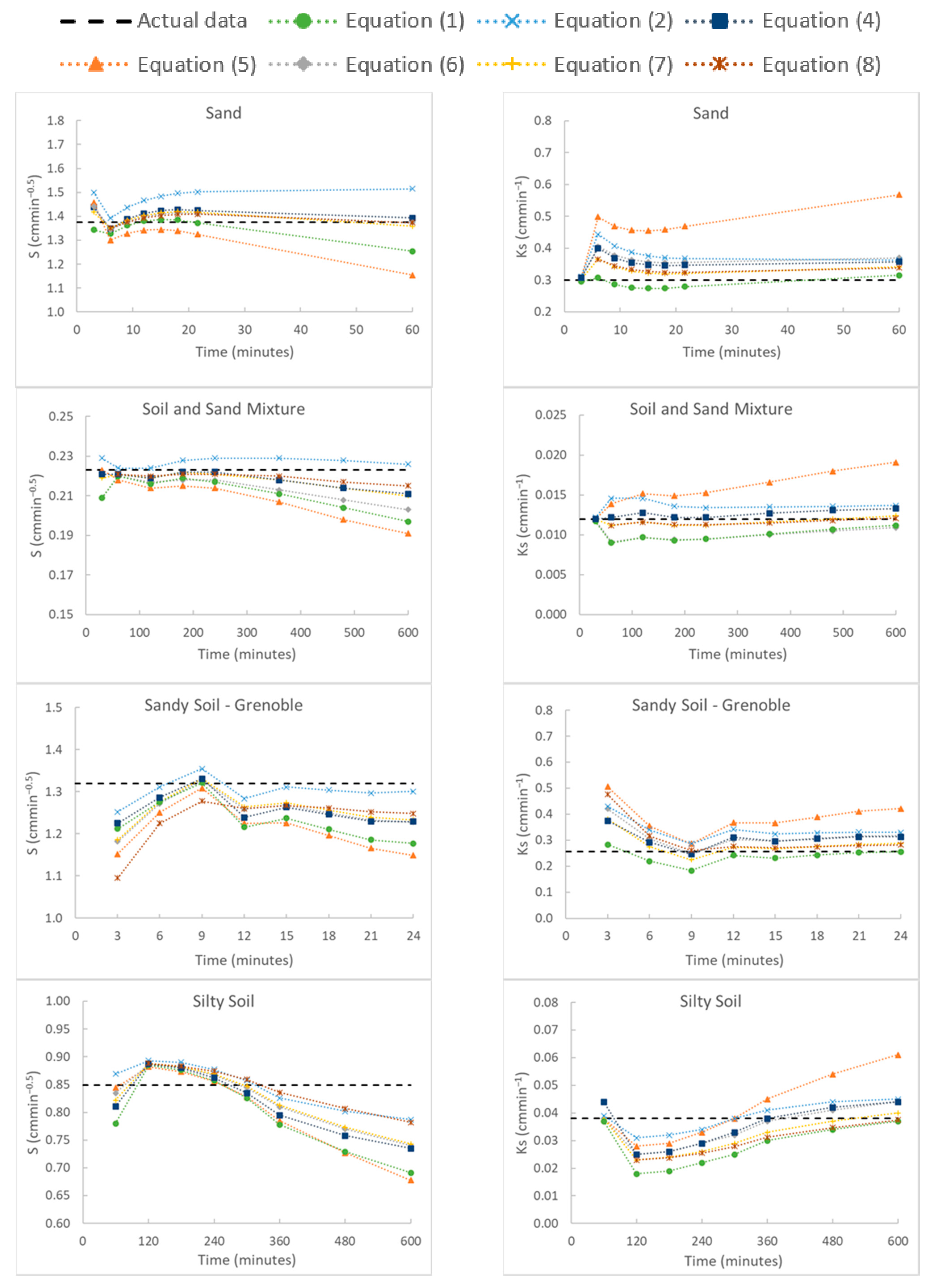
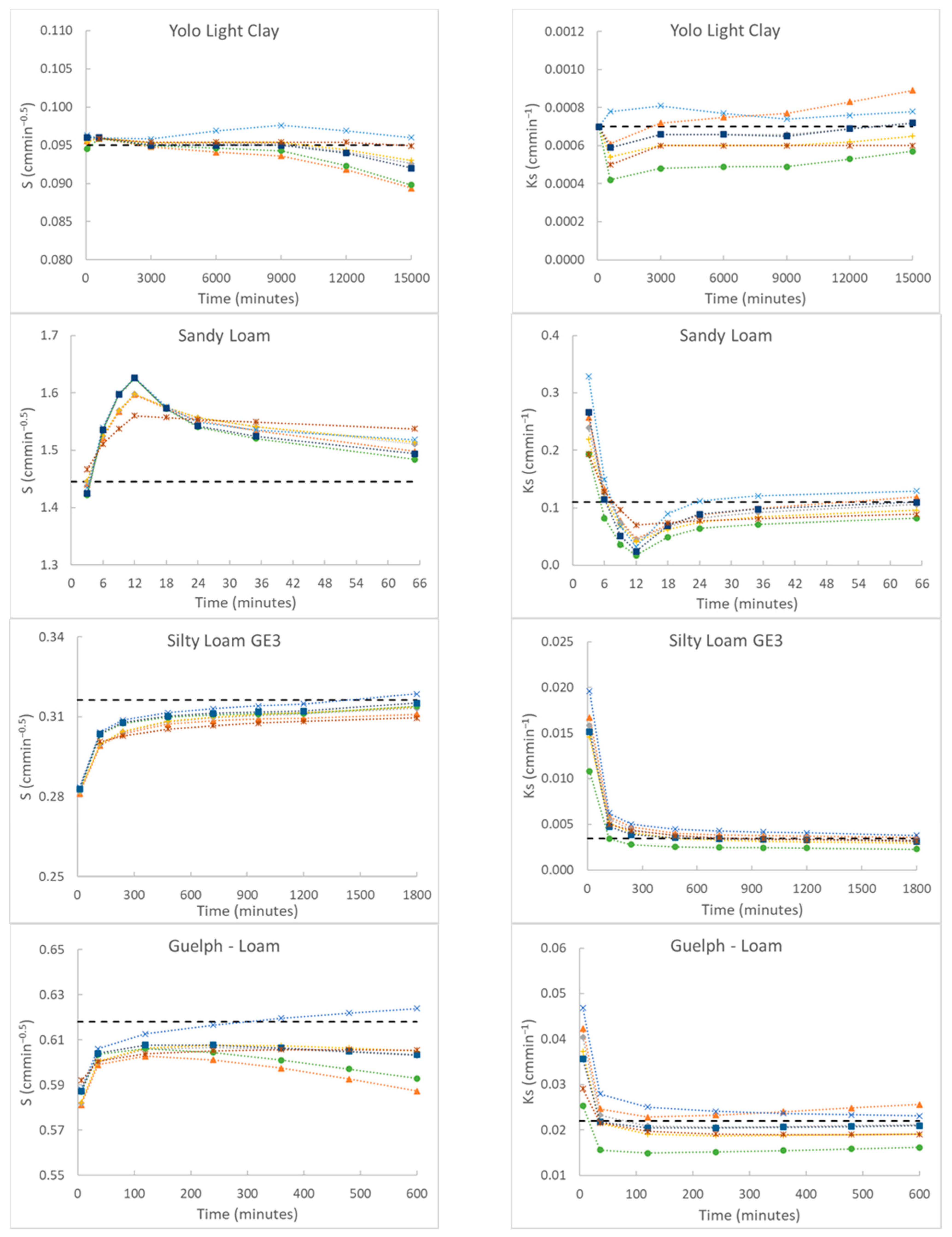
2.3. The Effect of Infiltration Time on the Estimation of S and Ks by the Various Methods Used
2.4. Statistical Analysis
3. Results and Discussion
3.1. Results from Nonlinear Optimization for Estimation of S and Ks Parameters
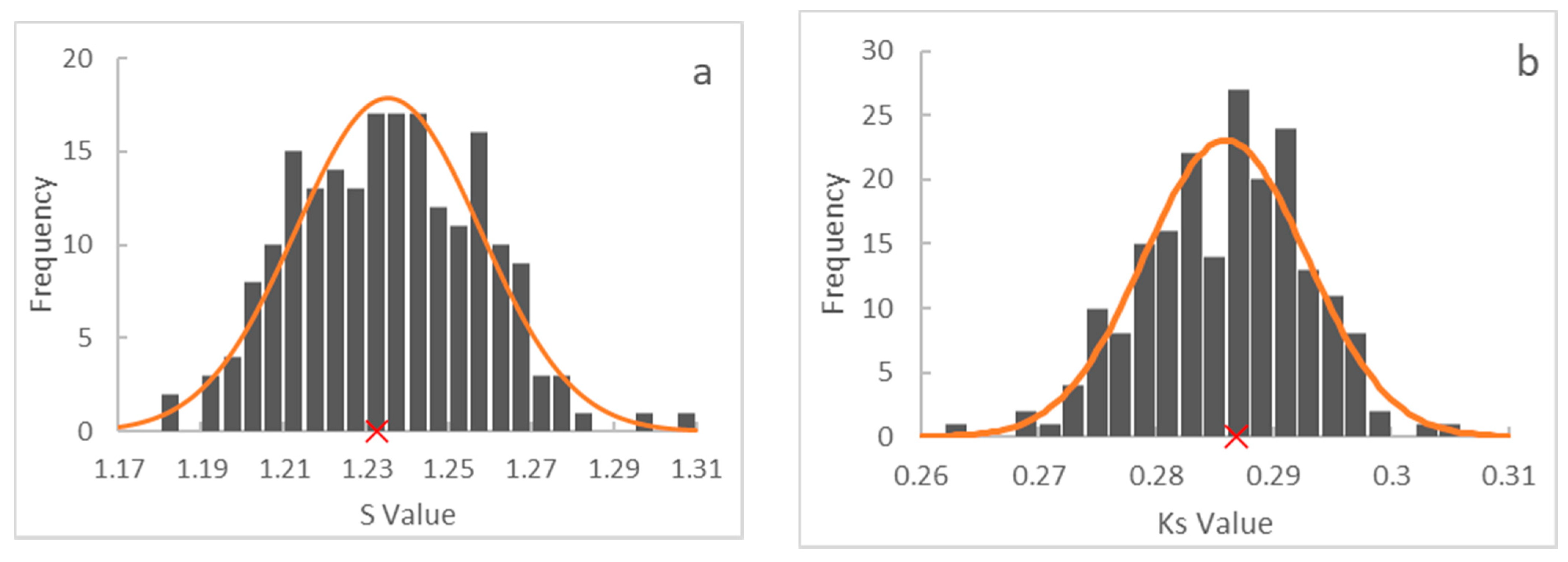
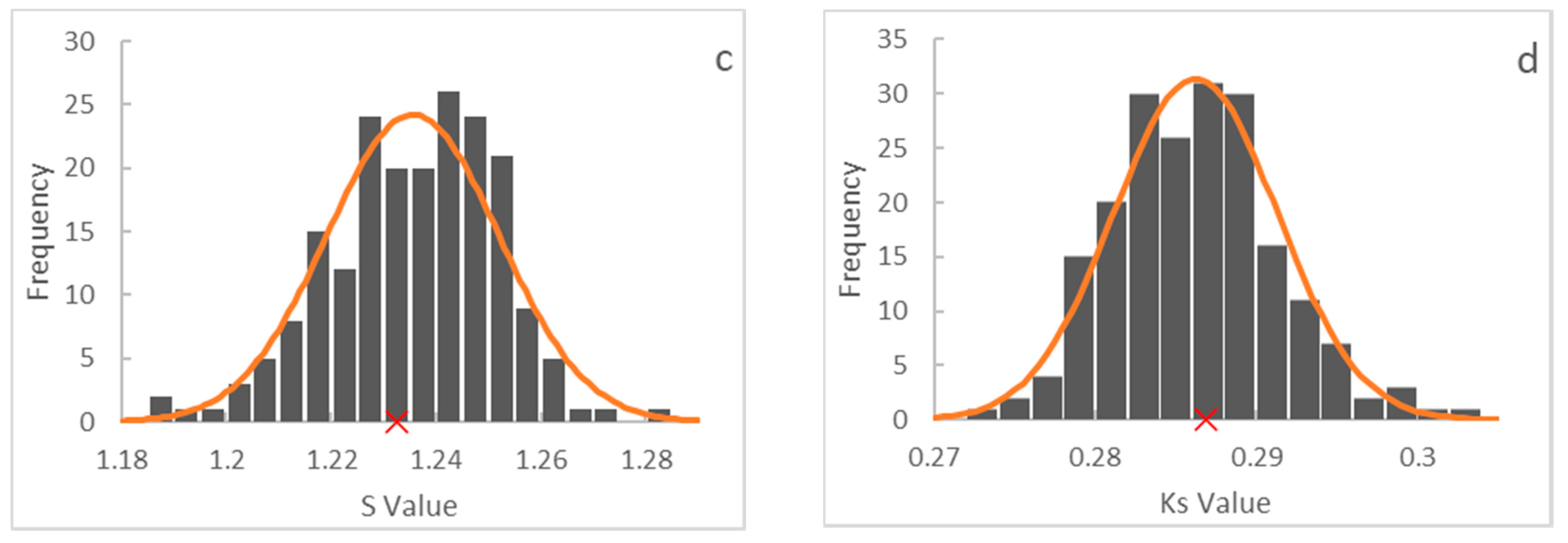
3.2. Results from the Latorre et al. Approach for S and Ks Estimation
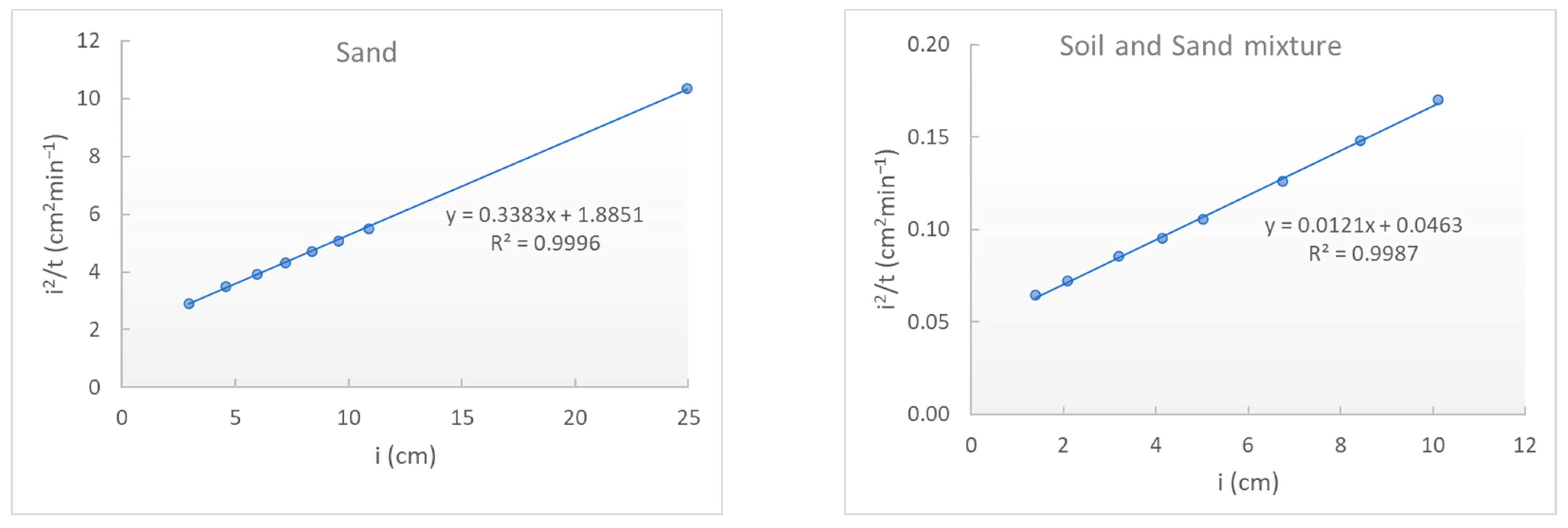
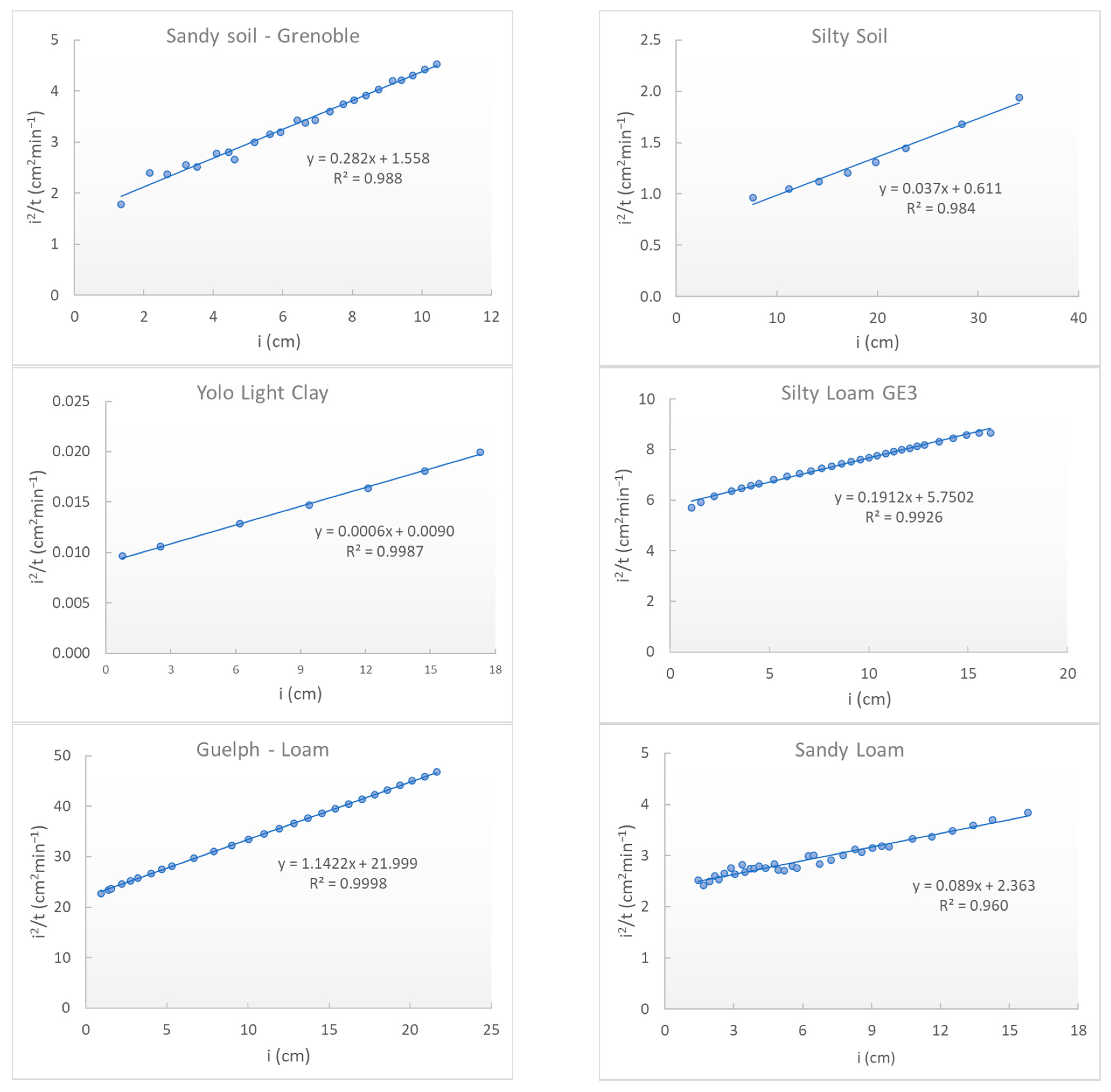
3.3. Results from the Linearization Method with Valiantzas Equation
3.4. Fixed β = 0.6 vs. Variable β Generated from Nonlinear Optimization Equations
3.5. Evaluation of S and Ks through Time from Nonlinear Optimization and Linear Equation of Valiantzas
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Kargas, G.; Londra, P.A. Effect of tillage practices on hydraulic properties of a loamy soil. Desalin. Water Treat. 2015, 54, 2138–2146. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on Soil Physics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Talsma, T.; Parlange, J.-Y. One-dimensional vertical infiltration. Aust. J. Soil Res. 1972, 10, 143. [Google Scholar] [CrossRef]
- Parlange, J.Y.; Lisle, I.; Braddock, R.D.; Smith, R.E. The three-parameter infiltration equation. Soil Sci. 1982, 133, 337–341. [Google Scholar] [CrossRef]
- Haverkamp, R.; Parlange, J.Y.; Starr, J.L.; Schmitz, G.; Fuentes, C. Infiltration under ponded conditions: 3. A predictive equation based on physical parameters. Soil Sci. 1990, 149, 292–300. [Google Scholar] [CrossRef]
- Haverkamp, R.; Ross, P.J.; Smettem, K.R.J.; Parlange, J.Y. Three-dimensional analysis of infiltration from the disc infiltrometer: 2. Physically based infiltration equation. Water Resour. Res. 1994, 30, 2931–2935. [Google Scholar] [CrossRef] [Green Version]
- Valiantzas, J.D. New linearized two-parameter infiltration equation for direct determination of conductivity and sorptivity. J. Hydrol. 2010, 384, 1–13. [Google Scholar] [CrossRef]
- Kargas, G.; Londra, P.A. Comparison of two-parameter vertical ponded infiltration equations. Environ. Model. Assess. 2021, 26, 179–186. [Google Scholar] [CrossRef]
- Jaiswal, P.; Gao, Y.; Rahmati, M.; Vanderborght, J.; Šimůnek, J.; Vereecken, H.; Vrugt, J.A. Parasite inversion for determining the coefficients and time-validity of Philip’s two-term infiltration equation. Vadose Zone J. 2022, 21, e20166. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gao, Y. On the three-parameter infiltration equation of Parlange et al. (1982): Numerical solution, experimental design, and parameter estimation. Vadose Zone J. 2022, 21, e20167. [Google Scholar] [CrossRef]
- Vandervaere, J.P.; Vauclin, M.; Elrick, D.E. Transient flow from tension infiltrometers I. The two-parameter equation. Soil Sci. Soc. Am. J. 2000, 64, 1263–1272. [Google Scholar] [CrossRef] [Green Version]
- Angulo-Jaramillo, R.; Bagarello, V.; Iovino, M.; Lassabatere, L. Infiltration Measurements for Soil Hydraulic Characterization; Springer International Publishing: Cham, Switzerland, 2016; pp. 193–218. [Google Scholar]
- Smiles, D.E.; Knight, J.H. A note on the use of the Philip infiltration equation. Soil Res. 1976, 14, 103–108. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T. Estimating unsaturated soil hydraulic properties from tension disc infiltrometer data by numerical inversion. Water Resour. Res. 1996, 32, 2683–2696. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Gribb, M.M.; Hopmans, J.W. Parameter estimation of unsaturated soil hydraulic properties from transient flow processes. Soil Tillage Res. 1998, 47, 27–36. [Google Scholar] [CrossRef]
- Šimůnek, J.; Hopmans, J.W. Parameter Optimization and Nonlinear Fitting. In Methods of Soil Analysis, Part 4: Physical Methods; Soil Science Society of America, Inc.: Madison, WI, USA, 2018; pp. 139–157. [Google Scholar]
- Lassabatere, L.; Angulo-Jaramillo, R.; Soria-Ugalde, J.M.; Šimůnek, J.; Haverkamp, R. Numerical evaluation of a set of analytical infiltration equations. Water Resour. Res. 2009, 45, W12415. [Google Scholar] [CrossRef] [Green Version]
- Latorre, B.; Peña, C.; Lassabatere, L.; Angulo-Jaramillo, R.; Moret-Fernández, D. Estimate of soil hydraulic properties from disc infiltrometer three-dimensional infiltration curve. Numerical analysis and field application. J. Hydrol. 2015, 527, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Rahmati, M.; Vanderborght, J.; Simunek, J.; Vrugt, J.A.; Moret-Fernández, D.; Latorre, B.; Lassabatere, L.; Vereecken, H. Soil hydraulic properties estimation from one-dimensional infiltration experiments using characteristic time concept. Vadose Zone J. 2020, 19, e20068. [Google Scholar] [CrossRef]
- Rahmati, M.; Latorre, B.; Lassabatere, L.; Angulo-Jaramillo, R.; Moret-Fernández, D. The relevance of Philip theory to Haverkamp quasi-exact implicit analytical formulation and its uses to predict soil hydraulic properties. J. Hydrol. 2019, 570, 816–826. [Google Scholar] [CrossRef]
- Latorre, B.; Moret-Fernández, D.; Lassabatere, L.; Rahmati, M.; López, M.V.; Angulo-Jaramillo, R.; Comin, F.; Sorando, R.; Jiménez, J.J. Influence of the β parameter of the Haverkamp model on the transient soil water infiltration curve. J. Hydrol. 2018, 564, 222–229. [Google Scholar] [CrossRef]
- Clothier, B.E.; Scotter, D. Unsaturated water transmission parameters obtained from infiltration. In Methods of Soil Analysis: Part 4. Physical Methods; Dane, J.H., Topp, G.C., Eds.; SSSA Book Series 5; SSSA: Madison, WI, USA, 2002; pp. 879–888. [Google Scholar]
- Haverkamp, R.; Kutilek, M.; Parlange, J.Y.; Rendon, L.; Krejca, M. Infiltration under ponded conditions: 2. infiltration equations tested for parameter time-dependence and predictive use. Soil Sci. 1988, 145, 317–329. [Google Scholar] [CrossRef]
- Poulovassilis, A.; Elmaloglou, S.; Kerkides, P.; Argyrokastritis, I. A variable sorptivity infiltration equation. Water Resour. Manag. 1989, 3, 287–298. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Šimůnek, J.; Angulo-Jaramillo, R.; Schaap, M.G.; Vandervaere, J.P.; Van Genuchten, M.T. Using an inverse method to estimate the hydraulic properties of crusted soils from tension-disc infiltrometer data. Geoderma 1998, 86, 61–81. [Google Scholar] [CrossRef]
- Wraith, J.M.; Or, D. Nonlinear parameter estimation using spreadsheet software. J. Nat. Resour. Life Sci. Educ. 1998, 27, 13–19. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. Revue française d’automatique, informatique, recherche opérationnelle. Rech. Opérationnelle 1974, 8, 73–103. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Xie, J.; Chau, H.W.; Si, B.C. Evaluation of parameter uncertainties in nonlinear regression using Microsoft Excel Spreadsheet. Environ. Syst. Res. 2015, 4, 4. [Google Scholar] [CrossRef] [Green Version]
| Soil | H (cm) | S (cm min−0.5) | Ks (cm min−1) |
|---|---|---|---|
| Sand (Poulovassilis et al. [26]) | 0 | 1.375 | 0.3 |
| Soil and Sand mixture (Poulovassilis et al. [26]) | 0 | 0.223 | 0.012 |
| Sandy Soil—Grenoble (Haverkamp et al. [25]) | 2.25 | 1.319 | 0.255 |
| Silty Soil (Poulovassilis et al. [26]) | 0 | 0.849 | 0.038 |
| Yolo Light Clay (Poulovassilis et al. [26]) | 0 | 0.095 | 0.0007 |
| Silty Loam GE3 (van Genuchten [27]) | 0 | 0.3162 | 0.0034 |
| Guelph—loam (van Genuchten [27]) | 0 | 0.6181 | 0.0219 |
| Sandy Loam | 3 | 1.445 | 0.11 |
| Soil | Equation (1) with Solver | Equation (2) with Solver | Equation (4) with Solver | |||
| S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | |
| Sand | 1.254 | 0.315 | 1.515 | 0.363 | 1.393 | 0.358 |
| Soil and Sand mixture | 0.197 | 0.011 | 0.226 | 0.0137 | 0.211 | 0.0133 |
| Sandy Soil—Grenoble | 1.177 | 0.255 | 1.301 | 0.33 | 1.229 | 0.313 |
| Silty Soil | 0.691 | 0.037 | 0.787 | 0.045 | 0.735 | 0.044 |
| Yolo Light Clay | 0.09 | 0.00057 | 0.096 | 0.00078 | 0.092 | 0.00072 |
| Silty Loam GE3 | 0.314 | 0.0023 | 0.319 | 0.0038 | 0.315 | 0.0031 |
| Guelph—loam | 0.593 | 0.0162 | 0.624 | 0.0231 | 0.6034 | 0.0209 |
| Sandy Loam | 1.484 | 0.082 | 1.518 | 0.129 | 1.494 | 0.11 |
| Soil | Equation (5) with Solver | Equation (6) with Solver | Equation (7) with Solver | |||
| S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | |
| Sand | 1.154 | 0.568 | 1.374 | 0.37 | 1.359 | 0.341 |
| Soil and Sand mixture | 0.191 | 0.0191 | 0.203 | 0.0109 | 0.21 | 0.0124 |
| Sandy Soil—Grenoble | 1.149 | 0.422 | 1.228 | 0.318 | 1.233 | 0.287 |
| Silty Soil | 0.678 | 0.061 | 0.74 | 0.044 | 0.743 | 0.04 |
| Yolo Light Clay | 0.0894 | 0.00089 | 0.0926 | 0.00072 | 0.093 | 0.00065 |
| Silty Loam GE3 | 0.311 | 0.0036 | 0.313 | 0.0032 | 0.314 | 0.003 |
| Guelph—loam | 0.587 | 0.0256 | 0.603 | 0.0211 | 0.605 | 0.0191 |
| Sandy Loam | 1.498 | 0.119 | 1.511 | 0.106 | 1.514 | 0.096 |
| Soil | Equation (8) (Linearization) | Latorre et al. Approach | Actual Data | |||
| S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | |
| Sand | 1.373 | 0.3383 | 1.946 | 0.2874 | 1.375 2 | 0.3 2 |
| Soil and Sand mixture | 0.215 | 0.0121 | 0.214 | 0.0131 | 0.223 2 | 0.012 2 |
| Sandy Soil—Grenoble | 1.248 | 0.282 | 1.225 | 0.315 | 1.319 1 | 0.255 1 |
| Silty Soil | 0.782 | 0.037 | 0.7186 | 0.0445 | 0.849 1 | 0.038 1 |
| Yolo Light Clay | 0.0949 | 0.0006 | 0.093 | 0.0007 | 0.095 2 | 0.0007 2 |
| Silty Loam GE3 | 0.31 | 0.0032 | 0.3122 | 0.0033 | 0.316 2 | 0.0034 2 |
| Guelph—loam | 0.606 | 0.019 | 0.6042 | 0.0208 | 0.618 2 | 0.0219 2 |
| Sandy Loam | 1.537 | 0.089 | 1.481 | 0.115 | 1.445 1 | 0.11 1 |
| RE (%) | ||||||
| Soil | Equation (1) with Solver | Equation (2) with Solver | Equation (4) with Solver | |||
| S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | S (cm min−0.5) | Ks (cm min−1) | |
| Sand | −8.77 | 5.12 | 10.15 | 20.98 | 1.32 | 19.27 |
| Soil and Sand mixture | −11.46 | −6.53 | 1.52 | 14.43 | −5.39 | 11.00 |
| Sandy Soil—Grenoble | −10.79 | −0.05 | −1.35 | 29.23 | −6.86 | 22.87 |
| Silty Soil | −18.55 | −3.89 | −7.25 | 19.00 | −13.46 | 15.08 |
| Yolo Light Clay | −5.46 | −19.27 | 1.00 | 11.22 | −3.13 | 2.75 |
| Silty Loam GE3 | −0.63 | −32.35 | 0.82 | 11.76 | −0.32 | −8.82 |
| Guelph—loam | −4.08 | −26.03 | 0.94 | 5.48 | −2.38 | −4.57 |
| Sandy Loam | 2.71 | −25.29 | 5.07 | 17.32 | 3.36 | 0.40 |
| Soil | Equation (5) with Solver | Equation (6) with Solver | Equation (7) with Solver | |||
| S (cmmin−0.5) | Ks (cmmin−1) | S (cmmin−0.5) | Ks (cmmin−1) | S (cmmin−0.5) | Ks (cmmin−1) | |
| Sand | −16.07 | 89.46 | −0.04 | 23.33 | −1.15 | 13.61 |
| Soil and Sand mixture | −14.52 | 59.29 | −8.84 | −9.36 | −5.63 | 3.02 |
| Sandy Soil—Grenoble | −12.91 | 65.65 | −6.91 | 24.75 | −6.55 | 12.50 |
| Silty Soil | −20.10 | 60.01 | −12.80 | 16.32 | −12.49 | 5.05 |
| Yolo Light Clay | −5.91 | 27.60 | −2.54 | 2.62 | −2.14 | −7.51 |
| Silty Loam GE3 | −1.58 | 5.88 | −0.95 | −5.88 | −0.70 | −11.76 |
| Guelph—loam | −4.98 | 16.89 | −2.44 | −3.65 | −2.10 | −12.79 |
| Sandy Loam | 3.67 | 8.20 | 4.60 | −3.93 | 4.79 | −12.67 |
| Soil | Equation (8) (Linearization) | Latorre et al. Approach | ||||
| S (cm min−0.5) | Ks (cmmin−1) | S (cm min−0.5) | Ks (cm min−1) | |||
| Sand | −0.15 | 12.77 | 41.53 | −4.20 | ||
| Soil and Sand mixture | −3.59 | 0.83 | −4.04 | 9.50 | ||
| Sandy Soil—Grenoble | −5.38 | 10.59 | −7.13 | 23.53 | ||
| Silty Soil | −7.89 | −2.63 | −15.36 | 17.00 | ||
| Yolo Light Clay | −0.11 | −14.29 | −2.11 | 0.29 | ||
| Silty Loam GE3 | −1.90 | −5.88 | −1.20 | −2.94 | ||
| Guelph—loam | −2.04 | −13.24 | −2.25 | −5.02 | ||
| Sandy Loam | 6.37 | −19.09 | 2.49 | 4.55 | ||
| Soil | Equation (4) with Solver | Equation (5) with Solver | Equation (6) with Solver | ||||||
|---|---|---|---|---|---|---|---|---|---|
| β | S (cm min−0.5) | Ks (cm min−1) | β | S (cm min−0.5) | Ks (cm min−1) | β | S (cm min−0.5) | Ks (cm min−1) | |
| Sand | 0.808 | 1.458 | 0.361 | 0.439 | 1.154 | 0.51 | 0.914 | 1.446 | 0.395 |
| Soil and Sand mixture | 1.215 | 0.234 | 0.0139 | 0.508 | 0.191 | 0.0179 | 1.286 | 0.232 | 0.0153 |
| Sandy Soil—Grenoble | 1.146 | 1.329 | 0.333 | 0.504 | 1.149 | 0.395 | 1.321 | 1.337 | 0.368 |
| Silty Soil | 4.39 | 1.116 | 0.047 | 0.542 | 0.678 | 0.058 | 2.532 | 0.98 | 0.042 |
| Yolo Light Clay | 1.401 | 0.1 | 0.00081 | 0.566 | 0.0894 | 0.00087 | 1.340 | 0.0984 | 0.00088 |
| Silty Loam GE3 | 0.013 | 0.314 | 0.0023 | 0.591 | 0.311 | 0.0036 | 0.0138 | 0.3126 | 0.0024 |
| Guelph—loam | 0.764 | 0.6107 | 0.022 | 0.590 | 0.5873 | 0.0254 | 0.851 | 0.6096 | 0.0235 |
| Sandy Loam | 1.502 | 1.571 | 0.146 | 0.583 | 1.498 | 0.118 | 1.680 | 1.586 | 0.158 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kargas, G.; Koka, D.; Londra, P.A. Determination of Soil Hydraulic Properties from Infiltration Data Using Various Methods. Land 2022, 11, 779. https://doi.org/10.3390/land11060779
Kargas G, Koka D, Londra PA. Determination of Soil Hydraulic Properties from Infiltration Data Using Various Methods. Land. 2022; 11(6):779. https://doi.org/10.3390/land11060779
Chicago/Turabian StyleKargas, George, Dimitrios Koka, and Paraskevi A. Londra. 2022. "Determination of Soil Hydraulic Properties from Infiltration Data Using Various Methods" Land 11, no. 6: 779. https://doi.org/10.3390/land11060779
APA StyleKargas, G., Koka, D., & Londra, P. A. (2022). Determination of Soil Hydraulic Properties from Infiltration Data Using Various Methods. Land, 11(6), 779. https://doi.org/10.3390/land11060779








