Abstract
This study modelled the relationships between vegetation response and available water below the soil surface using Terra’s moderate resolution imaging spectroradiometer (MODIS), Normalised Difference Vegetation Index (NDVI), and soil water content (SWC). The Soil & Water Assessment Tool (SWAT) interface known as ArcSWAT was used in ArcGIS for the groundwater analysis. The SWAT model was calibrated and validated in SWAT-CUP software using 10 years (2001–2010) of monthly streamflow data. The average Nash-Sutcliffe efficiency during the calibration and validation was 0.54 and 0.51, respectively, indicating that the model performances were good. Nineteen years (2002–2020) of monthly MODIS NDVI data for three different types of vegetation (forest, shrub, and grass) and soil water content for 43 sub-basins were analysed using the WEKA, machine learning tool with a selection of two supervised machine learning algorithms, i.e., support vector machine (SVM) and random forest (RF). The modelling results show that different types of vegetation response and soil water content vary in the dry and wet seasons. For example, the model generated high positive relationships (r = 0.76, 0.73, and 0.81) between the measured and predicted NDVI values of all vegetation in the sub-basin against the groundwater flow (GW), soil water content (SWC), and combination of these two variables, respectively, during the dry season. However, these relationships were reduced by 36.8% (r = 0.48) and 13.6% (r = 0.63) against GW and SWC, respectively, in the wet season. Our models also predicted that vegetation in the top location (upper part) of the sub-basin is highly responsive to GW and SWC (r = 0.78, and 0.70) during the dry season. Although the rainfall pattern is highly variable in the study area, the summer rainfall is very effective for the growth of the grass vegetation type. The results predicted that the growth of vegetation in the top-point location is highly dependent on groundwater flow in both the dry and wet seasons, and any instability or long-term drought can negatively affect these floodplain vegetation communities. This study has enriched our knowledge of vegetation responses to groundwater in each season, which will facilitate better floodplain vegetation management.
1. Introduction
Floodplain vegetation plays an important role in catchment hydrology and energy flow. Floodplain vegetation distribution is directly influenced by several factors, including rainfall, temperature, and groundwater [1]. Rainfall, temperature, and groundwater are highly variable in arid and semi-arid regions [2]. The annual rainfall in arid regions is much less than the annual potential evapotranspiration and surface water flows (i.e., surface runoff), which provides limited water supply for vegetation systems [3]. Therefore, groundwater becomes the only water source in arid regions affecting the spatial and temporal distribution of soil water content (SWC) which, in turn, affects the growth of vegetation [4]. An accurate understanding of the distribution of SWC in arid regions is important since water deficit is gradually becoming one of the major factors limiting agricultural productivity and ecological development [5]. As one of the driest continents in the world, Australia has been facing severe droughts over the last 50 years, noticeably in the south-eastern part of the country [6]. This area will become drier in the coming decades due to increasing annual average temperatures and decreasing rainfall [7]. Therefore, understanding the vegetation response to SWC is critical for sustainable ecosystem improvements in arid regions [8].
SWC can be estimated using both direct and indirect methods. The direct method, such as the oven drying technique, is widely used because of its reliability and simplicity [9]; however, the direct method is labour-intensive, time-consuming, and costly for continuous application in large catchments. On the other hand, hydrological simulation and remote sensing techniques can be used for the same purpose at a catchment or global scale [10]. SWC can also be estimated for previous years using remote sensing techniques, which is not possible to obtain from experimental measurements [10]. Therefore, model-simulated results can fulfil temporal and spatial data requirements and improve SWC and vegetation response relationship studies.
The SWC also influences vegetation productivity and water stress [11,12]. The amount of soil water availability in drought regions for vegetation intake affects the length of the growing period [13]. However, groundwater is the main source of water for vegetation growth in arid regions [14]. Any changes in the groundwater tables decrease the accessibility of the dependent vegetation and may create water stress [15]. Moreover, water stress can trigger a longer growing period and photosynthesis reduction, thereby resulting in reduced productivity and increased vegetation mortality [12]. The reduction in accessible soil water availability under a changing climate may exaggerate ecological droughts during the plantation season [16]. Researchers have identified that the change in groundwater depth affects the vegetation physiology and dynamics [17,18]. Another study also focused on individual vegetation responses by examining the leaf, tree, canopy, and population [19]. However, according to our knowledge, accessible water in soil and vegetation response modelling is still lacking. This research focuses on SWC that is accessible to floodplain vegetation and understanding their relationship in a seasonal context.
The Soil and Water Assessment Tool (SWAT) is a physically based and semi-distributed hydrological model widely used for quantitative hydrological modelling [20,21]. Many researchers have used SWAT for evaluating soil water at the catchment scale [22,23,24]. Previous studies have shown that changes in the water balance components, specifically soil water storage, evapotranspiration, land use/land cover dynamics, and water yield, are more sensitive under wet climate and heterogeneous soils [25,26]. The SWAT model has also been successfully applied in the U.S. to estimate SWC for drought monitoring and predicting crop production [27]. However, the SWAT application in the Australian region is limited [28]. In our study, a SWAT model was used to estimate SWC for the Burrinjuck Dam sub-catchment within the Murrumbidgee River catchment. The suitability of the model simulation for long-term SWC datasets was assessed using a combination of physically measured and remotely sensed data. This type of simulation helps to correlate with long-term historical vegetation data.
The Normalised Difference Vegetation Index (NDVI), which can be derived from remote sensing, is frequently applied for studies on vegetation dynamics over large scales [29,30,31,32]. Researchers used NDVI to understand the relationships between terrestrial vegetation and climate [31]. Several studies found a linear relationship between NDVI and climate variables in arid regions [33,34,35]. Relationships also were investigated for NDVI and groundwater levels and groundwater flow discharge [36,37,38]. However, none of these previous studies analysed the relationship between NDVI and hydrological model simulated SWC in an arid region.
This study aims to analyse and model the relationships between seasonal SWC variability and floodplain vegetation responses using MODIS-derived NDVI data and machine learning algorithms for 20 years (2001–2020). The specific objectives of this study are the following: (a) to understand the relationship between different types of vegetation responses (NDVI) and groundwater variables as simulated by the SWAT model at the basin level; (b) to assess the correlation between the vegetation response (as measured by NDVI) and SWAT-simulated variables at different positions (top and bottom) within the sub-basin; and (c) to model seasonal vegetation responses to groundwater variables at the basin level using the WEKA machine learning tool developed by the University of Waikato, New Zealand [39,40].
The WEKA tool is a collection of machine learning algorithms for data mining activities that supports data pre-processing, clustering, classification, regression, and visualization [41]. This software can be run under the General Public License (GNU) with a selected classifier compared to other data mining tools [42].
The results of this study provide qualitative information on catchment hydrology and water resources on temporal and spatial dimensions at the sub-catchment level. A calibrated model at this scale can be used for various analyses such as sedimentation, water pollution, and future stream flow prediction. This study also contributes to developing sustainable water resource management for the dry and wet season in an efficient way. The modelling results may be used to improve domestic agricultural production by selecting appropriate crops and plants that can grow commercially in similar regions. An understanding of seasonal vegetation water requirements from this study can be implemented to review the floodplain water management policies for better water management.
2. Materials and Methods
2.1. Study Area
The study area resides within the Upper Murrumbidgee catchment (Figure 1) in the south-east of the Murray Darling Basin (MDB), in south-eastern Australia. The Burrinjuck Dam catchment area size is 13,000 km2 (approx.) which is one-seventh that of the Murrumbidgee River catchment [43]. The latitude and longitude of the study area are 34.53° S–35.14° S and 148.31° E–148.55° E. The Burrinjuck Dam is situated within the upper catchment of the Murrumbidgee River basin, which was built (1910–1927) to develop an irrigation project after the devastating drought in 1902. The Murrumbidgee River rises at an altitude of around 1500 m in Kosciuszko National Park and flows approximately 316 km before entering Burrinjuck Reservoir at an altitude of 370 m (approx.). The topography of the Burrinjuck Dam area consists of gentle and moderate slopes and the elevation varies from 370 to 934 m [44]. The upper mountainous section of the Murrumbidgee River flow is regulated by dams for hydroelectric power generation and water supply [45]. The main land use in this part is forest and pasture. However, this area also contributes to agricultural production by growing wheat and cereals [46]. Having a diverse climate in the upper and lower Murrumbidgee, the mean annual rainfall varies 350 mm in the Riverina plains and 1700 mm in the Snowy Mountains [47]. According to the Köppen-Geiger climate classification system, the climate of the study area is temperate, without a dry season mostly hot summer with average 22 °C temperature in the hottest months [48]. The Burrinjuck Dam and surrounding area contribute to the maximum river flow by adding 24% of the total rainfall as runoff [49]. The climate has enriched the Burrinjuck reserve possesses a high diversity of vegetation types and ecosystems.
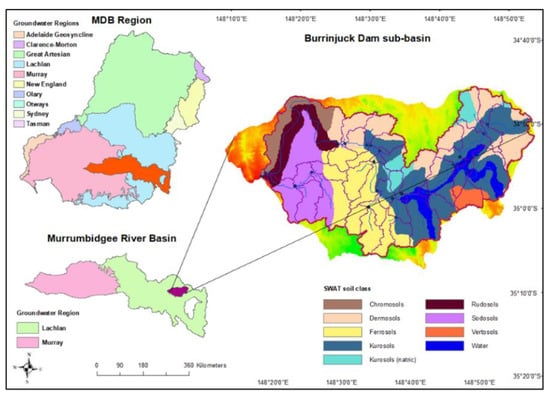
Figure 1.
Study area of the Burrinjuck Dam sub-catchment of the Murrumbidgee River catchment within the Murray-Darling Basin region.
2.2. Methods
Figure 2 presents an overview of the research methods applied in this study. The SWC and groundwater flow (GW) were simulated in ArcSWAT. The datasets used in this study were obtained from various local and international data portals, such as the Australian Bureau of Meteorology (BOM) and U.S. Geological Survey (USGS). We used the ArcGIS tool [50] and Microsoft Excel [51] for spatial and attribute data pre-processing and formatted the data to apply in the ArcSWAT hydrological model. We analysed the model output data using the WEKA machine learning tool [52] with different vegetation responses as measured by MODIS NDVI values. Different machine learning algorithms have been applied to model the relationships between vegetation types, and their location within the sub-basin and seasonal groundwater variability.
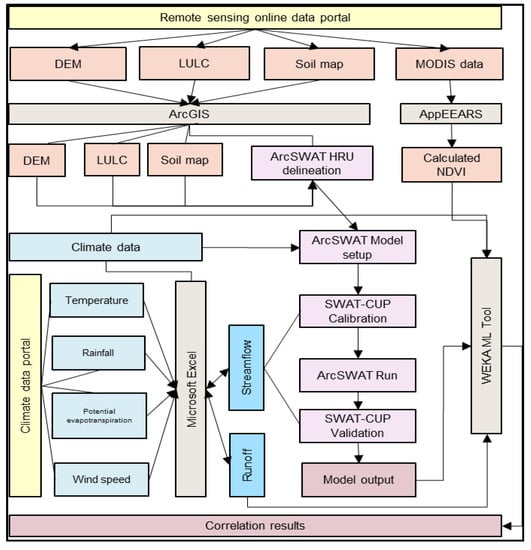
Figure 2.
An overview of the research methodology for vegetation responses and groundwater variables modelling using machine learning algorithms.
2.3. Hydrological Model Setup
An ArcSWAT interface of the SWAT2012 model was used in this study [21]. We installed compatible ArcGIS version 10.6 on a desktop to run SWAT2012 from the user interface. The SWAT model is a continuous physically based distributed parameter model that operates on a daily time-step. This model is capable of simulating catchment hydrology, land use impact on water, sediments, plant growing, agricultural-chemical yields, etc., within agricultural watersheds [21,53]. SWAT divides the watershed into multiple sub-basins based on spatial characteristics. These sub-basins are further subdivided into hydrological response units (HRUs) that consist of unique land use, soils, and slope characteristics [54]. Each HRU is simulated for SWC, groundwater flow, nutrient cycles, sedimentation, crop growth, and management practices [44]. The simulated results from the HRUs represent the sub-basin scale. SWAT [53] simulates the hydrological cycle based on the following daily water balance equation:
where SWt is the ultimate water content in (mm), SW0 is the amount of water content on the first soil of the day i (mm), t is time (days), Rday is the amount of rainfall on day i (mm), Qsurf is the amount of surface runoff on specific day i (mm), Ea is the amount of evapotranspiration on day i (mm), Wseep is the amount of water percolated into the vadose zone from the soil profile on day i (mm), and Qgw is the amount of return flow on day i (mm).
The SWAT model was delineated from a 30 m resolution digital elevation model (DEM) (Figure 3). A threshold drainage area of 1342 km2 was selected based on the DEM and Murrumbidgee River network to divide the watershed into 43 sub-basins, which were later categorised into 350 HRUs depending on land cover and land use, soil types, and slope. The model was run for 20 years of data, starting from 2001 and ending in 2020. The SWC data for Australia was obtained from the Australian Water Resource Assessment Landscape water balance model (AWRA-L), which was calibrated against the streamflow data. It is not best practice to use data from a different model simulation to run a hydrological model as it may not provide good modelling results. To avoid this confusion, the model was calibrated and validated against observed streamflow data instead of SWC.
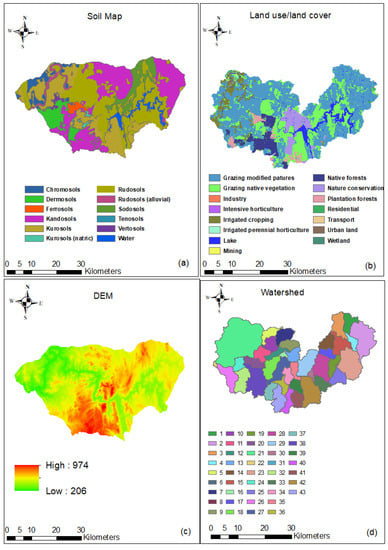
Figure 3.
In the above figure four images are captured: (a) Study area soil map, (b) Land use/land cover map, (c) DEM, and (d) Delineated watershed.
2.3.1. Data Preparation
A combination of climatological and land properties data were required to develop a semi-distributed model using the ArcSWAT interface (Appendix A). Some data such as DEM, soil, land use, and weather data are mandatory to run the dynamics of the watershed; however, streamflow, reservoir information, sediment, water quality, chemical, and pesticide data are non-mandatory. The data used in this study and their sources are listed in Table 1.

Table 1.
The datasets used in this study including their descriptions and sources.
2.3.2. Study Period
The study period (2001–2020) was selected to include a long-term drought (2001–2006) and flooding (2007–2010) phases. Both dry and wet phases were included in the study to ensure any long-term change in the vegetation condition was identified in the NDVI data. The annual data were divided into two seasons: (i) dry and (ii) wet, which were categorised based on rainfall and temperature anomalies. The average dry season (Oct–Mar) and wet season (Apr–Sep) rainfall are 52.4 mm, 66.45 mm and 70.74 mm, 73.91 mm in the drought and flooding periods, respectively.
2.3.3. DEM
The sub-basin parameters (gradient and length of the slope) and stream network characteristics (slope, width, and length of the channel) were obtained from the DEM file. For this study, we used a 30 m resolution DEM downloaded from the Shuttle Rader Topography Mission (STRM) using the USGS data portal [55]. DEM for the Burrinjuck Dam study area was masked for the SWAT application (Figure 3c).
2.3.4. Land Use/Land Cover Data
The land use data for the study area used in the ArcSWAT HRU delineation was developed by the NSW Office of Environment and Heritage. These satellite imagery data were derived for the period of 2001 to 2005 and verified with Google Earth and a field survey of specific land cover types. The raster files were processed in ArcGIS to reclassify for the SWAT model (Figure 3b).
2.3.5. Soil Data
The SWAT model requires soil information of the basin area including a database table of soil texture, pH number, available water content, hydraulic conductivity, bulk density, and organic carbon content for each soil type [44,56]. The soil map of the study area was downloaded from the Digital Atlas of Australian Soil [8] (Figure 3a). A ‘usersoil’ database table was prepared for this study from the available soil information and lookup tables, and then replaced the default ‘usersoil’ table in the SWAT database.
2.3.6. Climate Data
The climate data we used in this study included daily rainfall, temperature (maximum and minimum), wind speed, solar radiation, and relative humidity. They were obtained from the Australian Bureau of Meteorology [57]. The climate data was obtained for a period of 21 years (from 2000 to 2020) in daily time series format. These data were processed using the Microsoft Excel tool to fill 0.2 of the missing data by the linear interpolation method [58].
2.3.7. Sensitivity Analysis and Hydrological Model Calibration
We applied sensitivity analysis following the guidelines explained in the previous studies [59], using the SWAT Calibration and Uncertainty Programs (SWAT-CUP). The SWAT-CUP has five algorithm options for model calibration (SUFI-2, PSO, GLUE, ParaSol, and MCMC), 11 functions (mult, sum, R2, chi2, NS, br2, ssqr, PBIAS, KGE, RSR, MNS) and integrated features such as plot visualisation [60]. The sensitivity analysis was done using SUFI-2, considering the one-at-a-time method of 15 parameters related to the processes of streamflow, recharge, evapotranspiration, percolation, and infiltration from the list to identify the most sensitive ones for the model simulations at the Burrinjuck Dam. According to previous studies [61], the Curve Number for moisture condition II (CN2) and the coefficient of water percolation to the deep aquifer (RCHRG_DP) were identified as the two most important sensitive parameters. Based on the literature review, among the two sensitive parameters, CN2 was chosen for the model calibration of this study. However, some other parameters such as the surface runoff lag coefficient (SURLAG) and Manning’s roughness coefficient (CH_N2) were also analysed, which were not as sensitive as in the previous modelling done by Saha and Zeleke [44]. The fact is that the previous study was done in the Yass River gauging station, which was upstream of the Burrinjuck Dam basin, while the present study focuses on the whole basin. Acquiring knowledge from several previous studies that applied the SWAT model close to the study area helps parameter selection for sensitivity analysis. Thirteen parameters were chosen to do sensitivity analysis (Table 2) based on previous SWAT model applications in the Kyeamba Creek basin [28] and Yass River basin [44]. The difference in basin scale could interfere in the sensitivity analysis. Therefore, the parameters used for calibration in this study are not necessarily the same proposed by Saha [44].

Table 2.
The table below shows the number of parameters applied, their definitions, and ranking in the SWAT-CUP simulation.
In this study, we used the sequential uncertainty fitting algorithm (SUFI-2) and selected the Nash–Sutcliffe model efficiency (NS) coefficient as a target function for calibration procedures. In the calibration process, SUFI-2 captures the uncertainties of the model run. The six parameters applied in the calibration process were selected from the sensitivity analysis table based on their ranking (Table 2). A researcher [61] found that the calibration process and uncertainties are closely related, and identifying these relationships are important. In the SUFI-2 interface, the input parameter uncertainty is expressed as ranges, whereas the output parameter’s uncertainties are expressed from the 95 PPU (95% probability distribution), which is calculated using Latin American hypercube sampling from the cumulative distribution of an output variable at 2.5% and 97.5%. The adjustment between the simulation results and observed data can be done by the p-factor (the fraction of measured data bracketed by the 95PPU band) and the R-factor (ratio of the average width of the 95PPU band and the standard deviation of the measured variable) known as statistical indices [61]. The p-factor value > 0.7 and R-factor value <1.5 are desirable for streamflow discharge depending on the situation [62].
The SWAT model was calibrated (2004–2007) and validated (2008–2010) with a warm-up period of three years (2000–2002). The calibration and validation processes were done in monthly timestep at two different points within the watershed, starting from the upstream of the streamflow station (Yass station) and then to the downstream station (Burrinjuck Dam station).
2.3.8. Hydrological Model Performance Evaluation
In this study, we assessed model calibration performance using the coefficient of determination (R2), Nash-Sutcliffe efficiencies (NSE), and percent bias (PBIAS) quantitative statistics, which were used in previous studies [56,63,64]. Moreover, we applied 15 parameters in the SWAT-CUP simulation and ranked them following the model performance acceptance guidelines documented by Arnold et al., [21], which are presented in Table 2.
The Nash–Sutcliffe simulation efficiency (NSE) coefficient is a dimensionless statistic, indicating the accuracy of simulated versus observed data against the 1:1 line [65]. NSE is the most widely used statistical indicator for hydrological model performance, in which the NSE value 1 represents observed and simulated values as the same, while negative NSE value means simulations are extremely poor. NSE is defined as:
where n is the number of time steps, , i is the observed flow at time step i (daily here), is the mean of the observed flow, and , i is the simulated flow. The range of NSE is [−∞,1], where 1 represents a perfect match between the observed and simulated flow.
A hydrological model with higher R2 is considered as a good result [66]. R2 is defined as:
where, and are representing the measured and simulated data for ith observation and and are the mean of the measured and simulated data, respectively.
The percent bias (PBIAS) determines the average tendency to be greater or smaller simulated values than their observed data [63]. The maximum PBIAS value is zero, indicating the simulation is exactly the same as the observed data. In general, a smaller PBIAS value signifies accurate model simulation. PBIAS is calculated as:
where and are representing the measured and simulated data for the ith observation, respectively.
2.3.9. Remote Sensing Data
Moderate resolution imaging spectroradiometer (MODIS) data are available from the U.S. Geological Survey website for free of cost [55]. We used the MODIS (Terra) 16-Day Global 250 m composite product of MOD13Q1 (version V006) to identify the vegetation condition. The NDVI values were selected from the available vegetation indices in the MOD13Q1 product from imagery acquired during the period 2001 to 2020. We have selected six plots of different vegetation types (average size between 1 and 2 km2) within the study area (such as grass, shrub, and tree). These plots were selected randomly (i.e., stratified random sampling) based on the specific vegetation type dominant in the selected plot area. We also selected point areas (500 m radius) at the bottom and top of each sub-basin (Figure 4). A total of 60 areas (point area) were calculated for 40 sub-basins (three sub-basins were too small to create a point). These plots have been converted into polygons in the Google Earth Pro and then saved as KML files, which were later processed into shapefiles in ArcGIS [50]. A pre-processing tool called the Application for Extracting and Exploring Analysis Ready Samples (AppEEARS) was selected to obtain pre-processed NDVI time-series data for those shapefiles prepared earlier.
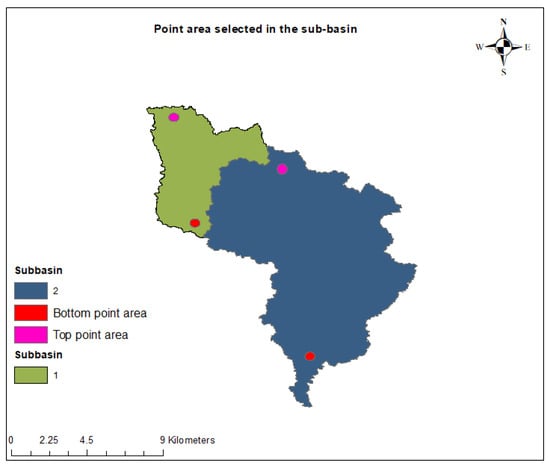
Figure 4.
The vegetation NDVI was also calculated for the point area with a radius of 500m selected both from the top and bottom location within all sub-basins. The above figure only shows the point locations of sub-basin 1 and 2.
2.3.10. Normalised Difference Vegetation Index (NDVI)
The NDVI data were processed using the AppEEARS tool [67]. The MODIS sensor captures a range of broad spectrum of reflected sunlight from tree leaves. The healthy vegetation mostly absorbs light from the red spectrum and reflects light from the near-infrared (NIR) spectrum. NDVI utilises the contrast of strong reflectance in the near-infrared region and the strongly absorbed reflectance in the red wavelength region. The NDVI calculation was performed applying the difference between the red and near-infrared bands and normalising it over the sum of the red and near-infrared bands (Equation (5)).
Three types of vegetation indices were obtained using the Google Earth map and U.S. Geological Survey website. Firstly, the plots were selected for forest type vegetation within the watershed in Google Earth Pro and saved into KML files. These KML files were then processed in ArcGIS to convert into shapefiles and later used to obtain 20 years (2001–2020) of NDVI data from USGS. These similar steps were followed to obtain NDVI data for shrub and grass type vegetation within the watershed. We also calculated NDVI for each of the 43 sub-basins for the same period (2001–2020).
2.3.11. Machine Learning Algorithms for Data Analysis
A machine learning (ML) algorithm is a set of computational codes that can process a large amount of data in a complex way [68]. It is also known as data-driven methods that build models based on evidence obtained from a sample data set. The algorithms read and processed data to learn the maximum possible patterns about the data [49]. In this study, we applied the Waikato Environment for Knowledge Analysis (WEKA) tool, developed by the University of Waikato, New Zealand [39,40]. Firstly, the WEKA tool was set up to run a random forest model using 43 different datasets. These datasets included the combination of SWC, groundwater flow towards stream, and different types of vegetation responses (NDVI values). Each dataset was initially set for linear regression to find the collinear and non-collinear variables. Secondly, the machine learning tool was prepared to run a support vector machine (SVM) model using the same datasets.
The performance of all models was assessed in two ways: (a) using a 10-fold cross-validation, which is a leave-one-out approach, and (b) using the 80 and 20 per cent split-sample method. These two approaches were performed to compute the root mean square error (RMSE) and correlation coefficient (r) between the SWAT output variables (SW and GW) and predicted vegetation response (NDVI value) of each model. We selected models with higher correlation coefficient (r) values and smaller RMSEs to analyse the relationship against soil water content (SWC) and groundwater flow (GW). We also analysed these relationships based on rainfall intensity such as dry season (October to March) for less intensity and wet season (April to September) for high intensity.
3. Results
3.1. Hydrological Model Calibration and Validation
Table 2 shows the sensitivity ranking of the different model parameters and their ranges applied during the calibration. The model was calibrated and validated at two different stations (Figure 5), for which the results are listed in Table 3. The results explained that manual calibration performed better than auto-calibration. The 0.51 NSE value for the manual calibration performance parameters can be marked as ‘satisfactory’ for the SWAT model developed in the study area. The model in the study area was able to simulate about 51% of the variance on observed streamflow data.
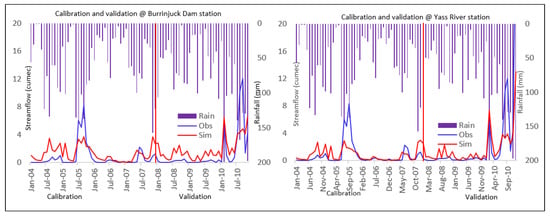
Figure 5.
In this study, the SWAT-CUP tool was applied for the model calibration and validation at two different locations based on the available station, (i) Burrinjuck Dam, and (ii) Yass River station.

Table 3.
The table below shows the number of parameters applied, their definitions, and ranking in the SWAT-CUP simulation.
The statistical indicators reflected a regression between observed and simulated streamflow for those two points with NSE 0.51, PBIAS 54.2, R2 0.72, p-factor 0.63 and NSE 0.54, PBIAS 58.6, R2 0.73, and p-factor 0.68, respectively. The hydrographs show that the observed and simulated values have a noticeable difference in the plots. Additionally, the model slightly overestimated the low flow during the calibration and validation periods.
3.2. Relationships of Vegetation Responses and Groundwater
The average monthly SWC and groundwater data were presented in Table 4. The average correlation coefficient of different vegetation types and SWAT model output variables over the study period in shown in Figure 6. The different correlation patterns of vegetation types of responses and SWC (SWC) suggested that vegetations were influenced considerably by SWC. The linear regression results show that shrub vegetation NDVI is highly correlated (R2 = 0.82) to SWC than forest and grass type vegetation NDVI (R2 = 0.78, and R2 = 0.72, respectively). However, grass type vegetation response is higher (R2 = 0.59) to groundwater (GW) compared to forest vegetation (R2 = 0.24) and shrub vegetation (R2 = 0.25).

Table 4.
ArcSWAT produced simulated soil water content (SWC) and groundwater flow (GW) data presented as average monthly for the study area.
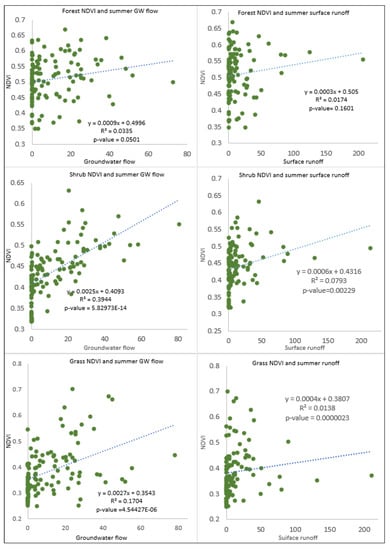
Figure 6.
The forest, shrub, and grass type vegetation NDVI datasets are plotted against model-simulated surface runoff and groundwater flow (GW) to calculate the co-efficient of determination (R2).
The WEKA modelling results show that sub-basin NDVI (including all vegetation types within the sub-basin no 28) was highly responsive (r = 0.78) compared with forest NDVI (r = 0.61) when the ML algorithms were applied against SWC and GW (Table 5). Similarly, sub-basin NDVI (including all vegetation types within the sub-basin no 19 and 28) was highly responsive (r = 0.76 and r = 0.74 respectively) than shrub and grass type vegetation (r = 0.67 and r = 0.56 respectively) (Table 6 and Table 7).

Table 5.
The WEKA-generated modelling results for forest, sub-basin, top-point, and bottom-point NDVI against SWAT-simulated variables, soil water content (SWC), and groundwater flow (GW). The r represents the correlation coefficient.

Table 6.
The WEKA machine learning produced modelling results for vegetation NDVI from shrub, sub-basin, top point, and bottom point against the SWAT variables soil water content (SWC) and groundwater flow (GW). The r represents the correlation coefficient in the below results.

Table 7.
The WEKA machine learning modelling results for grass type vegetation NDVI (sub-basin combined, vegetation located at the top point, and vegetation located at the bottom point) against SWAT variables. The correlation coefficient (r) for the random forest and support vector machine algorithms are listed in the below table.
3.3. Vegetation Responses Considering Their Location within the Watershed
The results shown in Figure 6 were calculated from the average data for 40 sub-basins. The monthly average correlation coefficient result shows that vegetation in the top-point location in a sub-basin is more sensitive (R2 = 0.77) to SWC when compared with vegetation in the bottom point location (R2 = 0.72). On the other hand, vegetation in the bottom point location is more correlated to groundwater (R2 = 0.62) than vegetation in the top point location (R2 = 0.57).
The average correlation coefficient of top-point (distant from outlet) and bottom-point (close to outlet) NDVI and SWC is shown in Figure 7. The modelling results show that vegetation in the top-point location of the sub-basin has moderate r values against GW and SWC (0.67 and 0.69 respectively) compared with vegetation in the bottom location (0.25, and 0.46 respectively). Moreover, the result shows strong correlations for the top point vegetation NDVI against these two variables (r = 0.81 and r = 0.79, respectively) (Table 6 and Table 7). The negative value of r (−0.0069) shows that vegetation in the bottom location of sub-basin #23 has no response to the GW (Table 7).
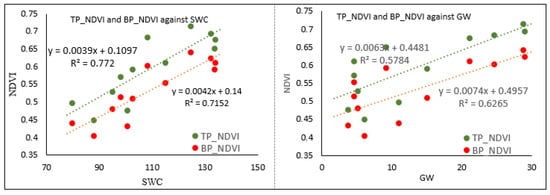
Figure 7.
The NDVI collected from the top-point and bottom-point areas as vegetation response are plotted against the Soil Water Content (SWC) and groundwater flow (GW) to calculate the co-efficient of determination (R2).
3.4. Seasonal Vegetation Responses
The results of the linear correlation analysis for different vegetation types for two distinct seasons are shown in Figure 8. The correlation results show that shrub and forest vegetations are highly correlated (R2 = 0.89 and R2 = 0.82, respectively) to SWC during the wet season compared with grass type vegetation (R2 = 0.47). However, grass vegetation shows a better response during the dry season (R2 = 0.52) compared with the shrub and forest (R2 = 0.45 and R2 = 0.43, respectively).
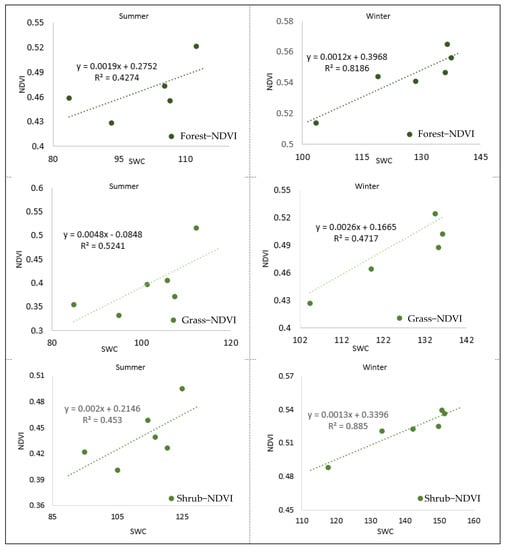
Figure 8.
The vegetation responses (NDVI) against the SWC in dry and wet seasons in the study area are plotted to calculate the co-efficient of determination (R2).
The vegetation responses were observed for different locations within the sub-basin (Figure 9). The regression analysis shows that vegetation in the top point and bottom point locations of the sub-basin are highly correlated to GW in the dry (R2 = 0.79 and R2 = 0.84, respectively) and wet season (R2 = 0.81 and R2 = 0.85, respectively). However, vegetation in these two locations is moderately correlated to SWC during the wet season (R2 = 0.66 and R2 = 0.71, respectively) than the dry season (R2 = 0.51 and R2 = 0.54, respectively).
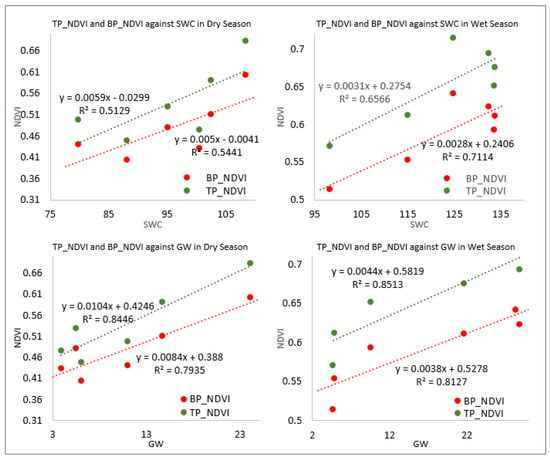
Figure 9.
Seasonal vegetation responses (NDVI) from different locations (top point and bottom point) against soil water content (SWC) and groundwater flow are plotted to identify the co-efficient of determination (R2).
The WEKA modelling results show that shrub vegetation is moderately responsive to GW and SWC (r = 0.62 and r = 0.63, respectively) in the dry season. However, forest and grass type vegetation are less responsive to GW and SWC (r = 0.52, r = 0.48, r = 0.27, and r = 0.38, respectively) in the dry season (Table 8). All three types of vegetation were less responsive to GW and SWC in the wet season.

Table 8.
The below table shows the modelling results for different types of vegetation responses and vegetation located at different points in the sub-basin. This result shows the relationship during the dry season. The r value shows the correlation coefficient of the modelling results.
In contrast to the sub-basin level, the vegetation NDVI is highly responsive to GW and SWC (r = 0.75 and r = 0.73, respectively) in the dry season. Furthermore, the sub-basin NDVI shows a strong relationship with SWC and GW (r = 0.81) (Table 8) in the dry season, and moderate relation (r = 0.62) in the wet season (Table 9). This result clearly indicates that the vegetation in the sub-basin is positively influenced by groundwater flow both in the dry and wet seasons.

Table 9.
The below table shows the modelling results for different types of vegetation responses and vegetation located at different points in the sub-basin. This result shows the relationship during the wet season. The r value shows the correlation coefficient of the modelling results.
The vegetation in the top-point location within the sub-basin is also highly responsive to GW and SWC (r = 0.78 and r = 0.70, respectively) than vegetation in the bottom-point location (r = 0.42 and r = 0.32, respectively) in the dry season. The vegetation in the top-point location has a higher r value (r = 0.79) when correlated against GW and SWC in the dry season. However, vegetation in the top-point location has moderate responses to GW and SWC (r = 0.64 and r = 0.61, respectively), and highly responsive (r = 0.75) against these two variables together (Table 9).
4. Discussion
4.1. Relationship between Vegetation Responses (NDVI) and ArcSWAT Model Simulated Soil Water Content (SWC) and Groundwater Flow (GW) Considering Vegetation Types and Their Locations
This study presents a robust analysis of the relationships between groundwater availability and vegetation responses vigour in the floodplain zone. The hydrological model simulated different groundwater variables by calculating a range of meteorological variables, which were later analysed in relation to NDVI using different machine learning algorithms. Among random forest (RF) and support vector machine learning (SVM) algorithms, the SVM represented higher r values (r = 0.78, r = 0.75, r = 0.74 etc.) compared with RF (r = 0.73, r = 0.68, and r = 0.65 etc.) when analysed by different types of vegetation. A previous study also mentioned outperformance of random forest in terms of vegetation and water relationship modelling. Before the analysis, the SWAT model calibration was completed and produced the 0.51 NSE value. This might reflect the high volume of groundwater loss and disconnection of the deep aquifer in SWAT [10]. We found that the simulated variables (SWC and GW) and vegetation NDVI relationships vary with vegetation types when we applied data from the same sub-basin (watershed). The shrub-type vegetation is highly correlated to SWC over forest and grass vegetation; however, grass vegetation shows a high correlation to GW compared to forest and shrub vegetation [69]. The first objective of this study to understand different types of vegetation responses to SWC and groundwater is thus successful. Previous studies have found a strong correlation between different types of vegetation and SWAT-simulated SWC [32]. However, in their studies, different types of floodplain vegetation such as forest, shrub, or grass vegetation responses have not been included.
We also noticed from our study that the vegetated location within the sub-basin also impacts these relationships to SWC and GW. The vegetation located in the top point within the sub-basin, which are distant to the water outlet or stream, showed higher response to SWC (r = 0.69, 0.78 etc.). The SWC volume rate is usually high near the water outlet, and that is why the vegetation located in the bottom point zone can easily access SWC for their growth. This saturated soil enables surface and sub-surface flows and activates connectivity between soils and streams [68,70]. Moreover, vegetation located in the top point showed higher response to GW (R = 0.62) than vegetation located in the bottom point. The modelling results also showed the correlation coefficient (r) value has increased by 42% against GW for vegetation located at the top point compared to the bottom point. The correlation coefficient (r) was highly positive (0.81) for top-point vegetation when SWC and GW variables were considered together as relationship predictors. This means vegetation located in the top point can grow well when SWC and groundwater flow increases within the sub-basin.
4.2. Seasonal Variability in Each Vegetation Type
In the seasonal domain, the vegetation responses become stronger in the wet season when rainfall increases in the study area. As rainfall is the main source of water in the area of interest, the average SWC and GW values increased by 22% and 32.68%, respectively, during the wet season. Considering the inter seasonal water variability, the vegetation responses to SWC and groundwater flow varied over different types of vegetation. We found the grass vegetation response decreased by 10.6% in the wet season compared to the dry season. This variation may also be related to inter-seasonal temperature differences. During the wet season, the average temperature in the study area is 18.45 °C (average from 2001 to 2020), which negatively impacts vegetation growth in winter months [4,70]. However, forest and shrub vegetation types are highly responsive to the sub-basin’s SWC during the wet season. Therefore, forest and shrub responses were increased by 48.8% and 49.43%, respectively, in the wet season when compared to the dry season.
Similarly, we analysed vegetation responses and groundwater relationships against SWC and groundwater flow during the dry season using machine learning algorithms. The vegetation NDVI (including all vegetation in the sub-basin) against GW and SWC produced highly positive correlation coefficient values (r) (0.76, and 0.73 respectively). However, when the model was run against GW and SWC together, the r value becomes higher (0.81). The overall RF model performance was 7.3% better against runoff over the SVM classifier. The result shows that the RF classifier performs better than the SVM algorithm in the predictions. This result supports the findings of other studies where RF is widely used for crop mapping, urban studies and particularly for land use/land cover applications [71]. In this study, the WEKA model produced different r values when we applied a combined vegetation NDVI dataset at the sub-basin level. For example, the values of r between the sub-basin NDVI and GW, SWC were 0.75, 0.73, and 0.81, respectively. This means that vegetation in the sub-basin within a floodplain is highly responsive to groundwater flow and SWC during the dry season.
Not surprisingly, we found that shrub and forest type vegetation are highly responsive to GW (r = 0.63 and 0.58, respectively) compared to grass (r = 0.30). These results support that woody vegetation type is highly responsive to groundwater, while the non-woody vegetation type immediately responds to rainfall by seed or rhizome regeneration [72]. However, both shrub and forest vegetation were moderately responsive to SWC and GW (r = 0.66 and 0.59, respectively). This means tree and shrub vegetation can grow well when SWC and groundwater flow increase after the rainfall in dry season. Moreover, this study suggests the grass vegetation type is highly dependent on groundwater during the dry and winter season for their growth, and any instability or long-term drought can negatively affect these floodplain vegetation communities.
A comprehensive documentation of different types of vegetation and groundwater relationships can be prepared for efficient floodplain vegetation management based on the results of this study. Agricultural production in similar regions around the world can be increased by selecting appropriate crops based on their seasonal response to groundwater.
Authors should discuss the results and how they can be interpreted from the perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.
5. Conclusions
The analytical results show that the vegetation system is highly dependent on groundwater hydrology during the dry season in this study area, especially shrub and grass type vegetation that are located distant from the water outlet in the HRU. This suggests that small- and medium-rooted vegetation, for instance, quince, feijoa, wheat, and oats etc., can grow well in similar floodplains globally, with possible implications for water management during the dry season.
The results of the study conclude the relationship between floodplain vegetation and catchment hydrology is two-way, and any change in the environment can directly influence the vegetation response to groundwater. For example, suitable growing temperature and available water can boost vegetation growth which, in turn, contributes to increasing the potential evapotranspiration rate. On the other hand, grass type vegetation growth helps to increase the infiltration. The hydrological simulation results suggested that rainfall dominates the study area catchment water balance, in which groundwater flow increases in the wetting period between April and September. Any changes in groundwater in the basin area can directly impact vegetation conditions, which need to be included in future studies applying LAI in the hydrological modelling. As rainfall dominates the catchment hydrology, any future changes in the rainfall pattern need to be considered carefully for better floodplain management. Measuring the field soil moisture data and applying that data for model calibration could be another option to compare model simulation to support the output results.
In summary, this study contributes scientific insight into groundwater-vegetation relationship and outlines a methodology for modelling the relationship in contrast to seasonal groundwater variations. The research outcomes can potentially support sustainable floodplain vegetation system development in arid environments. However, there are still some drawbacks. This study considered vegetation types and their distance from the streamflow while assessing their responses to the groundwater variables. There could be other factors, e.g., vegetation density and depth of root can be included in the future studies.
Further research should consider improving the modelling results applying more data for intense rainfall and drought years. Thus, the multiple regression including a time lag, temperature, or rainfall frequency as well as future climate projections may give better understanding on ecosystem hydrology.
Author Contributions
N.M.: Conceptualization, Methodology, Software, Data gathering, Formal analysis, Investigation, Validation, Writing original draft preparation, Review and Editing. A.A.A.: Supervision, Conceptualization, Validation, Review and Editing. T.N.M.: Validation, Review and Editing. G.T.A.: Software, Validation, Review and Editing, and acquisition of APC. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by University of Southern Queensland Research Training Program. Gebiaw T Ayele funded the APC.
Data Availability Statement
The data that support the findings of this study are publicly available in Figshare which can be accessed from this link 10.6084/m9.figshare.21625994.
Acknowledgments
This research was supported by the University of Southern Queensland Research Training Program (RTP). Thanks are extended to the Australian Bureau of Meteorology, for providing the Australian meteorological dataset, to the USGS and National Aeronautics and Space Administration (NASA) for offering the MODIS NDVI product. Gebiaw T. Ayele received funding and acknowledges Griffith Graduate Research School, the Australian Rivers Institute and School of Engineering, Griffith University, Queensland, Australia.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Figure A1.
ArcSWAT interface shows the model set up in the Burrinjuck Dam sub-basin study area which is applied to understand the catchment hydrology.
References
- Ponting, J.; Kelly, T.J.; Verhoef, A.; Watts, M.J.; Sizmur, T. The impact of increased flooding occurrence on the mobility of potentially toxic elements in floodplain soil—A review. Sci. Total Environ. 2021, 754, 142040. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, B.; Salah, O.; Driss, O.; Abdelghani, C. Global warming and groundwater from semi-arid areas: Essaouira region (Morocco) as an example. SN Appl. Sci. 2020, 2, 1245. [Google Scholar] [CrossRef]
- Condon, L.E.; Atchley, A.L.; Maxwell, R.M. Evapotranspiration depletes groundwater under warming over the contiguous United States. Nat. Commun. 2020, 11, 873. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Zhang, D.; Chen, X. Vegetation Response to Groundwater Variation in Arid Environments: Visualization of Research Evolution, Synthesis of Response Types, and Estimation of Groundwater Threshold. Int. J. Environ Res. Public Health 2019, 16, 1849. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Yang, W.; Zhan, H.; Jiang, Q.; Shi, M.; Wang, Y. On the Origin of Deep Soil Water Infiltration in the Arid Sandy Region of China. Water 2020, 12, 2409. [Google Scholar] [CrossRef]
- Ma, X.; Huete, A.; Moran, S.; Ponce-Campos, G.; Eamus, D. Abrupt shifts in phenology and vegetation productivity under climate extremes. J. Geophys. Res. Biogeosciences 2015, 120, 2036–2052. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. WIREs Clim. Change 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.; Yu, J.; Fu, G.; Ao, F. Vegetation dynamics induced by groundwater fluctuations in the lower Heihe River Basin, northwestern China. J. Plant Ecol. 2011, 4, 77–90. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Jackson, T.J.; McKim, H.L. Survey of methods for soil moisture determination. Water Resour. Res. 1980, 16, 961–979. [Google Scholar] [CrossRef]
- Uniyal, B.; Dietrich, J.; Vasilakos, C.; Tzoraki, O. Evaluation of SWAT simulated soil moisture at catchment scale by field measurements and Landsat derived indices. Agric. Water Manag. 2017, 193, 55–70. [Google Scholar] [CrossRef]
- Porporato, A.; Daly, E.; Rodriguez-Iturbe, I. Soil water balance and ecosystem response to climate change. Am. Nat. 2004, 164, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Tian, S.; Renzullo, L.J.; van Dijk, A.I.J.M.; Tregoning, P.; Walker, J.P. Global joint assimilation of GRACE and SMOS for improved estimation of root-zone soil moisture and vegetation response. Hydrol. Earth Syst. Sci. 2019, 23, 1067–1081. [Google Scholar] [CrossRef]
- Leenaars, J.G.; Claessens, L.; Heuvelink, G.B.; Hengl, T.; González, M.R.; van Bussel, L.G.; Guilpart, N.; Yang, H.; Cassman, K.G. Mapping rootable depth and root zone plant-available water holding capacity of the soil of sub-Saharan Africa. Geoderma 2018, 324, 18–36. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Wu, Y.; Drake, S. A survey: Obstacles and strategies for the development of ground-water resources in arid inland river basins of Western China. J. Arid. Environ. 2004, 59, 351–367. [Google Scholar] [CrossRef]
- Naumburg, E.; Mata-Gonzalez, R.; Hunter, R.G.; McLendon, T.; Martin, D.W. Phreatophytic Vegetation and Groundwater Fluctuations: A Review of Current Research and Application of Ecosystem Response Modeling with an Emphasis on Great Basin Vegetation. Environ. Manag. 2005, 35, 726–740. [Google Scholar] [CrossRef]
- Schlaepfer, D.R.; Bradford, J.B.; Lauenroth, W.K.; Munson, S.M.; Tietjen, B.; Hall, S.A.; Wilson, S.D.; Duniway, M.C.; Jia, G.; Pyke, D.A.; et al. Climate change reduces extent of temperate drylands and intensifies drought in deep soils. Nat. Commun. 2017, 8, 14196. [Google Scholar] [CrossRef]
- Tomlinson, M.; Boulton, A.J. Ecology and management of subsurface groundwater dependent ecosystems in Australia—A review. Mar. Freshw. Res. 2010, 61, 936–949. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, Y.; Ren, L.; Lü, H.; Zhao, W.; Yuan, F.; Xu, M. Ecosystem restoration and conservation in the arid inland river basins of Northwest China: Problems and strategies. Ecol. Eng. 2016, 94, 629–637. [Google Scholar] [CrossRef]
- Eamus, D.; Zolfaghar, S.; Villalobos-Vega, R.; Cleverly, J.; Huete, A. Groundwater-dependent ecosystems: Recent insights from satellite and field-based studies. Hydrol. Earth Syst. Sci. 2015, 19, 4229–4256. [Google Scholar] [CrossRef]
- Adhikari, R.K.; Mohanasundaram, S.; Shrestha, S. Impacts of land-use changes on the groundwater recharge in the Ho Chi Minh city, Vietnam. Environ Res. 2020, 185, 109–440. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Jha, M.K. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Cuceloglu, G.; Abbaspour, K.C.; Ozturk, I. Assessing the Water-Resources Potential of Istanbul by Using a Soil and Water Assessment Tool (SWAT) Hydrological Model. Water 2017, 9, 814. [Google Scholar] [CrossRef]
- Francesconi, W.; Srinivasan, R.; Pérez-Miñana, E.; Willcock, S.P.; Quintero, M. Using the Soil and Water Assessment Tool (SWAT) to model ecosystem services: A systematic review. J. Hydrol. 2016, 535, 625–636. [Google Scholar] [CrossRef]
- Pisinaras, V.; Petalas, C.; Gikas, G.D.; Gemitzi, A.; Tsihrintzis, V.A. Hydrological and water quality modeling in a medium-sized basin using the Soil and Water Assessment Tool (SWAT). Desalination 2010, 250, 274–286. [Google Scholar] [CrossRef]
- Silva-Júnior, R.O.D.; Salomão, G.N.; Tavares, A.L.; Santos, J.F.D.; Santos, D.C.; Dias, L.C.; Rocha, E.J.P.D. Response of Water Balance Components to Changes in Soil Use and Vegetation Cover Over Three Decades in the Eastern Amazon. Front. Water 2021, 3, 1. [Google Scholar] [CrossRef]
- Yonaba, R.; Biaou, A.C.; Koïta, M.; Tazen, F.; Mounirou, L.A.; Zouré, C.O.; Queloz, P.; Karambiri, H.; Yacouba, H. A dynamic land use/land cover input helps in picturing the Sahelian paradox: Assessing variability and attribution of changes in surface runoff in a Sahelian watershed. Sci. Total Environ. 2021, 757, 143792. [Google Scholar] [CrossRef] [PubMed]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Saha, P.; Zeleke, K. Assessment of streamflow and catchment water balance sensitivity to climate change for the Yass River catchment in south eastern Australia. Environ. Earth Sci. 2014, 73, 6229–6242. [Google Scholar] [CrossRef]
- Fu, B.; Burgher, I. Riparian vegetation NDVI dynamics and its relationship with climate, surface water and groundwater. J. Arid. Environ. 2015, 113, 59–68. [Google Scholar] [CrossRef]
- Mallick, J.; AlMesfer, M.; Singh, V.; Falqi, I.; Singh, C.; Alsubih, M.; Kahla, N. Evaluating the NDVI–Rainfall Relationship in Bisha Watershed, Saudi Arabia Using Non-Stationary Modeling Technique. Atmosphere 2021, 12, 593. [Google Scholar] [CrossRef]
- Nouri, H.; Anderson, S.; Sutton, P.; Beecham, S.; Nagler, P.; Jarchow, C.J.; Roberts, D.A. NDVI, scale invariance and the modifiable areal unit problem: An assessment of vegetation in the Adelaide Parklands. Sci. Total Environ. 2017, 584–585, 11–18. [Google Scholar] [CrossRef]
- Park, J.-Y.; Ahn, S.-R.; Hwang, S.-J.; Jang, C.-H.; Park, G.-A.; Kim, S.-J. Evaluation of MODIS NDVI and LST for indicating soil moisture of forest areas based on SWAT modeling. Paddy Water Environ. 2014, 12, 77–88. [Google Scholar] [CrossRef]
- Groeneveld, D.P.; Baugh, W.M.; Sanderson, J.S.; Cooper, D.J. Annual Groundwater Evapotranspiration Mapped from Single Satellite Scenes. J. Hydrol. 2007, 344, 146–156. [Google Scholar] [CrossRef]
- Nanzad, L.; Zhang, J.; Tuvdendorj, B.; Nabil, M.; Zhang, S.; Bai, Y. NDVI anomaly for drought monitoring and its correlation with climate factors over Mongolia from 2000 to 2016. J. Arid. Environ. 2019, 164, 69–77. [Google Scholar] [CrossRef]
- Wen, L.; Macdonald, R.; Morrison, T.; Hameed, T.; Saintilan, N.; Ling, J. From hydrodynamic to hydrological modelling: Investigating long-term hydrological regimes of key wetlands in the Macquarie Marshes, a semi-arid lowland floodplain in Australia. J. Hydrol. 2013, 500, 45–61. [Google Scholar] [CrossRef]
- Aguilar, C.; Zinnert, J.C.; Polo, M.J.; Young, D.R. NDVI as an indicator for changes in water availability to woody vegetation. Ecol. Indic. 2012, 23, 290–300. [Google Scholar] [CrossRef]
- Bhanja, S.N.; Malakar, P.; Mukherjee, A.; Rodell, M.; Mitra, P.; Sarkar, S. Using Satellite-Based Vegetation Cover as Indicator of Groundwater Storage in Natural Vegetation Areas. Geophys. Res. Lett. 2019, 46, 8082–8092. [Google Scholar] [CrossRef]
- Seeyan, S.; Merkel, B.; Abo, R. Investigation of the Relationship between Groundwater Level Fluctuation and Vegetation Cover by using NDVI for Shaqlawa Basin, Kurdistan Region—Iraq. J. Geogr. Geol. 2014, 6, 187. [Google Scholar] [CrossRef]
- Eibe, F.; Mark, A.H.; Ian, H.W. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”, 4th ed.; Kaufmann, M., Ed.; University of Waikato: Burlington, MA, USA, 2016. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Marin, D.B.; Ferraz, G.A.E.S.; Santana, L.S.; Barbosa, B.D.S.; Barata, R.A.P.; Osco, L.P.; Ramos, A.P.M.; Guimarães, P.H.S. Detecting coffee leaf rust with UAV-based vegetation indices and decision tree machine learning models. Comput. Electron. Agric. 2021, 190, 106476. [Google Scholar] [CrossRef]
- Sharma, A.K.; Kumar, A.; Saxena, S.; Beniwal, M. Evaluating WEKA over the Open Source Web Data Mining Tools. Int. J. Eng. Res. Technol. 2015, 8, 128–132. [Google Scholar]
- Brown, A.E.; Podger, G.M.; Davidson, A.J.; Dowling, T.I.; Zhang, L. Predicting the impact of plantation forestry on water users at local and regional scales: An example for the Murrumbidgee River Basin, Australia. For. Ecol. Manag. 2007, 251, 82–93. [Google Scholar] [CrossRef]
- Saha, P.; Zeleke, K.; Hafeez, M. Streamflow modeling in a fluctuant climate using SWAT: Yass River catchment in south eastern Australia. Environ. Earth Sci. 2013, 71, 5241–5254. [Google Scholar] [CrossRef]
- Wallbrink, P.J.; Olley, J.M.; Murray, A.S. The Contribution of Subsoil to Sediment Yield in the Murrumbidgee River Basin, New South Wales, Australia; IAHS: Wallingford, UK, 1996. [Google Scholar]
- Verstraeten, G.; Prosser, I.P.; Fogarty, P. Predicting the spatial patterns of hillslope sediment delivery to river channels in the Murrumbidgee catchment, Australia. J. Hydrol. 2007, 334, 440–454. [Google Scholar] [CrossRef]
- Green, D.; Petrovic, J.; Moss, P.; Burrell, M. Water Resources and Management Overview: Murrumbidgee Catchment; NSW Office of Water: Sydney, Australia, 2011.
- Peel, M.; Finlayson, B.; McMahon, T. Updated world map of the Köpper-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 439–472. [Google Scholar] [CrossRef]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Deskto2019; Environmental Systems Research Institute: Redlands, CA, USA, 2019. [Google Scholar]
- Microsoft Corporation. Microsoft Excel; Corporation, M., Ed.; Microsoft Corporation: Redmond, WA, USA, 2018. [Google Scholar]
- Smith, T.C.; Frank, E. Introducing machine learning concepts with WEKA. In Statistical Genomics; Humana Press: Totowa, NJ, USA, 2016; pp. 353–378. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. SWAT Theoretical Documentation Version 2009. Texas Water Resources Institute Technical Report No. 406; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Gassman, P.; Sadeghi, A.; Srinivasan, R. Applications of the SWAT Model Special Section: Overview and Insights. J. Environ. Qual. 2014, 43, 1–8. [Google Scholar] [CrossRef] [PubMed]
- USGS. Earth Explorer. US Geological Survey. Available online: https://earthexplorer.usgs.gov/ (accessed on 28 April 2022).
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. SWAT Model Application and Prediction Uncertainty Analysis in the Lake Tana Basin, Ethiopia. Hydrol. Process. 2009, 24, 357–367. [Google Scholar] [CrossRef]
- BOM. Climate Data Online. Australian Bureau of Meteorology. Available online: http://www.bom.gov.au/climate/data/index.shtml (accessed on 19 April 2022).
- Fassò, A.; Sommer, M.; von Rohden, C. Interpolation uncertainty of atmospheric temperature profiles. Atmos. Meas. Tech. 2020, 13, 6445–6458. [Google Scholar] [CrossRef]
- de Andrade, C.W.; Montenegro, S.M.; Montenegro, A.A.; Lima JR, D.S.; Srinivasan, R.; Jones, C.A. Soil moisture and discharge modeling in a representative watershed in northeastern Brazil using SWAT. Ecohydrol. Hydrobiol. 2019, 19, 238–251. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Vaghefi, S.A.; Srinivasan, R. A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference. Water 2018, 10, 6. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Zhang, L.; Li, H. Use of Remotely Sensed Actual Evapotranspiration to Improve Rainfall Runoff Modeling in Southeast Australia. J. Hydrometeorol. 2009, 10, 969–980. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Yang, Z.; Yu, Y.; Ma, X. Effects of single- and multi-site calibration strategies on hydrological model performance and parameter sensitivity of large-scale semi-arid and semi-humid watersheds. Hydrol. Process. 2022, 36, e14616. [Google Scholar] [CrossRef]
- EarthData. Application for Extracting and Exploring Analysis Ready Samples (AρρEEARS). 2021. Available online: https://appeears.earthdatacloud.nasa.gov/ (accessed on 26 April 2022).
- Sarkar, A. Deep Learning and the Evolution of Useful Information. Inf. Matters 2021, 1, 6. [Google Scholar] [CrossRef]
- Jiao, L.; An, W.; Li, Z.; Gao, G.; Wang, C. Regional variation in soil water and vegetation characteristics in the Chinese Loess Plateau. Ecol. Indic. 2020, 115, 106399. [Google Scholar] [CrossRef]
- He, B.; Chen, A.; Jiang, W.; Chen, Z. The response of vegetation growth to shifts in trend of temperature in China. J. Geogr. Sci. 2017, 27, 801–816. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Sandi, S.G.; Rodriguez, J.F.; Saintilan, N.; Wen, L.; Kuczera, G.; Riccardi, G.; Saco, P.M. Resilience to drought of dryland wetlands threatened by climate change. Sci. Rep. 2020, 10, 13232. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).