Opportunity Costs of In Situ Carbon Storage Derived by Multiple-Objective Stand-Level Optimization—Results from Case Studies in Portugal and Germany
Abstract
:1. Introduction
2. Materials and Methods
2.1. Portuguese Case Study Data
2.2. German Case Study Data
2.3. Discount Rate
2.4. Social Costs of Carbon as a Benchmark
3. Results
3.1. Opportunity Costs
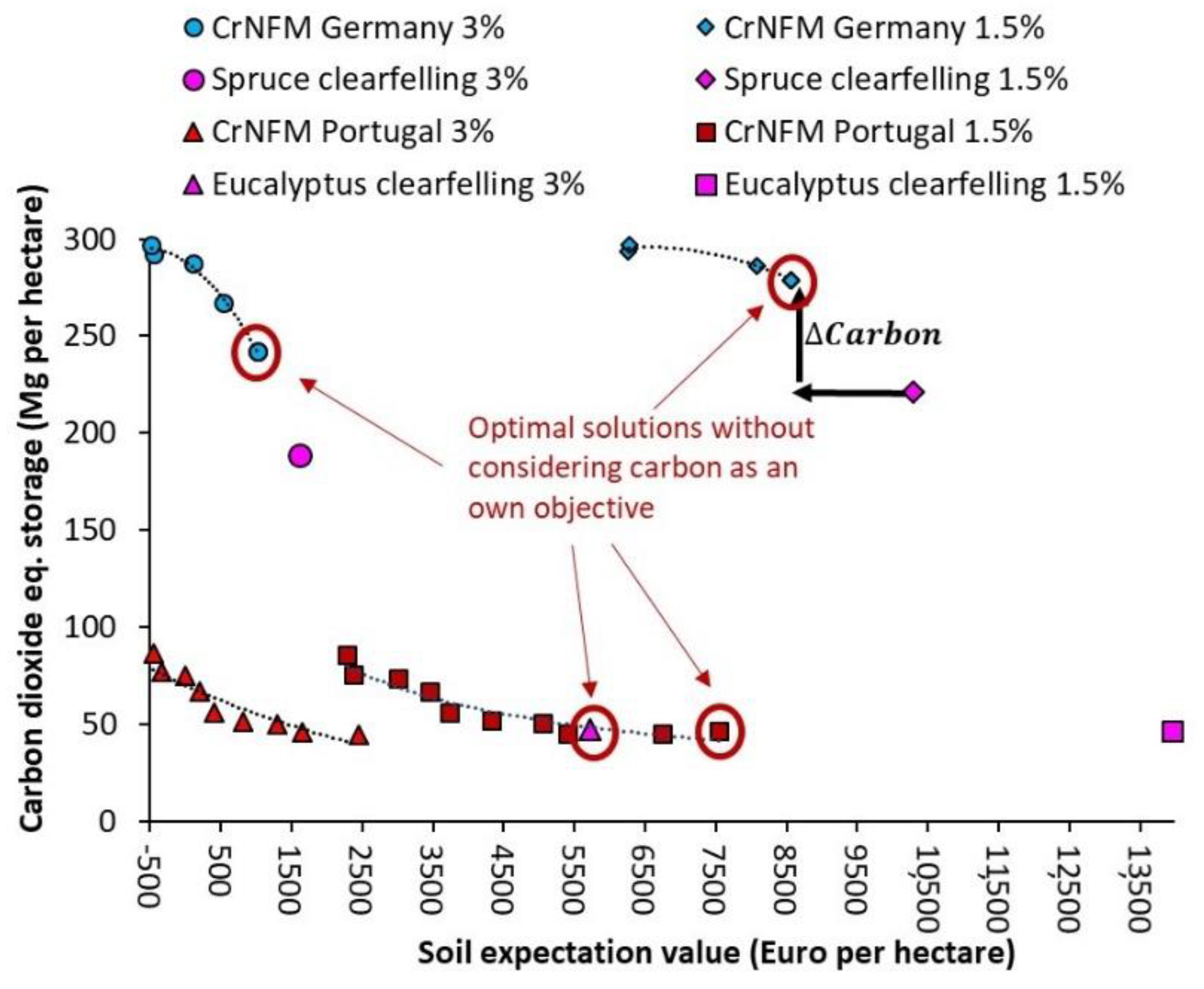
3.2. Trade-Offs between Economic Return and Carbon Storage
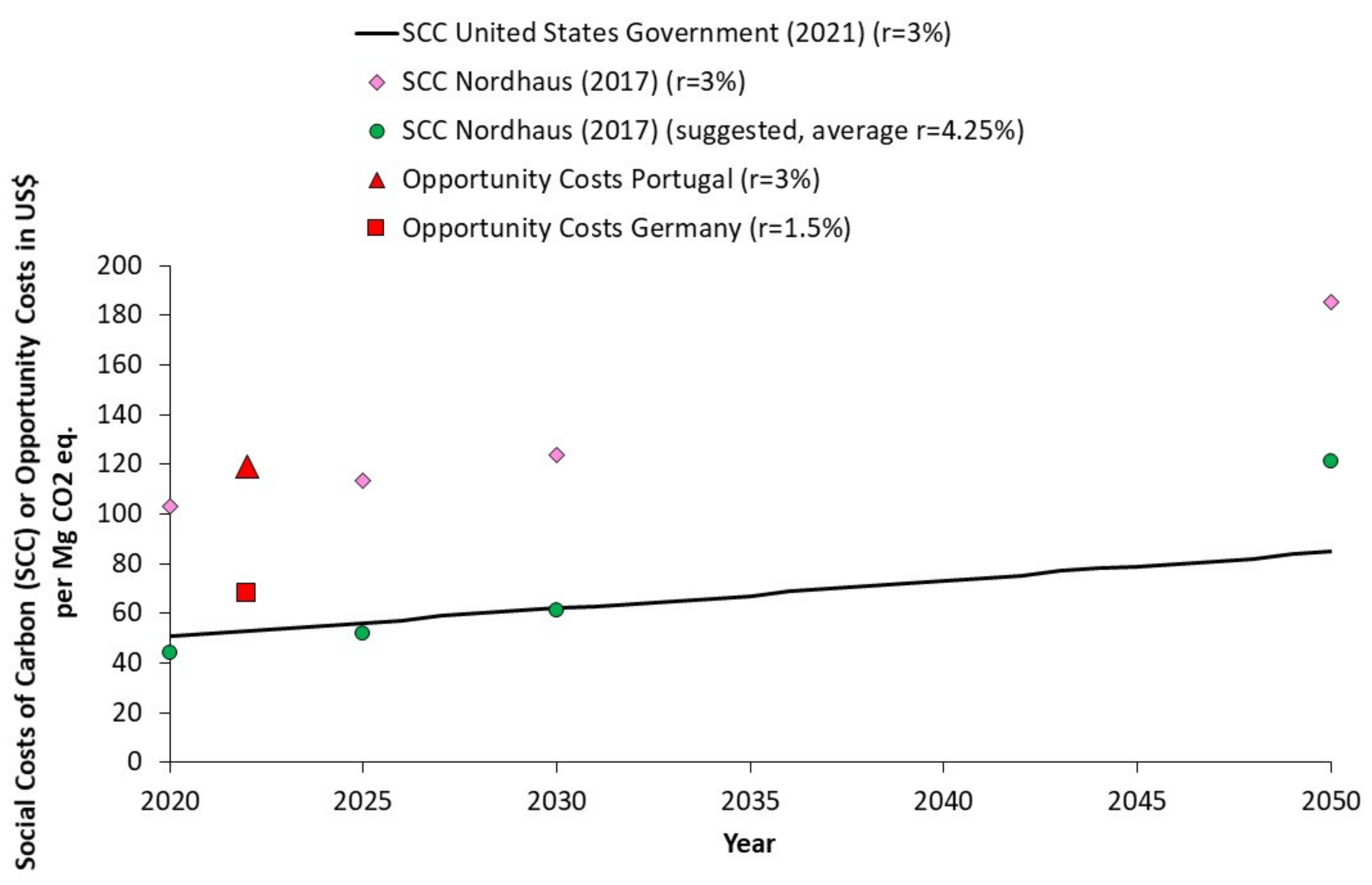
3.3. Social Costs of Carbon as a Benchmark
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lamb, W.F.; Wiedmann, T.; Pongratz, J.; Andrew, R.; Crippa, M.; Olivier, J.G.J.; Wiedenhofer, D.; Mattioli, G.; Khourdajie, A.A.; House, J.; et al. A review of trends and drivers of greenhouse gas emissions by sector from 1990 to 2018. Environ. Res. Lett. 2021, 16, 73005. [Google Scholar] [CrossRef]
- Hinzman, L.; Bettez, N.; Bolton, W.; Chapin, F.; Dyurgerov, M.; Fastie, C.L.; Griffith, B.; Hollister, R.D.; Hope, A.; Huntington, H.P.; et al. Evidence and implications of recent climate change in Northern Alaska and other arctic regions. Clim. Change 2005, 72, 251–298. [Google Scholar] [CrossRef]
- IPCC. Summary for policymakers. In Global Warming of 1.5 °C; An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-industrial Levels and Related Global Greenhouse Gas Emission Pathways, in The Context of Strengthening the Global Response; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Karlsson, I.; Rootzén, J.; Johnsson, F.; Erlandsson, M. Achieving net-zero carbon emissions in construction supply chains—A multidimensional analysis of residential building systems. Dev. Built Environ. 2021, 8, 100059. [Google Scholar] [CrossRef]
- Canadell, J.G.; Raupach, M.R. Managing forests for climate change mitigation. Science 2008, 320, 1456–1457. [Google Scholar] [CrossRef] [Green Version]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [Green Version]
- Sedjo, R.; Sohngen, B. Carbon Sequestration in Forests and Soils. Annu. Rev. Resour. Econ. 2012, 4, 127–144. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [Green Version]
- Gunn, J.S.; Ducey, M.J.; Whitman, A.A. Late-successional and old-growth forest carbon temporal dynamics in the Northern Forest (Northeastern USA). For. Ecol. Manag. 2014, 312, 40–46. [Google Scholar] [CrossRef]
- Noormets, A.; Epron, D.; Domec, J.C.; McNulty, S.G.; Fox, T.; Sun, G.; King, J.S. Effects of forest management on productivity and carbon sequestration: A review and hypothesis. For. Ecol. Manag. 2015, 355, 124–140. [Google Scholar] [CrossRef] [Green Version]
- Ontl, T.A.; Janowiak, M.K.; Swanston, C.W.; Daley, J.; Handler, S.; Cornett, M.; Hagenbuch, S.; Handrick, C.; Mccarthy, L.; Patch, N. Forest Management for Carbon Sequestration and Climate Adaptation. J. For. 2020, 118, 86–101. [Google Scholar] [CrossRef]
- Köthke, M.; Dieter, M. Effects of carbon sequestration rewards on forest management—An empirical application of adjusted Faustmann Formulae. For. Policy Econ. 2010, 12, 589–597. [Google Scholar] [CrossRef]
- West, T.A.; Wilson, C.; Vrachioli, M.; Grogan, K.A. Carbon payments for extended rotations in forest plantations: Conflicting insights from a theoretical model. Ecol. Econ. 2019, 163, 70–76. [Google Scholar] [CrossRef]
- Price, C. Declining discount rate and the social cost of carbon: Forestry consequences. J. For. Econ. 2018, 31, 39–45. [Google Scholar] [CrossRef]
- Pukkala, T. Carbon forestry is surprising. For. Ecosyst. 2018, 5, 11. [Google Scholar] [CrossRef] [Green Version]
- Rockström, J.; Gaffney, O.; Rogelj, J.; Meinshausen, M.; Nakicenovic, N.; Schellnhuber, H.J. A roadmap for rapid decarbonization. Science 2017, 355, 1269–1271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nunery, J.S.; Keeton, W.S. Forest carbon storage in the northeastern United States: Net effects of harvesting frequency, post-harvest retention, and wood products. For. Ecol. Manag. 2010, 259, 1363–1375. [Google Scholar] [CrossRef]
- Achim, A.; Moreau, G.; Coops, N.C.; Axelson, J.N.; Barrette, J.; Bédard, S.; Byrne, K.E.; Caspersen, J.; Dick, A.R.; D’Orangeville, L.; et al. The changing culture of silviculture. For. Int. J. For. Res. 2022, 95, 143–152. [Google Scholar] [CrossRef]
- Ledermann, T.; Braun, M.; Kindermann, G.; Jandl, R.; Ludvig, A.; Schadauer, K.; Schwarzbauer, P.; Weiss, P. Effects of Silvicultural Adaptation Measures on Carbon Stock of Austrian Forests. Forests 2022, 13, 565. [Google Scholar] [CrossRef]
- Assmuth, A.; Rämö, J.; Tahvonen, O. Optimal Carbon Storage in Mixed-Species Size-Structured Forests. Environ. Resour. Econ. 2021, 79, 249–275. [Google Scholar] [CrossRef]
- Kolo, H.; Kindu, M.; Knoke, T. Optimizing forest management for timber production, carbon sequestration and groundwater recharge. Ecosyst. Serv. 2020, 44, 101147. [Google Scholar] [CrossRef]
- Cattaneo, A.; Lubowski, R.; Busch, J.; Creed, A.; Strassburg, B.; Boltz, F.; Ashton, R. On international equity in reducing emissions from deforestation. Environ. Sci. Policy 2010, 13, 742–753. [Google Scholar] [CrossRef]
- Knoke, T.; Kindu, M.; Jarisch, I.; Gosling, E.; Friedrich, S.; Bödeker, K.; Paul, C. How considering multiple criteria, uncertainty scenarios and biological interactions may influence the optimal silvicultural strategy for a mixed forest. For. Policy Econ. 2020, 118, 102239. [Google Scholar] [CrossRef]
- Knoke, T.; Paul, C.; Friedrich, S.; Borchert, H.; Härtl, F.; Chang, S.J. The optimal rotation for a fully regulated forest is the same as, or shorter than, the rotation for a single even-aged forest stand: Comments on Helmedag’s (2018) paper. Eur. J. For. Res. 2020, 139, 133–143. [Google Scholar] [CrossRef]
- Roessiger, J.; Griess, V.C.; Knoke, T. May risk aversion lead to near-natural forestry? A simulation study. For. Int. J. For. Res. 2011, 84, 527–537. [Google Scholar] [CrossRef] [Green Version]
- Messerer, K.; Pretzsch, H.; Knoke, T. A non-stochastic portfolio model for optimizing the transformation of an even-aged forest stand to continuous cover forestry when information about return fluctuation is incomplete. Ann. For. Sci. 2017, 74, 45. [Google Scholar] [CrossRef] [Green Version]
- Bikhchandani, S.; Hirshleifer, J.; Riley, J.G. The Analytics of Uncertainty and Information, 2nd ed.; Cambridge University Press: New York, NY, USA, 2015; ISBN 9780521834087. [Google Scholar]
- Barreiro, S.; Rua, J.; Tomé, M. StandsSIM-MD: A Management Driven forest SIMulator. For. Syst. 2016, 25, eRC07. [Google Scholar] [CrossRef] [Green Version]
- Faias, S.P.; Palma, J.H.N.; Barreiro, S.M.; Paulo, J.A.; Tomé, M. Resource communication. sIMfLOR—Platform for Portuguese forest simulators. For. Syst. 2012, 21, 543. [Google Scholar] [CrossRef] [Green Version]
- Tomé, M.; Oliveira, T.; Soares, P. O Modelo GLOBULUS 3.0 Dados e Equações. Universidade Técnica de Lisboa, Instituto Superior de Agronomia, Centro de Estudos Florestais, Lisboa. Available online: https://www.repository.utl.pt/bitstream/10400.5/1760/1/REP-DEF-RC2%202006.pdf (accessed on 10 September 2022).
- Nunes, L.; Patrício, M.; Tomé, J.; Tomé, M. Modeling dominant height growth of maritime pine in Portugal using GADA methodology with parameters depending on soil and climate variables. Ann. For. Sci. 2011, 68, 311–323. [Google Scholar] [CrossRef] [Green Version]
- Nunes, L.; Tomé, J.; Tomé, M. Prediction of annual tree growth and survival for thinned and unthinned even-aged maritime pine stands in Portugal from data with different time measurement intervals. For. Ecol. Manag. 2011, 262, 1491–1499. [Google Scholar] [CrossRef]
- Monteiro, M.L.; Patrício, M.S. O castanheiro: Modelos de gestão. Rev. Florest. 1996, 9, 51–56. [Google Scholar]
- DGADR. CAOF—Comissão de Acompanhamento Para as Operações Florestais Acessível. Available online: https://www.dgadr.gov.pt/18-mecanizacao-agraria/127-caof (accessed on 10 September 2022).
- Marques, M.; Juerges, N.; Borges, J.G. Appraisal framework for actor interest and power analysis in forest management—Insights from Northern Portugal. For. Policy Econ. 2020, 111, 102049. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Schütze, G.; Uhl, E.; Rötzer, T. Forest stand growth dynamics in Central Europe have accelerated since 1870. Nat. Commun. 2014, 5, 4964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brandl, S.; Paul, C.; Knoke, T.; Falk, W. The influence of climate and management on survival probability for Germany’s most important tree species. For. Ecol. Manag. 2020, 458, 117652. [Google Scholar] [CrossRef]
- Paul, C.; Brandl, S.; Friedrich, S.; Falk, W.; Härtl, F.; Knoke, T. Climate change and mixed forests: How do altered survival probabilities impact economically desirable species proportions of Norway spruce and European beech? Ann. For. Sci. 2019, 76, 14. [Google Scholar] [CrossRef] [Green Version]
- Nordhaus, W.D. Revisiting the social cost of carbon. Proc. Natl. Acad. Sci. USA 2017, 114, 1518–1523. [Google Scholar] [CrossRef] [Green Version]
- Benítez, P.C.; McCallum, I.; Obersteiner, M.; Yamagata, Y. Global potential for carbon sequestration: Geographical distribution, country risk and policy implications. Ecol. Econ. 2007, 60, 572–583. [Google Scholar] [CrossRef]
- Möhring, B.; Rüping, U.; Leefken, G.; Ziegeler, M. The annuity—A “missing link” of the forest economy? Allg. Forst-Jagdztg. 2006, 177, 21–29. [Google Scholar]
- Price, R.; Thornton, S.; Nelson, S. The Social Cost of Carbon and the Shadow Price of Carbon: What They Are, and How to Use Them in Economic Appraisal in the UK; Department for Environment, Food and Rural Affairs: London, UK, 2007.
- United States Government. Table 1.1.9. Implicit Price Deflators for Gross Domestic Product. Available online: https://apps.bea.gov/iTable/iTable.cfm?reqid=19&step=3&isuri=1&1921=survey&1903=13#reqid=19&step=3&isuri=1&1921=survey&1903=13 (accessed on 16 June 2022).
- Larsen, J.B.; Angelstam, P.; Bauhus, J.; Carvalho, J.F.; Diaci, J.; Dobrowolska, D.; Gazda, A.; Gustafsson, L.; Krumm, F.; Knoke, T.; et al. From Science to Policy; European Forest Institute: Joensuu, Finland, 2022. [Google Scholar]
- United States Government. Technical Support Document: Social Cost of Carbon, Methane, and Nitrous Oxide Interim Estimates Under Executive Order 13990. Available online: https://www.whitehouse.gov/wp-content/uploads/2021/02/TechnicalSupportDocument_SocialCostofCarbonMethaneNitrousOxide.pdf (accessed on 29 May 2022).
- Knoke, T.; Weber, M. Expanding Carbon Stocks in Existing Forests—A Methodological Approach for Cost Appraisal at the Enterprise Level. Mitig. Adapt. Strateg. Glob. Change 2006, 11, 579–605. [Google Scholar] [CrossRef]
- Knoke, T.; Paul, C.; Gosling, E.; Jarisch, I.; Mohr, J.; Seidl, R. Assessing the Economic Resilience of Different Management Systems to Severe Forest Disturbance. Environ. Resour. Econ. 2022, in press. [Google Scholar] [CrossRef]
- Di Falco, S.; Perrings, C. Crop biodiversity, risk management and the implications of agricultural assistance. Ecol. Econ. 2005, 55, 459–466. [Google Scholar] [CrossRef] [Green Version]
- Baumgärtner, S.; Quaas, M.F. Managing increasing environmental risks through agrobiodiversity and agrienvironmental policies. Agric. Econ. 2010, 41, 483–496. [Google Scholar] [CrossRef] [Green Version]
- Espagne, E.; Pottier, A.; Fabert, B.P.; Nadaud, F.; Dumas, P. SCCs and the use of IAMs: Let’s separate the wheat from the chaff. Int. Econ. 2018, 155, 29–47. [Google Scholar] [CrossRef]
- Van den Bergh, J.; Botzen, W. Monetary valuation of the social cost of CO2 emissions: A critical survey. Ecol. Econ. 2015, 114, 33–46. [Google Scholar] [CrossRef]
- DePillis, L. Pace of Climate Change Sends Economists Back to Drawing Board; New York Times: New York, NY, USA, 2022. [Google Scholar]
- Roberts, D. The “Uncertainty Loop” Haunting Our Climate Models. Available online: https://www.vox.com/2015/10/23/9604120/climate-models-uncertainty (accessed on 15 September 2022).
- Stern, N.; Stiglitz, J.; Taylor, C. The economics of immense risk, urgent action and radical change: Towards new approaches to the economics of climate change. J. Econ. Methodol. 2022, 29, 181–216. [Google Scholar] [CrossRef]
- Lemoine, D. The Climate Risk Premium: How Uncertainty Affects the Social Cost of Carbon. J. Assoc. Environ. Resour. Econ. 2020, 8, 27–57. [Google Scholar] [CrossRef]
- US GAO. Social Cost of Carbon: Identifying a Federal Entity to Address the National Academies’ Recommendations Could Strengthen Regulatory Analysis; United States Government Accountability Office Report to Congressional Requesters No. GAO-20-254; US GAO: Washington, DC, USA, 2020.
- Dietz, S.; Rising, J.; Stoerk, T.; Wagner, G. Reply to Keen et al.: Dietz et al. modeling of climate tipping points is informative even if estimates are a probable lower bound. Earth Atmos. Planet. Sci. 2022, 119, e2201191119. [Google Scholar] [CrossRef]
- Dietz, S.; Rising, J.; Stoerk, T.; Wagner, G. Economic impacts of tipping points in the climate system. Proc. Natl. Acad. Sci. USA 2021, 118, e2103081118. [Google Scholar] [CrossRef]
- Keen, S.; Lenton, T.M.; Garrett, T.J.; Rae, J.W.B.; Hanley, B.P.; Grasselli, M. Estimates of economic and environmental damages from tipping points cannot be reconciled with the scientific literature. Proc. Natl. Acad. Sci. USA 2022, 119, e2117308119. [Google Scholar] [CrossRef]
- Franzke, C.L.E.; Ciullo, A.; Gilmore, E.A.; Matias, D.M.; Nagabhatla, N.; Orlov, A.; Paterson, S.K.; Scheffran, J.; Sillmann, J. Perspectives on tipping points in integrated models of the natural and human Earth system: Cascading effects and telecoupling. Environ. Res. Lett. 2022, 17, 15004. [Google Scholar] [CrossRef]
- Kemp, L.; Xu, C.; Depledge, J.; Ebi, K.L.; Gibbins, G.; Kohler, T.A.; Rockström, J.; Scheffer, M.; Schellnhuber, H.J.; Steffen, W.; et al. Climate Endgame: Exploring catastrophic climate change scenarios. Proc. Natl. Acad. Sci. USA 2022, 119, e2108146119. [Google Scholar] [CrossRef]
- Rising, J.A.; Taylor, C.; Ives, M.C.; Ward, R.E. Challenges and innovations in the economic evaluation of the risks of climate change. Ecol. Econ. 2022, 197, 107437. [Google Scholar] [CrossRef]
- Matthey, A.; Bünger, B. Methodological Convention 3.0 for the Assessment of Environmental Costs; No. Cost Rates Version 02/2019; Umwelt Bundesamt: Dessau-Roßlau, Germany, 2019. [Google Scholar]
- Wagner, G.; Anthoff, D.; Cropper, M.; Dietz, S.; Gillingham, K.T.; Groom, B.; Kelleher, J.P.; Moore, F.C.; Stock, J.H. Eight priorities for calculating the social cost of carbon. Nature 2021, 590, 548–550. [Google Scholar] [CrossRef] [PubMed]
- Ricke, K.; Drouet, L.; Caldeira, K.; Tavoni, M. Country-level social cost of carbon. Nat. Clim. Change 2018, 8, 895–900. [Google Scholar] [CrossRef] [Green Version]
- Augustynczik, A.L.; Asbeck, T.; Basile, M.; Jonker, M.; Knuff, A.; Yousefpour, R.; Hanewinkel, M. Reconciling forest profitability and biodiversity conservation under disturbance risk: The role of forest management and salvage logging. Environ. Res. Lett. 2020, 15, 0940a3. [Google Scholar] [CrossRef]
- Reith, E.; Gosling, E.; Knoke, T.; Paul, C. How Much Agroforestry Is Needed to Achieve Multifunctional Landscapes at the Forest Frontier?—Coupling Expert Opinion with Robust Goal Programming. Sustainability 2020, 12, 6077. [Google Scholar] [CrossRef]
- Aparício, B.A.; Alcasena, F.; Ager, A.; Chung, W.; Pereira, J.M.; Sá, A.C. Evaluating priority locations and potential benefits for building a nation-wide fuel break network in Portugal. J. Environ. Manag. 2022, 320, 115920. [Google Scholar] [CrossRef]
- Dobor, L.; Hlásny, T.; Rammer, W.; Zimová, S.; Barka, I.; Seidl, R. Spatial configuration matters when removing windfelled trees to manage bark beetle disturbances in Central European forest landscapes. J. Environ. Manag. 2020, 254, 109792. [Google Scholar] [CrossRef]
- Quine, C.P.; Gardiner, B.A.; Moore, J. Wind disturbance in forests: The process of wind created gaps, tree overturning, and stem breakage. In Plant Disturbance Ecology; Academic Press: Cambridge, MA, USA, 2021; pp. 117–184. [Google Scholar]
- Augustynczik, A.L.D.; Arce, J.E.; Yousefpour, R.; da Silva, A.C.L. Promoting harvesting stands connectivity and its economic implications in Brazilian forest plantations applying integer linear programming and simulated annealing. For. Policy Econ. 2016, 73, 120–129. [Google Scholar] [CrossRef]
- Bellavenutte, P.; Chung, W.; Diaz-Balteiro, L. Partitioning and solving large-scale tac-tical harvest scheduling problems for industrial plantation forests. Can. J. For. Res. 2020, 50, 811–818. [Google Scholar] [CrossRef]
- St John, R.; Tóth, S.F.; Zabinsky, Z.B. Optimizing the geometry of wildlife corridors in conservation reserve design. Oper. Res. 2018, 66, 1471–1485. [Google Scholar] [CrossRef] [Green Version]
- Jarisch, I.; Bödeker, K.; Bingham, L.R.; Friedrich, S.; Kindu, M.; Knoke, T. The influence of discounting ecosystem services in robust multi-objective optimization—An application to a forestry-avocado land-use portfolio. For. Policy Econ. 2022, 141, 102761. [Google Scholar] [CrossRef]
- Schulze, E.D.; Sierra, C.A.; Egenolf, V.; Woerdehoff, R.; Irslinger, R.; Baldamus, C.; Stupak, I.; Spellmann, H. The climate change mitigation effect of bioenergy from sustaina-bly managed forests in Central Europe. GCB Bioenergy 2020, 12, 186–197. [Google Scholar] [CrossRef]
- Borges, J.G.; Marques, S.; Garcia-Gonzalo, J.; Rahman, A.U.; Bushenkov, V.; Sottomayor, M.; Carvalho, P.O.; Nordström, E.-M. A multiple criteria approach for negotiating ecosystem services supply targets and forest owners’ programs. For. Sci. 2017, 63, 49–61. [Google Scholar] [CrossRef]
- Garcia-Gonzalo, J.; Borges, J.G.; Palma, J.H.N.; Zubizarreta-Gerendiain, A. A decision support system for management planning of Eucalyptus plantations facing climate change. Ann. For. Sci. 2014, 71, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Cabiyo, B.; Fried, J.S.; Collins, B.M.; Stewart, W.; Wong, J.; Sanchez, D.L. Innovative wood use can enable carbon-beneficial forest management in California. Proc. Natl. Acad. Sci. USA 2021, 118, e2019073118. [Google Scholar] [CrossRef]
- Gunn, J.S.; Ducey, M.J.; Buchholz, T.; Belair, E.P. Forest carbon resilience of eastern spruce budworm (Choristoneura fumiferana) salvage harvesting in the Northeastern United States. Front. For. Glob. Change 2020, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Härtl, F.H.; Höllerl, S.; Knoke, T. A new way of carbon accounting emphasises the crucial role of sustainable timber use for successful carbon mitigation strategies. Mitig. Adapt. Strateg. Glob. Change 2017, 22, 1163–1192. [Google Scholar] [CrossRef]
- Badgley, G.; Freeman, J.; Hamman, J.J.; Haya, B.; Trugman, A.T.; Anderegg, W.R.L.; Cullenward, D. Systematic over-crediting in California’s forest carbon offsets program. Glob. Change Biol. 2022, 28, 1433–1445. [Google Scholar] [CrossRef]
- Gifford, L. “You can’t value what you can’t measure”: A critical look at forest carbon accounting. Clim. Change 2020, 161, 291–306. [Google Scholar] [CrossRef]
| Portuguese Case Study | |
| Species | Data Sources |
| Maritime pine | [28,29,31,32,34,35] |
| Chestnut | [28,29,31,32,34,35] |
| Eucalyptus | [28,29,30,34,35] |
| Germany Case Study | |
| Species | Data Sources |
| Spruce | [23,36,37,38] |
| Silver fir | [23,37,38] |
| Beech | [23,36,37,38] |
| Discount Rate | |||||
|---|---|---|---|---|---|
| 1.5 | 3.0 | ||||
| Carbon Is No Objective | Carbon Is an Objective | Carbon Is No Objective | Carbon Is an Objective | ||
| Portugal | Tree species [%] | ||||
| Maritime pine | 17.5 | 0 | 0 | 0 | |
| Chestnut | 5.8 | 100 | 0 | 100 | |
| Eucalyptus | 76.7 | 0 | 100 | 0 | |
| Soil expectation value [EUR per hectare] | 7545 | 2249 | 5739 | −533 | |
| Average carbon storage [Mg CO2 equivalent per hectare] | 46.61 | 99.69 | 44.64 | 99.69 | |
| Opportunity costs [EUR per Mg CO2 equivalent] | 99.97 | 118.79 | |||
| Germany | Tree species [%] | ||||
| Spruce | 38.9 | 37.3 | 47.3 | 43.2 | |
| Silver fir | 49.6 | 46.3 | 50.3 | 48.9 | |
| Beech | 11.5 | 16.4 | 2.4 | 7.9 | |
| Soil expectation value [EUR per hectare] | 8560 | 8077 | 1012 | 541 | |
| Average carbon storage [Mg CO2 equivalent per hectare] | 279.02 | 297.23 | 242.19 | 266.94 | |
| Opportunity costs [EUR per Mg CO2 equivalent] | 68.12 | 18.95 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kindu, M.; Bingham, L.R.; Borges, J.G.; Marques, S.; Nahorna, O.; Eggers, J.; Knoke, T. Opportunity Costs of In Situ Carbon Storage Derived by Multiple-Objective Stand-Level Optimization—Results from Case Studies in Portugal and Germany. Land 2022, 11, 2085. https://doi.org/10.3390/land11112085
Kindu M, Bingham LR, Borges JG, Marques S, Nahorna O, Eggers J, Knoke T. Opportunity Costs of In Situ Carbon Storage Derived by Multiple-Objective Stand-Level Optimization—Results from Case Studies in Portugal and Germany. Land. 2022; 11(11):2085. https://doi.org/10.3390/land11112085
Chicago/Turabian StyleKindu, Mengistie, Logan Robert Bingham, José G. Borges, Susete Marques, Olha Nahorna, Jeannette Eggers, and Thomas Knoke. 2022. "Opportunity Costs of In Situ Carbon Storage Derived by Multiple-Objective Stand-Level Optimization—Results from Case Studies in Portugal and Germany" Land 11, no. 11: 2085. https://doi.org/10.3390/land11112085
APA StyleKindu, M., Bingham, L. R., Borges, J. G., Marques, S., Nahorna, O., Eggers, J., & Knoke, T. (2022). Opportunity Costs of In Situ Carbon Storage Derived by Multiple-Objective Stand-Level Optimization—Results from Case Studies in Portugal and Germany. Land, 11(11), 2085. https://doi.org/10.3390/land11112085










