Abstract
Cultivated land fragmentation (CLF) is a key obstacle to agricultural development and has a strong relationship with regional food security and global sustainable development. However, few studies have analyzed the spatio-temporal distribution pattern and evolution characteristics of CLF and the complex interactions among their influencing factors in rapidly developing regions. In this study, first, the GlobeLand30 datasets were used to obtain characteristic parameters of cultivated land in counties in Guangdong Province in 2000, 2010, and 2020. Then, the linear weighted comprehensive evaluation model based on the principal component analysis (PCA) was used to measure the extent of CLF. Finally, the exploratory spatial data analysis (ESDA) was used to analyze the spatio-temporal distribution pattern and evolution characteristics of CLF, and geodetector (GD) and random forest (RF) models were used to explore the factors influencing the spatial difference in CLF. The results showed that the spatial differences in the distribution of cultivated land resources in Guangdong Province are relatively large and the extent of agglomeration is generally low. The extent of CLF on the county scale is mainly medium and higher. The overall spatial distribution shows an increasing trend from the south to the north and from the west to the east, and the spatial distribution pattern with agglomeration and randomness remains relatively stable. From 2000 to 2020, the overall CLF continued to intensify and the evolution of CLF on the county scale mainly increased. The spatial difference in CLF is the result of that based on the natural environment and influenced by factors such as social, economic, and agricultural development. The interaction between influencing factors is very strong, dominated by nonlinear enhancement. The results are of great significance for promoting the intensive and efficient utilization of cultivated land resources and sustainable regional development.
1. Introduction
Cultivated land fragmentation (CLF) means the cultivated land plot has changed from a single, homogeneous, concentrated, and contiguous whole to a complex, heterogeneous, and divided patch mosaic [1,2]. CLF is driven by both natural and human factors and makes it difficult to carry out centralized contiguous operation and large-scale management [3]. As a typical feature of global cultivated land landscape and one of the main deterrents to agricultural development [4,5,6], CLF has a strong relationship with regional food security and global sustainable development [7]. CLF can restrict the use of agricultural machineries [8] and the construction of infrastructure [9] and hinder the centralized management and large-scale operation of cultivated land and the process of agricultural modernization and scale [10], resulting in low efficiency in agricultural production [11,12,13,14], waste of production materials [15], and increase in production cost [16,17,18]. In addition, the CLF process can seriously damage the cultivated soil, reduce soil fertility [19], lead to a decline in grain production capacity [20,21], and threaten national food security and social stability [22]. CLF can also change the regional microclimate [23,24], lead to the loss of biodiversity [25], and affect global soil carbon pools [26] and ecosystem functions [2,27,28,29]. Therefore, CLF has received extensive attention from academia and governments around the world and addressing the CLF problem has become a top priority for global agricultural policy [30,31]. Scientifically assessing the extent of CLF and analyzing its causes are key steps in promoting the intensive and efficient utilization of cultivated land resources, improving the productivity of cultivated land, promoting agricultural modernization and scale, and boosting rural development [21]. Conducting research works around this is of great significance in guaranteeing regional food security, maintaining ecological security patterns, and ensuring the sustainable development of the world.
Many scholars have carried out extensive research works on CLF and achieved rich results. The research mainly focuses on the definition of CLF [1,32], quantitative evaluation [15,33], detection of spatio-temporal patterns [34,35], analysis of influencing factors [3,36,37], and exploration of optimization methods [38,39]. The definition of CLF is the premise, the quantitative evaluation is the basis, the detection of spatio-temporal patterns is the important content, and the analysis of the influencing factors is the focus and the key to exploring optimization methods. Therefore, the current state of research on the influencing factors of CLF is elaborated in detail here. There are many methods (or models) for carrying out research on factors influencing CLF. These can be roughly divided into two types, methods based on correlation analysis and methods based on regression analysis. Methods based on correlation analysis reflect the relationship between two or more variables in the form of a correlation coefficient, such as the Pearson correlation coefficient [14], the Spearman correlation coefficient, or Moran’s I index [35]. However, the correlation coefficient only expresses the magnitude and direction of the extent of correlation between two variables. It neither states that the relationship is causal nor explains the specific relationship (the specific form of the mutual relationship) between the two variables.
Methods based on regression analysis are a continuation of the methods based on correlation analysis and can not only reveal the influence of independent variables on dependent variables but also perform quantitative prediction and control based on regression equations. Regression analysis can be divided into classical statistical regression [37] and spatial regression [29,40]. Using classical statistical regression for parameter estimation requires that the data satisfy assumptions such as independence, normal distribution, and homoscedasticity. However, according to the first law of geography (TFL) proposed by American geographer W. R. Tobler, “Everything is related to everything else, but near things are more related than distant things” [41], there is spatial autocorrelation between spatial things. It is difficult for classical statistical regression to reflect the real spatial characteristics of the dependent variable. Compared with classical statistical regression, spatial regression increases the consideration of spatial relationships. It combines attribute data with spatial position through a spatial relationship, which weakens the assumption that the data must satisfy the independence and homoscedasticity, as required in classical statistical regression. Spatial regression can better explain the spatial non-stationarity and spatial heterogeneity of geographic things. However, both classical statistical regression and spatial regression assume a linear relationship for model construction. In other words, the relationship described by these two methods is linear (a straight line), and CLF is a complex geographical phenomenon with obvious spatio-temporal differences and nonlinear characteristics. Therefore, methods such as classical statistical regression and spatial regression, which assume a linear relationship, are not applicable.
In addition, previous studies have mostly analyzed the strength of the individual effects of influencing factors but have given little or no attention to the interaction between influencing factors, although some studies have used the method of adding the sum or product of two influencing factors to the regression model and testing its significance to identify the extent of interaction between two influencing factors, assuming an additive or multiplicative interaction. However, the interaction between influencing factors is complex and not necessarily an additive or multiplicative relationship [42]. Therefore, we believe that to analyze the factors influencing regional CLF, it is important to introduce a nonlinear model that takes into account the complex interactions among influencing factors.
Considering the huge differences in China’s regional economic and urbanization development, the evolution trajectory of cultivated land in rapidly developing regions may be followed by less developed regions. Conducting research in these regions will not only help optimize local and national cultivated land protection approaches and strategies but also provide a reference for formulating cultivated land protection measures in less developed regions. Therefore, in this study, Guangdong Province, where the economy continues to develop rapidly and urbanization continues to accelerate, was selected as the study area. First, the GlobeLand30 datasets were used to obtain the characteristic parameters of cultivated land, such as the area, the spatial distribution, and the shape, in the study area in 2000, 2010, and 2020; then, the linear weighted comprehensive evaluation model based on the principal component analysis (PCA) was used to measure the extent of CLF; finally, the exploratory spatial data analysis (ESDA) was used to analyze the spatio-temporal distribution pattern and evolution characteristics of CLF, and geodetector (GD) and random forest (RF) models were used to explore the factors influencing the spatial difference in CLF. The main purpose of this study was to analyze the spatio-temporal distribution characteristics of cultivated land, measure the extent and explore the spatio-temporal distribution pattern and evolution characteristics of CLF, and detect the factors influencing the spatial difference in CLF in Guangdong Province from 2000 to 2020. These not only can provide scientific support for assessing the CLF and dissecting the driving mechanism of the CLF in rapidly developing regions but also can provide a data basis for formulating policies and measures to alleviate CLF, ultimately promoting the intensive and efficient utilization of cultivated land resources, promoting the modernization, scale, and sustainable development of agriculture, and ensuring food security.
2. Materials and Methods
2.1. Study Area
The study area, Guangdong Province (20°09′–25°31′ N, 109°45′–117°20′ E), is located in the southern coastal region of China (Figure 1). The terrain slopes from the north to the south. The northern region is dominated by mountains and hills, with a higher terrain, while the southern region is dominated by plains and platforms, with a lower terrain. A subtropical monsoon climate dominates, with an annual average temperature of 19.0–23.8 °C, an average annual precipitation of 1179.6–2320.9 mm, and an annual total solar radiation of 4200–5400 MJ/m2. The area is rich in light, heat, and water resources, and the rainy season and the hot season are synchronized. The superior geographical location and climate conditions are beneficial to agricultural production. In 2020, the total area of cultivated land in Guangdong Province was 2.59 million hectares, accounting for 14.43% of the total land area. The total planting area of grain crops was 2.20 million hectares, and the grain output was 12.68 million tons. Guangdong Province is the frontier of the “Reform and Openness” policy and the southern gate of China, and its society and economy have experienced continuous rapid development. The regional gross domestic production (GDP) exceeded CNY 11 trillion in 2020 (Guangdong Province ranked first among all provinces in China for 32 consecutive years). At the end of 2020, the permanent resident population was 126.24 million, with a population density of 702 person/km2, and the urban population accounted for 74.15% of the total.
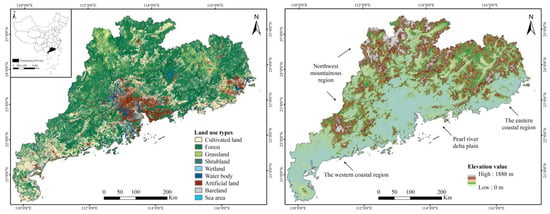
Figure 1.
Status of land use (2020) and elevation of the study area.
2.2. Data Sources
The main data sources for this study were as follows:
- (1)
- The cultivated land data were extracted from the global land cover data with a spatial resolution of 30 m, GlobeLand30, which is the first global geographic information public product provided by China to the United Nations and was praised by international peer experts as “a milestone in the openness and sharing of earth observation and geographic information”. The data results have been applied in nearly 120 countries across 5 continents, and the application fields include land cover mapping [43,44,45], land cover change monitoring [46,47,48], and ecosystem service value assessment [49]. GlobeLand30 provides high-quality scientific data for research on global environmental change and sustainable development [50,51]. The data include 10 land use types: cultivated land, forest, grassland, shrubland, wetland, water body, tundra, artificial land, bare land, and permanent snow and ice. The overall accuracy of the data in 2010 and 2020 was 83.50% and 85.72%, respectively, and the kappa coefficients were 0.78 and 0.82, respectively. Details of GlobeLand30 can be found at http://www.globallandcover.com, accessed on 11 December 2021.
- (2)
- The slope data were extracted from the ASTER GDEM V2 digital elevation model (DEM) with a spatial resolution of 30 m, which was downloaded from the geospatial data cloud platform (http://www.gscloud.cn, accessed on 11 December 2021).
- (3)
- The socioeconomic data were derived from Guangdong Yearbook (2021), Guangdong Statistical Yearbook (2021), and Guangdong Rural Statistical Yearbook (2021), as well as some local yearbooks.
2.3. Analytical Methods
To explore the spatio-temporal characteristics of and factors influencing CLF in Guangdong Province, (1) the Lorenz curve and the kernel density estimation (KDE) method were used to analyze the spatio-temporal distribution characteristics of cultivated land in Guangdong Province, (2) the linear weighted comprehensive evaluation model based on the PCA was used to measure the extent of CLF, and (3) the ESDA was used to analyze the spatio-temporal distribution pattern and evolution characteristics of CLF and GD and RF models were used to explore the factors influencing the spatial difference in CLF (Figure 2). GD and RF were combined to analyze the influencing factors, because these two methods do not assume a linear relationship and are immune to multi-independent variable collinearity. The former can not only identify the ability of each influencing factor to explain the spatial difference in CLF but also judge whether there is an interaction between any two influencing factors and identify the strength, direction, and linearity or nonlinearity of the interaction. The latter has the advantages of high operating efficiency, high model accuracy, and high tolerance to outliers and noise. Using it to build a regression model between CLF and influencing factors can help identify the importance of each factor influencing CLF. In addition, the analysis results of the two models can be compared and verified to a certain extent.
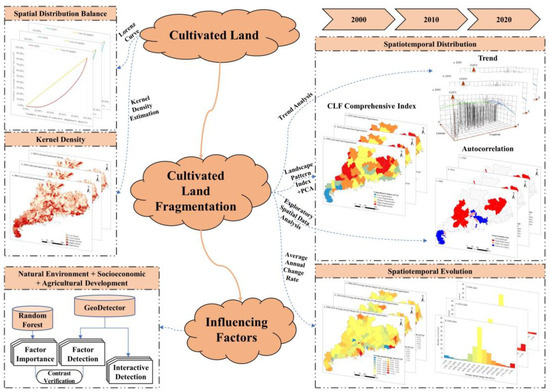
Figure 2.
General research framework.
2.3.1. Comprehensive Evaluation of CLF
- Selection of evaluation indicators and determination of their weights
Landscape ecology has obvious advantages in quantitatively identifying complex physical patterns in agricultural systems [29,52]. It provides quantitative indicators with high information content and strong description function [53] and landscape pattern indices that can reflect features of the landscape, such as structural composition and spatial configuration [54]. These quantitative indicators can also be used to describe the features of cultivated land, such as quantity, scale, shape, and spatial distribution [8,55,56,57]. Therefore, aiming at the realistic needs of current agricultural development, i.e., intensive and efficient development and moderate-scale operation, and referring to those indicators used to quantitatively evaluate the extent of CLF in existing studies [37,58,59,60], our study selected eight landscape pattern indices as indicators for evaluating CLF, covering three aspects: resource endowment, spatial aggregation and dispersion, and convenience of utilization. Table 1 presents the calculation formula and meaning of each landscape pattern index, and the specific calculation process was realized with the help of the Fragstats 4.2 software [61].

Table 1.
Evaluation index system of CLF on the county scale in Guangdong Province.
Since the landscape pattern indices used to evaluate CLF may be strongly correlated [29,62], which is not conducive to evaluating and analyzing CLF, it is necessary to perform a multicollinearity test first. Our study combined the variance inflation factor (VIF) and tolerance (Tol) for the multicollinearity test. It is generally believed that when VIF > 10 and Tol < 0.1, there is severe multicollinearity between one independent variable and the other independent variables. As shown in Table 2, the VIFs of all landscape pattern indices are less than 10, and the Tol values are greater than 0.1, indicating that there is no serious collinearity problem among the landscape pattern indices.

Table 2.
Test results of multicollinearity among landscape pattern indices.
The values of the selected landscape pattern indices have different connotative characteristics and dimensions and analyzing them directly may weaken the indices with lower values, leading to deviations in the results of the comprehensive analysis. Therefore, to standardize the values of the indicators, our study adopted the maximum difference normalization method. Note that if you are measuring the extent of CLF in a certain year, you need to conduct spatial global standardization on the values of each landscape pattern index only in that year. However, in our study, we also needed to analyze the evolution process of CLF. To ensure that the CLF evaluation results in different years are comparable, it is necessary to conduct global normalization in time series on the values of each landscape pattern index, that is, the global maximum and minimum values of each landscape pattern index in the time series direction are selected for normalization. However, existing studies often ignore this point [63]. The formula of the maximum difference normalization method is as follows:
where and are the normalized value and the actual value of the j-th indicator in the i-th year, respectively, and and are the minimum value and the maximum value of the actual value of the j-th indicator in the i-th year, respectively.
Considering the correlation among the landscape pattern indices [64] and the subjectivity of the Delphi method and the analytic hierarchy process (AHP) method in the process of setting weights, the principal component analysis (PCA) method was adopted to determine the weight of each landscape pattern index. The weight of a specific evaluation index is the normalization of the weighted average of the coefficients of the index in each linear combination of principal components, and the weight in the weighted average process is the variance contribution rate of each principal component. The advantage of this method is that the composite weight, which integrates the information of each index, is determined according to the property of the data themselves and the contribution to different principal components. This avoids the deviation caused by human subjective factors and different methods [63,65]. The process of principal component analysis was implemented in SPSS 23 software. As per the results, the value of the Kaiser–Meyer–Olkin test statistic, the measure of sampling adequacy, was 0.641, between 0.6 and 0.7. The chi-square value of Bartlett’s test of sphericity was 1538.123, and the significance was 0.000, less than 0.005, which is an extremely significant level.
- 2.
- Construction of the evaluation model
The linear weighted comprehensive evaluation model was used to measure the cultivated land fragmentation composite index (CLFCI) of each county. The formula for calculation is as follows:
where is the cultivated land fragmentation composite index, is the normalized value of the indicator , and is the weight of the indicator .
After that, the annual average rate of change in the CLFCI in each county was calculated using the following formula:
where is the annual average rate of change in the CLFCI, and are the value of the CLFCI at the beginning of the period and the value of the CLFCI at the end of the period, respectively, and is the study period (year).
2.3.2. Spatio-Temporal Characteristic Analysis of CLF
Due to the spatial heterogeneity of CLF, it is necessary to analyze the spatial distribution characteristics in order to formulate targeted improvement approaches. Exploratory spatial data analysis (ESDA) has the function of spatial identification and is mainly used to detect the non-randomness of spatial distribution. It can not only make up for the shortcomings of the regional difference measurement method in the spatial perspective but also visually describe the spatial distribution of the data, reveal the spatial structure and interaction mechanism of the data, and avoid the subjectivity and ambiguity errors caused by the direct judgment of the value map [66]. One of the main methods of ESDA is spatial autocorrelation analysis [34], including global spatial autocorrelation analysis and local spatial autocorrelation analysis [67]. In the former, Global Moran’s I is used to analyze the spatial relationship characteristics of a certain geographical phenomenon or a certain attribute value in the whole large area [68]. In the latter, Local Moran’s I is used to analyze the spatial relationship characteristics of a certain geographical phenomenon or a certain attribute value in the local small area unit in the whole large area [69], and it can be represented intuitively in the form of a LISA (local indicator of spatial association) diagram of the spatial agglomeration characteristics and spatial interaction of each regional unit within the region [70]. The spatial autocorrelation analysis process was implemented in GeoDa 1.8 software [71]. The formulas for calculating Global Moran’s I and Local Moran’s I are as follows:
where is the number of county-level administrative districts in the study area, and are the values of the cultivated land fragmentation composite index of county and county , respectively, is a spatial weight matrix, and and are the variance and average value of the values of cultivated land fragmentation composite index in all counties in the study area, respectively.
2.3.3. Detection of Factors Influencing Spatial Difference in CLF
Since the research methods based on correlation analysis can only obtain the magnitude and direction of the correlation between two variables, they neither state that the relationship is causal nor explain its specific form. Research methods based on regression analysis assume a linear relationship and so are not applicable for analyzing a geographical phenomenon with complex nonlinear characteristics. Moreover, due to the existence of multicollinearity, it is difficult to include more independent variables if using research methods based on regression analysis. Therefore, this study attempted to use geodetector (GD), a nonlinear model, to analyze the factors influencing spatial difference in CLF and the interaction among influencing factors. Meanwhile, the random forest model was used to analyze the importance of the factors, and the results were compared with the factor detection results of GD for validation.
- Geodetector Model
Geodetector (GD) is an important method for detecting the cause and mechanism of the spatial pattern of geographic elements [72]. It quantitatively measures the importance of each independent variable compared to the dependent variable by analyzing the overall differences between various types of geographic spaces [73]. The characteristics of this model are as follows: (1) There are few assumptions (almost none), which can effectively overcome the limitations of traditional calculation models, such as more assumptions and data requirements [74]. (2) The factor detector can be used to quantitatively analyze the explanatory power of each influencing factor regarding the spatial differentiation of cultivated land fragmentation [72]. (3) The interaction detector can be used to quantitatively analyze the existence, strength, and linearity or nonlinearity of the interaction between a certain two influencing factors [42]. The model is widely used in many fields of natural sciences, such as geology, meteorology, and environment, and social sciences, such as public health, regional economy, and land use [75]. It is mainly used to study the influence mechanism of social and economic factors and natural environment factors [76]. In view of the above advantages, our study introduced the GD model into the quantitative study of the factors influencing the spatial difference in CLF. The formula for calculation is as follows:
where is the explanatory power of the influencing factor, is the strata of the cultivated land fragmentation composite index or a certain influencing factor, , and are the number of samples in strata and the entire study area, respectively, is the variance in the value of the CLFCI in strata , and is the variance in the value of the CLFCI in the entire study area.
- 2.
- Random Forest Model
The random forest (RF) model is a machine learning algorithm based on classification trees proposed by Breiman and Adele in 2001 [76]. Compared with multiple linear regression (MLR), spatial autocorrelation, geographically weighted regression (GWR), and other models, the RF model has advantages such as insensitivity to multi-independent variable collinearity, high operating efficiency, high model accuracy, and high tolerance to outliers and noise [77]. The RF model is able to measure the importance of variables, which helps understand the mechanisms affecting the spatial difference in CLF. Therefore, our study introduced the RF model to measure the importance of each factor influencing the spatial difference in CLF, and the obtained results were compared and verified with the analysis results of influencing factors based on the GD model.
3. Results
3.1. Spatio-Temporal Distribution Characteristics of Cultivated Land
3.1.1. Balance of Spatio-Temporal Distribution of Cultivated Land
To analyze the balance of the spatial distribution of cultivated land resources in Guangdong Province in 2000, 2010, and 2020, Lorenz curves (Figure 3) were used. The curves were far away from the absolute mean line, and the degrees of bending were relatively large. Analysis showed that the spatial distribution of cultivated land resources in Guangdong Province in 2000, 2010, and 2020 was relatively scattered. To intuitively characterize the difference in the spatial distribution of cultivated land resources, the Gini coefficients of the spatial distribution of cultivated land resources in Guangdong Province in 2000, 2010, and 2020 were calculated and found to be 0.462, 0.468, and 0.481, respectively. The values were all between 0.4 and 0.6 and gradually increased, indicating that the spatial differences in the distribution of cultivated land resources in Guangdong Province were relatively large and showed a gradually increasing trend.
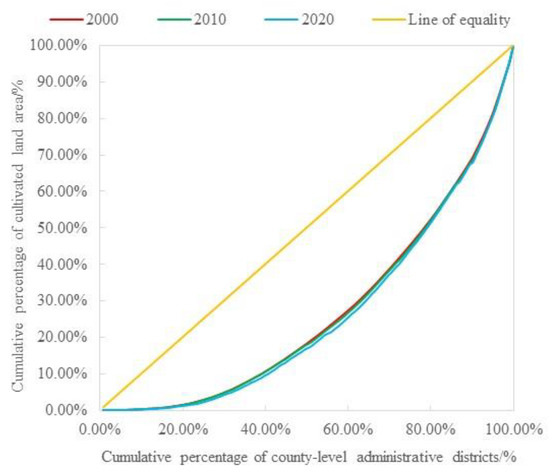
Figure 3.
Lorenz curves of spatial distribution of cultivated land resources in Guangdong Province in 2000, 2010, and 2020.
3.1.2. Spatial Agglomeration Distribution Characteristics of Cultivated Land
The kernel density of cultivated land can be used to characterize the aggregation of cultivated land plots. The larger the value, the more concentrated the spatial distribution of cultivated land. As shown in Figure 4, the cultivated land kernel density distribution in Guangdong Province in 2000, 2010, and 2020 was similar to grape bunches and the spatial distribution patterns were basically the same. The overall cultivated land kernel density showed an increasing trend from north to south and from west to east. Among all the kernel density grades of cultivated land, the area of the low-density-grade zone was the largest, followed by areas of lower density, medium density, higher density, and high density, indicating that the aggregate degree of cultivated land in Guangdong Province is generally low. The reasons are as follows: In the northern part of Guangdong Province, due to the large proportion of mountains and hills, the quantity of cultivated land was small and the spatial distribution was scattered, so the kernel density of cultivated land was low. In the Pearl River Delta Plain, due to the large radiation from the economic circle, the quantity of cultivated land was constantly decreasing, the reserve cultivated land resources were insufficient, the fragmentation was serious, and the kernel density of cultivated land was relatively low. In the Chaoshan Plain in the eastern coastal region and the platform along Leizhou Peninsula–Dianbai–Yangjiang on the western coast of Guangdong Province, there was a large amount of cultivated land, and the kernel density of cultivated land was relatively high. However, since the total area of these two regions was not large, the contribution to the overall value of the kernel density of cultivated land in Guangdong Province was small. From 2000 to 2020, the overall kernel density of cultivated land in Guangdong Province showed a continuous decreasing trend. Specifically, the areas of high-density-grade and higher-density-grade zones continued to decrease, and the areas of low-density-grade and lower-density-grade zones continued to increase (Table 3).
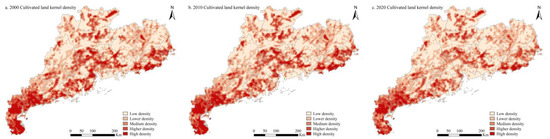
Figure 4.
Spatial distribution of cultivated land kernel density in Guangdong Province in 2000 (a), 2010 (b), and 2020 (c). The spatial distribution of cultivated land kernel density in Guangdong Province in 2000, 2010, and 2020 are displayed in (a,b), and (c), respectively.

Table 3.
The area ratio of each cultivated land kernel density grade zone in Guangdong Province in 2000, 2010, and 2020.
3.2. Spatio-Temporal Distribution Characteristics of CLF
3.2.1. Spatio-Temporal Distribution of CLF
The CLFCI of each county in Guangdong Province in 2000, 2010, and 2020 was calculated using formula (2), and the natural breaks method was used to divide them into five grades: low fragmentation (0.138–0.301), lower fragmentation (0.301–0.457), medium fragmentation (0.457–0.516), higher fragmentation (0.516-0.585), and high fragmentation (0.585–0.728). Overall, the average values of the CLFCI in Guangdong Province in 2000, 2010, and 2020 were 0.506, 0.508, and 0.516, respectively, and across all counties, the extent of CLF was dominated by medium fragmentation and higher fragmentation (Table 4). In terms of spatial distribution, the CLFCI values of all counties generally showed a “wave” shape, high in the north and low in the south, and an inverted “U” shape, high in the middle and low in the east and the west (Figure 5). In 2000, the extent of CLF in Meizhou and Heyuan in the northeastern region and Yunfu and Zhaoqing in the western region of Guangdong Province was relatively high, while the extent of CLF in Zhanjiang and Maoming in the western coastal region and Chaozhou and Shanwei in the eastern coastal region was relatively low. In 2010, the extent of CLF in each county in Guangdong Province increased slightly. The CLF in Yangjiang and Jiangmen in the western coastal region and Chaozhou in the eastern coastal region showed varying degrees of exacerbation. In 2020, the extent of CLF in each county in Guangdong Province increased significantly. The CLF in Guangzhou, Dongguan, and Foshan in the central region, Zhaoqing in the western region, Jieyang and Shantou in the eastern coastal region, Meizhou, Qingyuan, and Shaoguan in the northern region, and Zhanjiang and Maoming in the western coastal region all showed varying degrees of exacerbation (Figure 6).

Table 4.
Proportion of the number of counties of each CLF grade in Guangdong Province in 2000, 2010, and 2020.
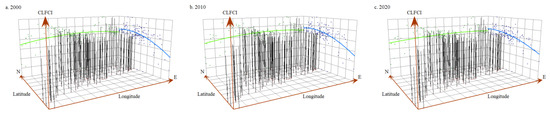
Figure 5.
Spatial distribution trend of CLF in Guangdong Province on the county scale in 2000 (a), 2010 (b), and 2020 (c). The spatial distribution trend of CLF in Guangdong Province on the county scale in 2000, 2010, and 2020 are displayed in (a,b), and (c), respectively.
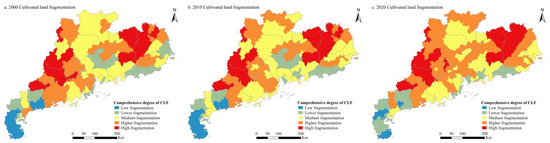
Figure 6.
Spatial distribution of CLF in Guangdong Province on the county scale in 2000 (a), 2010 (b), and 2020 (c). The spatial distribution of CLF in Guangdong Province in 2000, 2010, and 2020 are displayed in (a,b), and (c), respectively.
3.2.2. Spatial Agglomeration Features of CLF
To further explore the spatio-temporal characteristics of CLF in Guangdong Province from 2000 to 2020, we also carried out global spatial autocorrelation analysis and local spatial autocorrelation analysis in our study. As shown in Table 5, Global Moran’s I values of CLFCI on the county scale in Guangdong Province in 2000, 2010, and 2020 all showed a significant positive correlation at the 1% probability level, indicating obvious spatial agglomeration characteristics of the CLF in Guangdong Province, accompanied by the phenomenon of diffusion. The spatial agglomeration degree of CLF decreased slowly during 2000-2010 and increased slowly during 2010-2020. It showed a slow upward trend overall throughout the study period.

Table 5.
Univariate Global Moran’s I index of CLF in Guangdong Province on the county scale in 2000, 2010, and 2020.
The results of local spatial autocorrelation analysis were presented in the form of LISA graphs (Figure 7). The spatial pattern of agglomerated distribution and random distribution of CLF in Guangdong Province on the county scale remained relatively stable overall in 2000, 2010, and 2020. High–high clusters represent agglomeration areas of high values, concentrated in Heyuan and Meizhou in the northeastern region and some counties in Yunfu and Zhaoqing in the western region of Guangdong Province. Low–low clusters represent agglomeration areas of low values, concentrated in Zhanjiang in the western coastal region and some counties in Shenzhen, Zhuhai, Dongguan, Huizhou, and other cities in the southern coastal region of the Pearl River Delta. High–low clusters represent areas where the high value is surrounded by low values, mainly distributed in some counties in Dongguan, Guangzhou, Foshan, and other cities in the Pearl River Delta. Low–high clusters represent areas where the low value is surrounded by high values. This spatial relationship type involves fewer counties and was more dispersed in spatial distribution.
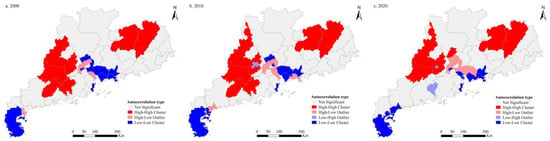
Figure 7.
Local indicators of the spatial association (LESA) map of CLF in Guangdong Province on the county scale in 2000 (a), 2010 (b), and 2020 (c). LESA map of CLF in Guangdong Province on the county scale in 2000, 2010, and 2020 are displayed in (a,b), and (c), respectively.
3.3. Spatio-Temporal Evolution Characteristics of CLF
The annual average change rate of CLFCI in each county in Guangdong Province was calculated using formula (3). As shown in Figure 8f, from 2000 to 2020, about 33% of the total counties in Guangdong Province remained relatively stable in terms of the CLFCI, the corresponding annual average change rate ranged from −0.1% to 0.1%, and the number of counties decreased with the increase in the absolute value of the annual average change rate. Of the total number of counties, 45.08% showed an increase in CLFCI. The above analysis shows that the extent of CLF in Guangdong Province has generally intensified. The locations of CLFCI changes are illustrated in Figure 8c. Counties with relatively large increases in CLFCI are located in Guangzhou, Foshan, Dongguan, Huizhou, and Zhuhai in the Pearl River Delta Plain, Chaozhou, Shantou, and Jieyang in the eastern coastal region, and some counties in Zhanjiang and Maoming in the western coastal region. Counties with relatively large decreases in CLFCI are located in some counties in Jiangmen, Zhaoqing, Huizhou, and other cities on the edge of the Pearl River Delta Plain.
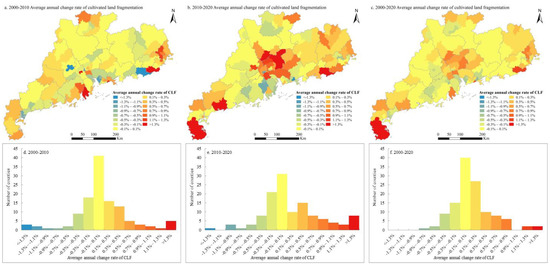
Figure 8.
Average annual change rate of CLF and its spatial distribution in Guangdong Province on the county scale during 2000–2010, 2010–2020, and 2000–2020. The spatial distribution and histogram of the average annual change rate of CLF during 2000–2010 are displayed in (a,d), respectively. The spatial distribution and histogram of the average annual change rate of CLF during 2010–2020 are displayed in (b,e), respectively. The spatial distribution and histogram of the average annual change rate of CLF during 2000–2020 are displayed in (c,f), respectively. Colors in the histograms correspond with the maps.
Focusing on the dynamic changes in CLF from a time-series perspective, the whole study period was divided into two stages: 2000–2010 and 2010–2020. About 34% and 25% of the total counties in Guangdong Province remained relatively stable for the CLFCI during 2000–2010 and 2010–2020, respectively. During both periods, the number of counties decreased with an increase in the absolute value of the annual average change rate. Figure 8d,e show that an increase in CLFCI predominates across counties, accounting for 36.89% and 44.26% of the total counties, respectively. During 2000–2010, some counties located in Zhuhai, Foshan, and Jiangmen in the Pearl River Delta Plain, and Chaozhou, Shantou, Jieyang, and other cities in the eastern coastal region, experienced relatively large increases in the CLFCI, while some counties located in Zhaoqing on the edge of the Pearl River Delta Plain and Shanwei in the eastern coastal region experienced relatively large decreases in CLFCI (Figure 8a). During 2010–2020, some counties located in Guangzhou, Foshan, Dongguan, and Huizhou on the Pearl River Delta Plain, Shanwei, Chaozhou, and Jieyang in the eastern coastal region, and Zhanjiang and Maoming in the western coastal region experienced relatively large increases in the CLFCI, while some counties located in Jiangmen on the edge of the Pearl River Delta Plain and Shaoguan in the northwest mountainous region experienced relatively large decreases in CLFCI (Figure 8b).
3.4. Factors Influencing Spatial Difference in CLF
The GD model and the RF model were successively used to analyze the factors influencing spatial difference in CLF in Guangdong Province on the county scale.
As per the results of GD, the mean values of the influence power (q) of social, economic, and agricultural development factors on CLF were 0.185, 0.154, and 0.150, respectively, all of which were significantly lower than the mean value of the influence power (q) of the natural environment factors (0.228). This indicated that the spatial difference in CLF in Guangdong Province on the county scale in 2020 was to a large extent driven by a combination of social, economic, and agricultural development factors based on natural environment conditions. As shown in Table 6, among the 14 influencing factors, the influence power (q) of population density, per capita regional GDP, forest area ratio, slope, altitude, agricultural practitioners, and the mean patch area of cultivated land on the CLF was greater than 0.20, indicating that these are the dominant factors driving the spatial difference in CLF in Guangdong Province. The influence power (q) of the agricultural output value, the proportion of industry and service industry, and the urbanization rate was between 0.15 and 0.20, making them important factors. The influence power (q) of per capita cultivated land area and construction land area ratio was between 0.10 and 0.15, making them relatively important factors. The influence power (q) of the per capita disposable income of all residents and grain production was less than 0.10, indicating the small influence of these two factors on the spatial difference in CLF in Guangdong Province.

Table 6.
Detection of factors influencing spatial difference in CLF in Guangdong Province.
The RF model analysis of the influencing factors showed that the most important influencing factors were slope, altitude, the mean patch area of cultivated land, population density, the proportion of industry and service industry, and forest area ratio.
To cross-validate the results of GD and RF, the absolute values of the influence power (q) and the importance score were arranged in descending order. In general, the contributions of each influencing factor to the spatial difference in CLF measured by the GD and RF models were basically consistent, and five of the top seven influencing factors were the same, with differences only in specific rankings.
With the help of the interaction detection module of GD, our study further detected the interactions between influencing factors. The results show that the effects of the influencing factors on the spatial difference in CLF in Guangdong Province were not mutually independent and the influence power (q) when two influencing factors interacted was greater than that of either of the two factors alone. The interaction was dominated by predominantly nonlinear enhancement (accounting for 72.53%), which was much higher than dual-factor enhancement (27.47%), and the mean value of the influence power (q) of the former (0.470) was greater than that of the latter (0.354). Among all interaction factors (Figure 9), the influence power (q) of interaction between the mean patch area of cultivated land and per capita regional GDP, between the mean patch area of cultivated land and construction land area ratio, and between forest area ratio and per capita regional GDP was above 0.690, indicating that interactions between the mean patch area of cultivated land and regional economic development led to a very strong level of the influencing power (q), and had a great impact on the spatial difference in CLF in Guangdong Province. The reason may be that along with the continuous improvement in the regional economic development level, the scale of construction land has gradually increased. The relatively concentrated and contiguous cultivated land in the plain area has been occupied continuously, and the supplementary cultivated land is scattered across the hills and mountainous areas with relatively high altitudes and slopes, which eventually leads to the cultivated land being fragmented as a whole.
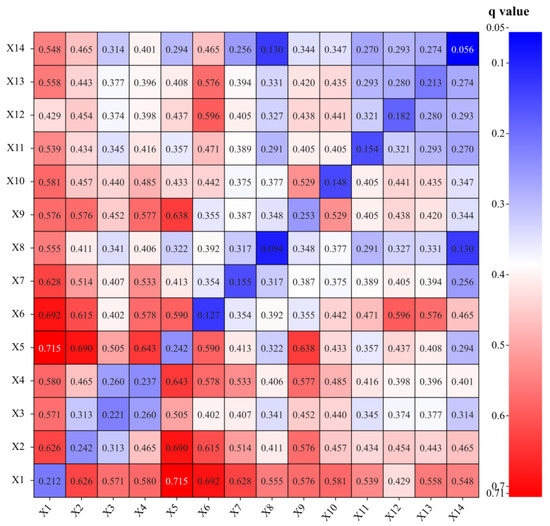
Figure 9.
Heatmap of the interaction between factors influencing spatial difference in CLF in Guangdong Province. X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13 and X14 refer to mean patch area of cultivated land, forest area ratio, altitude, slope, per capita regional GDP, construction land area ratio, proportion of industry and service industry, per capita disposable income of all residents, population density, per capita cultivated land area, urbanization rate, agricultural output value, agricultural practitioners and grain production, respectively.
4. Discussion
4.1. Comparison with Other Similar Studies
The landscape pattern index method is considered to be an effective means of characterizing CLF [56,78]. However, CLF is influenced by factors such as natural environment conditions and human activities and is diverse and complex, reflected in the edge, size, shape, and connectivity of cultivated land plots. A single or a few landscape pattern indices cannot reveal the true characteristics of CLF [14,55,79]. Issues such as redundancy and weight assignment also limit the use of landscape pattern indices [53,54]. The CLFCI proposed in our study was obtained through landscape pattern index primary selection, multicollinearity test, and weight assignment, which can help effectively quantify the characteristics of CLF. The results of our study show that from 2000 to 2020, the mean value of the CLFCI in Guangdong Province increased from 0.506 to 0.516, an increase of 2.0%, and CLF intensified in general, consistent with the overall trend of CLF in China [80,81]. In terms of spatial distribution, the extent of CLF in the mountainous and hilly areas in northern, northeastern, and northwestern Guangdong Province was significantly higher than that in the Pearl River Delta Plain in southern Guangdong Province, as well as in the plain and platform areas in the eastern and western coastal regions. The results are similar to the conclusions of the study by Qian et al. [35] on the spatial and temporal characteristics of CLF in different landform areas in northeast China and the study by Yucer et al. [38] on the CLF in Turkey, which showed that cultivated land in mountainous and hilly areas is more prone to fragmentation than that in the plain areas. The results of influencing factor detection by GD showed that the mean value of the influence power (q) of the natural environment factors is significantly higher than the mean values of social, economic, and agricultural development factors, which is in agreement with conclusions drawn by Xu et al. [3] and Sklenicka et al. [82], showing that natural environment factors are the main factors influencing CLF. In addition, interaction analysis showed that the effects of influencing factors on the spatial difference in CLF in Guangdong Province are not mutually independent, and the influence power (q) when two factors interact is greater than that of each of the two influence factors (dual-factor enhancement and nonlinear enhancement). A similar conclusion was obtained from the research concerning factors influencing CLF in the Huaihe River Basin of China [36].
4.2. Limitations and Prospects for Future Studies
CLF results from the heterogeneity of resource endowments, the historicity of policy management, and the diversity of agricultural development [1]. In our study, due to the limitation of data sources, only landscape fragmentation of cultivated land was considered in CLF evaluation, which includes the number, size, shape, and spatial distribution of cultivated land plots [83,84,85]. However, CLF also includes aspects such as different ownership and use rights of plots [58,86,87] and different fertility levels of plots [20,88]. CLF is a complex process under the combined effect of natural, social, economic, policy, and cultural factors. When analyzing the factors influencing CLF, we should not only pay attention to factors that are easy to quantify, such as the natural environmental conditions, the socio-economic development level, and the intensity of human activities, but also consider factors that are difficult to quantify but are important in terms of the influence on the spatial difference in CLF, such as the regulatory role of policies and regulations [89,90], culture and customs [86], and policy background [91]. Furthermore, the GD method was used to detect the factors influencing spatial difference in CLF in our study. The model requires the input independent variables to be categorical. If they are continuous variables, they need to be discretized first [42]. In our study, to discretize the data, we used natural breaks, which has been frequently used in existing studies [92]. The core idea of this method is to maximize the similarity within each group and maximize the dissimilarity between groups, while taking into account that the range and number of elements between groups are as close as possible. However, there are many other data discretization methods, such as the equal interval method, the quantile-based data discretization method, the data discretization method based on geometric interval, the k-means model, and the case-based reasoning method [93]. Different data discretization methods can have an impact on the results of GD (the zoning effect). To obtain the best results, it is necessary to carry out a comparative study of different discretization methods, which needs to be further improved by carrying out follow-up studies.
5. Conclusions
Assessing the extent of CLF, detecting its spatio-temporal distribution, and analyzing its formation mechanism are of great significance for promoting the intensive and efficient utilization of cultivated land resources, facilitating modernization, scale, and sustainable development of agriculture, and ensuring food security. In our study, on the basis of GlobeLand30 datasets, the extent of CLF in Guangdong Province, the frontier area of rapid economic development, was evaluated on the county scale, the spatio-temporal distribution pattern and evolution characteristics of CLF were detected, and influencing factors were explored. The main conclusions are as follows:
- (1)
- In 2000, 2010, and 2020, the spatial differences in the distribution of cultivated land resources in Guangdong Province were relatively large, with Gini coefficients of 0.462, 0.468, and 0.481, respectively, all between 0.4 and 0.5. The extent of agglomeration of cultivated land was generally low and the kernel density grades were dominated by low density and lower density. From 2000 to 2020, the spatial difference in the distribution of cultivated land in Guangdong Province gradually increased, while the kernel density continued to decrease.
- (2)
- In 2000, 2010, and 2020, the extent of CLF on the county scale was mainly medium and higher, and the average values of the CLFCI were 0.506, 0.508, and 0.516, respectively. The overall spatial distribution showed an increasing trend from the south to the north and from the west to the east, and there was a small, inverted U-shaped distribution in the east–west direction. There were significant agglomeration features in the spatial distribution of the CLF on the county scale, and the spatial distribution pattern with agglomeration and random remained relatively stable.
- (3)
- From 2000 to 2020, the overall CLF in Guangdong Province continued to intensify, and the evolution of the CLFCI on the county scale was increased (accounting for 45.08%), of which the proportions during 2000–2010 and 2010–2020 were 36.89% and 44.26%, respectively, showing an increasing trend. Counties with a relatively large increase in the CLFCI were mainly located in Guangzhou, Foshan, Dongguan, Huizhou, and Zhuhai in the Pearl River Delta Plain, Chaozhou, Shantou, and Jieyang in the eastern coastal region, and Zhanjiang and Maoming in the western coastal region.
- (4)
- The spatial difference in CLF was the result of that based on the natural environment and influenced by factors such as social, economic, and agricultural development, and the influence power (q) of each type of influencing factor was ranked as follows: natural environment factors (0.228) > social factors (0.185) > economic factors (0.154) > agricultural development factors (0.150). Population density, per capita regional GDP, and forest land area ratio were the dominant influencing factors. The interactions between influencing factors were very strong, mainly nonlinear enhancement. The interaction factor composed of mean patch area of cultivated land and per capita regional GDP, the interaction factor composed of mean patch area of cultivated land and construction land area ratio, and the interaction factor composed of forest land area ratio and per capita regional GDP were the dominant interaction factors.
We hope that the results of this study can act as scientific references for the assessment of CLF and analysis of influence mechanisms in regions with rapid economic development, so as to promote the intensive and efficient utilization of regional cultivated land resources, facilitate modernization, promote the scale and sustainable development of agriculture, and ensure food security.
Author Contributions
Conceptualization, D.W. and A.-X.Z.; methodology, D.W. and H.Y.; software, D.W.; investigation, D.W. and H.Y.; resources, Y.H. and X.M.; data curation, D.W.; writing—original draft preparation, D.W.; writing—review and editing, D.W., H.Y., and A.-X.Z.; visualization, D.W.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. U1901601) and Science and Technology Planning Project of Guangzhou (Grant No. 202206010163).
Data Availability Statement
Not applicable.
Acknowledgments
We gratefully acknowledge the paper writing assistance of Jianhua Li and Li Zhao.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Du, G.; Gai, Z.; Wang, H. Theoretical explanation and research framework of cultivated-land fragmentation in China. J. Earth Sci. Environ. 2021, 43, 997–1008. (In Chinese) [Google Scholar]
- Mitchell, M.G.E.; Suarez-Castro, A.F.; Martinez-Harms, M.; Maron, M.; McAlpine, C.; Gaston, K.J.; Johansen, K.; Rhodes, J.R. Reframing landscape fragmentation’s effects on ecosystem services. Trends Ecol. Evol. 2015, 30, 190–198. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Jin, X.; Liu, J.; Zhou, Y. Analysis of influencing factors of cultivated land fragmentation based on hierarchical linear model: A case study of Jiangsu Province, China. Land Use Policy 2021, 101, 105119. [Google Scholar] [CrossRef]
- Bakker, M.M.; Hatna, E.; Kuhlman, T.; Mücher, C.A. Changing environmental characteristics of European cropland. Agric. Syst. 2011, 104, 522–532. [Google Scholar] [CrossRef]
- Campbell, J.R. Development, global change and traditional food security in Pacific Island countries. Reg. Environ. Chang. 2015, 15, 1313–1324. [Google Scholar] [CrossRef]
- Jurgenson, E. Land reform, land fragmentation and perspectives for future land consolidation in Estonia. Land Use Policy 2016, 57, 34–43. [Google Scholar] [CrossRef]
- Power, A.G. Ecosystem services and agriculture: Tradeoffs and synergies. Philos. Trans. R. Soc. B-Biol. Sci. 2010, 365, 2959–2971. [Google Scholar] [CrossRef]
- Manjunatha, A.V.; Anik, A.R.; Speelman, S.; Nuppenau, E.A. Impact of land fragmentation, farm size, land ownership and crop diversity on profit and efficiency of irrigated farms in India. Land Use Policy 2013, 31, 397–405. [Google Scholar] [CrossRef]
- Lu, H.; Xie, H.; He, Y.; Wu, Z.; Zhang, X. Assessing the impacts of land fragmentation and plot size on yields and costs: A translog production model and cost function approach. Agric. Syst. 2018, 161, 81–88. [Google Scholar] [CrossRef]
- Han, H.; Lin, H. Patterns of Agricultural Diversification in China and Its Policy Implications for Agricultural Modernization. Int. J. Environ. Res. Public Health 2021, 18, 4978. [Google Scholar] [CrossRef]
- Rahman, S.; Rahman, M. Impact of land fragmentation and resource ownership on productivity and efficiency: The case of rice producers in Bangladesh. Land Use Policy 2009, 26, 95–103. [Google Scholar] [CrossRef]
- Ali, D.A.; Deininger, K. Is There a Farm Size–Productivity Relationship in African Agriculture? Evidence from Rwanda. Land Econ. 2015, 91, 317–343. [Google Scholar] [CrossRef]
- Deininger, K.; Savastano, S.; Carletto, C. Land Fragmentation, Cropland Abandonment, and Land Market Operation in Albania. World Dev. 2012, 40, 2108–2122. [Google Scholar] [CrossRef]
- Cheng, L.; Xia, N.; Jiang, P.; Zhong, L.; Pian, Y.; Duan, Y.; Huang, Q.; Li, M. Analysis of farmland fragmentation in China Modernization Demonstration Zone since “Reform and Openness”: A case study of South Jiangsu Province. Sci. Rep. 2015, 5, 11797. [Google Scholar] [CrossRef]
- Chen, W.; Feng, X.; Ma, R.; Hong, Q. Method of cultivated land fragmentation evaluation and empirical research: A case of Ningbo City in Zhejiang Province. China Land Sci. 2016, 30, 80–87. (In Chinese) [Google Scholar]
- Janus, J.; Mika, M.; Leń, P.; Siejka, M.; Taszakowski, J. A new approach to calculate the land fragmentation indicators taking into account the adjacent plots. Surv. Rev. 2016, 50, 1–7. [Google Scholar] [CrossRef]
- Latruffe, L.; Piet, L. Does land fragmentation affect farm performance? A case study from Brittany, France. Agric. Syst. 2014, 129, 68–80. [Google Scholar] [CrossRef]
- Sklenicka, P.; Janovska, V.; Salek, M.; Vlasak, J.; Molnarova, K. The Farmland Rental Paradox: Extreme land ownership fragmentation as a new form of land degradation. Land Use Policy 2014, 38, 587–593. [Google Scholar] [CrossRef]
- Song, W.; Liu, M. Farmland Conversion Decreases Regional and National Land Quality in China. Land Degrad. Dev. 2017, 28, 459–471. [Google Scholar] [CrossRef]
- Ciaian, P.; Guri, F.; Rajcaniova, M.; Drabik, D.; Paloma, S.G.Y. Land fragmentation and production diversification: A case study from rural Albania. Land Use Policy 2018, 76, 589–599. [Google Scholar] [CrossRef]
- Looga, J.; Jürgenson, E.; Sikk, K.; Matveev, E.; Maasikamäe, S. Land fragmentation and other determinants of agricultural farm productivity: The case of Estonia. Land Use Policy 2018, 79, 285–292. [Google Scholar] [CrossRef]
- Abrantes, P.; Fontes, I.; Gomes, E.; Rocha, J. Compliance of land cover changes with municipal land use planning: Evidence from the Lisbon metropolitan region (1990–2007). Land Use Policy 2016, 51, 120–134. [Google Scholar] [CrossRef]
- Haddad, N.M.; Brudvig, L.A.; Clobert, J.; Davies, K.F.; Gonzalez, A.; Holt, R.D.; Lovejoy, T.E.; Sexton, J.O.; Austin, M.P.; Collins, C.D.; et al. Habitat fragmentation and its lasting impact on Earth’s ecosystems. Sci. Adv. 2015, 1, e1500052. [Google Scholar] [CrossRef]
- Mitchell, M.G.E.; Bennett, E.M.; Gonzalez, A. Strong and nonlinear effects of fragmentation on ecosystem service provision at multiple scales. Environ. Res. Lett. 2015, 10, 94014. [Google Scholar] [CrossRef]
- Fitzgerald, L.A.; Walkup, D.; Chyn, K.; Buchholtz, E.; Angeli, N.; Parker, M. The Future for Reptiles: Advances and Challenges in the Anthropocene; Dellasala, D.A., Goldstein, M.I., Eds.; Elsevier Sci Ltd.: Oxford, UK, 2018; pp. 163–174. [Google Scholar]
- Chaplin-Kramer, R.; Sharp, R.P.; Mandle, L.; Sim, S.; Johnson, J.; Butnar, I.; Milà I Canals, L.; Eichelberger, B.A.; Ramler, I.; Mueller, C.; et al. Spatial patterns of agricultural expansion determine impacts on biodiversity and carbon storage. Proc. Natl. Acad. Sci. USA 2015, 112, 7402–7407. [Google Scholar] [CrossRef]
- Lee, Y.; Ahern, J.; Yeh, C. Ecosystem services in peri-urban landscapes: The effects of agricultural landscape change on ecosystem services in Taiwan’s western coastal plain. Landsc. Urban Plan. 2015, 139, 137–148. [Google Scholar] [CrossRef]
- Lee, Y.; Huang, S. Spatial emergy analysis of agricultural landscape change: Does fragmentation matter? Ecol. Indic. 2018, 93, 975–985. [Google Scholar] [CrossRef]
- Wei, L.; Luo, Y.; Wang, M.; Su, S.; Pi, J.; Li, G. Essential fragmentation metrics for agricultural policies: Linking landscape pattern, ecosystem service and land use management in urbanizing China. Agric. Syst. 2020, 182, 102833. [Google Scholar] [CrossRef]
- Gomes, E.; Banos, A.; Abrantes, P.; Rocha, J.; Kristensen, S.B.P.; Busck, A. Agricultural land fragmentation analysis in a peri-urban context: From the past into the future. Ecol. Indic. 2019, 97, 380–388. [Google Scholar] [CrossRef]
- Mekki, I.; Bailly, J.S.; Jacob, F.; Chebbi, H.; Ajmi, T.; Blanca, Y.; Zairi, A.; Biarnès, A. Impact of farmland fragmentation on rainfed crop allocation in Mediterranean landscapes: A case study of the Lebna watershed in Cap Bon, Tunisia. Land Use Policy 2018, 75, 772–783. [Google Scholar] [CrossRef]
- Ntihinyurwa, P.D.; de Vries, W.T. Farmland Fragmentation, Farmland Consolidation and Food Security: Relationships, Research Lapses and Future Perspectives. Land 2021, 10, 129. [Google Scholar] [CrossRef]
- Milne, G.; Byrne, A.W.; Campbell, E.; Graham, J.; McGrath, J.; Kirke, R.; McMaster, W.; Zimmermann, J.; Adenuga, A.H. Quantifying Land Fragmentation in Northern Irish Cattle Enterprises. Land 2022, 11, 402. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, D.; Yun, W.; Yang, L.; Tang, H.; Tang, C. Analysis on cultivated land fragmentation and spatial agglomeration pattern in Jiaxing city. Trans. Chin. Soc. Agric. Eng. 2012, 28, 235–242. (In Chinese) [Google Scholar]
- Qian, F.; Chi, Y.; Lal, R.; Lorenz, K. Spatio-temporal characteristics of cultivated land fragmentation in different landform areas with a case study in Northeast China. Ecosyst. Health Sustain. 2020, 6, 1800415. [Google Scholar] [CrossRef]
- Liang, J.; Pan, S.; Chen, W.; Li, J.; Zhou, T. Cultivated Land Fragmentation and Its Influencing Factors Detection: A Case Study in Huaihe River Basin, China. Int. J. Environ. Res. Public Health 2022, 19, 138. [Google Scholar] [CrossRef]
- Liu, J.; Jin, X.; Xu, W.; Sun, R.; Han, B.; Yang, X.; Gu, Z.; Xu, C.; Sui, X.; Zhou, Y. Influential factors and classification of cultivated land fragmentation, and implications for future land consolidation: A case study of Jiangsu Province in eastern China. Land Use Policy 2019, 88, 104185. [Google Scholar] [CrossRef]
- Yucer, A.A.; Kan, M.; Demirtas, M.; Kalanlar, S. The importance of creating new inheritance policies and laws that reduce agricultural land fragmentation and its negative impacts in Turkey. Land Use Policy 2016, 56, 1–7. [Google Scholar] [CrossRef]
- Zhang, B.; Niu, W.; Zuo, X.; Kong, X.; Yun, W.; Chen, H. Farmer-dominated pattern land consolidation to solve arable land fragmentation and its effectiveness evaluation in Guangxi. Trans. Chin. Soc. Agric. Eng. 2019, 35, 265–274. (In Chinese) [Google Scholar]
- Zhang, X.; Cai, Z.; Li, G.; Sun, J.; Li, G.; Chen, Z. Assessment of determinants of cultivated land fragmentation and its impacts on rural income. Sci. Surv. Mapp. 2020, 45, 134–141. (In Chinese) [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. (In Chinese) [Google Scholar]
- Balogun, A.; Mohd Said, S.A.; Sholagberu, A.T.; Aina, Y.A.; Althuwaynee, O.F.; Aydda, A. Assessing the suitability of GlobeLand30 for land cover mapping and sustainable development in Malaysia using error matrix and unbiased area Estimation. Geocarto Int. 2022, 37, 1607–1627. [Google Scholar] [CrossRef]
- Fonte, C.; Minghini, M.; Patriarca, J.; Antoniou, V.; See, L.; Skopeliti, A. Generating Up-to-Date and Detailed Land Use and Land Cover Maps Using OpenStreetMap and GlobeLand30. ISPRS Int. J. Geo-Inf. 2017, 6, 125. [Google Scholar] [CrossRef]
- Jokar Arsanjani, J.; See, L.; Tayyebi, A. Assessing the suitability of GlobeLand30 for mapping land cover in Germany. Int. J. Digit. Earth 2016, 9, 873–891. [Google Scholar] [CrossRef]
- Cadavid Restrepo, A.M.; Yang, Y.R.; Hamm, N.A.S.; Gray, D.J.; Barnes, T.S.; Williams, G.M.; Soares Magalhães, R.J.; McManus, D.P.; Guo, D.; Clements, A.C.A. Land cover change during a period of extensive landscape restoration in Ningxia Hui Autonomous Region, China. Sci. Total Environ. 2017, 598, 669–679. [Google Scholar] [CrossRef]
- Jokar Arsanjani, J. Characterizing and monitoring global landscapes using GlobeLand30 datasets: The first decade of the twenty-first century. Int. J. Digit. Earth 2019, 12, 642–660. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Minaei, M.; Feng, Y.; Pontius, R.G. GlobeLand30 maps show four times larger gross than net land change from 2000 to 2010 in Asia. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 240–248. [Google Scholar] [CrossRef]
- Arowolo, A.O.; Deng, X.; Olatunji, O.A.; Obayelu, A.E. Assessing changes in the value of ecosystem services in response to land-use/land-cover dynamics in Nigeria. Sci. Total Environ. 2018, 636, 597–609. [Google Scholar] [CrossRef]
- Chen, J.; Ban, Y.; Li, S. China: Open access to Earth land-cover map. Nature 2014, 514, 434. [Google Scholar]
- Chen, J.; Cao, X.; Peng, S.; Ren, H. Analysis and Applications of GlobeLand30: A Review. ISPRS Int. J. Geo-Inf. 2017, 6, 230. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, D.; Li, M. Farmland landscape fragmentation evolution and its driving mechanism from rural to urban: A case study of Changzhou City. J. Rural Stud. 2021, 82, 1–18. [Google Scholar]
- Su, S.; Xiao, R.; Jiang, Z.; Zhang, Y. Characterizing landscape pattern and ecosystem service value changes for urbanization impacts at an eco-regional scale. Appl. Geogr. 2012, 34, 295–305. [Google Scholar] [CrossRef]
- Rosa, I.M.D.; Gabriel, C.; Carreiras, J.M.B. Spatial and temporal dimensions of landscape fragmentation across the Brazilian Amazon. Reg. Envir. Chang. 2017, 17, 1687–1699. [Google Scholar] [CrossRef]
- Demetriou, D.; Stillwell, J.; See, L. A new methodology for measuring land fragmentation. Comput. Environ. Urban Syst. 2013, 39, 71–80. [Google Scholar] [CrossRef]
- Inkoom, J.N.; Frank, S.; Greve, K.; Walz, U.; Fürst, C. Suitability of different landscape metrics for the assessments of patchy landscapes in West Africa. Ecol. Indic. 2018, 85, 117–127. [Google Scholar] [CrossRef]
- Sun, R.; Jin, X.; Xiang, X.; Cao, S.; Xu, C.; Sui, X.; Liu, M.; Zhou, Y. Applicability analysis of indices in assessment on effect of land consolidation on cultivated land fragmentation. Trans. Chin. Soc. Agric. Eng. 2018, 34, 279–287. (In Chinese) [Google Scholar]
- Liu, J.; Jin, X.; Xu, W.; Yang, X.; Cao, S.; Xu, C.; Sui, X.; Liu, M.; Zhou, Y. Evaluation of cultivated land fragmentation and guidance of land consolidation at provincial level. Sci. Geogr. Sin. 2019, 39, 817–826. (In Chinese) [Google Scholar]
- Liu, J.; Jin, X.; Xu, W.; Zhou, Y. Evolution of cultivated land fragmentation and its driving mechanism in rural development: A case study of Jiangsu Province. J. Rural Stud. 2022, 91, 58–72. [Google Scholar] [CrossRef]
- Šímová, P.; Gdulová, K. Landscape indices behavior: A review of scale effects. Appl. Geogr. 2012, 34, 385–394. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Ene, E. FRAGSTATS V4: Spatial Pattern Analysis Program for Categorical and Continuous Maps; University of Massachusetts: Amherst, MA, USA, 2012. [Google Scholar]
- Peng, J.; Wang, Y.; Zhang, Y.; Wu, J.; Li, W.; Li, Y. Evaluating the effectiveness of landscape metrics in quantifying spatial patterns. Ecol. Indic. 2010, 10, 217–223. [Google Scholar] [CrossRef]
- Zhang, W.; Du, P.; Guo, S.; Lin, C.; Zheng, H.; Fu, P. Enhanced remote sensing ecological index and ecological environment evaluation in arid area. Natl. Remote Sens. Bull. 2022, 1–19. (In Chinese) [Google Scholar] [CrossRef]
- Plexida, S.G.; Sfougaris, A.I.; Ispikoudis, I.P.; Papanastasis, V.P. Selecting landscape metrics as indicators of spatial heterogeneity—A comparison among Greek landscapes. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 26–35. [Google Scholar] [CrossRef]
- Powell-Wiley, T.M.; Ayers, C.; Agyemang, P.; Leonard, T.; Berrigan, D.; Ballard-Barbash, R.; Lian, M.; Das, S.R.; Hoehner, C.M. Neighborhood-level socioeconomic deprivation predicts weight gain in a multi-ethnic population: Longitudinal data from the Dallas Heart Study. Prev. Med. 2014, 66, 22–27. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Chen, X. Application of spatial autocorrelation analysis to the spatial pattern of inbound tourism increase in China. World Reg. Stud. 2006, 15, 99–106. (In Chinese) [Google Scholar]
- Zhang, Y.; Huang, A.; Zu, J.; Liu, C.; Shi, Y.; Hao, J. Spatial and temporal evolution of construction land use intensity and its driving mechanism in China. Acta Sci. Nat. Univ. Pekin. 2020, 56, 893–906. (In Chinese) [Google Scholar]
- Moran, P.A.P. The Interpretation of Statistical. J. R. Stat. Soc. Ser. B-Stat. Methodol. 1948, 10, 243–251. [Google Scholar]
- Anselin, L. Local Indicators of Spatial Association-LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Yang, W.; Du, D.; Liu, C.; Ma, Y. Study on the spatial-temporal evolution and internal mechanism of geo-economic connections of China. Acta Geogr. Sin. 2016, 71, 956–969. (In Chinese) [Google Scholar]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, C.; Yang, F.; Wang, B.; Sun, D. Spatio-temporal evolution and the influencing factors of PM2.5 in China between 2000 and 2011. Acta Geogr. Sin. 2017, 72, 2079–2092. (In Chinese) [Google Scholar]
- Chen, W.; Li, J.; Zeng, J.; Ran, D.; Yang, B. Spatial heterogeneity and formation mechanism of eco-environmental effect of land use change in China. Geogr. Res. 2019, 38, 2173–2187. (In Chinese) [Google Scholar]
- Li, Y.; Feng, Y.; Peng, F.; Chen, S. Pattern evolvement of ecological land in Tianjin based on geodetector. Econ. Geogr. 2017, 37, 180–189. (In Chinese) [Google Scholar]
- Chang, Y.; Zhang, T.; Zhang, F.; Shi, J.; Xie, Z. Analysis on the spatiotemporal variability and driving factors of cultivated land fragmentation in the hilly region of eastern Gansu. Res. Soil Water Conserv. 2021, 28, 264–271. (In Chinese) [Google Scholar]
- Cheng, F.; Zhao, G.; Yang, M.; Liu, Y.; Li, F. Simulation of urban population distribution grid by integrating geodetector and random forest model. Bull. Surv. Mapp. 2020, 76–81. (In Chinese) [Google Scholar] [CrossRef]
- Tan, M.; Liu, K.; Liu, L.; Zhu, Y.; Wang, D. Spatialization of population in the Pearl River Delta in 30 m grids using random forest model. Prog. Geogr. 2017, 36, 1304–1312. (In Chinese) [Google Scholar]
- Morelli, F.; Benedetti, Y.; Šímová, P. Landscape metrics as indicators of avian diversity and community measures. Ecol. Indic. 2018, 90, 132–141. [Google Scholar] [CrossRef]
- Tian, Y.; Jim, C.Y.; Tao, Y.; Shi, T. Landscape ecological assessment of green space fragmentation in Hong Kong. Urban For. Urban Green. 2011, 10, 79–86. [Google Scholar] [CrossRef]
- Wang, X. Changes in Cultivated Land Loss and Landscape Fragmentation in China from 2000 to 2020. Land 2022, 11, 684. [Google Scholar] [CrossRef]
- Yu, Q.; Hu, Q.; van Vliet, J.; Verburg, P.H.; Wu, W. GlobeLand30 shows little cropland area loss but greater fragmentation in China. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 37–45. [Google Scholar] [CrossRef]
- Sklenicka, P.; Salek, M. Ownership and soil quality as sources of agricultural land fragmentation in highly fragmented ownership patterns. Landsc. Ecol. 2008, 23, 299–311. [Google Scholar] [CrossRef]
- De Vries, W.T. Post Disaster Consolidation of Land, Memory and Identity. In Proceedings of the FIG Working Week 2016—Recovery from Disaster, Christchurch, New Zealand, 2–6 May 2016. [Google Scholar]
- Jin, X.; Shao, Y.; Zhang, Z.; Resler, L.M.; Campbell, J.B.; Chen, G.; Zhou, Y. The evaluation of land consolidation policy in improving agricultural productivity in China. Sci. Rep. 2017, 7, 2792. [Google Scholar] [CrossRef]
- Qiu, L.; Zhu, J.; Pan, Y.; Wu, S.; Dang, Y.; Xu, B.; Yang, H. The positive impacts of landscape fragmentation on the diversification of agricultural production in Zhejiang Province, China. J. Clean Prod. 2020, 251, 119722. [Google Scholar] [CrossRef]
- Hartvigsen, M. Land reform and land fragmentation in Central and Eastern Europe. Land Use Policy 2014, 36, 330–341. [Google Scholar] [CrossRef]
- Ntihinyurwa, P.D.; de Vries, W.T.; Chigbu, U.E.; Dukwiyimpuhwe, P.A. The positive impacts of farm land fragmentation in Rwanda. Land Use Policy 2019, 81, 565–581. [Google Scholar] [CrossRef]
- Tian, M.; He, X. The fragmentation of agricultural land in China and how to manage it. J. Jiangxi Univ. Financ. Econ. 2015, 88–96. (In Chinese) [Google Scholar] [CrossRef]
- Liu, L.; Liu, Z.; Gong, J.; Wang, L.; Hu, Y. Quantifying the amount, heterogeneity, and pattern of farmland: Implications for China’s requisition-compensation balance of farmland policy. Land Use Policy 2019, 81, 256–266. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Liu, Y. Changes in quantity, quality, and pattern of farmland in a rapidly developing region of China: A case study of the Ningbo region. Landsc. Ecol. Eng. 2019, 15, 323–336. [Google Scholar] [CrossRef]
- Zang, L.; Araral, E.; Wang, Y. Effects of land fragmentation on the governance of the commons: Theory and evidence from 284 villages and 17 provinces in China. Land Use Policy 2019, 82, 518–527. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J. Geographic detection and optimizing decision of the differentiation mechanism of rural poverty in China. Acta Geogr. Sin. 2017, 72, 161–173. (In Chinese) [Google Scholar]
- Li, X.; Ye, J.; Liao, Q. Case-based reasoning (CBR) for land use classification using radar images. Natl. Remote Sens. Bull. 2004, 8, 246–253. (In Chinese) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).