Abstract
The aim of this article is to analyze the spatial clustering of pottery finds based on their occurrence at different depths in the Pobedim hillfort archaeological site (Western Slovakia), without reference to stratigraphic data. Two fuzzy sets methods (fuzzy linear function and fuzzy gamma operator) were used to analyze the distribution of Slavic pottery from the 9th century AD at six sectors (I–VI) located at the acropolis of the Pobedim hillfort in terms of their occurrence at different depths, their quantity at different depths, and the number of excavation pits. Using the mentioned fuzzy set methods, significant clusters of pottery were found in two sectors of the Pobedim site (sectors I and II). The results were compared with those obtained in previous research at this site, where the method of spatial autocorrelation was used. It was found that the most significant squares identified with the use of fuzzy set theory coincide with 14 squares where autocorrelation also found significant concentrations of pottery. However, the most significant squares identified by fuzzy methods (in the range 0.7–1) in all sectors of the Pobedim hillfort were 16% less than those identified by the positive spatial autocorrelation.
1. Introduction
The acropolis of the Pobedim hillfort from the 9th century AD is a well-known archeological site in Slovakia. The most significant discovery was a Slavic fortification from the period of the Pribina principality (approximately 833–1110 AD). The oldest settlement of the Pobedim area comes from the Late Stone Age (until 8300 BC), when the first peasants settled there. Evidence of their settlement is represented by potsherds and fragments of stone tools. During the archaeological research, other finds were also discovered, confirming the existence of settlement from the Early Bronze Age (1250–1000 BC). However, the most important settlement phase is from the Late Bronze Age (1000–700 BC). During the archeological research, a settlement belonging to the people of the Lusatian culture was discovered and documented. Several settlement remains were discovered as well as a cult place dedicated to the sun god. Among the finds, molds for casting bronze objects, pottery, processed bones, and mainly a rich collection of bronze objects (needles, scythes, knives, darts or jewelry) were documented. From a number of pottery fragments, it was possible to reconstruct jars of various types as well as small animal sculptures. The settlement from the Late Bronze Age (1000–700 BC) was an important trade and cult place in the central Považie region [1].
Notwithstanding the above, the most important part of Pobedim is the fortified center from the Slavic period, which had its own acropolis and nearby settlement. This fortified center constitutes one of the oldest hillforts of the Danube Slavs. It was fortified by a rampart. From the outside, a clay wall, reinforced with wood, protected the stone core and from the inside, the rampart was supported by leaning poles. A wooden palisade was installed on top of the rampart. There were watchtowers in certain parts of the rampart (Figure 1). The fortified center was inhabited by a nobleman together with his retinue and servants. There were workshops near the rampart, while the center of the fort was a place for gathering of the inhabitants of the surrounding settlements in times of danger. The Pobedim hillfort was also a center of trade in the Váh river basin. This is supported by the documentation of archaeological objects, especially the hryvnia, which served as primitive currency. The decay of the fortified settlement happened in the first and second third of the 9th century AD, which was the period when the territory of the Pribina principality became part of the Great Moravia. In the second half of the 9th and 10th centuries, Slavic settlements of agricultural character were located in the wider vicinity of the already extinct fortified settlement. During the 11–12th centuries AD, the site of the Pobedim hillfort became part of the territory of today’s municipality [2].
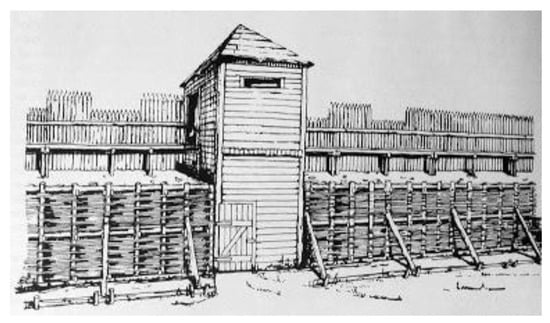
Figure 1.
Reconstruction of the watchtower according to Bialeková [1].
Archaeological research at the Pobedim hillfort revealed that several of the excavated features served as dwellings equipped with a stone kiln, while others served as production buildings. The total number of fragments of pottery vessels was 12,000 pieces. In some settlement remains, only a small number of potsherds was found. A relatively high number of axe-shaped bars attract most of the attention, while the finds also contained other iron objects. The hryvnia apparently served as pre-monetary currency.
Since pottery was one of the most numerous archaeological finds at the Pobedim acropolis, we therefore analyzed the quantity of pottery (the number of potsherds in general) in terms of its occurrence at different depths. This approach is similar to, for example, that of Orlando [3], who studied tombs at different depths or Fernandes et al. [4], who dealt with statistical methods for modeling occupation at an archaeological site also considering individual soil depths. Terrón et al. [5] also focused on the occurrence of archaeological finds at different depths, as well as Bitelli et al. [6] whose study concerned a small necropolis discovered in Rimini, where they documented the depths of individual graves uncovered at this site. Cornett and Ernenwein [7] studied depths at an archaeological site in Tennessee using object-oriented image analysis (OBIA) and digital photogrammetry. Masini et al. [8] used geophysical methods to determine the depths of archaeological finds (tombs) in the Henan area in China.
The advantages of fuzzyfication in geoinformation systems have been widely discussed and appear in several works, such as Bikdeli [9], who applied fuzzy logic and GIS for creating a model of land suitability in an area of suburb brown-fields, while Nabati et al. [10], Aghaloo and Chiu [11] and Seyedmohammadi et al. [12] used fuzzy sets for different aspects of agricultural research.
Archaeological research dealing with the fuzzy set theory was performed, for example, by Hammer et al. [13], who used this method to analyze the distribution of archaeological objects of reindeer and elk hunters in a study site in the north of Germany; Knitter et al. [14] used fuzzy sets to assess the extent of transformations between different archaeological phases from the Final Mesolithic until the Late Neolithic (4600–1700 BC) in the area of Oldenburger Graben, Schleswig-Holstein, Germany; Coughlan and Nelson [15] studied an archeological site in South Carolina using fuzzy set methods and other geospatial analyses; Taheri et al. [16] used fuzzy set methods to evaluate the sex of the bones found; and Belussi and Migliorini [17] who used this method in the spatio-temporal evaluation of archaeological data in Verona city, Italy. Moreover, the use of spatial statistics for the research of archaeological finds is presented in several works. Kempf [18] used spatial analysis in a regional case study of the Upper Rhine Valley for exemplifying the bias of archaeological records based on modern land use, construction and surface change. Zupancich et al. [19] used spatial statistics to study the usage of stone tools along the Esaro River in South Italy while Kaya [20] used spatial analysis to assess the vulnerability of the historic site of Prusias and Hypium (nowadays Konuralp Distric), particularly in the surroundings of the ancient amphitheater. Finally, Di Leo et al. [21] applied spatial analysis in the archaeological research of the Ionian sector of Basilicata in southern Italy to identify settlement patterns and dynamics of the site.
In this study, the occurrence of potsherds at different depths, the number of potsherds in different depth intervals and the total excavation pits performed in individual squares were analyzed using the fuzzy set theory. The fuzzy logic was used to find spatial clusters of potsherds, i.e., significant concentrations in spatial terms, without taking into account the stratigraphic data. The presented results were compared to the work of Vojteková et al. [22], where the amount of pottery (number of potsherds in general) in the Pobedim hillfort was studied in terms of its spatial distribution. The motivation of the authors for this research comes from the fact that the valuable data on pottery finds, which were collected in the field during the archaeological research, have not been used for any kind of spatial analysis so far, although they could eventually help to identify significant settlement remains in the studied site. Furthermore, one of the objectives of this study is to find similarities and differences in the results presented by Vojteková et al. [22] and to provide conclusions for what was achieved in both works.
All in all, the aim of this study is to analyze the spatial clustering of pottery based on their occurrence at different depths at the archaeological site of the Pobedim hillfort using the fuzzy set theory. Application of fuzzy logic and geographic information systems (GIS) is the first attempt in Slovakia to study this archaeological issue for this kind of archeological site. In particular, archaeological finds can be continuously distributed in certain areas and they usually do not conform to crisp and mutually exclusive classes, i.e., they are not defined by sharp boundaries. As a result, the use of classical set theory might misrepresent the reality, whereas fuzzy logic enables to move much closer toward real conditions. If we consider distribution of pottery as a spatially vague phenomenon, then the application of fuzzy logic is appropriate.
2. Materials and Methods
2.1. Study Site Description—Pobedim Hillfort
The archeological site of the Pobedim hillfort is located in the Trenčín Region (NUTS III), Nové Mesto nad Váhom District (NUTS IV), and in the south-western part of the Pobedim municipality on the border between the municipalities of Očkov and Podolie. The study site is situated between the rivers of Horný Dudváh and Dubová and is included in the geomorphological sub-unit called Dolnovážska niva (floodplain) at an altitude of approximately 163 m a. s. l. In terms of land use, the territory of the Pobedim hillfort has been utilized for agricultural purposes since the 18th century AD until today [22].
Niknami et al. [23] stated that prehistoric people built their dwellings in slightly elevated and grassy areas and near watercourses. This also applies in the turn of the 8th and 9th centuries AD when people in the Pobedim hillfort chose similar conditions for building their dwellings between the two rivers and on fertile land. The construction material was obtained from the nearest surroundings within a radius of 5–10 km. The limestone and sandstone for the construction of perimeter walls and the cover of the rampart top were obtained from the Malé Karpaty and Biele Karpaty mountains. The most accessible places were in the vicinity of today’s municipality of Čachtice and the town of Nové Mesto nad Váhom. In the Slavic period, this material was probably sailed on the rivers of Dudváh or Dubová to almost the hillfort. Some stones could have been extracted from the Váh River. Wood, especially oak, was obtained from the surrounding forests.
According to Bialeková [2], it is notable that a certain type of tree species predominated in different examined parts of the hillfort. This is evidence that that the fortification was not built in the same way along its entire length. While the basic construction type remained, different material was used for the construction of the skeleton, which required different building techniques while maintaining the same qualities and parameters of fortification. The fortified (nearby) settlement had a relatively uniform character (chamber type with a wheeled structure and with braided non-double walls). The use of different construction techniques on the same hillfort is undoubtedly a reflection of the staged construction of this fortified center (first the acropolis was fortified and then the nearby settlement), but even here, an economic logic was applied—the fortification of the nearby settlement was more cost-effective in terms of time and material used than the fortification in the acropolis. In particular, the wall was one meter narrower, and the chamber skeleton with a wheeled structure and braided walls was simpler. The construction of the fortification at the acropolis was also partially based on cost-effectiveness, particularly on the side of the acropolis, which was protected by the surrounding terrain, where building materials were saved.
When choosing the place of the Pobedim hillfort, not only the choice of the most suitable place from the point of view of defense played a role, although this was significant here, but the economic background of the existing environment was particularly important. Taking into account the former course of the Dudváh River, which probably meandered near the fortified settlement, it is assumed that the space between the river and the fortified settlement was always so swampy that it became a natural protection of the fortified settlement [1].
Together with Bojná, Pobedim belongs to two early medieval sites in Slovakia, which are known for the large occurrence of archaeological finds. The Pobedim hillfort can be characterized as one of the few typically lowland forts where the natural water regime was used as protection, as happens in other hillforts such as Mikulčice, Pohansko pri Břeclavi or Majcichov [24]. The oldest mentions of the ramparts of the original Slavic fortification come from the end of the 19th century AD. The rampart on the northern side of the Podebim hillfort was the border between the Pobedim and Očkov municipalities [1].
The size and internal division of the hillfort were determined by historical and social factors, but the shape of the fortification mostly adapted to the configuration of the terrain. The usable area of the acropolis is approximately 4.1 Ha, while the usable area of the nearby settlement is approximately 3.9 Ha. This study focuses only on the acropolis of the hillfort. Here, six sectors were analyzed and each sector was divided into squares (5 × 5 m) (Figure 2).
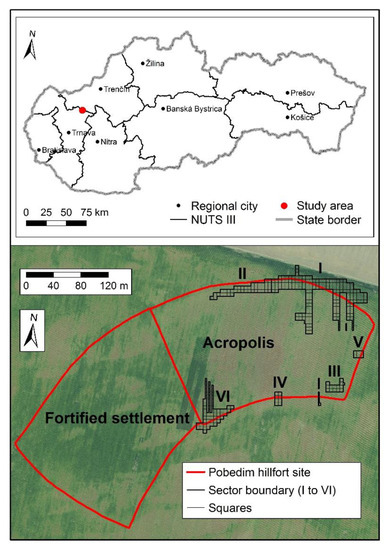
Figure 2.
Study site—Pobedim hillfort.
To visualize the current terrain surface at the Pobedim hillfort, airborne Light Detection And Ranging (LiDAR) data were used. The LiDAR data were represented by original point cloud (Source of products LLS: Geodesy, Cartography and Cadastre Authority of the Slovak Republic), which was laser-scanned during the period 11/2018–03/2019. The horizontal accuracy of the LiDAR data is 0.15 m, while the vertical accuracy is 0.05 m. As can be seen in Figure 3, some of the former features of the Pobedim hillfort are still visible, although the studied site has been levelled out for agricultural purposes (arable land) for a long time. Despite the fact that LiDAR data are very useful for interpreting archaeological topography, which has already been confirmed in a number of works [25,26,27,28,29,30,31], these data were not further analyzed in the presented study and were used for visualization purposes only.
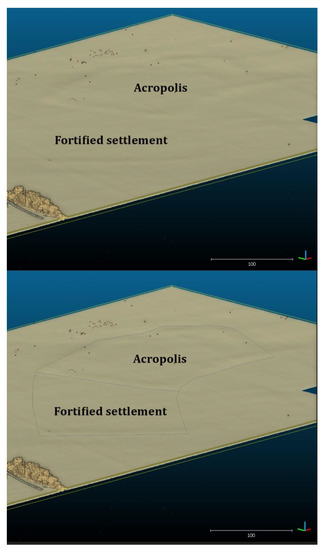
Figure 3.
LiDAR visualization of the former Pobedim hillfort using CloudCompare 2.12 software (Source of products LLS: Geodesy, Cartography and Cadastre Authority of the Slovak Republic). The study site is currently covered by the arable land.
2.2. Fieldwork Methodology
Pobedim is a lowland fortified settlement with small rivers in its surroundings, which were also used as protection against attacks. The geological bedrock is created from gneiss and granite. The elevation difference between the fort and the surrounding area at the time of the archaeological research was only less than one meter. During the uncovering, it was found that the acropolis and nearby fortified settlement were agriculturally cultivated and fruit trees had probably been planted on part of this area. However, they were removed about 30 years before the archaeological research. Therefore, the findings from a greater depth, essentially 30 cm from the surface at the time of the research, were considered as having a certain informative value. Fruit trees also left deeper damages, and in some sectors, it is necessary to believe that, during the planting and subsequent removal of trees, some archaeological features may have been destroyed. There is no data on when the trees were planted [1,2].
At the time of the archeological research, i.e., 1950s, heavy excavation equipment was available and most of the area was excavated manually. The area of the hillfort was precisely located with the aid of triangulation points. Subsequently, it was divided into a grid of 20 × 20 m squares, each one further divided into smaller 5 × 5 m squares (Figure 2).
After being uncovered by a bulldozer and subsequently cleared, darker surfaces, traces of housing remains, and especially, traces of fortification constructions began to emerge in the site. Potsherds and various iron objects were found in the remains of 21 houses, which did not overlap each other. Traces of timber construction and moats were found within the fortifications, but potsherds and other finds were not found here.
The remains of fortification could only be recorded through sections excavated in the most important sectors. Remains of houses were excavated manually and gradually in 20 cm layers. This method of artificial layers was used because there were no visible stratigraphic differences. The entire hillfort could not be researched for various reasons. While the hillfort was destroyed and partly burned, no human remains were found there [1,2].
Altogether, 12,000 potsherds were found in the studied area. Most of the housing remains were found at the acropolis, while only one house was found in the nearby fortified settlement. Only about a third of the potsherds were found in the 21 houses, with different quantities in each of them. Most of the potsherds were found outside these houses, with no obvious stratigraphic context, so their informative value is in principle lower than in the case of those recovered from any of the houses. As mentioned in a previous paragraph, potsherds both inside the houses and outside them were recorded using 20 cm artificial layers because there were no obvious differences in the natural stratigraphy (across the whole area). Potsherds from each house were evaluated as a whole because often fragments from one single vessel were found at different depths. One particular type of vessel found in the site belongs to a specific wavy handled type that is very rare and was only found in a few Slavic sites [1,2].
Each find has its relative coordinates with reference to the grid of squares. While the houses are not large, they usually extend over several squares. Both the exact location within a square and the depth were recorded for all the archaeological finds. When they were found inside houses, this was also recorded, including the depth in the house. The occurrence of each find is then also related to other settlements.
The individual houses do not overlap each other; therefore, it is not possible to talk about the respective stratigraphy of the settlements. In several houses, potsherds from one vessel were found in both the upper and lower layers, which means that many vessels were probably mixed. Due to the alteration of the upper layers of the site, it is not possible to draw sound conclusions about their spatial distribution. Based on all that, the Harris method could not be applied. Moreover, most of the pottery was composed of simple, common home-made productions with no decoration or a variety of shapes, meaning that a formal analysis was also not very useful [1,2].
2.3. Fuzzy Sets
GIS has expanded significantly in recent decades, becoming a powerful tool in not only geography, but also in other scientific fields, including archaeology. GIS is commonly used for the processing, management, analysis or synthesis of spatial data.
In most cases, the classical set theory is used for various GIS tasks. However, the use of the set theory or the Boolean logic involves a large number of limitations, especially for the spatial modeling of vaguely defined boundaries. In particular, archaeological finds can be continuously distributed in certain areas and they usually do not conform to crisp and mutually exclusive classes. Therefore, the conventional (classical) set theory might misrepresent the reality, whereas fuzzy logic enables the move towards much real conditions [32,33].
The use of fuzzy sets enables the expression of the fulfillment or failure to meet a condition by the so-called degree of membership to the set (number from the interval 0–1). On the contrary, Boolean logic allows for the expression of the fulfillment of a condition only by sharp values “yes” or “no” (1 or 0). Fuzzy logic is therefore a superset of conventional Boolean logic, extended by values in the interval between “absolutely true” and “absolutely false” statements [34,35]. Among other things, fuzzy logic in modeling uncertainty allows to use, for example, the potential of erroneous data (when the data is erroneous, but relatively close to the correct value) or categories of data with an unclear boundary [36,37,38].
Fuzzy set theory seeks to solve one of the basic problems of science, i.e., the relationship between accuracy and inaccuracy, which is elaborated in detail in several works [36,37,38]. The problem, which geographical (spatial) science faces most often, is the classification of objects according to certain attributes. Very exceptionally, there is an attribute for which it is possible to clearly, and without problems, define the classes into which the classification is carried out.
When analyzing spatial data (with tools such as intersection, union, buffer zone, attribute and spatial selections from data, and the like), the uncertainty of data is generally not taken into account. However, this approach is often not natural and close to human reasoning, in which queries can be expressed, for example, as follows: …near fluvial deposits; …on a moderate slope; or …on a slope; and the like.
All such situations can be mathematically modeled using fuzzy sets that specify individual spatial criteria. The application of fuzzy sets avoids the exclusion of suitable localities because it expresses the fulfillment or failure to meet the condition through a degree of membership from ⟨⟩. In contrast, Boolean logic uses only sharp classes “yes” or “no” (1 or 0) [35]. In this sense, let X be the so-called universe, x are elements of the universe, then classical sets A are unambiguously determined by a characteristic function as presented in Equation (1) [36]:
The basic idea of the fuzzy set theory is simple and natural. As we are not able to determine the exact boundaries of a class described by an indefinite term, we replace the decision on whether or not an element belongs to a given class with a measure selected from a scale of the membership function. Thus, it can be said that the fuzzy set is defined as a class that assigns uncertainty to an element in the form of the so-called degree of membership and it can be defined as follows: Fuzzy set A is a set of elements (X is the universe), where each of them is assigned a degree of membership , whose values are from the interval ⟨⟩, then the fuzzy set A can be written as in Equation (2) [36]:
The lower the degree of membership, the less chances the element x has to belong to the fuzzy set, and vice versa. Values of the characteristic function (degree of membership) between 0 and 1 express the extent to which elements belong to a given fuzzy set. The shape and parameters of the membership function can be determined in individual cases on the basis of practical experience or known properties of the phenomenon analyzed.
2.4. Analytical Workflow
The methodology applied in this case study included the following main steps, as presented in Figure 4:
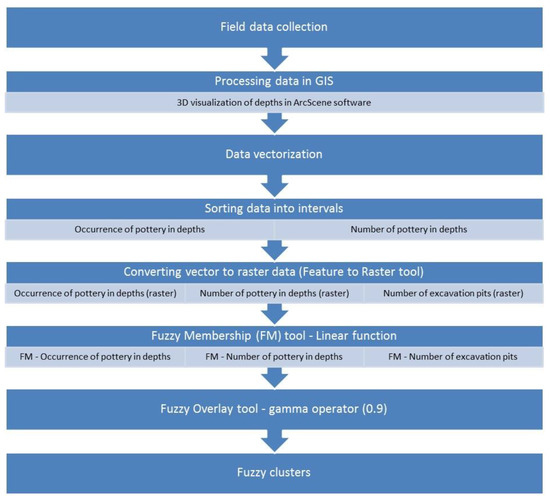
Figure 4.
Methodological workflow applied in this study.
- -
- Field data collection during the archaeological research.
- -
- 3D modeling of the depths of all archeological finds using the ArcScene 10.2.2 software (Figure 5). This particular visualization represents the maximum depth in each individual excavation pit. In this study, 3D models were used for visualization purposes only in order for the reader to have a better idea of the depths of the individual excavation pits.
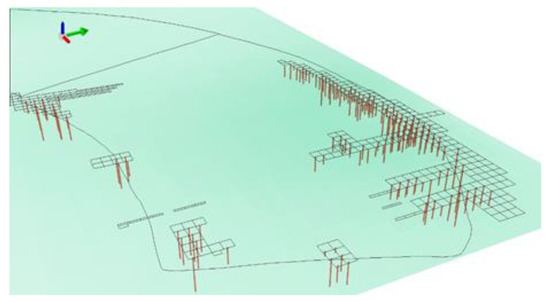 Figure 5. Depths of archeological finds (pottery) using ArcScene 10.2.2 software.
Figure 5. Depths of archeological finds (pottery) using ArcScene 10.2.2 software. - -
- Vectorization of data collected in the field using ArcGIS 10.2.2 software.
- -
- Classification of the occurrence of pottery finds and their quantity in specific depth layers, using five intervals (Table 1). Due to the number of excavation pits in individual squares, the interval sorting was not performed since the maximum number of excavation pits in one square was three. Since clusters of archaeological finds (pottery) were created on the basis of two observed criteria (existence of pottery finds and their quantity in specific depth layers), there will be 25 possible combinations (clusters) when using classical statistical methods. If we limit the number of clusters, i.e., they will be determined in advance, those features that will not meet the required criteria will not be classified at all. However, the use of fuzzy set methods allowed us, based on the use of a membership function, to include also those features in the cluster that met the given attribute only to the required level. In this case, the value of 0.9 was used, as mentioned also later.
 Table 1. Intervals for the occurrence and numbers of pottery in layers of depth.
Table 1. Intervals for the occurrence and numbers of pottery in layers of depth. - -
- Conversion of the vector layers to raster layers using the Feature to Raster tool for further raster analysis in ArcGIS. The reason for converting vector to raster layers is that fuzzy tools, which are mentioned in the next step, work only with raster data.
- -
- Use of fuzzy set theory methods in ArcGIS, specifically the Fuzzy Membership tool (Linear function) and the Fuzzy Overlay tool (gamma operator) to obtain fuzzy clusters.
2.5. Fuzzy Membership (Linear Function)
The fuzzification process defines the ideal definition for membership to the set, where the values of the phenomenon that are more central to the core of the definition of the set are assigned 1, while values that are definitely not part of the set are assigned 0. The values that occur between the two extremes are then included in the transition zone of the set. The values that move away from the ideal of the set are assigned a decreasing value on a scale from 1 to 0, which means a lower possibility of being a member of that set. For values below 0.5, the likelihood of membership to the set is increasingly low [33,36,37,39,40].
The structure of the membership function enables determination of the extent to which potential membership differs from the optimal value [41]. In this study, a linear function between the user-specified minimum and maximum values was applied. Anything below the minimum is assigned 0 (definitely not a member of a set) and anything above the maximum is assigned 1 (definitely a member of a set) [33,40]. As a result, fuzzy membership decreases at a constant rate. The following Equation (3) shows an increasing linear or decreasing linear membership between two input values by a linearized sigmoid shape [42]:
where min and max are user inputs.
2.6. Fuzzy Overlay (Gamma Operator)
The fuzzy overlay method analyzes the possibility of an observation belonging to multiple sets applying a multicriteria overlay analysis. There are different fuzzy overlay techniques (operators), which can be used [43]. For the purposes of this study, the gamma operator was used.
This operator is an algebraic product of fuzzy product and fuzzy sum, which are then raised to the power of gamma, as shown in Equation (4) [42]:
where γ is the user input variable selected in the range 0–1.
When γ = 0, the combination equals the fuzzy algebraic product and when γ = 1, the combination equals the fuzzy algebraic sum. The gamma operator is thus a compromise between the increasing tendencies of the fuzzy sum and the decreasing effect of the fuzzy product [44]. In this study, a fuzzy gamma operator with a value of 0.9 was used. Eventually, the fuzzy overlay tool was used to combine the fuzzy membership rasters (occurrence of pottery in depths, quantity of pottery in depths, and number of excavation pits) into a final raster of fuzzy clusters.
3. Results
Altogether, 303 excavation pits were carried out in 168 squares of the 5 × 5 m grid at the acropolis of Pobedim.
Across the whole site, pottery was found in depths from 10 cm to 130 cm, mostly between 10–70 cm, and far less between 90 and 130 cm.
First, the fuzzy membership function was used for determining the degree of membership (0–1) of individual studied factors within the fuzzy sets (Figure 6). The application of the fuzzy approach thus represents the exclusion of suitable localities because it allows us to express the fulfillment or failure to meet the condition of the degree of membership to a set (number from the interval 0–1).
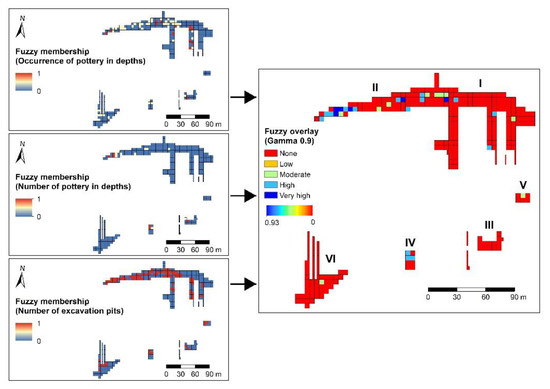
Figure 6.
Results of the fuzzy membership and fuzzy overlay methods used in this study.
After creating fuzzy raster layers using the fuzzy membership function, the synthesis of multiple fuzzy rasters was performed using the fuzzy overlay function in order to create the resulting raster. After the application of the fuzzy overlay method, six most significant squares (very high class in Figure 6), i.e., squares that were closest to 1, were found. In terms of the occurrence of potsherds at individual depths as well as the depth and number of excavation pits in the range from 0.7 to 1 (high and very high classes in Figure 6), sectors I and II were found to be the most significant. In addition, sector IV had three significant squares (Figure 6). In total, there were 31 sectors identified by the fuzzy set method of which 21 were significant (high and very high class in Figure 6) in the range from 0.7 to 1, which represents 12.5% of all studied squares in the studied area. The largest number of significant squares (10), which were identified by the fuzzy set method, were located in sector II.
The results obtained by the fuzzy set method were compared with the results obtained by the spatial autocorrelation method, which was used and described in detail for the same study site by Vojteková et al. [22]. By calculating the Moran coefficient of spatial autocorrelation, it was found that there were seven High–High clusters and three High–Low clusters, specifically, in sectors I, II, III, and IV [22].
Comparing the results obtained by fuzzy set method and positive spatial autocorrelation for the acropolis of the Pobedim hillfort, it can be seen that the most significant squares identified by the fuzzy set method (interval 0.7–1) coincide in 14 squares where the existence of positive spatial autocorrelation of pottery occurrence was confirmed (Figure 7) [22]. When analyzing the studied factors (occurrence of pottery at individual depths, their number in individual depths as well as the number of excavation pits) by the fuzzy set method, there were 16% (interval 0.7–1) of statistically significant squares less compared to the squares identified by the spatial autocorrelation. The coincidence between the squares identified as the most significant by both methods (if we assume that the most significant square has the fuzzy membership value in the range of 0.9 to 1) is in six squares, which represent 42.9% of all significant squares identified by both methods. The significant squares, which were identified by the fuzzy set method in the range from 0.7 to 1 and were located outside the squares in which the existence of positive spatial autocorrelation of pottery occurrence was not confirmed, were located in sectors I, II, V, and IV. They create 19.4% of squares from the total number of squares identified by the fuzzy set method. On the contrary, 25% of the squares, out of the total number of squares in which the existence of positive spatial autocorrelation of pottery occurrence was confirmed, were outside the squares identified by the fuzzy set method. They were located in sectors I, II, III, and IV.
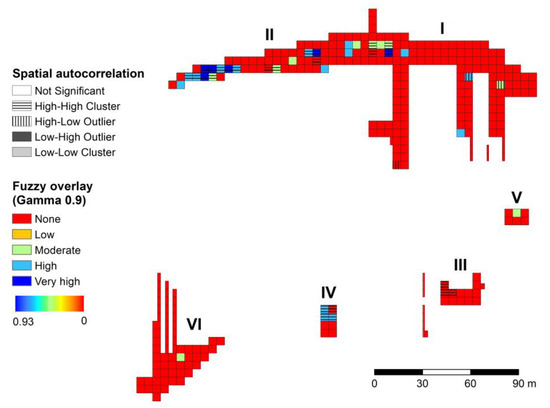
Figure 7.
Comparison of results using the fuzzy overlay method (gamma operator equals 0.9) and spatial autocorrelation method (as presented by Vojteková et al. [22]).
4. Discussion
Based on the comparison of the results of fuzzy set and spatial autocorrelation methods [22], which was applied here for the same case study, the following similarities and differences can be highlighted:
Sector I
Using the spatial autocorrelation method, six significant clusters encompassing nine squares were identified, three of which, covering six squares, showed a positive spatial autocorrelation of high number of potsherds. In its turn, the fuzzy set method found eight clusters encompassing 13 squares, eight of which can be described as significant (in the range 0.7–1). The squares with positive spatial autocorrelation and the most significant squares identified by the fuzzy set method coincide in two cases in this sector.
Sector II
Three clusters in 12 squares were identified by spatial autocorrelation in this sector. All of them showed positive spatial autocorrelation (High–High cluster) with a high number of potsherds. However, the fuzzy set method identified four clusters in 13 squares, 10 of which were in the interval 0.7–1. The squares with positive spatial autocorrelation and the most significant squares identified by the fuzzy set method coincide in nine cases in this sector.
Sector III
As for this sector, only one cluster, comprised of three squares, was identified by the spatial autocorrelation method, all of them showing a positive spatial autocorrelation. On the contrary, no clusters were identified in this sector with the use of the fuzzy set method.
Sector IV
The spatial autocorrelation method was able to identify one cluster covering four squares. All of them showed a positive spatial autocorrelation. Using the fuzzy set method, one cluster in three squares was identified, which fall into the interval 0.7–1. The coincidence between both methods in this sector happened in three squares.
Sector V
No clusters were recorded in this sector using the spatial autocorrelation method. However, the fuzzy set method identified one cluster corresponding to one square. This square does not belong to the interval 0.7–1, which means that it is not considered significant for this analysis.
Sector VI
Similarly to sector V, no cluster was recorded in this sector by the spatial autocorrelation method. Using the fuzzy set method, one cluster in one square was identified, as in sector V. In addition, this square does not belong to the interval 0.7–1, and thus, it is not significant.
After comparing the results of both methods, it was found that the most significant sector from the point of view of this research is sector II, as the highest number of significant squares (9) were identified in this sector by both methods.
These results can be compared with similar approaches developed in other archaeological contexts. For instance, the work by Gordienko [45] similarly deals with the distribution of pottery in individual depths in the medieval settlement of Borovikovo. In this research, the author studied pottery finds at different depths from 40 cm to 320 cm, which eventually proved that the settlement of people from the Batyrskaya and Molchanovka cultures in the site. In our research, however, the settlement of the Pobedim hillfort by several cultures was not confirmed on the basis of the discovered pottery. Generally, here pottery finds were uncovered at shallower depths (maximum depth was 130 cm, with only three pieces) than in the work by Gordienko [45].
Furthermore, the works by Alwan et al. [46], Espada [47] and Tafreshi et al. [48] confirm the utility of using the fuzzy overlay function, especially the gamma function with the 0.9 degree of membership. The limitations of the fuzzy set method compared to the classical approach using map algebra is that it is not possible to determine which of the three studied factors (occurrence of archaeological finds of pottery in individual depths, their quantity in individual depths, and number of excavation pits) has more influence in each location. Using the fuzzy set method, it is possible to find out in which square the individual studied factors operate with a minimum or maximum value [49]. While the fuzzy-based analysis increases the amount of information, the results are more difficult to interpret. In this sense, it is difficult to calculate the exact values of spatial clusters compared to Boolean classification methods, which could also be considered as one of the limitations of a fuzzy-based analysis. Another limitation for our particular case study can be seen from the fact that after the year 1959, archaeological research could not continue due various reasons, and the site was largely destroyed by an agricultural cooperative as part of land consolidation. We can assume that, if research had continued, more pottery could have been found, which would enrich the potential of a spatial analysis. However, if the site was not severely damaged, it would have been possible to validate the results achieved in this study as well as in the study by Vojteková et al. [22].
The results presented in this work can also be compared to works that deal with the comparison of fuzzy sets and more classical approaches (map algebra). For example, Vojteková and Vojtek [33] made a comparison between the overlay method and the fuzzy set theory in their research of stable surfaces in the landscape. Murphy et al. [50] compared fuzzy sets and regular, cumulative and probability methods in visibility research. Our approach is also supported by the work of Hermon and Niccolucci [51], who studied spatio-temporal boundaries of archaeological cultures comparing traditional map algebra methods with fuzzy sets, which they recommend should be preferred in archaeological research. Another relevant example is Malinverni and Fangi [52], who compared several methods, including fuzzy sets, for the analysis of an archaeological site in north-western Peru.
5. Conclusions
Based on the results obtained by analyzing the distribution of Slavic pottery from the acropolis of the Pobedim hillfort, it can be stated that using the fuzzy sets method with respect to the occurrence of finds at depths, the number of pottery at individual depths and the number of excavation pits, the most significant clusters were identified in sectors I, II, and IV. As was mentioned, based on the spatial autocorrelation used in the previous work of Vojteková et al. [22], the most significant clusters had been identified in sectors II and III.
By comparing the results of both studies, it was found that the largest number of clusters analyzed by spatial autocorrelation was found in sector II. Similarly, the largest number of significant squares identified by fuzzy logic (interval 0.7–1) in terms of the occurrence of the three criteria used (existence and quantity of potsherds at individual depth layers and number of excavation pits) was located in sector II. This matches with the findings of Vojteková et al. [22], who stated that sector II is extremely significant from the point of view of archaeological research carried out at the Pobedim hillfort. It was found that, during the fire that happened in this sector, remains of the fortification fell over a house, and thanks to this, the archaeological finds remained in-situ. The archaeological research discovered not only eight vessels, that could be fully reconstructed but also many iron objects, which consisted of iron headlands, agricultural and craft tools. It is interesting that some of the iron objects were very well preserved and those that were damaged were probably used as a raw material for the production of new objects. It is notable that six vessels and iron objects were found in such a position as if they were originally placed on a hanging shelf and due to the fire in the house, they fell to the ground. It can be assumed that there were significant housing constructions in sector II, such as the residence of a rich person, a pottery workshop, and the like [22]. Since starting new archaeological research at the Pobedim site is not possible due to agricultural activities, future research directions are thus limited. From the spatial point of view, the obtained field data could be further analyzed with the use of various spatial analyses and statistics or machine learning algorithms, which are coming to the fore in various scientific fields in recent years.
Author Contributions
Conceptualization, A.T., J.V., M.V. and I.V.; methodology, J.V., A.T. and M.V.; software, J.V. and M.V.; formal analysis, J.V. and A.T.; resources, J.V. and I.V.; data curation J.V. and A.T.; writing—original draft preparation, J.V., A.T. and M.V.; writing—review and editing, M.V. and J.V.; visualization, J.V. and M.V. All authors discussed the results and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Slovak Research and Development Agency under the Contract no. APVV-18-0185 and by the VEGA agency (Scientific Grant Agency of the Ministry of Education, Science, Research and Sport of the Slovak Republic and the Slovak Academy of Sciences) under the grant number 1/0934/17.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bialeková, D. Výskum a Rekonštrukcia Fortifikácie na Slovanskom Hradisku v Pobedime; Slovenská Archeológia: Nitra, Slovakia, 1978; Volume XXVI-1. [Google Scholar]
- Bialeková, D. Pobedim v Praveku, Pobedim v Dobe Rímskej a v Dobe St’ahovania Národov, Pobedim v Dobe Slovanskej; SAV: Bratislava, Slovakia, 1992. [Google Scholar]
- Orlando, L. GPR to constrain ERT data inversion in cavity searching: Theoretical and practical applications in archeology. J. Appl. Geophys. 2013, 89, 35–47. [Google Scholar] [CrossRef]
- Fernandes, R.; Geeven, G.; Soetens, S.; Klontza-Jaklova, V. Deletion/Substitution/Addition (DSA) model selection algorithm applied to the study of archaeological settlement patterning. J. Archaeol. Sci. 2011, 38, 2293–2300. [Google Scholar] [CrossRef]
- Terrón, J.M.; Mayoral, V.; Salgado, J.A.; Galea, F.A.; Pérez, V.H.; Odriozola, C.; Mateos, O.; Pizzo, A. Use of Soil Apparent Electrical Resistivity Contact Sensors for the Extensive Study of Archaeological Sites. Archaeol. Prospect. 2015, 22, 269–281. [Google Scholar] [CrossRef]
- Bitelli, G.; Girelli, V.A.; Sammarini, G. 4-dimensional recording and visualization of urban archeological excavations. Appl. Geomat. 2018, 10, 415–426. [Google Scholar] [CrossRef]
- Cornett, R.L.; Ernenwein, E.G. Object-Based Image Analysis of Ground-Penetrating Radar Data for Archaic Hearths. Remote Sens. 2020, 12, 2539. [Google Scholar] [CrossRef]
- Masini, N.; Capozzoli, L.; Chen, P.P.; Chen, F.L.; Romano, G.; Lu, P.; Tang, P.P.; Sileo, M.; Ge, Q.F.; Lasaponara, R. Towards an Operational Use of Geophysics for Archaeology in Henan (China): Methodological Approach and Results in Kaifeng. Remote Sens. 2017, 9, 809. [Google Scholar] [CrossRef]
- Bikdeli, S. Redevelopment modeling for land suitability evaluation of the suburb brown-fields using fuzzy logic and GIS, northeastern Iran. Environ. Dev. Sustain. 2020, 22, 6213–6232. [Google Scholar] [CrossRef]
- Nabati, J.; Nezami, A.; Neamatollahi, E.; Akbari, M. GIS-based agro-ecological zoning for crop suitability using fuzzy inference system in semi-arid regions. Ecol. Indic. 2020, 117, 6646. [Google Scholar] [CrossRef]
- Aghaloo, K.; Chiu, Y.R. Identifying Optimal Sites for a Rainwater-Harvesting Agricultural Scheme in Iran Using the Best-Worst Method and Fuzzy Logic in a GIS-Based Decision Support System. Water 2020, 12, 1913. [Google Scholar] [CrossRef]
- Seyedmohammadi, J.; Navidi, M.N.; Esmaeelnejad, L. Geospatial modeling of surface soil texture of agricultural land using fuzzy logic, geostatistics and GIS techniques. Commun. Soil Sci. Plant Anal. 2019, 50, 1452–1464. [Google Scholar] [CrossRef]
- Hamer, W.B.; Knitter, D.; Grimm, S.B.; Serbe, B.; Eriksen, B.V.; Nakoinz, O.; Duttmann, R. Location Modeling of Final Palaeolithic Sites in Northern Germany. Geosciences 2019, 9, 430. [Google Scholar] [CrossRef]
- Knitter, D.; Brozio, J.P.; Doerfler, W.; Duttmann, R.; Feeser, I.; Hamer, W.; Kirleis, W.; Mueller, J.; Nakoinz, O. Transforming landscapes: Modeling land-use patterns of environmental borderlands. Holocene 2019, 29, 1572–1586. [Google Scholar] [CrossRef]
- Coughlan, M.R.; Nelson, D.R. Geostatistical analysis of historical contingency and land use footprints in the prehistoric settlement dynamics of the South Carolina Piedmont, North America. J. Archaeol. Sci. 2019, 107, 1–9. [Google Scholar] [CrossRef]
- Taheri, S.M.; Ghadim, F.I.; Kabirian, M. Application of Fuzzy Inference Systems in Archaeology. In Proceedings of the 7th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Bojnord, Iran, 29–31 January 2019; pp. 79–82. [Google Scholar]
- Belussi, A.; Migliorini, S. A spatio-temporal framework for managing archeological data. Ann. Math. Artif. Intell. 2017, 80, 175–218. [Google Scholar] [CrossRef]
- Kempf, M. Modeling multivariate landscape affordances and functional ecosystem connectivity in landscape archeology. Archaeol. Anthr. Sci. 2020, 12, 159. [Google Scholar] [CrossRef]
- Zupancich, A.; Mutri, G.; Caricola, I.; Carra, M.L.; Radini, A.; Cristiani, E. The application of 3D modeling and spatial analysis in the study of groundstones used in wild plants processing. Archaeol. Anthr. Sci. 2019, 11, 4801–4827. [Google Scholar] [CrossRef]
- Kaya, A.T. A Spatial Analysis of the Ancient Theater in Konuralp with Respect to the Urban Fabric. In Cultural Sustainable Tourism; Springer: Cham, Germany, 2019; pp. 3–11. [Google Scholar]
- Di Leo, P.; Bavusi, M.; Corrado, G.; Danese, M.; Giammatteo, T.; Gioia, D.; Schiattarella, M. Ancient settlement dynamics and predictive archaeological models for the Metapontum coastal area in Basilicata, southern Italy: From geomorphological survey to spatial analysis. J. Coast. Conserv. 2018, 22, 865–877. [Google Scholar] [CrossRef]
- Vojteková, J.; Vojtek, M.; Tirpáková, A.; Vlkolinská, I. Spatial Analysis of Pottery Presence at the Former Pobedim Hillfort (an Archeological Site in Slovakia). Sustainability 2019, 11, 6873. [Google Scholar] [CrossRef]
- Niknami, K.A.; Amirkhiz, A.C.; Jalali, F. Spatial pattern of archaeological site distributions on the eastern shores of Lake Urmia, northwestern Iran. Archeol. Calc. 2009, 20, 261–276. [Google Scholar]
- Chropovský, B. K otázke postavenia slovanských hradísk na Slovensku a úloha ich výskumu. In Zborník FF Historica 15; Comenius University: Bratislava, Slovakia, 1964; pp. 9–29. [Google Scholar]
- Lieskovský, T.; Faixová Chalachanová, J. The assessment of the chosen LiDAR data sources in Slovakia for the archaeological spatial analysis. In Advances and Trends in Geodesy, Cartography and Geoinformatics II, Proceedings of the 11th International Scientific and Professional Conference on Geodesy, Cartography and Geoinformatics (GCG 2019), Demänovská Dolina, Low Tatras, Slovakia, 10–13 September 2019; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Golden, C.; Murtha, T.; Cook, B.; Shaffer, D.S.; Schroder, W.; Hermitt, E.J.; Firpi, O.A.; Scherer, A.K. Reanalyzing environmental lidar data for archaeology: Mesoamerican applications and implications. J. Archaeol. Sci. Rep. 2016, 9, 293–308. [Google Scholar] [CrossRef]
- Fisher, C.T.; Fernández-Diaz, J.C.; Cohen, A.S.; Neil Cruz, O.; Gonzáles, A.M.; Leisz, S.J.; Pezzutti, F.; Shrestha, R.; Carter, W. Identifying Ancient Settlement Patterns through LiDAR in the Mosquitia Region of Honduras. PLoS ONE 2016, 11, e0159890. [Google Scholar] [CrossRef] [PubMed]
- Inomata, T.; Pinzón, F.; Ranchos, J.L.; Haraguchi, T.; Nasu, H.; Fernandez-Diaz, J.C.; Aoyama, K.; Yonenobu, H. Archaeological Application of Airborne LiDAR with Object-Based Vegetation Classification and Visualization Techniques at the Lowland Maya Site of Ceibal, Guatemala. Remote Sens. 2017, 9, 563. [Google Scholar] [CrossRef]
- Chase, A.F.; Chase, D.Z.; Weishampel, J.F.; Drake, J.B.; Shrestha, R.L.; Slatton, K.C.; Awe, J.J.; Carter, W.E. Airborne LiDAR, archaeology, and the ancient Maya landscape at Caracol, Belize. J. Archaeol. Sci. Rep. 2011, 38, 387–398. [Google Scholar] [CrossRef]
- Opitz, R.S.; Cowley, D.C. Interpreting Archaeological Topography: Airborne Laser Scanning, 3D Data and Ground Observation; Oxbow Books: Oxford, UK, 2013. [Google Scholar]
- Kokalj, Ž.; Somrak, M. Why Not a Single Image? Combining Visualizations to Facilitate Fieldwork and On-Screen Mapping. Remote Sens. 2019, 11, 747. [Google Scholar] [CrossRef]
- Robinson, V.B. A perspective on the fundamentals of fuzzy sets and their use in geographical information systems. Trans. GIS 2003, 7, 3–30. [Google Scholar] [CrossRef]
- Vojteková, J.; Vojtek, M. GIS-Based Landscape Stability Analysis: A Comparison of Overlay Method and Fuzzy Model for the Case Study in Slovakia. Prof. Geog. 2019, 71, 631–644. [Google Scholar] [CrossRef]
- Hall, G.B.; Wang, F.; Subaryono, F. Comparison of Boolean and fuzzy classification methods in land suitability analysis by using geographical information systems. Environ. Plan. A 1992, 24, 497–516. [Google Scholar] [CrossRef]
- Ďuračiová, R. Multikriteriálne rozhodovanie pomocou fuzzy množín v prostredí GIS a jeho využitie v archeologickej predikcii. Geod. Carto. Rev. 2011, 57, 205–215. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zimmerman, H.J. Fuzzy Set Theory—and Its Applications; Springer: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Zimmerman, H.J. Fuzzy decision support systems. In Computational Intelligence: Soft Computing and Fuzzy-Neuro Integration with Applications; Kaynak, O., Zadeh, L.A., Türkşen, B., Rudas, I.J., Eds.; NATO ASI Series (Series F: Computer and Systems Sciences); Springer: Berlin, Germany, 1998; pp. 198–229. [Google Scholar]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic: New York, NY, USA, 1980. [Google Scholar]
- ESRI. ArcGIS Resources. 2014. Available online: http://resources.arcgis.com (accessed on 2 December 2020).
- MacMillian, W.D. An introduction to the theory of fuzzy sets in the context of the construction of representational spatial economic theory. In Towards the Dynamic Analysis of Spatial Systems; Martin, R.L., Thrift, N.J., Bennett, R.J., Eds.; Pion: London, UK, 1978; pp. 36–52. [Google Scholar]
- Nyimbili, P.H.; Erden, T. A Combined Model of GIS and Fuzzy Logic Evaluation for Locating Emergency Facilities: A Case Study of Istanbul. In Proceedings of the 8th International Conference on Cartography and GIS, Nessebar, Bulgaria, 15–20 June 2020; Bandrova, T., Konečný, M., Marinova, S., Eds.; pp. 191–203. [Google Scholar]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modeling with GIS; Pergamon: Oxford, UK, 1994. [Google Scholar]
- Bianchini, S.; Solari, L.; Del Soldato, M.; Raspini, F.; Montalti, R.; Ciampalini, A.; Casagli, N. Ground Subsidence Susceptibility (GSS) Mapping in Grosseto Plain (Tuscany, Italy) Based on Satellite InSAR Data Using Frequency Ratio and Fuzzy Logic. Remote Sens. 2019, 11, 2015. [Google Scholar] [CrossRef]
- Gordienko, A.V. The Medieval Batyrskaya Settlement Borovikovo. Tomsk State Univ. J. 2019, 440, 106–116. [Google Scholar] [CrossRef]
- Alwan, I.A.; Aziz, N.A.; Hamoodi, M.N. Potential Water Harvesting Sites Identification Using Spatial Multi-Criteria Evaluation in Maysan Province, Iraq. ISPRS Int. J. Geo-Inf. 2020, 9, 235. [Google Scholar] [CrossRef]
- Espada, R. Integrating information and communications technology (ICT) assets in assessing tropical cyclone risk in the Philippines. Int. J. Disaster Risk Red. 2019, 39, 101141. [Google Scholar] [CrossRef]
- Tafreshi, A.M.; Tafreshi, G.M.; Keshavarzi, M.H.B. Qualitative zoning of groundwater to assessment suitable drinking water using fuzzy logic spatial modelling via GIS. Water Environ. J. 2018, 32, 607–620. [Google Scholar] [CrossRef]
- Kominácká, J. Moderní Informační Technologie pro Podporu Vyhodnocení Prostorových Indikátorů Kvality Života; Konvoj: Brno, Czech Republic, 2011. [Google Scholar]
- Murphy, K.M.; Gittings, B.; Crow, J. Visibility analysis of the Roman communication network in southern Scotland. J. Archaeol. Sci. Rep. 2018, 17, 111–124. [Google Scholar] [CrossRef]
- Hermon, S.; Niccolucci, F. Formally Defining the Time-Space-Archaeological Culture Relation: Problems and Prospects. Archaeol. Calc. 2017, 28, 93–108. [Google Scholar]
- Malinverni, E.S.; Fangi, G. Comparative cluster analysis to localize emergencies in archaeology. J. Cult. Herit. 2009, 10, e10–e19. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).