Long-Term Assessment of Climate Change Impacts on Tennessee Valley Authority Reservoir Operations: Norris Dam
Abstract
:1. Introduction
2. Materials and Methods
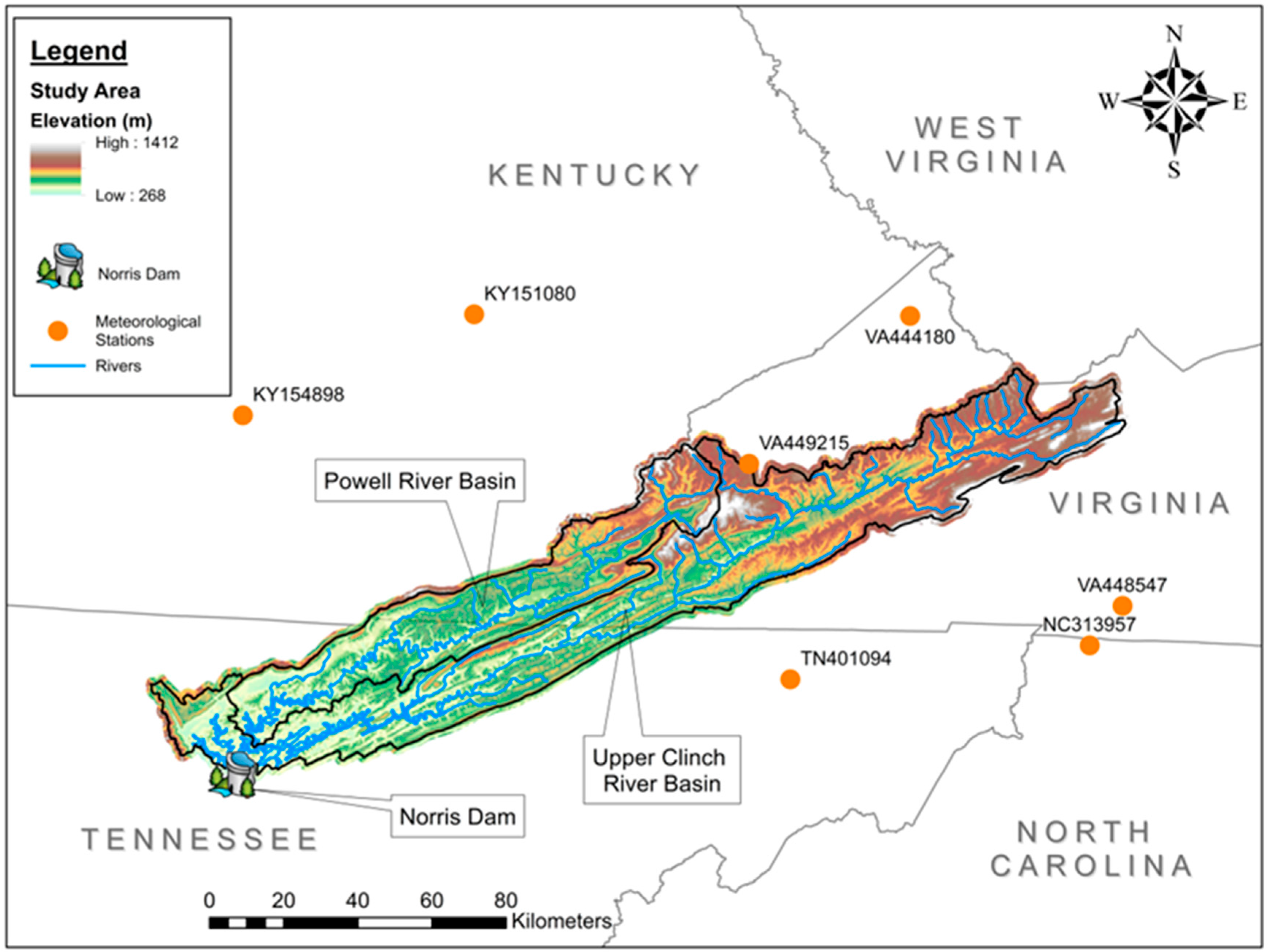
2.1. Study Area
2.2. Data Sources
2.2.1. Climatic Data
2.2.2. Climate Projection Data
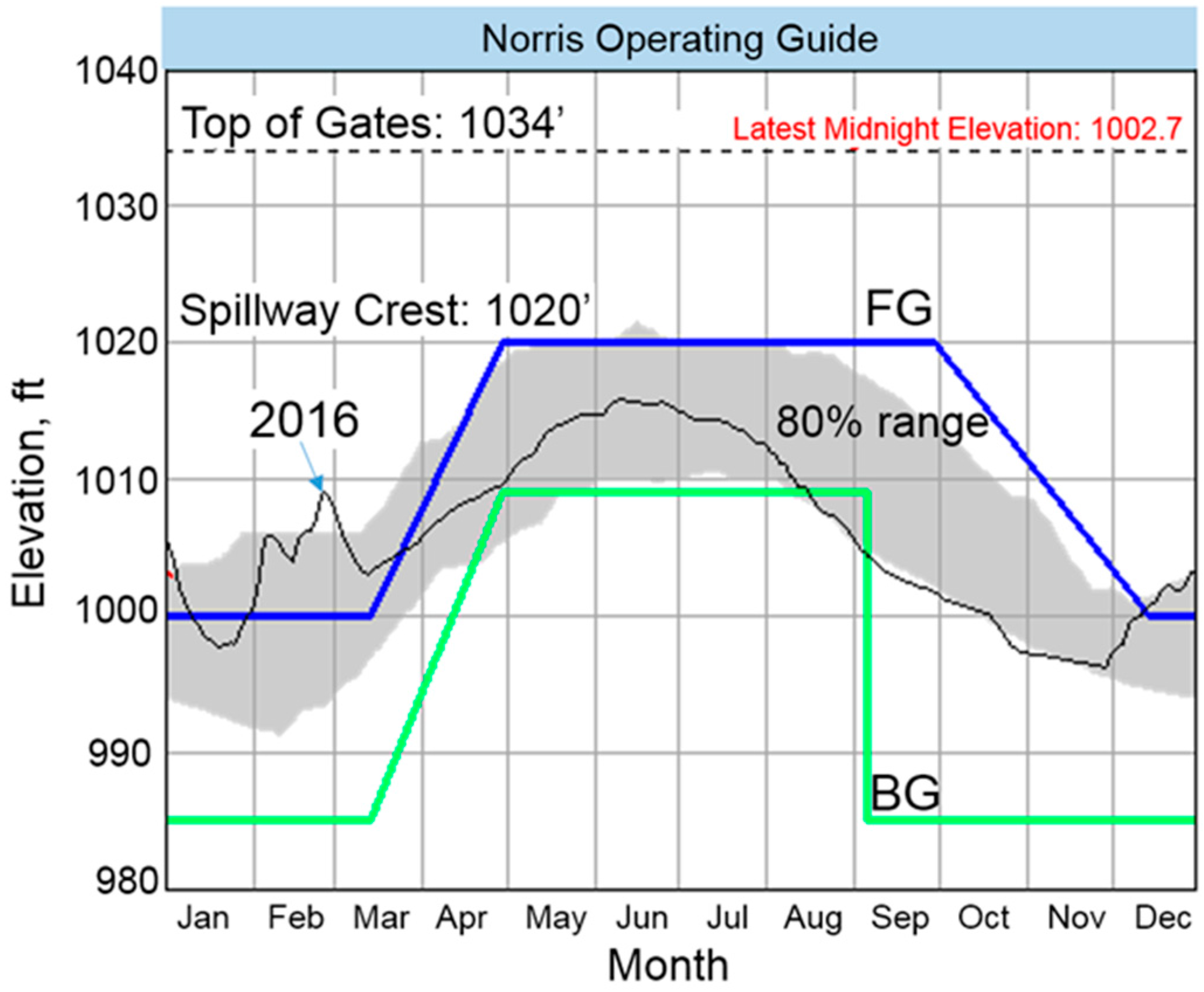
2.2.3. Dam Operations
2.3. Spatial Interpolation
2.4. Climatic Data Reproduction
2.5. Hydrologic Model
2.6. Reservoir Routing Optimization
2.7. Reservoir Assessment
3. Results
3.1. Generation of Composite Climate Data
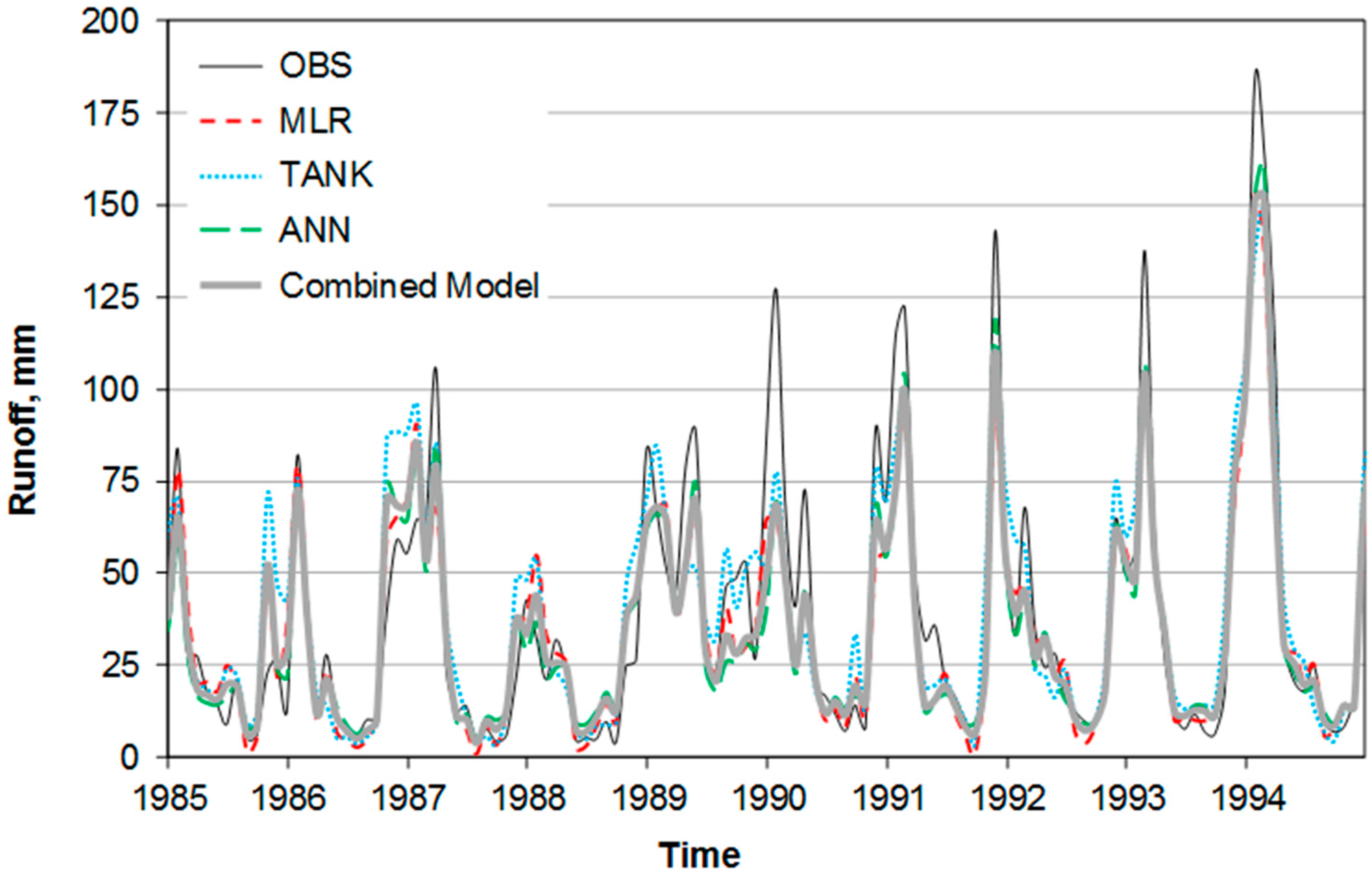
3.2. Hydrologic Model Evaluation
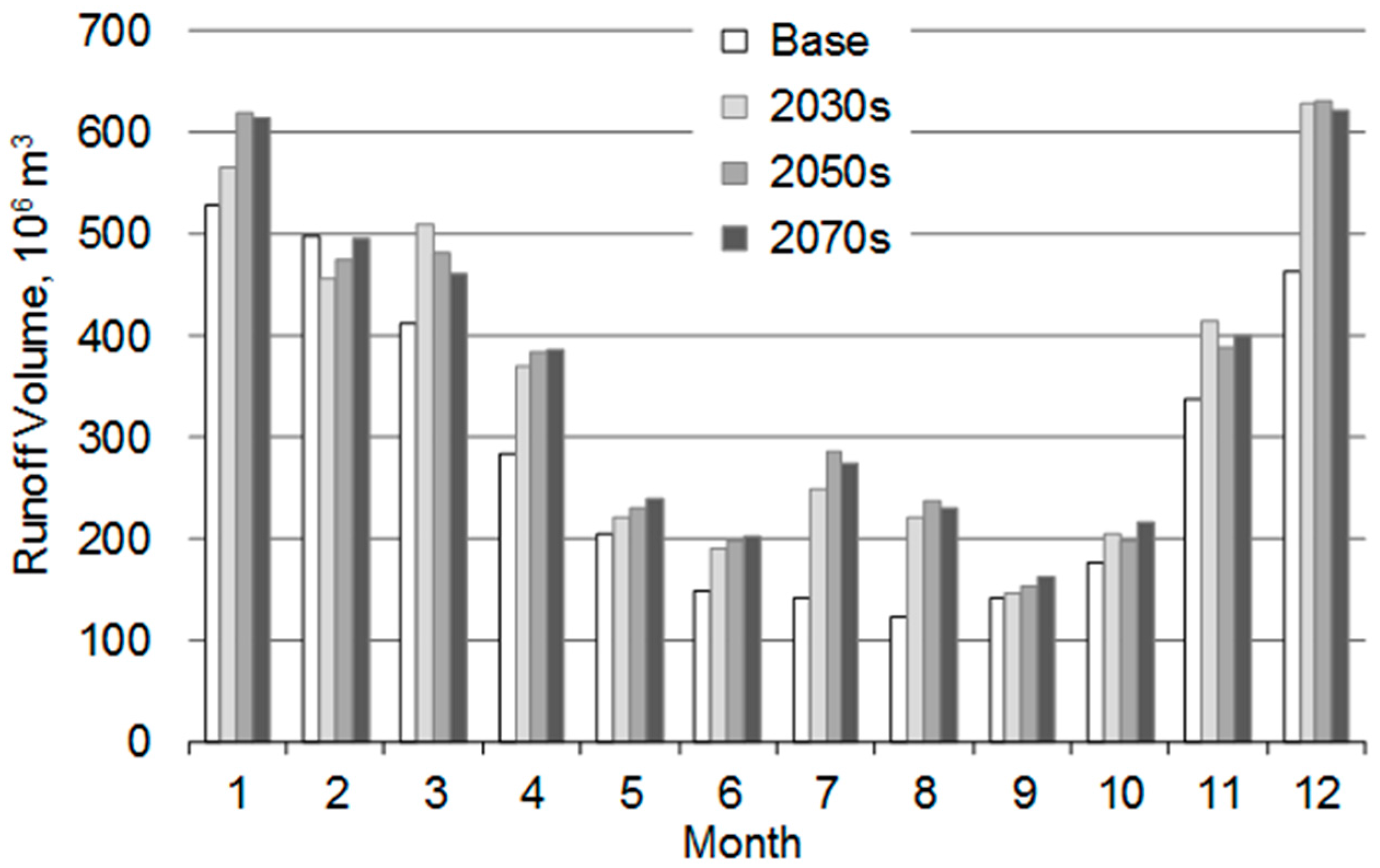
3.3. Projected Changes in Runoff
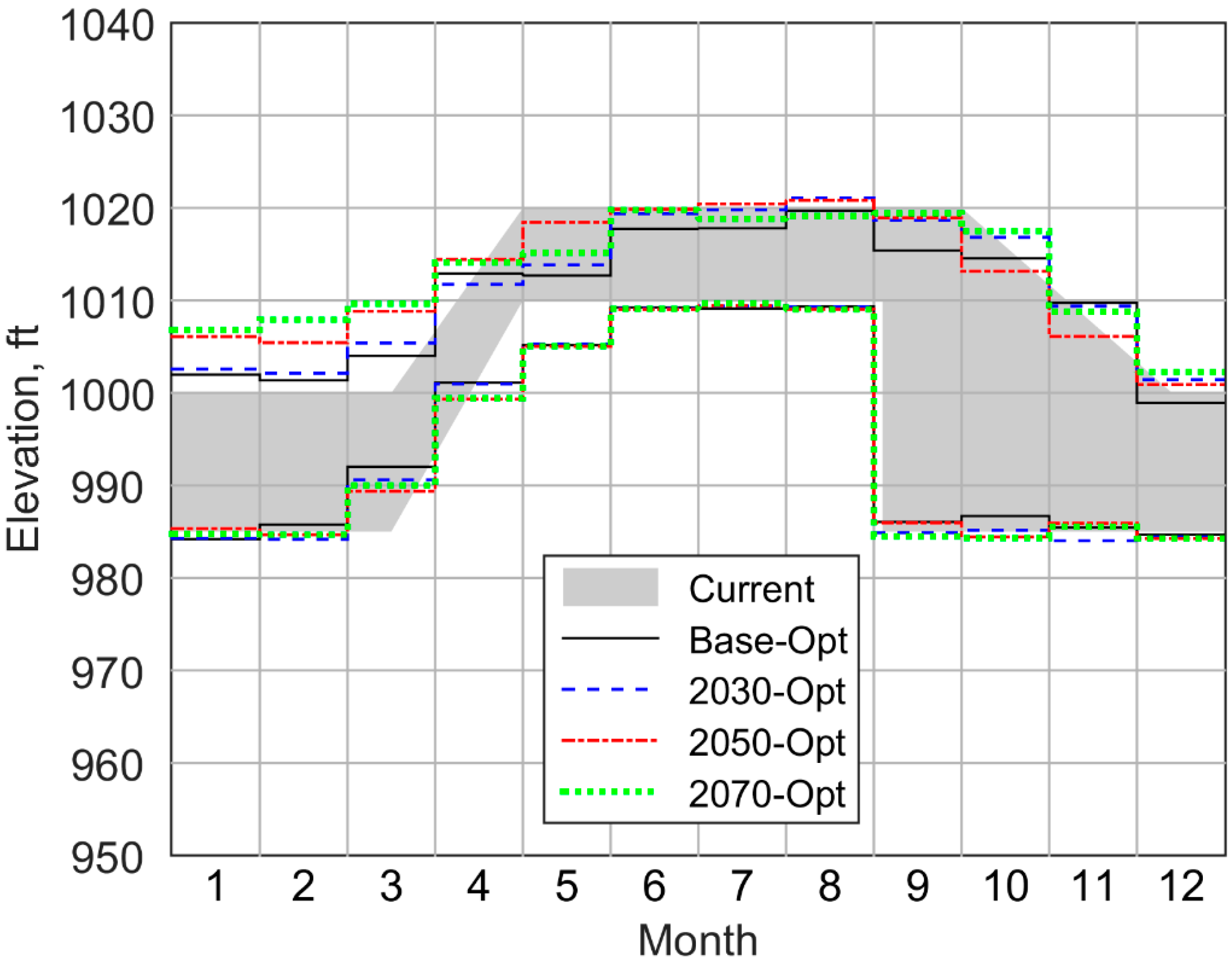
3.4. Reservoir Routing and Optimization
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Inventory of Dams. Available online: nid.usace.army.mil (accessed on 28 August 2017).
- Frederick, K.D.; Major, D.C. Climate Change and Water Resources. In Climate Change and Water Resources Planning Criteria; Frederick, K.D., Major, D.C., Stakhiv, E.Z., Eds.; Springer: Dordrecht, The Netherlands, 1997; pp. 7–23. [Google Scholar]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V. IPCC, 2013: Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Midgley, P.M., Ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.L.; Sloan, L.C.; Snyder, M.A. Regional changes in extreme climatic events: A future climate scenario. J. Clim. 2004, 17, 81–87. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, J.S.; Drake, J.B.; Liu, Y.; Lamarque, J.F. Projected changes of extreme weather events in the eastern United States based on a high resolution climate modeling system. Environ. Res. Lett. 2012, 7, 44025. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Statement on the Status of the Global Climate in 2013; WMO: Geneva, Switzerland, 2013. [Google Scholar]
- Karl, T.R. Global Climate Change Impacts in the United States; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Choi, Y.G. Potential Impacts of Climate Change on Water Resources and Water Quality of Norris Lake, Tennessee. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2011. [Google Scholar]
- Christensen, N.S.; Wood, A.W.; Voisin, N.; Lettenmaier, D.P.; Palmer, R.N. The effects of climate change on the hydrology and water resources of the Colorado River basin. Clim. Chang. 2004, 62, 337–363. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- Payne, J.; Wood, A.; Hamlet, A. Mitigating the effects of climate change on the water resources of the Columbia River Basin. Clim. Chang. 2004, 62, 233–256. [Google Scholar] [CrossRef]
- Arnell, N.W. Climate change and global water resources. Glob. Environ. Chang. 1999, 9, S31–S49. [Google Scholar] [CrossRef]
- Askew, A.J. Climate Change and Water Resources. In The Influence of Climate Change and Climatic Variability on the Hydrologic Regin and Water Resources, Proceedings of the Vancouver Symposium Soloman, Vancouver, BC, Canada, 9–22 August 1987; Solomon, S.I., Beran, M., Hogg, W., Eds.; IAHS Press: Wallingford, Oxfordshire, UK, 1987. [Google Scholar]
- Guegan, M.; Madani, K.; Uvo, C.B. Climate Change Effects on the High Elevation Hydropower System with Consideration of Warming Impacts on Electricity Demand and Pricing; A White Paper from the California Energy Commission’s California Climate Change Center; California Energy Commission: Sacramento, CA, USA, 2012. [Google Scholar]
- Markoff, M.S.; Cullen, A.C. Impact of climate change on Pacific Northwest hydropower. Clim. Chang. 2008, 87, 451–469. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Lettenmaier, D.P. Effects of climate change on hydrology and water resources in the Columbia River Basin1. J. Am. Water Res. Assoc. 1999, 35, 1597–1623. [Google Scholar] [CrossRef]
- Stone, M.C.; Hotchkiss, R.H.; Hubbard, C.M.; Fontaine, T.A.; Mearns, L.O.; Arnold, J.G. Impacts of climate change on Missouri River Basin water yield. J. Am. Water Res. Assoc. 2001, 37, 1119–1129. [Google Scholar] [CrossRef]
- Lee, S.Y.; Hamlet, A.F.; Fitzgerald, C.J.; Burges, S.J. Optimized flood control in the Columbia River Basin for a global warming scenario. J. Water Res. Plan. Manag. 2009, 135, 440–450. [Google Scholar] [CrossRef]
- Tennessee Valley Authority. Reservoir Operations Study Final Programmatic Environmental Impact Statement; Tennessee Valley Authority: Knoxville, TN, USA, 2004.
- The United States Environmental Protection Agency (USEPA). Powell Valley Watershed Ecological Risk Assessment; USEPA: Washington, DC, WA, USA, 2002.
- Tennessee Valley Authority: Norris Reservoir. Available online: http://www.tva.gov/sites/norris.htm (accessed on 28 August 2017).
- Parker, J.M. The Influence of Hydrological Patterns on Brook Trout (Salvelinus Fontinalis) and Rainbow Trout (Oncorhynchus Mykiss) Population Dynamics in the Great Smoky Mountains. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2008. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Black, P.E. Revisiting the Thornthwaite and Mather water balance. J. Am. Water Res. Assoc. 2007, 43, 1604–1605. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.; Amatya, D. A Comparison of six potential evapotranspiration methods for regional use in the Southeastern United States. J. Am. Water Res. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- McCabe, G.J.; Wolock, D.M. Sensitivity of irrigation demand in a humid-temperate region to hypothetical climatic change. J. Am. Water Res. Assoc. 1992, 28, 535–543. [Google Scholar] [CrossRef]
- Palmer, W.C.; Havens, A.V. A graphical technique for determining evapotranspiration by the Thornthwaite method. Mon. Weather Rev. 1958, 86, 123–128. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Y.; Gao, Y.; Fu, J.S.; Johnson, B.A.; Huang, C.; Kim, Y.M.; Liu, Y. Estimation and uncertainty analysis of impacts of future heat waves on mortality in the Eastern United States. Environ. Health Perspect. 2014, 122, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Wang, B. Future change of global monsoon in the CMIP5. Clim. Dyn. 2014, 42, 101–119. [Google Scholar] [CrossRef]
- Moss, R.; Edmonds, J.; Hibbard, K.; Manning, M.; Rose, S.; Van Vuuren, D.; Carter, T.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.E.; Balaji, V.; Hankin, S.; Juckes, M.; Lawrence, B. CMIP5 Data Reference Syntax (DRS) and Controlled Vocabularies. Available online: http://cmip-pcmdi.llnl.gov/cmip5/docs/cmip5_data_reference_syntax.pdf (accessed on 28 August 2017).
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E.; et al. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Chang. 2011, 109, 77–94. [Google Scholar] [CrossRef]
- Tennessee Valley Authority Norris Operating Guide. Available online: https://www.tva.gov/Environment/Lake-Levels/Norris/Norris-Operating-Guide (accessed on 28 August 2017).
- Guo, S.; Guo, J.; Zhang, J.; Chen, H. VIC distributed hydrological model to predict climate change impact in the Hanjiang basin. Sci. China Ser. E Technol. Sci. 2009, 52, 3234–3239. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.L.; Liu, W.Z. Spatiotemporal characteristics of reference evapotranspiration during 1961–2009 and its projected changes during 2011–2099 on the Loess Plateau of China. Agric. For. Meteorol. 2012, 154–155, 147–155. [Google Scholar] [CrossRef]
- Kim, U.; Kaluarachchi, J.J. Application of parameter estimation and regionalization methodologies to ungauged basins of the Upper Blue Nile River Basin, Ethiopia. J. Hydrol. 2008, 362, 39–56. [Google Scholar] [CrossRef]
- Boughton, W.; Chiew, F. Estimating runoff in ungauged catchments from rainfall, PET and the AWBM model. Environ. Model. Softw. 2007, 22, 476–487. [Google Scholar] [CrossRef]
- Heuvelmans, G.; Muys, B.; Feyen, J. Regionalisation of the parameters of a hydrological model: Comparison of linear regression models with artificial neural nets. J. Hydrol. 2006, 319, 245–265. [Google Scholar] [CrossRef]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalisation methods for catchment model parameters. Hydrol. Earth Syst. Sci. Discuss. 2005, 9, 157–171. [Google Scholar] [CrossRef]
- Seelbach, P.W.; Hinz, L.C.; Wiley, M.J.; Cooper, A.R. Use of multiple linear regression to estimate flow regimes for all rivers across Illinois, Michigan, and Wisconsin. Fish. Res. Rep. 2011, 2095, 1–35. [Google Scholar]
- Wagener, T.; Wheater, H.S. Parameter estimation and regionalization for continuous rainfall-runoff models including uncertainty. J. Hydrol. 2006, 320, 132–154. [Google Scholar] [CrossRef]
- Chen, R.S.; Pi, L.C.; Hsieh, C.C. Application of parameter optimization method for calibrating tank model. J. Am. Water Res. Assoc. 2005, 41, 389–402. [Google Scholar] [CrossRef]
- Jain, S.K. Calibration of conceptual models for rainfall-runoff simulation. Hydrol. Sci. J. 1993, 38, 431–441. [Google Scholar] [CrossRef]
- Sugawara, M. The flood forecasting by a series of storage type model. Proc. Int. Symp. Floods Comput. 1969, 1, 555–560. [Google Scholar]
- Yokoo, Y.; Kazama, S.; Sawamoto, M.; Nishimura, H. Regionalization of lumped water balance model parameters based on multiple regression. J. Hydrol. 2001, 246, 209–222. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network ToolboxTM 7 User’s Guide; The Mathworks: Natick, MA, USA, 2010. [Google Scholar]
- Dawson, C.W.; Wilby, R.L. Hydrological modelling using artificial neural networks. Progress Phys. Geogr. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Kisi, Ö. Streamflow forecasting using different artificial neural network algorithms. J. Hydrol. Eng. 2007, 12, 532–539. [Google Scholar] [CrossRef]
- Tokar, A.S.; Johnson, P.A. Rainfall-runoff modeling using artificial neural networks. J. Hydrol. Eng. 1999, 4, 232–239. [Google Scholar] [CrossRef]
- Zealand, C.M.; Burn, D.H.; Simonovic, S.P. Short term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef]
- Tennessee Valley Authority. A Comprehensive Report of the Planning Design, Constructions, and Initial Operations of the Tenneessee Valley Authority’s First Water Control Project; Tennessee Valley Authority: Knoxville, TN, USA, 1940.
- Tennessee Valley Authority. Review of TVA’s Reservoir Operations; Tennessee Valley Authority: Knoxville, TN, USA, 2010.
- Chaves, P.; Kojiri, T. Deriving reservoir operational strategies considering water quantity and quality objectives by stochastic fuzzy neural networks. Adv. Water Res. 2007, 30, 1329–1341. [Google Scholar] [CrossRef]
- Raje, D.; Mujumdar, P.P. Reservoir performance under uncertainty in hydrologic impacts of climate change. Adv. Water Res. 2010, 33, 312–326. [Google Scholar]
- Chen, L. Real coded genetic algorithm optimization of long term reservoir operation1. J. Am. Water Res. Assoc. 2003, 39, 1157–1165. [Google Scholar] [CrossRef]
- Cheng, C.T.; Wang, W.C.; Xu, D.M.; Chau, K.W. Optimizing hydropower reservoir operation using hybrid genetic algorithm and chaos. Water Res. Manag. 2008, 22, 895–909. [Google Scholar] [CrossRef]
- Wardlaw, R.; Sharif, M. Evalutaion of genetic algorithms for optimal reservoir system operation. J. Water Res. Plan. Manag. 1999, 125, 25–33. [Google Scholar] [CrossRef]
- Feddema, J.J.; Oleson, K.W.; Bonan, G.B. The importance of land-cover change in simulating future climates. Science 2005, 310, 1674–1678. [Google Scholar] [CrossRef] [PubMed]

| No. | Notation | Description | Violation | Note |
|---|---|---|---|---|
| Penalty Function (ft2) | ||||
| 0 | FG-BG | Elevation between the flood and balancing guides | 0 | Normal operation |
| 1 | FG | Elevation (EL) above the flood guide | (EL-FG)2 | Flood control |
| 2 | BG | Elevation below the balancing guide | (BG-EL)2 | Basic operation |
| 3 | HM | Elevation above the historical maximum 314.06 m (1030.38 ft) | 1000 | Flood control |
| 4 | NAV | Elevation below 219.08 m (955 ft) | 1000 | Navigation |
| 5 | TG | Elevation above 315.16 m (1034 ft) (top of gates) | 10,000 | Dam stability |
| 6 | COOL | Failure to provide cooling requirement flows for Bull Run Fossil Plant (seasonally 46 MCM~114 MCM per month) | 1000 | Service |
| 7 | ECOPOW | Failure to provide requirements for ecosystem and hydropower generation (19.96 MCM per month) | 10,000 | Ecology and hydropower |
| 8 | FLD | Flow exceeding maximum flow causing inundation (1028 MCM per month) | 10,000 | Flood control |
| Test | Equation | MLR | TANK | ANN | Combined Model |
|---|---|---|---|---|---|
| R2 (t = 1~m months) | 0.75 | 0.73 | 0.81 * | 0.81 | |
| Mean Absolute Error (MAE) (mm) (m = number of months) | 12.22 | 13.66 | 11.00 * | 11.04 | |
| Annual Runoff MAE (mm) (n = number of years) | 19.49 * | 37.16 | 28.54 | 20.55 | |
| High Flow Season MAE (mm) (i = November~April) | 3.44 * | 4.93 | 4.91 | 3.67 | |
| Low Flow Season MAE (mm) (i = May~October) | 0.19 | 1.25 | 0.15 * | 0.25 | |
| Low Runoff MAE (mm) (OBS < 10th percentile) | 4.47 * | 5.05 | 5.33 | 4.21 | |
| High Runoff MAE (mm) (OBS > 90th percentile) | 35.95 | 28.22 * | 28.57 | 30.50 | |
| 25–75th Quartile MAE (mm) (OBS inside interquartile) | 10.38 | 13.91 | 8.93 * | 9.22 |
| Time Span | Operating Guide Scenarios | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Sum |
|---|---|---|---|---|---|---|---|---|---|---|
| FG | BG | HM | NAV | TG | COOL | ECOPOW | FLD | |||
| Base | Current | 12,452 | 35,670 | 0 | 0 | 0 | 5460 | 0 | 0 | 53,582 |
| Base-Opt | 6497 | 29,610 | 0 | 0 | 0 | 5460 | 0 | 0 | 41,567 | |
| GCM-Opt | 6497 | 29,610 | 0 | 0 | 0 | 5460 | 0 | 0 | 41,567 | |
| 2030s | Current | 10,512 | 22,120 | 0 | 0 | 0 | 6450 | 0 | 6700 | 45,782 |
| Base-Opt | 5047 | 16,940 | 0 | 0 | 0 | 6450 | 0 | 6700 | 35,137 | |
| 2030-Opt | 4349 | 12,060 | 0 | 0 | 0 | 6450 | 0 | 6700 | 29,559 | |
| 2050s | Current | 10,280 | 20,880 | 0 | 0 | 0 | 7150 | 0 | 7000 | 45,310 |
| Base-Opt | 4961 | 16,130 | 0 | 0 | 0 | 7150 | 0 | 7000 | 35,241 | |
| 2050-Opt | 3662 | 11,810 | 0 | 0 | 0 | 7150 | 0 | 7000 | 29,622 | |
| 2070s | Current | 10,095 | 19,770 | 0 | 0 | 0 | 6220 | 0 | 3400 | 39,485 |
| Base-Opt | 4863 | 15,350 | 0 | 0 | 0 | 6220 | 0 | 3400 | 29,833 | |
| 2070-Opt | 3757 | 11,500 | 0 | 0 | 0 | 6220 | 0 | 3400 | 24,877 |
| Time Span | ∆ Penalty from Current when Using Base-Opt (%) | ∆ Penalty from Current When Using GCM-Opt (%) |
|---|---|---|
| Base | −22.4 | −22.4 |
| 2030s | −23.3 | −35.4 |
| 2050s | −22.2 | −34.6 |
| 2070s | −24.4 | −37.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rungee, J.; Kim, U. Long-Term Assessment of Climate Change Impacts on Tennessee Valley Authority Reservoir Operations: Norris Dam. Water 2017, 9, 649. https://doi.org/10.3390/w9090649
Rungee J, Kim U. Long-Term Assessment of Climate Change Impacts on Tennessee Valley Authority Reservoir Operations: Norris Dam. Water. 2017; 9(9):649. https://doi.org/10.3390/w9090649
Chicago/Turabian StyleRungee, Joseph, and Ungtae Kim. 2017. "Long-Term Assessment of Climate Change Impacts on Tennessee Valley Authority Reservoir Operations: Norris Dam" Water 9, no. 9: 649. https://doi.org/10.3390/w9090649
APA StyleRungee, J., & Kim, U. (2017). Long-Term Assessment of Climate Change Impacts on Tennessee Valley Authority Reservoir Operations: Norris Dam. Water, 9(9), 649. https://doi.org/10.3390/w9090649





