Numerical Investigation of the Influence of Water Jumping on the Local Scour beneath a Pipeline under Steady Flow
Abstract
:1. Introduction
2. Numerical Method
2.1. Flow Model
2.2. Turbulence Closure Model
2.3. Sediment Transport Equations
2.3.1. Bed Load Transport Equations
2.3.2. Suspended Load Transport Equations
2.3.3. Boundary Condition
2.4. Scour Model
2.5. Dynamic Mesh Model
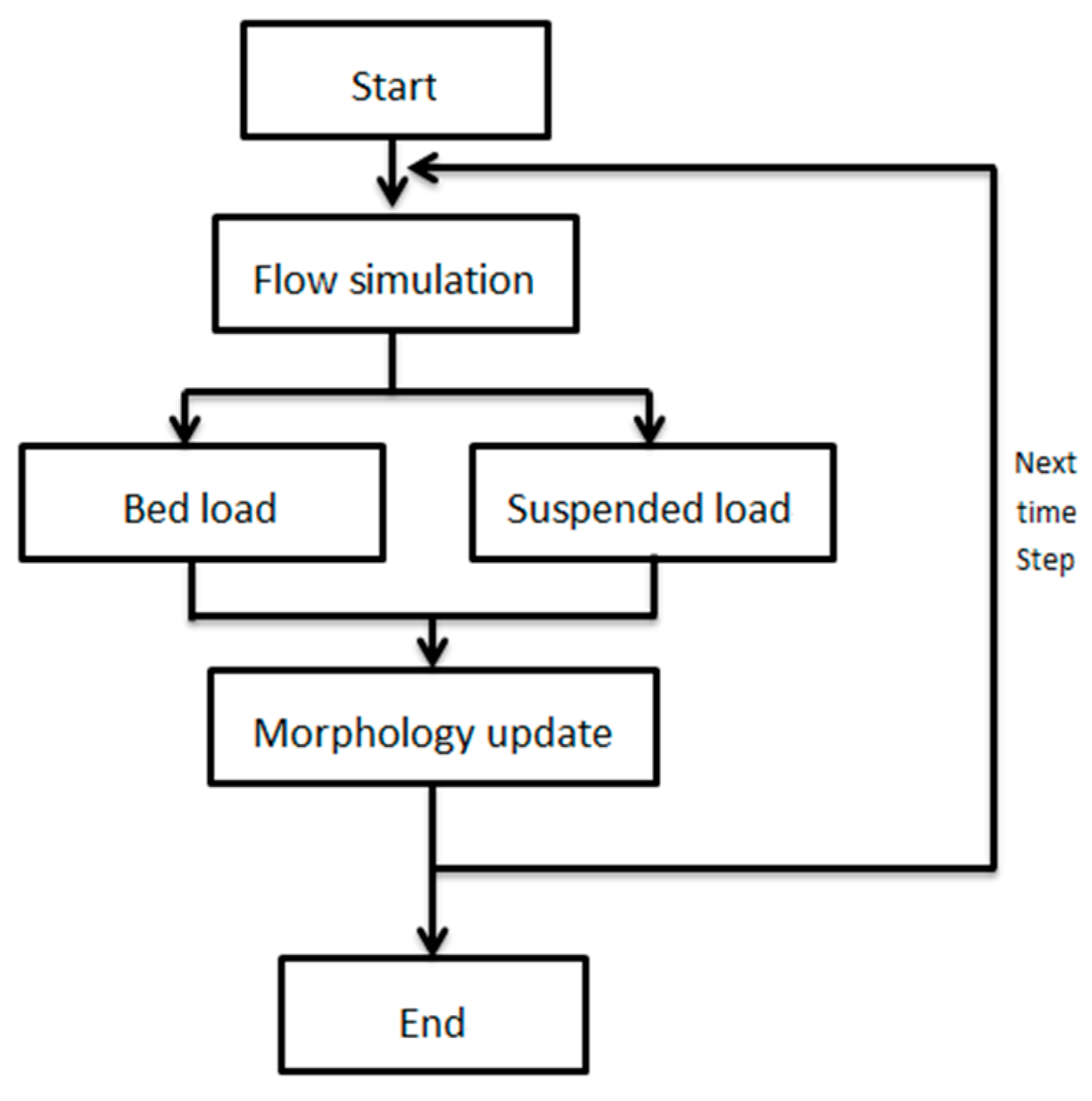
3. Numerical Method
3.1. Numerical Schemes of the Flow Model
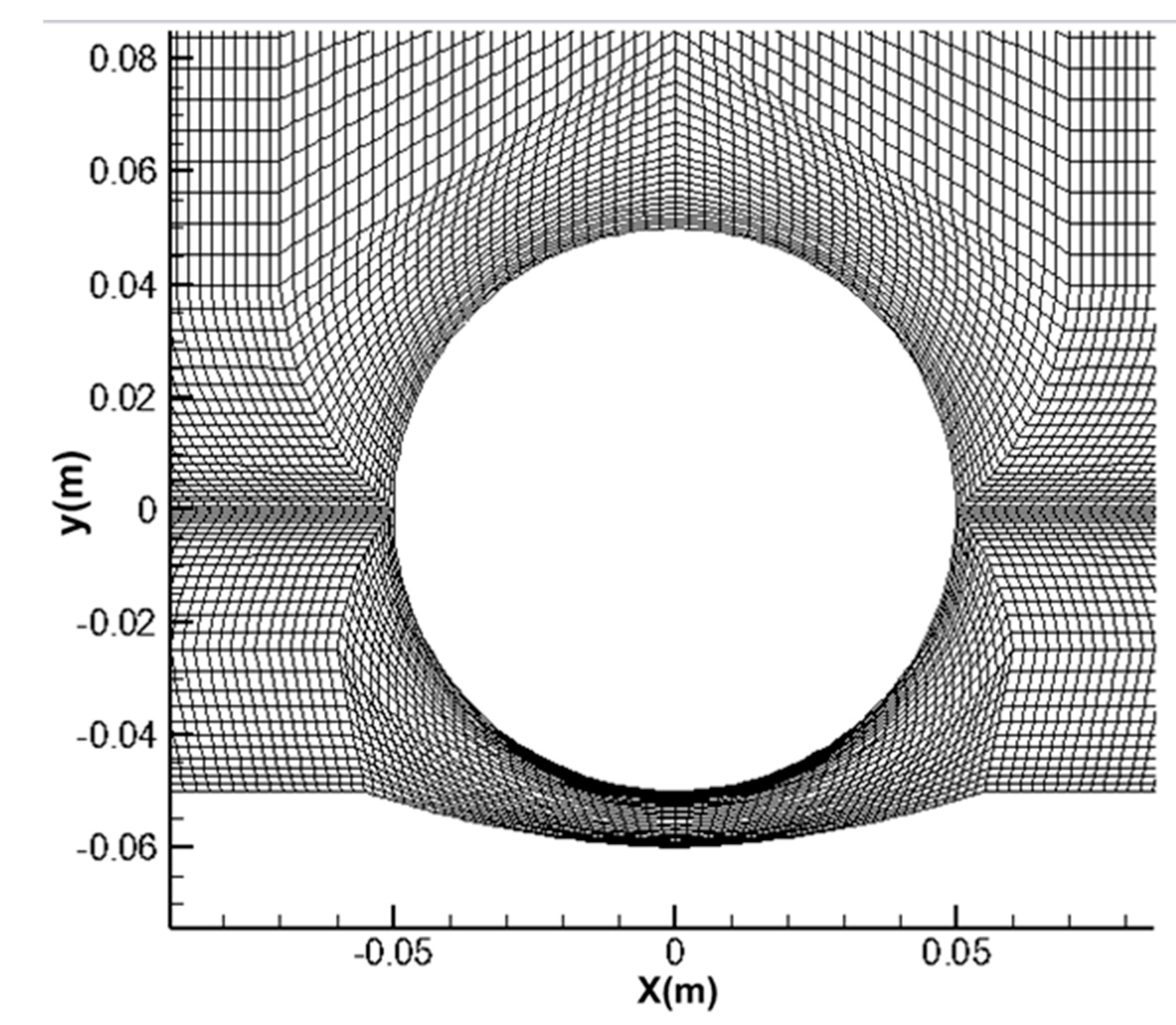
3.2. Numerical Schemes for Sediment Transport and Scour Model
4. Model Validation
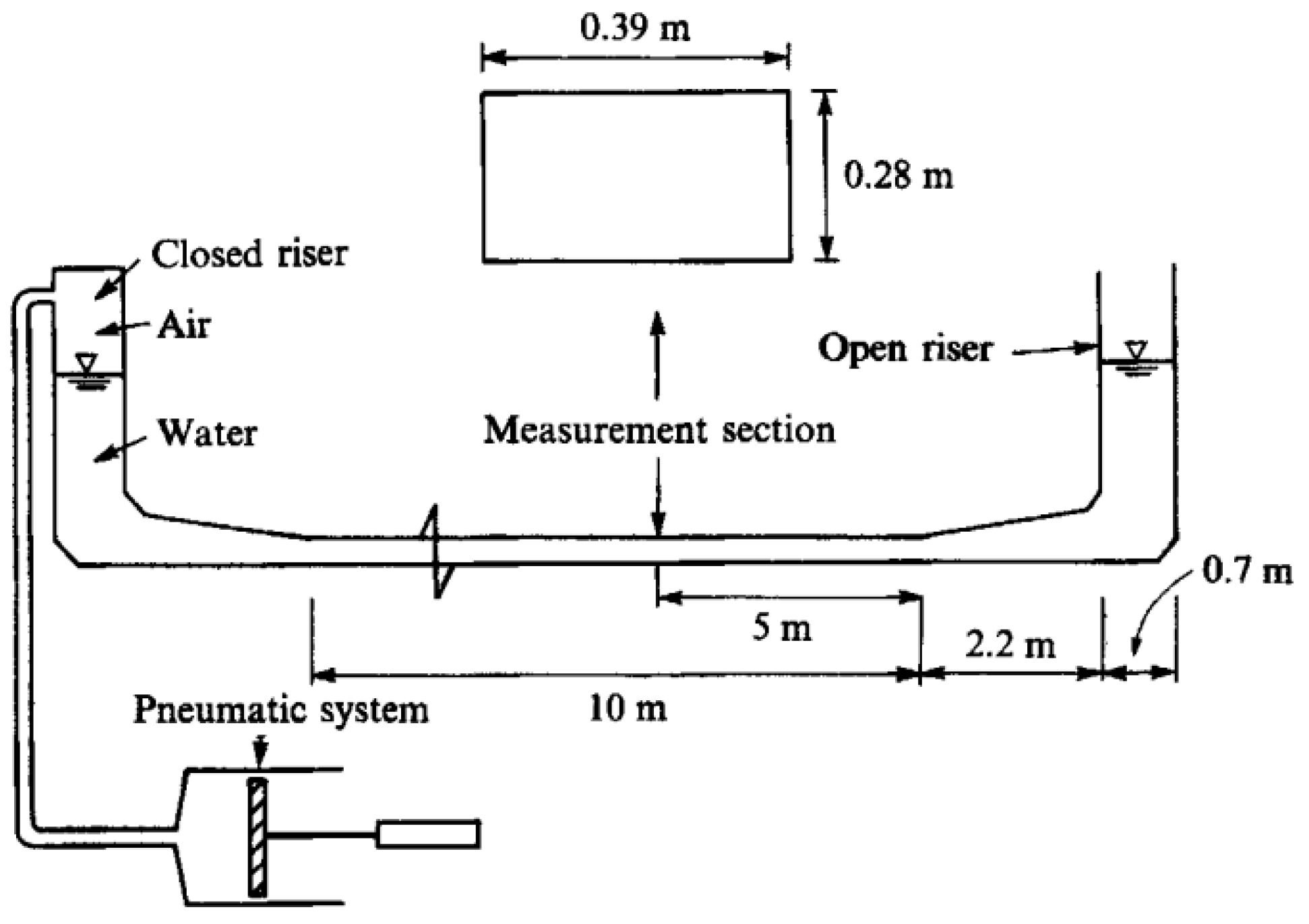
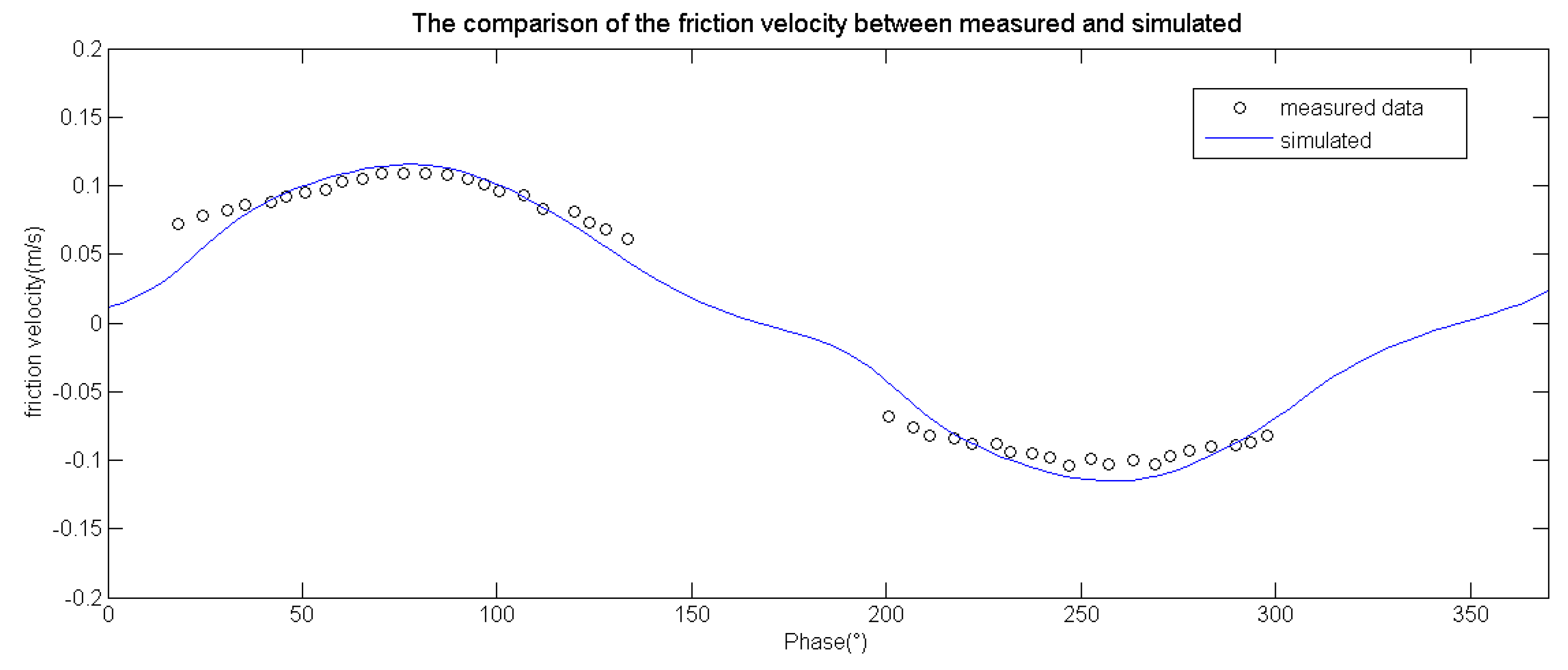
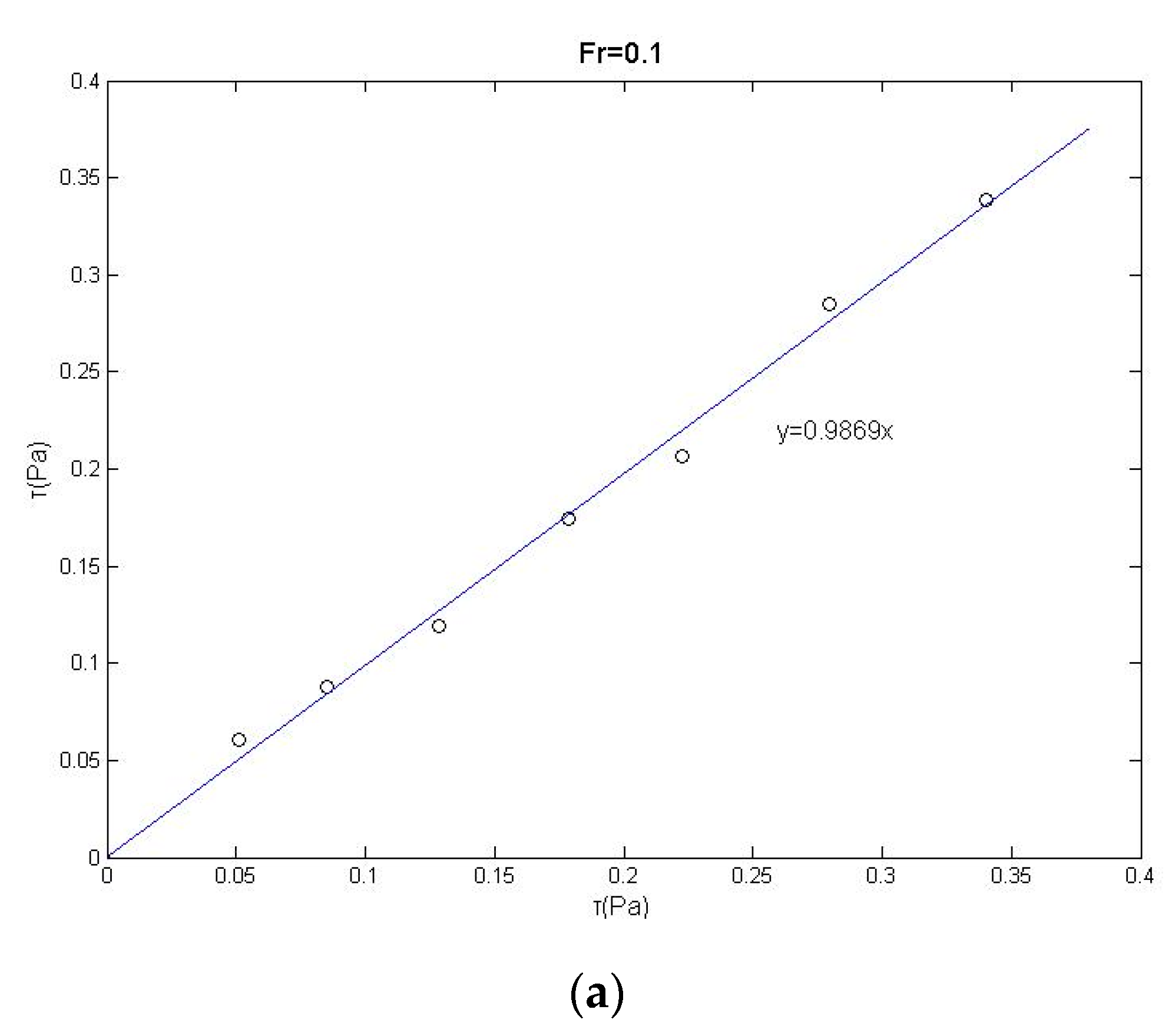
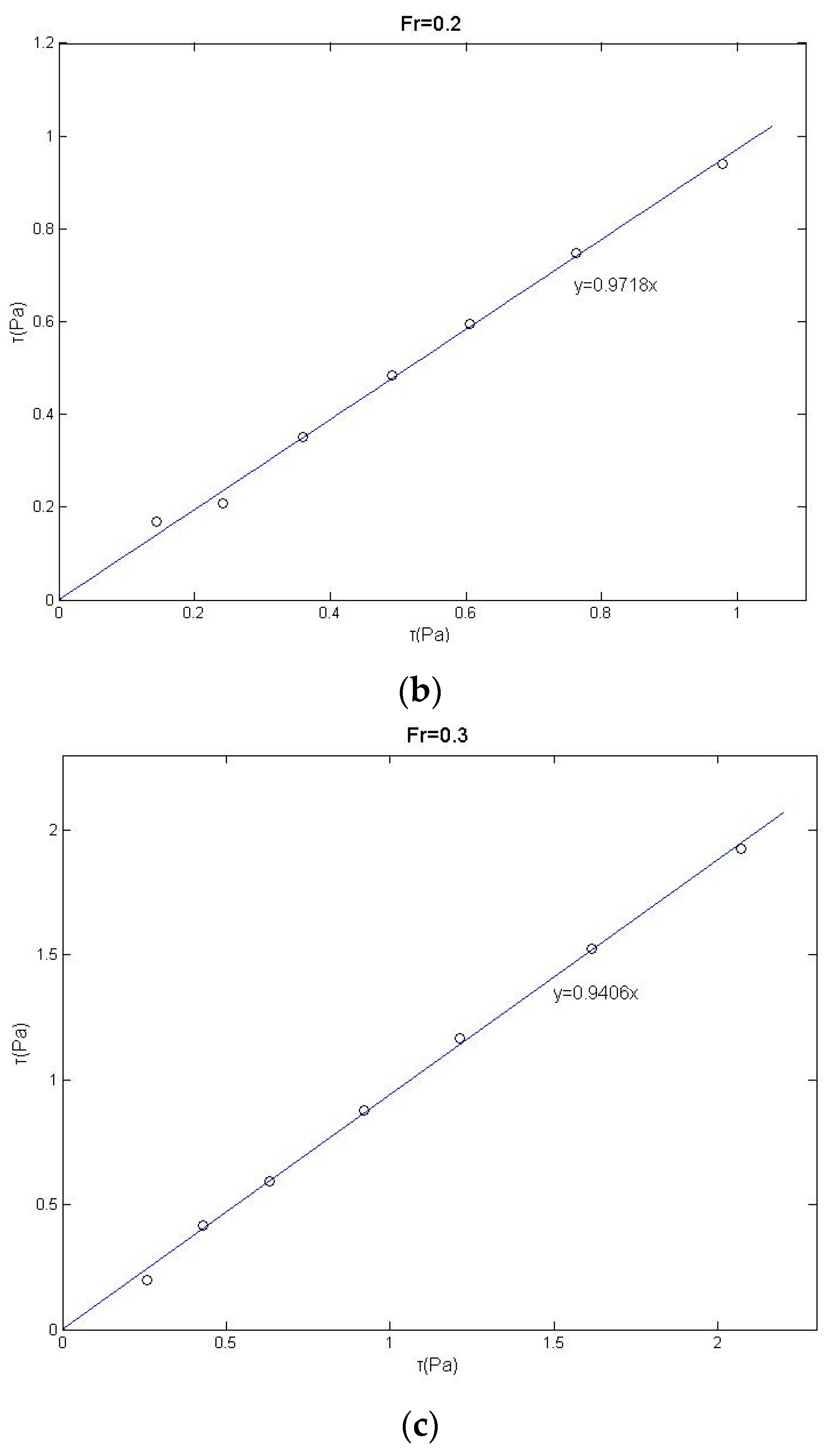
4.1. Bed Shear Stress
4.2. Suspended Load Model
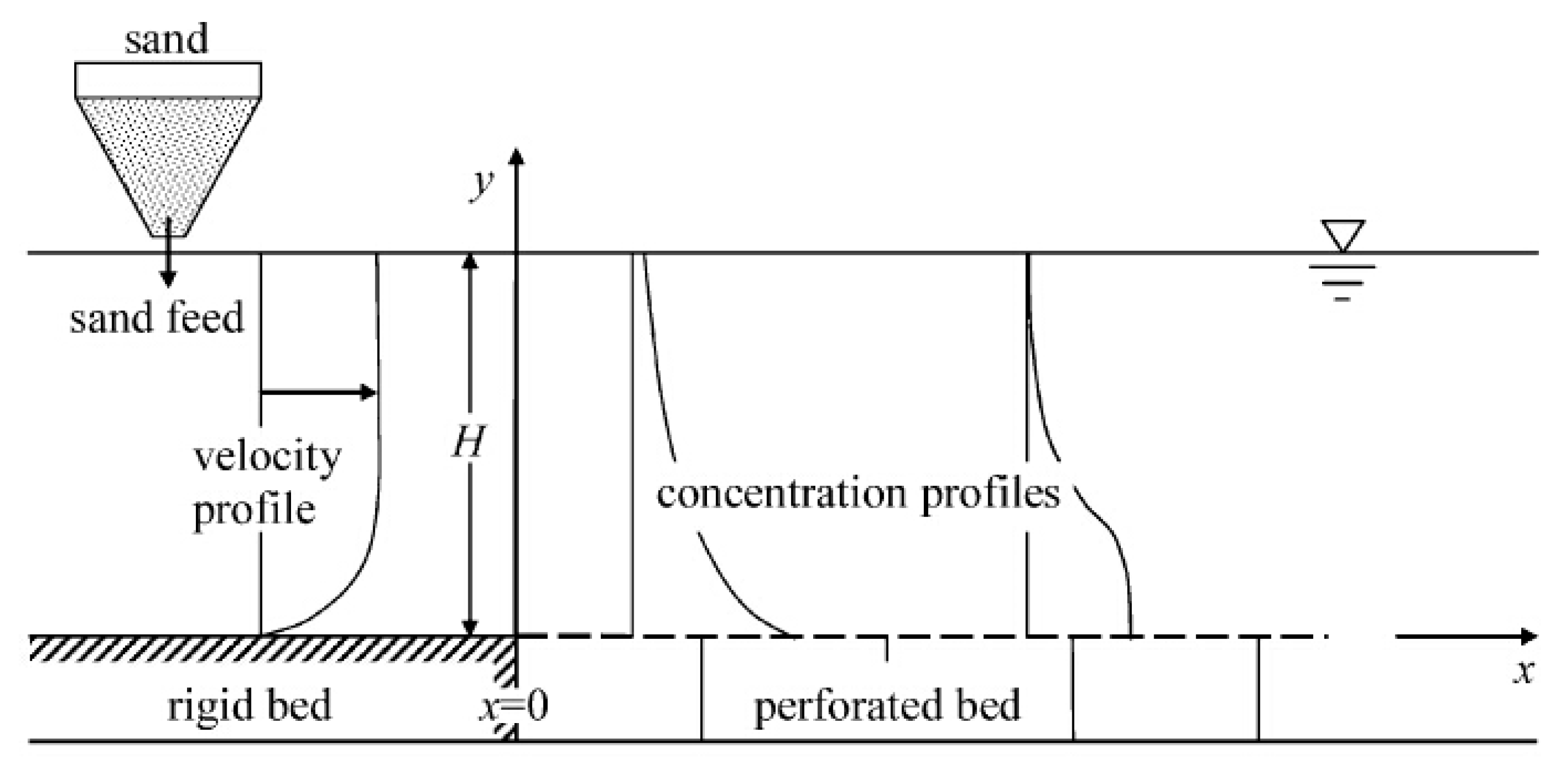
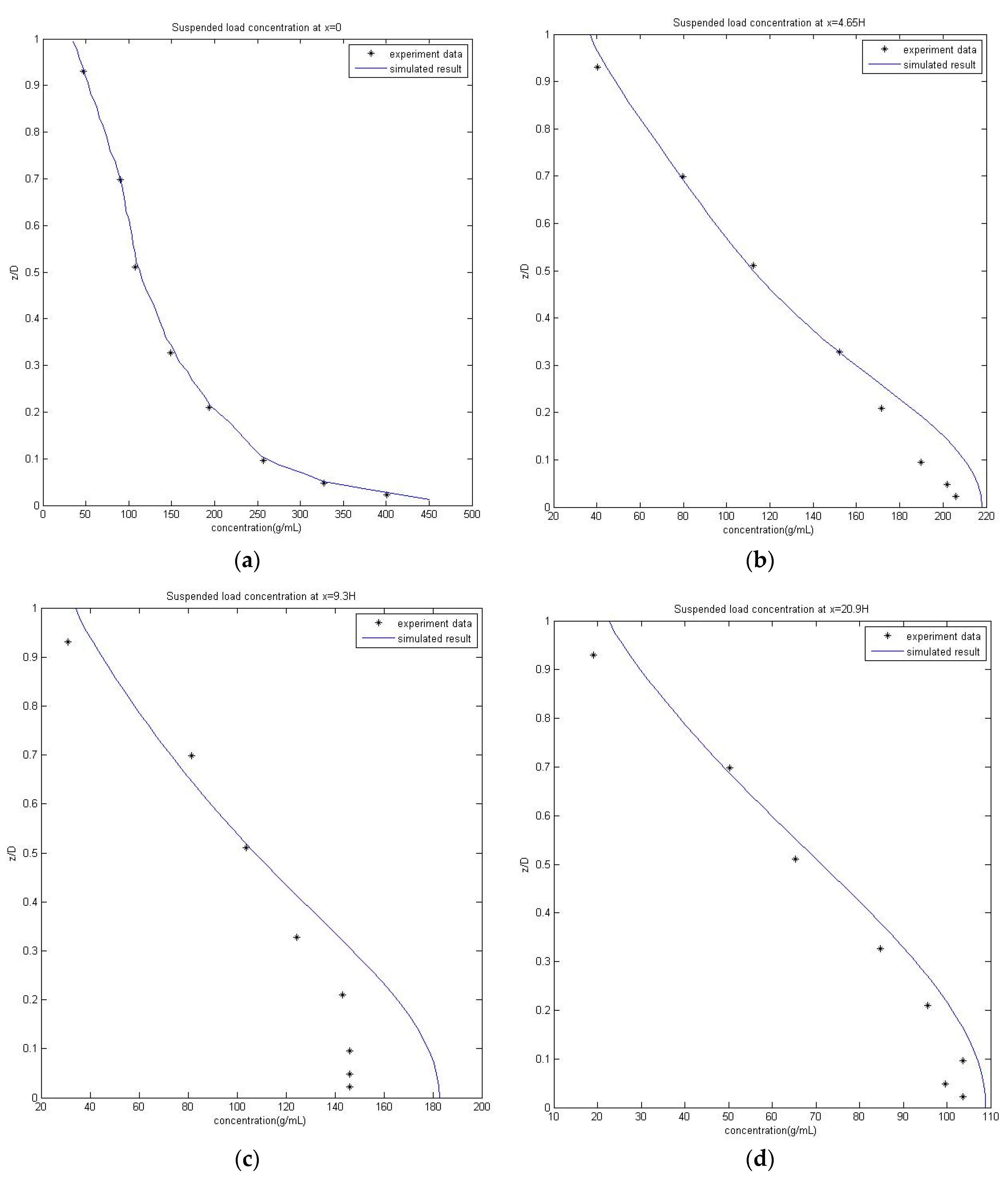
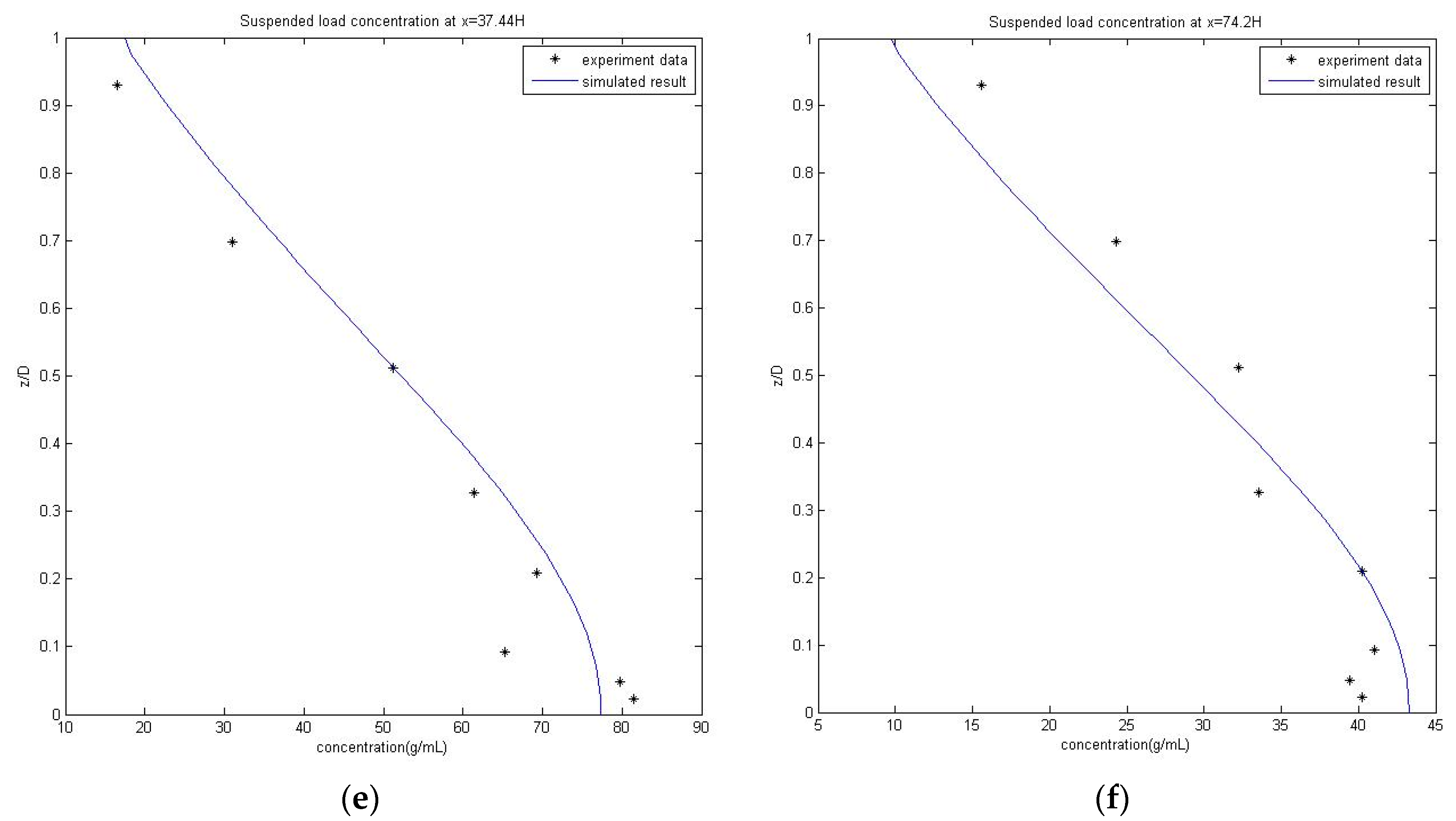
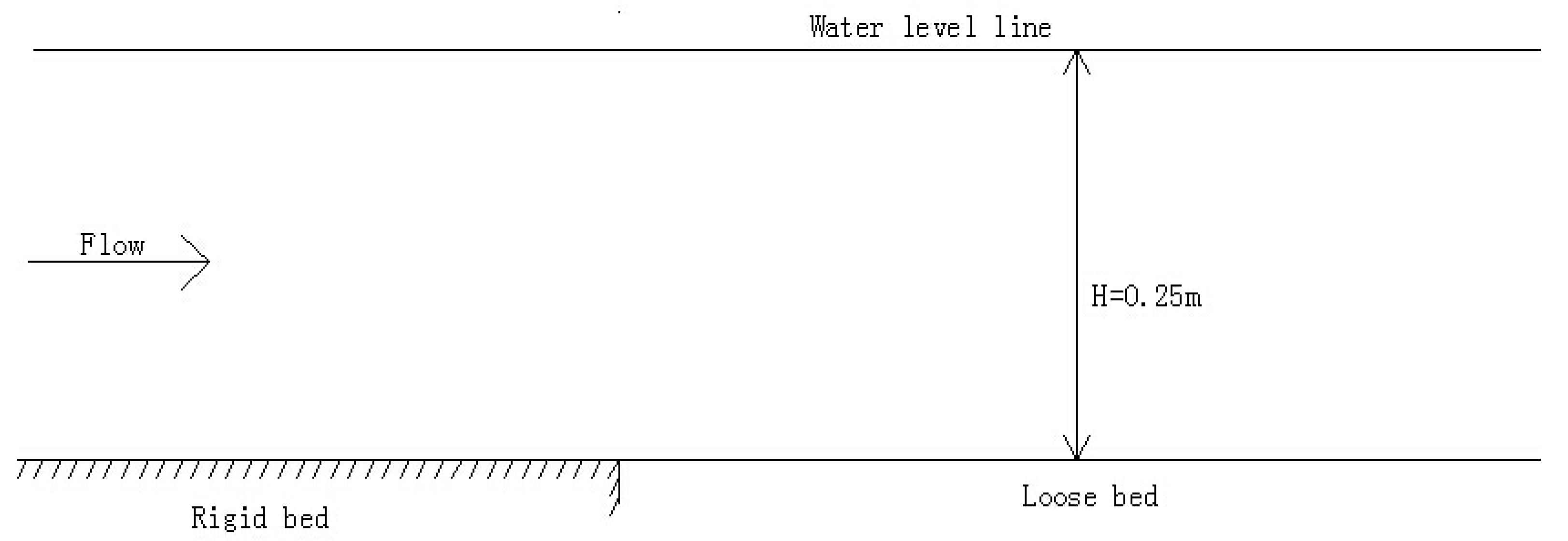
4.2.1. Zero Entrainment Experiment
4.2.2. Net Entrainment Experiment
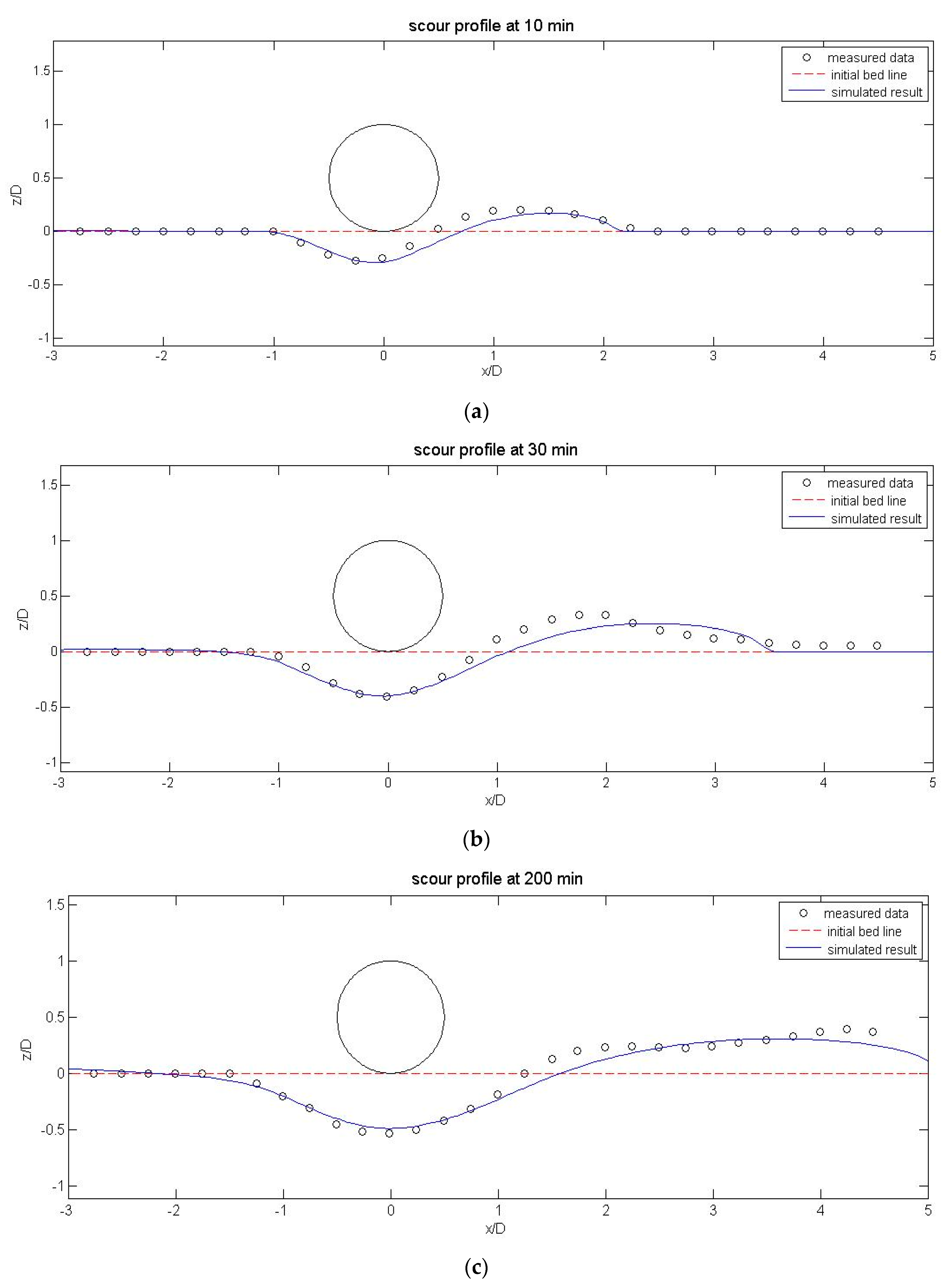
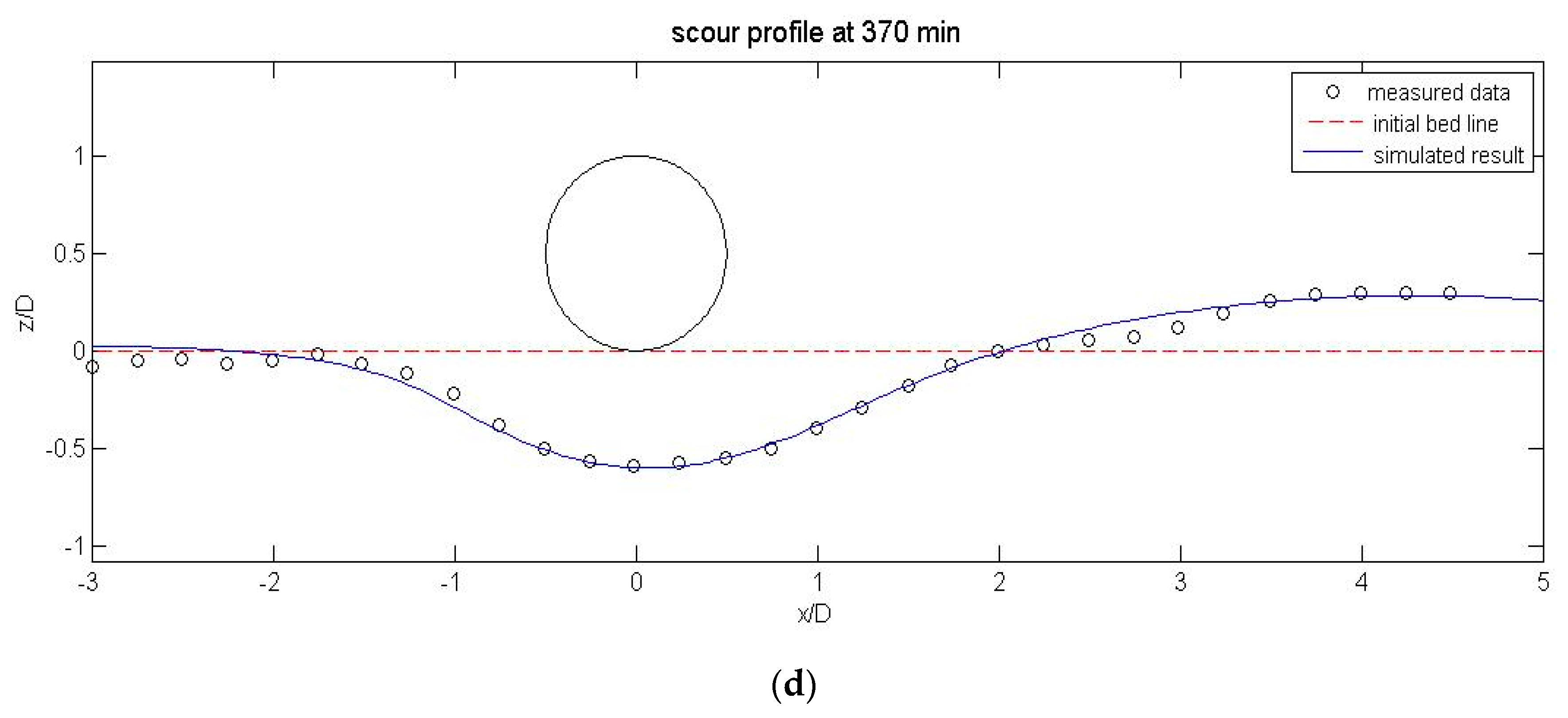
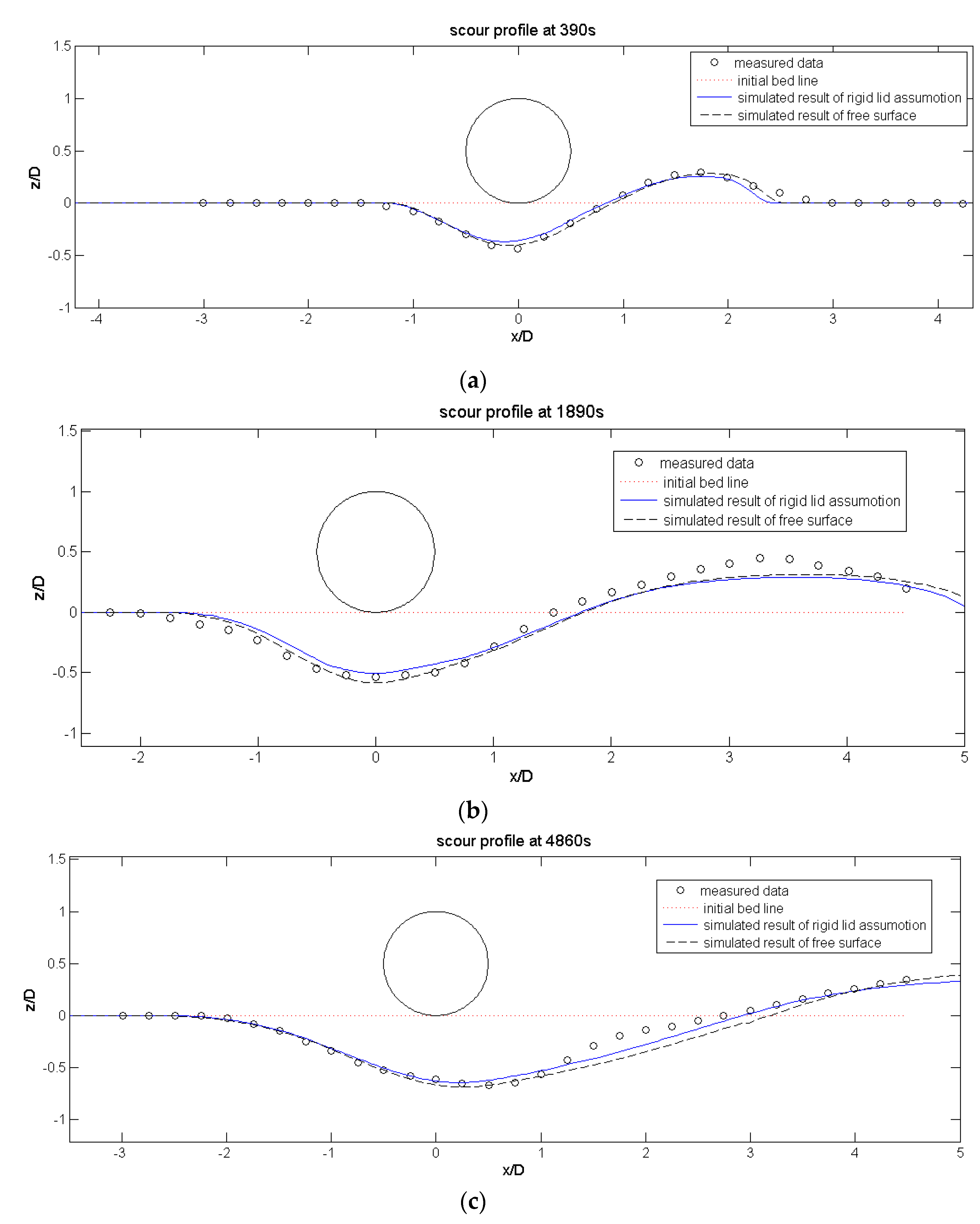
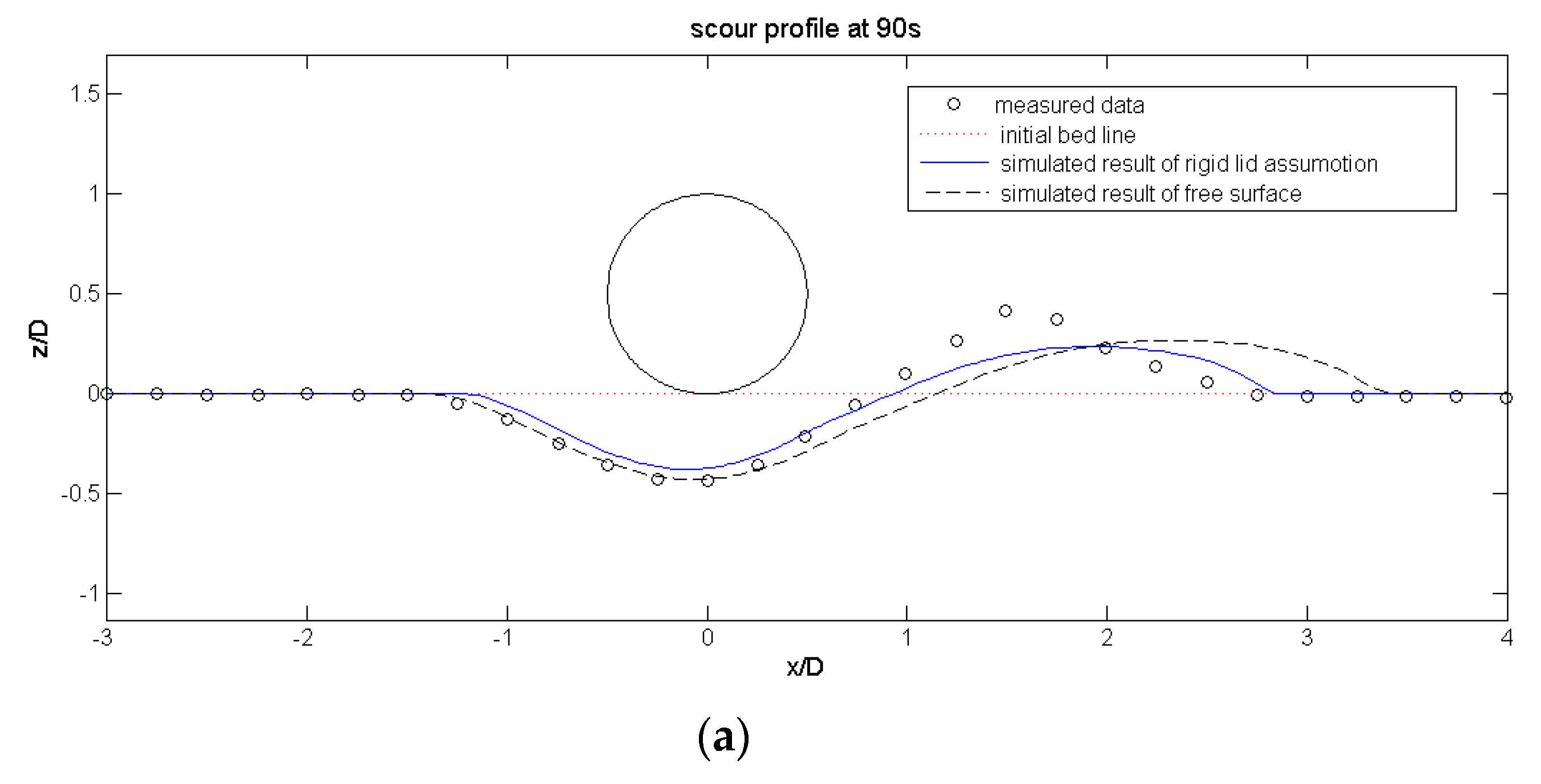
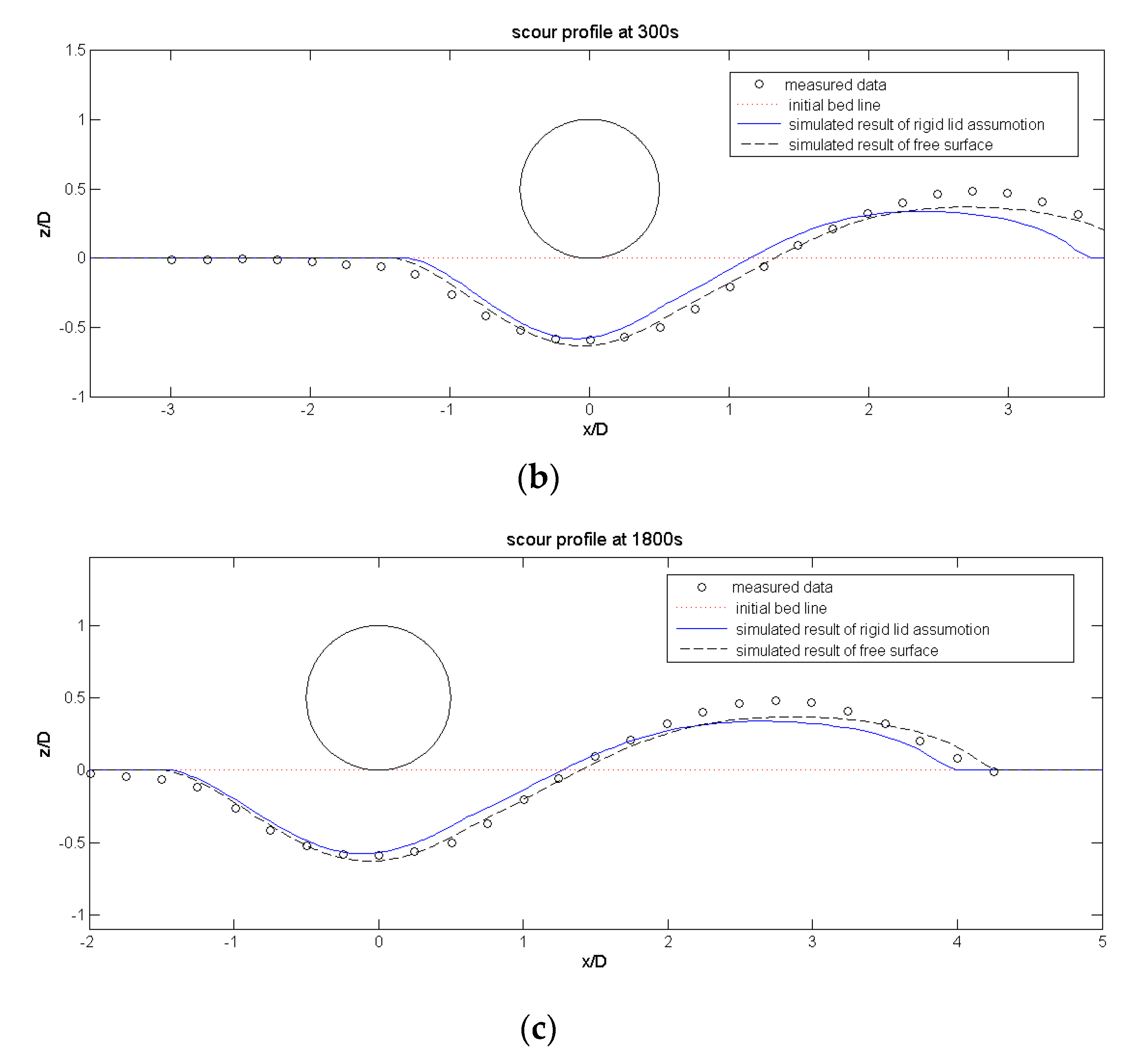
4.3. Local Scour under a Pipeline
5. Discussion
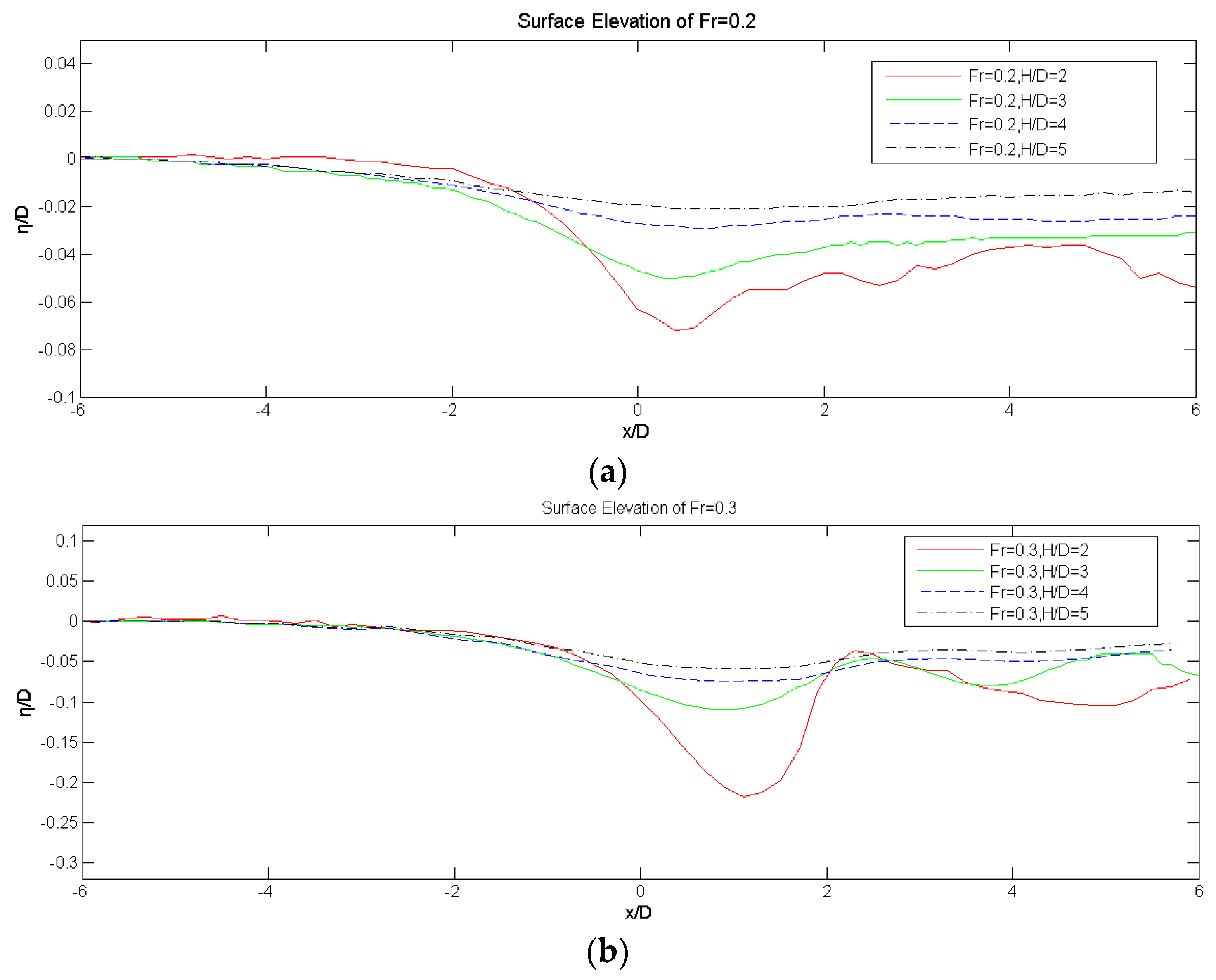
5.1. The Channel without a Pipeline
5.2. The Channel with a Pipeline
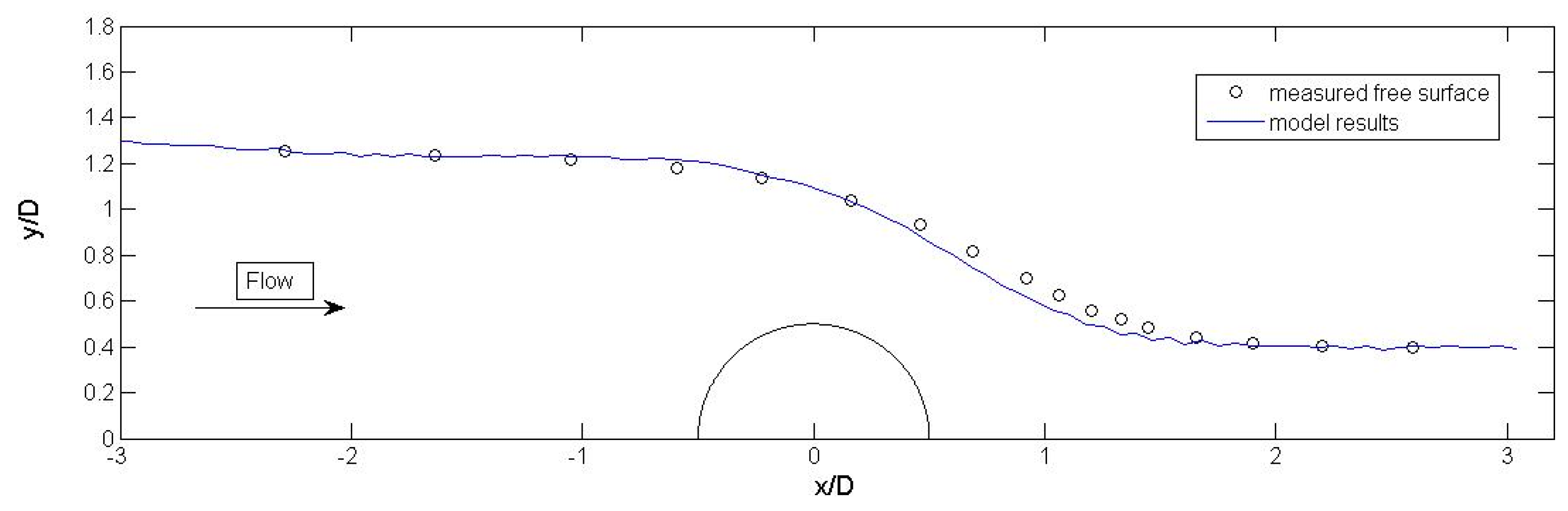
5.2.1. Validation of the Free Surface
5.2.2. The Surface Elevation and Bed Shear Stress
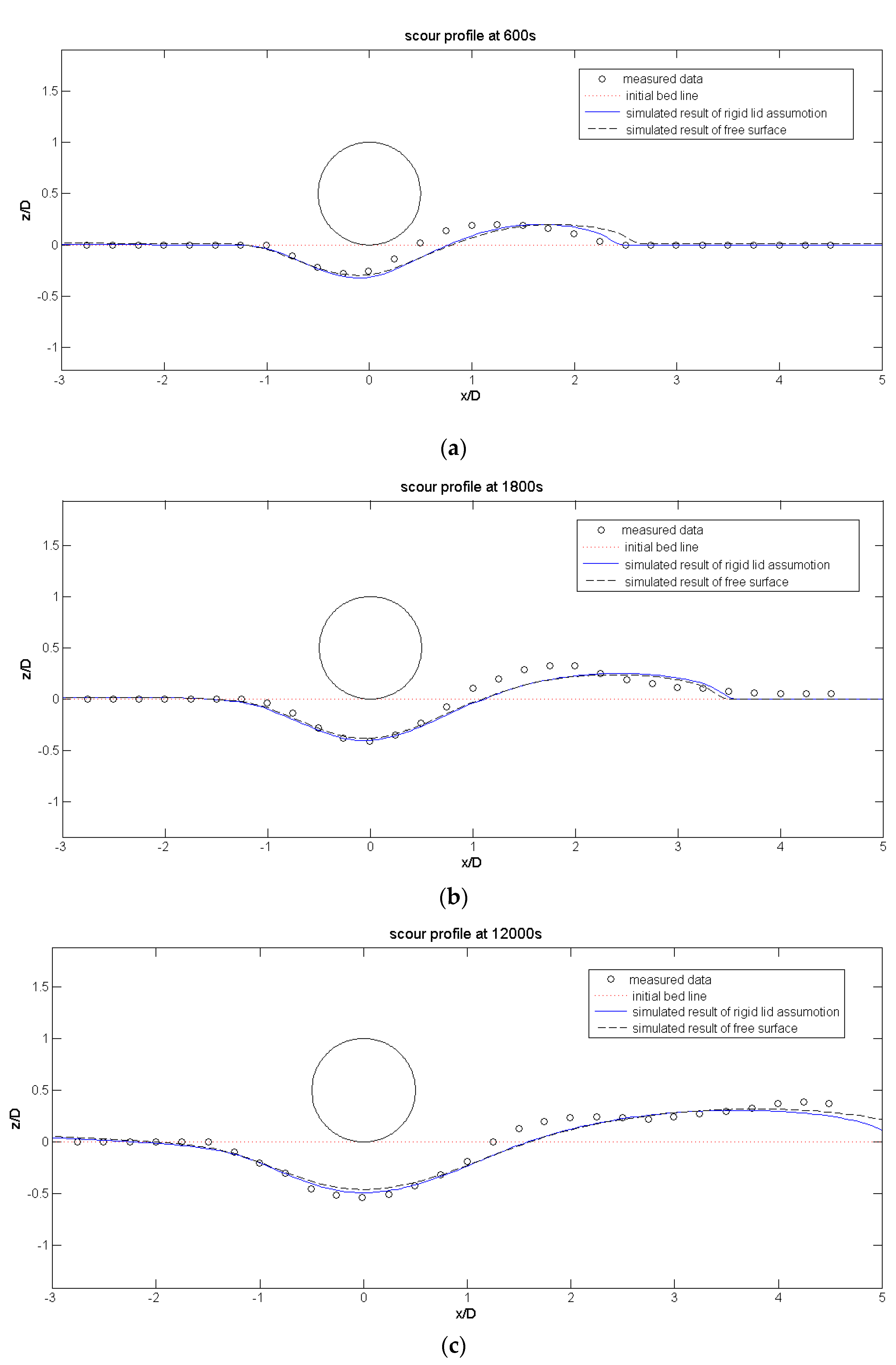
5.2.3. The Scour Hole
6. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mao, Y. The Interaction between a Pipeline and an Erodible Bed. Ph.D. Thesis, Technical University of Danmark, Kgs. Lyngby, Danmark, 1986. [Google Scholar]
- Jensen, H.R.; Jensen, B.L.; Sumer, B.M.; Fredsøe, J. Flow visualization and numerical simulation of the flow around marine pipelines on an erodible bed in waves. Underw. Pipelines 1989, 62, 37–55. [Google Scholar]
- Mattioli, M.; Alsina, J.M.; Mancinelli, A.; Miozzi, M.; Brocchini, M. Experiment investigation of the nearbed dynamics around a submarine pipeline laying on different types of seabed: The interaction between turbulent structures and particles. Adv. Water Resour. 2012, 48, 31–46. [Google Scholar] [CrossRef]
- Mattioli, M.; Mancinelli, A.; Brocchini, M. Experiment inverstigation of the wave-induced flow around a surface-touching cylinder. J. Fluids Struct. 2013, 37, 62–87. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zang, Z.; Li, F. 3D scour below pipelines under waves and combined waves and currents. Coast. Eng. 2014, 83, 137–149. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zhang, Z.; Teng, B. Three-dimensional scour below offshore pipelines in steady flow. Coast. Eng. 2009, 56, 577–590. [Google Scholar] [CrossRef]
- Qin, Z.; Draper, S.; Liang, C.; An, H. Scour below a subsea pipeline in time varying flow condition. Appl. Ocean Res. 2016, 55, 151–162. [Google Scholar] [CrossRef]
- Burak, K.; Esin, C. Scour below submarine pipelines under irregular wave attack. Coast. Eng. 2013, 79, 1–8. [Google Scholar] [CrossRef]
- Liang, D.F. Numerical modeling of flow and scour below a pipeline in currents, Part II. Scour simulation. Coast. Eng. 2005, 52, 43–62. [Google Scholar] [CrossRef]
- Fuhrman, D.R.; Baykal, C. Numerical simulation of wave induced scour and backfilling processes beneath submarine pipelines. Coast. Eng. 2014, 94, 10–22. [Google Scholar] [CrossRef]
- Zhao, M.; Shailesh, V. Local scour around two pipelines in tandem in steady current. Coast. Eng. 2015, 98, 1–15. [Google Scholar] [CrossRef]
- Liu, M.M. Numerical modeling of local scour and forces for submarine pipeline under surface waves. Coast. Eng. 2016, 94, 10–22. [Google Scholar] [CrossRef]
- Bjarke, E.L.; David, R.F. Simulation of wave plus current scour beneath submarine pipelines. J. Waterw. Port Coast. Ocean Eng. 2016. [Google Scholar] [CrossRef]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R. Numerical investigation of flow and scour around a vertical circular cylinder. Phil. Trans. R. Soc. 2015. [Google Scholar] [CrossRef] [PubMed]
- Roulund, A.; Sumer, B.M. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L. Numerical investigation of Local scour below vibrating pipeline under steady currents. Coast. Eng. 2010, 57, 397–406. [Google Scholar] [CrossRef]
- Liu, X.F. Three-dimensional numerical model with free water surface and mesh deformation for local sediment scour. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 203–217. [Google Scholar] [CrossRef]
- Fan, F.; Liang, B.; Bai, Y.; Zhu, Z.; Zhu, Y. Numerical Modeling of Local Scour Around Hydraulic Structure in Sandy Beds by Dynamic Mesh Method. J. Ocean Univ. China 2017, 16, 738–746. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Mathematical Modelling of Morphological processes in the case of suspended sediment Transport. Delft Hyrrul. Commun. 1987, 382, 44–48. [Google Scholar]
- Smith, J.D.; McLean, S. Spatially averaged flow over a wavy surface. J. Geophys. Res. 1977, 83, 1735–1746. [Google Scholar] [CrossRef]
- Mayer, S.; Garapon, A.; Sorensen, L. A fractional step method for unsteady free-surface flow with application to non-linear wave dynamics. Int. J. Numer. Methods Fluids 1998, 282, 293–315. [Google Scholar] [CrossRef]
- Soulsby, R.; Whitehouse, R. Threshold of sediment motion in coastal environments. In Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Christchurch, New Zealand, 7–11 September 1997. [Google Scholar]
- Huai, W.X. Numerical simulation of sandy bed erosion by 2D vertical jet. Sci. China Technol. Sci. 2011, 54, 3265–3274. [Google Scholar] [CrossRef]
- Niels, G.J. A Full Hydro- and Morphodynamic Description of Breaker Bar Development. Ph.D. Thesis, Technical University of Denmark, Kgs. Lyngby, Denmark, 2011. [Google Scholar]
- Van Rijn, L.C. Sediment transport. Part III: Bed forms and alluvial roughness. J. Hydraul. Eng. 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Deltares. Sediment transport and morphology. In Delft 3D-Flow Manual: Simulation of Multi-Dimensional Hydrodynamic Flows and Transport Phenomena, Including Sediments; Deltares: Delft, The Netherlands, 2011; pp. 329–408. [Google Scholar]
- Niels, G.J. Mass conservation in computational morphodynamics: Uniform sediment and infinite availability. Int. J. Numer. Methods Fluids 2015, 78, 233–256. [Google Scholar] [CrossRef]
- Jensen, B.L.; Sumer, B.M. Turbulent Oscillatory Boundary layers at High Reynolds numbers. J. Fluid Mech. 1989, 206, 265–297. [Google Scholar] [CrossRef]
- Wang, Z.B.; Ribbeerink, J.S. The validity of a depth integrated model for suspended sediment transport. J. Hydraul. Res. 1986, 24, 53–66. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Mathematical modeling of suspended sediment in non-uniform flows. J. Hydraul. Eng. 1986, 112, 433–455. [Google Scholar] [CrossRef]
- Frobes, L.K.; Schwartz, L.Z. Free-surface flow over a semicircular obstruction. J. Fluid Mech. 1982, 144, 299–314. [Google Scholar] [CrossRef]



| Location | X = 0D | X = 2D | |
|---|---|---|---|
| Cases | |||
| Experiment data | 0.038 | 0.011 | |
| Case1 (mesh size 1 cm) | 0.0326 | 0.0073 | |
| Case2 (mesh size 5 mm) | 0.0349 | 0.0089 | |
| Case3 (mesh size 1 mm) | 0.0364 | 0.0100 | |
| Case4 (mesh size 0.5 mm) | 0.0372 | 0.0105 | |
| Case5 (mesh size 0.1 mm) | 0.0374 | 0.0106 | |
| Cases | Fr = 0.1 | Fr = 0.2 | Fr = 0.3 | |||
|---|---|---|---|---|---|---|
| H (m) | U (m/s) | Re (104) | U (m/s) | Re (104) | U (m/s) | Re (104) |
| 0.1 | 0.1 | 1.0 | 0.2 | 4 | 0.3 | 9 |
| 0.225 | 0.15 | 1.5 | 0.3 | 6 | 0.45 | 13.5 |
| 0.4 | 0.2 | 2.0 | 0.4 | 8 | 0.6 | 19 |
| 0.625 | 0.25 | 2.5 | 0.5 | 10 | 0.75 | 22.5 |
| 0.9 | 0.3 | 3.0 | 0.6 | 12 | 0.9 | 27 |
| 1.225 | 0.35 | 3.5 | 0.7 | 14 | 1.05 | 31.5 |
| 1.6 | 0.4 | 4.0 | 0.8 | 16 | 1.2 | 36 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, F.; Liang, B.; Li, Y.; Bai, Y.; Zhu, Y.; Zhu, Z. Numerical Investigation of the Influence of Water Jumping on the Local Scour beneath a Pipeline under Steady Flow. Water 2017, 9, 642. https://doi.org/10.3390/w9090642
Fan F, Liang B, Li Y, Bai Y, Zhu Y, Zhu Z. Numerical Investigation of the Influence of Water Jumping on the Local Scour beneath a Pipeline under Steady Flow. Water. 2017; 9(9):642. https://doi.org/10.3390/w9090642
Chicago/Turabian StyleFan, Fei, Bingchen Liang, Yaru Li, Yuchuan Bai, Yanjun Zhu, and Zhixia Zhu. 2017. "Numerical Investigation of the Influence of Water Jumping on the Local Scour beneath a Pipeline under Steady Flow" Water 9, no. 9: 642. https://doi.org/10.3390/w9090642
APA StyleFan, F., Liang, B., Li, Y., Bai, Y., Zhu, Y., & Zhu, Z. (2017). Numerical Investigation of the Influence of Water Jumping on the Local Scour beneath a Pipeline under Steady Flow. Water, 9(9), 642. https://doi.org/10.3390/w9090642




