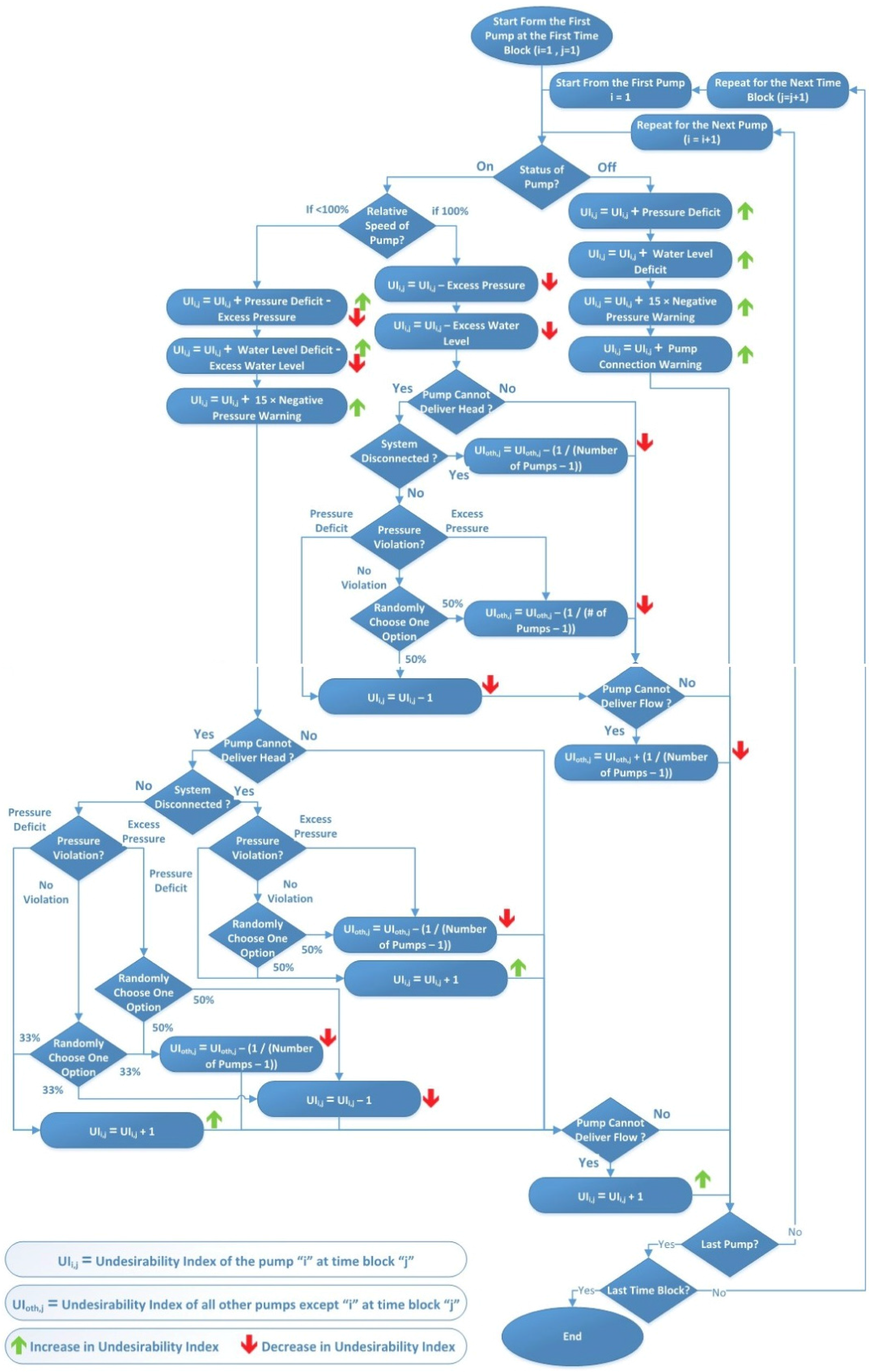
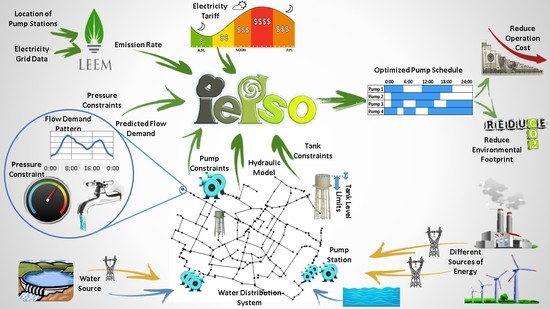
1. Introduction
In the modern world, many systems are designed based on scientific analysis and engineering techniques, but it does not mean that these systems are developed and operated in an optimal way. In recent decades, due to improvement in the computational power of machines and development of new optimization techniques, engineers have focused more on using computer models and deterministic or meta heuristic optimization techniques to optimize the design and operation of systems. There are many optimization efforts related to water systems including piping design optimization, pump operation optimization, sensor placement improvement, model calibration, leakage detection and reduction, system reliability, etc. [
1].
About 4% of electricity usage in the US is attributed to the supply, conveyance, and treatment of water and wastewater at the cost of approximately 4 billion US dollars per year. Moreover, due to increasing urban and industrial water demands and a decrease in access to high-quality water resources, it is predicted that the energy consumption of this sector will increase more than 50% by 2050 [
2]. According to the US Department of Energy, approximately 75% of the operating costs of municipal water supply, treatment and distribution facilities is attributed to electricity demand [
3]. As noted by several researchers, optimizing pump operation has a considerable effect on the water industries, which can offer a reduction of up to 10% in the annual expenditure of energy and other related costs [
4,
5]. Using hydraulic models to investigate the potential of energy usage and associated pollution emission reduction in water systems has been studied by different researchers. For instance, Perez-Sanchez and his colleagues, by using EPANET model of an irrigation system, showed that theoretically 188.23 MWh/year energy-equivalent to 137.4 ton CO
2/year-can be recovered from the system [
6,
7]. León-Celi, C et al. also used EPANET toolkit and two optimization algorithms to find the optimum flowrate distribution in water systems with multiple pump stations and minimize energy usage and potential leakage [
8].
Time-of-use tariff and change in sources of energy in time may increase or decrease the electricity cost or pollution emissions (associated with the generation of energy) of the system, even if the total energy consumption of the system does not change. Elevated storage tanks in the system provide flexibility for operators to shift energy usage of the system. Shifting energy consumption may allow the operator to take advantage of cheaper energy and less polluting generator sources.
Uncertainties in demand of the system and complexity of the possible combination of pump status that can potentially answer operational requirements of the WDS, increase the tendency of operators to maintain water pressure in the system higher than the minimum required pressure. This increases energy usage, water leakage and consequently water and energy waste. Therefore, developing an optimization tool that can automatically react to changes in various inputs and generate a near optimum pump schedule may decrease electricity cost and the environmental footprint of the system.
2. Literature Review
About four decades ago, when researchers started to work on optimization of WDSs, most of them focused on construction cost (reducing the cost of piping) and operation cost (minimizing the cost of energy usage and the power demand of the pump station). However, after a while, other objectives such as increasing reliability and water quality or decreasing environmental footprint were included in the optimization process. In the last decade, the attention toward the environmental effect of energy usage and sustainability of WDSs increased due to increase in public and scientific awareness of climate change and the effect of pollutant emissions from power generation [
9]. At first, most researchers considered the WDS optimization problem as a single objective problem. However, some researchers adopt multi-objective methods for optimization of the operation of the WDS [
10].
One of the main objectives of the pump operation optimization is reducing the operation cost of pumps. The real electricity tariffs, in many cases, include a peak power demand charge (
$/kW) in addition to the energy consumption charge (
$/kWh). So, it is evident that a useful optimization tool should be able to use complicated electricity tariffs including both energy consumption and peak power demand costs. There are different examples in previous research of energy consumption charge and peak power demand charge being used. Wang et al. used a time-of-use electricity tariff in their optimization study [
10]. Baran et al. also used a time-dependent electricity tariff that was defined based on on-peak and off-peak hours [
11]. Shamir and Salomon used a more complicated electricity tariff. They used the real and complex electricity tariff of Haifa city, Israel, which includes three time periods, representing high, medium, and low energy costs. The tariff was different for the weekend and holidays and the various seasons of the year [
12]. Working multiple pumps at the same time may cause an increase in required power. This may increase the total electricity cost of the system. There are some examples of researchers taking the power demand charge into account. For instance, Fracasso and Barnes included the amount of peak power demand (kW) as an objective of the optimization process [
13].
In addition to the electricity cost, pollutant emissions associated with the electricity consumption is another objective that needs to be optimized to have a sustainable WDS. Wu et al. included the effect of variable emission rates and electricity tariffs in their WDS design optimization study [
14]. Stokes et al. also suggested a framework for the modeling and optimization of Greenhouse Gases (GHG) emissions associated with energy usage and pump operation [
15]. In most of these efforts, the emission rate of energy usage was considered as a constant value and was linearly related to the amount of consumed energy. However, most of the time, the source of electrical energy is a mix of various types of power generators. As this combination of generators may change in time, the emitted amount of pollutants per unit of consumed energy may change. Researchers at Wayne State University developed the LEEM methodology to calculate the amount of pollutant emissions associated with energy generation at different points in space and time. LEEM is an acronym for Locational Emissions Estimation Methodology and provides real-time and predicted marginal emission factors (kg/MWh) based on location and time of energy consumption [
16].
Besides the two above-mentioned objectives, some constraints help to direct the algorithm to solutions that satisfy operational requirements of the WDS. For instance, frequent pump starts can increase the maintenance costs of the system [
17]. Some researchers placed some limits on the maximum number of pump starts. Similarly, water pressures at junctions or water flow rate in pipes can be bounded. Constraints can be handled explicitly or can be converted to objectives and handled implicitly during the optimization process. One of the common methods of converting a constraint to an objective is using penalty formula. By this approach, violation from a constraint can be converted to a penalty value and reducing the penalty can be considered as an objective. Zecchin et al. used the pressure penalty to add a pressure constraint to the objective function of the ant colony (AC) algorithm that they used for WDS design optimization [
18]. Lopez-Ibanez investigated the effect of constraint on the maximum number of pump starts. He found that a lower limit of the maximum number of pump starts that does not hinder the search for an optimum solution is related to characteristics of the network [
19].
In addition to the maximum number of pump starts, other constraints such as minimum and maximum allowed water level in tanks, maximum and minimum allowed pressure at different points of the water network and maximum and minimum allowed velocity of water in different pipes can be considered during optimization. The effect of all of these constraints can be translated to penalty values. Reducing total penalties of a pump operation schedule can be formulated as an objective of optimization. So, reducing electricity usage cost, pollution emissions (associated with electricity usage) and penalties can be considered as three objectives of a pump operation optimization problem.
A multi-objective optimization problem can be solved with multi-objective methods or can be converted to a single objective problem and solved with a single objective optimization algorithm. For instance, Wu and Behandish calculated the amount of the objective function by the total weighted cost of energy and amount of three penalties [
20]. Abiodun and Ismail completed a bi-objective optimization that aimed to reduce the electricity cost and maintenance problems [
5]. In other studies, researchers used the multi-objective optimization method to solve a multi-objective problem directly and find the Pareto frontier of solutions. For instance, Fu and Kapelan used a multi-objective optimization method for finding the best WDS design based on pipe cost and system robustness [
21]. Pollutant Emission Pump Station Optimization (PEPSO) is a platform developed by the water research team at Wayne State University for optimizing the pump schedule of the WDS [
16]. The initial version of PEPSO used weighting factors to calculate a single combined objective from electricity usage, pollutant emissions and penalties [
22]. However, the newer version of this tool is equipped with a multi-objective optimization algorithm to optimize each objective independent of others and find the Pareto frontiers of solutions.
Converting the multi-objective problem to a single objective problem increases the simplicity of the optimization algorithm. Also, the optimum result is a single solution that can be used directly. On the other hand, by using multi-objective methods, finding optimum solutions with respect to one objective does not have any effect on the process of finding the optimum value of other objectives. Also, there is not any need for normalizing and weighting operations. Defining a meaningful method to combine different objectives such as the cost of electricity usage and weight of pollution emissions and coming up with a single objective is a challenging process. Additionally, the multi-objective approach creates a range optimal solutions as a Pareto frontier that provides some flexibilities for users to select the preferred solution based on their requirements. Finally, a multi-objective algorithm can search the solution space of a multi-objective optimization problem with more freedom. This cannot be achieved with a single objective algorithm and when the effect of one objective on the combined objective is much more considerable than the effect of other objectives.
In the last two decades, many researchers have shifted the focus of WDS optimization from traditional and deterministic techniques, based on linear and nonlinear programming, to the implementation of methods that were generally based on heuristics derived from nature [
18,
23]. In recent years, Evolutionary Computation has proven to be a powerful tool to solve optimal pump-scheduling problems [
11]. The great advantage of metaheuristic algorithms over deterministic methods is that they can be used for almost all types of optimization problems without considering the linearity or convexity of the problem. However, while using metaheuristic algorithms, constraints related to the hydraulic behavior of the solution must be checked separately or should be converted to an objective [
24].
Genetic Algorithm (GA) is one of the most used algorithms in the optimization field and especially in water-related problems [
25,
26]. At first, Simpson et al. suggested using GA in the mid-90s for WDS optimization [
27]. Lopez-Ibanez investigated various representations of pump schedule in his thesis and suggested that time-controlled trigger-based representation can lead to a better result and ensure maximum limit of switches per pump in comparison with level-controlled trigger representation. However, his result also showed that time-controlled trigger-based representation did not have considerable advantages on the common binary representation [
19]. In this study, we used a customized version of the multi-objective Non-Dominated Sorting Genetic Algorithm (NSGA II) with the binary representation of solutions to develop that WDS or water transmission lines. These networks have a handful of pipes, junctions, pumps and occasionally one or two optimization tool.
One of the most famous free and publicly available software for modeling the WDS is EPANET2 that is published by the US EPA [
7]. Lopez-Ibanez reviewed about 20 articles from 1995 to 2004 and reported that most of the researchers used complete hydraulic simulation to evaluate the effect of decision variables on the status of the hydraulic network [
19]. We also used EPANET 2.00.12 as the hydraulic solver of the optimizer tool [
7].
Most of the previous studies focused on a small-scale elevated tanks [
5,
10,
28]. A small portion of real systems are similar to small test networks of these researches, but most of the time we face large networks with a couple of hundred pipes, junctions, and a considerable number of pumps, valves, tanks, etc. There are a few studies that tried to optimize a real and large-size WDS [
4,
29,
30]. Most of the systems that were used in WDS optimization studies do not have variable speed pumps. The WDS of Monroe City, MI, previously used for comparing three pump operation optimization tools, has both fixed and variable speed pumps [
31]. The WDS of Richmond, UK, is also used in several types of research. This model is publicly available for the researcher and is suggested to be used for operation optimization studies of WDSs [
32]. In this study, we used both Monroe and Richmond WDS models to test the developed optimization tool.
5. Results and Discussion
In total, 60 optimization runs have been done on two WDS models. The required time for completing an optimization run of the Monroe WDS is 02:14:44 ± 00:03:43. This time, for the skeletonized version of the Richmond WDS model, is 00:35:38 ± 00:01:36. PEPSO reports the electricity cost of the final solution. However, before comparing the electricity cost of different solutions, we should consider that the final volume of stored water in the system might not be equal in all solutions. Although the final level of water was in the acceptable range from a system operation point of view, filling or draining an elevated tank can be regarded as storing energy into or draining energy from the system. Therefore, the net energy consumption of the system is calculated considering the change in volume of stored water. Similarly, the net electricity cost and net CO2 emissions of each solution is calculated before comparing the results. It is assumed that a long-run deficit or surplus water volume at the end of each day will be balanced by the change of operation in different hours of upcoming days. Therefore, the average electricity charge ($/kWh) and CO2 emission factor (kg/MWh) were used to take into account the effect of this deficit or surplus water volume and calculate the net electricity cost and net CO2 emissions.
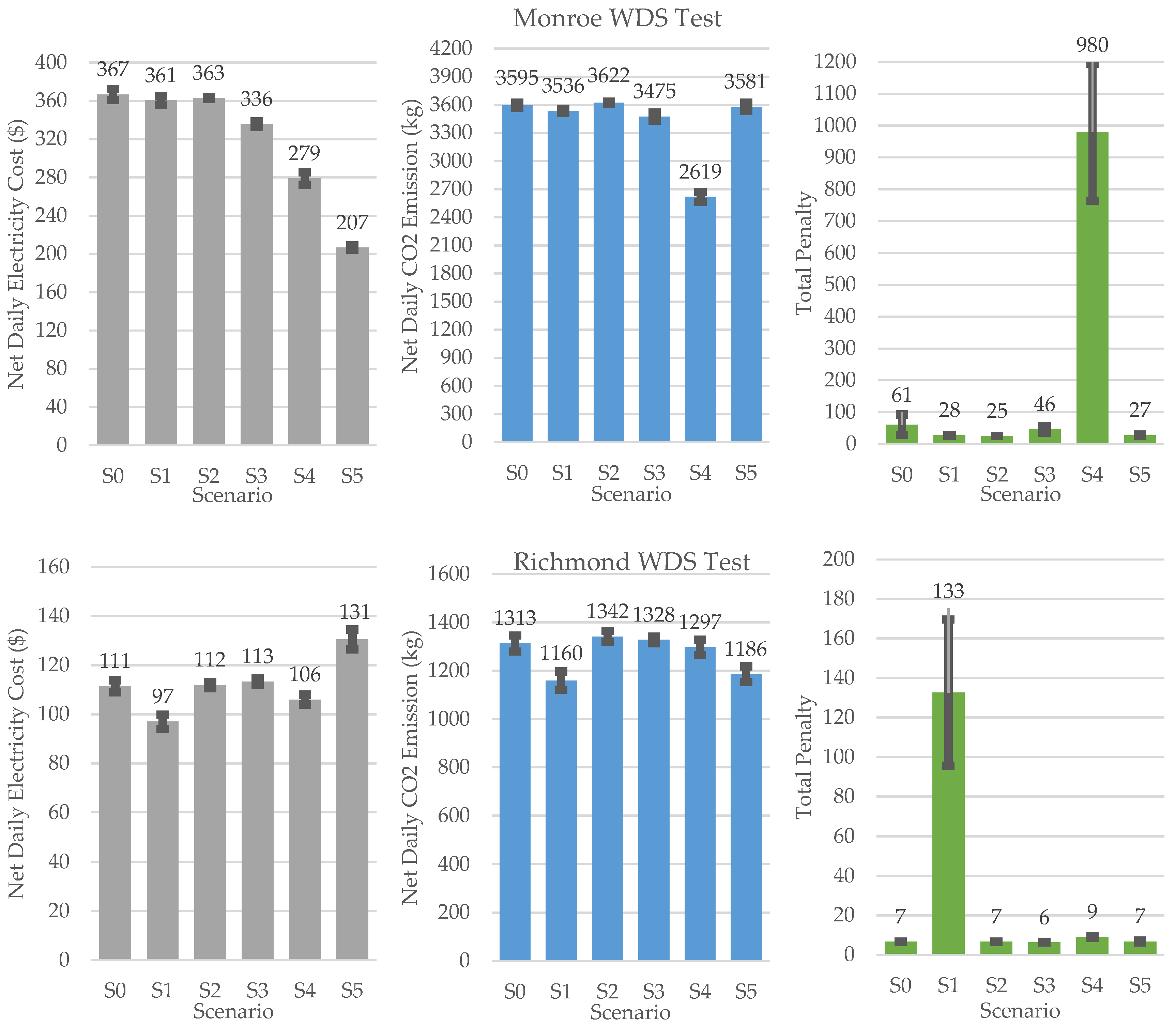
Net electricity cost (
$) (left), net CO
2 emissions (kg) (middle) and total penalty (right) of all five scenarios of the Monroe WDS (top) and the Richmond skeletonized WDS (bottom) tests are displayed in bar charts in
Figure 2. Each column shows the average result of five repeated tests and the error bar on top of it displays the SEM value. Except for columns that show high total penalty values, the SEMs of all the other results are relatively small. This shows the consistency in the outcome of PEPSO runs. Since penalty values are related to the amount of violation raised to the power of 1.5, it is expected to see that the moderate change in violation value results in a more severe change in penalty values.
Comparing results of scenarios S0, S1 and S2 showed, in both WDSs, optimizing based on three objectives (S1) is the most effective strategy for reducing objectives and obtaining a practical result. Theoretically, we expect to see the lowest amount of electricity cost in the result of the S0 scenario, but the result showed that in the majority of tests, both the electricity cost and CO2 emissions of the S1 scenario are less than S0. On average, the electricity cost and CO2 emissions of S1 scenarios are 12.9% and 11.7% in Richmond tests and 1.7% and 1.7% in Monroe tests less than S0 results respectively. Since, in most cases, reducing energy usage decreases both the electricity cost and pollution emissions, optimizing based on all three objectives (S1) helps PEPSO to better explore the solution space. So, despite our theoretical expectation to see the minimum electricity cost in the result of the S0 scenario, in practice, the S1 scenario is more efficient at finding low energy consumption solutions in a limited amount of time.
As expected, optimizing just based on total penalty (S2) results in less penalty with respect to the outcome of both S0 and S1 scenarios. The total penalty of the S1 scenario of the Richmond test was considerably higher than the S0 and S2 scenarios. Investigating the detailed results, in this case, showed that there are two solution groups that can be selected as the optimum solution. In the first group, pumps are using more energy and pressure at junctions and water levels in tanks are slightly below the upper boundary of the desirable range. So, total penalties of this solution group are low. The second solution group has considerably less energy consumption and correspondingly less CO2 emissions. However, in these solutions, pressure at a couple of junctions and water level at some tanks are below the desired level which increases the total penalty of these solutions. Although the violations in these cases are not beyond the acceptable range, from the optimizer perspective, these are dominated solutions when there is only one objective (total penalty). So, PEPSO does not choose the final solution from the second group. However, in the S1 scenario, when all three objectives are considered, a solution from the second group, which has some penalties but has a considerably lower electricity cost and CO2 emissions, is reported as the optimum solution.
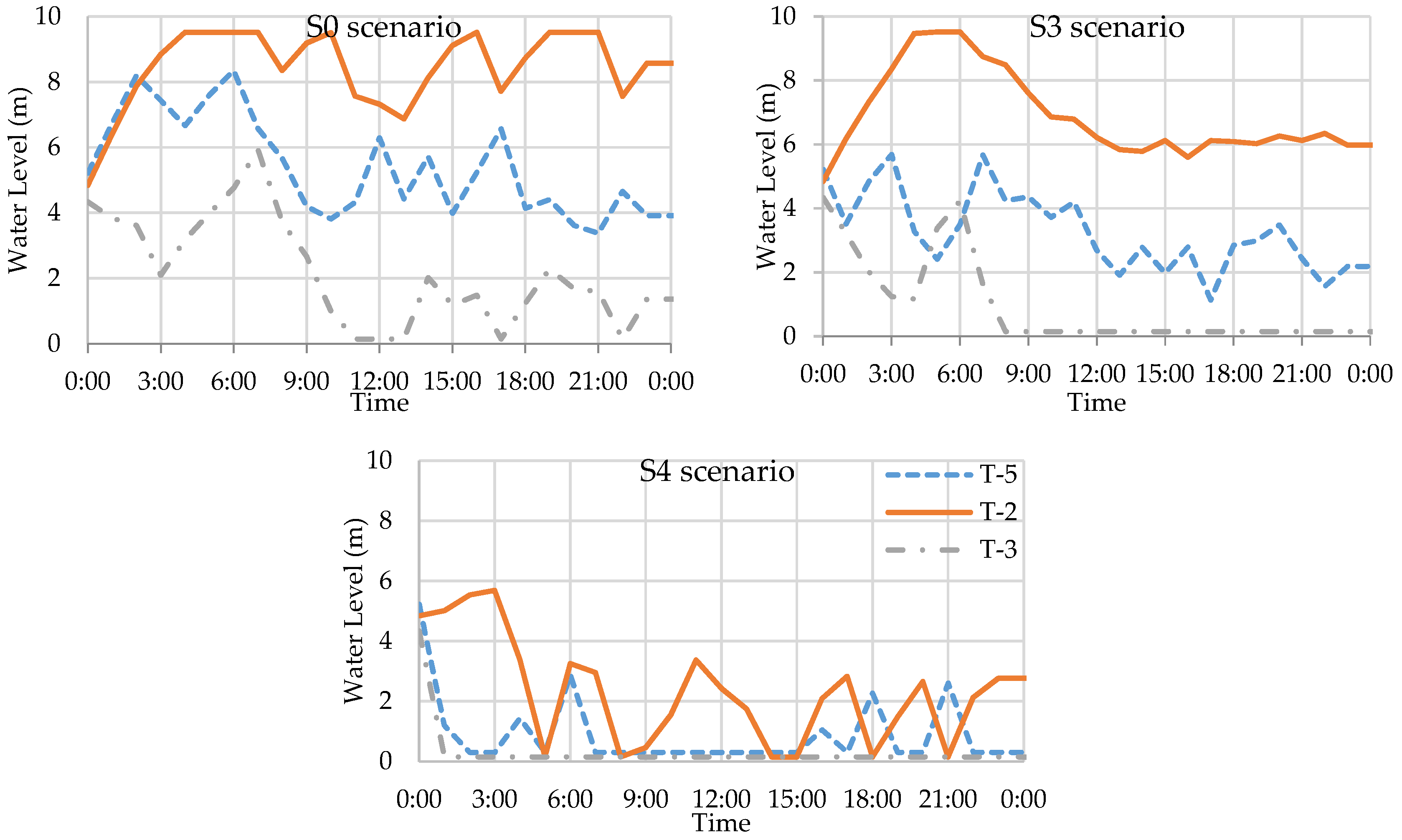
Comparing results of the S0 scenario with those of the S3 scenario showed that, when the UI is used in the optimization run of the Monroe WDS, on average, the net electricity cost is reduced by 8.5%. Although, at first sight, it seems that using the UI reduced the effectivity of the optimization algorithm, a closer look at the results revealed that the result of the S0 scenario is more practical than the S3 scenario. During the whole operation period, the stored volume of water in tanks in the S3 scenario is, on average, 5.6% lower than S0. The final volume of stored water in tanks for the S3 scenario is 10.9% lower than the final volume of stored water in the S0 scenario. Also, solutions of the S0 scenario, on average, have less than two warnings about pumps that cannot deliver head, but S3 results, on average, have about four and one warnings for pumps that cannot deliver head and flow respectively.
Figure 3 displays the water level pattern in tanks of typical results of S0 (top left) and S3 (top right) scenarios. It can be seen that the solution of S3 tends to drain tanks more than that of S0.
The hydraulic model of the skeletonized version of the Richmond WDS was simpler than the Monroe WDS. So, in this case, optimizing with or without the undesirability calculation did not considerably change the results. Results of both S0 and S3 scenarios are close with respect to total penalty, electricity cost and the number of warnings. It seems that the undesirability calculation helped a little bit to find solutions with slightly lower CO2 emissions (2.2%). However, it should be considered that calculating undesirability is an additional computation load on the optimization process. On average, calculating and using the UI in the optimization process of the Monroe WDS increased the required time for the optimization run by 8.9%. Based on these results, we can say that calculating the UI increased the required time for 16,600 solution evaluations in an optimization run. However, the final result was more practical and of higher quality. Obtaining a final solution with the same level of quality without using the UI needs more iterations and solution evaluations that increase the length of the optimization process. We expected that using the UI, by quantifying positive and negative effects of pump statuses on hydraulic responses of the water network, adds some intelligence to the process of producing the next generation and makes possible more purposeful crossover, mutation and elitism steps. Although calculating the UI increases the computational load of each iteration, we expected to see that within the same number of iterations, using the UI can provide better results. The outcome of these tests showed promising results regarding the use of the UI. However, this area still needs further research. More studies on complicated networks with vast solution space can help to show and quantify the level of effectiveness of the UI. It is possible that, in the case of a complex system with multiple pumps and vast solution space, traditional blind crossover, mutation and elitism steps (without using UI) cannot find an acceptable solution within a reasonable number of iterations. Results of the S4 scenario showed that giving PEPSO the possibility to operate pumps without tank level constraints, on average, reduces the electricity cost and CO2 emissions of the system by 24.0% and 27.2%.
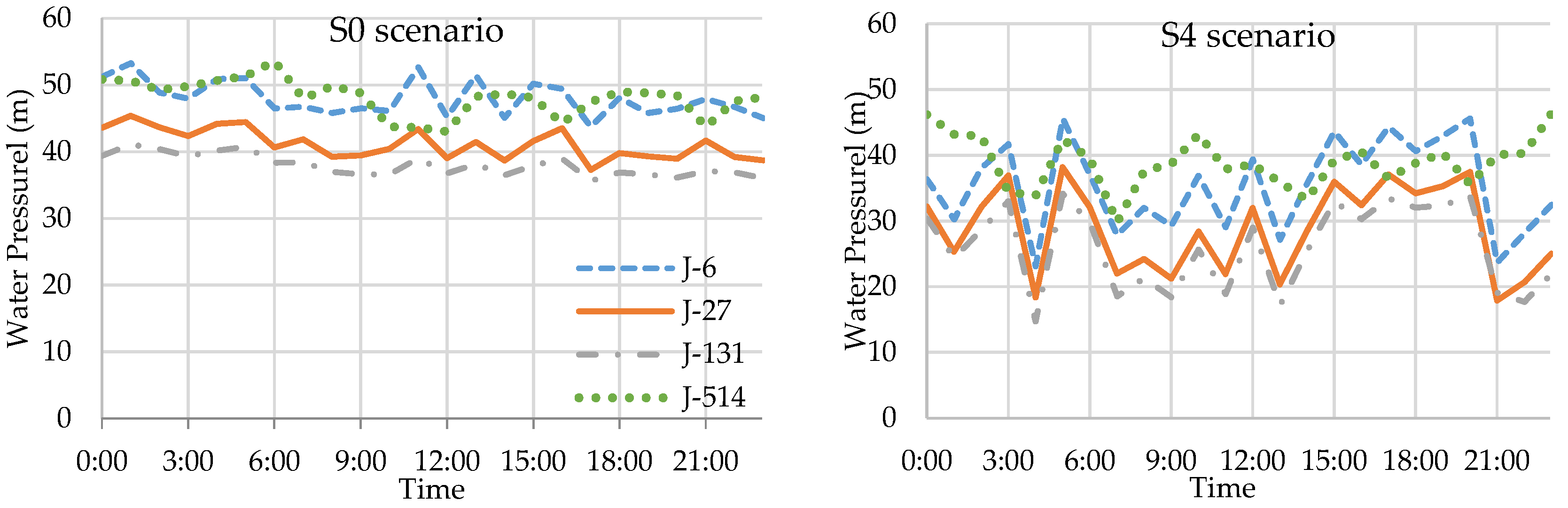
Despite the fact that removing water level constraints reduces the electricity cost and CO
2 emissions, it considerably increased the water level violation of tanks and water pressure violation at strategic junctions. In the S4 scenario, the pressure of junctions has some fluctuations that caused considerable low and high-pressure penalties. The water level penalty of tanks of the S4 scenario is four times more than for the S0 scenario. Comparing patterns of the water level in tanks (see
Figure 3) and water pressure at junctions (see
Figure 4) of the S4 and S0 scenarios can clearly show these differences.
On average, constraining the water levels of tanks during the operation cycle led to a reduction of more than 32% in the final volume of stored water. Monroe test results indicate that water level constraint effectively helps to keep the final tank level balanced and prevents tanks from draining during the whole operation period. Similarly, optimizing the pump operation of the Richmond WDS without water level constraints for tanks (S4), on average, reduces the net electricity cost and CO2 emissions by 4.8% and 1.2% respectively. However, this increases the total penalty by 35.1%.
Results of the test on the Monroe WDS showed that having a flat rate electricity tariff, on average, can lead to a 9.7% increase in peak power demand (kW) while the total consumed energy (kWh) is almost unchanged. Although the total energy consumption in both S0 and S5 scenarios is almost unchanged, 2.1% of the total energy consumption in the S5 scenario shifted from off-peak hours to on-peak hours. These results confirm that the power demand charge and time-of-use electricity tariffs will force PEPSO to find an optimized solution with more energy consumption during off-peak times and with a reduced peak power demand.
The overall electricity cost in the Richmond system is related to the time-dependent energy consumption charge. However, in the S5 requirement of the system. PEPSO uses a customized version of the NSGA II to find the Pareto frontier and then select the best solution as the optimum pump scenario, the flat rate electricity tariff, on average, reduced the total energy use (kWh) from the off-peak hours by 3%and added half of that to the on-peak hours. By this change, the remaining 1.5% of energy is saved. Previously, due to the use of a time-of-use electricity tariff, PEPSO needed to shift energy usage to reduce the electricity cost of the system. This shift of energy usage caused a 1.5% energy loss due to head losses while filling and draining tanks. It is interesting to see that the solution of the S0 scenario drained 21.6% of the stored volume of water in tanks of the Richmond WDS. While the S5 scenario just drained 12.0% of this volume.