Modelling Fine Sediment Dynamics: Towards a Common Erosion Law for Fine Sand, Mud and Mixtures
Abstract
:1. Introduction
2. Strategy and Modelling Background
2.1. Strategy for Assessing an Erosion Law, and Its Application to the BoBCS
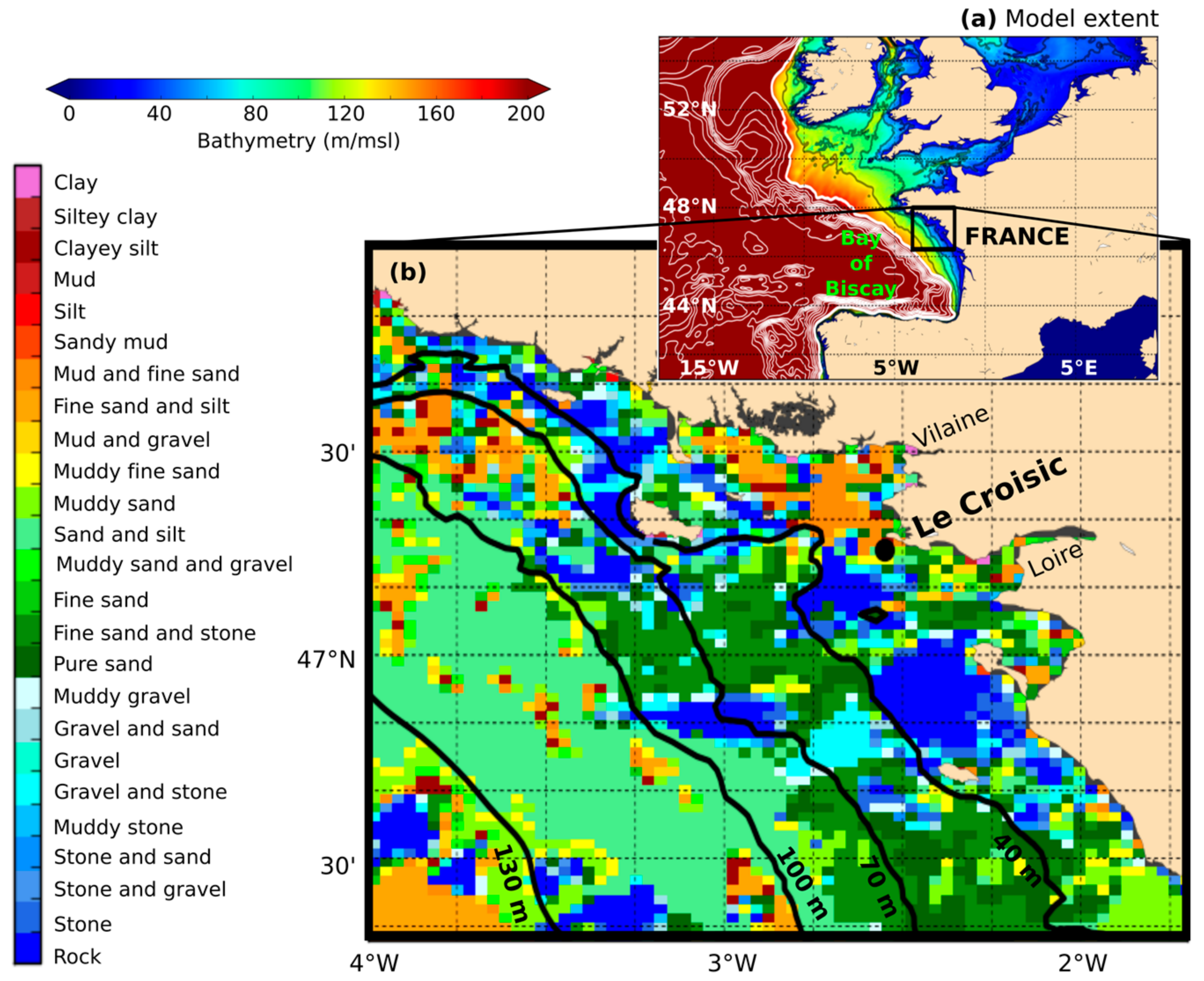
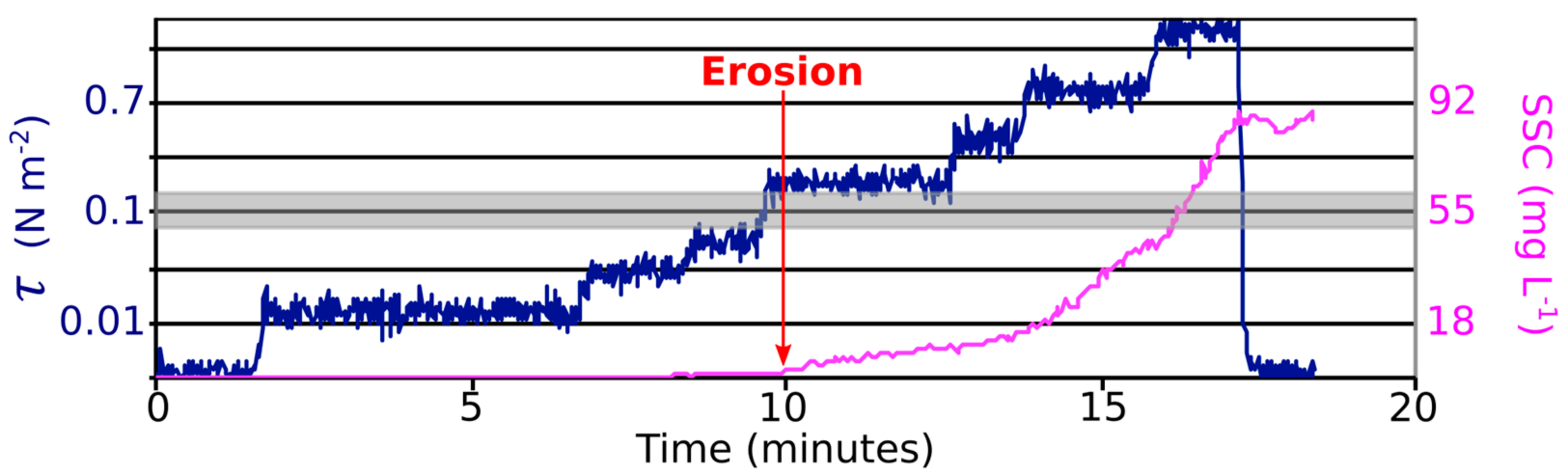
2.2. Measurements Used for Erosion Law Assessment and Model Validation
2.3. Hydrodynamics Models (Waves, Currents)
2.3.1. Brief Description
2.3.2. Hydrodynamic Validation of the Model
2.4. Sediment Transport Model
2.4.1. Managing Sediment Deposition
2.4.2. Sediment Discretization within the Seabed
2.4.3. Sediment Facies Initialization for the Application to the BoBCS
3. Erosion Law Setting: Building and Numerical Experiment
3.1. General Formulation
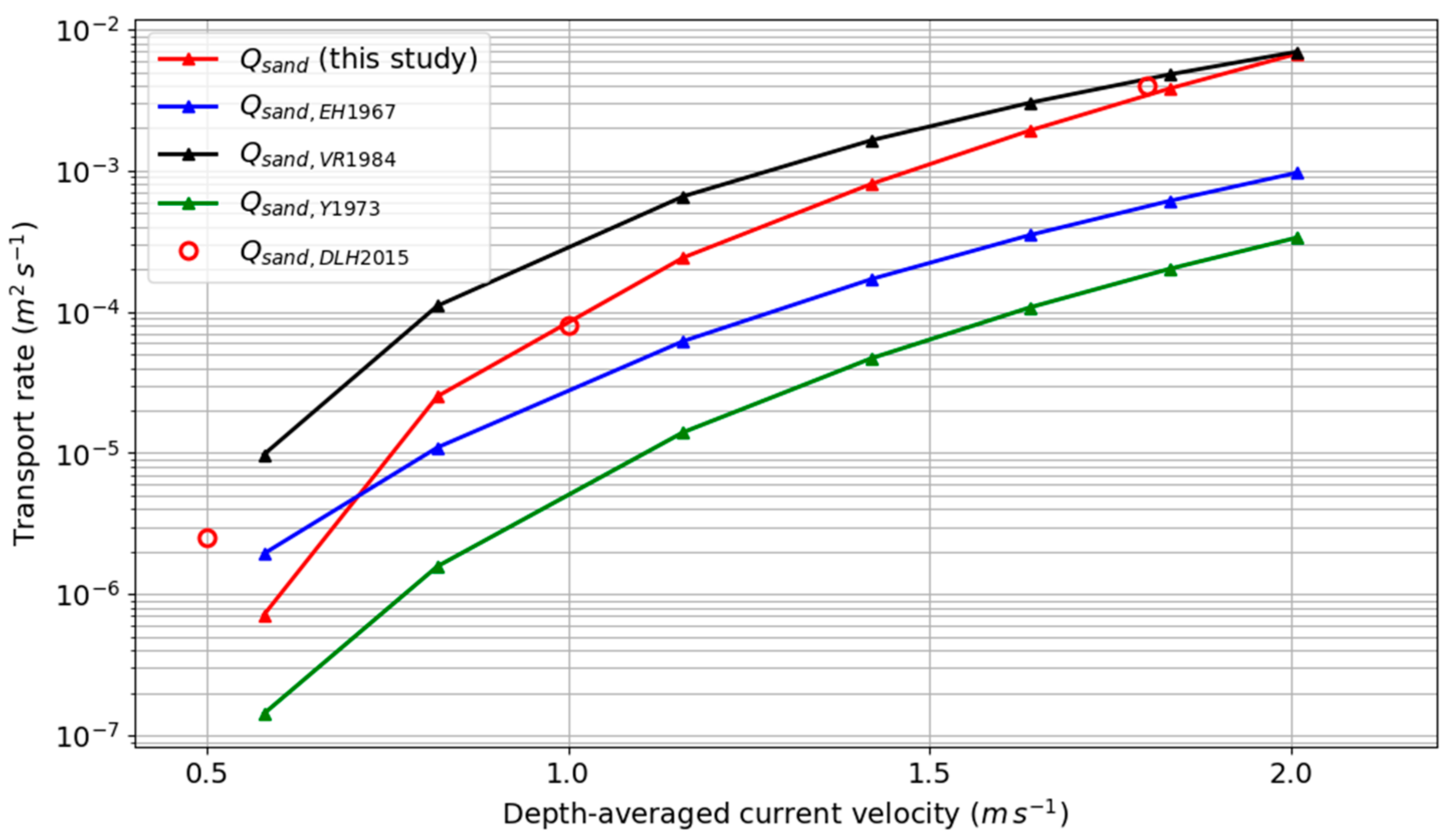
3.2. Pure Sand Erosion
3.3. Pure Mud Erosion
3.4. Erosion of Transitional Sand/Mud Mixtures: Selection of Transition Formulations to be Tested
4. Results
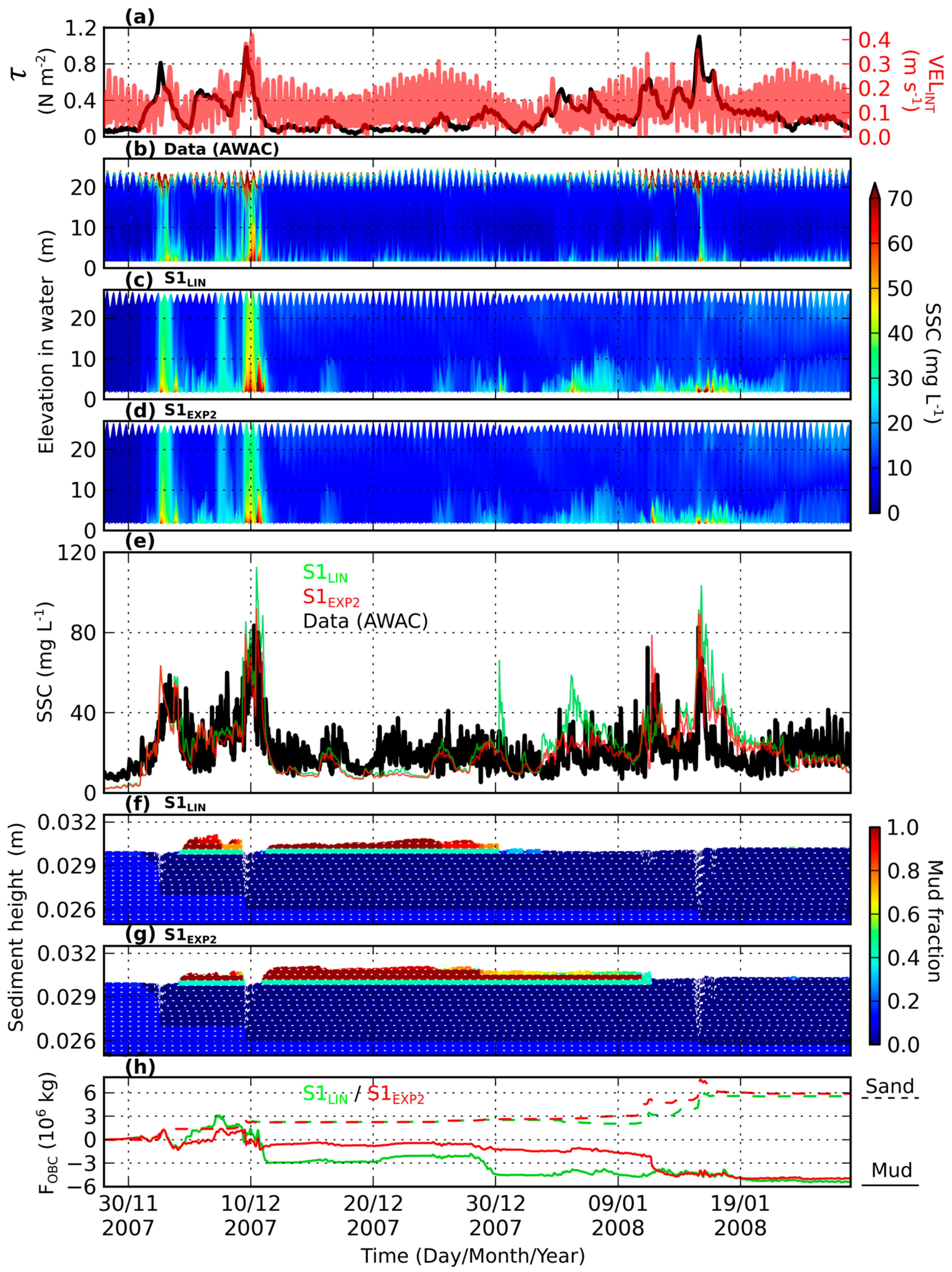
4.1. Influence of the Transition Trend between Non-Cohesive and Cohesive Erosion Modes in the Erosion Law
4.2. Influence of Critical Mud Fractions
5. Discussion
5.1. Setting Describing Erosion of a Sand/Mud Mixture
5.2. Limitations of the Approach and Remaining Uncertainties
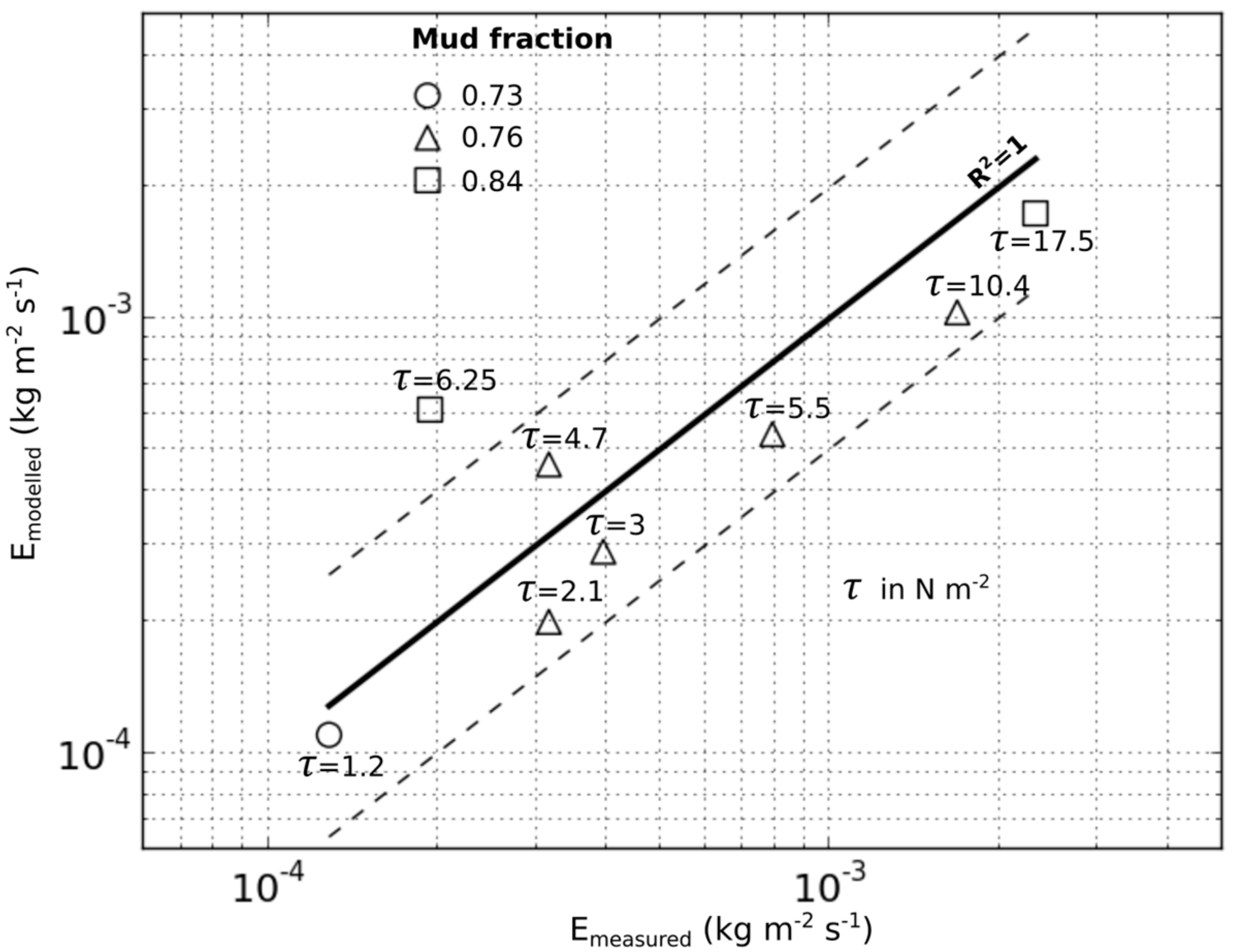
5.2.1. Mud Erosion Law
5.2.2. Initial Condition of the Sediment and Time Variation of the Seabed
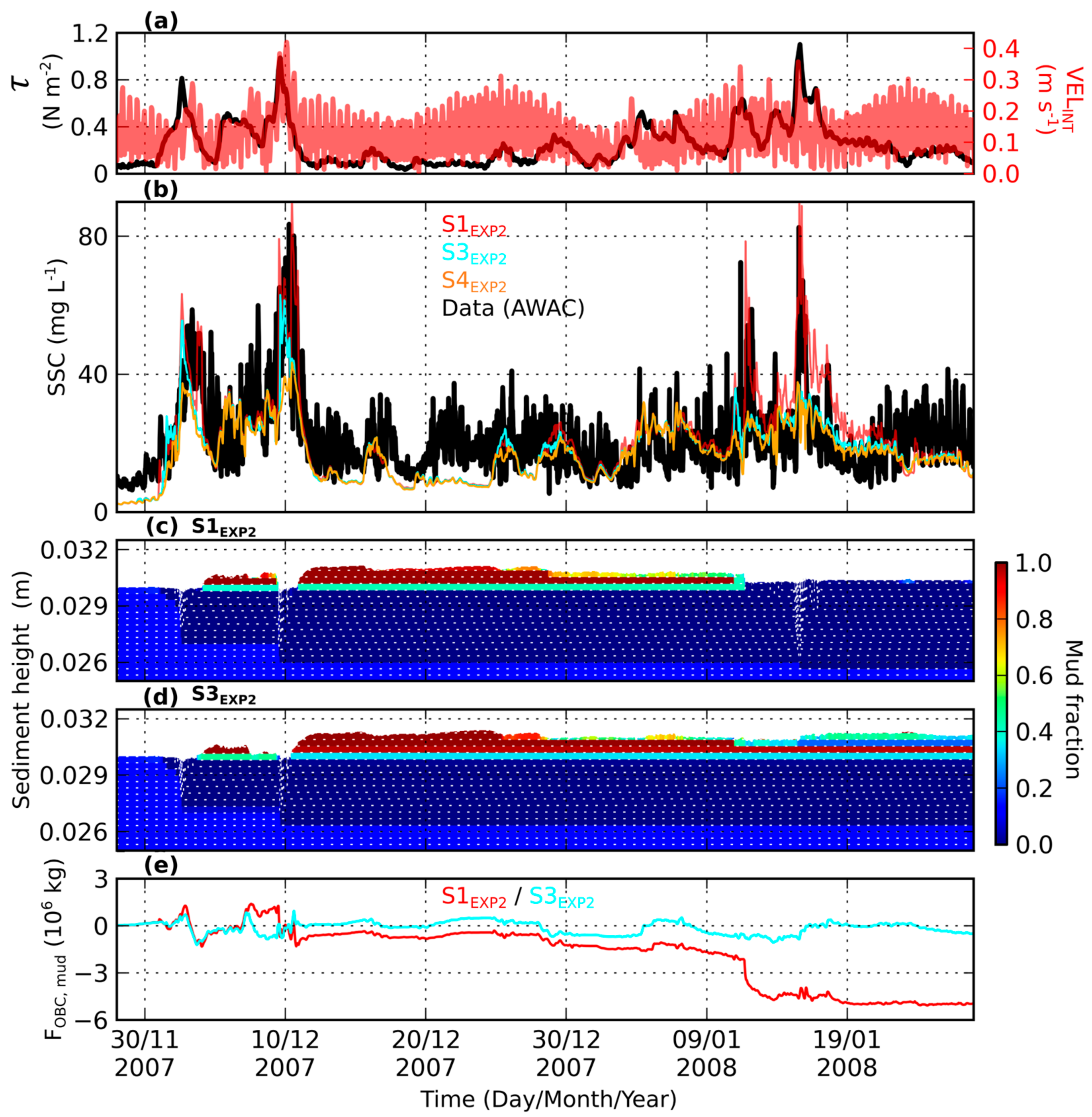
5.2.3. Applicability of the Sand/Mud Mixture Erosion Law
6. Conclusions
- Using an abrupt exponential transition, e.g., an erodibility parameter decrease of 2.5 orders of magnitude over a 10% (respectively, 3%) mud (respectively, clay) content range, improves SSC model results regarding measurements, compared to results obtained with linear or less abrupt exponential transitions. This conclusion agrees with recent experimental studies in the literature on the erosion of sand/mud mixtures, which mention a drastic change in erosion mode for only a small percentage of clay added in the mixture.
- A first critical mud fraction (above which the erosion mode begins to change) of 10–20% is required to ensure a relevant model response in turbidity. By reasoning in terms of the clay fraction, the corresponding critical clay fraction ranges between 3% and 6%. Once again, this conclusion agrees with experimental studies in the literature reporting that 2% to 10% of clay minerals in a sediment mixture are sufficient to control the soil properties.
- The erosion flux of mixed sediments appears to be very sensitive to the clay fraction of the surficial sediment, and then is likely to change considerably at a given location, according to erosion and deposition events.
- The need to perform 3D simulations to account for advection, which considerably influences sediment dynamics in terms of export of resuspended sediments, sediment inflows from adjacent cells, and consequent changes in the surficial seabed (nature and thickness of deposits).
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Le Hir, P.; Cayocca, F.; Waeles, B. Dynamics of sand and mud mixtures: A multiprocess-based modelling strategy. Cont. Shelf Res. 2011, 31, S135–S149. [Google Scholar] [CrossRef]
- Righetti, M.; Lucarelli, C. May the Shields theory be extended to cohesive and adhesive benthic sediments? J. Geophys. Res. 2007, 112, C05039. [Google Scholar] [CrossRef]
- Kimiaghalam, N.; Clark, S.P.; Ahmari, H. An experimental study on the effects of physical, mechanical, and electrochemical properties of natural cohesive soils on critical shear stress and erosion rate. Int. J. Sediment Res. 2016, 31, 1–15. [Google Scholar] [CrossRef]
- Williamson, H.J.; Ockenden, M.C. Laboratory and field investigations of mud and sand mixtures. In Proceedings of the First International Conference on Hydro-Science and Engineering, Advances in Hydro-Science and Engineering, Washington, DC, USA, 7–11 June 1993; Wang, S.S.Y., Ed.; Volume 1, pp. 622–629. [Google Scholar]
- Le Hir, P.; Monbet, Y.; Orvain, F. Sediment erodability in sediment transport modelling: Can we account for biota effects? Cont. Shelf Res. 2007, 27, 1116–1142. [Google Scholar] [CrossRef]
- Jacobs, W.; Le Hir, P.; Van Kesteren, W.; Cann, P. Erosion threshold of sand–mud mixtures. Cont. Shelf Res. 2011, 31, S14–S25. [Google Scholar] [CrossRef]
- Le Hir, P.; Cann, P.; Waeles, B.; Jestin, H.; Bassoullet, P. Erodibility of natural sediments: Experiments on sand/mud mixtures from laboratory and field erosion tests. In Sediment and Ecohydraulics: INTERCOH 2005 (Proceedings in Marine Science); Kusuda, T., Yamanishi, H., Spearman, J., Gailani, J.Z., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 9, pp. 137–153. [Google Scholar]
- Van Rijn, L.C. Sediment pick-up functions. J. Hydraul. Eng. 1984, 110, 1494–1502. [Google Scholar] [CrossRef]
- Emadzadeh, A.; Cheng, N.S. Sediment pickup rate in uniform open channel flows. In Proceedings of the River Flow 2016, Iowa City, IA, USA, 11–14 July 2016; Constantinescu, G., Garcia, M., Hanes, D., Eds.; Taylor & Francis Group: London, UK, 2016; Volume 1, pp. 450–457. [Google Scholar]
- Partheniades, E. A Study of Erosion and Deposition of Cohesive Soils in Salt Water. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1962. [Google Scholar]
- Ariathurai, C.R. A Finite Element Model of Cohesive Sediment Transportation. Ph.D. Thesis, University of California, Davis, CA, USA, 1974. [Google Scholar]
- Van Ledden, M.; Van Kesteren, W.G.M.; Winterwerp, J.C. A conceptual framework for the erosion behaviour of sand–mud mixtures. Cont. Shelf Res. 2004, 24, 1–11. [Google Scholar] [CrossRef]
- Flemming, B.W. A revised textural classification of gravel-free muddy sediments on the basis of ternary diagrams. Cont. Shelf Res. 2000, 20, 1125–1137. [Google Scholar]
- Mitchener, H.; Torfs, H. Erosion of mud/sand mixtures. Coast. Eng. 1996, 29, 1–25. [Google Scholar] [CrossRef]
- Panagiotopoulos, I.; Voulgaris, G.; Collins, M.B. The influence of clay on the threshold of movement of fine sandy beds. Coast. Eng. 1997, 32, 19–43. [Google Scholar] [CrossRef]
- Ye, Z.; Cheng, L.; Zang, Z. Experimental study of erosion threshold of reconstituted sediments. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; American Society of Mechanical Engineers: New York, NY, USA; Volume 7, pp. 973–983. [Google Scholar] [CrossRef]
- Smith, S.J.; Perkey, D.; Priestas, A. Erosion thresholds and rates for sand-mud mixtures. In Proceedings of the 13th International Conference on Cohesive Sediment Transport Processes (INTERCOH), Leuven, Belgium, 7–11 September 2015; Toorman, E., Mertens, T., Fettweis, M., Vanlede, J., Eds.; [Google Scholar]
- Gailani, J.Z.; Jin, L.; McNeil, J.; Lick, W. Effects of Bentonite Clay on Sediment Erosion Rates. DOER Technical Notes Collection. Available online: http://www.dtic.mil/docs/citations/ADA390214 (accessed on 21 July 2017).
- Waeles, B.; Le Hir, P.; Lesueur, P. A 3D morphodynamic process-based modelling of a mixed sand/mud coastal environment: The Seine estuary, France. In Sediment and Ecohydraulics: INTERCOH 2005, Proceedings in Marine Science; Kusuda, T., Yamanishi, H., Spearman, J., Gailani, J.Z., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 9, pp. 477–498. [Google Scholar]
- Bi, Q.; Toorman, E.A. Mixed-sediment transport modelling in Scheldt estuary with a physics-based bottom friction law. Ocean Dyn. 2015, 65, 555–587. [Google Scholar] [CrossRef]
- Migniot, C. Tassement et rhéologie des vases—Première partie. La Houille Blanche 1989, 1, 11–29. (In French) [Google Scholar] [CrossRef]
- Dickhudt, P.J.; Friedrichs, C.T.; Sanford, L.P. Mud matrix solids fraction and bed erodibility in the York River estuary, USA, and other muddy environments. Cont. Shelf Res. 2011, 31, S3–S13. [Google Scholar] [CrossRef]
- Carniello, L.; Defina, A.; D’Alpaos, L. Modeling sand-mud transport induced by tidal currents and wind waves in shallow microtidal basins: Application to the Venice Lagoon (Italy). Estuar. Coast. Shelf Sci. 2012, 102, 105–115. [Google Scholar] [CrossRef]
- Van Ledden, M. Sand-Mud Segregation in Estuaries and Tidal Basins. Ph.D. Thesis, Delft University of Civil Engineering, Delft, The Netherlands, 2003. [Google Scholar]
- Ahmad, M.F.; Dong, P.; Mamat, M.; Wan Nik, W.B.; Mohd, M.H. The critical shear stresses for sand and mud mixture. Appl. Math. Sci. 2011, 5, 53–71. [Google Scholar]
- Wiberg, P.L.; Drake, D.E.; Harris, C.K.; Noble, M. Sediment transport on the Palos Verdes shelf over seasonal to decadal time scales. Cont. Shelf Res. 2002, 22, 987–1004. [Google Scholar] [CrossRef]
- Ulses, C.; Estournel, C.; Durrieu de Madron, X.; Palanques, A. Suspended sediment transport in the Gulf of Lions (NW Mediterranean): Impact of extreme storms and floods. Cont. Shelf Res. 2008, 28, 2048–2070. [Google Scholar] [CrossRef]
- Fard, I.K.P. Modélisation des Échanges Dissous Entre L’estuaire de la Loire et les Baies Côtières Adjacentes. Ph.D. Thesis, University of Bordeaux, Bordeaux, France, 2015. [Google Scholar]
- Lurton, X. An Introduction to Underwater Acoustics: Principles and Applications; Springer: Berlin, Germany, 2002. [Google Scholar]
- Tessier, C.; Le Hir, P.; Lurton, X.; Castaing, P. Estimation de la matière en suspension à partir de l’intensité rétrodiffusée des courantomètres acoustiques à effet Doppler (ADCP). C. R. Geosci. 2008, 340, 57–67. (In French) [Google Scholar] [CrossRef]
- Lazure, P.; Dumas, F. An external–internal mode coupling for a 3D hydrodynamical model for applications at regional scale (MARS). Adv. Water Resour. 2008, 31, 233–250. [Google Scholar] [CrossRef]
- Song, Y.; Haidvogel, D. A semi-implicit ocean circulation model using a generalized topography-following coordinate system. J. Comput. Phys. 1994, 115, 228–244. [Google Scholar] [CrossRef]
- Rodi, W. Turbulence Models and Their Application in Hydraulics, 3rd ed.; IAHR Monograph: Delft, The Netherlands, 1993. [Google Scholar]
- Ferry, N.; Parent, L.; Garric, G.; Barnier, B.; Jourdain, N.C. Mercator global Eddy permitting ocean reanalysis GLORYS1V1: Description and results. Mercator-Ocean Q. Newsl. 2010, 36, 15–27. [Google Scholar]
- Boudière, E.; Maisondieu, C.; Ardhuin, F.; Accensi, M.; Pineau-Guillou, L.; Lepesqueur, J. A suitable metocean hindcast database for the design of Marine energy converters. Int. J. Mar. Energy 2013, 3–4, e40–e52. [Google Scholar] [CrossRef]
- Déqué, M.; Dreveton, C.; Braun, A.; Cariolle, D. The ARPEGE/IFS atmosphere model: A contribution to the French community climate modelling. Clim. Dyn. 1994, 10, 249–266. [Google Scholar] [CrossRef]
- Lyard, F.; Lefèvre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Jonsson, I.G. Wave boundary layers and friction factors. In Proceedings of the 10th International Conference on Coastal Engineering, Tokyo, Japan, September 1966; American Society of Civil Engineers: New York, NY, USA, 1966; pp. 127–148. [Google Scholar]
- Soulsby, R.L.; Hamm, L.; Klopman, G.; Myrhaug, D.; Simons, R.R.; Thomas, G.P. Wave-current interaction within and outside the bottom boundary layer. Coast. Eng. 1993, 21, 41–69. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford: London, UK, 1997. [Google Scholar]
- Grasso, F.; Le Hir, P.; Bassoullet, P. Numerical modelling of mixed-sediment consolidation. Ocean Dyn. 2015, 65, 607–616. [Google Scholar] [CrossRef]
- Van Leussen, W. Estuarine Macroflocs and Their Role in Fine-Grained Sediment Transport. Ph.D. Thesis, University of Utrecht, Utrecht, The Netherlands, 1994. [Google Scholar]
- Tessier, C.; Le Hir, P.; Dumas, F.; Jourdin, F. Modélisation des turbidités en Bretagne sud et validation par des mesures in situ. Eur. J. Environ. Civ. Eng. 2008, 12, 179–190. [Google Scholar] [CrossRef]
- Verney, R.; Gangloff, A.; Chapalain, M.; Le Berre, D.; Jacquet, M. Floc features in estuaries and coastal seas. In Proceedings of the 5th Particles in Europe Conference, Budapest, Hungary, 3–5 October 2016. [Google Scholar]
- Dyer, K.R. Coastal and Estuarine Sediment Dynamics; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Mengual, B. Variabilité Spatio-Temporelle des Flux Sédimentaires Dans le Golfe de Gascogne: Contributions Relatives des Forçages Climatiques et des Activités De Chalutage. Ph.D. Thesis, University of Western Brittany, Brest, France, 2016. [Google Scholar]
- Bouysse, P.; Lesueur, P.; Klingebiel, A. Carte Des Sédiments Superficiels du Plateau Continental du Golfe de Gascogne: Partie Septentrionale au 1/500 000. Co-Éditée par le BRGM Et l’IFREMER, 1986. Available online: http://sextant.ifremer.fr/record/ea0b61b0-71c6-11dc-b1e4-000086f6a62e/ (accessed on 21 July 2017).
- Mengual, B.; Cayocca, F.; Le Hir, P.; Draye, R.; Laffargue, P.; Vincent, B.; Garlan, T. Influence of bottom trawling on sediment resuspension in the “Grande-Vasière” area (Bay of Biscay, France). Ocean Dyn. 2016, 66, 1181–1207. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Unified view of sediment transport by currents and waves. II: Suspended transport. J. Hydraul. Eng. 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part II: Suspended load transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams; Teknish Forlag, Technical Press: Copenhagen, Denmark, 1967. [Google Scholar]
- Yang, C.T. Incipient motion and sediment transport. J. Hydraul. Div. 1973, 99, 1679–1704. [Google Scholar]
- Dufois, F.; Le Hir, P. Formulating Fine to Medium Sand Erosion for Suspended Sediment Transport Models. J. Mar. Sci. Eng. 2015, 3, 906–934. [Google Scholar] [CrossRef]
- Winterwerp, J.C. Flow-Induced Erosion of Cohesive Beds; A Literature Survey. Rijkswaterstaat—Delft Hydraulics, Cohesive Sediments Report 25, February 1989. Available online: http://publicaties.minienm.nl/download-bijlage/45703/164198.pdf (accessed on 21 July 2017).
- Tessier, C. Caractérisation et Dynamique des Turbidités en Zone Côtière: L’exemple de la Région Marine Bretagne Sud. Ph.D. Thesis, University of Bordeaux 1, Bordeaux, France, 2006. [Google Scholar]
- Raudkivi, A.J. Loose Boundary Hydraulics, 3rd ed.; Pergamon Press: Oxford, UK, 1990. [Google Scholar]
- Bassoullet, P.; Le Hir, P.; Gouleau, D.; Robert, S. Sediment transport over an intertidal mudflat: Field investigations and estimation of fluxes within the “Baie de Marennes-Oléron” (France). Cont. Shelf Res. 2000, 20, 1635–1653. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; Van Kesteren, W.G.M. Introduction to the Physics of Cohesive Sediment Dynamics in the Marine Environment; Developments in Sedimentology; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]


| Forcing | Source |
|---|---|
| Initial & boundary conditions (3D velocities, temperature, salinity) | GLORYS global ocean reanalysis [34] |
| Wave (Significant height, peak period, bottom excursion and orbital velocities) | WaveWatch III hindcast [35] |
| Meteorological conditions (Atmospheric pressure, wind, temperature, relative humidity, cloud cover) | ARPEGE model [36] |
| Tide (14 components) | FES2004 solution [37] |
| River discharge (flow and SSC) | Daily runoff data (French freshwater office) |
| Erosion Regime | E0 (kg·m−2·s−1) | τe (N·m−2) | n |
|---|---|---|---|
| Non-cohesive (pure sand) | E0,sand = 5.94 × 10−3 | τe,sand = 0.15 | nsand = 1.5 |
| Cohesive (pure mud) | E0,mud = 10−5 | τe,mud = 0.1 | nmud = 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mengual, B.; Hir, P.L.; Cayocca, F.; Garlan, T. Modelling Fine Sediment Dynamics: Towards a Common Erosion Law for Fine Sand, Mud and Mixtures. Water 2017, 9, 564. https://doi.org/10.3390/w9080564
Mengual B, Hir PL, Cayocca F, Garlan T. Modelling Fine Sediment Dynamics: Towards a Common Erosion Law for Fine Sand, Mud and Mixtures. Water. 2017; 9(8):564. https://doi.org/10.3390/w9080564
Chicago/Turabian StyleMengual, Baptiste, Pierre Le Hir, Florence Cayocca, and Thierry Garlan. 2017. "Modelling Fine Sediment Dynamics: Towards a Common Erosion Law for Fine Sand, Mud and Mixtures" Water 9, no. 8: 564. https://doi.org/10.3390/w9080564
APA StyleMengual, B., Hir, P. L., Cayocca, F., & Garlan, T. (2017). Modelling Fine Sediment Dynamics: Towards a Common Erosion Law for Fine Sand, Mud and Mixtures. Water, 9(8), 564. https://doi.org/10.3390/w9080564




