Halosteric Sea Level Changes during the Argo Era
Abstract
:1. Introduction
2. Data and Methods
2.1. Gridded Temperature and Salinity Products
2.2. Methods
3. Results
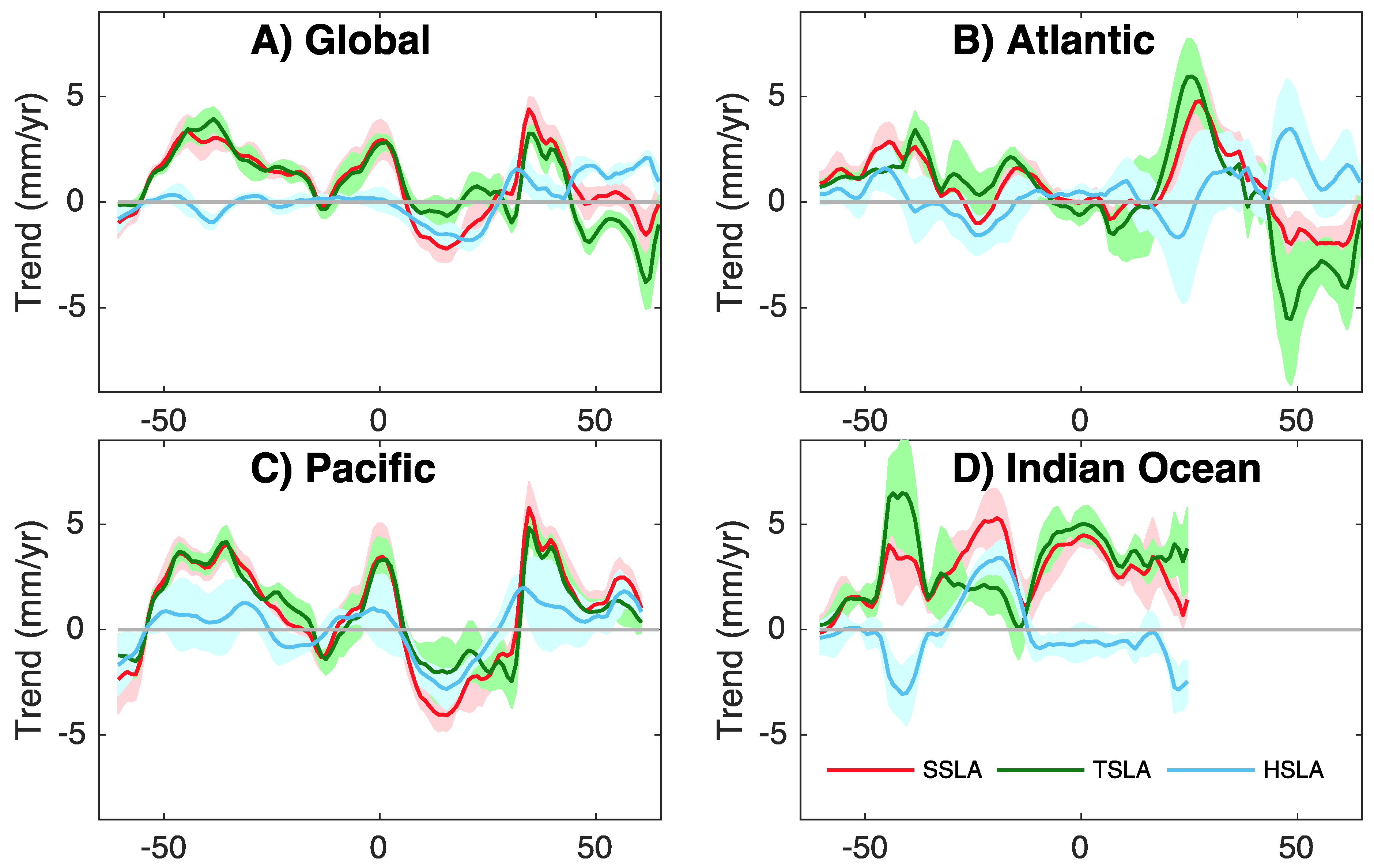
3.1. Time Evaluation of Global HSLA
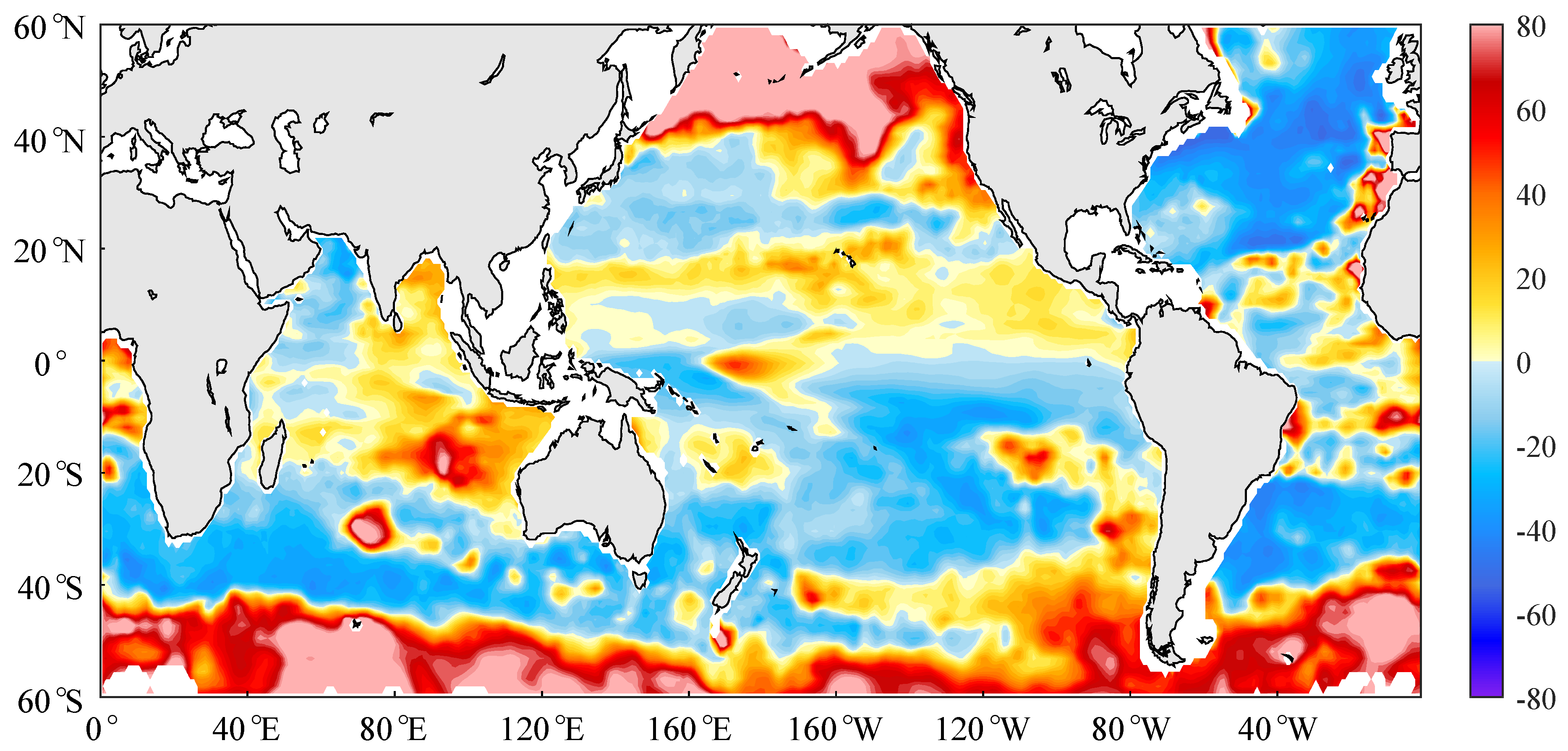
3.2. Spatial Pattern of Long-Term HSLA Change
3.3. The Role of Salinity in Regional SSLA
4. Summary and Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Johnson, G.C.; Wijffels, S.E. Ocean Density Change Contributions to Sea Level Rise. Oceanography 2011, 24, 112–121. [Google Scholar] [CrossRef]
- Antonov, J.I.; Levitus, S.; Boyer, T.P. Steric sea level variations during 1957–1994: Importance of salinity. J. Geophys. Res. Oceans 2002, 107, 8013. [Google Scholar] [CrossRef]
- Willis, J.K.; Roemmich, D.; Cornuelle, B. Interannual variability in upper ocean heat content, temperature, and thermosteric expansion on global scales. J. Geophys. Res. Oceans 2004, 109, C12036. [Google Scholar] [CrossRef]
- Lombard, A.; Cazenave, A.; Letraon, P.; Ishii, M. Contribution of thermal expansion to present-day sea-level change revisited. Glob. Planet. Chang. 2005, 47, 1–16. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Mishonov, A.V.; Reagan, J.R.; Seidov, D.; Yarosh, E.S.; et al. World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys. Res. Lett. 2012, 39, L10603–L10607. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J.; Konikow, L.F.; Domingues, C.M.; Cogley, J.G.; Rignot, E.; Gregory, J.M.; van den Broeke, M.R.; Monaghan, A.J.; Velicogna, I. Revisiting the Earth’s sea-level and energy budgets from 1961 to 2008. Geophys. Res. Lett. 2011, 38, L18601. [Google Scholar] [CrossRef]
- Llovel, W.; Willis, J.K.; Landerer, F.W.; Fukumori, I. Deep-ocean contribution to sea level and energy budget not detectable over the past decade. Nat. Clim. Chang. 2014, 4, 1031–1035. [Google Scholar] [CrossRef]
- Boyer, T.P.; Antonov, J.I.; Baranova, O.K.; Coleman, C.; Garcia, H.E.; Grodsky, A.; Johnson, D.R.; Locarnini, R.; Mishonov, A.; O’Brien, T.D.; et al. World Ocean Database 2013; NOAA Atlas NESDIS: Silver Spring, MD, USA, 2013. [Google Scholar]
- Durack, P.J.; Wijffels, S.A.; Gleckler, P.J. Long-term Sea-level Change Revisited: The Role of Salinity. Environ. Res. Lett. 2014, 9, 114017. [Google Scholar] [CrossRef]
- Maes, C. Estimating the influence of salinity on sea level anomaly in the ocean. Geophys. Res. Lett. 1998, 25, 3551–3554. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Garcia, H.E.; Locarnini, R.A. Linear trends of zonally averaged thermosteric, halosteric, and total steric sea level for individual ocean basins and the world ocean, (1955–1959)–(1994–1998). Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Suzuki, T.; Ishii, M. Long-term regional sea level changes due to variations in water mass density during the period 1981–2007. Geophys. Res. Lett. 2011, 38, L21604. [Google Scholar] [CrossRef]
- Sato, O.T.; Polito, P.S.; Liu, W.T. Importance of salinity measurements in the heat storage estimation from TOPEX/POSEIDON. Geophys. Res. Lett. 2000, 27, 549–551. [Google Scholar] [CrossRef]
- Wunsch, C.; Rui, M.P.; Heimbach, P. Decadal Trends in Sea Level Patterns: 1993–2004. J. Clim. 2007, 20, 5889–5911. [Google Scholar] [CrossRef]
- Yu, L. A global relationship between the ocean water cycle and near-surface salinity. J. Geophys. Res. 2011, 116, C10025. [Google Scholar] [CrossRef]
- Hasson, A.E.A.; Delcroix, T.; Dussin, R. An assessment of the mixed layer salinity budget in the tropical Pacific Ocean. Observations and modelling (1990–2009). Ocean Dyn. 2013, 63, 179–194. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Feng, M.; Wang, T.; Zhang, N.; Wijffels, S. Decadal trends of the upper ocean salinity in the tropical Indo-Pacific since mid-1990s. Sci. Rep. 2015, 5, 16050. [Google Scholar] [CrossRef] [PubMed]
- Ponte, R.M.; Vinogradova, N.T. An assessment of basic processes controlling mean surface salinity over the global ocean. Geophys. Res. Lett. 2016, 43, 7052–7058. [Google Scholar] [CrossRef]
- Durack, P.J.; Wijffels, S.E. Fifty-Year Trends in Global Ocean Salinities and Their Relationship to Broad-Scale Warming. J. Clim. 2010, 23, 4342–4362. [Google Scholar] [CrossRef]
- Skliris, N.; Marsh, R.; Josey, S.A.; Good, S.A.; Liu, C.; Allan, R.P. Salinity changes in the World Ocean since 1950 in relation to changing surface freshwater fluxes. Clim. Dyn. 2014, 43, 709–736. [Google Scholar] [CrossRef]
- Hosoda, S.; Suga, T.; Shikama, N.; Mizuno, K. Global surface layer salinity change detected by Argo and its implication for hydrological cycle intensification. J. Oceanogr. 2009, 65, 579–586. [Google Scholar] [CrossRef]
- Durack, P.J.; Wijffels, S.E.; Matear, R.J. Ocean salinities reveal strong global water cycle intensification during 1950 to 2000. Science 2012, 336, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wu, L. Can Oceanic Freshwater Flux Amplify Global Warming? J. Clim. 2012, 25, 3417–3430. [Google Scholar] [CrossRef]
- Levitus, S. Interpentadal variability of steric sea level and geopotential thickness of the north Atlantic Ocean, 1970–1974 versus 1955–1959. J. Geophys. Res. Atmos. 1990, 95, 5233–5238. [Google Scholar] [CrossRef]
- Ishii, M.; Kimoto, M.; Sakamoto, K.; Iwasaki, S.-I. Steric Sea Level Changes Estimated from Historical Ocean Subsurface Temperature and Salinity Analyses. J. Oceanogr. 2006, 62, 155–170. [Google Scholar] [CrossRef]
- Talley, L.D.; Pickard, G.L.; Emery, W.J. (Eds.) Descriptive Physical Oceanography: An Introduction, 6th ed.; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2011. [Google Scholar]
- Fasullo, J.T.; Boening, C.; Landerer, F.W.; Nerem, R.S. Australia’s unique influence on global sea level in 2010–2011. Geophys. Res. Lett. 2013, 40, 4368–4373. [Google Scholar] [CrossRef]
- Fasullo, J.; Nerem, R. Interannual Variability in Global Mean Sea Level Estimated from the CESM Large and Last Millennium Ensembles. Water 2016, 8, 491. [Google Scholar] [CrossRef]
- Llovel, W.; Lee, T. Importance and origin of halosteric contribution to sea level change in the southeast Indian Ocean during 2005–2013. Geophys. Res. Lett. 2015, 42, 1148–1157. [Google Scholar] [CrossRef]
- Cheng, L.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Abraham, J.; Zhu, J. Improved estimates of ocean heat content from 1960 to 2015. Sci. Adv. 2017, 3, e1601545. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Zhu, J. Benefits of CMIP5 multimodel ensemble in reconstructing historical ocean subsurface temperature variations. J. Clim. 2016, 29, 5393–5416. [Google Scholar] [CrossRef]
- Barnes, S.L. A technique for maximizing details in numerical weather map analysis. J. Appl. Meteorol. 1964, 3, 396–409. [Google Scholar] [CrossRef]
- Jayne, S.R.; Wahr, J.M.; Bryan, F.O. Observing ocean heat content using satellite gravity and altimetry. J. Geophys. Res. Atmos. 2003, 108, 295–314. [Google Scholar] [CrossRef]
- McDougall, T.J. Neutral Surface. J. Phys. Oceanogr. 1987, 17, 1950–1964. [Google Scholar] [CrossRef]
- Cazenave, A.; Dieng, H.-B.; Meyssignac, B.; von Schuckmann, K.; Decharme, B.; Berthier, E. The rate of sea-level rise. Nat. Clim. Chang. 2014, 4, 358–361. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Oxford, UK, 2011; Volume 100. [Google Scholar]
- Yu, L.; Jin, X.; Josey, S.A.; Lee, T.; Kumar, A.; Wen, C.; Xue, Y. The Global Ocean Water Cycle in Atmospheric Reanalysis, Satellite, and Ocean Salinity. J. Clim. 2017, 30, 3829–3852. [Google Scholar] [CrossRef]
- Purkey, S.G.; Johnson, G.C. Antarctic Bottom Water Warming and Freshening: Contributions to Sea Level Rise, Ocean Freshwater Budgets, and Global Heat Gain. J. Clim. 2013, 26, 6105–6122. [Google Scholar] [CrossRef]
- Menezes, V.V.; Macdonald, A.M.; Schatzman, C. Accelerated freshening of Antarctic Bottom Water over the last decade in the Southern Indian Ocean. Sci. Adv. 2017, 3, e1601426. [Google Scholar] [CrossRef] [PubMed]
- Boyer, T.; Levitus, S.; Antonov, J.; Locarnini, R.; Mishonov, A.; Garcia, H.; Josey, S.A. Changes in freshwater content in the North Atlantic Ocean 1955–2006. Geophys. Res. Lett. 2007, 34, 159–166. [Google Scholar] [CrossRef]
- Cazenave, A.; Henry, O.; Munier, S.; Delcroix, T.; Gordon, A.L.; Meyssignac, B.; Llovel, W.; Palanisamy, H.; Becker, M. Estimating ENSO Influence on the Global Mean Sea Level, 1993–2010. Mar. Geod. 2012, 35, 82–97. [Google Scholar] [CrossRef]
- Stammer, D.; Cazenave, A.; Ponte, R.M.; Tamisiea, M.E. Causes for Contemporary Regional Sea Level Changes. Annu. Rev. Mar. Sci. 2013, 5, 21–46. [Google Scholar] [CrossRef] [PubMed]
- Lago, V.; Wijffels, S.E.; Durack, P.J.; Church, J.A.; Bindoff, N.L.; Marsland, S.J. Simulating the role of surface forcing on observed multidecadal upper ocean salinity changes. J. Clim. 2015, 29, 5575–5588. [Google Scholar] [CrossRef]
- Llovel, W.; Meyssignac, B.; Cazenave, A. Steric sea level variations over 2004–2010 as a function of region and depth: Inference on the mass component variability in the North Atlantic Ocean. Geophys. Res. Lett. 2011, 38, 601–612. [Google Scholar] [CrossRef]
- Curry, R.G.; McCartney, M.S.; Joyce, T.M. Oceanic transport of subpolar climate signals to mid-depth subtropical waters. Nature 1998, 391, 575–577. [Google Scholar] [CrossRef]
- Köhl, A.; Sena Martins, M.; Stammer, D. Impact of assimilating surface salinity from SMOS on ocean circulation estimates. J. Geophys. Res. Oceans 2014, 119, 5449–5464. [Google Scholar] [CrossRef]
- Lu, Z.; Cheng, L.; Zhu, J.; Lin, R. The complementary role of SMOS sea surface salinity observations for estimating global ocean salinity state. J. Geophys. Res. Oceans 2016, 121, 3672–3691. [Google Scholar] [CrossRef]
- Wijffels, S.; Roemmich, D.; Monselesan, D.; Church, J.; Gilson, J. Ocean temperatures chronicle the ongoing warming of Earth. Nat. Clim. Chang. 2016, 6, 116–118. [Google Scholar] [CrossRef]
- Llovel, W.; Terray, L. Observed southern upper-ocean warming over 2005? 2014 and associated mechanisms. Environ. Res. Lett. 2016, 11, 124023. [Google Scholar] [CrossRef]
- Volkov, D.L.; Lee, S.-K.; Landerer, F.W.; Lumpkin, R. Decade-long deep-ocean warming detected in the subtropical South Pacific: Deep-Ocean Warming in the South Pacific. Geophys. Res. Lett. 2017, 44, 927–936. [Google Scholar] [CrossRef]
- Hu, S.; Sprintall, J. Observed strengthening of interbasin exchange via the Indonesian seas due to rainfall intensification. Geophys. Res. Lett. 2017, 44, 1448–1456. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-K.; Park, W.; Baringer, M.O.; Gordon, A.L.; Huber, B.; Liu, Y. Pacific origin of the abrupt increase in Indian Ocean heat content during the warming hiatus. Nat. Geosci. 2015, 8, 445–449. [Google Scholar] [CrossRef]
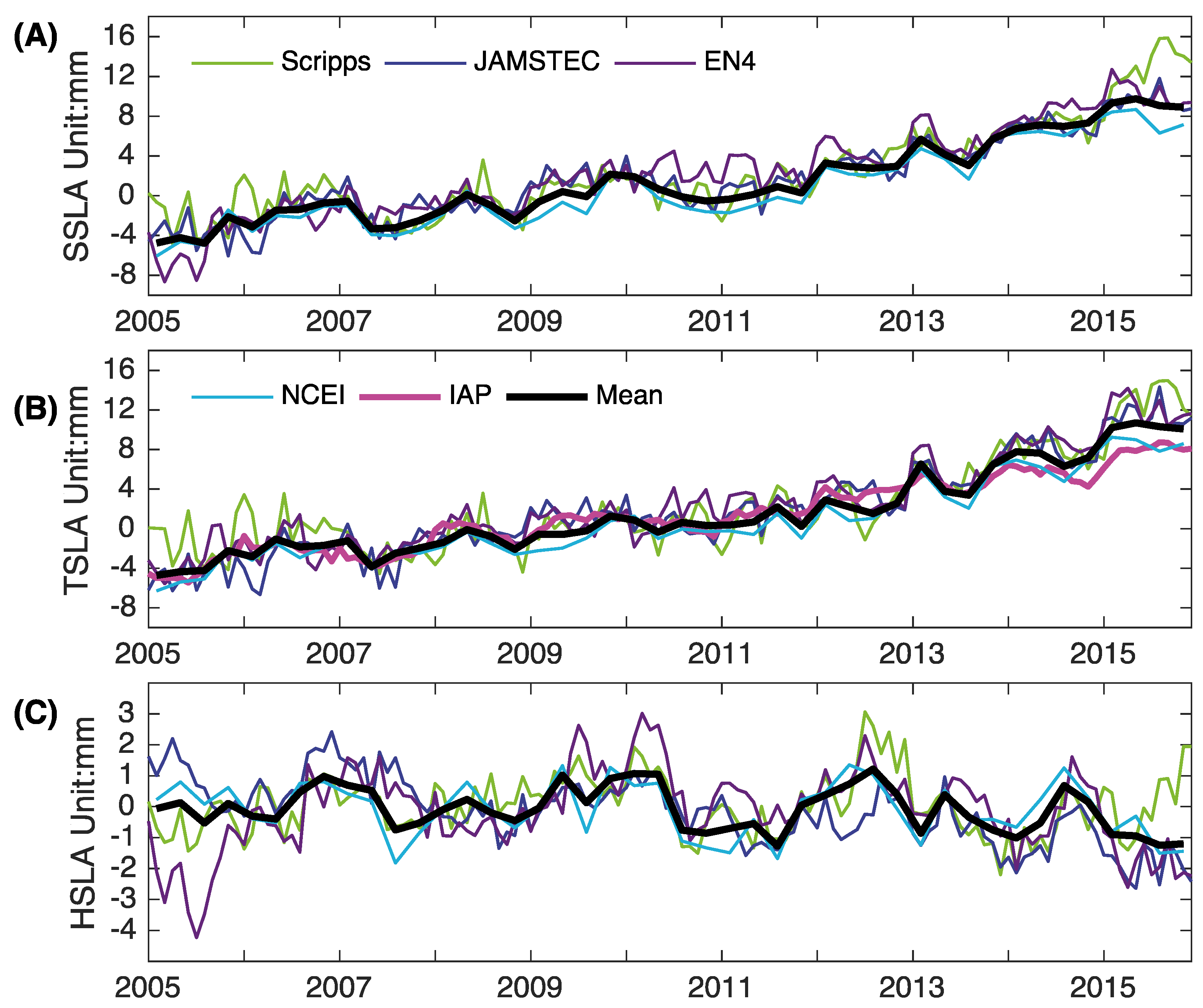
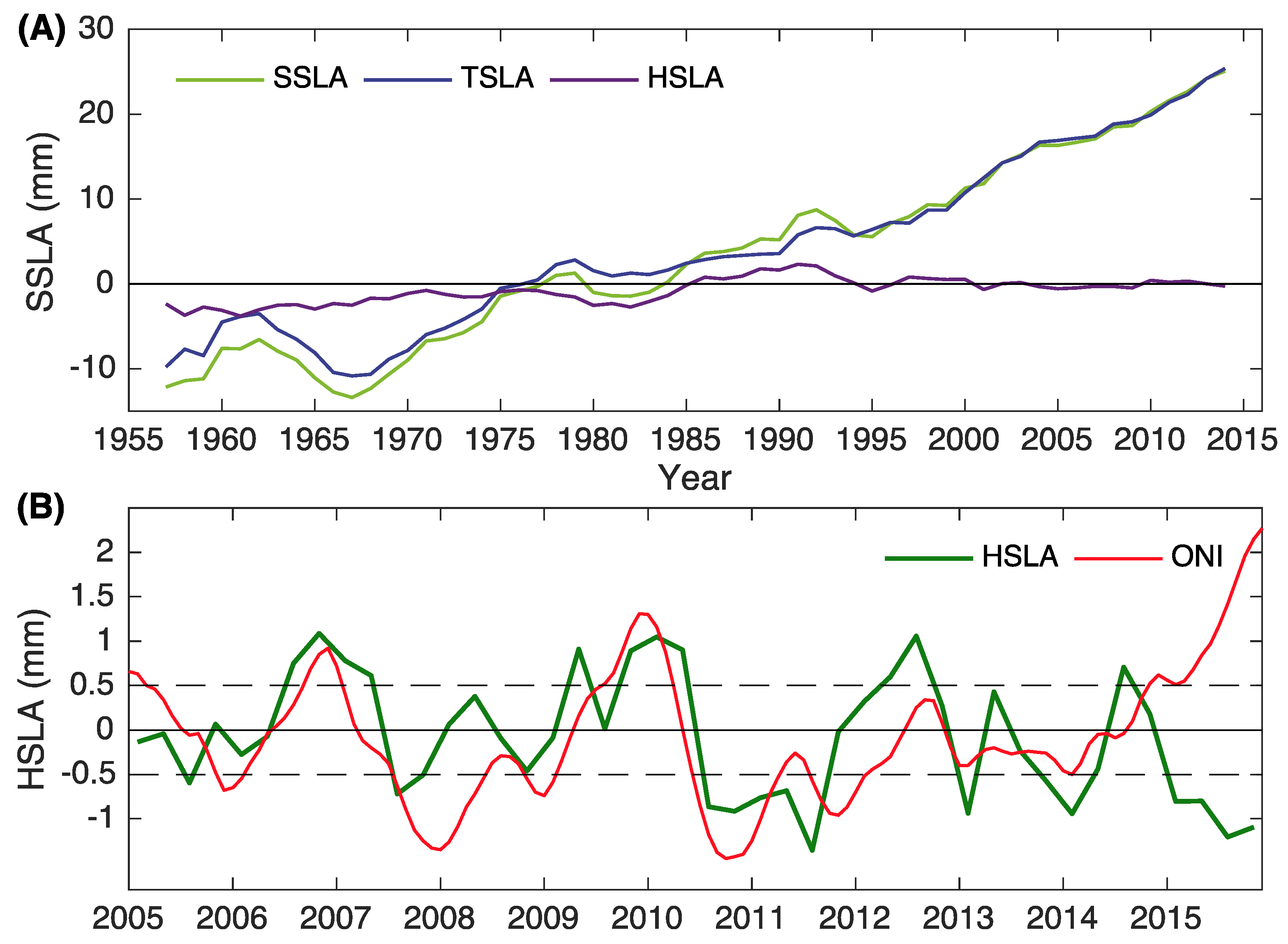
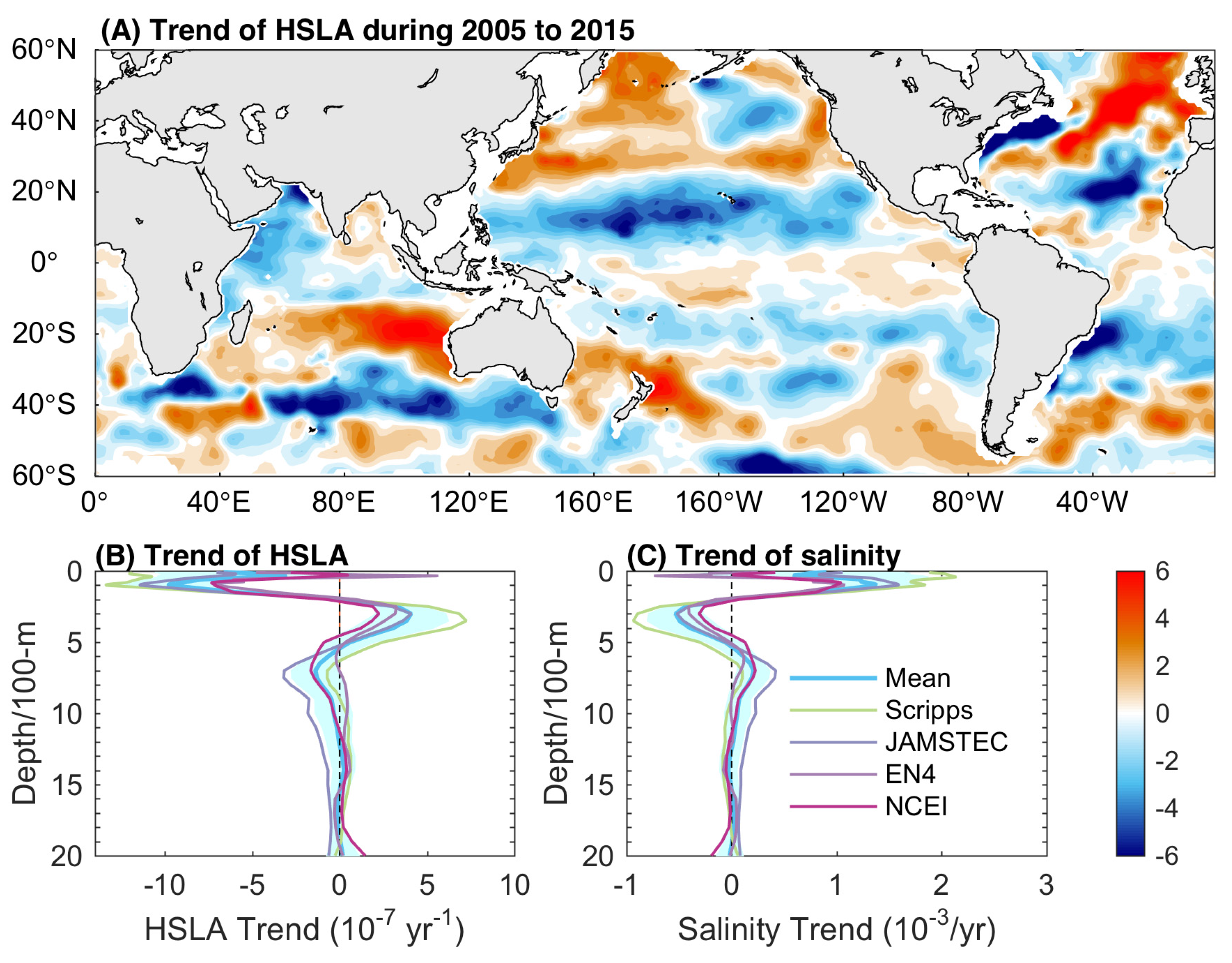
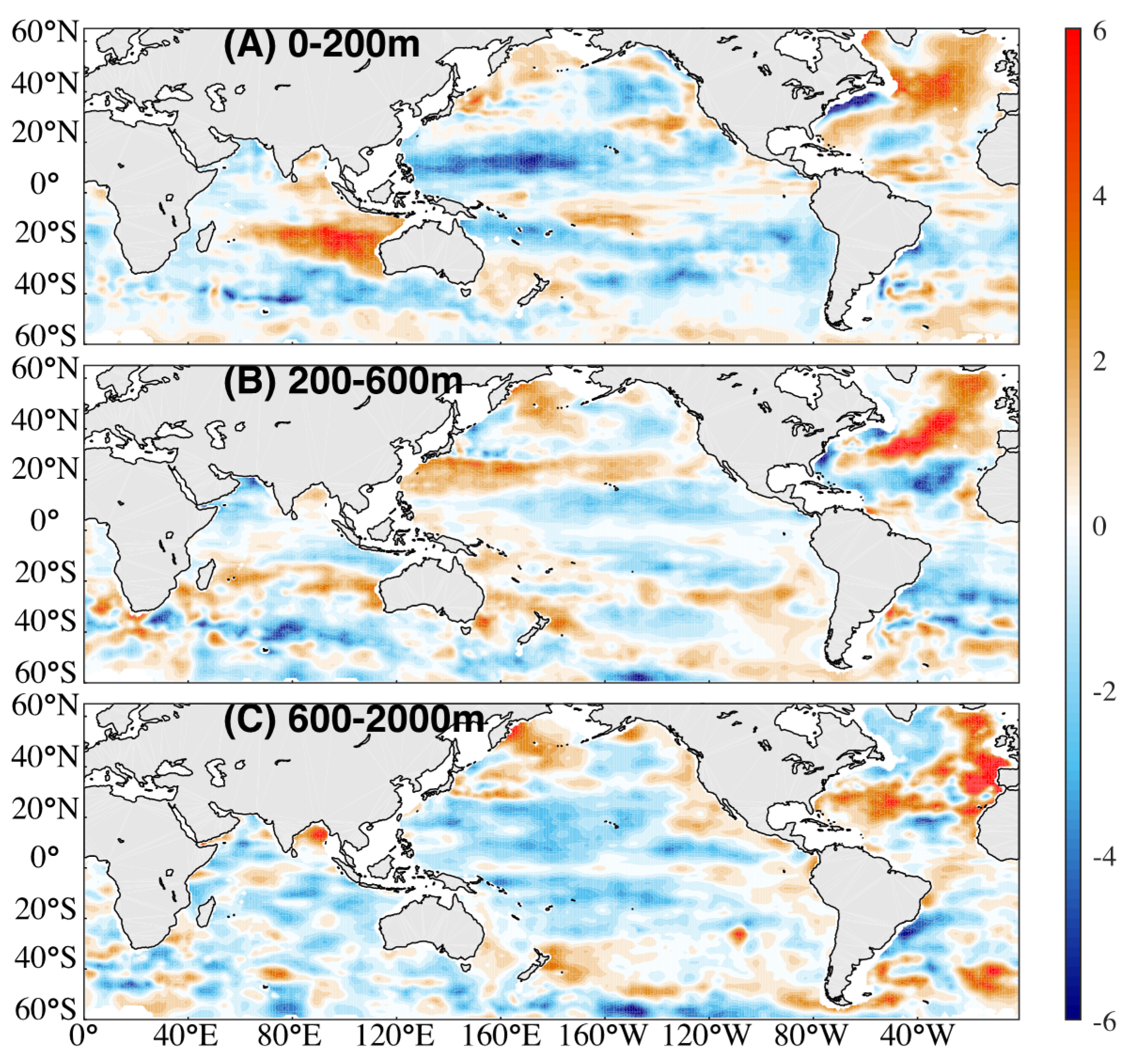
| Trend | SSLA | TSLA | HSLA |
|---|---|---|---|
| SCRIPPS | 0.86 ± 0.13 | 0.88 ± 0.14 | −0.02 ± 0.01 |
| JAMSTEC | 0.83 ± 0.10 | 1.01 ± 0.12 | −0.18 ± 0.02 |
| EN4 | 0.97 ± 0.10 | 0.96 ± 0.12 | 0.01 ± 0.04 |
| NCEI | 0.84 ± 0.17 | 0.89 ± 0.19 | −0.05 ± 0.03 |
| IAP | ‒ | 0.81 ± 0.08 | ‒ |
| Mean | 0.86 ± 0.18 | 0.89 ± 0.19 | −0.05 ± 0.03 |
| NCEI (1955–2016) | 0.63 ± 0.02 | 0.58 ± 0.02 | 0.06 ± 0.01 |
| Atlantic | Indian | Pacific | Southern | Global | |
|---|---|---|---|---|---|
| SSLA | 0.77 ± 0.32 | 2.42 ± 0.45 | 0.0 ± 0.12 | 1.18 ± 0.25 | 0.80 ± 0.17 |
| TSLA | 0.74 ± 0.39 | 1.95 ±0.37 | 0.22 ± 0.10 | 1.41 ± 0.28 | 0.85 ± 0.18 |
| HSLA | 0.04 ± 0.12 | 0.52 ± 0.10 | −0.21 ± 0.05 | −0.31 ± 0.12 | −0.06 ± 0.03 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Cheng, L.; Boyer, T.; Li, C. Halosteric Sea Level Changes during the Argo Era. Water 2017, 9, 484. https://doi.org/10.3390/w9070484
Wang G, Cheng L, Boyer T, Li C. Halosteric Sea Level Changes during the Argo Era. Water. 2017; 9(7):484. https://doi.org/10.3390/w9070484
Chicago/Turabian StyleWang, Gongjie, Lijing Cheng, Timothy Boyer, and Chongyin Li. 2017. "Halosteric Sea Level Changes during the Argo Era" Water 9, no. 7: 484. https://doi.org/10.3390/w9070484
APA StyleWang, G., Cheng, L., Boyer, T., & Li, C. (2017). Halosteric Sea Level Changes during the Argo Era. Water, 9(7), 484. https://doi.org/10.3390/w9070484




