Runoff Responses to Climate and Land Use/Cover Changes under Future Scenarios
Abstract
:1. Introduction
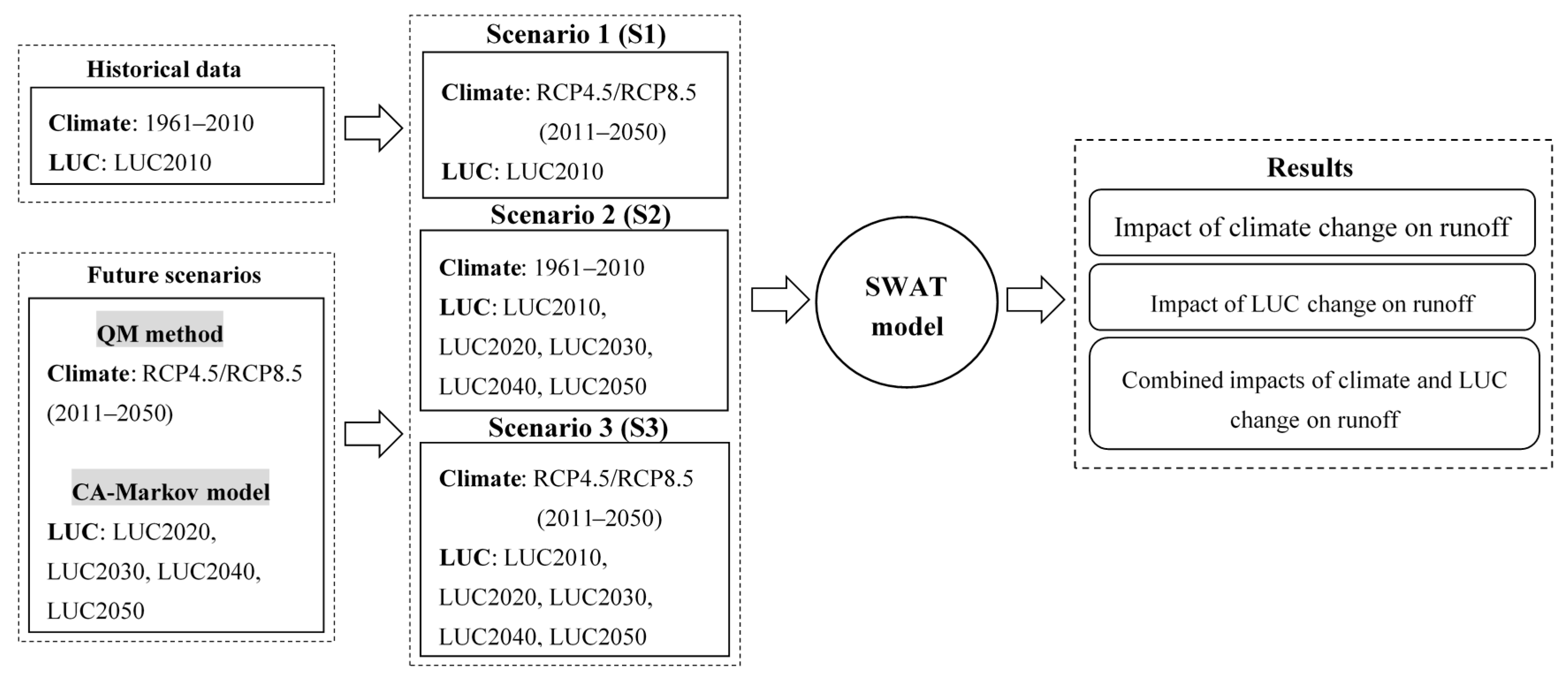
2. Methodology
2.1. Establishment of Future Climate Scenarios
2.2. Establishment of Future LUC Scenarios
2.3. SWAT Model
3. Study Area and Data
3.1. Study Area
3.2. Dataset
4. Results and Discussion
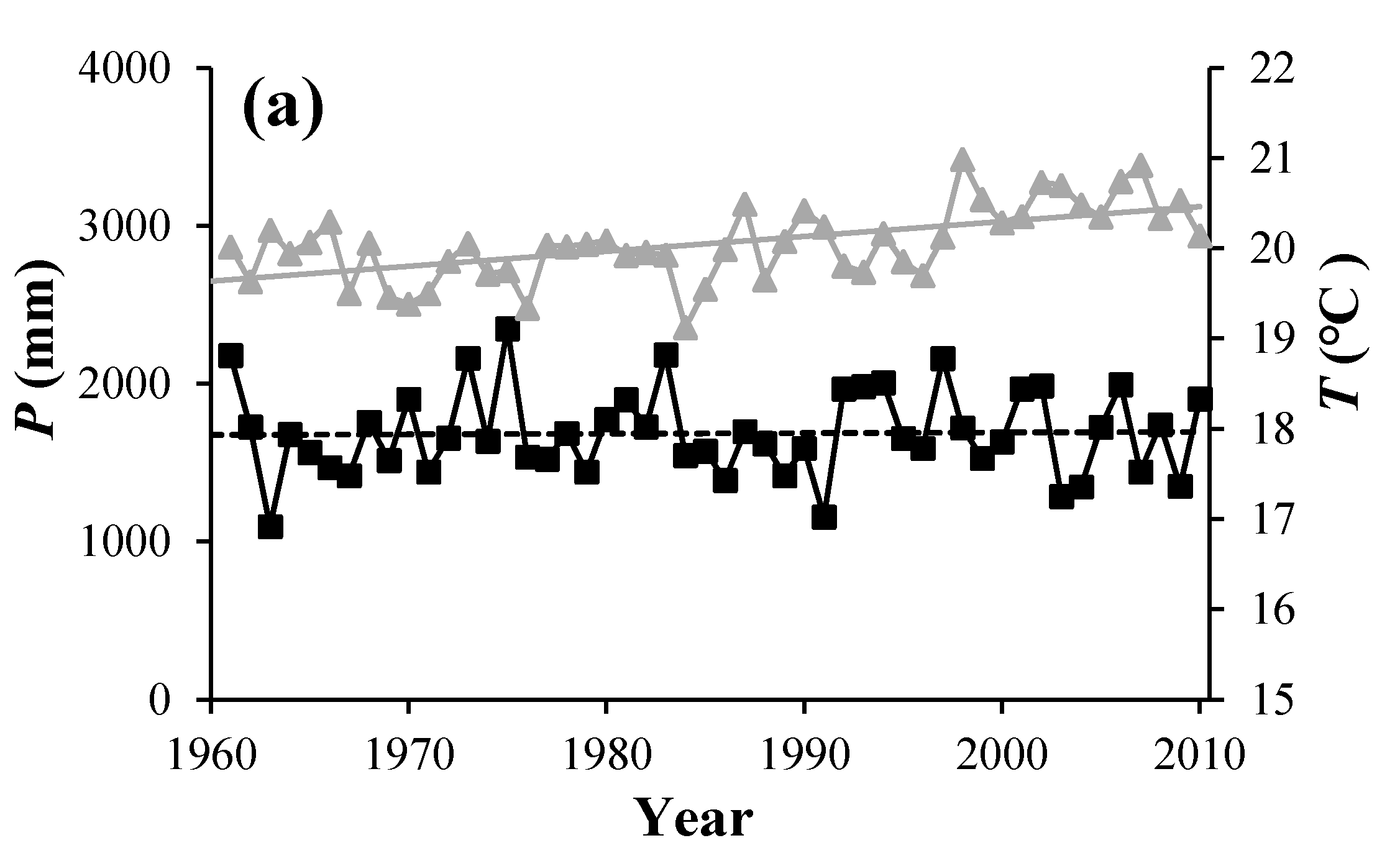
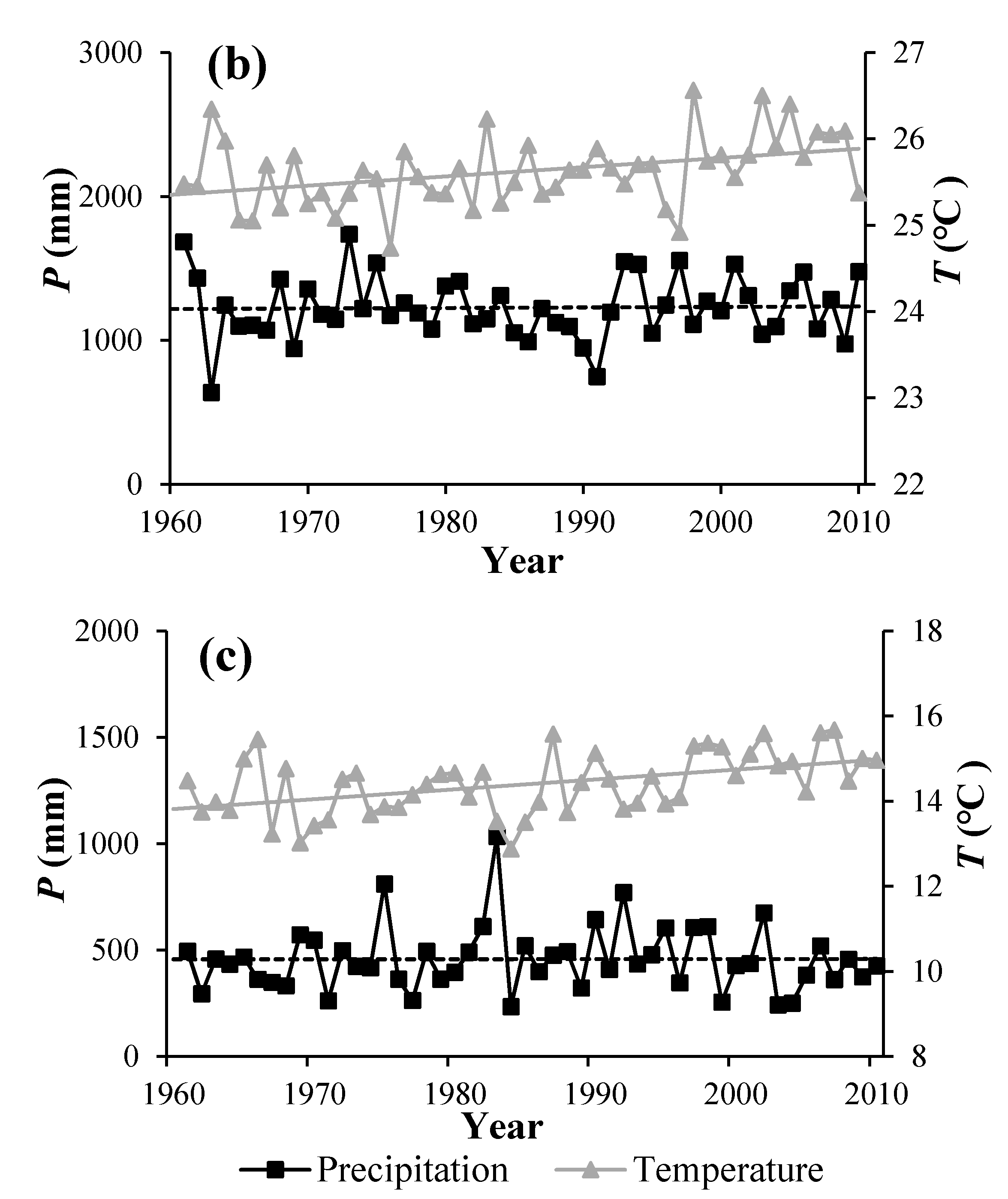
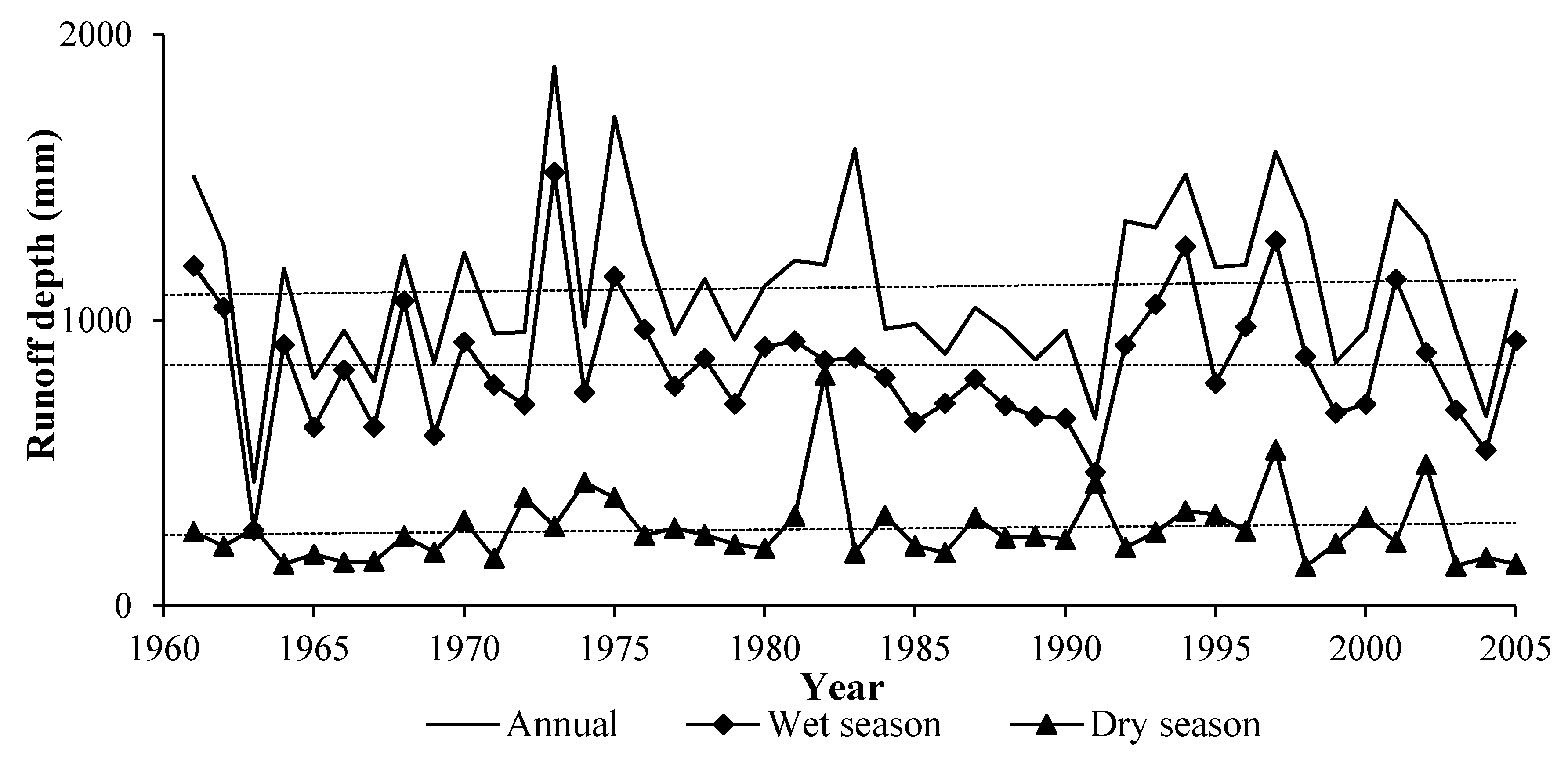
4.1. Historical Climate, LUC and Runoff Changes
4.2. Model Performance
4.2.1. Performance of QM
4.2.2. Performance of the CA-Markov Model
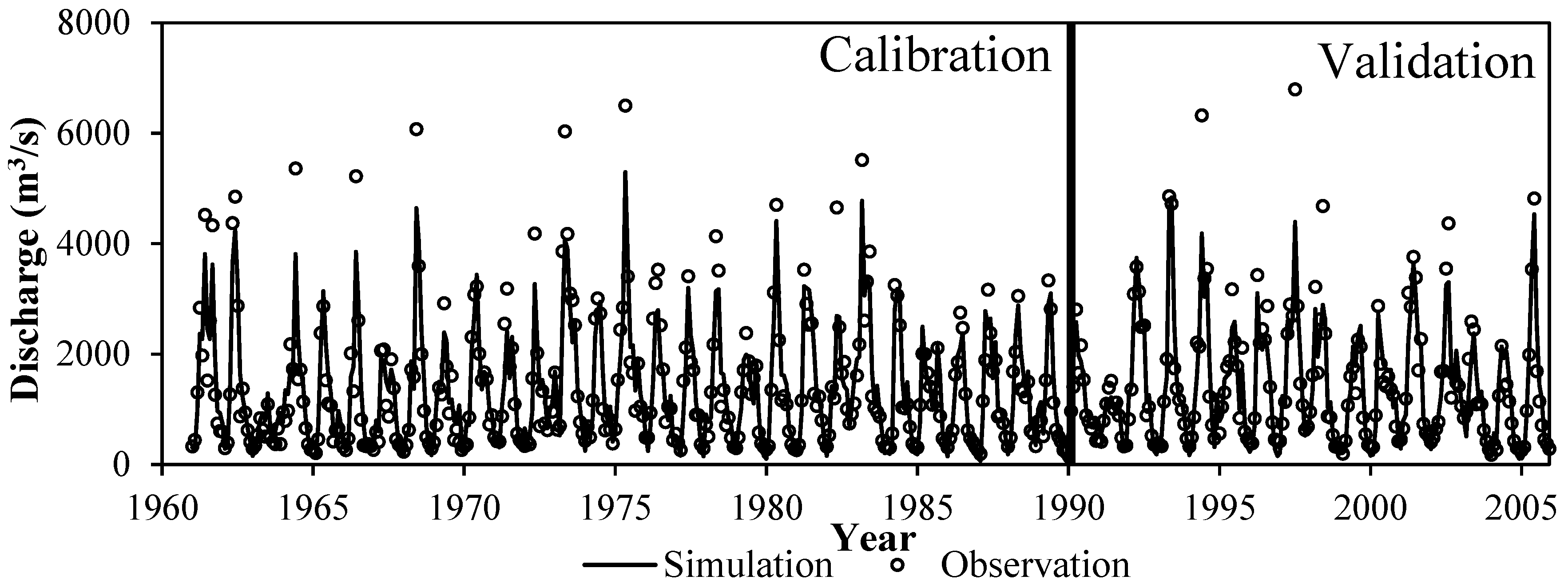
4.2.3. Performance of the SWAT Model
4.3. Future Climate and LUC Scenarios
4.4. Runoff Response to Climate and LUC Changes
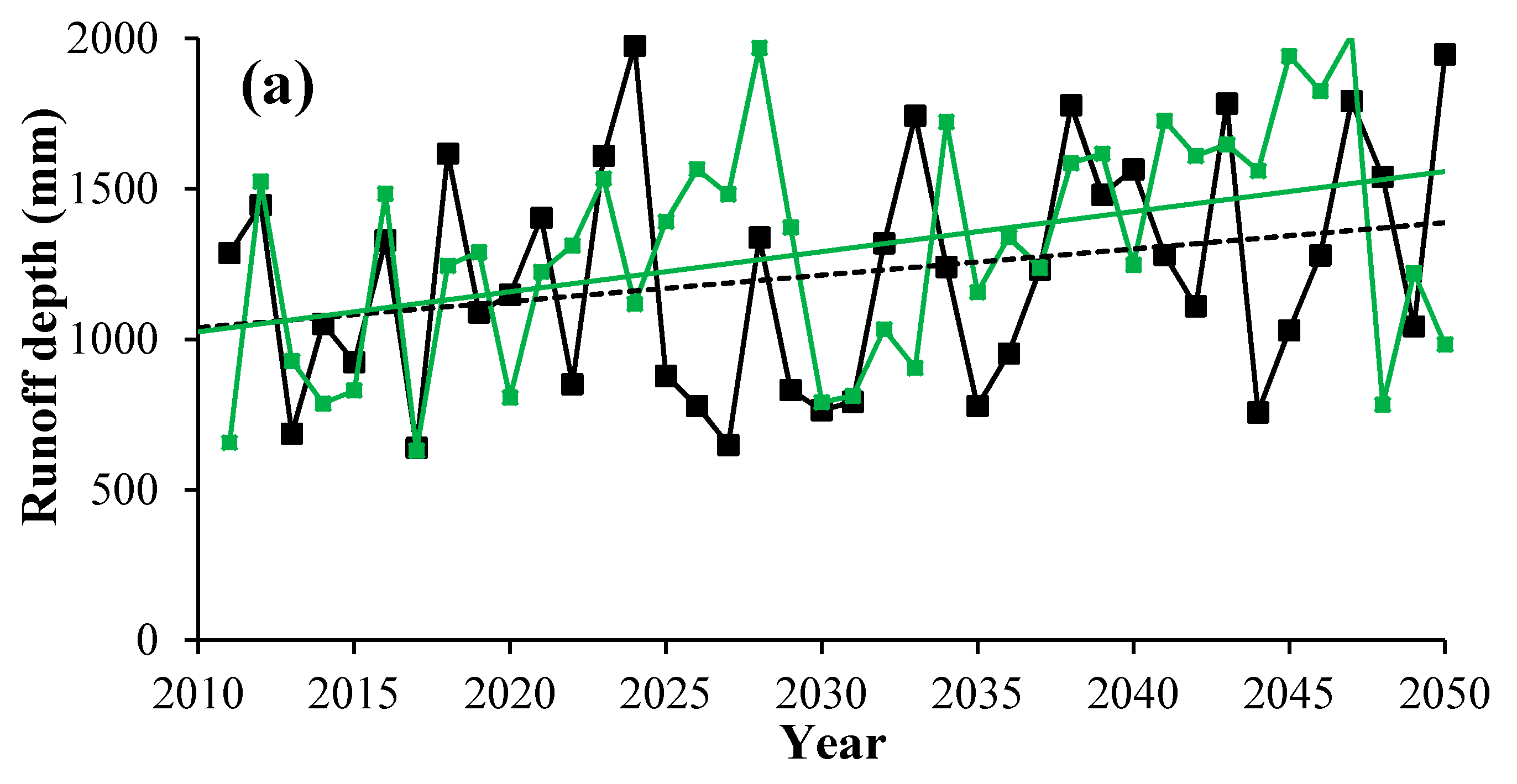
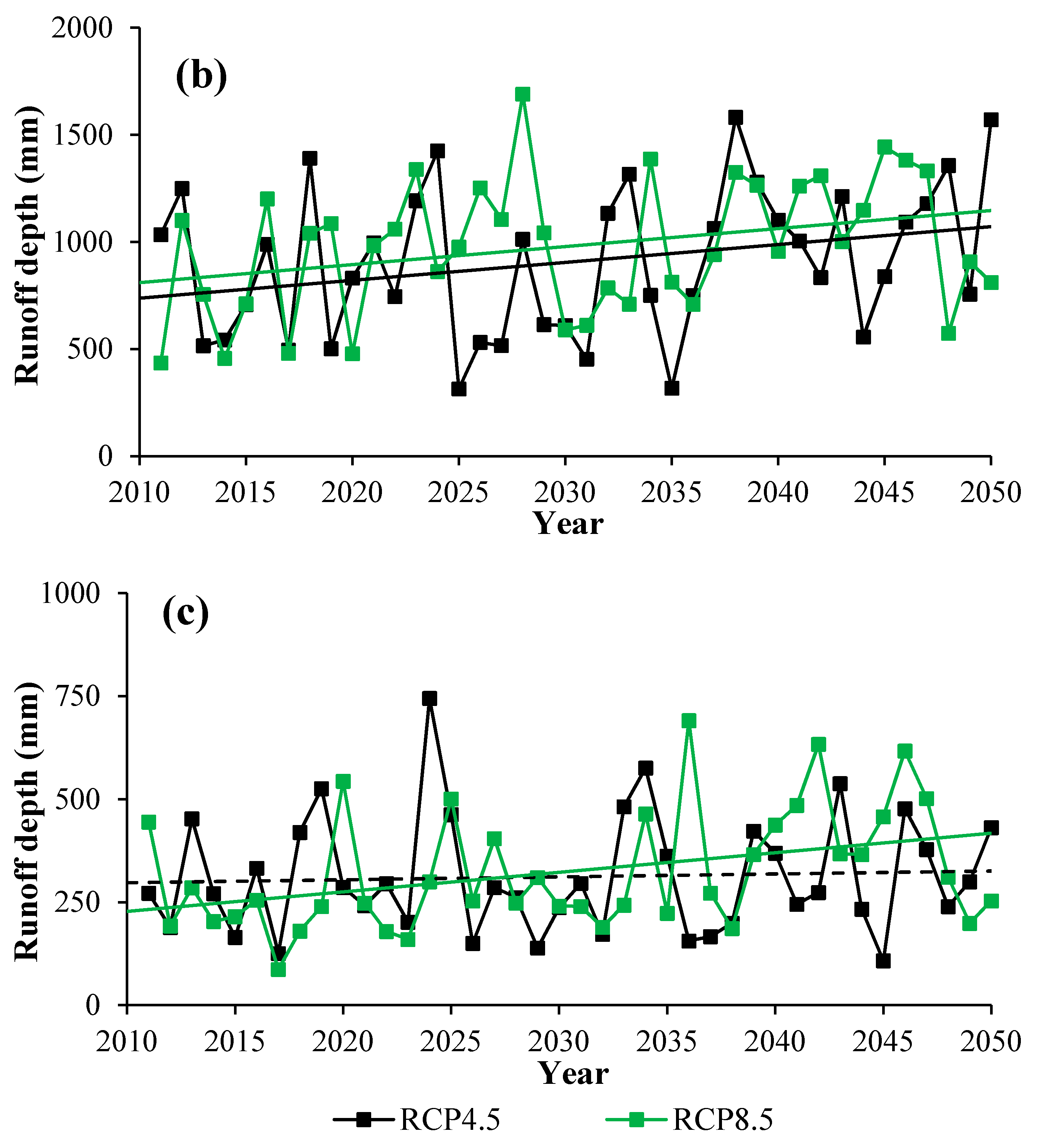
4.4.1. Impact of Climate Change on Runoff Process
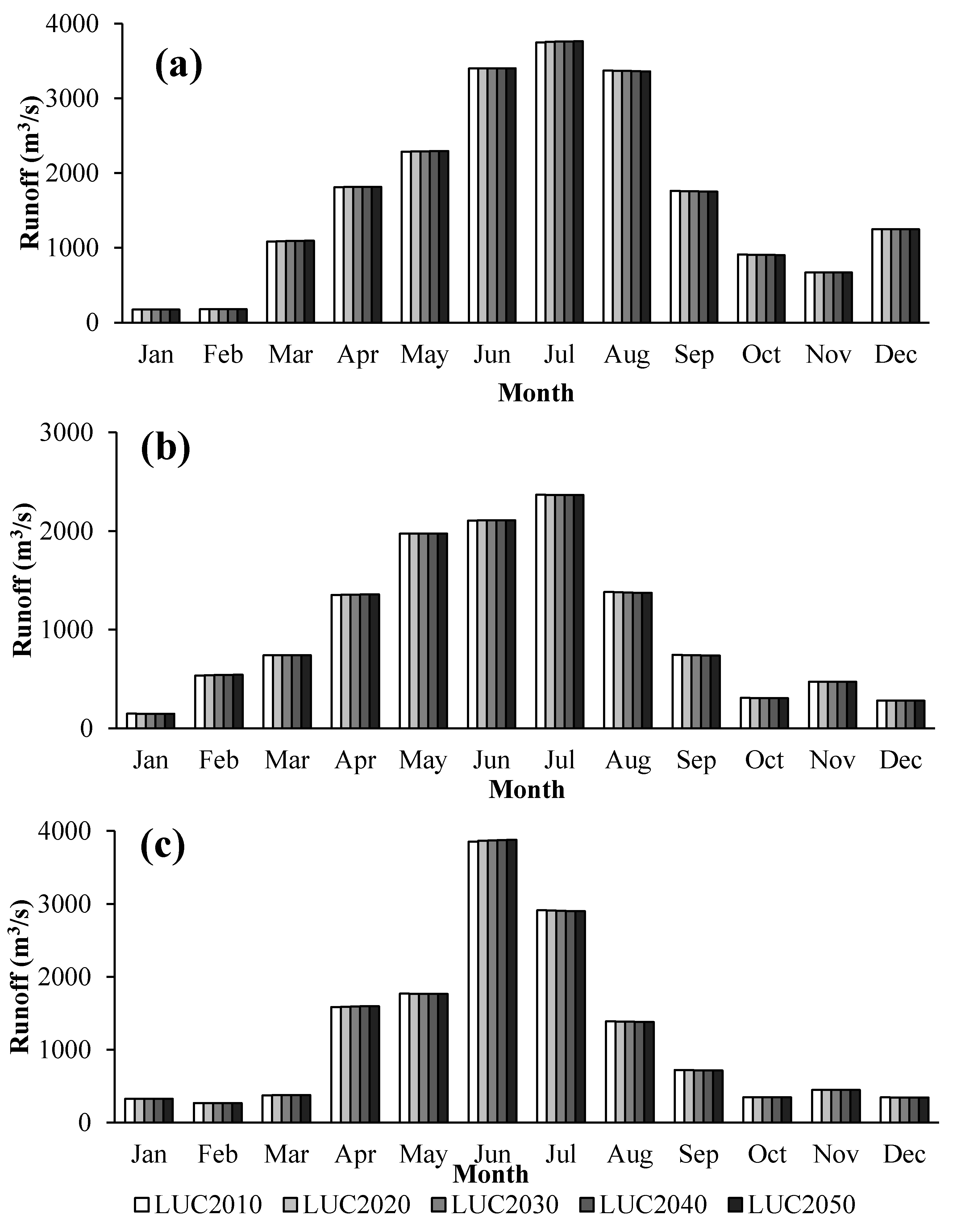
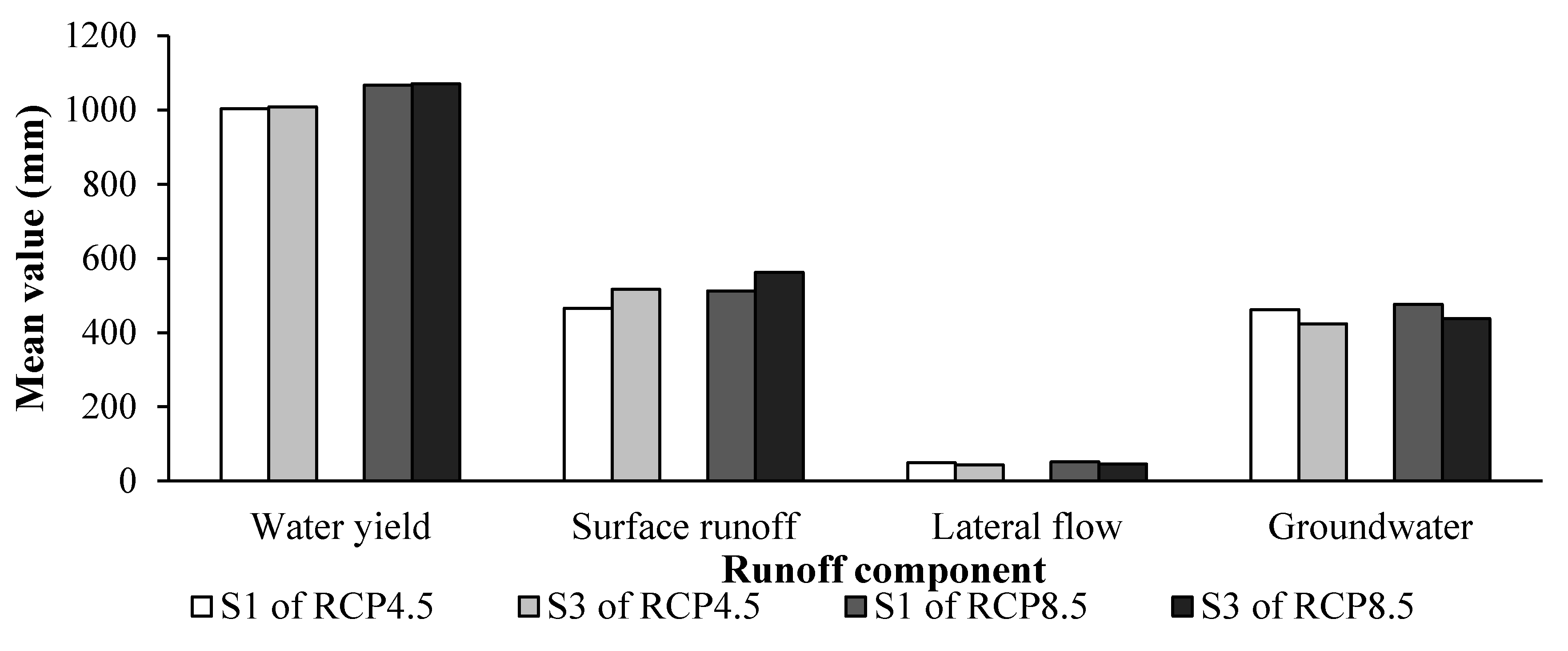
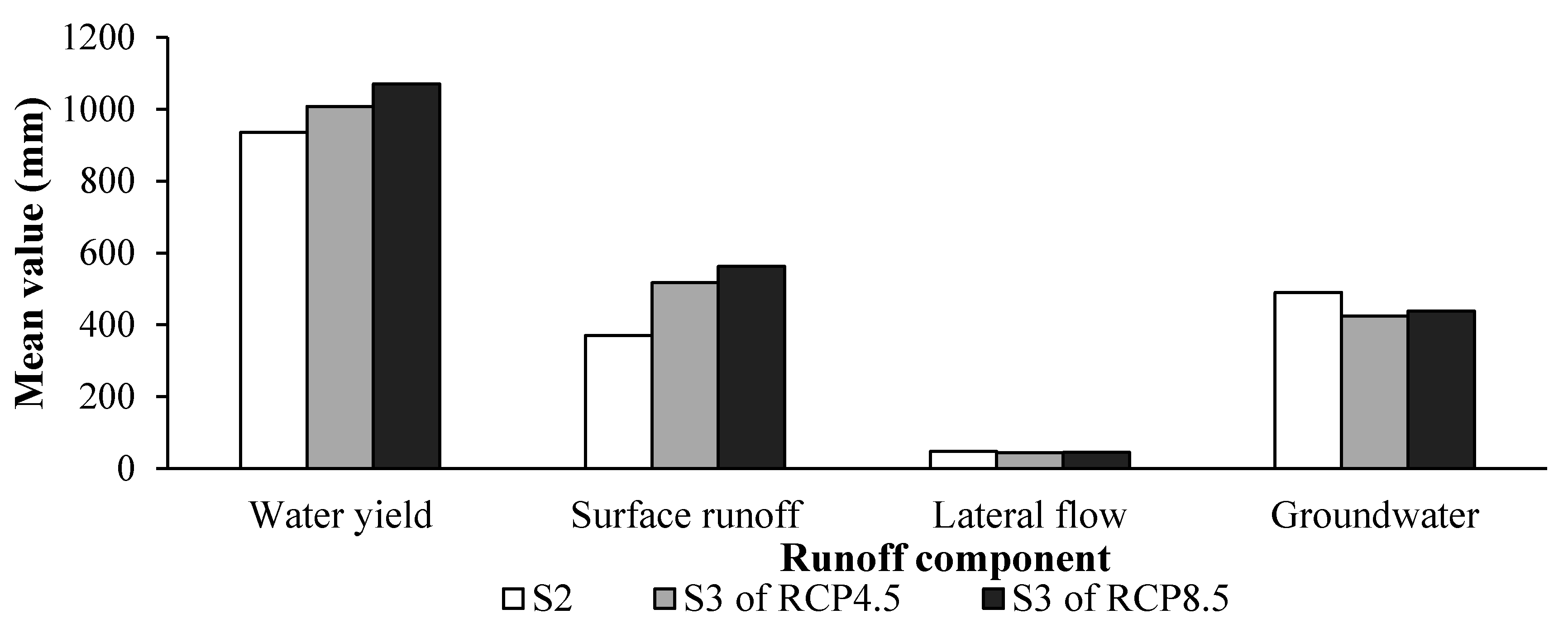
4.4.2. Impact of LUC Change on Runoff Process
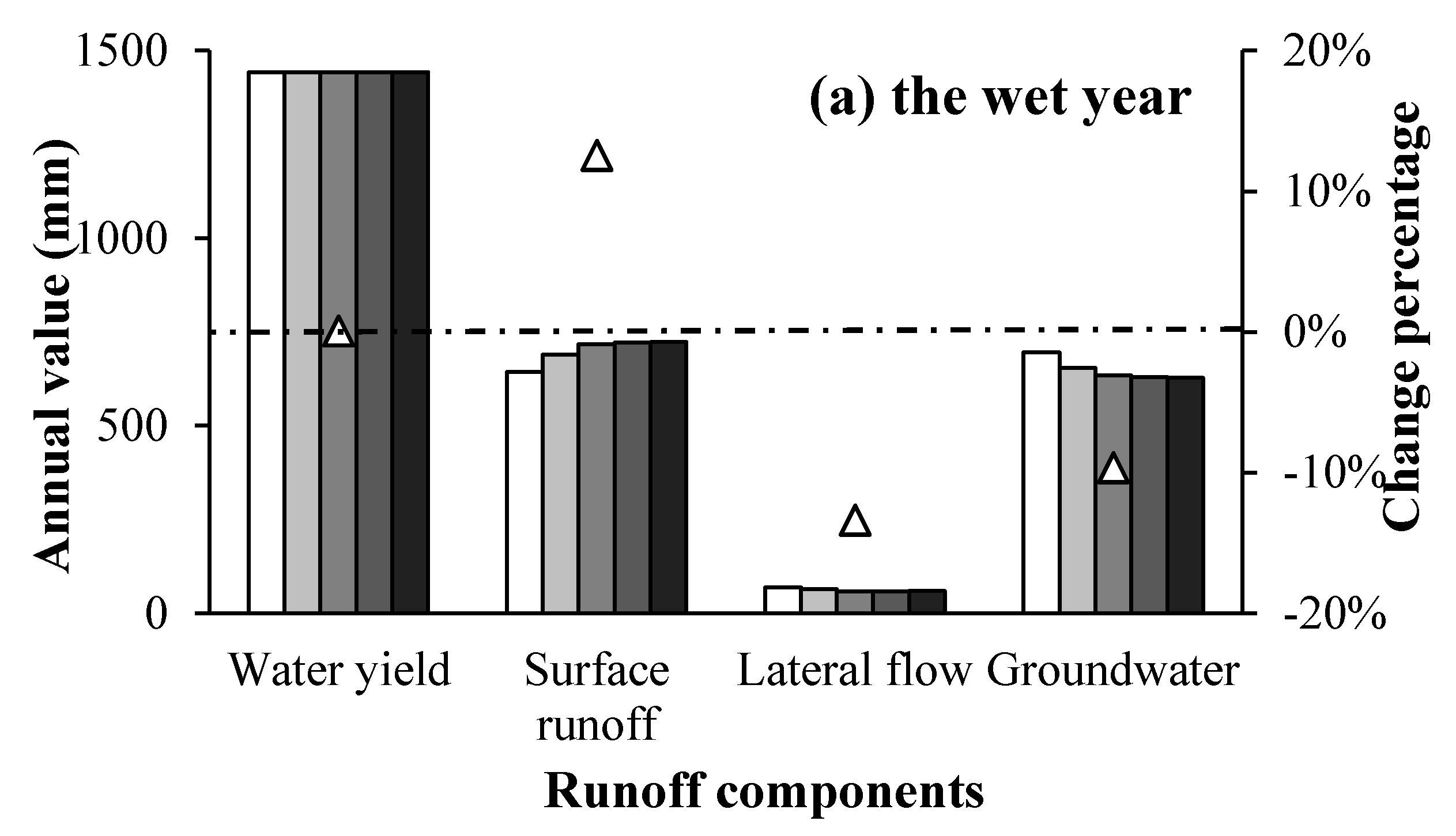
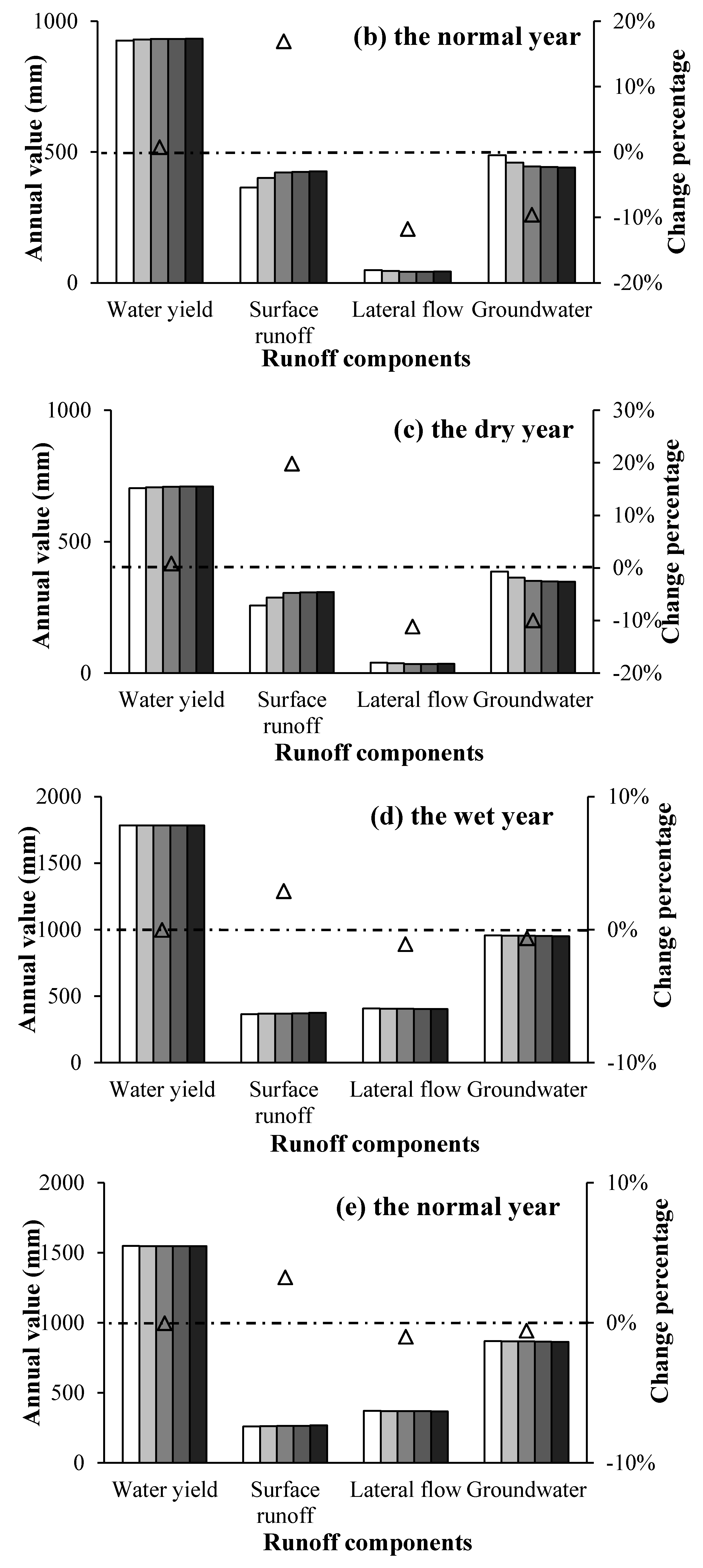
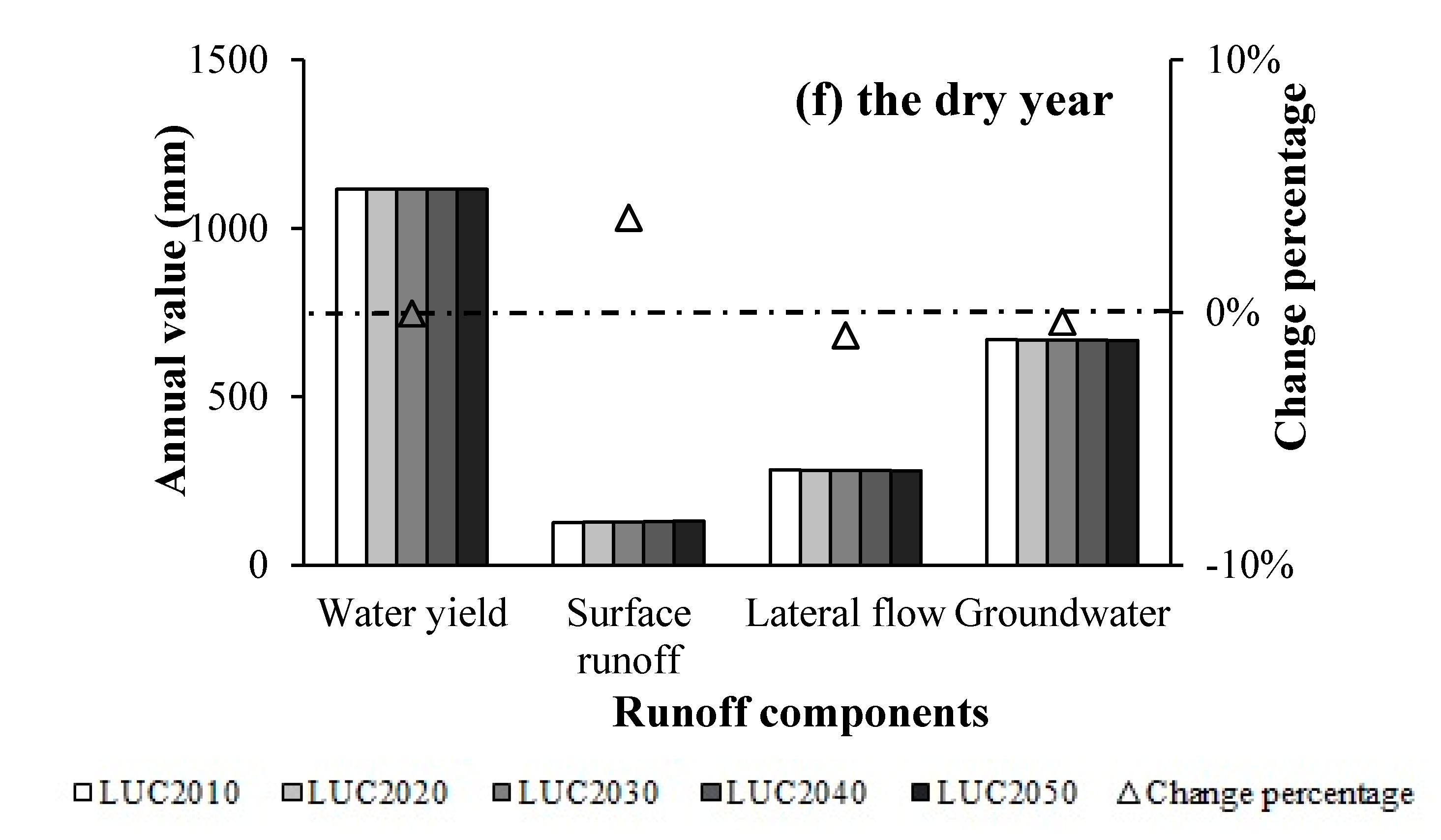
4.4.3. Impact of Climate and LUC Changes on Runoff Process
5. Conclusions
- (1)
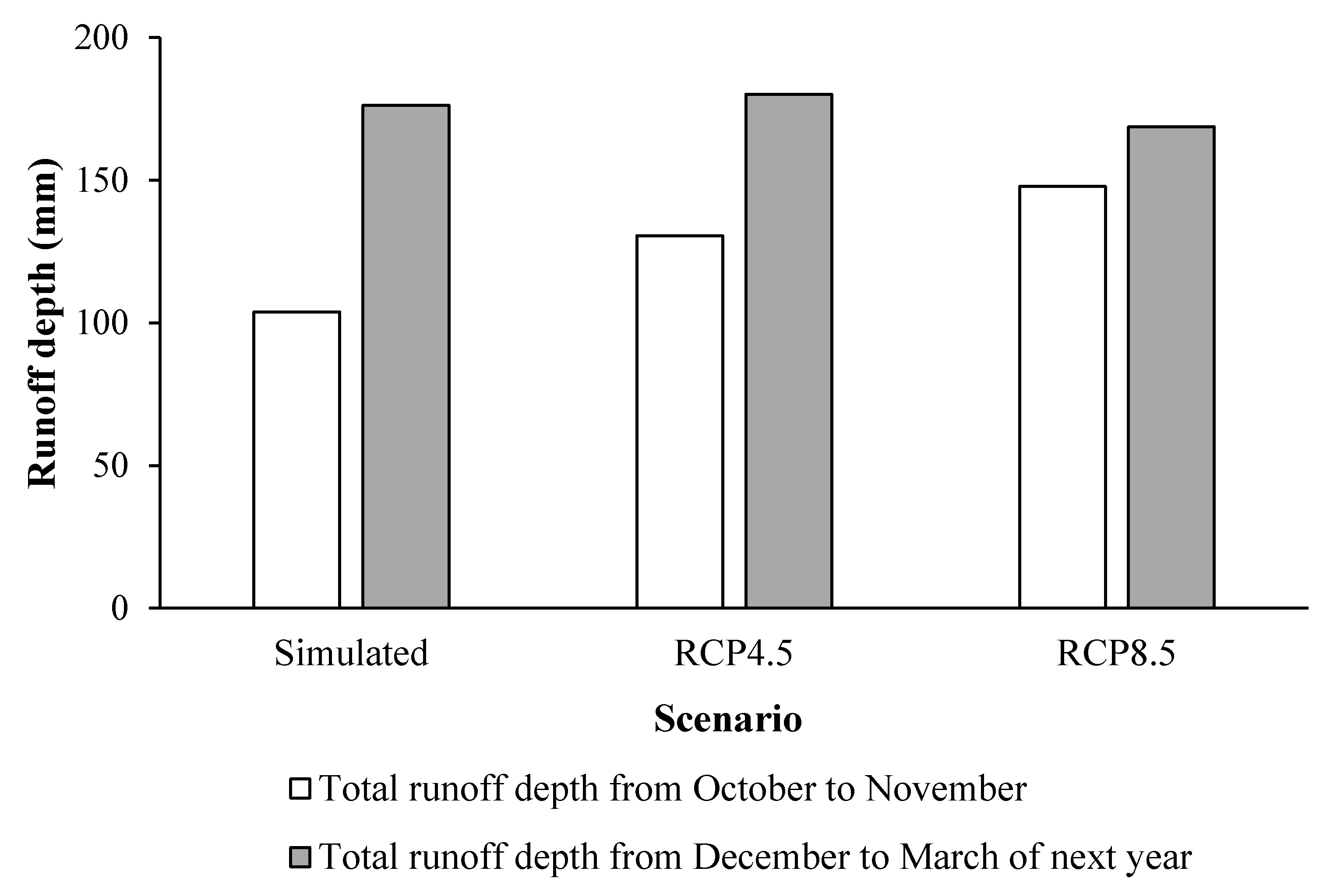
- The impact of climate change on runoff is significant. Runoff depth is projected to increase in both wet and dry seasons under future climate change for both RCP 4.5 and RCP 8.5.
- (2)
- LUC change has an insignificant influence on runoff at the basin level, since there are few differences in outlet runoff under different LUC scenarios. However, changes in runoff components are more important at the sub-watershed level. The impact of urbanization on runoff components can be better understood at the sub-watershed level, and urbanization has less impact on water yield than on surface runoff and groundwater. The impact of LUC change on runoff components differs obviously among the wet, normal and dry years in urbanized regions. The increase in surface runoff caused by urbanization is highest in the wet year.
- (3)
- With simultaneous changes in climate and LUC, runoff depth in the study area is predicted to increase in the future. Climate change brings increases in water yield and surface runoff, whereas LUC change leads to changes in the allocation of surface runoff and groundwater in urban areas.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Changnon, S.A.; Demissie, M. Detection of changes in streamflow and floods resulting from climate fluctuations and land use-drainage changes. Clim. Chang. 1996, 32, 411–421. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; Jeu, R.D.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.H.; Botta, A.; Cardille, J.A. Effects of large-scale changes in land cover on the discharge of the Tocantins River, Southeastern Amazonia. J. Hydrol. 2003, 283, 206–217. [Google Scholar] [CrossRef]
- Jones, J.A. Hydrologic processes and peak discharge response to forest removal, regrowth, and roads in 10 small experimental basins, western Cascades, Oregon. Water Resour. Res. 2000, 36, 2621–2642. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. Soil conservation service curve number (SCS-CN) methodology. Water Sci. Technol. Libr. 2003, 22, 355–362. [Google Scholar]
- Tao, F.L.; Yokozawa, M.; Hayashi, Y.; Lin, E. Future climate change, the agricultural water cycle, and agricultural production in China. Agric. Ecosyst. Environ. 2003, 95, 203–215. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.H.; Liu, D.D.; Hu, T.S.; Xu, C.Y. Frequency analysis of nonstationary annual maximum flood series using the time-varying two-component mixture distributions. Hydrol. Process. 2017, 31, 69–89. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Xu, J.C.; Noordwijk, M.V. Sensitivity of streamflow from a Himalayan catchment to plausible changes in land cover and climate. Hydrol. Process. 2010, 24, 1379–1390. [Google Scholar] [CrossRef]
- Chawla, I.; Mujumdar, P.P. Isolating the impacts of land use and climate change on streamflow. Hydrol. Earth Syst. Sci. 2015, 19, 3633–3651. [Google Scholar] [CrossRef]
- Tranga, N.T.T.; Shresthaa, S.; Shresthaa, M.; Dattab, A.; Kawasakic, A. Evaluating the impacts of climate and land-use change on the hydrology and nutrient yield in a transboundary river basin: A case study in the 3S River Basin (Sekong, Sesan, and Srepok). Sci. Total Environ. 2017, 576, 586–598. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.F.; Kang, S.Z.; Zhang, L.; Li, F.S. Modelling hydrological response to different land-use and climate change scenarios in the Zamu River basin of northwest China. Hydrol. Process. 2008, 22, 2502–2510. [Google Scholar] [CrossRef]
- Goyal, M.K.; Burn, D.H.; Ojha, C.S.P. Statistical downscaling of temperatures under climate change scenarios for Thames river basin, Canada. Int. J. Glob. Warm. 2012, 4, 13–30. [Google Scholar] [CrossRef]
- Li, F.P.; Zhang, Y.Q.; Xu, Z.X.; Teng, J.; Liu, C.M.; Liu, W.F.; Mpelasoka, F. The impact of climate change on runoff in the southeastern Tibetan Plateau. J. Hydrol. 2013, 505, 188–201. [Google Scholar] [CrossRef]
- Gan, R.; Luo, Y.; Zuo, Q.T.; Sun, L. Effects of projected climate change on the glacier and runoff generation in the Naryn River Basin, Central Asia. J. Hydrol. 2015, 523, 240–251. [Google Scholar] [CrossRef]
- Dhar, S.; Mazumdar, A. Hydrological modelling of the Kangsabati river under changed climate scenario: Case study in India. Hydrol. Process. 2009, 23, 2394–2406. [Google Scholar] [CrossRef]
- Chen, H.; Xu, C.Y.; Guo, S.L. Comparison and evaluation of multiple GCMs, statistical downscaling and hydrological models in the study of climate change impacts on runoff. J. Hydrol. 2012, 434–435, 36–45. [Google Scholar] [CrossRef]
- Bosch, J.M.; Hewlett, J.D. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol. 1982, 55, 3–23. [Google Scholar] [CrossRef]
- Hornbeck, J.W.; Adams, M.B.; Corbett, E.S.; Verry, E.S.; Lynch, J.A. Long-term impacts of forest treatments on water yield: A summary for northeastern USA. J. Hydrol. 1993, 150, 323–344. [Google Scholar] [CrossRef]
- Stednick, J.D. Monitoring the effects of timber harvest on annual water yield. J. Hydrol. 1996, 176, 79–95. [Google Scholar] [CrossRef]
- Brown, A.E.; Zhang, L.; McMahon, T.A.; Western, A.W.; Vertessy, R.A. A review of paired catchment studies for determining changes in water yield resulting from alterations in vegetation. J. Hydrol. 2005, 310, 28–61. [Google Scholar] [CrossRef]
- Onstad, C.A.; Jamieson, D.G. Modelling the effect of land use modifications on runoff. Water Resour. Res. 1970, 6, 1287–1295. [Google Scholar] [CrossRef]
- Calder, I.R.; Hall, R.L.; Bastable, H.G.; Gunston, H.M.; Shela, O.; Chirwa, A.; Kafundu, R. The impact of land use change on water resources in sub-Saharan Africa: A modelling study of Lake Malawi. J. Hydrol. 1995, 170, 123–135. [Google Scholar] [CrossRef]
- Fohrer, N.; Haverkamp, S.; Frede, H.G. Assessment of the effects of land use patterns on hydrologic landscape functions: Development of sustainable land use concepts for low mountain range areas. Hydrol. Process. 2005, 19, 659–672. [Google Scholar] [CrossRef]
- Li, L.J.; Jiang, D.J.; Hou, X.Y.; Li, J.Y. Simulated runoff responses to land use in the middle and upstream reaches of Taoerhe River basin, Northeast China, in wet, average and dry years. Hydrol. Process. 2013, 27, 3484–3494. [Google Scholar] [CrossRef]
- Mwangi, H.M.; Julich, S.; Patil, S.D.; McDonald, M.A.; Feger, K.H. Modelling the impact of agroforestry on hydrology of MaraRiver Basin in East Africa. Hydrol. Process. 2016, 30, 3139–3155. [Google Scholar] [CrossRef]
- Li, F.P.; Zhang, G.X.; Xu, Y.J. separating the impacts of climate variation and human activities on runoff in the songhua river basin, northeast China. Water 2014, 6, 3320–3338. [Google Scholar] [CrossRef]
- Zhan, C.S.; Jiang, S.S.; Sun, F.B.; Jia, Y.W.; Niu, C.W.; Yue, W.F. Quantitative contribution of climate change and human activities to runoff changes in the Wei River basin, China. Hydrol. Earth Syst. Sci. 2014, 18, 3069–3077. [Google Scholar] [CrossRef]
- Zhang, X.P.; Zhang, L.; Zhao, J.; Rustomji, P; Hairsine, P. Responses of streamflow to changes in climate and land use/cover in the Loess Plateau, China. Water Resour. Res. 2008, 44, W00A07. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F.L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Cuo, L.; Zhang, Y.X.; Gao, Y.H.; Hao, Z.C.; Cairang, L. The impacts of climate change and land cover/use transition on the hydrology in the upper Yellow River Basin, China. J. Hydrol. 2013, 502, 37–52. [Google Scholar] [CrossRef]
- Zhang, L.; Karthikeyan, R.; Bai, Z.K.; Srinivasan, R. Analysis of streamflow responses to climate variability and land use change in the Loess Plateau region of China. Catena 2017, 154, 1–11. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Mouria, G.; Nakanob, K.; Tsuyamac, I.; Tanakac, N. The effects of future nationwide forest transition to discharge in the 21st century with regard to general circulation model climate change scenarios. Environ. Res. 2016, 149, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Themeßl, M.J.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W. A CMIP5 multimodel projection of future temperature, precipitation, and climatological drought in China. Int. J. Climatol. 2014, 34, 2059–2078. [Google Scholar] [CrossRef]
- Ngai, S.T.; Tangang, F.; Juneng, L. Bias correction of global and regional simulated daily precipitation and surface mean temperature over Southeast Asia using quantile mapping method. Glob. Planet. Chang. 2017, 149, 79–90. [Google Scholar] [CrossRef]
- Maraun, D. Bias correction, quantile mapping, and downscaling: Revisiting the inflation issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Mpelasoka, F.S.; Chiew, F.H.S. Influence of rainfall scenario construction methods on runoff projections. J. Hydrometeorol. 2009, 10, 1168–1183. [Google Scholar] [CrossRef]
- Hyandye, C.; Martz, L.W. A Markovian and cellular automata land-use change predictive model of the Usangu Catchment. Int. J. Remote Sens. 2017, 38, 64–81. [Google Scholar] [CrossRef]
- Nouri, J.; Gharagozlou, A.; Arjmandi, R.; Faryadi, S.; Adl, M. Predicting urban land use changes using a CA-Markova model. Arab. J. Sci. Eng. 2014, 39, 5565–5573. [Google Scholar] [CrossRef]
- Halmy, M.W.A.; Gessler, P.E.; Hicke, J.A.; Salem, B.B. Land use/land cover change detection and prediction in the north-western coastal desert of Egypt using Markov-CA. Appl. Geogr. 2015, 63, 101–112. [Google Scholar] [CrossRef]
- Memarian, H.; Balasundram, S.K.; Talib, J.B.; Sung, C.T.B.; Sood, A.M.; Abbaspour, K. Validation of CA-Markov for simulation of land use and cover change in the langat basin, Malaysia. J. Geogr. Inf. Syst. 2012, 4, 542–554. [Google Scholar] [CrossRef]
- Guan, D.J.; Li, H.F.; Inohae, T.; Su, W.C.; Nagaie, T.; Hokao, K. Modeling urban land use change by the integration of cellular automaton and Markov model. Ecol. Model. 2011, 222, 3761–3772. [Google Scholar] [CrossRef]
- Scott, W.A. The reliability of content analysis: The case of nominal scale coding. Pub. Opin. Q. 1955, 19, 321–325. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment. Part 1. Model development. J. Am. Water Resour. Assoc. 1998, 34, 1–17. [Google Scholar] [CrossRef]
- Mango, L.M.; Melesse, A.M.; McClain, M.E.; Gann, D.; Setegn, S.G. Land use and climate change impacts on the hydrology of the upper Mara River Basin, Kenya: Results of a modeling study to support better resource management. Hydrol. Earth Syst. Sci. 2011, 15, 2245–2258. [Google Scholar] [CrossRef]
- Wagner, P.D.; Kumar, S.; Schneider, K. An assessment of land use change impacts on the water resources of the Mula and Mutha Rivers catchment upstream of Pune, India. Hydrol. Earth Syst. Sci. 2013, 17, 2233–2246. [Google Scholar] [CrossRef]
- Mehdi, B.; Ludwig, R.; Lehner, B. Evaluating the impacts of climate change and crop land use change on streamflow, nitrates and phosphorus: A modeling study in Bavaria. J. Hydrol. Reg. Stud. 2015, 4, 60–90. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.T.; Yu, W.J.; Ge, Y.C. Hydrological responses to land-use change scenarios under constant and changed climatic conditions. Environ. Manag. 2016, 57, 412–431. [Google Scholar] [CrossRef] [PubMed]
- Eckhardt, K.; Ulbrich, U. Potential impacts of climate change on groundwater recharge and streamflow in a central European low mountain range. J. Hydrol. 2003, 284, 244–252. [Google Scholar] [CrossRef]
- Bouraoui, F.; Grizzetti, B.; Granlund, K.; Rekolainen, S.; Bidoglio, G. Impact of climate change on the water cycle and nutrient losses in a Finnish catchment. Clim. Chang. 2004, 66, 109–126. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation, Version 2009. Available online: http://swat.tamu.edu/documentation/ (accessed on 28 June 2017).
- Zhou, F.; Xu, Y.P.; Chen, Y.; Xu, C.Y.; Gao, Y.Q.; Du, J.K. Hydrological response to urbanization at different spatio-temporal scales simulated by coupling of CLUE-S and the SWAT model in the Yangtze River Delta region. J. Hydrol. 2013, 485, 113–125. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.H.; Wang, Z.L. A tentative discussion on the impact of human activities on the variability of runoff series of the Beijiang River basin. J. Nat. Resour. 2006, 21, 910–915. (In Chinese) [Google Scholar]
- Andréassian, V.; Parent, E.; Michel, C. A distribution-free test to detect gradual changes in 358 watershed behavior. Water Resour. Res. 2003, 39, 333–342. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Time stability of catchment model parameters: Implications for climate impact analyses. Water Resour. Res. 2011, 47, 2144–2150. [Google Scholar] [CrossRef]
- Westra, S.; Thyer, M.; Leonard, M.; Kavetski, D.; Lambert, M. A strategy for diagnosing and interpreting hydrological model nonstationarity. Water Resour. Res. 2014, 50, 5090–5113. [Google Scholar] [CrossRef]
- Patil, S.D.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef]


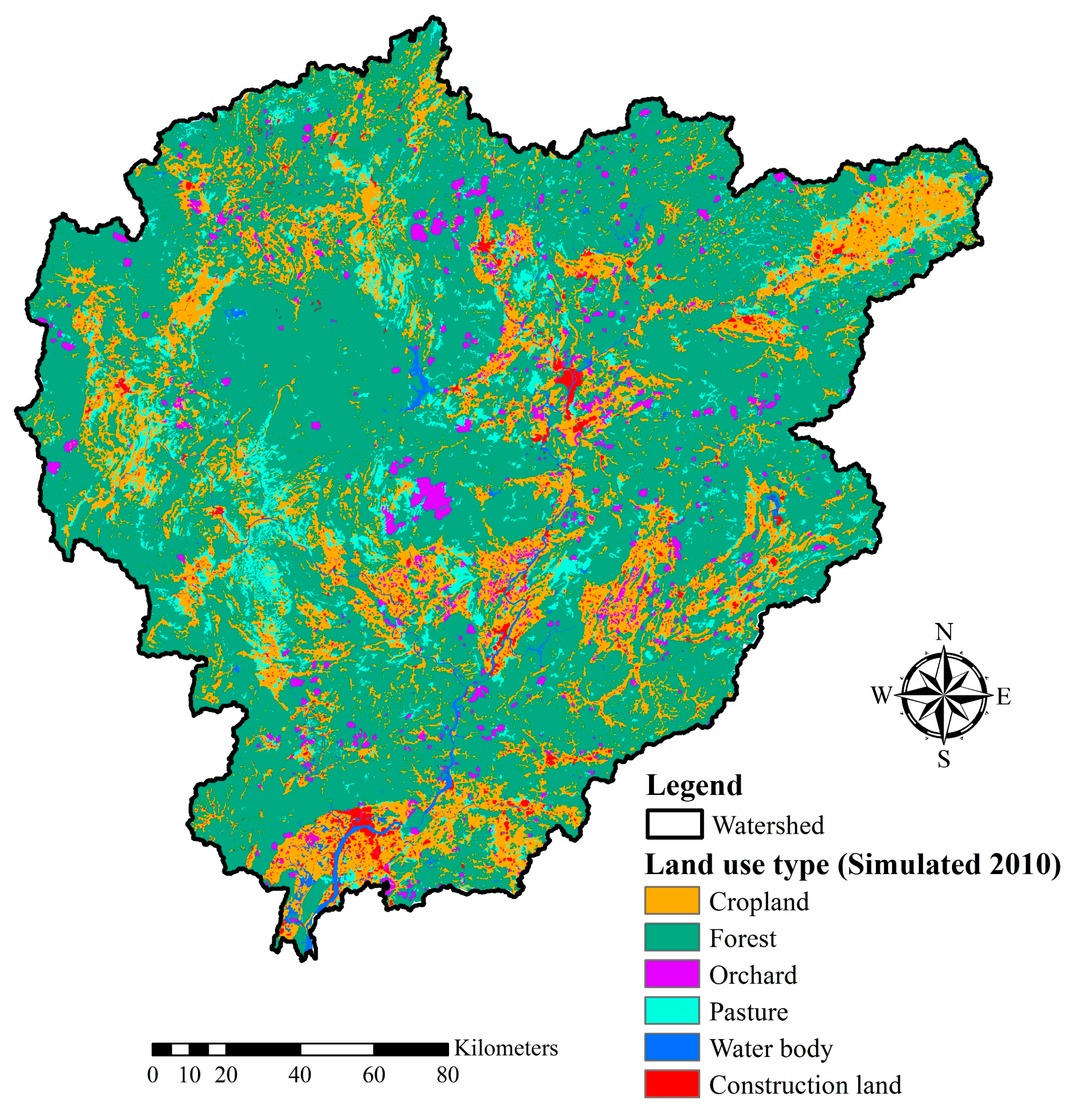
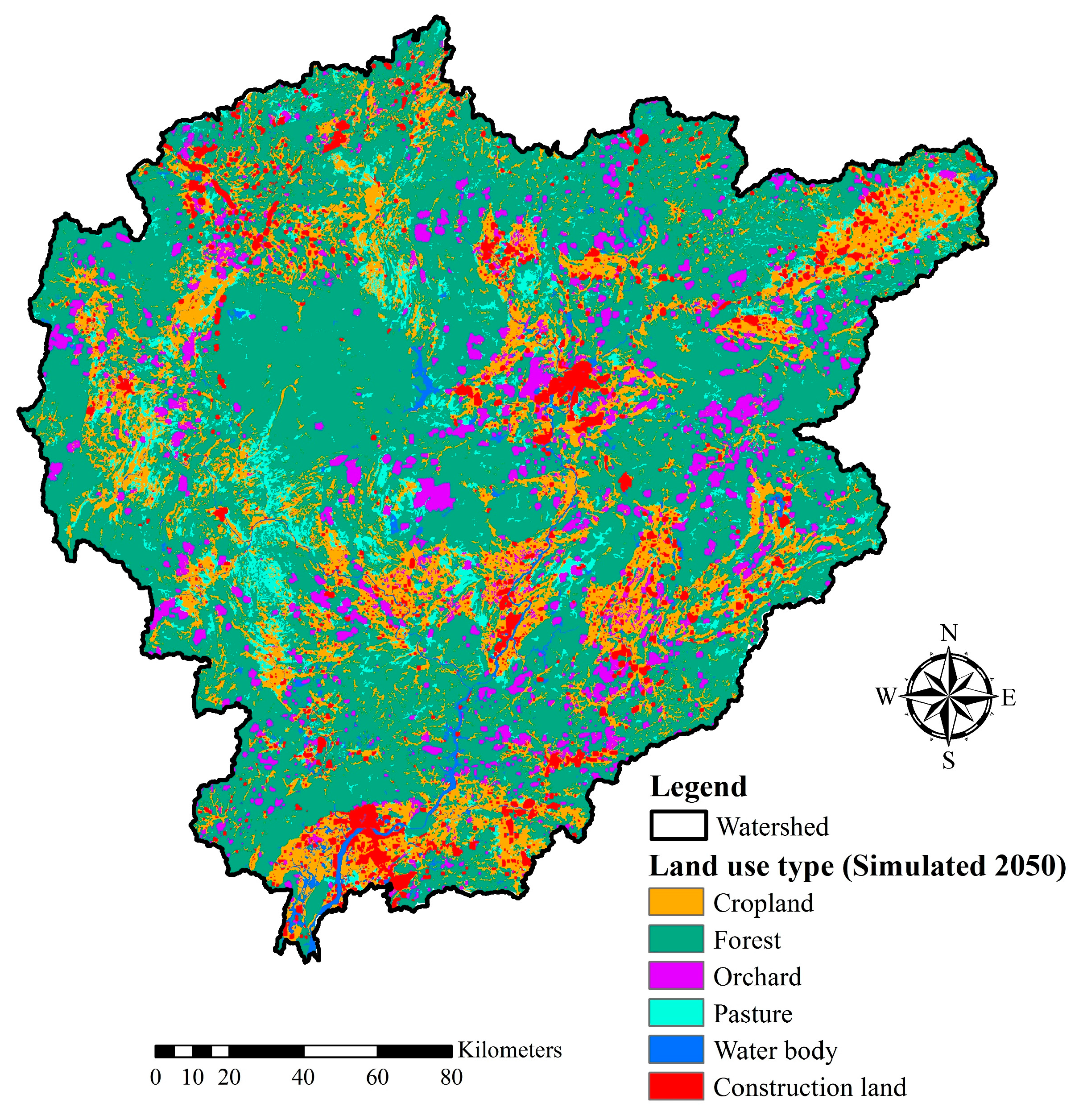
| LUC Type | The Observed Map | The Predicted Map | |||||
|---|---|---|---|---|---|---|---|
| 1990 | 2000 | 2010 | 2020 | 2030 | 2040 | 2050 | |
| Cropland | 20.8 | 20.8 | 19.4 | 18.8 | 18.6 | 18.4 | 18.3 |
| Forest | 68.2 | 68.1 | 67.5 | 63.6 | 62.7 | 62.1 | 61.7 |
| Orchard | 1.4 | 1.5 | 3.5 | 7.0 | 7.6 | 7.9 | 8.0 |
| Pasture | 6.6 | 6.6 | 5.6 | 5.3 | 5.1 | 4.9 | 4.8 |
| Water body | 1.4 | 1.5 | 1.8 | 2.0 | 2.0 | 2.1 | 2.1 |
| Construction land | 1.6 | 1.6 | 2.2 | 3.3 | 3.9 | 4.5 | 5.1 |
| Statistics | Periods | Calibration | Validation | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P (mm/d) | T (°C) | P (mm/d) | T (°C) | ||||||
| QM | Observed | QM | Observed | QM | Observed | QM | Observed | ||
| Mean | Annual | 4.58 | 4.60 | 19.83 | 19.84 | 4.63 | 4.68 | 20.00 | 20.33 |
| Wet | 6.62 | 6.67 | 25.48 | 25.48 | 6.85 | 6.86 | 25.71 | 25.76 | |
| Dry | 2.54 | 2.52 | 14.16 | 14.17 | 2.31 | 2.51 | 14.26 | 14.88 | |
| Standard deviation | Annual | 11.72 | 11.85 | 7.42 | 7.42 | 12.71 | 12.30 | 7.58 | 7.07 |
| Wet | 14.32 | 14.71 | 3.73 | 3.72 | 15.11 | 15.56 | 3.84 | 3.46 | |
| Dry | 7.76 | 7.36 | 5.66 | 5.66 | 7.41 | 7.56 | 5.89 | 5.37 | |
| 95th percentile | Annual | 26.04 | 25.98 | 29.36 | 29.36 | 25.63 | 26.51 | 29.71 | 29.49 |
| Wet | 35.08 | 35.04 | 29.93 | 29.93 | 33.70 | 35.62 | 30.22 | 30.08 | |
| Dry | 14.70 | 14.64 | 23.59 | 23.58 | 13.75 | 14.99 | 24.22 | 23.89 | |
| 75th percentile | Annual | 2.94 | 2.94 | 26.41 | 26.41 | 2.81 | 2.84 | 26.68 | 26.47 |
| Wet | 6.22 | 6.21 | 28.16 | 28.16 | 6.62 | 6.26 | 28.58 | 28.16 | |
| Dry | 1.00 | 1.01 | 18.52 | 18.51 | 0.77 | 0.92 | 19.02 | 18.95 | |
| Item | P | T | ||||
|---|---|---|---|---|---|---|
| Annual | Wet | Dry | Annual | Wet | Dry | |
| Change percentage of RCP4.5 | 3% | 6% | −1% | 0.5 °C | 0.7 °C | 1.5 °C |
| Change percentage of RCP8.5 | 8% | 13% | −3% | 1.8 °C | 1.8 °C | 2.0 °C |
| Scenario | Description |
|---|---|
| S1 | Only climate change scenario: RCP4.5 and RCP8.5 (2011–2050). LUC is LUC2010. |
| S2 | Only LUC change scenario: Changing LUC (LUC2010, LUC2020, LUC2030, LUC2040 and LUC2050) with three typical hydrological years. |
| S3 | Simultaneous climate and LUC change scenario in the future: RCP4.5/RCP8.5 (2011–2020) + LUC2020; RCP4.5/RCP8.5 (2021–2030) + LUC2030; RCP4.5/RCP8.5 (2031–2040) + LUC2040; RCP4.5/RCP8.5 (2041–2050) + LUC2050. |
| Season | Robs (mm) | Rsim (mm) | Prediction under RCP 4.5 | Prediction under RCP 8.5 | ||
|---|---|---|---|---|---|---|
| Change Amount (mm) | Change Percentage (%) | Change Amount (mm) | Change Percentage (%) | |||
| Annual | 1116 | 1118 | +98 | +9 | +178 | +16 |
| Wet | 844 | 836 | +70 | +8 | +144 | +17 |
| Dry | 272 | 282 | +28 | +10 | +34 | +12 |
| Sub-Watershed | LUC Scenarios | Cropland | Forest | Orchard | Pasture | Water body | Construction Land |
|---|---|---|---|---|---|---|---|
| Sub12 | LUC2010 | 20.1 | 32.9 | 10.6 | 5.0 | 8.9 | 22.5 |
| LUC2020 | 16.2 | 22.8 | 12.5 | 4.6 | 10.3 | 33.6 | |
| LUC2030 | 15.1 | 17.8 | 12.6 | 4.3 | 10.6 | 39.6 | |
| LUC2040 | 15.1 | 17.3 | 12.6 | 4.0 | 10.6 | 40.4 | |
| LUC2050 | 15.2 | 17.0 | 12.1 | 3.9 | 11.1 | 40.7 | |
| Sub31 | LUC2010 | 13.0 | 73.7 | 3.7 | 1.0 | 7.4 | 1.1 |
| LUC2020 | 13.1 | 71.6 | 6.2 | 0 | 7.9 | 1.2 | |
| LUC2030 | 13.1 | 71.4 | 6.4 | 0 | 8.0 | 1.2 | |
| LUC2040 | 13.2 | 71.3 | 6.2 | 0 | 8.0 | 1.4 | |
| LUC2050 | 13.4 | 70.0 | 7.0 | 0 | 8.1 | 1.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, S.; Liu, D.; Wang, Z.; Zhao, Q.; Zou, H.; Hou, Y.; Liu, P.; Xiong, L. Runoff Responses to Climate and Land Use/Cover Changes under Future Scenarios. Water 2017, 9, 475. https://doi.org/10.3390/w9070475
Pan S, Liu D, Wang Z, Zhao Q, Zou H, Hou Y, Liu P, Xiong L. Runoff Responses to Climate and Land Use/Cover Changes under Future Scenarios. Water. 2017; 9(7):475. https://doi.org/10.3390/w9070475
Chicago/Turabian StylePan, Sihui, Dedi Liu, Zhaoli Wang, Qin Zhao, Hui Zou, Yukun Hou, Pan Liu, and Lihua Xiong. 2017. "Runoff Responses to Climate and Land Use/Cover Changes under Future Scenarios" Water 9, no. 7: 475. https://doi.org/10.3390/w9070475
APA StylePan, S., Liu, D., Wang, Z., Zhao, Q., Zou, H., Hou, Y., Liu, P., & Xiong, L. (2017). Runoff Responses to Climate and Land Use/Cover Changes under Future Scenarios. Water, 9(7), 475. https://doi.org/10.3390/w9070475







