Modelling of Ozone Mass-Transfer through Non-Porous Membranes for Water Treatment
Abstract
:1. Introduction
1.1. Theoretical Development
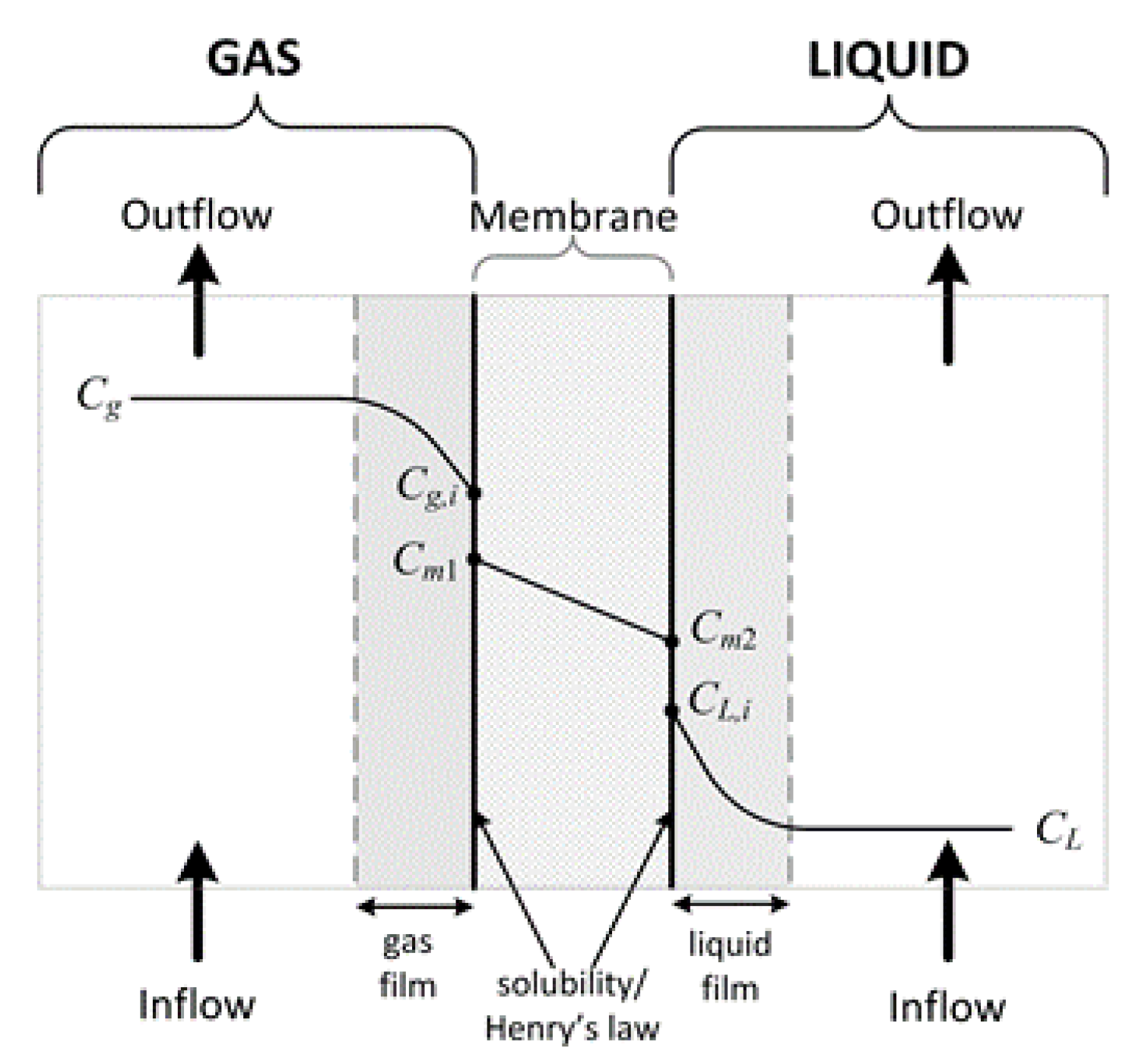
1.1.1. Gas Phase
1.1.2. Membrane
1.1.3. Liquid Phase
2. Numerical Modelling
2.1. Model Domain and Geometry
2.2. Meshing and Scaling
2.3. Governing Equations
- Axial symmetry: no flow crossing the boundary, i.e., when , .
- Membrane wall: no-slip, i.e., when , .
- The velocity in the r-directions at all the boundaries are almost zero, i.e., .
- Tube inlet: flow is fully developed and velocity profile is parabolic, i.e., when , where is the mean axial velocity in the gas phase.
- Tube outlet: flow is fully developed, i.e., when , .
- Axial symmetry: no material flow across the boundary, i.e., when , .
- Tube inlet: the inlet concentrations in the gas phase were defined based on a small ozone and oxygen percentage by volume, .
- Tube outlet: the gas flux is predominantly by convection i.e., when , .
- Gas–membrane interface: the gas concentration is specified using the point-wise constraint boundary condition. The interfacial transport was defined by the solubility laws [26], i.e., when , , where Sj is the solubility of j in the membrane.
- Membrane inlet and outlet: the two boundaries are insulated, i.e., at, and .
- The velocity in the r-directions at all the boundaries are almost zero, i.e.,
- Membrane wall: no-slip, i.e., when , .
- Inlet: average velocity is specified at the inlet, i.e., when , .
- Outlet: flow is fully developed, i.e., when , .
- Inlet: concentrations of O2 and O3 at the liquid inlet are assumed zero, i.e., .
- Membrane–liquid interface: the gas concentration is specified using the point-wise constraint boundary condition. The interfacial transport was defined by the solubility laws [13], i.e., when , , where Hj is the Henry’s constant of j in the liquid.
2.4. Mass Transfer Correlation
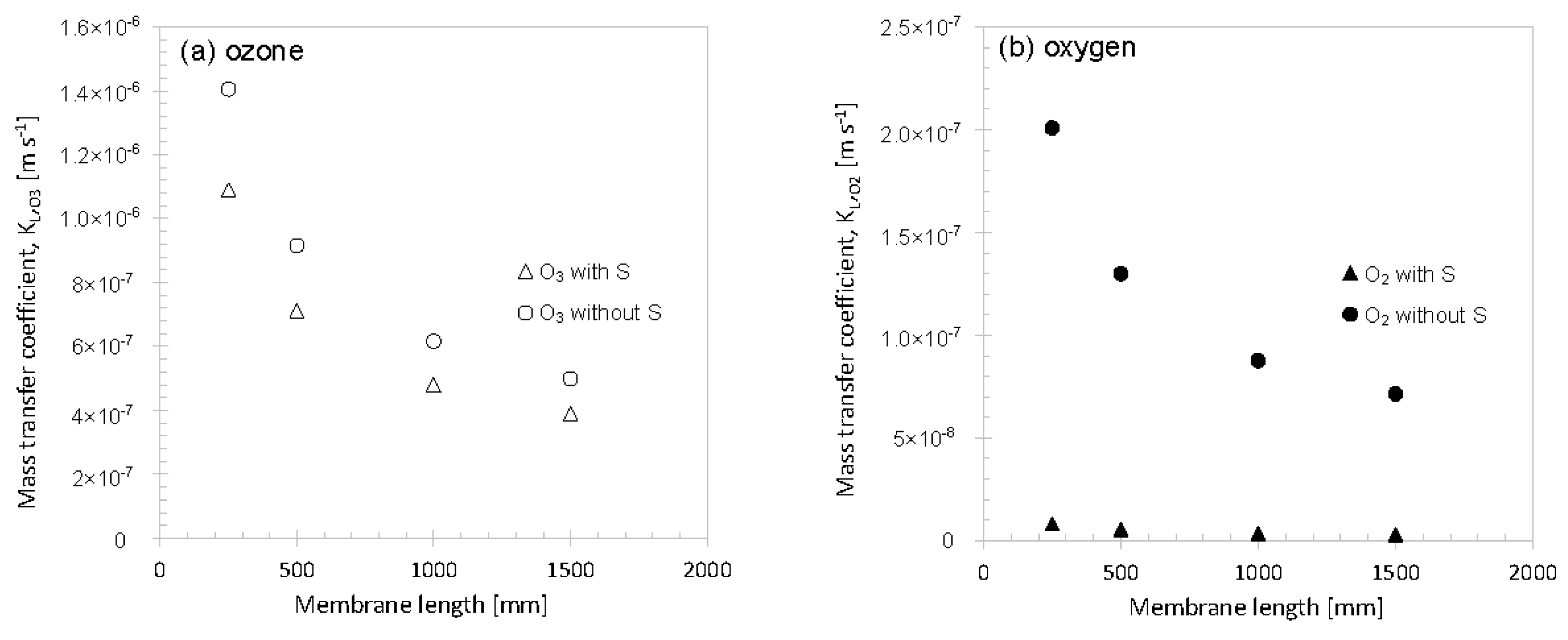
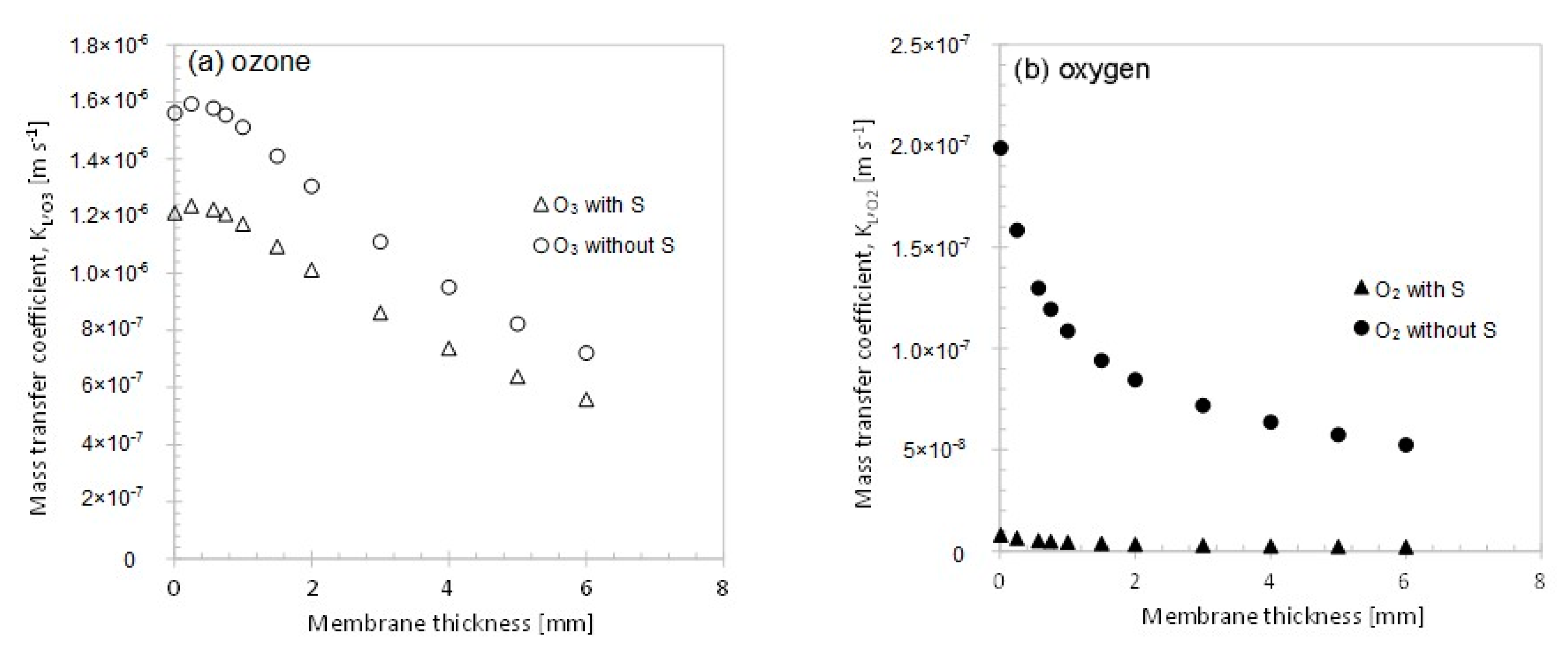
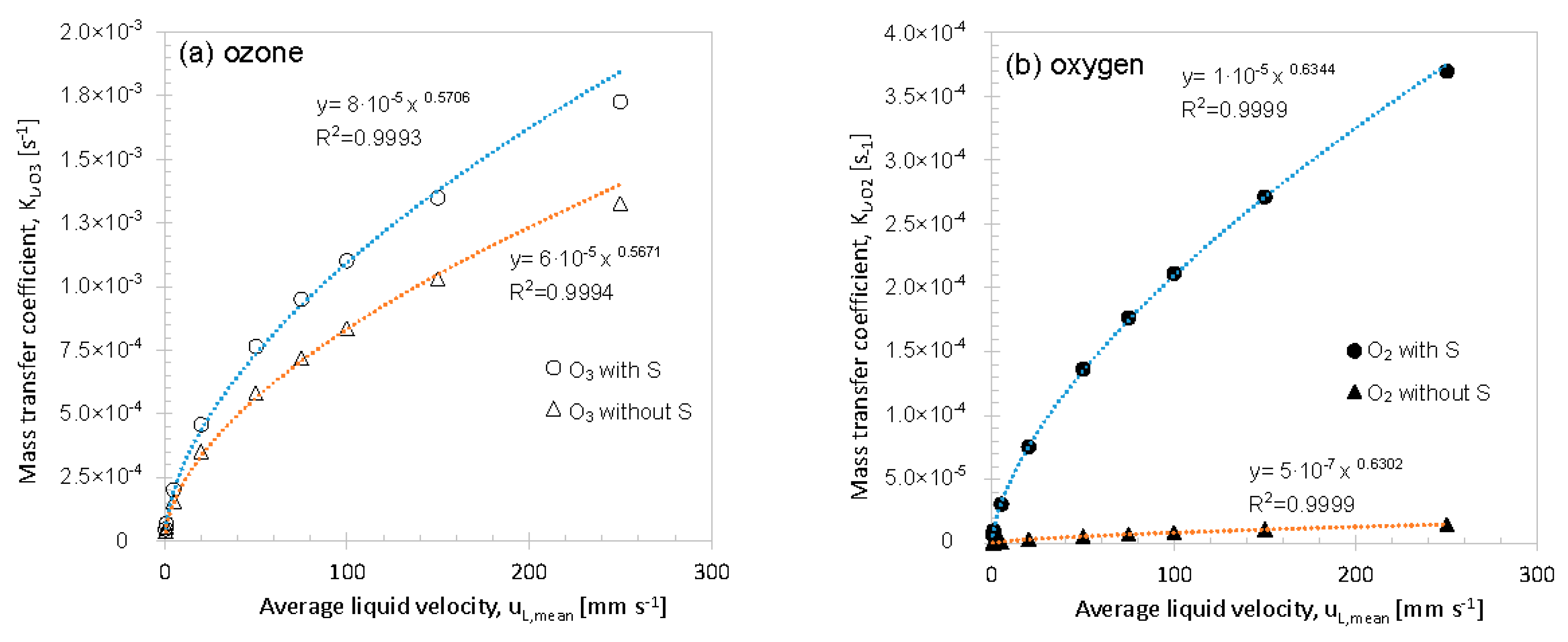
3. Results and Discussion
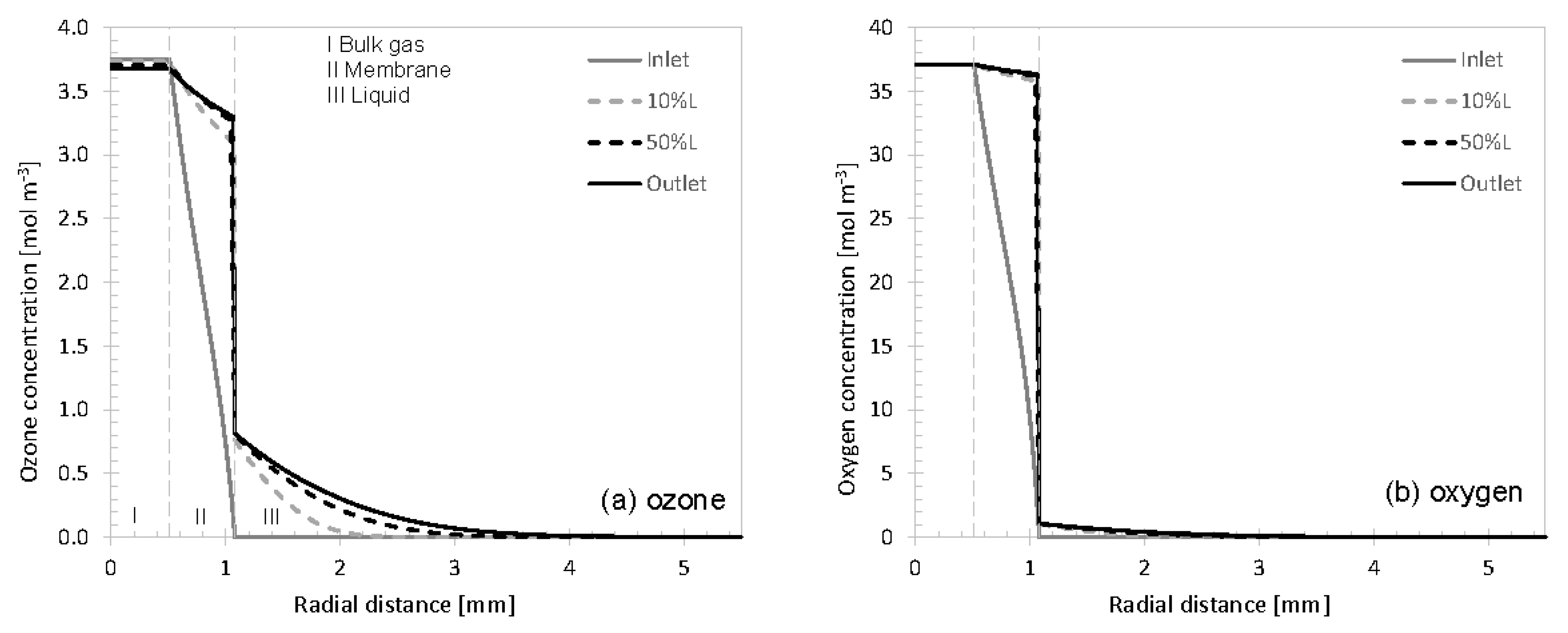
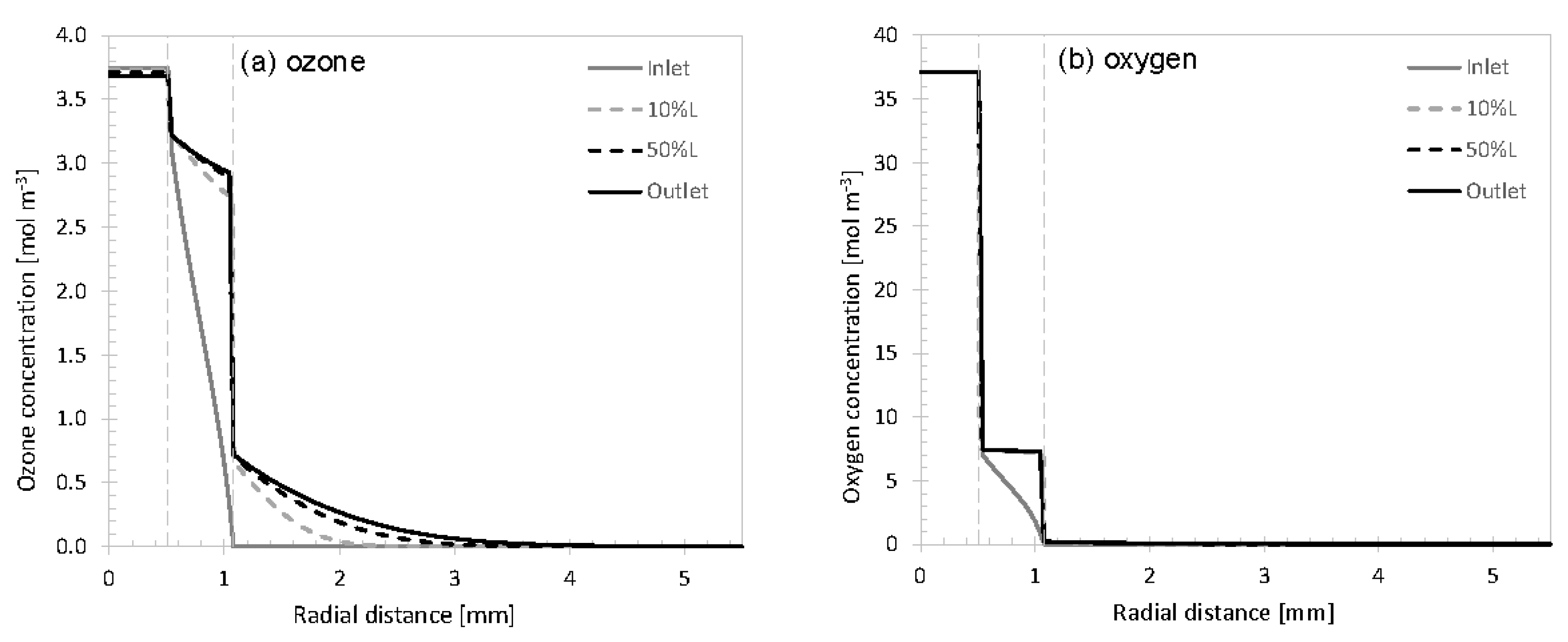
3.1. Concentration Profiles
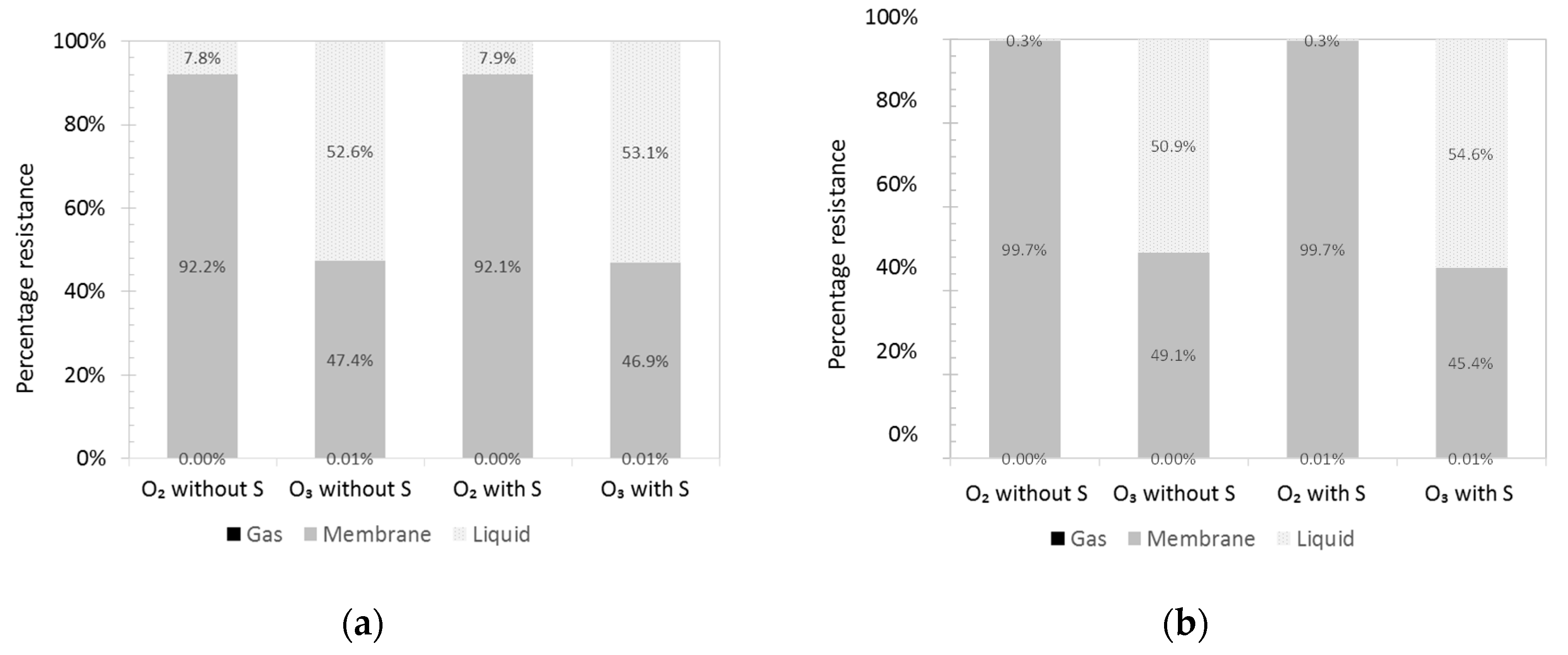
3.2. Variation of Model Parameters
3.2.1. Tube Length
3.2.2. Membrane Thickness
3.2.3. Liquid Side Velocity
3.3. Mass Transfer Correlation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Nomenclature | ||
| a | Interfacial surface area of membrane per unit volume of liquid | m2 m−3 |
| C | Concentration | mol m−3 |
| D | Diffusivity | m2 s−1 |
| H | Henry’s Law constant | - |
| k | Mass transfer coefficient | m s−1 |
| KL | Overall mass transfer coefficient | m s−1 |
| L | Length | m |
| N | Molar flux | mol m−2 s−1 |
| p | Pressure | Pa |
| r | Radial coordinate | m |
| R | Mass transfer resistance | m s−1 |
| R | Radius | m |
| Ri | Inner membrane radius | m |
| Rg | Universal gas constant | J mol−1 K−1 |
| Re | Reynold’s Number | - |
| S | Solubility coefficient | - |
| Si, o3 | Solubility of ozone in PDMS = 3.55 × 10−1 [26] | mol m−3 Pa−1 |
| Sc | Schmidt Number | - |
| Sh | Sherwood Number | - |
| T | Temperature | K |
| Qm,o3 | Permeability coefficient of ozone in PDMS = 1.05 × 10−9 [31] | (mol m) m−2 s−1 Pa−1 |
| u | Velocity vector | m s−1 |
| u | Velocity | m s−1 |
| z | Axial coordinate | m |
| μ | Viscosity | Pa s |
| ρ | Density | kg m−3 |
| Subscripts | ||
| c | Characteristic | |
| g | Gas phase | |
| i | Interface | |
| inner | Inner | |
| j | Component j | |
| L | Liquid phase | |
| m | Membrane | |
| mean | Mean or average value | |
| 0 | Inlet | |
| O2 | Oxygen | |
| O3 | Ozone | |
| outer | Outer | |
| Out | Outlet | |
| tot | Total | |
| w | Characteristic length scale of water phase | |
| Acronyms | ||
| CFD | Computational fluid dynamics | |
| PDMS | Polydimethylsiloxane | |
| PTFE | Polytetrafluoroethylene | |
| PVDF | Polyvinylidene difluoride | |
References
- Loeb, B.L.; Thompson, C.M.; Drago, J.; Takahara, H.; Baig, S. Worldwide ozone capacity for treatment of drinking water and wastewater: A review. Ozone Sci. Eng. 2012, 34, 64–77. [Google Scholar] [CrossRef]
- Gottschalk, C.; Libra, J.A.; Saupe, A. Ozonation of Water and Waste Water a Practical Guide to Understanding Ozone and Its Applications, 2nd ed.; Wiley: Weinheim, Germany, 2010; p. 362. [Google Scholar]
- Rakness, K.L. Ozone in Drinking Water Treatment: Process Design, Operation, and Optimization; American Water Works Association: Denver, CO, USA, 2011; p. 305. [Google Scholar]
- Dodd, M.C.; Zuleeg, S.; von Gunten, U.; Pronk, W. Ozonation of source-separated urine for resource recovery and waste minimization: Process modeling, reaction chemistry, and operational considerations. Environ. Sci. Technol. 2008, 42, 9329–9337. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Smith, D.W.; Stanley, S.J. Modeling of dissolved ozone concentration profiles in bubble columns. J. Environ. Eng. 1994, 120, 821–840. [Google Scholar] [CrossRef]
- Zhou, H.; Smith, D.W. Ozone mass transfer in water and wastewater treatment: Experimental observations using a 2d laser particle dynamics analyzer. Water Res. 2000, 34, 909–921. [Google Scholar] [CrossRef]
- Hollender, J.; Zimmermann, S.G.; Koepke, S.; Krauss, M.; McArdell, C.S.; Ort, C.; Singer, H.; von Gunten, U.; Siegrist, H. Elimination of organic micropollutants in a municipal wastewater treatment plant upgraded with a full-scale post-ozonation followed by sand filtration. Environ. Sci. Technol. 2009, 43, 7862–7869. [Google Scholar] [CrossRef] [PubMed]
- Langlais, B.; Reckhow, D.A.; Brink, D.R. Ozone in Water Treatment: Application and Engineering: Cooperative Research Report; CRC Press (Lewis Publishers): Boca Raton, FL, USA, 1991. [Google Scholar]
- Battimelli, A.; Millet, C.; Delgenès, J.P.; Moletta, R. Anaerobic digestion of waste activated sludge combined with ozone post-treatment and recycling. Water Sci. Technol. 2003, 48, 61–68. [Google Scholar] [PubMed]
- Oneby, M.A.; Bromley, C.O.; Borchardt, J.H.; Harrison, D.S. Ozone treatment of secondary effluent at U.S. Municipal wastewater treatment plants. Ozone Sci. Eng. 2010, 32, 43–55. [Google Scholar] [CrossRef]
- Kerry, F.G. Industrial Gas Handbook: Gas Separation and Purification; CRC Press: Boca Raton, FL, USA, 2007; p. 550. [Google Scholar]
- Gabelman, A.; Hwang, S.T. Hollow fiber membrane contactors. J. Membr. Sci. 1999, 159, 61–106. [Google Scholar] [CrossRef]
- Pines, D.S.; Min, K.N.; Ergas, S.J.; Reckhow, D.A. Investigation of an ozone membrane contactor system. Ozone Sci. Eng. 2005, 27, 209–217. [Google Scholar] [CrossRef]
- Drioli, E.; Criscuoli, A.; Curcio, E. Membrane contactors fundamentals, applications and potentialities. In Membrane Science and Technology Series 11; Elsevier: Amsterdam, The Netherlands, 2006; p. 516. [Google Scholar]
- Li, N.N.; Fane, A.G.; Ho, W.S.W.; Matsuura, T. Advanced Membrane Technology and Applications; Wiley-Blackwell: Oxford, UK, 2008; p. 994. [Google Scholar]
- Ismail, A.F.; Khulbe, C.; Matsuura, T. Gas Separation Membranes; Springer: Berlin, Germany, 2015; p. 331. [Google Scholar]
- Mulder, M. Basic Principles of Membrane Technology, 2nd ed.; Kluwer: Dordrecht, The Netherlands; London, UK, 1996; p. 564. [Google Scholar]
- Shen, Z.; Semmens, M.J.; Collins, A.G. A novel approach to ozone—Water mass transfer using hollow—Fiber reactors. Environ. Technol. 1990, 11, 597–608. [Google Scholar] [CrossRef]
- Dos Santos, F.R.A.; Borges, C.P.; da Fonseca, F.V. Polymeric materials for membrane contactor devices applied to water treatment by ozonation. Mater. Res. 2015, 18, 1015–1022. [Google Scholar] [CrossRef]
- Janknecht, P.; Wilderer, P.A.; Picard, C.; Larbot, A. Ozone-water contacting by ceramic membranes. Sep. Purif. Technol. 2001, 25, 341–346. [Google Scholar] [CrossRef]
- Picard, C.; Larbot, A.; Sarrazin, J.; Janknecht, P.; Wilderer, P. Ceramic membranes for ozonation in wastewater treatment. Ann. Chim. Sci. Mater. 2001, 26, 13–22. [Google Scholar] [CrossRef]
- Stylianou, S.K.; Szymanska, K.; Katsoyiannis, I.A.; Zouboulis, A.I. Novel water treatment processes based on hybrid membrane-ozonation systems: A novel ceramic membrane contactor for bubbleless ozonation of emerging micropollutants. J. Chem. 2015, 1–12, 214927. [Google Scholar] [CrossRef]
- Stylianou, S.K.; Kostoglou, M.; Zouboulis, A.I. Ozone mass transfer studies in a hydrophobized ceramic membrane contactor: Experiments and analysis. Ind. Eng. Chem. Res. 2016, 55, 7587–7597. [Google Scholar] [CrossRef]
- Heng, S.; Yeung, K.L.; Djafer, M.; Schrotter, J.C. A novel membrane reactor for ozone water treatment. J. Membr. Sci. 2007, 289, 67–75. [Google Scholar] [CrossRef]
- Atchariyawut, S.; Phattaranawik, J.; Leiknes, T.; Jiraratananon, R. Application of ozonation membrane contacting system for dye wastewater treatment. Sep. Purif. Technol. 2009, 66, 153–158. [Google Scholar] [CrossRef]
- Dingemans, M.; Dewulf, J.; van Hecke, W.; van Langenhove, H. Determination of ozone solubility in polymeric materials. Chem. Eng. J. 2008, 138, 172–178. [Google Scholar] [CrossRef]
- Leiknes, T.; Phattaranawik, J.; Boller, M.; von Gunten, U.; Pronk, W. Ozone transfer and design concepts for nom decolourization in tubular membrane contactor. Chem. Eng. J. 2005, 111, 53–61. [Google Scholar] [CrossRef]
- Bamperng, S.; Suwannachart, T.; Atchariyawut, S.; Jiraratananon, R. Ozonation of dye wastewater by membrane contactor using PVDF and PTFE membranes. Sep. Purif. Technol. 2010, 72, 186–193. [Google Scholar] [CrossRef]
- Jansen, R.H.S.; de Rijk, J.W.; Zwijnenburg, A.; Mulder, M.H.V.; Wessling, M. Hollow fiber membrane contactors—A means to study the reaction kinetics of humic substance ozonation. J. Membr. Sci. 2005, 257, 48–59. [Google Scholar] [CrossRef]
- Shanbhag, P.V.; Guha, A.K.; Sirkar, K.K. Membrane-based ozonation of organic compounds. Ind. Eng. Chem. Res. 1998, 37, 4388–4398. [Google Scholar] [CrossRef]
- Shanbhag, P.V.; Sirkar, K.K. Ozone and oxygen permeation behavior of silicone capillary membranes employed in membrane ozonators. J. Appl. Polym. Sci. 1998, 69, 1263–1273. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Leiknes, T.; Pronk, W. Mass transfer studies in flat-sheet membrane contactor with ozonation. J. Membr. Sci. 2005, 247, 153–167. [Google Scholar] [CrossRef]
- Zhang, J.; Tejada-Martinez, A.E.; Lei, H.; Zhang, Q. Indicators for technological, environmental and economic sustainability of ozone contactors. Water Res. 2016, 101, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Cockx, A.; Do-Quang, Z.; Liné, A.; Roustan, M. Use of computational fluid dynamics for simulating hydrodynamics and mass transfer in industrial ozonation towers. Chem. Eng. Sci. 1999, 54, 5085–5090. [Google Scholar] [CrossRef]
- Ghasem, N.; Al-Marzouqi, M.; Abdul Rahim, N. Modelling of CO2 absorption in a membrane contactor considering solvent evaporation. Sep. Purif. Technol. 2013, 110, 1–10. [Google Scholar] [CrossRef]
- Al-Saffar, H.B.; Ozturk, B.; Hughes, R. A comparison of porous and non-porous gas-liquid membrane contactors for gas separation. Chem. Eng. Res. Des. 1997, 75, 685–692. [Google Scholar] [CrossRef]
- Mansourizadeh, A. Experimental study of CO2 absorption/stripping via PVDF hollow fiber membrane contactor. Chem. Eng. Res. Des. 2012, 90, 555–562. [Google Scholar] [CrossRef]
- Coulson, J.M.; Richardson, J.F. Coulson & Richardson's Chemical Engineering: Fluid Flow, Heat Transfer, and Mass Transfer, 6th ed.; Elsevier (Butterworth-Heinemann): Oxford, UK, 1999; p. 895. [Google Scholar]
- Tu, J.; Yeoh, G.H.; Liu, C. Computational Fluid Dynamics: A Practical Approach; Elsevier (Butterworth-Heinemann): Oxford, UK, 2012; p. 456. [Google Scholar]
- Massman, W.J. A review of the molecular diffusivities of H2O, CO2, CH4, CO, O3, SO2, NH3, N2O, NO, and NO2 in air, O2 and N2 near STP—Polar and polyatomic gases. Atmos. Environ. 1998, 32, 1111–1127. [Google Scholar] [CrossRef]
- Tritton, D.J. Physical Fluid Dynamics; Springer: Dordrecht, The Netherlands, 2012; p. 362. [Google Scholar]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Dhingra, S.S.; Marand, E. Mixed gas transport study through polymeric membranes. J. Membr. Sci. 1998, 141, 45–63. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Oxford, UK, 2007; p. 905. [Google Scholar]
- Bergman, T.L.; Incropera, F.P.; de Witt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Oxford, UK, 2011. [Google Scholar]
- Yampolskii, Y. Polymeric gas separation membranes. Macromolecules 2012, 8, 3298–3311. [Google Scholar] [CrossRef]
- Merle, T.; Pronk, W.; von Gunten, U. MEMBRO3X, a novel combination of a membrane contactor with advanced oxidation (O3/H2O2) for simultaneous micropollutant abatement and bromate minimization. Environ. Sci. Technol. Lett. 2017, 4, 180–185. [Google Scholar] [CrossRef]


| Membrane System | Gases Explored | Main Findings | Reference |
|---|---|---|---|
| PDMS, non-porous, capillary membrane contactor | O2, O3, N2 | Gas permeability, ozone permeability is four times greater than oxygen, PDMS solubility for gases increases after ozone exposure | [31] |
| PTFE, PVDF, porous and nonporous, flat sheet | O3 | Developed mass transfer coefficients and mass transfer correlations | [13] |
| Al2O3 ceramic, porous, tubular membrane contactor | O3 | Developed mass transfer coefficients | [22] |
| PVDF, porous, flat sheet | O3, O2 | Ozone mass transfer coefficient developed indirectly from oxygen transport | [32] |
| Parameter | Value (Range) | Unit | Reference |
|---|---|---|---|
| Inner membrane radius, Ri | 0.51 | mm | Manufacturer information a |
| Membrane thickness, Lm | 0.57 (0.05–4.50) | mm | Manufacturer information a |
| Water layer thickness, LW | 4.42 | mm | Estimated parameter b |
| Membrane length, L | 500 (250–1250) | mm | Study parameter |
| O3 diffusivity in gas phase, Dg,o3 | 1.454 × 10−5 | m2 s−1 | [40] |
| O3 diffusivity in water, DL,o3 | 1.76 × 10−9 | m2 s−1 | [2] |
| O3 diffusivity in the membrane, Dm,o3 | 2.96 × 10−9 | m2 s−1 | Calculated via the PDMS-ozone permeability coefficient Qm,o3 and the solubility coefficient of O3 in PDMS, So3 c |
| O3 membrane permeability, Qm,o3 | 1.05 × 10−12 | mol m−1 s−1 Pa−1 | [31] |
| O2 diffusivity in gas phase, Dg,o2 | 1.862 × 10−5 | m2 s−1 | [41] |
| O2 diffusivity in water, DL,o2 | 2.025 × 10−9 | m2 s−1 | [2] |
| O2 diffusivity in membrane, Dm,o2 | 2.1 × 10−9 | m2 s−1 | [31] |
| O3 inlet concentration in gas, Cg,o3,0 | 3.75 (0.41–6.25) | mol m−3 | Equates to 13% (wt) of ozone in ozonated oxygen under specified temperature and pressure conditions |
| O3 inlet concentration in water, CL,o3,0 | 0 | mol m−3 | Specified parameter |
| O2 inlet concentration in water, CL,o2,0 | 0 | mol m−3 | Specified parameter |
| Average gas velocity, ug,mean | 0.1 | m s−1 | Experimental parameter |
| Average water velocity, uL,mean | 8 × 10−4 (4 × 10−4–0.15) | m s−1 | The flow regime is assumed laminar in this work i.e., simulating the worst case scenario for mass transfer |
| Temperature, T | 298.15 | K | Isothermal condition was assumed throughout |
| Universal gas constant, R | 8.314 | J mol−1 K−1 | |
| Total pressure at gas inlet, ptot | 101325 | Pa | Pressure at inlet is assumed to be atmospheric |
| Total gas concentration at inlet, Ctot | mol m−3 | ||
| O2 inlet concentration in gas, Cg,o2,0 | 37.12 (40.46–34.62) | mol m−3 | |
| O3 solubility in water, Ho3 | 1 × 10−4 RTg | - | [42] |
| O2 solubility in water, Ho2 | 1.2 × 10−5 RTg | - | [42] |
| O3 solubility in PDMS membrane, So3 | 0.881 | - | [26] |
| O2 solubility in PDMS membrane, So2 | 0.201 | - | [31] |
| Membrane System | Correlation | Reference |
|---|---|---|
| PDMS, non-porous, without solubility (S) | This study | |
| PDMS, non-porous, with solubility (S) | This study | |
| Teflon, non-porous, without solubility (S) | [13] | |
| Film model [Heat and mass transfer analogy] | [45] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berry, M.J.; Taylor, C.M.; King, W.; Chew, Y.M.J.; Wenk, J. Modelling of Ozone Mass-Transfer through Non-Porous Membranes for Water Treatment. Water 2017, 9, 452. https://doi.org/10.3390/w9070452
Berry MJ, Taylor CM, King W, Chew YMJ, Wenk J. Modelling of Ozone Mass-Transfer through Non-Porous Membranes for Water Treatment. Water. 2017; 9(7):452. https://doi.org/10.3390/w9070452
Chicago/Turabian StyleBerry, Matthew J., Caitlin M. Taylor, William King, Y. M. John Chew, and Jannis Wenk. 2017. "Modelling of Ozone Mass-Transfer through Non-Porous Membranes for Water Treatment" Water 9, no. 7: 452. https://doi.org/10.3390/w9070452
APA StyleBerry, M. J., Taylor, C. M., King, W., Chew, Y. M. J., & Wenk, J. (2017). Modelling of Ozone Mass-Transfer through Non-Porous Membranes for Water Treatment. Water, 9(7), 452. https://doi.org/10.3390/w9070452







