Daily Based Morgan–Morgan–Finney (DMMF) Model: A Spatially Distributed Conceptual Soil Erosion Model to Simulate Complex Soil Surface Configurations
Abstract
:1. Introduction
- A modified temporal scale of the model from an annual basis to daily basis. This is better suited to regions with intensive seasonal rainfall
- Inclusion of impervious surface covers (e.g., plastic mulching and artificial structures such as concrete ditches and pavements)
- Revision of the effective rainfall equation, the interflow equation, and equations relevant to flow velocity.
2. Model Description
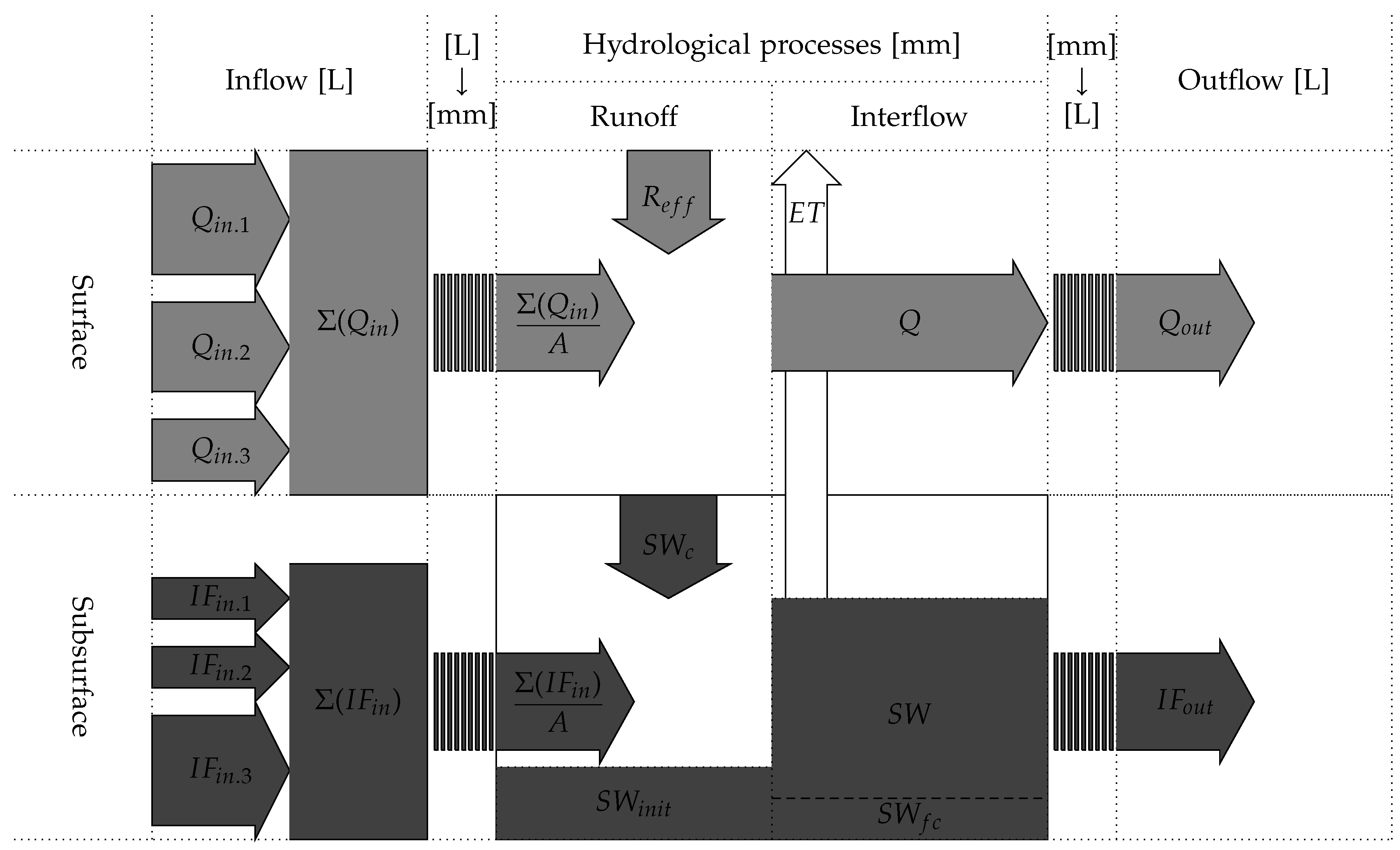
2.1. The DMMF Model
2.2. Hydrological Phase
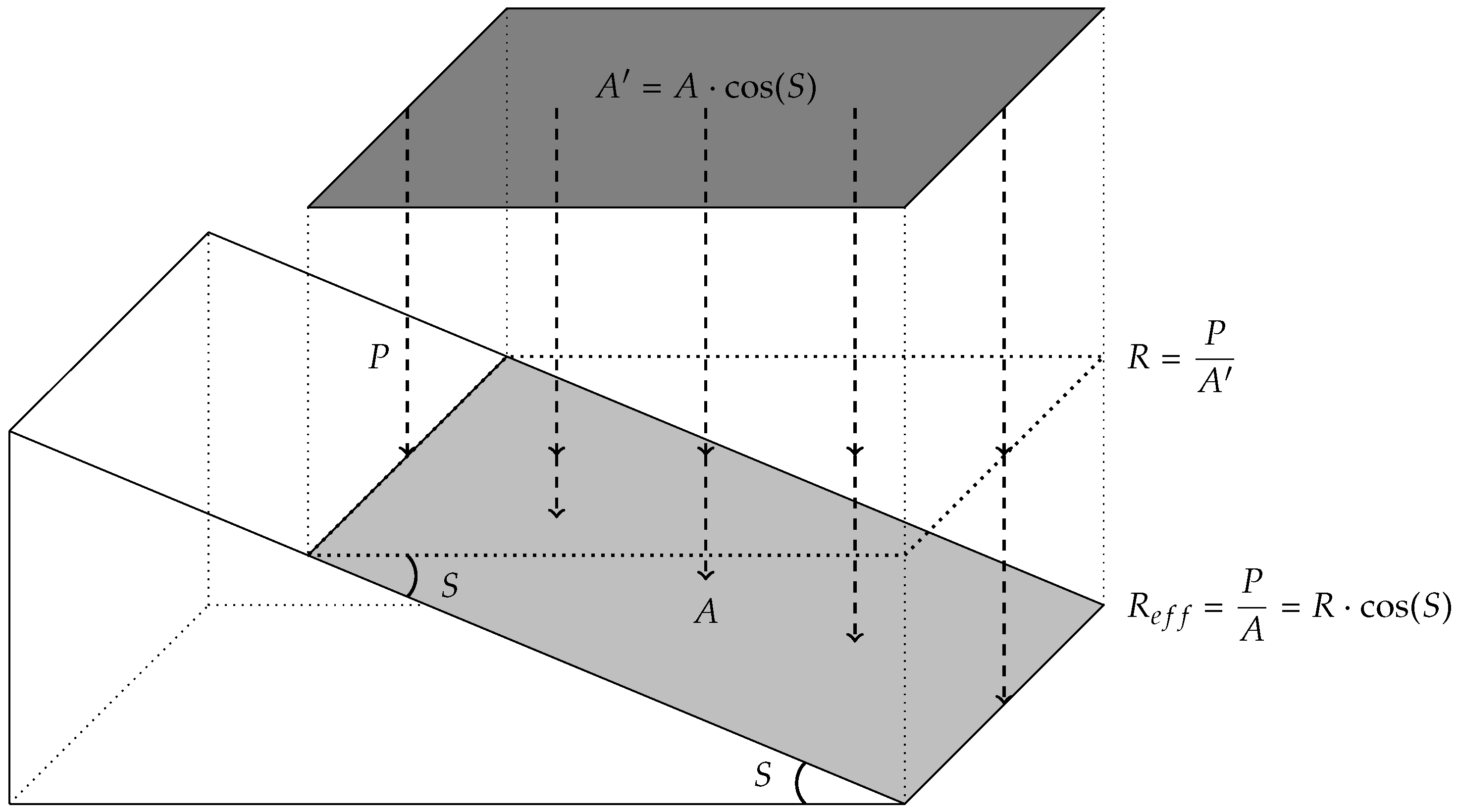
2.2.1. Surface Runoff Process
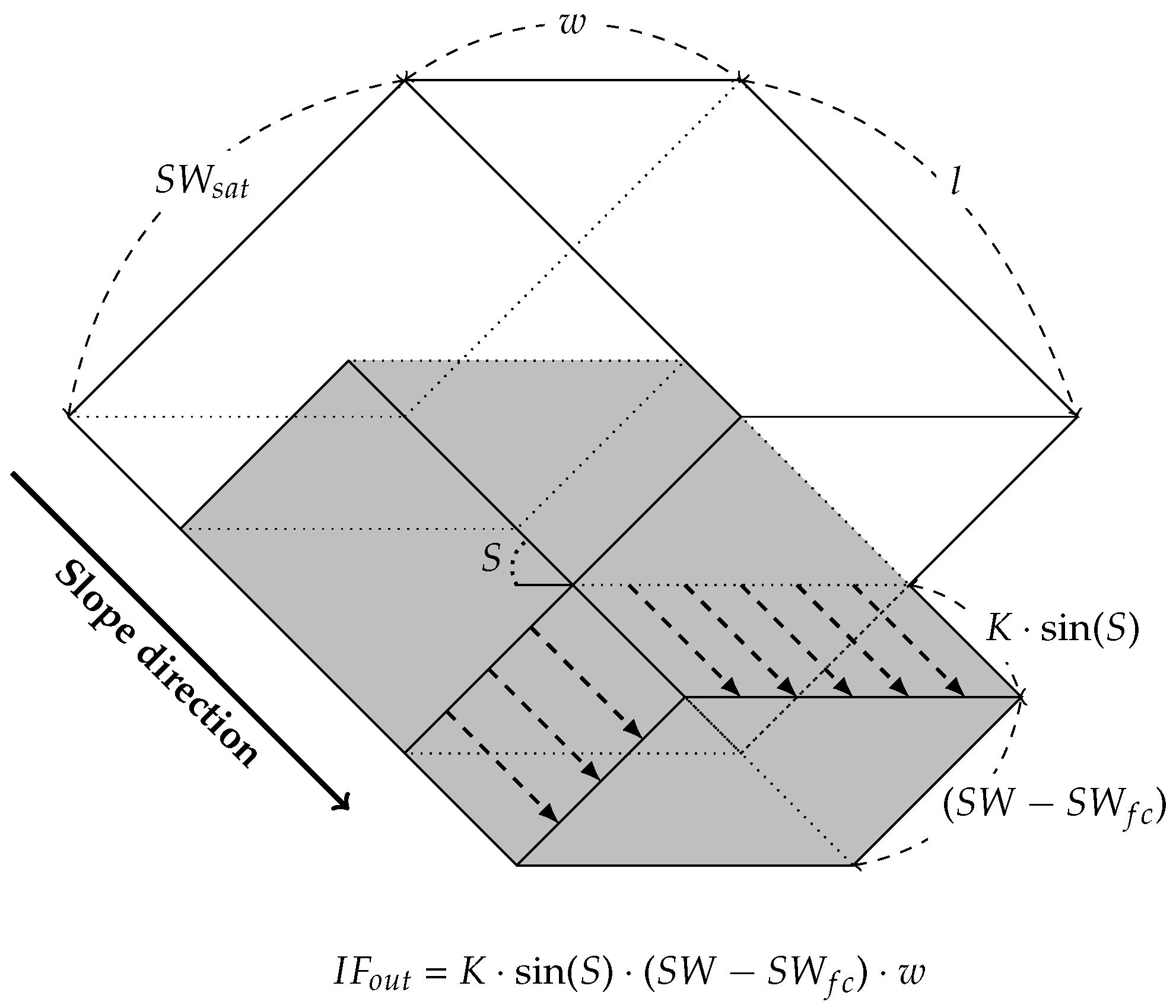
2.2.2. Interflow Process
2.3. Sediment Phase
2.3.1. Sediment Delivery to Surface Runoff
2.3.2. Gravitational Deposition of Suspended Sediments
2.3.3. Estimation of Sediment Loss from an Element
2.4. Estimation of Total Runoff and Soil Erosion for Rainfall Period
3. Testing the DMMF Model
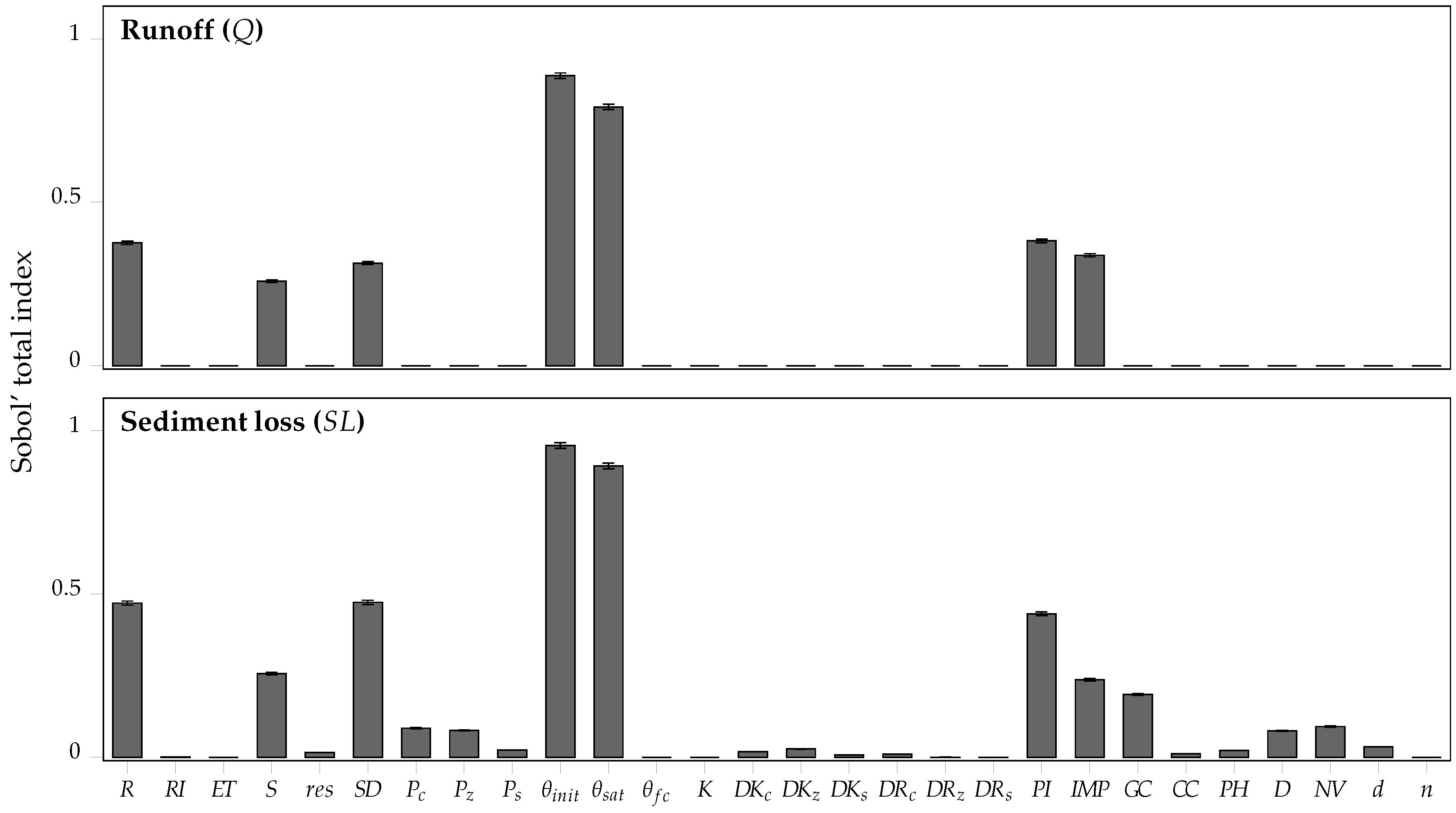
3.1. Sensitivity Analysis of the Model
3.2. Testing the DMMF Model in the Field
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pimentel, D.; Kounang, N. Ecology of soil erosion in ecosystems. Ecosystems 1998, 1, 416–426. [Google Scholar] [CrossRef]
- Sidle, R.C.; Ziegler, A.D.; Negishi, J.N.; Nik, A.R.; Siew, R.; Turkelboom, F. Erosion processes in steep terrain—Truths, myths, and uncertainties related to forest management in Southeast Asia. For. Ecol. Manage. 2006, 224, 199–225. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion and Conservation, 3rd ed.; Blackwell Publishing: Malden, MA, USA, 2005. [Google Scholar]
- Onori, F.; De Bonis, P.; Grauso, S. Soil erosion prediction at the basin scale using the revised universal soil loss equation (RUSLE) in a catchment of Sicily (southern Italy). Environ. Geol. 2006, 50, 1129–1140. [Google Scholar] [CrossRef]
- Napoli, M.; Cecchi, S.; Orlandini, S.; Mugnai, G.; Zanchi, C.A. Simulation of field-measured soil loss in Mediterranean hilly areas (Chianti, Italy) with RUSLE. Catena 2016, 145, 246–256. [Google Scholar] [CrossRef]
- Zema, D.A.; Denisi, P.; Taguas Ruiz, E.V.; Gómez, J.A.; Bombino, G.; Fortugno, D. Evaluation of Surface Runoff Prediction by AnnAGNPS Model in a Large Mediterranean Watershed Covered by Olive Groves. Land Degrad. Dev. 2016, 27, 811–822. [Google Scholar] [CrossRef]
- Huon, S.; Evrard, O.; Gourdin, E.; Lefévre, I.; Bariac, T.; Reyss, J.L.; des Tureaux, T.H.; Sengtaheuanghoung, O.; Ayrault, S.; Ribolzi, O. Suspended sediment source and propagation during monsoon events across nested sub-catchments with contrasted land uses in Laos. J. Hydrol. Reg. Stud. 2017, 9, 69–84. [Google Scholar] [CrossRef]
- Boardman, J. Soil erosion science: Reflections on the limitations of current approaches. Catena 2006, 68, 73–86. [Google Scholar] [CrossRef]
- Hu, L.J.; Flanagan, D.C. Towards new-generation soil erosion modeling: Building a unified omnivorous model. J. Soil Water Conserv. 2013, 68, 100A–103A. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting rainfall erosion losses—A guide to conservation planning. In Agriculture Handbook; Number 537, United States Department of Agriculture (USDA): Washington, DC, USA, 1978; pp. 1–58. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised universal soil loss equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Williams, J.R. Sediment-yield prediction with Universal Equation using runoff energy factor. In Present and prospective technology for predicting sediment yield and sources: Proceedings of the Sediment-Yield Workshop; United States Department of Agriculture (USDA): New Orleans, LA, USA, 1975; Volume ARS-S-40, pp. 244–252. [Google Scholar]
- Morgan, R.P.C.; Morgan, D.D.V.; Finney, H.J. A predictive model for the assessment of soil erosion risk. J. Agric. Eng. Res. 1984, 30, 245–253. [Google Scholar] [CrossRef]
- Morgan, R.P.C. A simple approach to soil loss prediction: A revised Morgan–Morgan–Finney model. Catena 2001, 44, 305–322. [Google Scholar] [CrossRef]
- Lal, R. Soil degradation by erosion. Land Degrad. Dev. 2001, 12, 519–539. [Google Scholar] [CrossRef]
- Merritt, W.; Letcher, R.; Jakeman, A. A review of erosion and sediment transport models. Environ. Modell. Softw. 2003, 18, 761–799. [Google Scholar] [CrossRef]
- Lilhare, R.; Garg, V.; Nikam, B. Application of GIS-Coupled Modified MMF Model to Estimate Sediment Yield on a Watershed Scale. J. Hydrol. Eng. 2014, 20, C5014002. [Google Scholar] [CrossRef]
- Avwunudiogba, A.; Hudson, P.F. A Review of Soil Erosion Models with Special Reference to the needs of Humid Tropical Mountainous Environments. Eur. J. Sustain. Dev. 2014, 3, 299–310. [Google Scholar] [CrossRef]
- Morgan, R.P.C.; Quinton, J.N.; Smith, R.E.; Govers, G.; Poesen, J.W.A.; Auerswald, K.; Chisci, G.; Torri, D.; Styczen, M.E. The European Soil Erosion Model (EUROSEM): A dynamic approach for predicting sediment transport from fields and small catchments. Earth Surf. Processes Landforms 1998, 23, 527–544. [Google Scholar] [CrossRef]
- De Roo, A.P.J.; Wesseling, C.G.; Ritsema, C.J. LISEM: A single-event physically based hydrological and soil erosion model for drainage basins. I: Theory, Input and Output. Hydrol. Processes 1996, 10, 1107–1117. [Google Scholar] [CrossRef]
- von Werner, M. GIS-orientierte Methoden der digitalen Reliefanalyse zur Modellierung von Bodenerosion in kleinen Einzugsgebieten. Ph.D. Thesis, Department of Earth Sciences, Free University of Berlin, Berlin, Germany, 1995. [Google Scholar]
- Nearing, M.A.; Foster, G.R.; Lane, L.J.; Finkner, S.C. A process-based soil erosion model for USDA-Water Erosion Prediction Project technology. Trans. ASAE 1989, 32, 1587–1593. [Google Scholar] [CrossRef]
- Beasley, D.B.; Huggins, L.F.; Monke, E.J. ANSWERS: A Model for Watershed Planning. Trans. ASAE 1980, 23, 938–944. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Bergström, S.; Forsman, A. Development of a conceptual deterministic rainfall-runoff model. Nord. Hydrol. 1973, 4, 147–170. [Google Scholar]
- Devia, G.K.; Ganasri, B.; Dwarakish, G. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Morgan, R.P.C.; Duzant, J.H. Modified MMF (Morgan–Morgan–Finney) model for evaluating effects of crops and vegetation cover on soil erosion. Earth Surf. Processes Landforms 2008, 32, 90–106. [Google Scholar] [CrossRef]
- De Jong, S.M.; Paracchini, M.L.; Bertolo, F.; Folving, S.; Megier, J.; De Roo, A.P.J. Regional assessment of soil erosion using the distributed model SEMMED and remotely sensed data. Catena 1999, 37, 291–308. [Google Scholar] [CrossRef]
- Vigiak, O.; Okoba, B.O.; Sterk, G.; Groenenberg, S. Modelling catchment-scale erosion patterns in the East African Highlands. Earth Surf. Processes Landforms 2005, 30, 183–196. [Google Scholar] [CrossRef]
- López-Vicente, M.; Navas, A.; Machín, J. Modelling soil detachment rates in rainfed agrosystems in the south-central Pyrenees. Agric. Water Manage. 2008, 95, 1079–1089. [Google Scholar] [CrossRef]
- Vieira, D.C.S.; Prats, S.A.; Nunes, J.P.; Shakesby, R.A.; Coelho, C.O.A.; Keizer, J.J. Modelling runoff and erosion, and their mitigation, in burned Portuguese forest using the revised Morgan–Morgan–Finney model. For. Ecol. Manage. 2014, 314, 150–165. [Google Scholar] [CrossRef]
- Baartman, J.E.; Jetten, V.G.; Ritsema, C.J.; de Vente, J. Exploring effects of rainfall intensity and duration on soil erosion at the catchment scale using openLISEM: Prado catchment, SE Spain. Hydrol. Processes 2012, 26, 1034–1049. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Alexander, L.V.; Allen, S.K.; Bindoff, N.L.; Bréon, F.M.; Church, J.A.; Cubasch, U.; Emori, S.; et al. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; chapter Technical Summary; pp. 33–115. [Google Scholar]
- Espí, E.; Salmerón, A.; Fontecha, A.; García, Y.; Real, A.I. Plastic Films for Agricultural Applications. J. Plast. Film Sheeting 2006, 22, 85–102. [Google Scholar] [CrossRef]
- Shuster, W.D.; Bonta, J.; Thurston, H.; Warnemuende, E.; Smith, D.R. Impacts of impervious surface on watershed hydrology: A review. Urban Water J. 2005, 2, 263–275. [Google Scholar] [CrossRef]
- Pappas, E.A.; Smith, D.R.; Huang, C.; Shuster, W.D.; Bonta, J.V. Impervious surface impacts to runoff and sediment discharge under laboratory rainfall simulation. Catena 2008, 72, 146–152. [Google Scholar] [CrossRef]
- Arnhold, S.; Ruidisch, M.; Bartsch, S.; Shope, C.; Huwe, B. Simulation of runoff patterns and soil erosion on mountainous farmland with and without plastic-covered ridge-furrow cultivation in South Korea. Trans. ASABE 2013, 56, 667–679. [Google Scholar] [CrossRef]
- Ruidisch, M.; Kettering, J.; Arnhold, S.; Huwe, B. Modeling water flow in a plastic mulched ridge cultivation system on hillslopes affected by South Korean summer monsoon. Agric. Water Manage. 2013, 116, 204–217. [Google Scholar] [CrossRef]
- Choi, K.; Huwe, B.; Reineking, B. Commentary on ‘Modified MMF (Morgan–Morgan–Finney) model for evaluating effects of crops and vegetation cover on soil erosion’ by Morgan and Duzant (2008). Available online: https://arxiv.org/abs/1612.08899 (accessed on 13 April 2017).
- Kirkby, M.J. Hydrological Slope Models: The Influence of Climate. In Geomorphology and Climate; Derbyshire, E., Ed.; Wiley: London, UK, 1976; pp. 247–267. [Google Scholar]
- Petryk, S.; Bosmajian, G. Analysis of flow through vegetation. ASCE J. Hydraul. Div. 1975, 101, 871–884. [Google Scholar]
- Veihmeyer, F.J.; Hendrickson, A.H. The moisture equivalent as a measure of the field capacity of soils. Soil Sci. 1931, 32, 181–194. [Google Scholar] [CrossRef]
- Meyer, L.D.; Wischmeier, W.H. Mathematical simulation of the process of soil erosion by water. Trans. ASAE 1969, 12, 754–758. [Google Scholar]
- Brandt, C.J. Simulation of the size distribution and erosivity of raindrops and throughfall drops. Earth Surf. Processes Landforms 1990, 15, 687–698. [Google Scholar] [CrossRef]
- Shin, S.S.; Park, S.D.; Choi, B.K. Universal Power Law for Relationship between Rainfall Kinetic Energy and Rainfall Intensity. Adv. Meteorol. 2016, 2016, 2494681. [Google Scholar] [CrossRef]
- Poesen, J. An improved splash transport model. Z. Geomorphol. 1985, 29, 193–211. [Google Scholar]
- Tollner, E.W.; Barfield, B.J.; Haan, C.T.; Kao, T.Y. Suspended Sediment Filtration Capacity of Simulated Vegetation. Trans. ASAE 1976, 19, 678–682. [Google Scholar] [CrossRef]
- Sobol’, I. Sensitivity Analysis for Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, C.; Chu, J.; Zhou, H. Sobol’ ’s sensitivity analysis for TOPMODEL hydrological model: A case study for the Biliu River Basin, China. J. Hydrol. Environ. Res. 2013, 1, 1–10. [Google Scholar]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Modell. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Modell. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Pujol, G.; Iooss, B.; Janon, A.; Boumhaout, K.; Da Veiga, S.; Fruth, J.; Gilquin, L.; Guillaume, J.; Le Gratiet, L.; Lemaitre, P.; et al. Sensitivity: Global Sensitivity Analysis of Model Outputs, R package version 1.12.1; Available online: https://CRAN.R-project.org/package=sensitivity (accessed on 15 May 2016).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- World Meteorological Organization’s World Weather & Climate Extremes Archive. Available online: wmo.asu.edu/content/world-meteorological-organization-global-weather-climate-extremes-archive (accessed on 16 November 2016).
- Senay, G.; Verdin, J.; Lietzow, R.; Melesse, A. Global Daily Reference Evapotranspiration Modeling and Evaluation. J. Am. Water Resour. Assoc. 2008, 44, 969–979. [Google Scholar] [CrossRef]
- Jia, L.; Xi, G.; Liu, S.; Huang, C.; Yan, Y.; Liu, G. Regional estimation of daily to annual regional evapotranspiration with MODIS data in the Yellow River Delta wetland. Hydrol. Earth Syst. Sci. 2009, 13, 1775–1787. [Google Scholar] [CrossRef]
- Pandey, A.; Mathur, A.; Mishra, S.K.; Mal, B.C. Soil erosion modeling of a Himalayan watershed using RS and GIS. Environ. Earth Sci. 2009, 59, 399–410. [Google Scholar] [CrossRef]
- Canadell, J.; Jackson, R.B.; Ehleringer, J.B.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. Maximum rooting depth of vegetation types at the global scale. Oecologia 1996, 108, 583–595. [Google Scholar] [CrossRef] [PubMed]
- Saxton, K.E.; Rawls, W.J.; Romberger, J.S.; Papendick, R.I. Estimating generalized soil-water characteristics from texture. Soil Sci. Soc. Am. J. 1986, 50, 1031–1036. [Google Scholar] [CrossRef]
- Irmay, S. Hydrodynamics in soils. In Physical Principles of Water Percolation and Seepage; Bear, J., Zaslavsky, D., Irmay, S., Eds.; UNESCO: Paris, France, 1968; Volume 29, p. 60. [Google Scholar]
- MODIS Collection 5 Land Products Global Subsetting and Visualization Tool; ORNL DAAC: Oak Ridge, TN, USA, 2009; Available online: http://dx.doi.org/10.3334/ORNLDAAC/1241 (accessed on 22 September 2015).
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Brooks, E.S.; Boll, J.; McDaniel, P.A. A hillslope-scale experiment to measure lateral saturated hydraulic conductivity. Water Resour. Res. 2004, 40, W04208. [Google Scholar] [CrossRef]
- Boll, J.; Brooks, E.S.; Campbell, C.R.; Stockle, C.O.; Young, S.K.; Hammel, J.E.; McDaniel, P.A. Progress toward development of a GIS based water quality management tool for small rural watersheds: Modification and application of a distributed model. In Proceedings of the ASAE Annual International Meeting, Orlando, FL, USA, 12–16 July 1998. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Global Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Ardia, D.; Mullen, K.M.; Peterson, B.G.; Ulrich, J. DEoptim: Differential Evolution in R, R package version 2.2-3; Available online: http://CRAN.R-project.org/package=DEoptim (accessed on 11 November 2016).
- Mullen, K.; Ardia, D.; Gil, D.; Windover, D.; Cline, J. DEoptim: An R Package for Global Optimization by Differential Evolution. J. Stat. Softw. 2011, 40, 1–26. [Google Scholar] [CrossRef]
- Joseph, J.; Guillaume, J. Using a parallelized MCMC algorithm in R to identify appropriate likelihood functions for SWAT. Environ. Modell. Softw. 2013, 46, 292–298. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.C.; Simpson, A.R. Investigating the run-time searching behavior of the differential evolution algorithm applied to water distribution system optimization. Environ. Modell. Softw. 2015, 69, 292–307. [Google Scholar] [CrossRef]
- Quansah, C. Laboratory Experimentation for the Statistical Derivation of Equations for Soil Erosion Modelling and Soil Conservation Design. Ph.D. Thesis, Cranfield Institute of Technology, England, UK, April 1982. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Panagos, P.; Liedekerke, M.V.; Jones, A.; Montanarella, L. European Soil Data Centre: Response to European policy support and public data requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]

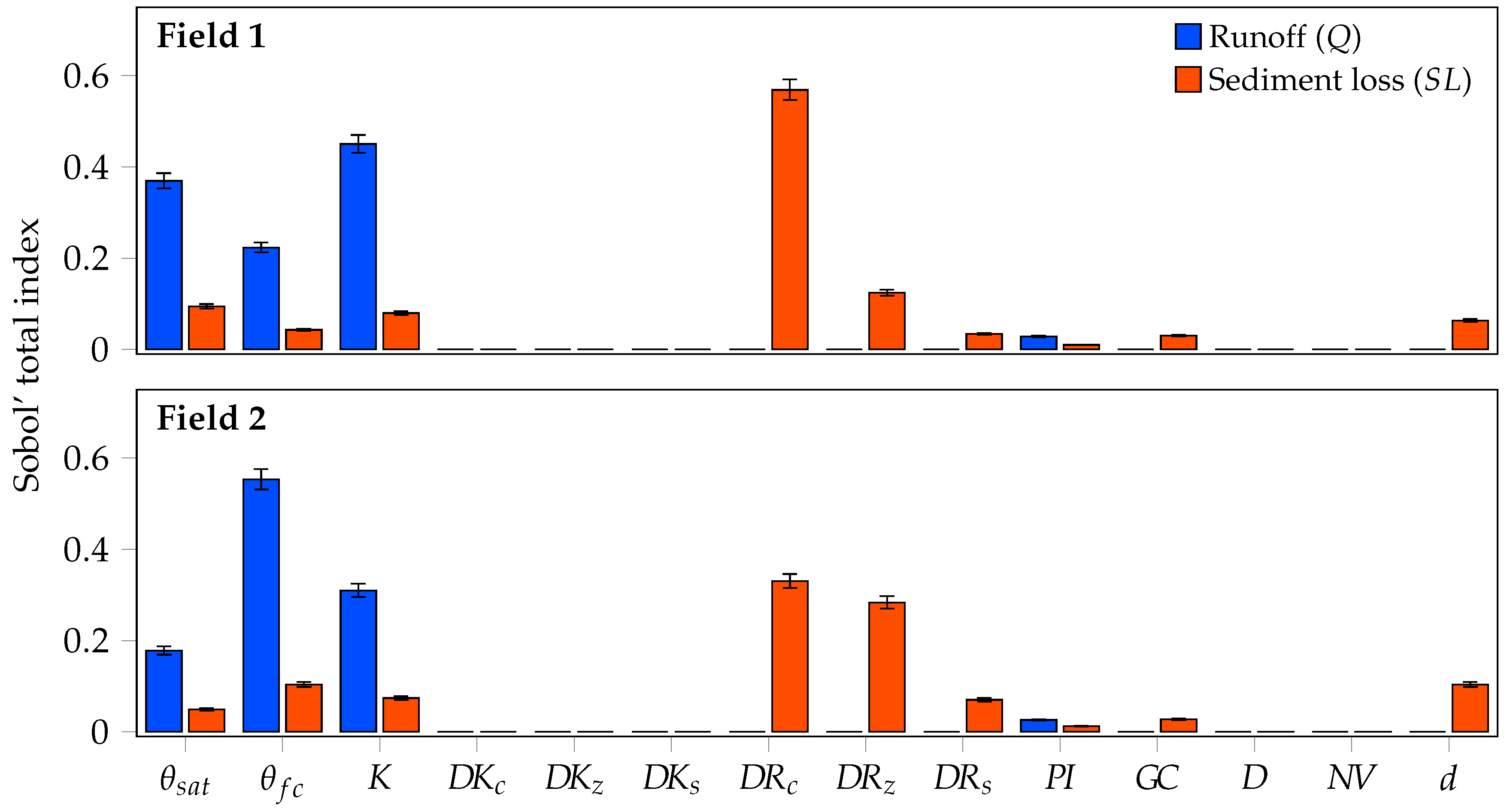
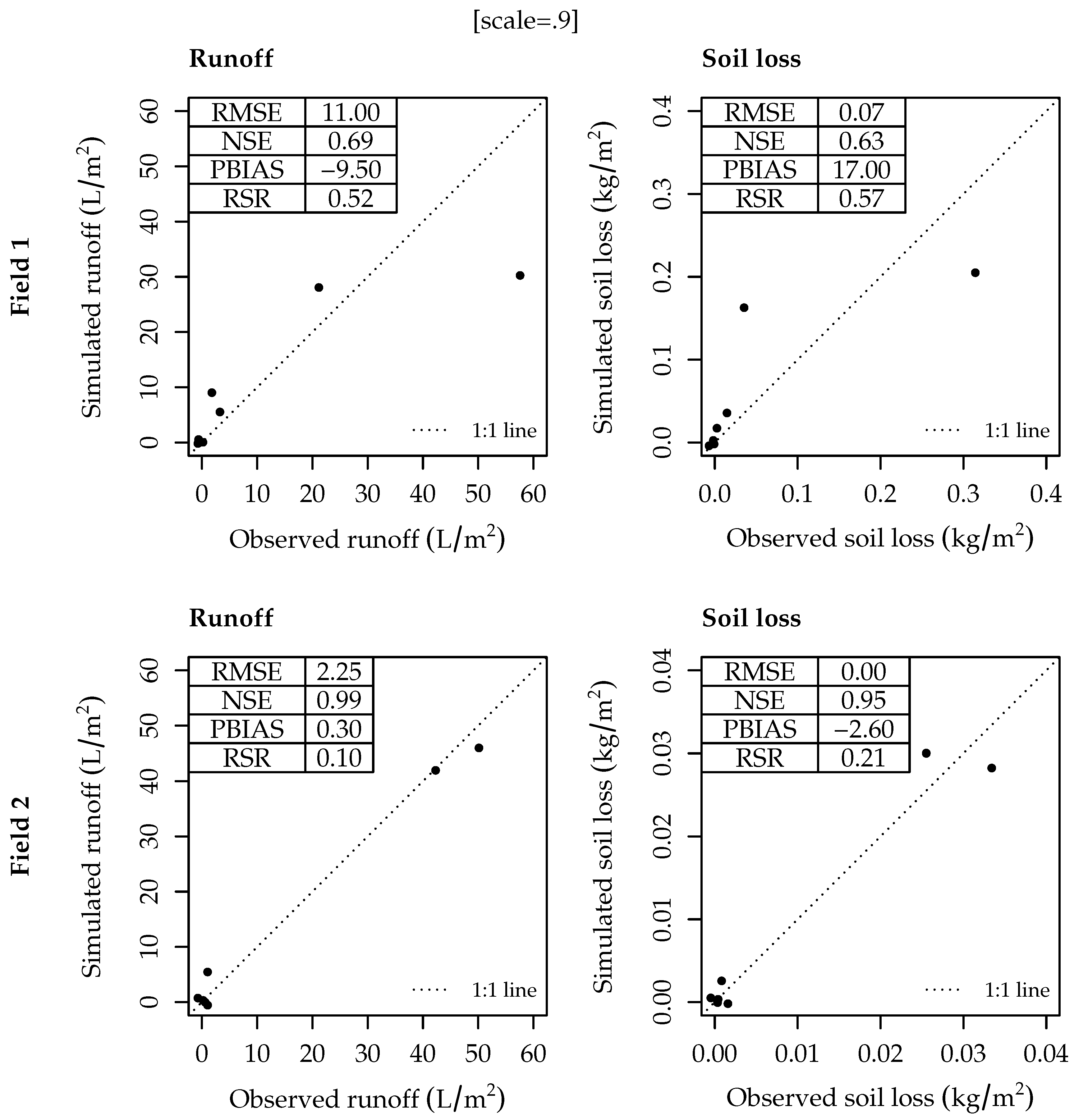
| Parameter | Description | Unit | Range |
|---|---|---|---|
| R | Daily rainfall | [mm] | 1–1825 (a) |
| Mean rainfall intensity of a day | [mm ] | 15.0–305.0 (a) | |
| Daily evapotranspiration | [mm] | 0.0–15.0 (b) | |
| S | Slope angle | [] | 0.0–1.5 (c) |
| Grid size of a raster map for the width (w) and the length (l)of an element that are equal to and | [] | 0.25–100 (d) | |
| Proportion of clay of the surface soil | [proportion] | 0–1 | |
| Proportion of silt of the surface soil | [proportion] | 0–1 | |
| Proportion of sand of the surface soil | [proportion] | 0–1 | |
| Soil depth | [] | 0.3–68.0 (e) | |
| Initial soil water content of entire soil profile | [] | 0.00– (f) | |
| Saturated water content of entire soil profile | [] | 0.31–0.56 (f) | |
| Soil water content at field capacity of entire soil profiles | [] | 0.10– (f) | |
| K | Saturated soil lateral hydraulic conductivity | [] | 1–230 (g) |
| Detachability of clay particles by rainfall | [] | 0.10–1.50 (h) | |
| Detachability of silt particles by rainfall | [] | 0.50–5.15 (h) | |
| Detachability of sand particles by rainfall | [] | 0.15–4.15 (h) | |
| Detachability of clay particles by surface runoff | [] | 0.020–2.0 (h) | |
| Detachability of silt particles by surface runoff | [] | 0.016–1.6 (h) | |
| Detachability of sand particles by surface runoff | [] | 0.015–1.5 (h) | |
| Area proportion of the permanent interception of rainfall | [proportion] | 0–1 | |
| Area proportion of the impervious ground cover | [proportion] | 0–1 | |
| Area proportion of the ground cover of the soil surfaceprotected by vegetation or crop cover on the ground | [proportion] | 0–1 | |
| Area proportion of the canopy cover of the soil surfaceprotected by vegetation or crop canopy | [proportion] | 0–1 | |
| Average height of vegetation or crop cover of an elementwhere leaf drainage starts to fall | [] | 0–30 (h) | |
| D | Average diameter of individual plant elements at the surface | [] | 0.00001–3.0 (h) |
| Number of individual plant elements per unit area | [] | 0.00001–2000 (h) | |
| d | Typical flow depth of surface runoff in an element | [] | 0.005–3 (h) |
| n | Manning’s roughness coefficient of the soil surface | [] | 0.01–0.05 (i) |
| Field | K | D | d | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Field 1 | Sup. | 0.454 | 0.351 | 17.9 | 0.144 | 0.48 | 5.4 | 0.12 | 1.50 | 5.15 | 4.15 | 2.0 | 1.6 | 1.5 | 0.010 |
| Inf. | 0.351 | 0.345 | 0.29 | 0.096 | 0.32 | 3.6 | 0.08 | 0 | 0 | 0 | 0 | 0 | 0 | 0.005 | |
| Field 2 | Sup. | 0.494 | 0.435 | 5.22 | 0.144 | 0.48 | 5.4 | 0.12 | 1.50 | 5.15 | 4.15 | 2.0 | 1.6 | 1.5 | 0.010 |
| Inf. | 0.435 | 0.407 | 0.15 | 0.096 | 0.32 | 3.6 | 0.08 | 0 | 0 | 0 | 0 | 0 | 0 | 0.005 |
| K | d | ||||||
|---|---|---|---|---|---|---|---|
| Field 1 | 0.500 | 0.362 | 0.345 | 0.015 | 0.012 | 0.011 | 0.010 |
| Field 2 | 0.284 | 0.453 | 0.435 | 0.007 | 0.005 | 0.005 | 0.005 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, K.; Arnhold, S.; Huwe, B.; Reineking, B. Daily Based Morgan–Morgan–Finney (DMMF) Model: A Spatially Distributed Conceptual Soil Erosion Model to Simulate Complex Soil Surface Configurations. Water 2017, 9, 278. https://doi.org/10.3390/w9040278
Choi K, Arnhold S, Huwe B, Reineking B. Daily Based Morgan–Morgan–Finney (DMMF) Model: A Spatially Distributed Conceptual Soil Erosion Model to Simulate Complex Soil Surface Configurations. Water. 2017; 9(4):278. https://doi.org/10.3390/w9040278
Chicago/Turabian StyleChoi, Kwanghun, Sebastian Arnhold, Bernd Huwe, and Björn Reineking. 2017. "Daily Based Morgan–Morgan–Finney (DMMF) Model: A Spatially Distributed Conceptual Soil Erosion Model to Simulate Complex Soil Surface Configurations" Water 9, no. 4: 278. https://doi.org/10.3390/w9040278
APA StyleChoi, K., Arnhold, S., Huwe, B., & Reineking, B. (2017). Daily Based Morgan–Morgan–Finney (DMMF) Model: A Spatially Distributed Conceptual Soil Erosion Model to Simulate Complex Soil Surface Configurations. Water, 9(4), 278. https://doi.org/10.3390/w9040278






