Comparison of IMERG Level-3 and TMPA 3B42V7 in Estimating Typhoon-Related Heavy Rain
Abstract
:1. Introduction
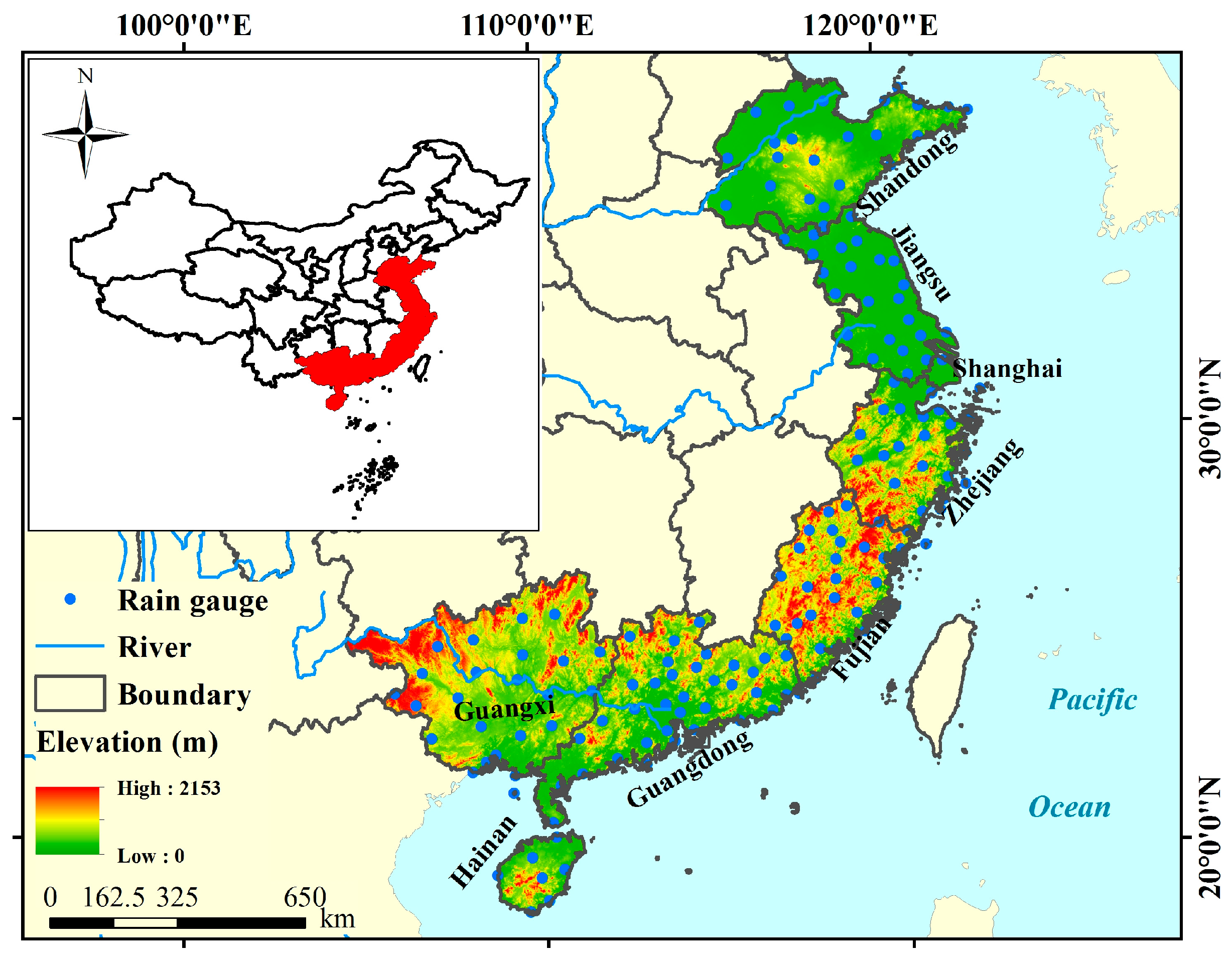
2. Study Area and Datasets
2.1. Study Area
2.2. Typhoon Events
2.3. Gauge Observations
2.4. TMPA 3B42V7
2.5. IMERG Final Run
3. Methods
4. Results
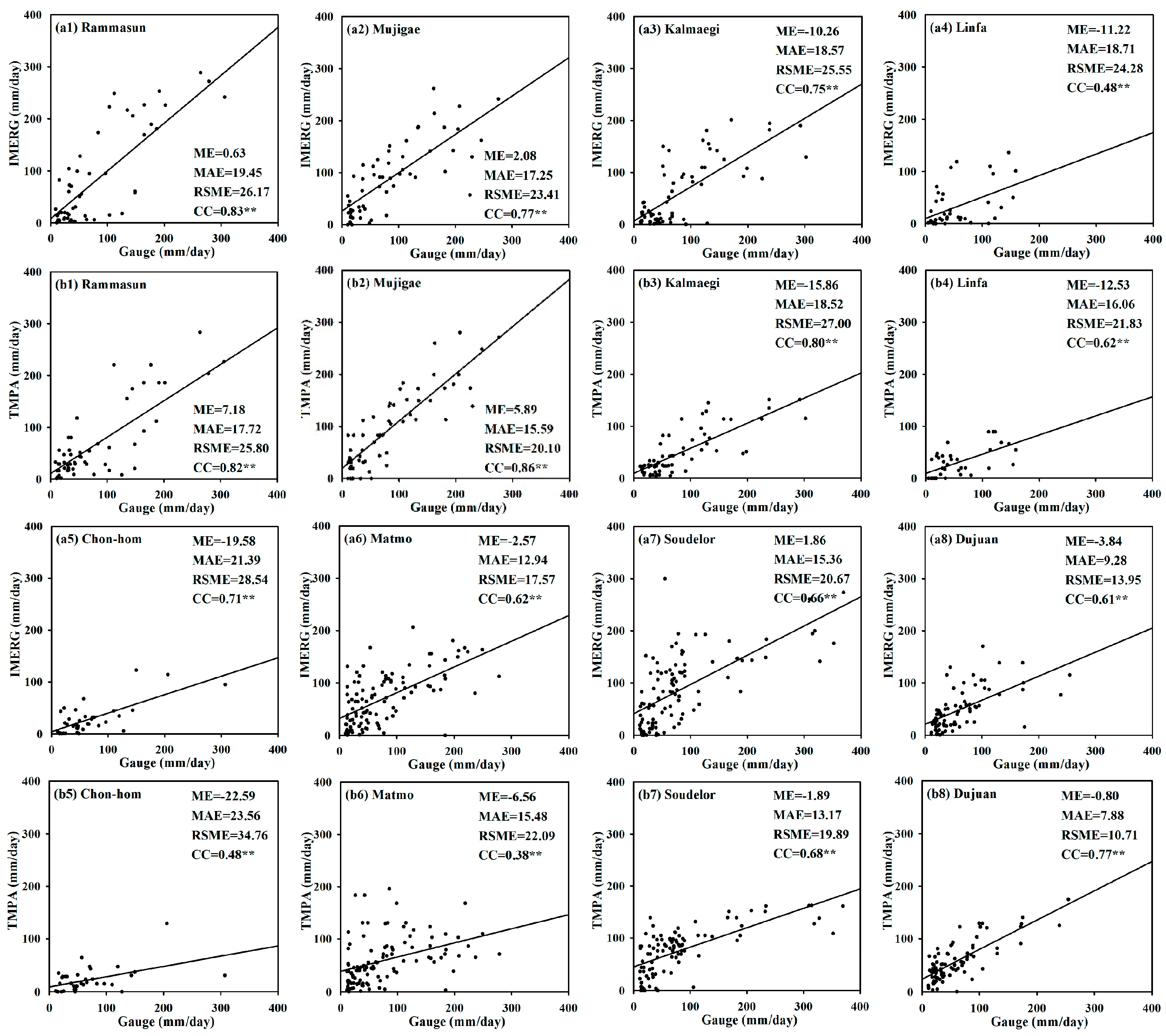
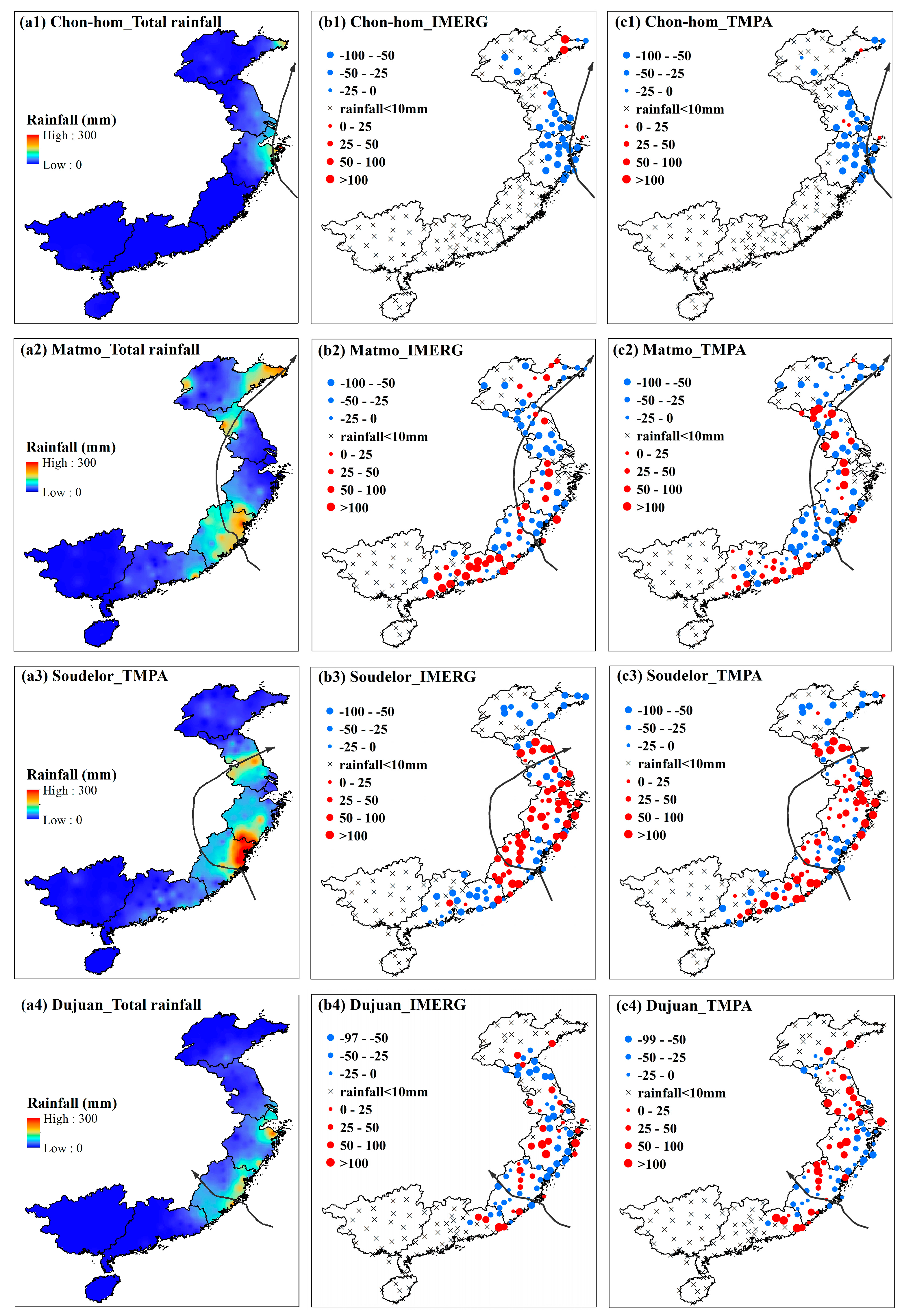
4.1. Characteristics of the Metrics
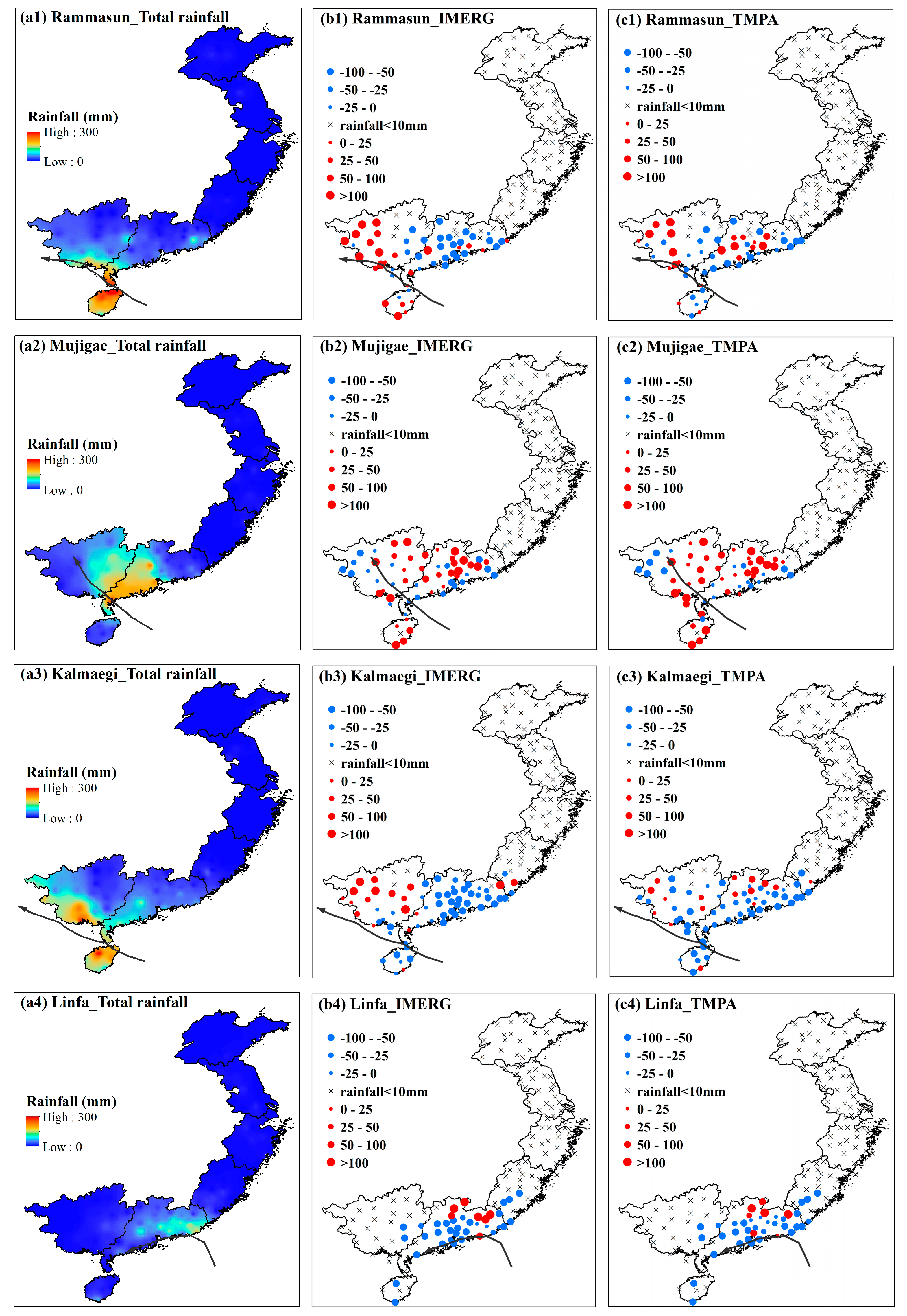
4.2. Applicability Associated with Rain Intensity and Typhoon Track
5. Discussion
6. Summary
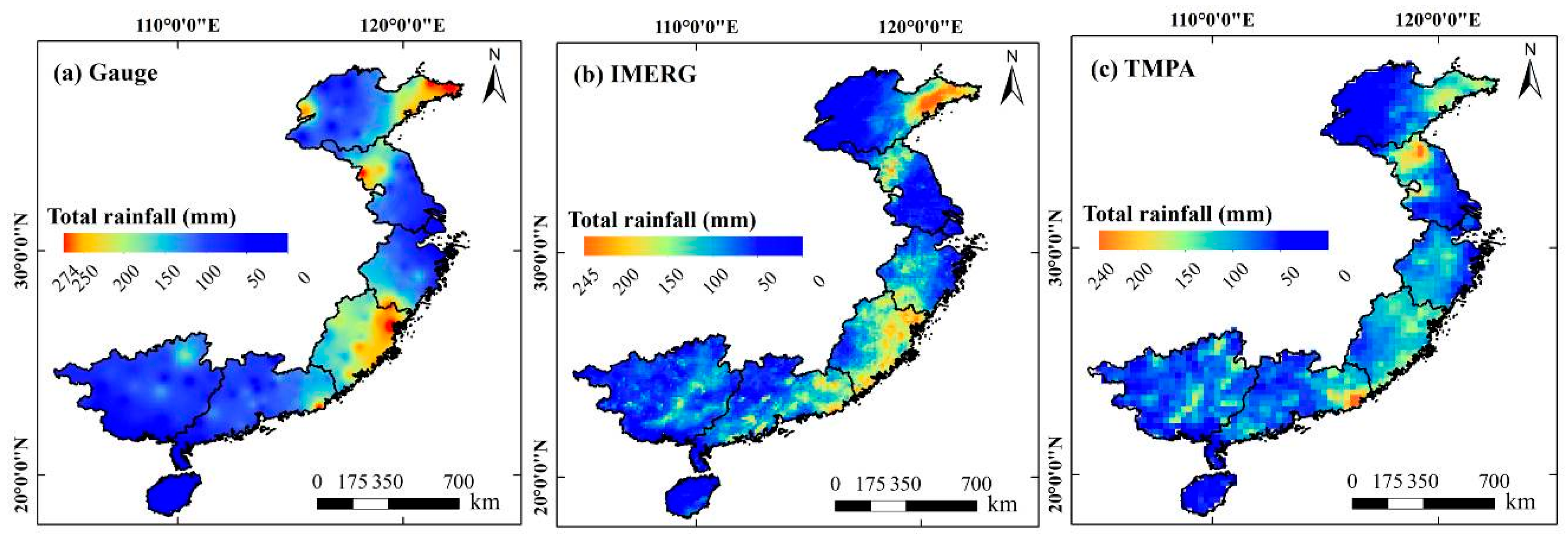
- All correlation coefficients (CCs) both of IMERG and TMPA for the investigated typhoon events are significant at the 0.01 level, but they tend to underestimate a total amount of heavy rainfall, especially around the storm center.
- The IMERG final run shows an overall better performance than TMPA 3B42V7.
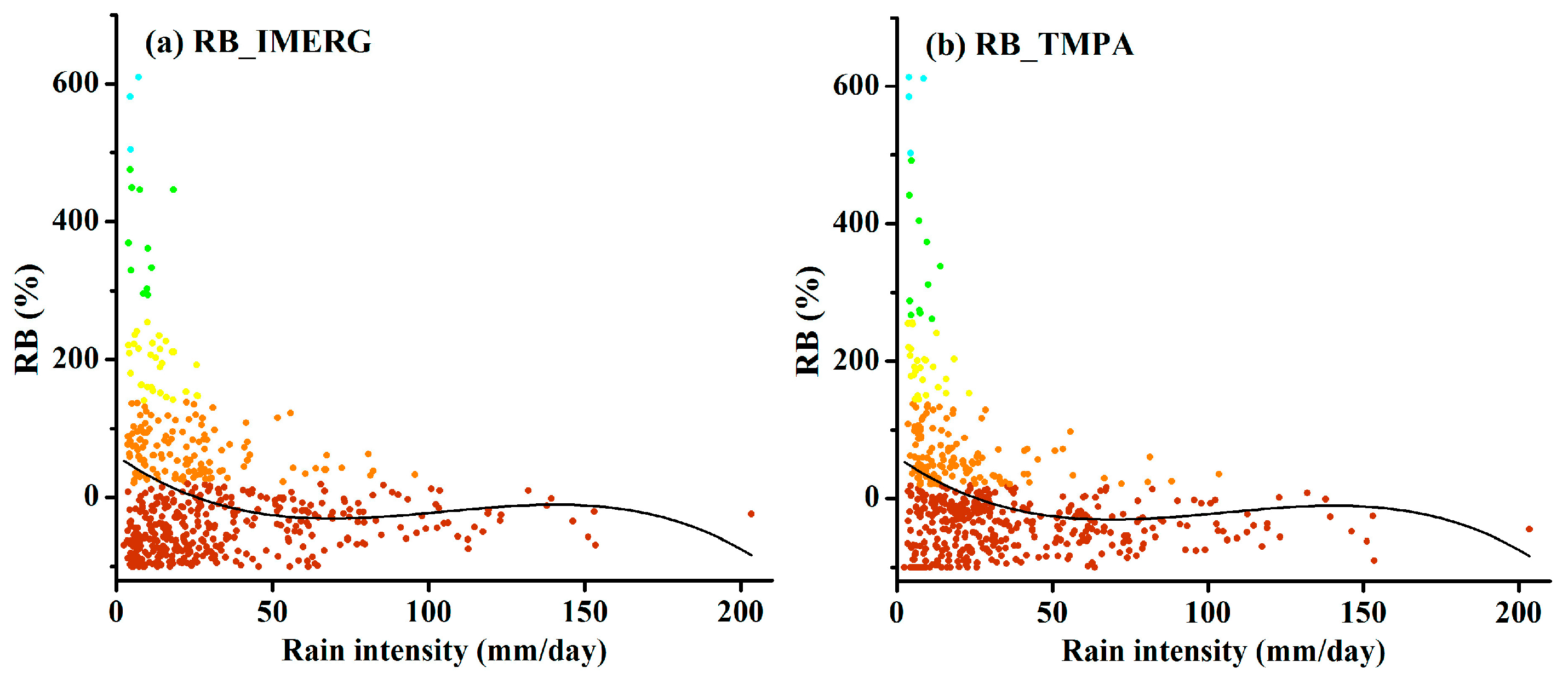
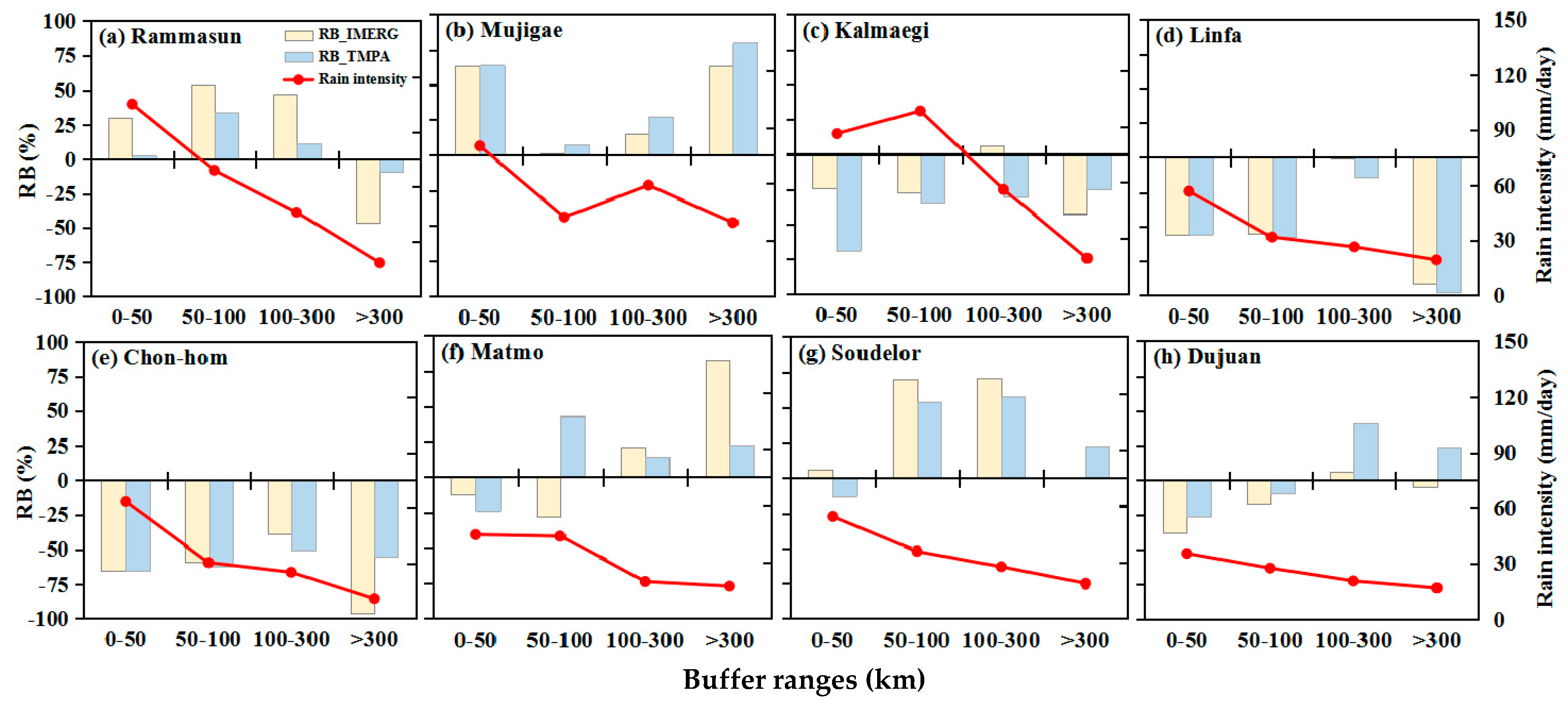
- Both IMERG and TMPA exhibit a better performance (i.e., smaller absolute RB) when rain intensities are within 20–40 and 80–100 mm/day than those of 40–80 mm/day and larger than 100 mm/day. Meanwhile, both products generally have the best applicability in the range of 50–100 km away from typhoon tracks, and have the worst applicability beyond a 300-km range.
- It needs to be emphasized that the study lacks physical insights to strengthen the statistical analysis. Future works, which will be devoted to further understand the limits of the applicability and accuracy of such satellite products in monitoring typhoon rainfall, should be focused on the physical process of typhoon rainfall, with consideration for the moving speed and direction of the typhoon, and the underlying topography.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.Q. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Ban, N.; Schmidli, J.; Schar, C. Heavy precipitation in a changing climate: Does short-term summer precipitation increase faster? Geophys. Res. Lett. 2015, 42, 1165–1172. [Google Scholar] [CrossRef]
- Yang, T.H.; Yang, S.C.; Ho, J.Y.; Lin, G.F.; Hwang, G.D.; Lee, C.S. Flash flood warnings using the ensemble precipitation forecasting technique: A case study on forecasting floods in Taiwan caused by typhoons. J. Hydrol. 2015, 520, 367–378. [Google Scholar] [CrossRef]
- Habib, E.; Henschke, A.; Adler, R.F. Evaluation of TMPA satellite-based research and real-time rainfall estimates during six tropical-related heavy rainfall events over Louisiana, USA. Atmos. Res. 2009, 94, 373–388. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Mazari, N.; Zeitler, J.; Sharif, H.; Hammond, W. Evaluation of a near-real time NEXRAD DSP product in evolution of heavy rain events on the Upper Guadalupe River Basin, Texas. J. Hydroinform. 2013, 15, 464–485. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Pai, D.S. Error characterization of TRMM Multisatellite Precipitation Analysis (TMPA-3B42) products over India for different seasons. J. Hydrol. 2015, 529, 1302–1312. [Google Scholar] [CrossRef]
- Mehran, A.; AghaKouchak, A. Capabilities of satellite precipitation datasets to estimate heavy precipitation rates at different temporal accumulations. Hydrol. Process. 2014, 28, 2262–2270. [Google Scholar] [CrossRef]
- Bharti, V.; Singh, C. Evaluation of error in TRMM 3B42V7 precipitation estimates over the Himalayan region. J. Geophys. Res. 2015, 120, 12458–12473. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Hyun, J.Y.; Rockaway, T.D.; French, M.N. Ground-level rainfall variation in Jefferson County, Kentucky. J. Hydrol. Eng. 2016, 21, 05016029. [Google Scholar] [CrossRef]
- Kitzmiller, D.; Miller, D.; Fulton, R.; Feng, D. Radar and multisensor precipitation estimation techniques in National Weather Service hydrologic operations. J. Hydrol. Eng. 2013, 18, 133–142. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined–sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteor. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Hou, A.Y.; Skofronick-Jackson, G.; Kummerow, C.D.; Shepherd, J.M. Global precipitation measurement. In Precipitation: Advances in Measurement, Estimation and Prediction; Silas, M., Ed.; Springer: Belin/Heidelberg, Germany, 2008; pp. 131–169. [Google Scholar]
- AghaKouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation data sets. Geophys. Res. Lett. 2012, 39, L09406. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nasrollahi, N.; Habib, E. Accounting for uncertainties of the TRMM satellite estimates. Remote Sens. 2009, 1, 606–619. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Yong, B.; Kirstetter, P.E.; Hu, J.; Hardy, J.; et al. Evaluation of the successive V6 and V7 TRMM multisatellite precipitation analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
- Goldstein, A.; Foti, R.; Montalto, F. Effect of spatial resolution in modeling stormwater runoff for an urban block. J. Hydrol. Eng. 2016, 21, 06016009. [Google Scholar] [CrossRef]
- Liao, S.L.; Li, G.; Sun, Q.Y.; Li, Z.F. Real-time correction of antecedent precipitation for the Xinanjiang model using the genetic algorithm. J. Hydroinform. 2016, 18, 803–815. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) Version 4.4 for the NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); NASA: Greenbelt, MD, USA, 2014; pp. 1–30.
- Huffman, G.J.; Bolvin, D.T. TRMM and Other Data Precipitation Data Set Documentation. Available online: ftp://precip.gsfc.nasa.gov/pub/trmmdocs/3B42_3B43_doc.pdf (accessed on 13 April 2017).
- Mitra, A.K.; Momin, I.M.; Rajagopal, E.N.; Basu, S.; Rajeevan, M.N.; Krishnamurti, T.N. Gridded daily Indian monsoon rainfall for 14 seasons: Merged TRMM and IMD gauge analyzed values. J. Earth Syst. Sci. 2013, 122, 1173–1182. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J.; et al. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X. Statistical and hydrological comparisons between TRMM and GPM Level-3 products over a midlatitude basin: Is Day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Chen, F.; Li, X. Evaluation of IMERG and TRMM 3B43 monthly precipitation products over Mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of Integrated Multisatellite Retrievals for GPM (IMERG) and TRMM Multisatellite Precipitation Analysis (TMPA) monthly precipitation products: Initial results. J. Hydrometeorol. 2016, 17, 777–790. [Google Scholar] [CrossRef]
- Sahlu, D.; Nikolopoulos, E.; Moges, S.; Anagnostou, E.; Hailu, D. First evaluation of the Day-1 IMERG over the upper Blue Nile Basin. J. Hydrometeorol. 2016, 17, 2875–2882. [Google Scholar] [CrossRef]
- Wang, D.; Wang, X.; Liu, L.; Wang, D.; Huang, H.; Pan, C. Evaluation of CMPA precipitation estimate in the evolution of typhoon-related storm rainfall in Guangdong, China. J. Hydroinform. 2016, 18, 1055–1068. [Google Scholar] [CrossRef]
- Kang, B. Statistical analysis of typhoon events in China. China Flood Drought Manag. 2016, 26, 36–40. (In Chinese) [Google Scholar]
- China Typhoon Online. Available online: http://typhoon.weather.com.cn/ (accessed on 13 April 2017).
- National Meteorological Center: Typhoon and Marine Weather Monitoring and Warning. Available online: http://typhoon.nmc.cn/web.html (accessed on 13 April 2017).
- Toreti, A.; Kuglitsch, F.; Xoplaki, E.; Della-Marta, P.; Aguilar, E.; Prohom, M.; Luterbacher, J. A note on the use of the standard normal homogeneity test to detect inhomogeneities in climatic time series. Int. J. Climatol. 2011, 31, 630–632. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in Ethiopia. J. Appl. Meteorol. Clim. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- NASA’s Precipitation Measurement Missions. Available online: http://pmm.nasa.gov/data-access (accessed on 13 April 2017).
- Skofronick-Jackson, G.; Huffman, G.; Stocker, E.; Walter, P. Successes with the Global Precipitation Measurement (GPM) Mission. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3910–3912. [Google Scholar]
- Nastos, P.T.; Kapsomenakis, J.; Philandras, K.M. Evaluation of the TRMM 3B43 gridded precipitation estimates over Greece. Atmos. Res. 2016, 169, 497–514. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Inter. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Huang, J.C.; Yu, C.K.; Lee, J.Y.; Cheng, L.W.; Lee, T.Y.; Kao, S.J. Linking typhoon tracks and spatial rainfall patterns for improving flood lead time predictions over a mesoscale mountainous watershed. Water Resour. Res. 2012, 48, W09540. [Google Scholar] [CrossRef]
- Chen, Y.; Ebert, E.E.; Walsh, K.J.E.; Davidson, N.E. Evaluation of TRMM 3B42 precipitation estimates of tropical cyclone rainfall using PACRAIN data. J. Geophys. Res. 2013, 118, 2184–2196. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Kirstetter, P.E.; Gourley, J.J.; Qi, Y.; Zhang, J.; Howard, K.; Hu, J.; Wang, J. Performance evaluation of radar and satellite rainfalls for Typhoon Morakot over Taiwan: Are remote-sensing products ready for gauge denial scenario of extreme events? J. Hydrol. 2013, 506, 4–13. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
| Group | Typhoon Event | Period | Mainly Affected Province (City) | Number of Investigated Station | Maximum Daily Rainfall |
|---|---|---|---|---|---|
| Group I | Rammasun | 18–19 July 2014 | Guangdong, Guangxi, Hainan | 55 | 303.6 mm |
| Mujigae | 4–5 October 2015 | Hainan, Guangdong, Guangxi | 58 | 192.9 mm | |
| Kalmaegi | 16–17 September 2014 | Hainan, Guangdong, Guangxi | 67 | 296.5 mm | |
| Linfa | 9–10 July 2015 | Guangdong, Fujian | 39 | 158.8 mm | |
| Group II | Chon-hom | 11–12 July 2015 | Zhejiang, Jiangsu, Fujian, Shanghai | 37 | 267.7 mm |
| Matmo | 23–25 July 2014 | Fujian, Guangdong, Jiangsu, Shandong | 98 | 238.3 mm | |
| Soudelor | 8–10 August 2015 | Fujian, Zhejiang, Jiangsu, Guangdong | 104 | 232.1 mm | |
| Dujuan | 28–30 September 2015 | Fujian, Zhejiang, Jiangsu | 80 | 170.9 mm |
| Typhoon Events | IMERG | TMPA | |||
|---|---|---|---|---|---|
| Overestimate | Underestimate | Overestimate | Underestimate | ||
| Group I | Rammasun | 47.27 | 52.73 | 38.18 | 61.82 |
| Mujigae | 58.62 | 41.38 | 67.24 | 32.76 | |
| Kalmaegi | 26.87 | 73.13 | 23.88 | 76.12 | |
| Linfa | 25.51 | 74.49 | 17.95 | 82.05 | |
| Group II | Chon-hom | 8.11 | 91.89 | 8.11 | 91.89 |
| Matmo | 39.80 | 60.20 | 35.71 | 64.29 | |
| Soudelor | 55.77 | 44.23 | 50.96 | 49.04 | |
| Dujuan | 38.75 | 61.25 | 46.25 | 53.75 | |
| Rain Intensity | IMERG | TMPA | ||||
|---|---|---|---|---|---|---|
| Over-Per | Under-Per | RB | Over-Per | Under-Per | RB | |
| 0–20 | 44.31 | 55.69 | 31.51 | 54.90 | 45.10 | 45.23 |
| 20–40 | 39.86 | 60.14 | −9.23 | 33.11 | 66.89 | −19.58 |
| 40–60 | 33.33 | 66.66 | −12.14 | 21.57 | 78.43 | −23.77 |
| 60–80 | 18.18 | 81.82 | −27.92 | 18.18 | 81.82 | −41.13 |
| 80–100 | 50.00 | 50.00 | −7.87 | 25.00 | 75.00 | −22.50 |
| >100 | 12.50 | 87.50 | −30.17 | 12.50 | 87.50 | −34.81 |
| Buffer Ranges (km) | IMERG | ||||||||
| Group I | Group II | Mean | |||||||
| Rammasun | Mujigae | Kalmaegi | Linfa | Chon-hom | Matmo | Soudelor | Dujuan | ||
| <50 | 30.18 | 63.66 | −24.11 | −55.77 | −65.57 | −11.76 | 6.32 | −37.47 | −11.82 |
| 50–100 | 54.36 | 1.31 | −17.26 | −55.49 | −58.78 | −28.33 | 69.95 | −17.47 | −6.46 |
| 100–300 | 47.02 | 15.00 | 6.19 | −1.13 | −38.93 | 21.10 | 70.48 | 6.37 | 15.76 |
| >300 | −46.94 | 63.79 | −42.82 | −91.89 | −96.40 | 82.81 | 0.84 | −4.92 | −16.94 |
| Buffer Ranges (km) | TMPA | ||||||||
| Group I | Group II | Mean | |||||||
| Rammasun | Mujigae | Kalmaegi | Linfa | Chon-hom | Matmo | Soudelor | Dujuan | ||
| <50 | 2.65 | 63.83 | −69.00 | −55.57 | −65.57 | −23.96 | −13.21 | −26.76 | −23.45 |
| 50–100 | 34.03 | 7.64 | −35.35 | −57.20 | −62.21 | 43.31 | 54.52 | −9.42 | −3.09 |
| 100–300 | 11.50 | 27.12 | −30.00 | −13.73 | −50.51 | 14.50 | 58.09 | 40.88 | 7.23 |
| >300 | −9.30 | 79.40 | −24.80 | −98.11 | −55.34 | 22.23 | 22.23 | 23.90 | −4.97 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Chen, J.; Wang, X. Comparison of IMERG Level-3 and TMPA 3B42V7 in Estimating Typhoon-Related Heavy Rain. Water 2017, 9, 276. https://doi.org/10.3390/w9040276
Wang R, Chen J, Wang X. Comparison of IMERG Level-3 and TMPA 3B42V7 in Estimating Typhoon-Related Heavy Rain. Water. 2017; 9(4):276. https://doi.org/10.3390/w9040276
Chicago/Turabian StyleWang, Ren, Jianyao Chen, and Xianwei Wang. 2017. "Comparison of IMERG Level-3 and TMPA 3B42V7 in Estimating Typhoon-Related Heavy Rain" Water 9, no. 4: 276. https://doi.org/10.3390/w9040276
APA StyleWang, R., Chen, J., & Wang, X. (2017). Comparison of IMERG Level-3 and TMPA 3B42V7 in Estimating Typhoon-Related Heavy Rain. Water, 9(4), 276. https://doi.org/10.3390/w9040276







