Spatial and Temporal Variations of Snow Cover in the Karoon River Basin, Iran, 2003–2015
Abstract
:1. Introduction
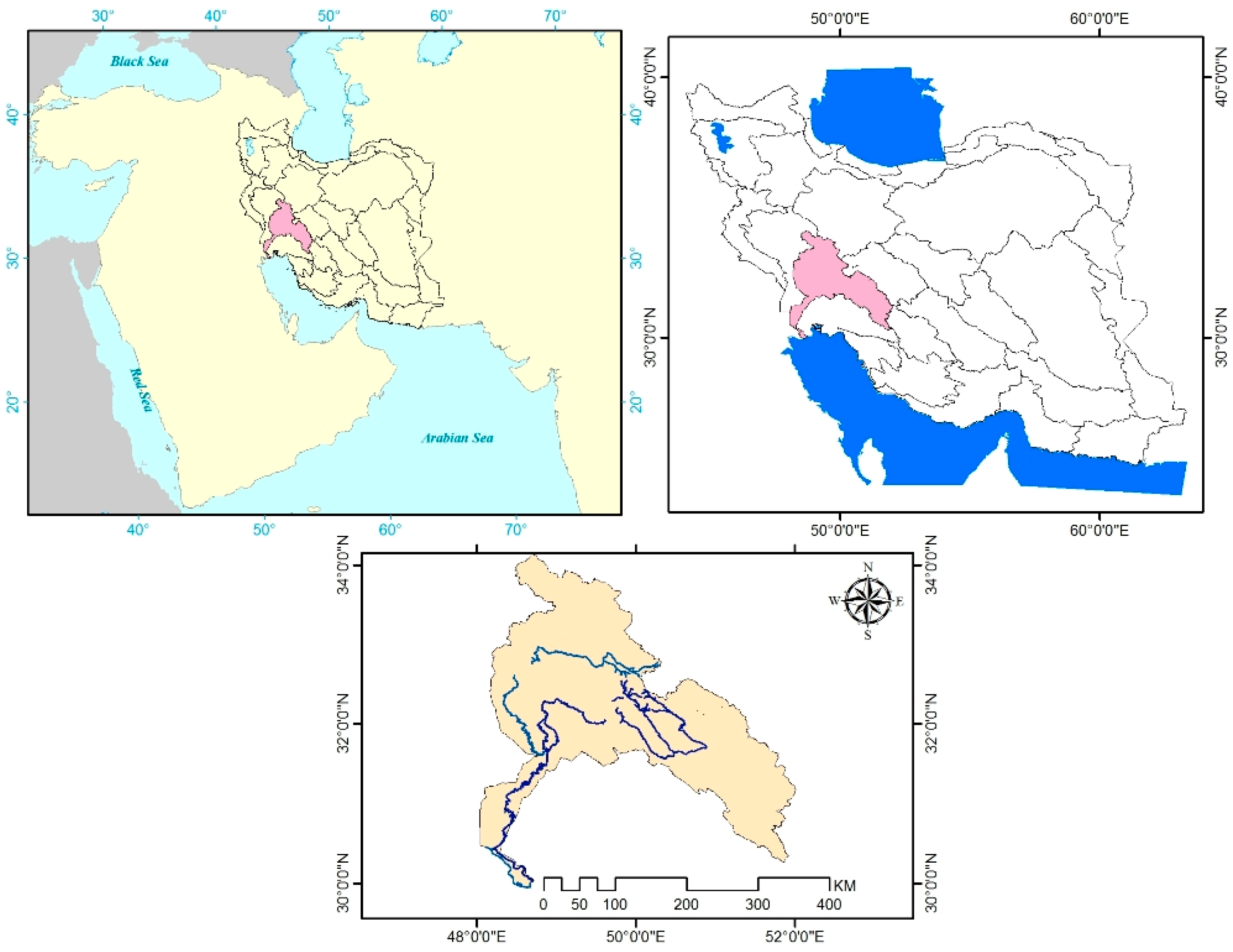
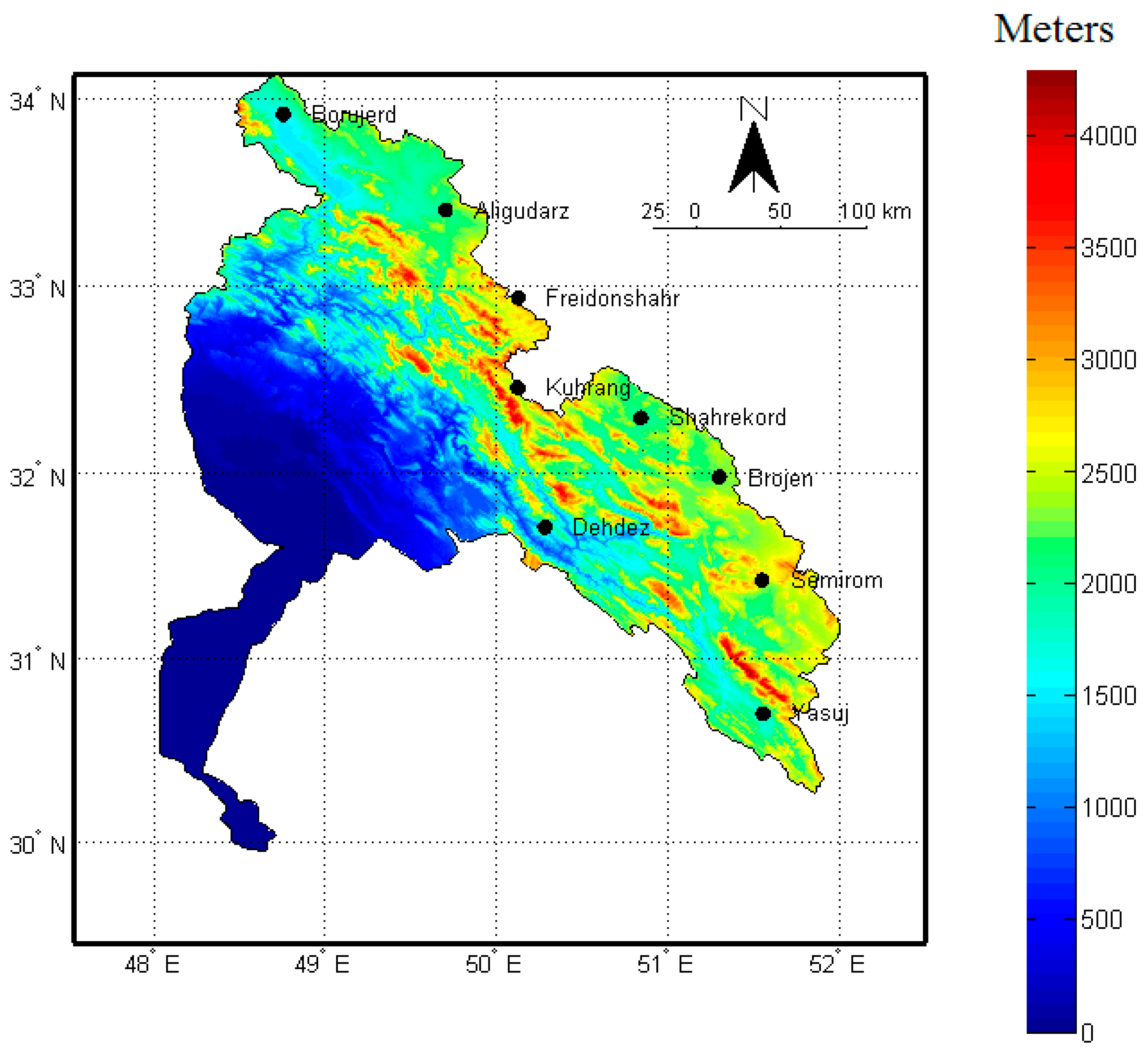
2. Study Region
3. Data and Methods
3.1. Data
3.1.1. Snow Cover Products
3.1.2. Station Data
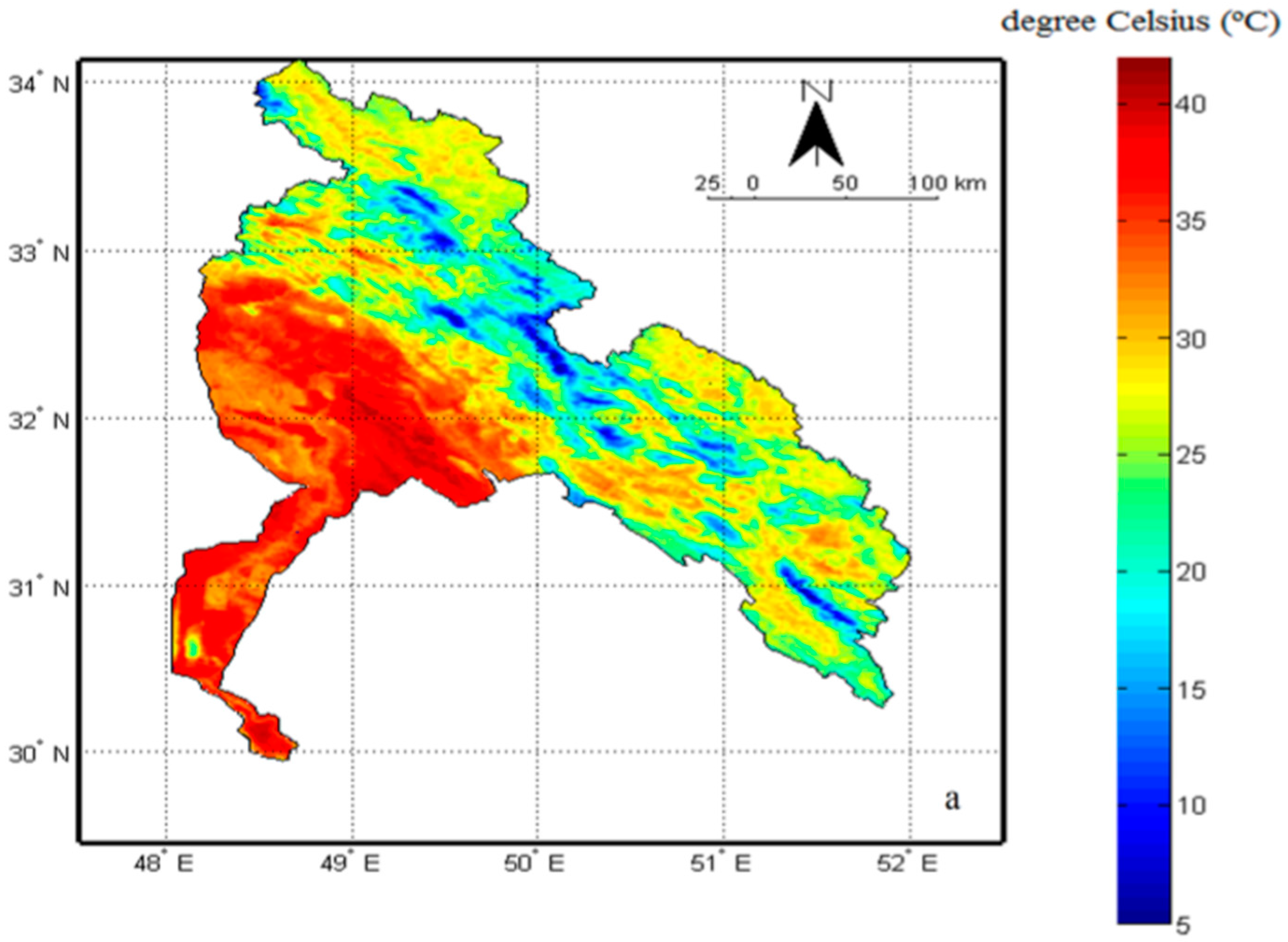
3.1.3. Land Surface Temperature Data
3.1.4. Digital Elevation Model (DEM)
3.2. Methods
3.2.1. Cloud Gap-Filling Methods
3.2.2. Trend Analysis
4. Results
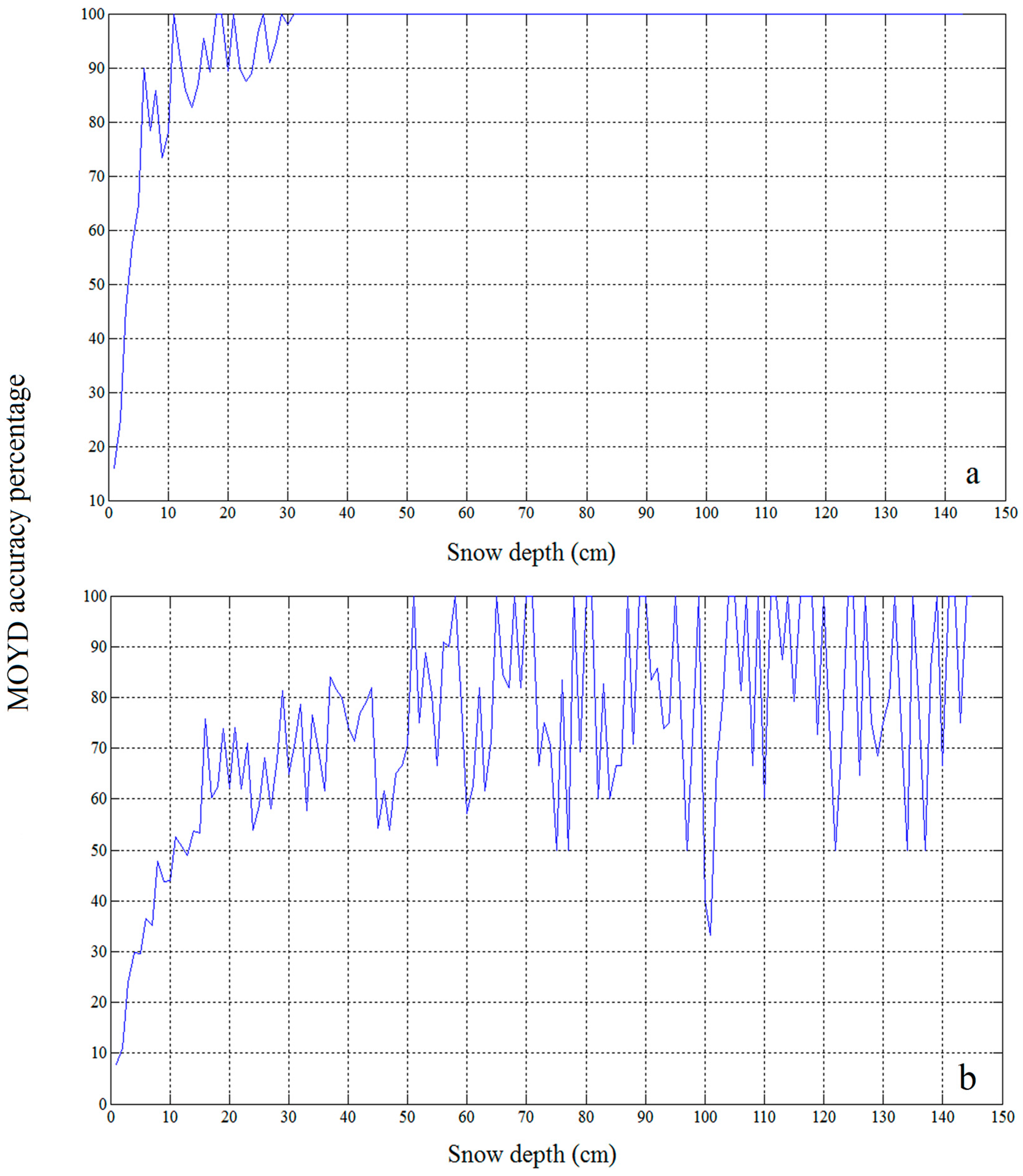
4.1. Accuracy Assessment
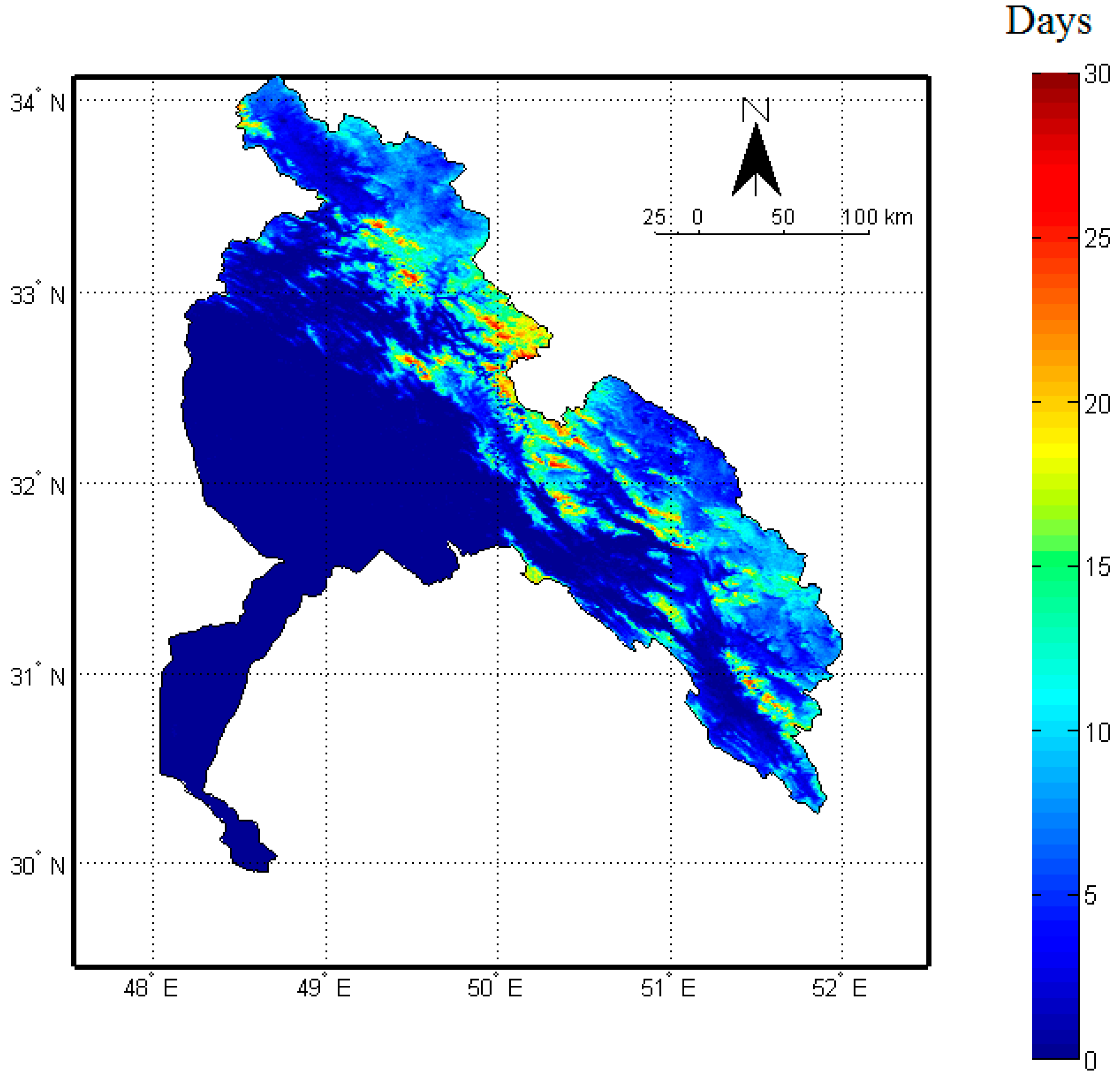
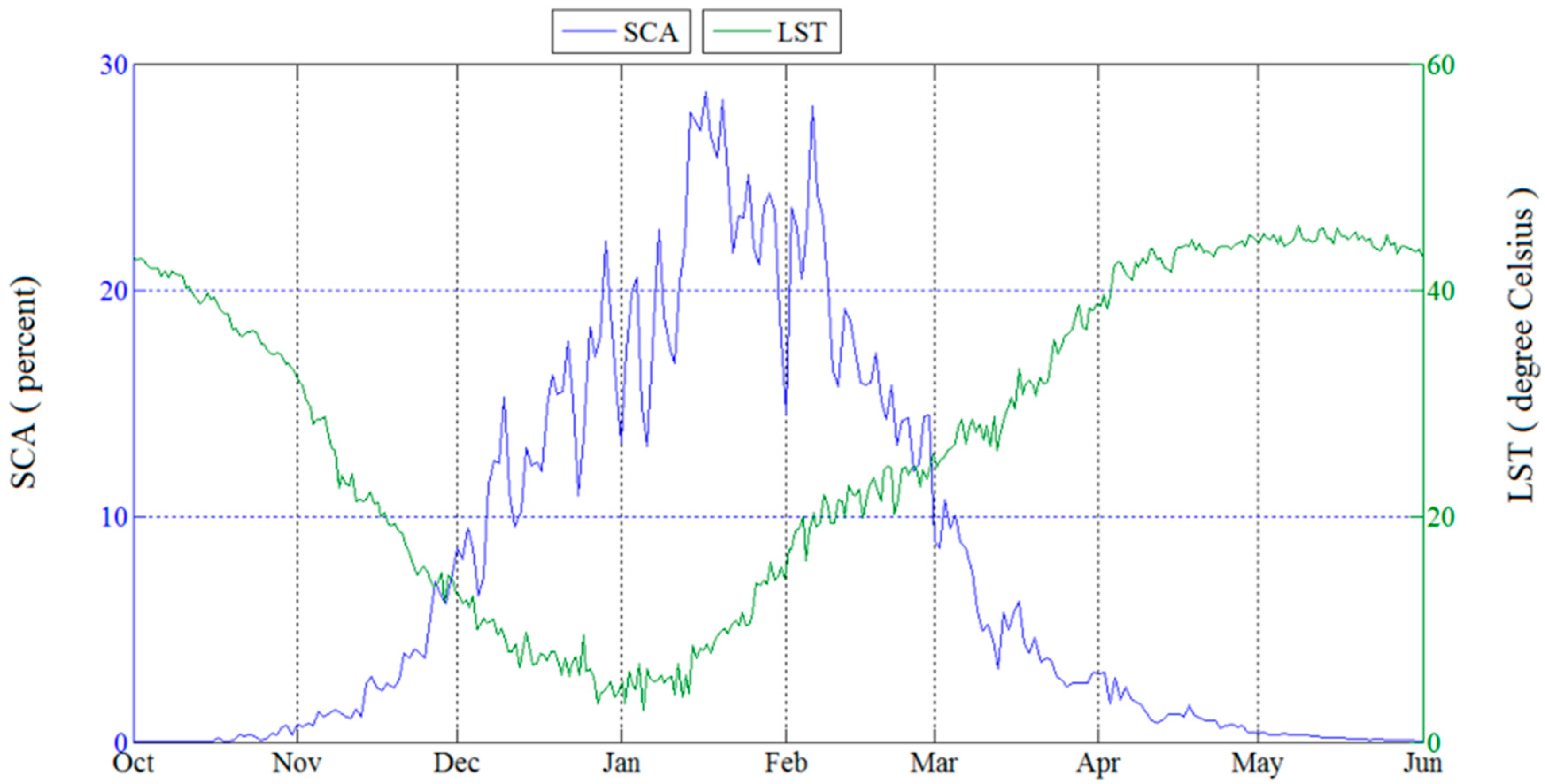
4.2. Karoon River Basin Snow Cover
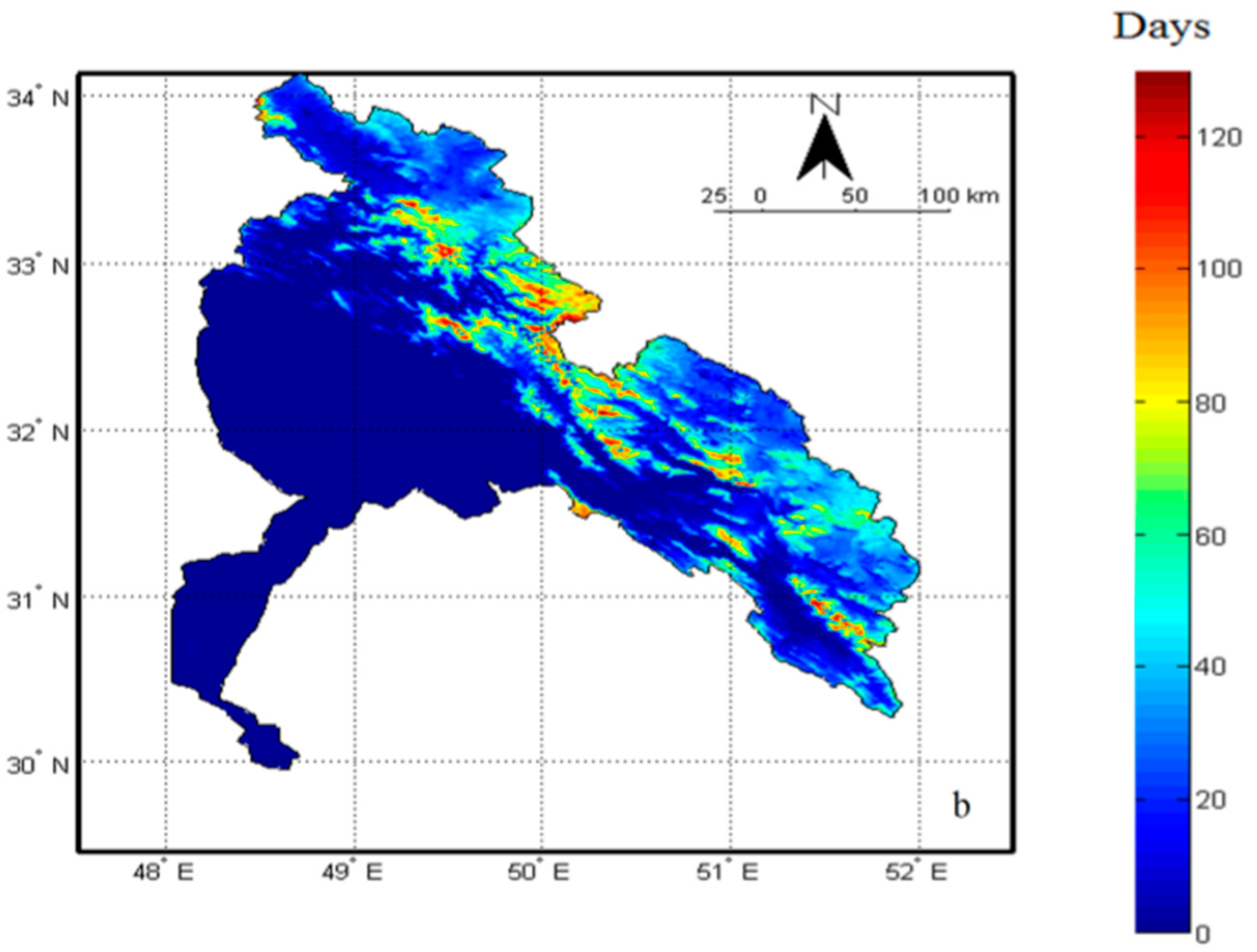
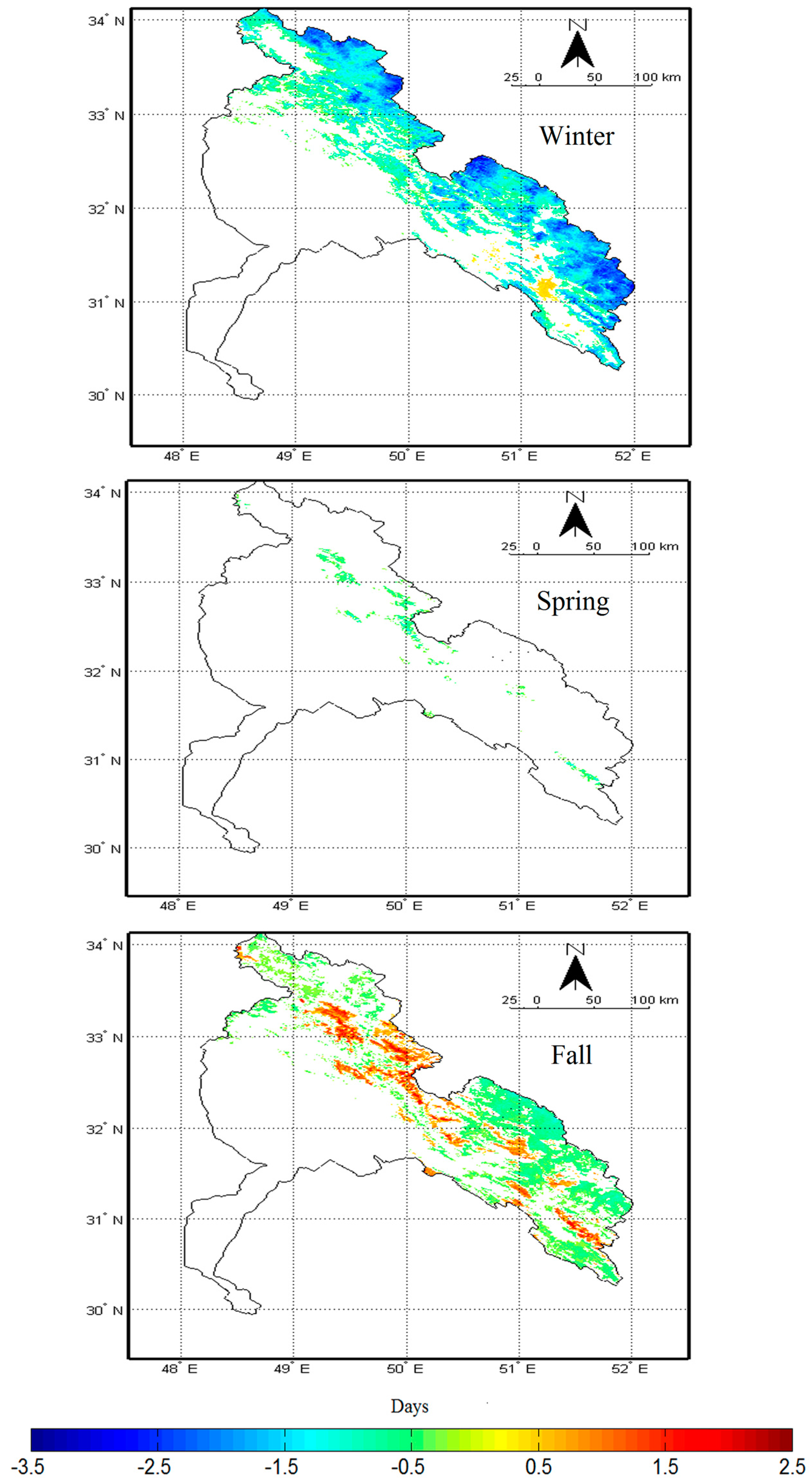
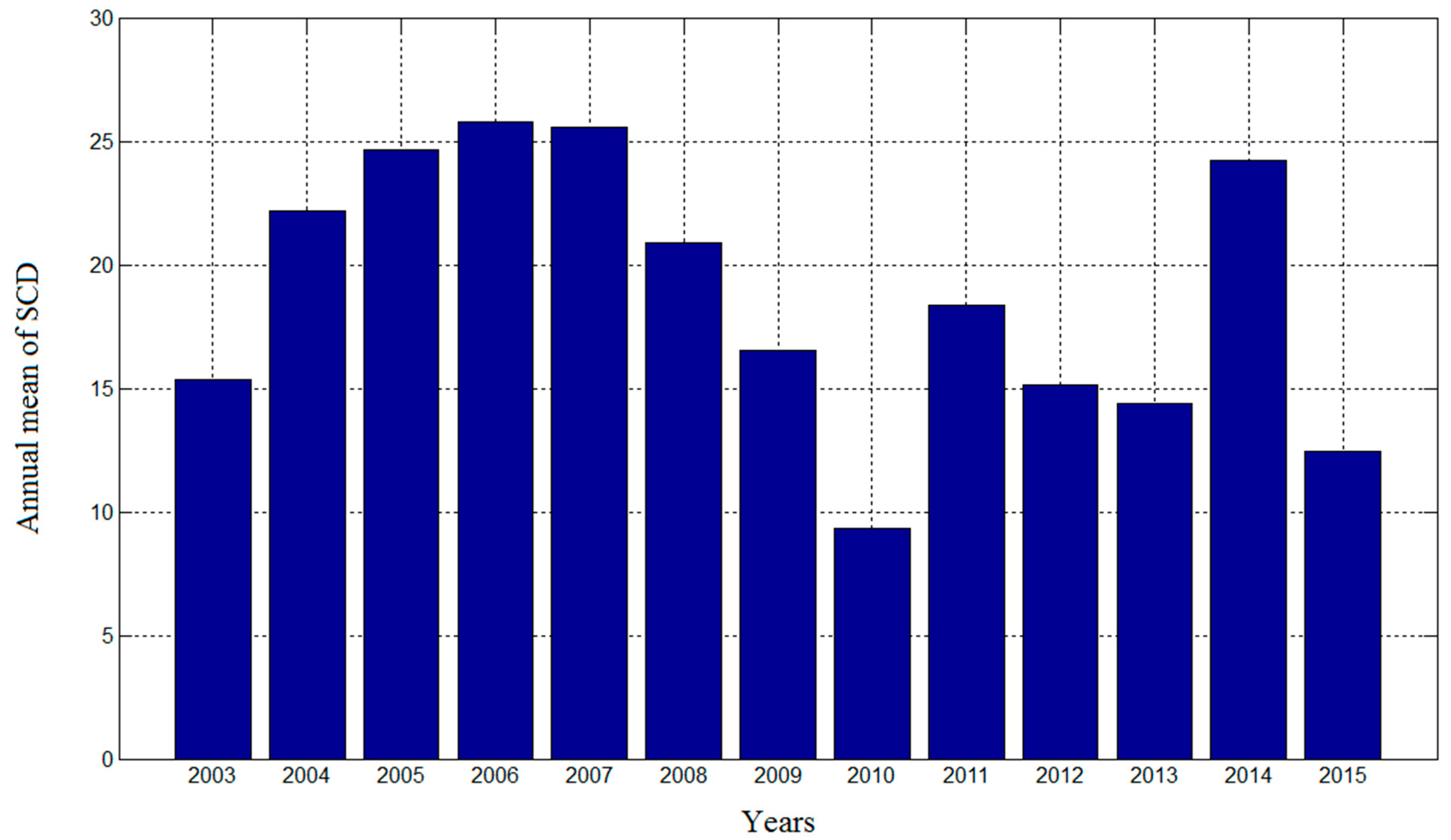
4.3. Trends in SCA and SCD
4.4. Trend in SCD in Elevation Classes
5. Discussion
6. Conclusions
Supplementary Materials
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brown, R.D. Northern hemisphere snow cover variability and change, 1915–97. J. Clim. 2000, 13, 2339–2355. [Google Scholar] [CrossRef]
- Leathers, D.J.; Mote, T.L.; Grendstein, A.J.; Robinson, D.A.; Felter, K.; Conrad, K.; Sedywitz, L. Associations between continental-scale snow cover anomalies and air mass frequencies across eastern North America. Int. J. Climatol. 2002, 22, 1473–1494. [Google Scholar] [CrossRef]
- Turner, J. Atlas of satellite observations related to global change. Weather 1994, 49, 226–227. [Google Scholar] [CrossRef]
- Tekeli, Y.; Tekeli, A.E. A technique for improving MODIS standard snow products for snow cover monitoring over Eastern Turkey. Arab. J. Geosci. 2012, 5, 353–363. [Google Scholar] [CrossRef]
- Elder, K.; Dozier, J.; Michaelsen, J. Snow accumulation and distribution in an alpine watershed. Water Resour. Res. 1991, 27, 1541–1552. [Google Scholar] [CrossRef]
- Anderton, S.P.; White, S.M.; Alvera, B. Evaluation of spatial variability in snow water equivalent for a high mountain catchment. Hydrol. Process. 2004, 18, 435–453. [Google Scholar] [CrossRef]
- Trujillo, E.; Ramfrez, J.A.; Elder, K.J. Topographic, meteorologic, and canopy controls on scaling characteristics of the spatial distribution of snow depth fields. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Zhou, X.; Xie, H.; Hendrickx, J.M.H. Statistical evaluation of remotely sensed snow-cover products with constraints from streamflow and SNOTEL measurements. Remote Sens. Environ. 2005, 94, 214–231. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, J.; Li, H.; Yan, L. Spatiotemporal changes of snow cover over the Tibetan plateau based on cloud-removed moderate resolution imaging spectroradiometer fractional snow cover product from 2001 to 2011. J. Appl. Remote Sens. 2013, 7. [Google Scholar] [CrossRef]
- Maskey, S.; Uhlenbrook, S.; Ojha, S. An analysis of snow cover changes in the Himalayan region using MODIS snow products and in-situ temperature data. Clim. Chang. 2011, 108, 391–400. [Google Scholar] [CrossRef]
- Singh, S.K.; Rathore, B.P.; Bahuguna, I.M.; Ajai. Snow cover variability in the Himalayan—Tibetan region. Int. J. Climatol. 2011, 34, 446–452. [Google Scholar] [CrossRef]
- Wang, W.; Huang, X.; Deng, J.; Xie, H.; Liang, T. Spatio-temporal change of snow cover and its response to climate over the Tibetan Plateau based on and improved daily cloud-free snow cover product. Remote Sens. 2015, 7, 169–194. [Google Scholar] [CrossRef]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Ashraf, M.; Bhatti, M.T. Snow cover trend and hydrological characteristics of the Astore River Basin (Western Himalayas) and its comparison to the Hunza Basin (Karakoram region). Sci. Total Environ. 2015, 505, 748–761. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Ke, C.Q.; Xu, Y.Y.; Li, X.C. Spatial and temporal variations of snow cover in the Loess Plateau, China. Int. J. Climatol. 2014, 35, 1721–1731. [Google Scholar] [CrossRef]
- Riggs, G.; Hall, D.; Salomonson, V. MODIS Snow Products User Guide to Collection 5, 2006, Retrieved 15 January 2013. Available online: http://www.nsidc.org/data/docs/daac/modis_v5/dorothy_snow_doc.pdf (accessed on 21 October 2016).
- Crosson, W.L.; Al-Hamdan, M.Z.; Hemmings, S.N.J.; Wade, G.M. A daily merged MODIS Aqua–Terra land surface temperature data set for the conterminous United States. Remote Sens. Environ. 2012, 119, 315–324. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Klein, A.G.; Barnett, A.C. Validation of daily MODIS snow cover maps of the Upper Rio Grande River Basin for the 2000–2001 snow year. Remote Sens. Environ. 2003, 86, 162–176. [Google Scholar] [CrossRef]
- Maurer, E.P.; Rhoads, J.D.; Dubayah, R.O.; Lettenmaier, D.P. Evaluation of the snow-covered area data product from MODIS. Hydrol. Process. 2003, 17, 59–71. [Google Scholar] [CrossRef]
- Simic, A.; Fernandes, R.; Brown, R.; Romanov, P.; Park, W. Validation of vegetation, MODIS, and GOESCSSM/I snow-cover products over Canada based on surface snow depth observations. Hydrol. Process. 2004, 18, 1089–1104. [Google Scholar] [CrossRef]
- Parajika, J.; Blosch, G. Validation of MODIS snow cover images over Austria. Hydrol. Earth Syst. Sci. 2006, 10, 679–689. [Google Scholar] [CrossRef]
- Huang, X.; Liang, T.; Zhang, X.; Guo, Z. Validation of MODIS snow cover products using Landsat and ground measurements during the 2001–2005 snow seasons over Northern Xinjiang, China. Int. J. Remote Sens. 2011, 32, 133–152. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Liang, T.; Huang, X. Comparison and validation of MODIS standard and new combination of Terra and Aqua snow cover products in Northern Xinjiang, China. Hydrol. Process. 2009, 23, 419–429. [Google Scholar] [CrossRef]
- Xie, H.; Wang, X.; Liang, T. Development and assessment of combined Terra and Aqua snow cover products in Colorado Plateau, USA and Northern Xinjiang, China. J. Appl. Remote Sens. 2009, 3. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Lu, N.; Yao, T.; Liang, T. Toward advanced daily cloud-free snow cover and snow water equivalent products from Terra-Aqua MODIS and Aqua AMSR-E measurements. J. Hydrol. 2010, 385, 23–35. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Yao, T.; Xue, C. Integrated assessment on multi-temporal and multi-sensor combinations for reducing cloud obscuration of MODIS snow cover products of the Pacific Northwest USA. Remote Sens. Environ. 2010, 114, 1662–1675. [Google Scholar] [CrossRef]
- Paudel, K.P.; Andersen, P. Monitoring snow cover variability in an agropastoral area in the Trans Himalayan Region of Nepal using MODIS data with improved cloud removal methodology. Remote Sens. Environ. 2011, 115, 1234–1246. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Foster, J.L.; Kumar, S.V. Development and evaluation of a cloud-gap-filled MODIS daily snow-cover product. Remote Sens. Environ. 2010, 114, 496–503. [Google Scholar] [CrossRef]
- She, J.; Zhang, Y.; Li, X.; Feng, X. Spatial and Temporal Characteristics of Snow Cover in the Tizinafu Watershed of the Western Kunlun Mountains. Remote Sens. 2015, 7, 3426–3445. [Google Scholar] [CrossRef]
- Kolmogorov, A. Confidence limits for an unknown distribution function. Ann. Math. Stat. 1941, 12, 461–463. [Google Scholar] [CrossRef]
- Smirnov, N.V. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Birnbaum, Z.W. Numerical tabulation of the distribution of Kolmogorov’s statistic for finite sample values. J. Am. Stat. Assoc. 1952, 47, 425–441. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Liang, T. Evaluation of MODIS snow cover and cloud mask and its application in Northern Xinjiang, China. Remote Sens. Environ. 2008, 112, 1497–1513. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). 2013: Annex I: Atlas of Global and Regional Climate Projections; van Oldenborgh, G.J., Collins, M., Arblaster, J., Christensen, J.H., Marotzke, J., Power, S.B., Rummukainen, M., Zhou, T., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Sönmez, I.; Tekeli, A.E.; Erdi, E. Snow cover trend analysis using Interactive Multisensor Snow and Ice Mapping System data over Turkey. Int. J. Climatol. 2014, 34, 2349–2361. [Google Scholar] [CrossRef]
- Khadka, D.; Babel, M.S.; Shrestha, S.; Tripathi, N.K. Climate change impact on glacier and snow melt and runoff in Tamakoshi Basin in the Hindu Kush Himalayan (HKH) region. J. Hydrol. 2014, 511, 49–60. [Google Scholar] [CrossRef]
- Verdhen, A.; Chahar, B.R.; Ashwagosha, G.; Sharma, O.M.P. Modeling Snow Line Altitudes in the Himalayan Watershed. J. Hydrol. Eng. 2015, 21. [Google Scholar] [CrossRef]
- Svoma, B.M. Trends in snow level elevation in the mountains of central Arizona. Int. J. Climatol. 2011, 31, 87–94. [Google Scholar] [CrossRef]
- Ellis, A.W.; Sauter, K. The significance of snow to surface water supply: An empirical case study from the Southwestern United States. Phys. Geogr. 2017, 38, 211–230. [Google Scholar] [CrossRef]
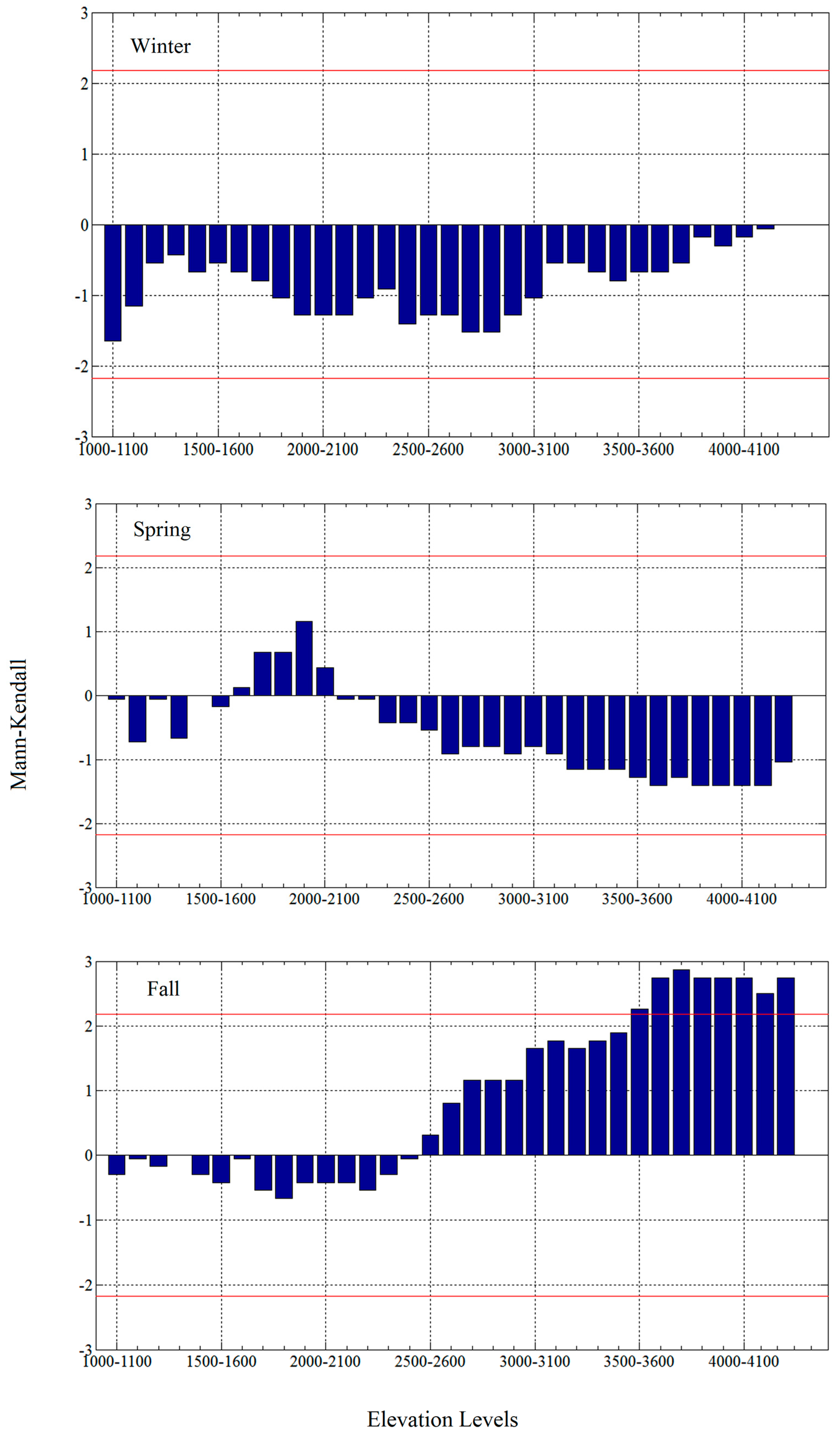
| Decreasing Trend | No Trend | Increasing Trend | |
|---|---|---|---|
| Winter | 42.98 | 55.61 | 1.40 |
| Spring | 3.48 | 96.49 | 0.01 |
| Fall | 25.35 | 64.26 | 10.38 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keikhosravi Kiany, M.S.; Masoodian, S.A.; Balling, R.C.; Svoma, B.M. Spatial and Temporal Variations of Snow Cover in the Karoon River Basin, Iran, 2003–2015. Water 2017, 9, 965. https://doi.org/10.3390/w9120965
Keikhosravi Kiany MS, Masoodian SA, Balling RC, Svoma BM. Spatial and Temporal Variations of Snow Cover in the Karoon River Basin, Iran, 2003–2015. Water. 2017; 9(12):965. https://doi.org/10.3390/w9120965
Chicago/Turabian StyleKeikhosravi Kiany, Mohammad Sadegh, Seyed Abolfazl Masoodian, Robert C. Balling, and Bohumil M. Svoma. 2017. "Spatial and Temporal Variations of Snow Cover in the Karoon River Basin, Iran, 2003–2015" Water 9, no. 12: 965. https://doi.org/10.3390/w9120965
APA StyleKeikhosravi Kiany, M. S., Masoodian, S. A., Balling, R. C., & Svoma, B. M. (2017). Spatial and Temporal Variations of Snow Cover in the Karoon River Basin, Iran, 2003–2015. Water, 9(12), 965. https://doi.org/10.3390/w9120965




