Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses
Abstract
:1. Introduction
2. Study Area and Data
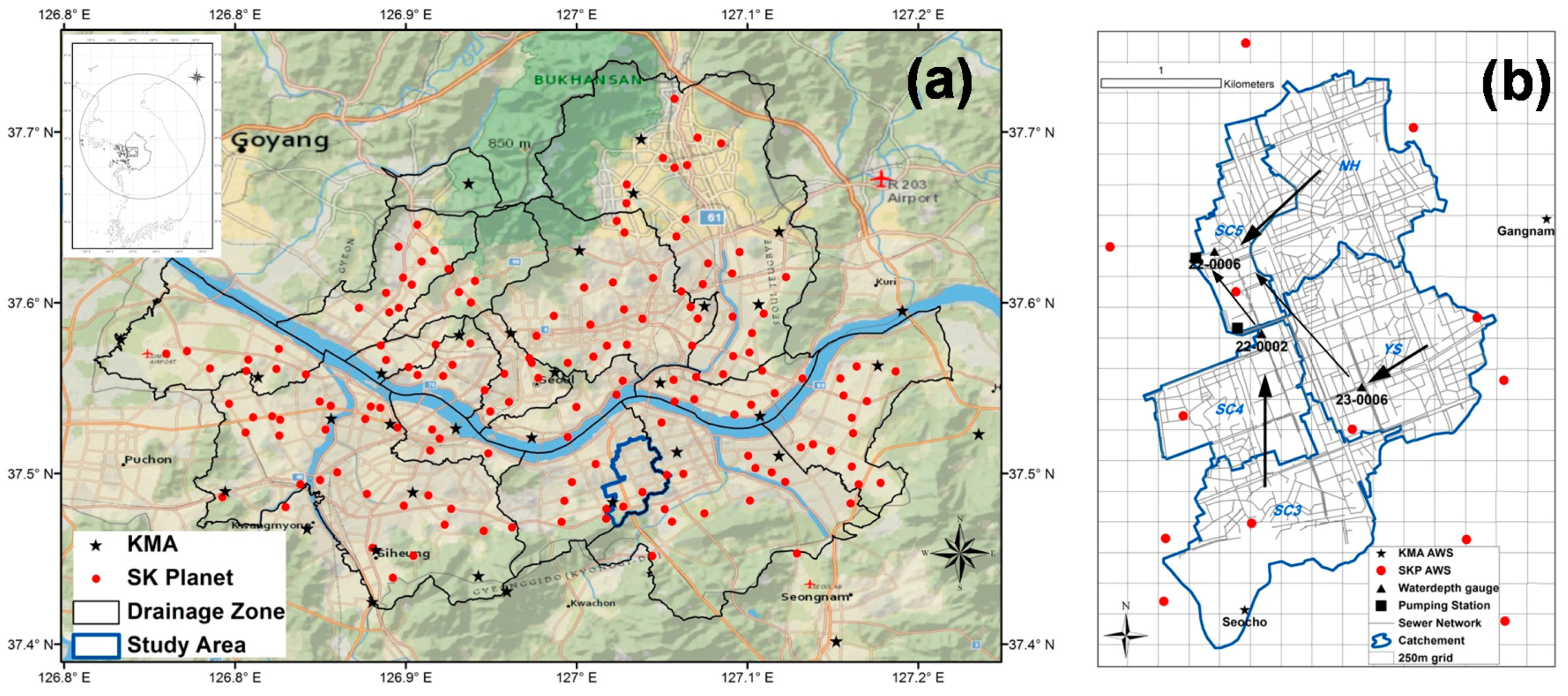
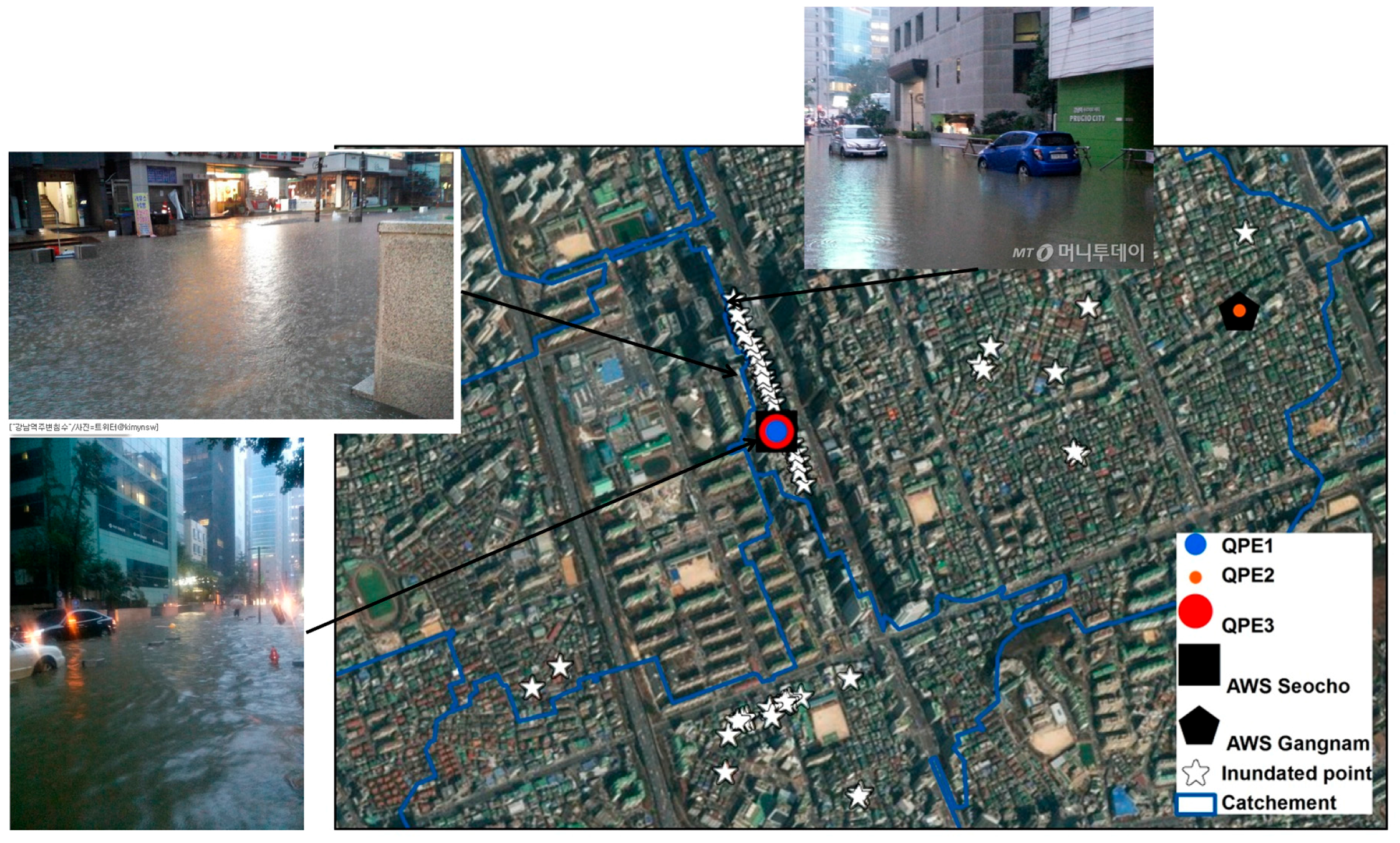
2.1. Study Area
2.2. High-Density Rain-Gauge Network
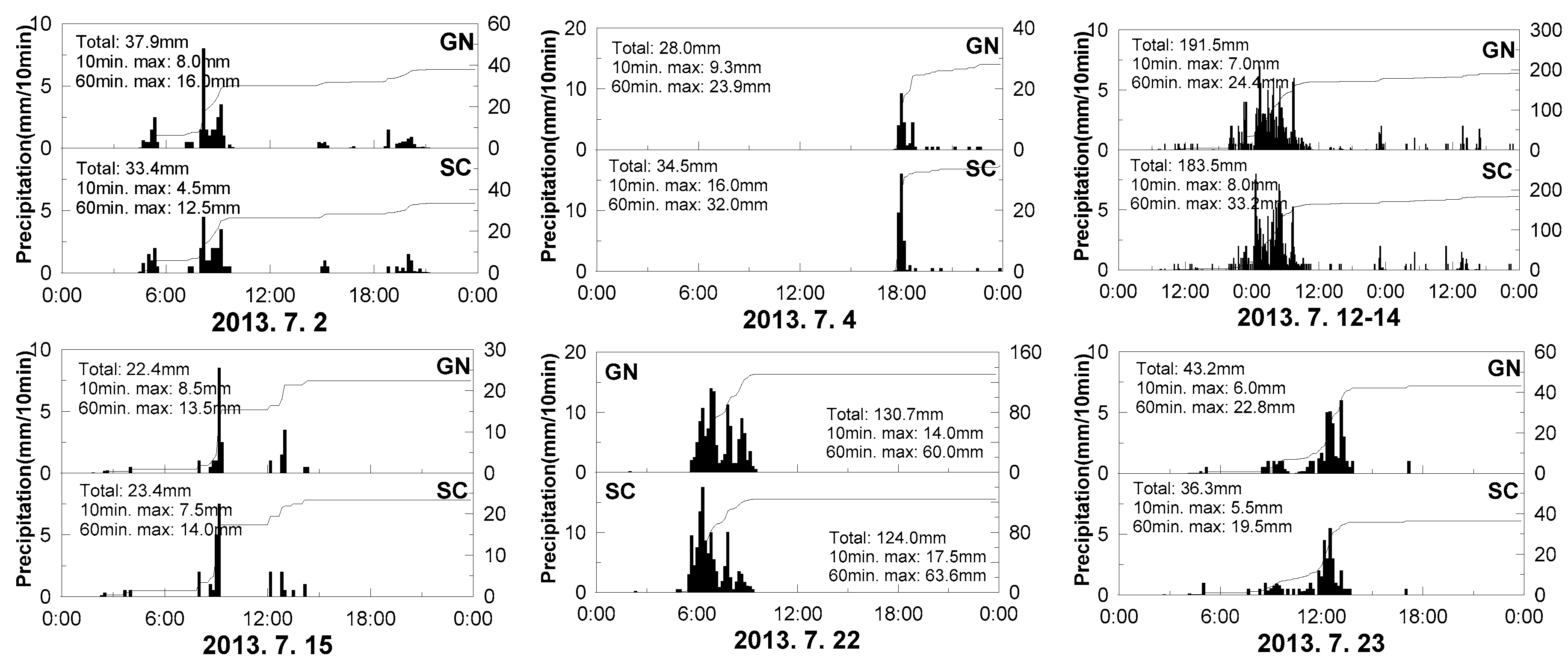
2.3. Weather Radar Data
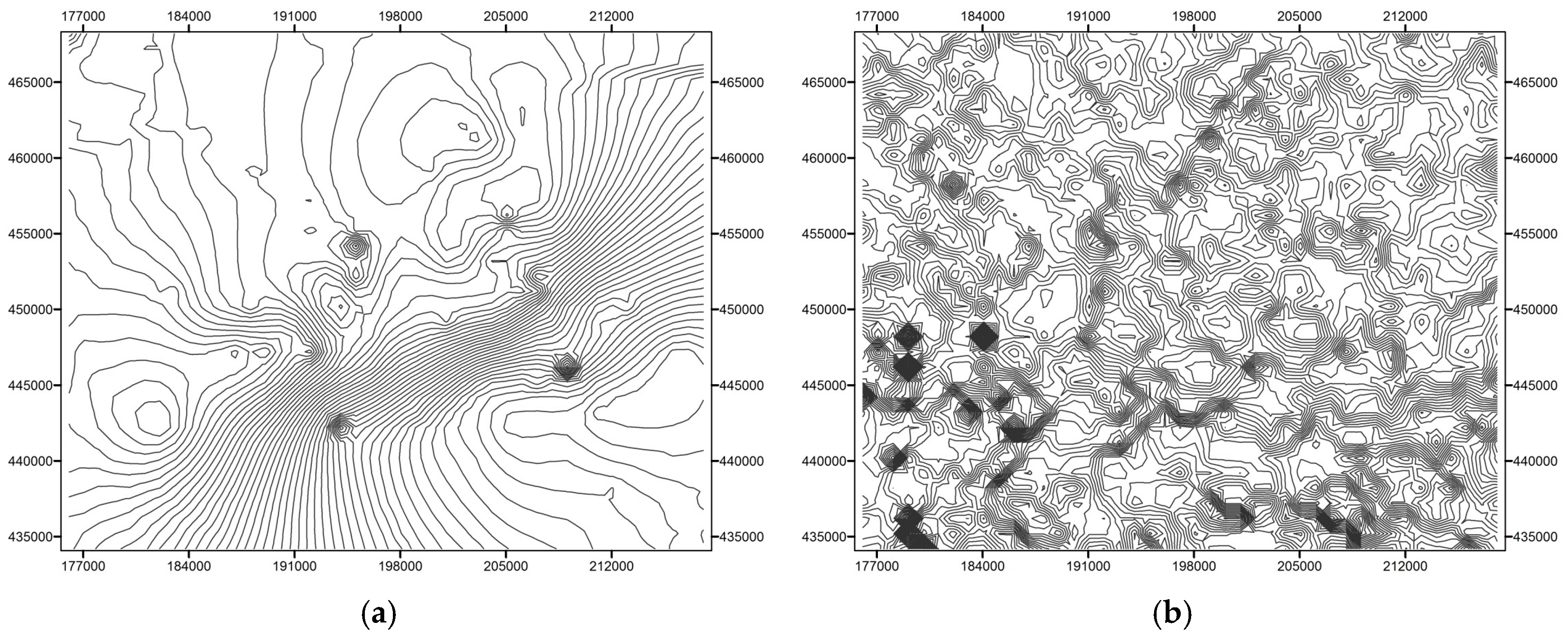
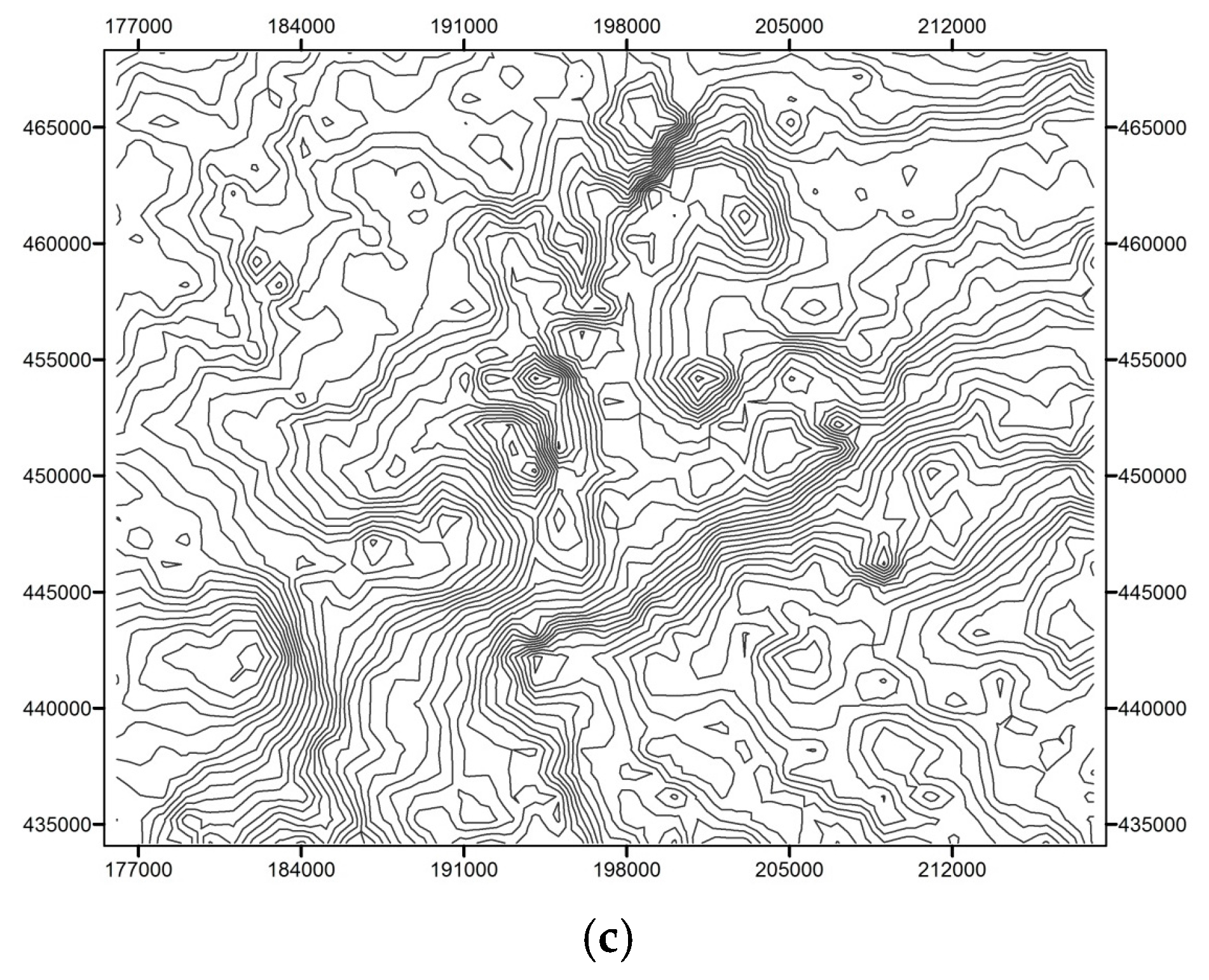
2.4. Drainage Network and Topographic Data
3. Methodology
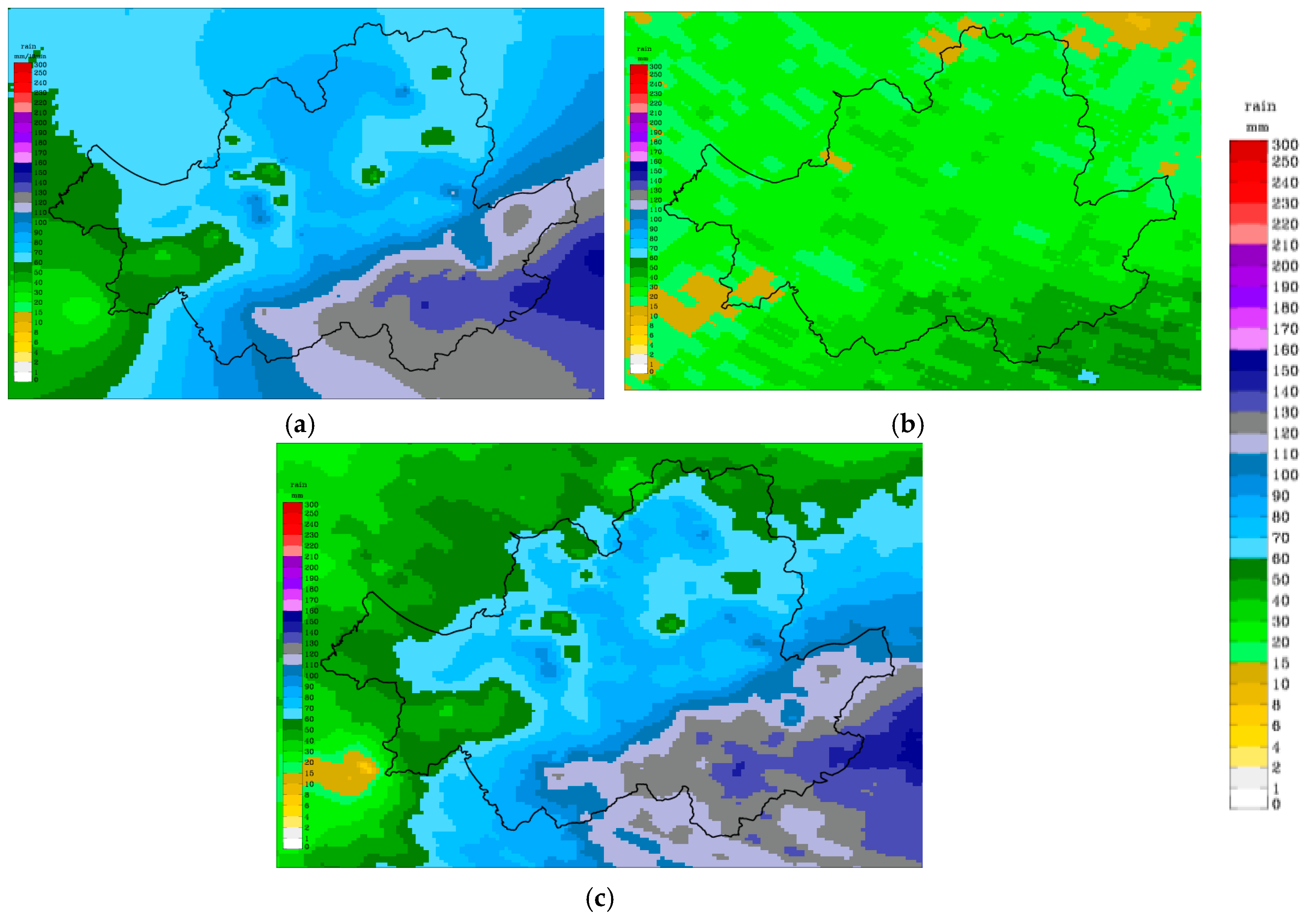
3.1. Quantitative Precipitation Estimation
3.2. Urban Runoff Simulation
4. Applications and Results
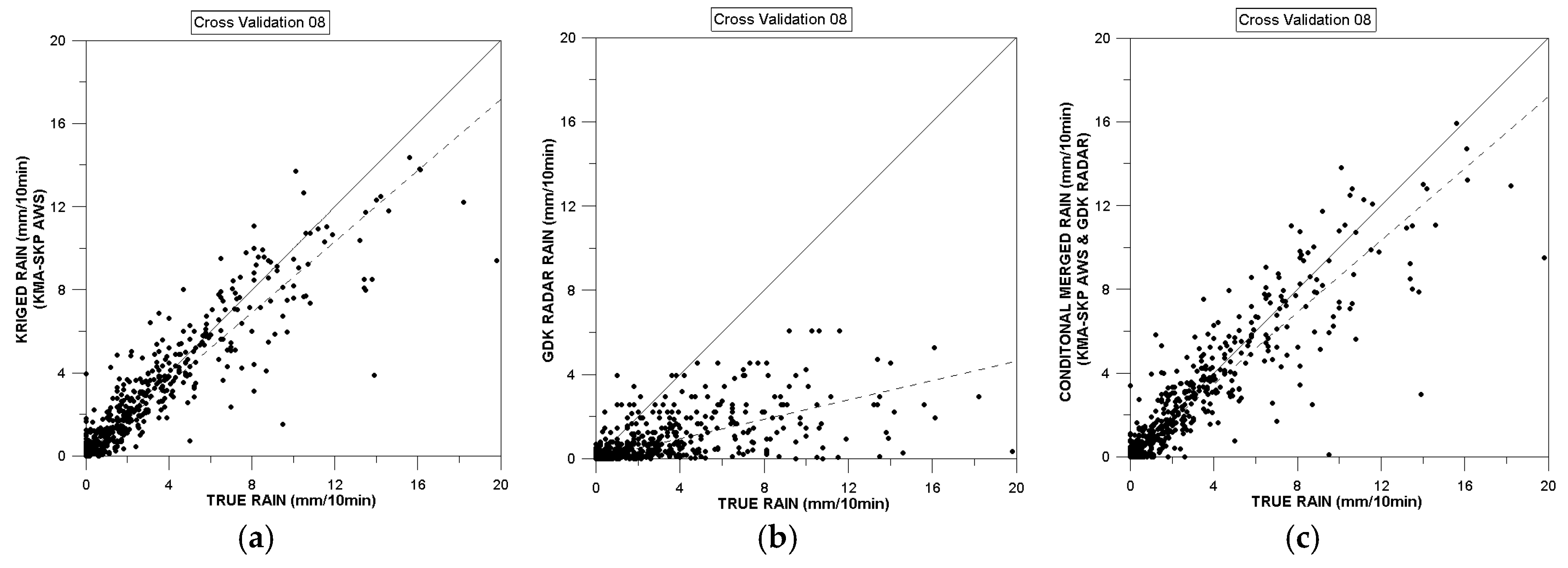
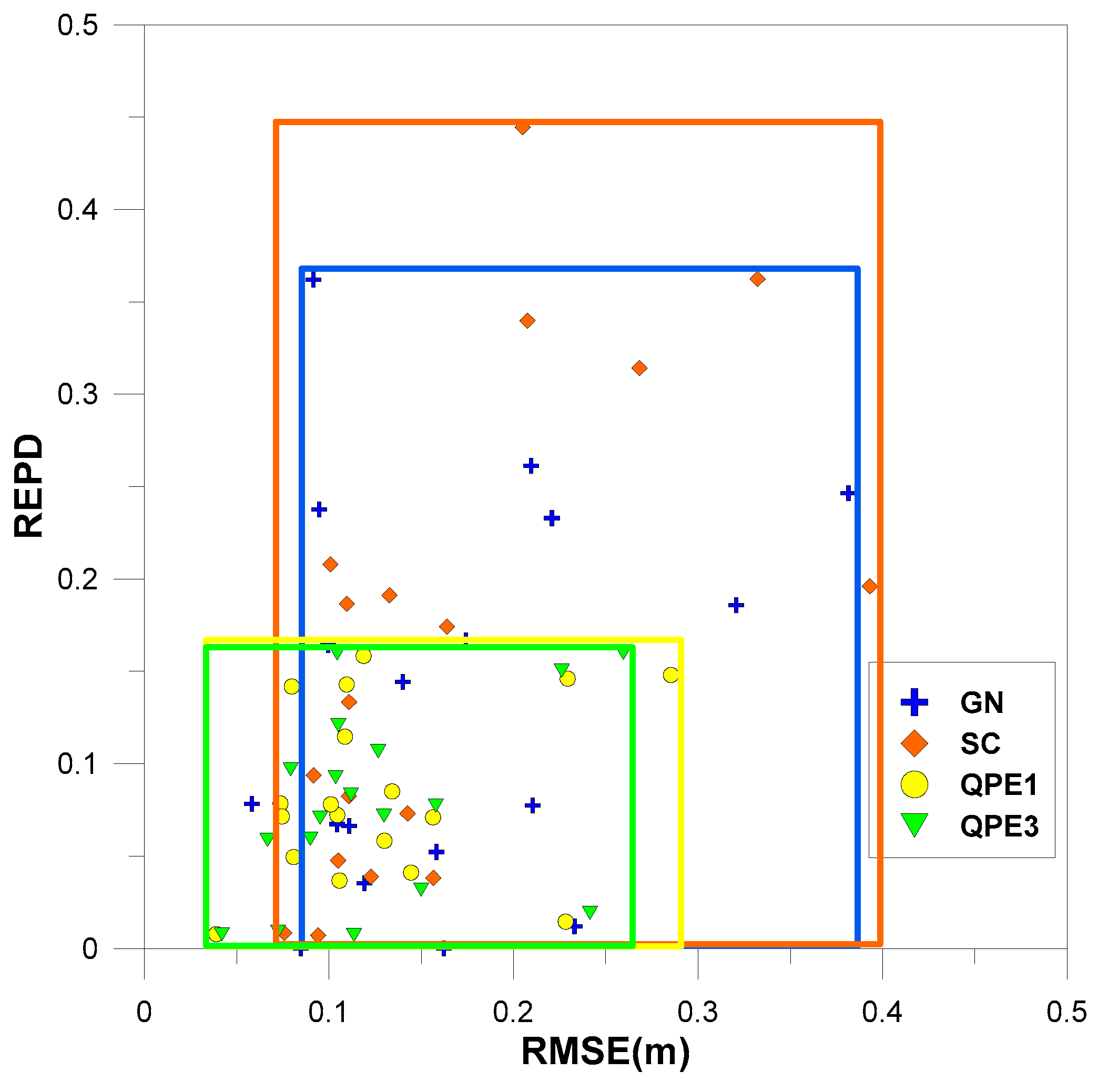
4.1. Cross Validation of Quantitative Precipitation Estimates
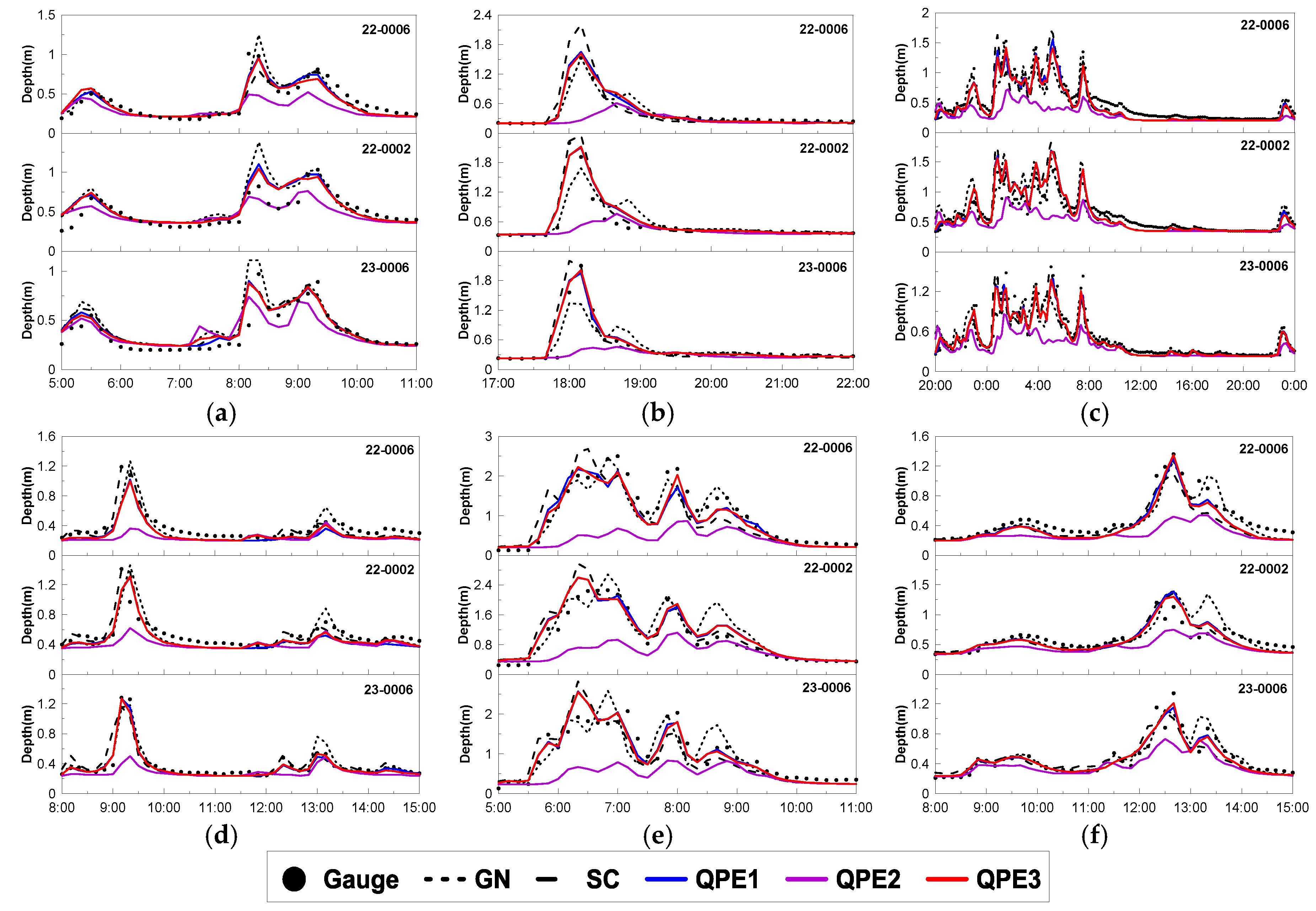
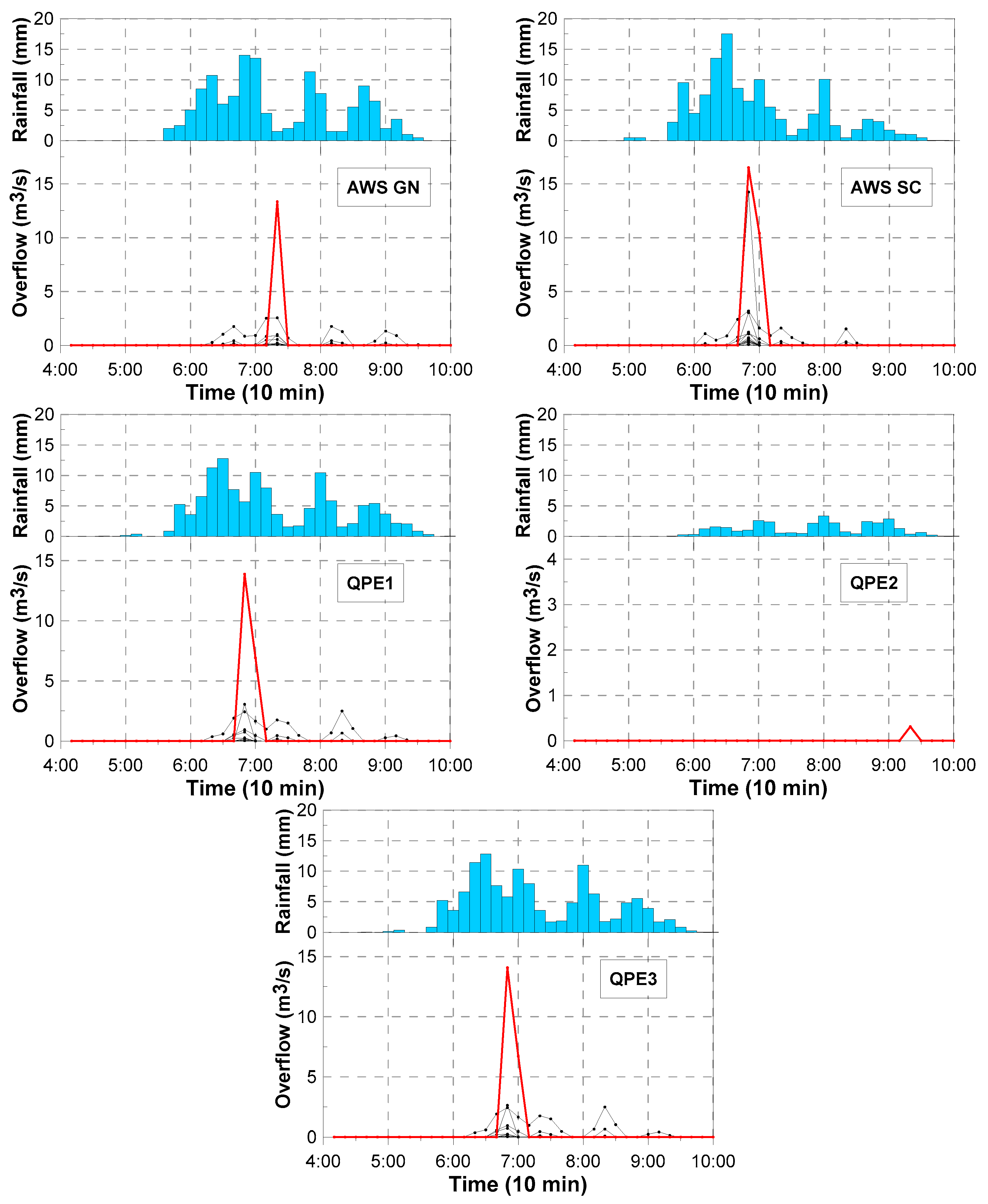
4.2. Urban Runoff Simulation with Various QPE Products
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yoon, D.K. Disaster and development examining global issues and cases. In Disaster Policies and Emergency Management in Korea; Kapucu, N., Liou, K.T., Eds.; Springer: Cham, Switzerland, 2014; pp. 149–164. [Google Scholar]
- Thorndahl, S.; Einfalt, T.; Wilems, P.; Nielsen, J.E.; Veldhuis, M.C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Chen, D.; Ou, T.H.; Gong, L.B.; Xu, C.Y.; Li, W.J.; Ho, C.H.; Qian, W.H. Spatial interpolation of daily precipitation in China: 1951–2005. Adv. Atmos. Sci. 2010, 27, 1221–1232. [Google Scholar] [CrossRef]
- Michaud, J.D.; Sorooshian, S. Effect of rainfall-sampling errors on simulations of desert flash floods. Water Resour. Res. 1994, 30, 2765–2775. [Google Scholar] [CrossRef]
- Dong, X.; Dohmen-Janssen, C.M.; Booij, M.J. Appropriate spatial sampling of rainfall or flow simulation. Hydrol. Sci. J. 2005, 50, 279–298. [Google Scholar] [CrossRef]
- Srinivasan, G.; Nair, S. Daily rainfall characteristics from a high-density rain gauge network. Curr. Sci. 2005, 6, 942–946. [Google Scholar]
- Xu, H.; Xu, C.Y.; Chen, H.; Zhang, Z.; Li, L. Assessing the influence of rain gauge density and distribution on hydrological model performance in a humid region of China. J. Hydrol. 2013, 205, 1–12. [Google Scholar] [CrossRef]
- Vieux, B.; Vieux, J. Rainfall Accuracy Considerations Using Radar and Rain Gauge Networks for Rainfall-Runoff Monitoring. J. Water Manag. Model. 2005. [Google Scholar] [CrossRef]
- Schilling, W. Rainfall data for urban hydrology: What do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolu tion of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 1995, 531, 389–407. [Google Scholar] [CrossRef]
- Sempere-Torres, D.; Corral, C.; Raso, J.; Malgrat, P. Use of weather radar of combined sewer overflows monitoring and control. J. Environ. Eng. 1999, 123, 372–380. [Google Scholar] [CrossRef]
- James, W.P.; Robinson, C.G.; Bell, J.F. Radar-assisted real-time flood forecasting. J. Water Resour. Plan. Manag. 1993, 119, 32–44. [Google Scholar] [CrossRef]
- Pessoa, M.L.; Rafael, L.B.; Earle, R.W. Use of weather radar for flood forecasting in the Sieve river basin: A sensitivity analysis. J. Appl. Meteorol. 1993, 32, 462–475. [Google Scholar] [CrossRef]
- Mimikou, M.A.; Baltas, E.A. Flood forecasting based on radar rainfall Measurements. J. Water Resour. Plan. Manag. 1996, 122, 151–156. [Google Scholar] [CrossRef]
- Sun, X.; Mein, R.G.; Keenan, T.D.; Elliott, J.F. Flood Estimation using Radar and Raingauge Data. J. Hydrol. 2000, 239, 4–18. [Google Scholar] [CrossRef]
- Kim, B.S.; Kim, B.K.; Kim, H.S. Flood simulation using the gauge-adjusted radar rainfall and physics-based distributed hydrologic model. Hydrol. Process. 2008, 22, 4400–4414. [Google Scholar]
- Krajewski, W.F. Cokriging radar-rainfall and rain gauge data. J. Geophys. Res. 1987, 92, 9571–9580. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Seo, D.J.; Breidenbach, J.; Fulton, R.; Miller, D.; O’Bannon, T. Real-time adjustment of range dependent biases in WSR-88D rainfall estimates due to nonuniform vertical profile of reflectivity. J. Hydrometeorol. 2000, 1, 222–240. [Google Scholar] [CrossRef]
- Michelson, D.B. Quality Control of Weather Radar Data for Quantitative Application. Ph.D. Thesis, Telford Institute of Environmental Systems, University of Salford, Salford, UK, 2003. [Google Scholar]
- Liu, C.; Heckman, S. The application of the total lightning detection for severe storm prediction. In Proceedings of the WMO Technical Conference on Meteorological and Environmental Instruments and Methods of Observation (TECO-2010), Helsinki, Finland, 30 August–1 September 2010. [Google Scholar]
- Blumenfeld, K.A.; Skaggs, R.H. Using a high-density rain gauge network to estimate extreme rainfall frequencies in Minnesota. Appl. Geogr. 2011, 31, 5–11. [Google Scholar] [CrossRef]
- Tsuboya, H.; Kymagai, K.; Furuta, Y.; Miyajima, A. Environmental Sensor Network for NTT DOCOMO. J. Disaster Manag. 2016, 11, 334–339. [Google Scholar] [CrossRef]
- Korea Meteorological Agency. “Real-Time Quality Control System for Meteorological Gauged Data (I) Application.” 11-1360000-000206-01; Tech. Note 2006-2; Korea Meteorological Agency: Seoul, Korea, 2006; p. 157.
- Wade, C.G. A quality control program for surface mesometeorological data. J. Atmos. Ocean. Technol. 1987, 4, 435–453. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Guidelines on Quality Control Procedures for Data from Automatic Weather Stations; WMO: Geneva, Switzerland, 2004; p. 10. [Google Scholar]
- Heo, B.H.; Lee, J.A.; Chu, Y.O.; Kim, J.H.; Park, N.C.; Cho, J.Y.; Oh, S.J.; Noh, M.S.; Lee, Y.J. Statistical procedure of AWS gauged data to determine the threshold value for the RQMOD (real-time quality control system for meteorological gauged data). In Proceedings of the Autumn Meeting of Korean Meteorological Society, Seoul, Korea, 25 October 2005; pp. 390–391. [Google Scholar]
- Madsen, H. Semi-automatic Quality Control of Daily Precipitation Measurements. In Proceedings of the 5th International Meeting on Statistical Climatology, Toronto, ON, Canada, 22–26 June 1992; pp. 375–377. [Google Scholar]
- Madsen, H. Algorithms for correction of error types in a semi-automatic data collection. In Proceedings of the Precipitation Measurements and Quality Control: International Symposium on Precipitation and Evaporation, Bratislava, Slovakia, 20–24 September 1993; Sevruk, B., Lapin, M., Eds.; Slovak Hydrometeorological Institute: Bratislava, Slovakia, 1993. [Google Scholar]
- Yoon, S.S.; Lee, B.; Choi, Y. Deduction of Data Quality Control Strategy for High Density Rain Gauge Network in Seoul Area. J. Korea Water Resour. Assoc. 2015, 48, 245–255. (In Korean) [Google Scholar] [CrossRef]
- Mohr, C.G.; Vaughan, R.L. An economical procedure for Cartesian interpolation and display of reflectivity factor data in three-dimensional space. Bull. Am. Meteorol. Soc. 1979, 18, 661–670. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation, 4th ed.; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Yoon, S.S. Development of Optimal Radar Rainfall Estimation with Orographic Effect and Urban Flood Forecasting Application Technique. Ph.D. Thesis, Sejong University, Seoul, Korea, 2011. (In Korean). [Google Scholar]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Yoon, S.S.; Bae, D.H. Optimal Rainfall Estimation by Considering Elevation at the Han River Basin, South Korea. J. Appl. Meteorol. Climatol. 2013, 52, 802–818. [Google Scholar] [CrossRef]
- Huber, W.C.; Heaney, J.P.; Nix, S.J.; Dickinson, R.E.; Polmann, D.J. Storm Water Management Model User’s Manuall Version III; US Environmental Protection Agency: Cininnati, OH, USA, 1984. [Google Scholar]
- Huber, W.C.; Dickinson, R.E. Storm Water Management Model, Version 4: User’s Manual; Environmental Research Laboratory, EPA: Athens, GA, USA, 1988. [Google Scholar]
- Jensen, N.E.; Pedersen, L. Spatial variablilty of rainfall: Variations within a single radar pixel. J. Atmos. Res. 2005, 77, 269–277. [Google Scholar] [CrossRef]
- Pedersen, L.; Jensen, N.E.; Christensen, L.E.; Madsen, H. Quantification of the spatial varibility of rainfall based on a dense network of rain gauges. Atmos. Res. 2010, 95, 441–454. [Google Scholar] [CrossRef]
- Tokay, A.; Roche, R.J.; Bashor, P.G. An Experimental study of spatial variability of rainfall. J. Hydrometeorol. 2014, 15, 801–812. [Google Scholar] [CrossRef]

| Status | Criteria |
|---|---|
| Missing value | Recorded observation data as “NULL” value |
| Outlier |
|
| Event | Item | Test Stations | QPE1 | QPE2 | QPE3 |
|---|---|---|---|---|---|
| Case 1 | Total rainfall | 4174.221 | 4186.78 | 1653.51 | 4024.08 |
| C-CORR | - | 0.95 | 0.66 | 0.94 | |
| RMSE (mm) | - | 0.34 | 0.91 | 0.37 | |
| ME (mm) | - | 0.001 | −0.23 | −0.01 | |
| MAE (mm) | - | 0.10 | 0.29 | 0.11 | |
| Case 2 | Total rainfall | 193.38 | 197.77 | 72.07 | 159.52 |
| C-CORR | - | 0.92 | 0.49 | 0.88 | |
| RMSE (mm) | - | 0.15 | 0.36 | 0.20 | |
| ME (mm) | - | 0.002 | −0.04 | −0.01 | |
| MAE (mm) | - | 0.04 | 0.07 | 0.04 | |
| Case 3 | Total rainfall | 1647.38 | 1635.78 | 519.06 | 1606.39 |
| C-CORR | - | 0.93 | 0.73 | 0.93 | |
| RMSE (mm) | - | 0.69 | 1.54 | 0.72 | |
| ME (mm) | - | 0.001 | −0.41 | −0.01 | |
| MAE (mm) | - | 0.17 | 0.44 | 0.18 | |
| Case 4 | Total rainfall | 910.85 | 909.08 | 331.17 | 877.06 |
| C-CORR | - | 0.96 | 0.77 | 0.96 | |
| RMSE (mm) | - | 0.29 | 0.84 | 0.31 | |
| ME (mm) | - | −0.0006 | −0.21 | −0.01 | |
| MAE (mm) | - | 0.08 | 0.23 | 0.09 |
| Rainfall Type | GN | SC | QPE1 | QPE2 | QPE3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Event | Station | RMSE (mm) | REPD (%) | RMSE (mm) | REPD (%) | RMSE (mm) | REPD (%) | RMSE (mm) | REPD (%) | RMSE (mm) | REPD (%) |
| Case 1 | 22-0006 | 0.16 | 5.23 | 0.21 | 33.99 | 0.13 | 8.50 | 0.44 | 52.94 | 0.13 | 7.19 |
| 22-0002 | 0.21 | 7.74 | 0.16 | 17.42 | 0.16 | 7.10 | 0.31 | 60.65 | 0.16 | 7.74 | |
| 23-0006 | 0.21 | 26.12 | 0.16 | 3.82 | 0.11 | 11.47 | 0.36 | 69.43 | 0.11 | 12.10 | |
| Case 2 | 22-0006 | 0.10 | 6.72 | 0.08 | 0.84 | 0.11 | 14.29 | 0.20 | 69.75 | 0.10 | 15.97 |
| 22-0002 | 0.12 | 3.55 | 0.09 | 0.71 | 0.10 | 7.80 | 0.18 | 56.03 | 0.10 | 7.09 | |
| 23-0006 | 0.06 | 7.81 | 0.09 | 9.38 | 0.04 | 0.78 | 0.18 | 60.94 | 0.04 | 0.78 | |
| Case 3 | 22-0006 | 0.23 | 1.20 | 0.39 | 19.60 | 0.31 | 25.60 | 0.88 | 72.80 | 0.26 | 16.00 |
| 22-0002 | 0.32 | 18.58 | 0.27 | 31.42 | 0.23 | 15.04 | 0.66 | 68.14 | 0.23 | 15.04 | |
| 23-0006 | 0.38 | 24.64 | 0.33 | 36.23 | 0.23 | 3.38 | 0.69 | 61.84 | 0.24 | 1.93 | |
| Case 4 | 22-0006 | 0.11 | 6.62 | 0.13 | 19.12 | 0.11 | 3.68 | 0.27 | 61.77 | 0.11 | 0.74 |
| 22-0002 | 0.17 | 16.67 | 0.11 | 13.33 | 0.12 | 15.83 | 0.17 | 37.50 | 0.11 | 8.33 | |
| 23-0006 | 0.10 | 16.42 | 0.11 | 18.66 | 0.08 | 14.18 | 0.16 | 45.52 | 0.08 | 9.70 | |
| Case 5 | 22-0006 | 0.10 | 23.76 | 0.10 | 20.79 | 0.08 | 4.95 | 0.18 | 51.49 | 0.09 | 5.94 |
| 22-0002 | 0.16 | 0.00 | 0.12 | 3.88 | 0.13 | 5.83 | 0.13 | 26.21 | 0.13 | 10.68 | |
| 23-0006 | 0.14 | 14.43 | 0.11 | 8.25 | 0.11 | 7.22 | 0.14 | 23.71 | 0.10 | 9.28 | |
| Case 6 | 22-0006 | 0.09 | 0.00 | 0.21 | 44.44 | 0.07 | 7.84 | 0.32 | 60.13 | 0.07 | 5.88 |
| 22-0002 | 0.22 | 23.29 | 0.14 | 7.31 | 0.14 | 4.11 | 0.42 | 65.30 | 0.15 | 3.20 | |
| 23-0006 | 0.09 | 36.19 | 0.11 | 4.76 | 0.07 | 7.14 | 0.19 | 78.10 | 0.07 | 0.92 | |
| Average | 0.165 | 13.276 | 0.162 | 16.331 | 0.129 | 9.152 | 0.327 | 56.792 | 0.127 | 7.695 | |
| Item | GN | SC | QPE1 | QPE2 | QPE3 |
|---|---|---|---|---|---|
| No. of Flooded Nodes | 29 | 71 | 33 | 1 | 38 |
| Hours Flooded | 2.38 | 2.12 | 2.56 | 0.16 | 2.57 |
| Maximum Rate (CMS) | 13.00 | 25.75 | 14.88 | 0.33 | 15.31 |
| Total Flood Volume (106 Ltr) | 22.07 | 34.89 | 25.52 | 0.10 | 25.14 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, S.-S.; Lee, B. Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses. Water 2017, 9, 931. https://doi.org/10.3390/w9120931
Yoon S-S, Lee B. Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses. Water. 2017; 9(12):931. https://doi.org/10.3390/w9120931
Chicago/Turabian StyleYoon, Seong-Sim, and Byongju Lee. 2017. "Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses" Water 9, no. 12: 931. https://doi.org/10.3390/w9120931
APA StyleYoon, S.-S., & Lee, B. (2017). Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses. Water, 9(12), 931. https://doi.org/10.3390/w9120931




